Wzory sinus cosinus tangens cotangens. Sinus, cosinus, tangens, cotangens kąta ostrego. Funkcje trygonometryczne
Przeczytaj także
Trygonometria to dział matematyki zajmujący się badaniem funkcji trygonometrycznych i ich wykorzystaniem w geometrii. W tym czasie rozpoczął się rozwój trygonometrii starożytna Grecja. W średniowieczu naukowcy z Bliskiego Wschodu i Indii wnieśli istotny wkład w rozwój tej nauki.
Ten artykuł jest o podstawowe koncepcje i definicje trygonometrii. Omówiono definicje głównych funkcji trygonometrycznych: sinusa, cosinusa, tangensa i cotangensa. Wyjaśniono i zilustrowano ich znaczenie w kontekście geometrii.
Yandex.RTB R-A-339285-1
Początkowo definicje funkcji trygonometrycznych, których argumentem jest kąt, były wyrażane przez stosunek boków trójkąta prostokątnego.
Definicje funkcji trygonometrycznych
Sinus kąta (sin α) jest stosunkiem nogi przeciwnej do tego kąta do przeciwprostokątnej.
Cosinus kąta (cos α) to stosunek sąsiedniej nogi do przeciwprostokątnej.
Tangens kąta (t g α) jest stosunkiem przeciwległego ramienia do sąsiedniego.
Cotangens kąta (ct g α) to stosunek sąsiedniego ramienia do przeciwległego.
Te definicje są podane dla kąt ostry trójkąt prostokątny!
Podajmy ilustrację.
W trójkącie ABC o kącie prostym C, sinus kąta A jest równy stosunkowi odnoga BC do przeciwprostokątnej AB.
Definicje sinusa, cosinusa, tangensa i cotangensa umożliwiają obliczenie wartości tych funkcji ze znanych długości boków trójkąta.
Ważne do zapamiętania!
Zakres wartości sinusa i cosinusa: od -1 do 1. Innymi słowy, sinus i cosinus przyjmują wartości od -1 do 1. Zakres wartości tangens i cotangens to cała oś liczbowa, czyli te funkcje mogą przyjmować dowolną wartość.
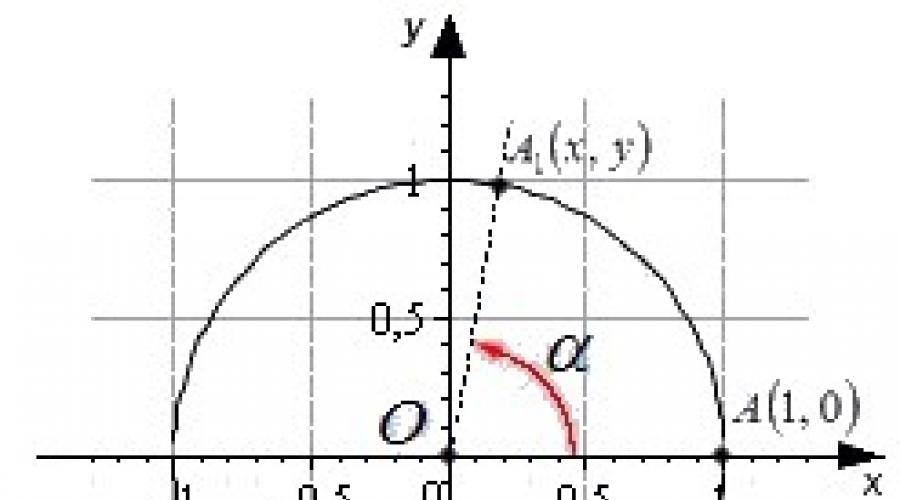
Podane powyżej definicje odnoszą się do kątów ostrych. W trygonometrii wprowadza się pojęcie kąta obrotu, którego wartość, w przeciwieństwie do kąta ostrego, nie jest ograniczona ramkami od 0 do 90 st. Kąt obrotu w stopniach lub radianach wyraża się dowolną liczbą rzeczywistą od - ∞ do + ∞.
W tym kontekście można zdefiniować sinus, cosinus, tangens i cotangens kąta o dowolnej wielkości. Wyobraź sobie okrąg jednostkowy wyśrodkowany na początku kartezjańskiego układu współrzędnych.

Punkt początkowy A o współrzędnych (1 , 0) obraca się wokół środka okręgu jednostkowego o pewien kąt α i przechodzi do punktu A 1 . Definicja jest podana poprzez współrzędne punktu A 1 (x, y).
Sinus (sin) kąta obrotu
Sinus kąta obrotu α jest rzędną punktu A 1 (x, y). sinα = y
Cosinus (cos) kąta obrotu
Cosinus kąta obrotu α jest odciętą punktu A 1 (x, y). cos α = x
Tangens (tg) kąta obrotu
Tangens kąta obrotu α jest stosunkiem rzędnej punktu A 1 (x, y) do jego odciętej. t g α = y x
Cotangens (ctg) kąta obrotu
Cotangens kąta obrotu α jest stosunkiem odciętej punktu A 1 (x, y) do jego rzędnej. c t g α = x y
Sinus i cosinus są definiowane dla dowolnego kąta obrotu. Jest to logiczne, ponieważ odciętą i rzędną punktu po obrocie można wyznaczyć pod dowolnym kątem. Inaczej jest z tangensem i cotangensem. Styczna nie jest zdefiniowana, gdy punkt po obrocie przechodzi do punktu z zerową odciętą (0 , 1) i (0 , - 1). W takich przypadkach wyrażenie na styczną t g α = y x po prostu nie ma sensu, ponieważ zawiera dzielenie przez zero. Podobnie jest z cotangensem. Różnica polega na tym, że cotangens nie jest zdefiniowany w przypadkach, gdy znika rzędna punktu.
Ważne do zapamiętania!
Sinus i cosinus są zdefiniowane dla dowolnych kątów α.
Styczna jest zdefiniowana dla wszystkich kątów z wyjątkiem α = 90° + 180° k , k ∈ Z (α = π 2 + π k , k ∈ Z)
Cotangens jest zdefiniowany dla wszystkich kątów z wyjątkiem α = 180° k, k ∈ Z (α = π k, k ∈ Z)
Decydując praktyczne przykłady nie mów "sinus kąta obrotu α". Słowa „kąt obrotu” są po prostu pominięte, co sugeruje, że z kontekstu już wiadomo, o co toczy się gra.
Liczby
A co z definicją sinusa, cosinusa, tangensa i cotangensa liczby, a nie kąta obrotu?
Sinus, cosinus, tangens, cotangens liczby
Sinus, cosinus, tangens i cotangens liczby t wywoływana jest liczba, która jest odpowiednio równa sinusowi, cosinusowi, tangensowi i cotangensowi in t radian.
Na przykład sinus 10 π równy sinusowi kąt obrotu 10 π rad.
Istnieje inne podejście do definicji sinusa, cosinusa, tangensa i cotangensa liczby. Rozważmy to bardziej szczegółowo.
Dowolna liczba rzeczywista t punkt na okręgu jednostkowym jest umieszczany zgodnie ze środkiem w początku prostokątnego kartezjańskiego układu współrzędnych. Sinus, cosinus, tangens i cotangens są definiowane w kategoriach współrzędnych tego punktu.
Punktem początkowym na okręgu jest punkt A o współrzędnych (1 , 0).
Liczba dodatnia t
Liczba ujemna t odpowiada punktowi, do którego przesunie się punkt początkowy, jeśli przesunie się w kierunku przeciwnym do ruchu wskazówek zegara po okręgu i przejdzie drogę t .
Teraz, gdy ustalono związek między liczbą a punktem na okręgu, przechodzimy do definicji sinusa, cosinusa, tangensa i cotangensa.
Sin (sin) liczby t
Sinus liczby t- rzędna punktu okręgu jednostkowego odpowiadającego liczbie t. grzech t = y
Cosinus (cos) z t
Cosinus liczby t- odcięta punktu okręgu jednostkowego odpowiadającego liczbie t. cos t = x
Tangens (tg) z t
Tangens liczby t- stosunek rzędnej do odciętej punktu okręgu jednostkowego odpowiadającego liczbie t. t g t = y x = sin t cos t
Te ostatnie definicje są zgodne i nie są sprzeczne z definicją podaną na początku tej sekcji. Punkt na okręgu odpowiadającym liczbie t, pokrywa się z punktem, do którego przechodzi punkt początkowy po skręcie o kąt t radian.
Funkcje trygonometryczne argumentu kątowego i liczbowego
Każda wartość kąta α odpowiada pewnej wartości sinusa i cosinusa tego kąta. Tak jak wszystkie kąty α inne niż α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) odpowiada pewnej wartości tangensa. Cotangens, jak wspomniano powyżej, jest zdefiniowany dla wszystkich α, z wyjątkiem α = 180 ° k , k ∈ Z (α = π k , k ∈ Z).
Możemy powiedzieć, że sin α , cos α , t g α , c t g α są funkcjami kąta alfa lub funkcjami argumentu kątowego.
Podobnie można mówić o sinus, cosinus, tangens i cotangens jako funkcjach argumentu liczbowego. Każda liczba rzeczywista t odpowiada określonej wartości sinusa lub cosinusa liczby t. Wszystkie liczby inne niż π 2 + π · k , k ∈ Z odpowiadają wartości tangensa. Cotangens jest podobnie zdefiniowany dla wszystkich liczb z wyjątkiem π · k , k ∈ Z.
Podstawowe funkcje trygonometrii
Sinus, cosinus, tangens i cotangens to podstawowe funkcje trygonometryczne.
Z kontekstu zwykle wynika, z jakim argumentem funkcji trygonometrycznej ( argument kątowy lub argument liczbowy), z którym mamy do czynienia.
Wróćmy do danych na samym początku definicji i kąta alfa, który zawiera się w przedziale od 0 do 90 stopni. Definicje trygonometryczne sinus, cosinus, tangens i cotangens są w pełni zgodne z definicje geometryczne, dany przez stosunki boków trójkąta prostokątnego. Pokażmy to.

Weźmy okrąg jednostkowy wyśrodkowany na prostokątnym kartezjańskim układzie współrzędnych. Obróćmy punkt początkowy A (1, 0) o kąt do 90 stopni i narysujmy od wynikowego punktu A 1 (x, y) prostopadle do osi x. W powstałym trójkącie prostokątnym kąt A 1 O H równy kątowi skręt α, długość nogi O H jest równa odciętej punktu A 1 (x, y) . Długość odnogi przeciwległej do narożnika jest równa rzędnej punktu A 1 (x, y), a długość przeciwprostokątnej jest równa jedynce, ponieważ jest to promień okręgu jednostkowego.
Zgodnie z definicją z geometrii, sinus kąta α jest równy stosunkowi przeciwległej nogi do przeciwprostokątnej.
grzech α \u003d A 1 H O A 1 \u003d y 1 \u003d y
Oznacza to, że definicja sinusa kąta ostrego w trójkącie prostokątnym przez współczynnik kształtu jest równoważna definicji sinusa kąta obrotu α, gdzie alfa mieści się w zakresie od 0 do 90 stopni.
Podobnie, zgodność definicji można wykazać dla cosinusa, tangensa i cotangensa.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter
Tam, gdzie rozważano zadania rozwiązywania trójkąta prostokątnego, obiecałem przedstawić technikę zapamiętywania definicji sinusa i cosinusa. Używając go, zawsze szybko zapamiętasz, która noga należy do przeciwprostokątnej (sąsiadująca lub przeciwna). Postanowiłem nie odkładać tego w nieskończoność, niezbędny materiał poniżej, proszę zobaczyć
Faktem jest, że wielokrotnie obserwowałem, jak uczniowie klas 10-11 mają trudności z zapamiętaniem tych definicji. Bardzo dobrze pamiętają, że noga odnosi się do przeciwprostokątnej, ale która…- zapomnij i zmieszany. Ceną pomyłki, jak wiadomo na egzaminie, jest stracony wynik.
Informacje, które przedstawię bezpośrednio matematyce, nie mają nic wspólnego. Jest związana z myślenie figuratywne, oraz metodami połączenia werbalno-logicznego. Zgadza się, ja sam raz na zawsze zapamiętanydane definicji. Jeśli nadal o nich zapomnisz, to przy pomocy przedstawionych technik zawsze łatwo je zapamiętać.
Przypomnę definicje sinusa i cosinusa w trójkącie prostokątnym:
Cosinus kąt ostry w trójkącie prostokątnym to stosunek sąsiedniej nogi do przeciwprostokątnej:

Zatoka kąt ostry w trójkącie prostokątnym to stosunek przeciwprostokątnej do przeciwprostokątnej:

Jakie skojarzenia wywołuje w tobie słowo cosinus?
Prawdopodobnie każdy ma swojeZapamiętaj link:
W ten sposób natychmiast będziesz mieć wyraz w swojej pamięci -
«… stosunek sąsiedniej nogi do przeciwprostokątnej».
Problem z definicją cosinusa został rozwiązany.
Jeśli chcesz zapamiętać definicję sinusa w trójkącie prostokątnym, to pamiętając definicję cosinusa, możesz łatwo ustalić, że sinus kąta ostrego w trójkącie prostokątnym jest stosunkiem przeciwnej nogi do przeciwprostokątnej. W końcu są tylko dwie nogi, jeśli sąsiednia noga jest „zajęta” przez cosinus, to dla sinusa pozostaje tylko przeciwna strona.
A co z tangensem i cotangensem? To samo zamieszanie. Uczniowie wiedzą, że jest to stosunek nóg, ale problem polega na tym, aby pamiętać, która z nich odnosi się do której - albo przeciwnie do sąsiednich, albo odwrotnie.
Definicje:
Tangens kąt ostry w trójkącie prostokątnym to stosunek przeciwnej nogi do sąsiedniej:

Cotangens kąt ostry w trójkącie prostokątnym to stosunek sąsiedniej nogi do przeciwnej:

Jak zapamiętać? Są dwa sposoby. Jedno również wykorzystuje połączenie werbalno-logiczne, drugie - matematyczne.
METODA MATEMATYCZNA
Jest taka definicja - tangens kąta ostrego to stosunek sinusa kąta do jego cosinusa:

* Pamiętając wzór, zawsze możesz określić, że tangens kąta ostrego w trójkącie prostokątnym jest stosunkiem odnogi przeciwległej do sąsiedniej.
Podobnie.Cotangens kąta ostrego to stosunek cosinusa kąta do jego sinusa:

Więc! Pamiętając te formuły, zawsze możesz określić, że:
- tangens kąta ostrego w trójkącie prostokątnym to stosunek przeciwległego ramienia do sąsiedniego
- cotangens kąta ostrego w trójkącie prostokątnym to stosunek sąsiedniej nogi do przeciwległej.
METODA WERBALNO-LOGICZNA
O stycznej. Zapamiętaj link:

Oznacza to, że jeśli musisz zapamiętać definicję stycznej, korzystając z tego logicznego połączenia, możesz łatwo zapamiętać, co to jest
„...stosunek przeciwnej nogi do sąsiedniej”
Jeśli chodzi o cotangens, to pamiętając definicję tangensa, możesz łatwo wyrazić definicję cotangensa -
"... stosunek sąsiedniej nogi do przeciwnej"
Istnieje ciekawa technika zapamiętywania tangensa i cotangensa na stronie " Tandem matematyczny " , Popatrz.
METODA UNIWERSALNA
Możesz po prostu zmielić.Ale jak pokazuje praktyka, dzięki powiązaniom werbalno-logicznym człowiek zapamiętuje informacje na długi czas, nie tylko matematyczne.
Mam nadzieję, że materiał był dla Ciebie przydatny.
Z poważaniem Aleksander Krutitskikh
PS: Byłbym wdzięczny, gdybyś opowiedział o stronie w sieciach społecznościowych.
Jak znaleźć sinus?



Nauka geometrii pomaga rozwijać myślenie. Ten przedmiot jest zawarty w programie nauczania. W życiu znajomość tego tematu może się przydać – np. przy planowaniu mieszkania.
Z historii
W ramach kursu geometrii badana jest również trygonometria, która bada funkcje trygonometryczne. W trygonometrii badamy sinusy, cosinusy, tangensy i cotangensy kąta.
Ale dalej ten moment Zacznijmy od najprostszego - sinus. Przyjrzyjmy się bliżej pierwszej koncepcji - sinusowi kąta w geometrii. Czym jest sinus i jak go znaleźć?
Pojęcie „sinus kąta” i sinusoidy
Sinus kąta jest stosunkiem wartości przeciwnej nogi i przeciwprostokątnej trójkąta prostokątnego. Jest to bezpośrednia funkcja trygonometryczna, zapisana na piśmie jako „sin (x)”, gdzie (x) jest kątem trójkąta.
Na wykresie sinus kąta jest oznaczony sinusoidą o własnej charakterystyce. Sinusoida wygląda jak ciągła linia falista, która leży w pewnych granicach na płaszczyźnie współrzędnych. Funkcja jest nieparzysta, dlatego jest symetryczna względem 0 na płaszczyźnie współrzędnych (opuszcza początek współrzędnych).
Dziedzina tej funkcji leży w zakresie od -1 do +1 w kartezjańskim układzie współrzędnych. Okres funkcji sinusa wynosi 2 Pi. Oznacza to, że co 2 Pi wzór jest powtarzany, a sinusoida przechodzi pełny cykl.
Równanie sinusoidalne
- sin x = a / c
- gdzie a jest nogą przeciwną do kąta trójkąta
- c - przeciwprostokątna trójkąta prostokątnego
Własności sinusa kąta
- grzech(x) = - grzech(x). Ta cecha pokazuje, że funkcja jest symetryczna, a jeśli wartości x i (-x) są odłożone w układzie współrzędnych w obu kierunkach, to rzędne tych punktów będą przeciwne. Będą w równej odległości od siebie.
- Inną cechą tej funkcji jest to, że wykres funkcji rośnie na odcinku [- P / 2 + 2 Pn]; [P/2 + 2Pn], gdzie n jest dowolną liczbą całkowitą. Spadek wykresu sinusa kąta będzie obserwowany na odcinku: [P / 2 + 2 Pn]; [ 3P/2 + 2Pn].
- sin (x) > 0, gdy x należy do zakresu (2Pn, P + 2Pn)
- (x)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
Wartości sinusów kąta określają specjalne tabele. Takie tabele zostały stworzone, aby ułatwić proces liczenia. złożone formuły i równania. Jest łatwy w obsłudze i zawiera wartości nie tylko funkcje grzechu(x), ale także wartości innych funkcji.
Ponadto tabela standardowych wartości tych funkcji znajduje się w nauka obowiązkowa na pamięć, jak tabliczka mnożenia. Jest to szczególnie prawdziwe w przypadku klas z nastawieniem fizycznym i matematycznym. W tabeli można zobaczyć wartości głównych kątów stosowanych w trygonometrii: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 i 360 stopni.
Istnieje również tabela określająca wartości funkcji trygonometrycznych niestandardowych kątów. Wykorzystując różne stoły, możesz łatwo obliczyć sinus, cosinus, tangens i cotangens niektórych kątów.
Równania wykonuje się za pomocą funkcji trygonometrycznych. Rozwiązywanie tych równań jest łatwe, jeśli znasz proste tożsamości trygonometryczne i redukcje funkcji, na przykład, takie jak sin (P/2 + x) = cos (x) i inne. Dla takich odlewów przygotowano również osobną tabelę.
Jak znaleźć sinus kąta
Kiedy zadaniem jest znalezienie sinusa kąta, a pod warunkiem mamy tylko cosinus, tangens lub cotangens kąta, możemy łatwo obliczyć, czego potrzebujemy, używając tożsamości trygonometrycznych.
- grzech 2 x + cos 2 x = 1
Z tego równania możemy znaleźć zarówno sinus, jak i cosinus, w zależności od tego, która wartość jest nieznana. Odniesiemy sukces równanie trygonometryczne z jedną niewiadomą:
- grzech 2 x = 1 - cos 2 x
- sin x = ± √ 1 - cos 2 x
- ctg 2 x + 1 = 1 / grzech 2 x
Z tego równania można znaleźć wartość sinusa, znając wartość cotangensa kąta. Aby uprościć, zamień sin 2 x = y, a wtedy masz proste równanie. Na przykład wartość cotangensa wynosi 1, wtedy:
- 1 + 1 = 1/y
- 2 = 1 / y
- 2 lata = 1
- y = 1/2
Teraz wykonujemy odwrotną wymianę odtwarzacza:
- grzech 2 x = ½
- grzech x = 1 / √2
Ponieważ przyjęliśmy wartość cotangensa dla standardowego kąta (45 0), uzyskane wartości można sprawdzić w tabeli.
Jeśli masz wartość tangens, ale musisz znaleźć sinus, inna tożsamość trygonometryczna pomoże:
- tg x * ctg x = 1
Wynika, że:
- ctg x = 1 / tg x
Aby znaleźć sinus niestandardowego kąta, na przykład 240 0, należy skorzystać ze wzorów redukcji kąta. Wiemy, że π odpowiada nam 180 0. W ten sposób wyrazimy naszą równość za pomocą standardowych kątów przez rozwinięcie.
- 240 0 = 180 0 + 60 0
Musimy znaleźć następujące: grzech (180 0 + 60 0). W trygonometrii istnieją wzory redukcyjne, które w ta sprawa się przydać. Oto formuła:
- grzech (π + x) = - grzech (x)
Zatem sinus kąta 240 stopni wynosi:
- grzech (180 0 + 60 0) = - grzech (60 0) = - √3/2
W naszym przypadku odpowiednio x = 60 i P 180 stopni. Znaleźliśmy wartość (-√3/2) z tabeli wartości funkcji kątów standardowych.
W ten sposób można się rozkładać niestandardowe kąty, na przykład: 210 = 180 + 30.
Pojęcia sinus (), cosinus (), tangens (), cotangens () są nierozerwalnie związane z pojęciem kąta. Aby dobrze zrozumieć te na pierwszy rzut oka skomplikowane koncepcje (które wywołują u wielu uczniów stan przerażenia) i upewnić się, że „diabeł nie jest taki straszny, jak go malują”, zacznijmy od początku i zrozum pojęcie kąta.
Pojęcie kąta: radian, stopień
Spójrzmy na zdjęcie. Wektor „obrócił się” względem punktu o określoną wartość. Tak więc miarą tego obrotu w stosunku do pozycji początkowej będzie zastrzyk.
Co jeszcze musisz wiedzieć o pojęciu kąta? Oczywiście jednostki kąta!
Kąt, zarówno w geometrii, jak i trygonometrii, można mierzyć w stopniach i radianach.
Kąt (jeden stopień) to kąt środkowy okręgu, oparty na łuku kołowym równym części okręgu. Tak więc cały okrąg składa się z „kawałków” łuków kołowych lub kąt opisany przez okrąg jest równy.

Oznacza to, że powyższy rysunek pokazuje równy kąt, to znaczy ten kąt jest oparty na łuku kołowym o rozmiarze obwodu.
Kąt w radianach nazywany jest kątem środkowym okręgu, opartym na łuku kołowym, którego długość jest równa promieniowi okręgu. Cóż, zrozumiałeś? Jeśli nie, spójrzmy na zdjęcie.

Tak więc rysunek pokazuje kąt równy radianowi, to znaczy kąt ten opiera się na łuku kołowym, którego długość jest równa promieniowi okręgu (długość jest równa długości lub promieniowi równa długościłuki). Zatem długość łuku oblicza się według wzoru:
Gdzie jest kąt środkowy w radianach.
Wiedząc o tym, czy możesz odpowiedzieć, ile radianów zawiera kąt opisany przez okrąg? Tak, w tym celu musisz zapamiętać wzór na obwód koła. Tutaj jest:
Cóż, teraz skorelujmy te dwie formuły i uzyskajmy, że kąt opisany przez okrąg jest równy. To znaczy, skorelując wartość w stopniach i radianach, otrzymujemy to. Odpowiednio . Jak widać, w przeciwieństwie do „stopni”, słowo „radiany” jest pomijane, ponieważ jednostka miary jest zwykle jasna z kontekstu.
Ile jest radianów? Zgadza się!
Rozumiem? Następnie przewiń do przodu:
Jakieś trudności? Potem spójrz odpowiedzi:
Trójkąt prostokątny: sinus, cosinus, tangens, cotangens kąta
Tak więc, z koncepcją kąta. Ale jaki jest sinus, cosinus, tangens, cotangens kąta? Rozwiążmy to. W tym pomoże nam trójkąt prostokątny.

Jak nazywają się boki trójkąta prostokątnego? Zgadza się, przeciwprostokątna i nogi: przeciwprostokątna to strona, która leży po przeciwnej stronie prosty kąt(w naszym przykładzie jest to strona); nogi są dwoma pozostałymi bokami i (te, które sąsiadują z kątem prostym), ponadto, jeśli weźmiemy nogi pod kątem kąta, to noga jest nogą sąsiednią, a noga przeciwną. A teraz odpowiedzmy na pytanie: jaki jest sinus, cosinus, tangens i cotangens kąta?
Sinus kąta jest stosunkiem przeciwnej (dalekiej) nogi do przeciwprostokątnej.
w naszym trójkącie.
Cosinus kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
w naszym trójkącie.
Styczna kąta- jest to stosunek przeciwnej (dalekiej) nogi do sąsiedniej (bliskiej).
w naszym trójkącie.
Cotangens kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (daleko).
w naszym trójkącie.
Te definicje są niezbędne Zapamiętaj! Aby łatwiej było zapamiętać, którą nogę podzielić przez co, musisz to jasno zrozumieć w tangens oraz cotangens tylko nogi siedzą, a przeciwprostokątna pojawia się tylko w Zatoka oraz cosinus. A potem możesz wymyślić łańcuch skojarzeń. Na przykład ten:
cosinus→dotyk→dotyk→sąsiadujący;
Cotangens→dotyk→dotyk→sąsiadujący.
Przede wszystkim należy pamiętać, że sinus, cosinus, tangens i cotangens jako stosunki boków trójkąta nie zależą od długości tych boków (pod jednym kątem). Nie wierz? Następnie upewnij się, patrząc na zdjęcie:

Rozważmy na przykład cosinus kąta. Z definicji z trójkąta: , ale możemy obliczyć cosinus kąta z trójkąta: . Widzisz, długości boków są różne, ale wartość cosinusa jednego kąta jest taka sama. Zatem wartości sinusa, cosinusa, tangensa i cotangensa zależą wyłącznie od wielkości kąta.
Jeśli rozumiesz definicje, śmiało je napraw!
Dla trójkąta pokazanego na poniższym rysunku znajdujemy.

Cóż, dostałeś to? Następnie spróbuj sam: oblicz to samo dla rogu.
Koło jednostkowe (trygonometryczne)
Rozumiejąc pojęcia stopni i radianów, rozważyliśmy okrąg o promieniu równym. Taki krąg nazywa się pojedynczy. Jest bardzo przydatny w badaniach trygonometrii. Dlatego zajmiemy się tym bardziej szczegółowo.

Jak widać, okrąg ten zbudowany jest w kartezjańskim układzie współrzędnych. Promień okręgu jest równy jeden, natomiast środek okręgu leży w początku, początkowe położenie wektora promienia jest ustalone wzdłuż dodatniego kierunku osi (w naszym przykładzie jest to promień).
Każdy punkt okręgu odpowiada dwóm liczbom: współrzędnej wzdłuż osi i współrzędnej wzdłuż osi. Jakie są te liczby współrzędnych? A ogólnie, co mają wspólnego z omawianym tematem? Aby to zrobić, pamiętaj o rozważanym trójkącie prostokątnym. Na powyższym rysunku widać dwa całe prawe trójkąty. Rozważ trójkąt. Jest prostokątny, ponieważ jest prostopadły do osi.
Co jest równe z trójkąta? Zgadza się. Ponadto wiemy, że jest to promień okręgu jednostkowego, a więc . Podstaw tę wartość do naszego wzoru cosinusa. Oto, co się dzieje:
A co jest równe z trójkąta? Ależ oczywiście, ! Podstaw wartość promienia do tego wzoru i uzyskaj:
Czy możesz powiedzieć, jakie współrzędne ma punkt, należący do kręgu? Cóż, nie ma mowy? A jeśli zdajesz sobie z tego sprawę i to tylko liczby? Jakiej współrzędnej to odpowiada? Oczywiście współrzędne! Jakiej współrzędnej to odpowiada? Zgadza się, koordynuj! Tak więc punkt.

A co wtedy są równe i? Zgadza się, użyjmy odpowiednich definicji tangensa i cotangensa i zdobądźmy to.
Co jeśli kąt jest większy? Tutaj na przykład jak na tym obrazku:

Co się zmieniło w tym przykładzie? Rozwiążmy to. Aby to zrobić, ponownie zwracamy się do trójkąta prostokątnego. Rozważmy trójkąt prostokątny: kąt (jako sąsiadujący z kątem). Jaka jest wartość sinusa, cosinusa, tangensa i cotangensa kąta? Zgadza się, przestrzegamy odpowiednich definicji funkcji trygonometrycznych:
Jak widać, wartość sinusa kąta nadal odpowiada współrzędnej; wartość cosinusa kąta - współrzędna; oraz wartości tangensa i cotangensa do odpowiednich stosunków. Zatem te relacje mają zastosowanie do dowolnych obrotów wektora promienia.
Wspomniano już, że początkowe położenie wektora promienia leży wzdłuż dodatniego kierunku osi. Do tej pory obróciliśmy ten wektor w kierunku przeciwnym do ruchu wskazówek zegara, ale co się stanie, jeśli obrócimy go zgodnie z ruchem wskazówek zegara? Nic nadzwyczajnego, dostaniesz też kąt o określonej wielkości, ale tylko to będzie ujemne. Tak więc, obracając wektor promienia w kierunku przeciwnym do ruchu wskazówek zegara, otrzymujemy dodatnie kąty, a przy obrocie w prawo - negatywny.
Wiemy więc, że cały obrót wektora promienia wokół okręgu to lub. Czy można obrócić wektor promienia o lub o? Oczywiście, że możesz! Dlatego w pierwszym przypadku wektor promienia wykona jeden pełny obrót i zatrzyma się w pozycji lub.
W drugim przypadku wektor promienia wykona trzy pełne obroty i zatrzyma się w pozycji lub.
Zatem z powyższych przykładów możemy wywnioskować, że kąty różniące się o lub (gdzie jest dowolną liczbą całkowitą) odpowiadają temu samemu położeniu wektora promienia.
Poniższy rysunek przedstawia kąt. Ten sam obraz odpowiada narożnikowi i tak dalej. Ta lista może być kontynuowana w nieskończoność. Wszystkie te kąty można zapisać za pomocą ogólnego wzoru lub (gdzie jest dowolną liczbą całkowitą)

Teraz, znając definicje podstawowych funkcji trygonometrycznych i używając okręgu jednostkowego, spróbuj odpowiedzieć, jakie wartości są równe:
Oto krąg jednostek, który może ci pomóc:

Jakieś trudności? Więc zastanówmy się. Wiemy więc, że:
Stąd określamy współrzędne punktów odpowiadających pewnym miarom kąta. Cóż, zacznijmy w kolejności: róg w odpowiada punktowi o współrzędnych, a zatem:
Nie istnieje;
Ponadto, przestrzegając tej samej logiki, dowiadujemy się, że rogi odpowiadają odpowiednio punktom o współrzędnych. Wiedząc o tym łatwo wyznaczyć wartości funkcji trygonometrycznych w odpowiednich punktach. Najpierw spróbuj sam, a potem sprawdź odpowiedzi.
Odpowiedzi:
Nie istnieje
Nie istnieje
Nie istnieje
Nie istnieje
W ten sposób możemy wykonać następującą tabelę:

Nie trzeba pamiętać wszystkich tych wartości. Wystarczy pamiętać o zgodności współrzędnych punktów na okręgu jednostkowym z wartościami funkcji trygonometrycznych:
Ale wartości funkcji trygonometrycznych kątów w i podane w poniższej tabeli: trzeba pamiętać:

Nie bój się, teraz pokażemy jeden z przykładów dość proste zapamiętywanie odpowiednich wartości:
Aby skorzystać z tej metody, należy pamiętać wartości sinusa dla wszystkich trzech miar kąta () oraz wartość tangensa kąta w. Znając te wartości dość łatwo odtworzyć całą tabelę – wartości cosinusów są przekazywane zgodnie ze strzałkami, czyli:
Wiedząc o tym, możesz przywrócić wartości. Licznik „ ” będzie zgodny, a mianownik „ ” będzie zgodny. Wartości cotangens są przenoszone zgodnie ze strzałkami pokazanymi na rysunku. Jeśli to zrozumiesz i zapamiętasz schemat ze strzałkami, wystarczy zapamiętać całą wartość z tabeli.
Współrzędne punktu na okręgu
Czy można znaleźć punkt (jego współrzędne) na okręgu, znając współrzędne środka okręgu, jego promień i kąt obrotu?
Oczywiście, że możesz! Wydobądźmy ogólna formuła znaleźć współrzędne punktu.
Tutaj np. mamy taki krąg:

Dano nam, że punkt jest środkiem koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrót punktu o stopnie.
Jak widać na rysunku, współrzędna punktu odpowiada długości odcinka. Długość segmentu odpowiada współrzędnej środka koła, czyli jest równa. Długość segmentu można wyrazić za pomocą definicji cosinusa:
Wtedy mamy to dla punktu współrzędnej.
Zgodnie z tą samą logiką znajdujemy wartość współrzędnej y punktu. Zatem,
tak w ogólny widok współrzędne punktów wyznaczają wzory:
Współrzędne środka okręgu,
promień okręgu,
Kąt obrotu wektora promienia.
Jak widać, dla rozważanego okręgu jednostkowego wzory te są znacznie zmniejszone, ponieważ współrzędne środka wynoszą zero, a promień jest równy jeden:
Cóż, wypróbujmy te formuły dla smaku, ćwicząc znajdowanie punktów na kole?
1. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez włączenie punktu.
2. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez obrót punktu.
3. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez włączenie punktu.
4. Punkt - środek koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrócenie wektora promienia początkowego o.
5. Punkt - środek koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrócenie wektora promienia początkowego o.
Masz problem ze znalezieniem współrzędnych punktu na okręgu?
Rozwiąż te pięć przykładów (lub dobrze zrozum rozwiązanie), a dowiesz się, jak je znaleźć!
1.
Można zauważyć, że. I wiemy, co odpowiada pełnemu obrocie punktu wyjścia. W ten sposób żądany punkt będzie w tej samej pozycji, co podczas obracania się. Wiedząc o tym, znajdujemy pożądane współrzędne punktu:
2. Okrąg jest jednostką ze środkiem w punkcie, co oznacza, że możemy używać uproszczonych wzorów:
Można zauważyć, że. Wiemy, co odpowiada dwóm pełnym obrotom punktu początkowego. W ten sposób żądany punkt będzie w tej samej pozycji, co podczas obracania się. Wiedząc o tym, znajdujemy pożądane współrzędne punktu:
Sinus i cosinus są wartości tabeli. Zapamiętujemy ich wartości i otrzymujemy:
W ten sposób żądany punkt ma współrzędne.
3. Okrąg jest jednostką ze środkiem w punkcie, co oznacza, że możemy używać uproszczonych wzorów:
Można zauważyć, że. Przedstawmy rozważany przykład na rysunku:

Promień tworzy kąty z osią równą i. Wiedząc, że tabelaryczne wartości cosinusa i sinusa są równe i po ustaleniu, że cosinus ma tutaj wartość ujemną, a sinus jest dodatni, mamy:
Podobne przykłady są analizowane bardziej szczegółowo podczas studiowania wzorów redukcji funkcji trygonometrycznych w temacie.
W ten sposób żądany punkt ma współrzędne.
4.
Kąt obrotu wektora promienia (według warunku)
Aby wyznaczyć odpowiednie znaki sinusa i cosinusa, konstruujemy okrąg jednostkowy i kąt:

Jak widać, wartość, to znaczy jest dodatnia, a wartość, to znaczy jest ujemna. Znając wartości tabelaryczne odpowiednich funkcji trygonometrycznych otrzymujemy, że:
Otrzymane wartości podstawmy do naszego wzoru i znajdźmy współrzędne:
W ten sposób żądany punkt ma współrzędne.
5. Aby rozwiązać ten problem, używamy formuł w postaci ogólnej, gdzie
Współrzędne środka okręgu (w naszym przykładzie
Promień okręgu (według warunku)
Kąt obrotu wektora promienia (według warunku).
Zastąp wszystkie wartości formułą i uzyskaj:
oraz - wartości tabeli. Zapamiętujemy je i podstawiamy do formuły:
W ten sposób żądany punkt ma współrzędne.
PODSUMOWANIE I PODSTAWOWA FORMUŁA
Sinus kąta to stosunek przeciwnej (dalekiej) nogi do przeciwprostokątnej.
Cosinus kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
Tangens kąta to stosunek przeciwnej (dalekiej) nogi do sąsiedniej (bliskiej).
Cotangens kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (daleko).
Instrukcja
Użyj funkcji arcsine, aby obliczyć wartość kąta w stopniach, jeśli znasz wartość tego kąta. Jeśli zastrzyk oznaczone literą α, ogólnie rzecz biorąc, rozwiązanie można zapisać w następujący sposób: α = arcsin(sin(α)).
Jeśli masz możliwość korzystania z komputera, najłatwiej jest wykorzystać wbudowany system operacyjny do praktycznych obliczeń. W ostatnich dwóch wersjach systemu Windows możesz uruchomić go w ten sposób: naciśnij klawisz Win, wpisz „ka” i naciśnij Enter. We wcześniejszych wersjach tego systemu operacyjnego poszukaj łącza „Kalkulator” w podsekcji „Standardowe” w sekcji „Wszystkie programy” w menu głównym systemu.
Po uruchomieniu aplikacji przełącz ją w tryb umożliwiający pracę z funkcjami trygonometrycznymi. Można to zrobić, wybierając wiersz „Inżynieria” w sekcji „Widok” menu kalkulatora lub naciskając Alt + 2.
Wpisz wartość sinus. Domyślnie interfejs kalkulatora nie ma przycisku do obliczania arcus sinus. Aby móc korzystać z tej funkcji, należy odwrócić domyślne wartości przycisków - kliknij przycisk Inv w oknie programu. Więcej wczesne wersje ten przycisk jest zastąpiony polem wyboru o tym samym oznaczeniu - zaznacz to.
Możesz użyć w obliczeniach i różnych usługach, które są więcej niż wystarczające w Internecie. Na przykład wejdź na stronę http://planetcalc.com/326/, przewiń trochę w dół iw polu Input wpisz wartość sinusa. Aby rozpocząć procedurę obliczeniową, znajduje się przycisk o nazwie Oblicz - kliknij na niego. Wynik obliczeń znajdziesz w pierwszym wierszu tabeli pod tym przyciskiem. Oprócz arcus sinus wyświetla zarówno wartości, jak i arcus tangens wprowadzonej wartości.
Funkcja trygonometryczna odwrotnego sinusa nosi nazwę arcus sinus. Może przyjmować wartości mieszczące się w granicach połowy liczby pi, zarówno dodatnie, jak i ujemne. zła strona mierzone w radianach. Mierzone w stopniach wartości te będą mieściły się odpowiednio w zakresie od -90° do +90°.
Instrukcja
Niektóre „okrągłe” wartości nie muszą być obliczane, łatwiej je zapamiętać. Na przykład: - jeśli argumentem funkcji jest zero, to wartość arcsinus od niej również wynosi zero, - od 1/2 to 30 ° lub 1/6 Pi, jeśli zmierzono, - arcus sinus od -1/2 jest równy do -30° lub -1/6 pi w ;- arcsinus 1 to 90° lub 1/2 pi w radianach;- arcsinus -1 to -90° lub -1/2 pi w radianach;
Aby zmierzyć wartości tej funkcji z innych argumentów, najłatwiej jest użyć standardowego kalkulatora Windows, jeśli masz . Aby rozpocząć, otwórz menu główne na przycisku „Start” (lub naciskając klawisz WIN), przejdź do sekcji „Wszystkie programy”, a następnie do podsekcji „Akcesoria” i kliknij element „Kalkulator”.
Przełącz interfejs kalkulatora w tryb pracy, który umożliwia obliczanie funkcji trygonometrycznych. Aby to zrobić, otwórz sekcję „Widok” w jej menu i wybierz pozycję „Inżynieria” lub „Naukowe” (w zależności od używanego systemu operacyjnego).
Wprowadź wartość argumentu, na podstawie którego ma zostać obliczony łuk styczny. Można to zrobić, klikając myszą przyciski interfejsu kalkulatora lub naciskając klawisze na , albo kopiując wartość (CTRL + C), a następnie wklejając ją (CTRL + V) do pola wejściowego kalkulatora.
Wybierz jednostki, w których chcesz otrzymać wynik obliczenia funkcji. Poniżej pola wprowadzania znajdują się trzy opcje, z których należy wybrać (klikając myszą) jedną - , radiany lub rady.
Zaznacz pole wyboru, które odwraca funkcje wskazane na przyciskach interfejsu kalkulatora. Obok znajduje się krótki napis Inv.
Kliknij przycisk grzechu. Kalkulator odwróci dołączoną do niego funkcję, wykona obliczenia i przedstawi wynik w podanych jednostkach.
Powiązane wideo
Na trójkącie prostokątnym, jako najprostszym z wielokątów, różni naukowcy doskonalili swoją wiedzę w dziedzinie trygonometrii w tamtych czasach, kiedy nikt nawet tym słowem nie nazywał tego obszaru matematyki. Dlatego wskaż autora, który zidentyfikował wzory w stosunku długości boków do wartości kątów w tym mieszkaniu figura geometryczna dzisiaj nie jest możliwe. Takie relacje nazywane są funkcjami trygonometrycznymi i są podzielone na kilka grup, z których główne są konwencjonalnie uważane za funkcje „bezpośrednie”. Tylko dwie funkcje są przypisane do tej grupy, a jedna z nich jest sinus.

Instrukcja
Z definicji w trójkącie prostokątnym jeden z kątów jest równy 90°, a ponieważ suma jego kątów w geometrii euklidesowej musi być równa 180°, pozostałe dwa kąty to (czyli 90°). Regularności stosunków dokładnie tych kątów i długości boków opisują funkcje trygonometryczne.
Funkcja, zwana sinusem kąta ostrego, określa stosunek długości dwóch boków trójkąta prostokątnego, z których jeden leży naprzeciw tego kąta ostrego, a drugi sąsiaduje z nim i leży naprzeciw kąta prostego. Ponieważ strona przeciwna do kąta prostego w takim trójkącie nazywana jest przeciwprostokątną, a pozostałe dwie to nogi, funkcje sinusoidalne można sformułować jako stosunek długości nogi do przeciwprostokątnej.
Oprócz tak prostej definicji tej funkcji trygonometrycznej, istnieją bardziej złożone: przez okrąg we współrzędnych kartezjańskich, przez szereg, przez równania różniczkowe i funkcyjne. Funkcja ta jest ciągła, to znaczy jej argumenty ("dziedzina definicji") mogą być dowolną liczbą - od nieskończenie ujemnej do nieskończenie dodatniej. A maksymalne wartości tej funkcji są ograniczone zakresem od -1 do +1 - jest to „zakres jej wartości”. Minimalna wartość sinus przyjmuje się pod kątem 270 °, co odpowiada 3 / Pi, a maksimum uzyskuje się przy 90 ° (½ Pi). Wartości funkcji stają się zerowe przy 0°, 180°, 360° itd. Z tego wszystkiego wynika, że sinus jest funkcją okresową, a jego okres jest równy 360 ° lub dwukrotności liczby Pi.
Do praktycznych obliczeń wartości tej funkcji z danego argumentu można wykorzystać - zdecydowaną większość z nich (w tym wbudowany kalkulator programowy system operacyjny Twój komputer) ma odpowiednią opcję.
Powiązane wideo
Zatoka oraz cosinus- są to bezpośrednie funkcje trygonometryczne, dla których istnieje kilka definicji - poprzez okrąg w kartezjańskim układzie współrzędnych, poprzez rozwiązania równanie różniczkowe, poprzez kąty ostre w trójkącie prostokątnym. Każda z tych definicji pozwala wywnioskować związek między tymi dwiema funkcjami. Oto prawdopodobnie najprostszy sposób wyrażenia cosinus przez sinus - poprzez ich definicje dla kątów ostrych trójkąta prostokątnego.

Instrukcja
Wyraź sinus kąta ostrego trójkąta prostokątnego pod względem długości boków tej figury. Zgodnie z definicją, sinus kąta (α) musi być stosunkiem długości boku (a) przeciwległego - nogi - do długości boku (c) przeciwległego do kąta prostego - przeciwprostokątna: sin (α) = a/c.
Znajdź podobną formułę dla cosinus ale pod tym samym kątem. Z definicji wartość ta powinna być wyrażona jako stosunek długości boku (b) przylegającego do tego narożnika (druga noga) do długości boku (c) leżącej przeciwnie do kąta prostego: cos (a) \u003d a/c.
Przepisz równanie z twierdzenia Pitagorasa w taki sposób, aby wykorzystywało relacje między nogami i przeciwprostokątną wyprowadzone w dwóch poprzednich krokach. Aby to zrobić, najpierw podziel oba oryginały tego twierdzenia (a² + b² = c²) przez kwadrat przeciwprostokątnej (a² / c² + b² / c² = 1), a następnie przepisz wynikową równość w tej postaci: (a / c)² + (b / c )² = 1.
Zastąp w otrzymanym wyrażeniu stosunek długości nóg i przeciwprostokątnej funkcjami trygonometrycznymi, w oparciu o formuły pierwszego i drugiego kroku: sin² (a) + cos² (a) \u003d 1. Express cosinus z otrzymanej równości: cos(a) = √(1 - sin²(a)). Ten problem można rozwiązać w sposób ogólny.
Jeśli oprócz ogólnego wyniku potrzebujesz uzyskać wynik liczbowy, użyj na przykład kalkulatora wbudowanego w salę operacyjną system Windows. Link do jego uruchomienia w podsekcji „Standard” w sekcji „Wszystkie programy” w menu systemu operacyjnego. Ten link jest sformułowany zwięźle – „Kalkulator”. Aby móc obliczyć funkcje trygonometryczne z tego programu, włącz jego "inżynierski" interfejs - naciśnij kombinację klawiszy Alt + 2.
Wprowadź wartość sinusa kąta w warunkach i kliknij przycisk interfejsu z oznaczeniem x² - spowoduje to podniesienie do kwadratu pierwotnej wartości. Następnie wpisz *-1 na klawiaturze, naciśnij Enter, wpisz +1 i ponownie naciśnij Enter - w ten sposób odejmujesz kwadrat sinusa od jednostki. Kliknij przycisk radykalnej ikony, aby wyodrębnić kwadrat i uzyskać ostateczny wynik.
Badanie trójkątów było prowadzone przez matematyków od kilku tysiącleci. Nauka o trójkątach - trygonometria - wykorzystuje specjalne wielkości: sinus i cosinus.

Trójkąt prostokątny
Początkowo sinus i cosinus powstały ze względu na konieczność obliczania wielkości w trójkątach prostokątnych. Zauważono, że jeśli wartość miary stopnia kątów w trójkącie prostokątnym nie ulega zmianie, to proporcje, niezależnie od tego, jak bardzo zmieniają się te boki, zawsze pozostają takie same.
W ten sposób wprowadzono pojęcia sinusa i cosinusa. Sinus kąta ostrego w trójkącie prostokątnym jest stosunkiem przeciwprostokątnej do przeciwprostokątnej, a cosinus jest stosunkiem sąsiedniej nogi do przeciwprostokątnej.
Twierdzenia o cosinusach i sinusach
Ale cosinusy i sinusy mogą być używane nie tylko w trójkątach prostokątnych. Aby znaleźć wartość kąta rozwartego lub ostrego, czyli boku dowolnego trójkąta, wystarczy zastosować twierdzenie cosinus i sinus.
Twierdzenie o cosinusach jest dość proste: „Kwadrat boku trójkąta jest równy sumie kwadratów pozostałych dwóch boków minus dwukrotność iloczynu tych boków przez cosinus kąta między nimi”.
Istnieją dwie interpretacje twierdzenia sinus: mała i rozszerzona. Według małego: „W trójkącie kąty są proporcjonalne do przeciwnych boków”. Twierdzenie to jest często rozszerzane ze względu na właściwość koła opisanego wokół trójkąta: „W trójkącie kąty są proporcjonalne do przeciwnych boków, a ich stosunek jest równy średnicy koła opisanego”.
Pochodne
Pochodna to narzędzie matematyczne, które pokazuje, jak szybko zmienia się funkcja w odniesieniu do zmiany jej argumentu. Pochodne są używane w geometrii oraz w wielu dyscyplinach technicznych.
Rozwiązując problemy, musisz znać tabelaryczne wartości pochodnych funkcji trygonometrycznych: sinusa i cosinusa. Pochodną sinusa jest cosinus, a pochodną cosinusa jest sinus, ale ze znakiem minus.
Zastosowanie w matematyce
Szczególnie często w rozwiązywaniu używane są sinusy i cosinusy prawe trójkąty i zadania z nimi związane.
Wygoda sinusów i cosinusów znajduje również odzwierciedlenie w technologii. Kąty i boki były łatwe do oceny przy użyciu twierdzeń cosinusów i sinusów, dzieląc złożone kształty i obiekty na „proste” trójkąty. Inżynierowie i często zajmujący się obliczeniami współczynników kształtu i miar stopnia, spędzili dużo czasu i wysiłku na obliczaniu cosinusów i sinusów kątów nietabelowych.
Wtedy na ratunek przyszły tablice Bradis, zawierające tysiące wartości sinusów, cosinusów, tangensów i cotangensów różne kąty. W czasach sowieckich niektórzy nauczyciele zmuszali swoich podopiecznych do zapamiętywania stron tablic Bradisa.
Radiany — wielkość kątowałuki wzdłużne równy promieniowi lub 57.295779513 stopni.
Stopień (w geometrii) - 1/360 okręgu lub 1/90 kąta prostego.
π = 3,141592653589793238462… (przybliżona wartość pi).
Tabela cosinusów dla kątów: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Kąt x (w stopniach) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kąt x (w radianach) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3xπ/4 | 5xπ/6 | π | 7xπ/6 | 5xπ/4 | 4xπ/3 | 3xπ/2 | 5xπ/3 | 7xπ/4 | 11xπ/6 | 2xπ |
| bo x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |