Tabela wartości grzechu. Funkcje trygonometryczne
Przeczytaj także
Pojęcia sinus (), cosinus (), tangens (), cotangens () są nierozerwalnie związane z pojęciem kąta. Aby dobrze zrozumieć te na pierwszy rzut oka skomplikowane koncepcje (które wywołują u wielu uczniów stan przerażenia) i upewnić się, że „diabeł nie jest taki straszny, jak go malują”, zacznijmy od początku i zrozum pojęcie kąta.
Pojęcie kąta: radian, stopień
Spójrzmy na zdjęcie. Wektor „obrócił się” względem punktu o określoną wartość. Tak więc miarą tego obrotu w stosunku do pozycji początkowej będzie zastrzyk.
Co jeszcze musisz wiedzieć o pojęciu kąta? Oczywiście jednostki kąta!
Kąt, zarówno w geometrii, jak i trygonometrii, można mierzyć w stopniach i radianach.
Kąt (jeden stopień) to kąt środkowy okręgu, oparty na łuku kołowym równym części okręgu. Tak więc cały okrąg składa się z „kawałków” łuków kołowych lub kąt opisany przez okrąg jest równy.

Oznacza to, że powyższy rysunek pokazuje równy kąt, to znaczy ten kąt jest oparty na łuku kołowym o rozmiarze obwodu.
Kąt w radianach nazywany jest kątem środkowym okręgu, opartym na łuku kołowym, którego długość jest równa promieniowi okręgu. Cóż, zrozumiałeś? Jeśli nie, spójrzmy na zdjęcie.

Rysunek pokazuje więc kąt równy radianowi, to znaczy kąt ten opiera się na łuku kołowym, którego długość jest równa promieniowi okręgu (długość jest równa długości lub promień jest równy długość łuku). Zatem długość łuku oblicza się według wzoru:
Gdzie jest kąt środkowy w radianach.
Wiedząc o tym, czy możesz odpowiedzieć, ile radianów zawiera kąt opisany przez okrąg? Tak, w tym celu musisz zapamiętać wzór na obwód koła. Tutaj jest:
Cóż, teraz skorelujmy te dwie formuły i uzyskajmy, że kąt opisany przez okrąg jest równy. To znaczy, skorelując wartość w stopniach i radianach, otrzymujemy to. Odpowiednio . Jak widać, w przeciwieństwie do „stopni”, słowo „radiany” jest pomijane, ponieważ jednostka miary jest zwykle jasna z kontekstu.
Ile jest radianów? Zgadza się!
Rozumiem? Następnie przewiń do przodu:
Jakieś trudności? Potem spójrz odpowiedzi:
Trójkąt prostokątny: sinus, cosinus, tangens, cotangens kąta
Tak więc, z koncepcją kąta. Ale jaki jest sinus, cosinus, tangens, cotangens kąta? Rozwiążmy to. W tym pomoże nam trójkąt prostokątny.

Jak nazywają się boki trójkąta prostokątnego? Zgadza się, przeciwprostokątna i nogi: przeciwprostokątna to strona leżąca naprzeciwko kąta prostego (w naszym przykładzie jest to bok); nogi są dwoma pozostałymi bokami i (te, które sąsiadują z kątem prostym), ponadto, jeśli weźmiemy nogi pod kątem kąta, to noga jest nogą sąsiednią, a noga przeciwną. A teraz odpowiedzmy na pytanie: jaki jest sinus, cosinus, tangens i cotangens kąta?
Sinus kąta jest stosunkiem przeciwnej (dalekiej) nogi do przeciwprostokątnej.
w naszym trójkącie.
Cosinus kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
w naszym trójkącie.
Styczna kąta- jest to stosunek przeciwnej (dalekiej) nogi do sąsiedniej (bliskiej).
w naszym trójkącie.
Cotangens kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (daleko).
w naszym trójkącie.
Te definicje są konieczne Zapamiętaj! Aby łatwiej było zapamiętać, którą nogę podzielić przez co, musisz to jasno zrozumieć w tangens oraz cotangens tylko nogi siedzą, a przeciwprostokątna pojawia się tylko w Zatoka oraz cosinus. A potem możesz wymyślić łańcuch skojarzeń. Na przykład ten:
cosinus→dotyk→dotyk→sąsiadujący;
Cotangens→dotyk→dotyk→sąsiadujący.
Przede wszystkim należy pamiętać, że sinus, cosinus, tangens i cotangens jako stosunki boków trójkąta nie zależą od długości tych boków (pod jednym kątem). Nie wierz? Następnie upewnij się, patrząc na zdjęcie:

Rozważmy na przykład cosinus kąta. Z definicji z trójkąta: , ale możemy obliczyć cosinus kąta z trójkąta: . Widzisz, długości boków są różne, ale wartość cosinusa jednego kąta jest taka sama. Zatem wartości sinusa, cosinusa, tangensa i cotangensa zależą wyłącznie od wielkości kąta.
Jeśli rozumiesz definicje, śmiało je napraw!
Dla trójkąta pokazanego na poniższym rysunku znajdujemy.

Cóż, dostałeś to? Następnie spróbuj sam: oblicz to samo dla rogu.
Koło jednostkowe (trygonometryczne)
Rozumiejąc pojęcia stopni i radianów, rozważyliśmy okrąg o promieniu równym. Taki krąg nazywa się pojedynczy. Jest bardzo przydatny w badaniach trygonometrii. Dlatego zajmiemy się tym bardziej szczegółowo.

Jak widać, okrąg ten zbudowany jest w kartezjańskim układzie współrzędnych. Promień okręgu jest równy jeden, natomiast środek okręgu leży w początku, początkowe położenie wektora promienia jest ustalone wzdłuż dodatniego kierunku osi (w naszym przykładzie jest to promień).
Każdy punkt okręgu odpowiada dwóm liczbom: współrzędnej wzdłuż osi i współrzędnej wzdłuż osi. Jakie są te liczby współrzędnych? A ogólnie, co mają wspólnego z omawianym tematem? Aby to zrobić, pamiętaj o rozważanym trójkącie prostokątnym. Na powyższym rysunku widać dwa całe prawe trójkąty. Rozważ trójkąt. Jest prostokątny, ponieważ jest prostopadły do osi.
Co jest równe z trójkąta? Zgadza się. Ponadto wiemy, że jest to promień okręgu jednostkowego, a więc . Podstaw tę wartość do naszego wzoru cosinusa. Oto, co się dzieje:
A co jest równe z trójkąta? Ależ oczywiście, ! Podstaw wartość promienia do tego wzoru i uzyskaj:
Czy możesz mi powiedzieć, jakie są współrzędne punktu należącego do okręgu? Cóż, nie ma mowy? A jeśli zdajesz sobie z tego sprawę i to tylko liczby? Jakiej współrzędnej to odpowiada? Oczywiście współrzędne! Jakiej współrzędnej to odpowiada? Zgadza się, koordynuj! Tak więc punkt.

A co wtedy są równe i? Zgadza się, użyjmy odpowiednich definicji tangensa i cotangensa i zdobądźmy to.
Co jeśli kąt jest większy? Tutaj na przykład jak na tym obrazku:

Co się zmieniło w tym przykładzie? Rozwiążmy to. Aby to zrobić, ponownie zwracamy się do trójkąta prostokątnego. Rozważmy trójkąt prostokątny: kąt (jako sąsiadujący z kątem). Jaka jest wartość sinusa, cosinusa, tangensa i cotangensa kąta? Zgadza się, przestrzegamy odpowiednich definicji funkcji trygonometrycznych:
Jak widać, wartość sinusa kąta nadal odpowiada współrzędnej; wartość cosinusa kąta - współrzędna; oraz wartości tangensa i cotangensa do odpowiednich stosunków. Zatem te relacje mają zastosowanie do dowolnych obrotów wektora promienia.
Wspomniano już, że początkowe położenie wektora promienia leży wzdłuż dodatniego kierunku osi. Do tej pory obróciliśmy ten wektor w kierunku przeciwnym do ruchu wskazówek zegara, ale co się stanie, jeśli obrócimy go zgodnie z ruchem wskazówek zegara? Nic nadzwyczajnego, dostaniesz też kąt o określonej wielkości, ale tylko to będzie ujemne. Tak więc, obracając wektor promienia w kierunku przeciwnym do ruchu wskazówek zegara, otrzymujemy dodatnie kąty, a przy obrocie w prawo - negatywny.
Wiemy więc, że cały obrót wektora promienia wokół okręgu to lub. Czy można obrócić wektor promienia o lub o? Oczywiście, że możesz! Dlatego w pierwszym przypadku wektor promienia wykona jeden pełny obrót i zatrzyma się w pozycji lub.
W drugim przypadku wektor promienia wykona trzy pełne obroty i zatrzyma się w pozycji lub.
Zatem z powyższych przykładów możemy wywnioskować, że kąty różniące się o lub (gdzie jest dowolną liczbą całkowitą) odpowiadają temu samemu położeniu wektora promienia.
Poniższy rysunek przedstawia kąt. Ten sam obraz odpowiada narożnikowi i tak dalej. Ta lista może być kontynuowana w nieskończoność. Wszystkie te kąty można zapisać za pomocą ogólnego wzoru lub (gdzie jest dowolną liczbą całkowitą)

Teraz, znając definicje podstawowych funkcji trygonometrycznych i używając okręgu jednostkowego, spróbuj odpowiedzieć, jakie wartości są równe:
Oto krąg jednostek, który może ci pomóc:

Jakieś trudności? Więc zastanówmy się. Wiemy więc, że:
Stąd określamy współrzędne punktów odpowiadających pewnym miarom kąta. Cóż, zacznijmy w kolejności: róg w odpowiada punktowi o współrzędnych, a zatem:
Nie istnieje;
Ponadto, przestrzegając tej samej logiki, dowiadujemy się, że rogi odpowiadają odpowiednio punktom o współrzędnych. Wiedząc o tym łatwo wyznaczyć wartości funkcji trygonometrycznych w odpowiednich punktach. Najpierw spróbuj sam, a potem sprawdź odpowiedzi.
Odpowiedzi:
Nie istnieje
Nie istnieje
Nie istnieje
Nie istnieje
W ten sposób możemy wykonać następującą tabelę:

Nie trzeba pamiętać wszystkich tych wartości. Wystarczy pamiętać o zgodności współrzędnych punktów na okręgu jednostkowym z wartościami funkcji trygonometrycznych:
Ale wartości funkcji trygonometrycznych kątów w i podane w poniższej tabeli: trzeba pamiętać:

Nie bój się, teraz pokażemy jeden z przykładów dość proste zapamiętywanie odpowiednich wartości:
Aby skorzystać z tej metody, należy pamiętać wartości sinusa dla wszystkich trzech miar kąta () oraz wartość tangensa kąta w. Znając te wartości dość łatwo jest odtworzyć całą tabelę - wartości cosinusów są przenoszone zgodnie ze strzałkami, czyli:
Wiedząc o tym, możesz przywrócić wartości. Licznik „ ” będzie zgodny, a mianownik „ ” będzie zgodny. Wartości cotangens są przenoszone zgodnie ze strzałkami pokazanymi na rysunku. Jeśli to zrozumiesz i zapamiętasz schemat ze strzałkami, wystarczy zapamiętać całą wartość z tabeli.
Współrzędne punktu na okręgu
Czy można znaleźć punkt (jego współrzędne) na okręgu, znając współrzędne środka okręgu, jego promień i kąt obrotu?
Oczywiście, że możesz! Wydobądźmy ogólny wzór na znalezienie współrzędnych punktu.
Tutaj np. mamy taki krąg:

Dano nam, że punkt jest środkiem koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrót punktu o stopnie.
Jak widać na rysunku, współrzędna punktu odpowiada długości odcinka. Długość segmentu odpowiada współrzędnej środka koła, czyli jest równa. Długość segmentu można wyrazić za pomocą definicji cosinusa:
Wtedy mamy to dla punktu współrzędnej.
Zgodnie z tą samą logiką znajdujemy wartość współrzędnej y punktu. Zatem,
Tak więc, ogólnie rzecz biorąc, współrzędne punktów są określone wzorami:
Współrzędne środka okręgu,
promień okręgu,
Kąt obrotu wektora promienia.
Jak widać, dla rozpatrywanego okręgu jednostkowego wzory te są znacznie zmniejszone, ponieważ współrzędne środka wynoszą zero, a promień jest równy jeden:
Cóż, wypróbujmy te formuły dla smaku, ćwicząc znajdowanie punktów na kole?
1. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez włączenie punktu.
2. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez obrót punktu.
3. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez włączenie punktu.
4. Punkt - środek koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrócenie wektora promienia początkowego o.
5. Punkt - środek koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrócenie wektora promienia początkowego o.
Masz problem ze znalezieniem współrzędnych punktu na okręgu?
Rozwiąż te pięć przykładów (lub dobrze zrozum rozwiązanie), a dowiesz się, jak je znaleźć!
1.
Można zauważyć, że. I wiemy, co odpowiada pełnemu obrocie punktu wyjścia. W ten sposób żądany punkt będzie w tej samej pozycji, co podczas obracania się. Wiedząc o tym, znajdujemy pożądane współrzędne punktu:
2. Okrąg jest jednostką ze środkiem w punkcie, co oznacza, że możemy używać uproszczonych wzorów:
Można zauważyć, że. Wiemy, co odpowiada dwóm pełnym obrotom punktu początkowego. W ten sposób żądany punkt będzie w tej samej pozycji, co podczas obracania się. Wiedząc o tym, znajdujemy pożądane współrzędne punktu:
Sinus i cosinus to wartości tabelaryczne. Zapamiętujemy ich wartości i otrzymujemy:
W ten sposób żądany punkt ma współrzędne.
3. Okrąg jest jednostką ze środkiem w punkcie, co oznacza, że możemy używać uproszczonych wzorów:
Można zauważyć, że. Przedstawmy rozważany przykład na rysunku:

Promień tworzy kąty z osią równą i. Wiedząc, że tabelaryczne wartości cosinusa i sinusa są równe i po ustaleniu, że cosinus ma tutaj wartość ujemną, a sinus jest dodatni, mamy:
Podobne przykłady są analizowane bardziej szczegółowo podczas studiowania wzorów redukcji funkcji trygonometrycznych w temacie.
W ten sposób żądany punkt ma współrzędne.
4.
Kąt obrotu wektora promienia (według warunku)
Aby wyznaczyć odpowiednie znaki sinusa i cosinusa, konstruujemy okrąg jednostkowy i kąt:

Jak widać, wartość, to znaczy jest dodatnia, a wartość, to znaczy jest ujemna. Znając wartości tabelaryczne odpowiednich funkcji trygonometrycznych otrzymujemy, że:
Otrzymane wartości podstawmy do naszego wzoru i znajdźmy współrzędne:
W ten sposób żądany punkt ma współrzędne.
5. Aby rozwiązać ten problem, używamy formuł w postaci ogólnej, gdzie
Współrzędne środka okręgu (w naszym przykładzie
Promień okręgu (według warunku)
Kąt obrotu wektora promienia (według warunku).
Zastąp wszystkie wartości formułą i uzyskaj:
oraz - wartości tabeli. Zapamiętujemy je i podstawiamy do formuły:
W ten sposób żądany punkt ma współrzędne.
PODSUMOWANIE I PODSTAWOWA FORMUŁA
Sinus kąta to stosunek przeciwnej (dalekiej) nogi do przeciwprostokątnej.
Cosinus kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
Tangens kąta to stosunek przeciwnej (dalekiej) nogi do sąsiedniej (bliskiej).
Cotangens kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (daleko).
Ten artykuł zebrał tablice sinusów, cosinusów, tangensów i cotangensów. Najpierw podajemy tablicę podstawowych wartości funkcji trygonometrycznych, czyli tablicę sinusów, cosinusów, tangensów i cotangensów kątów 0, 30, 45, 60, 90, ..., 360 stopni ( 0, π/6, π/4, π/3, π/2, …, 2π radian). Następnie podamy tabelę sinusów i cosinusów, a także tabelę tangensów i cotangensów autorstwa V. M. Bradisa i pokażemy, jak korzystać z tych tabel podczas znajdowania wartości funkcji trygonometrycznych.
Nawigacja po stronach.
Tablica sinusów, cosinusów, tangensów i cotangensów dla kątów 0, 30, 45, 60, 90, ... stopni
Bibliografia.
- Algebra: Proc. na 9 komórek. śr. szkoła / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Wyd. S. A. Telyakovsky.- M.: Oświecenie, 1990.- 272 s.: Ill.- ISBN 5-09-002727-7
- Bashmakov MI Algebra i początek analizy: Proc. na 10-11 komórek. śr. szkoła - 3. ed. - M.: Oświecenie, 1993. - 351 s.: ch. - ISBN 5-09-004617-4.
- Algebra i początek analizy: Proc. na 10-11 komórek. ogólne wykształcenie instytucje / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn i inni; Wyd. A. N. Kolmogorova.- 14. wyd.- M.: Oświecenie, 2004.- 384 s.: il.- ISBN 5-09-013651-3.
- Gusiew V.A., Mordkovich A.G. Matematyka (podręcznik dla kandydatów do szkół technicznych): Proc. dodatek.- M.; Wyższy szkoła, 1984.-351 s., chor.
- Bradis V.M. Czterocyfrowe tablice matematyczne: dla edukacji ogólnej. podręcznik zakłady. - wyd. 2 - M.: Drop, 1999.- 96 s.: ch. ISBN 5-7107-2667-2
W artykule w pełni zrozumiemy, jak to wygląda tabela wartości trygonometrycznych, sinus, cosinus, tangens i cotangens. Rozważmy podstawową wartość funkcji trygonometrycznych pod kątem 0,30,45,60,90,...,360 stopni. Zobaczmy, jak wykorzystać te tabele do obliczania wartości funkcji trygonometrycznych.
Najpierw rozważ tabela cosinusa, sinusa, tangensa i cotangensa pod kątem 0, 30, 45, 60, 90,.. stopni. Zdefiniowanie tych wielkości umożliwia wyznaczenie wartości funkcji kątów 0 i 90 stopni:
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, cotangens 00 będzie niezdefiniowany
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, tangens 90 0 będzie niezdefiniowany
Jeśli weźmiemy trójkąty prostokątne, których kąty wynoszą od 30 do 90 stopni. Otrzymujemy:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Wszystkie uzyskane wartości przedstawiamy w formie tabela trygonometryczna:
Tablica sinusów, cosinusów, tangensów i cotangensów!
Jeśli użyjemy formuły redukcji, nasza tabela wzrośnie, zostaną dodane wartości dla kątów do 360 stopni. Będzie to wyglądać tak:

Również w oparciu o właściwości okresowości tablicę można zwiększyć, jeśli zastąpimy kąty przez 0 0 +360 0 *z .... 330 0 +360 0 *z, gdzie z jest liczbą całkowitą. W tej tabeli możliwe jest obliczenie wartości wszystkich kątów odpowiadających punktom w jednym okręgu.

Zobaczmy wyraźnie, jak wykorzystać tabelę w rozwiązaniu.
Wszystko jest bardzo proste. Ponieważ potrzebna nam wartość leży w punkcie przecięcia potrzebnych nam komórek. Na przykład weźmy cos o kącie 60 stopni, w tabeli będzie to wyglądać tak:

W końcowej tabeli głównych wartości funkcji trygonometrycznych postępujemy w ten sam sposób. Ale w tej tabeli można dowiedzieć się, jaka będzie styczna z kąta 1020 stopni, to = -√3 Sprawdźmy 1020 0 = 300 0 +360 0 *2. Znajdźmy stolik.

Stół Bradisa. Dla sinusa, cosinusa, tangensa i cotangensa.
Tablice Bradysa podzielone są na kilka części, składają się na nie tablice cosinusa i sinusa, tangensa i cotangensa – czyli podzielonej na dwie części (tg kąta do 90 stopni i ctg małych kątów).
Sinus i cosinus


kąt tg od 00 do 760, kąt ctg od 140 do 900.


tg do 900 i małe kąty ctg.
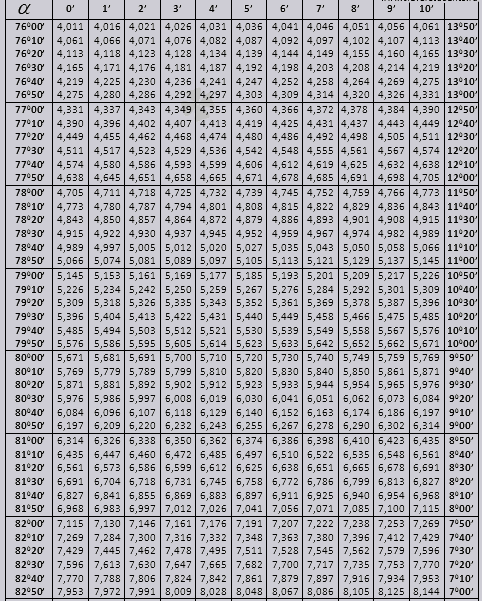

Zastanówmy się, jak używać tabel Bradisa do rozwiązywania problemów.
Znajdźmy oznaczenie sin (oznaczenie w kolumnie od lewej krawędzi) 42 minuty (oznaczenie znajduje się w górnym wierszu). Krzyżując szukamy oznaczenia, jest to = 0,3040.
Wartości minut są wskazywane w odstępie sześciu minut, co jeśli potrzebna nam wartość mieści się w tym przedziale. Weźmy 44 minuty, a w tabeli jest tylko 42. Bierzemy 42 jako podstawę i korzystamy z dodatkowych kolumn po prawej stronie, bierzemy drugą poprawkę i dodajemy do 0,3040 + 0,0006 otrzymujemy 0,3046.
Przy sin 47 min bierzemy za podstawę 48 min i odejmujemy od niej 1 poprawkę, czyli 0,3057 - 0,0003 = 0,3054
Przy obliczaniu cos działamy podobnie jak sin, tylko że za podstawę przyjmujemy dolny rząd tabeli. Na przykład cos 20 0 = 0,9397
Wartości tg o kącie do 90 0 i łóżeczku o małym kącie są prawidłowe i nie ma w nich poprawek. Na przykład znajdź tg 78 0 37 min = 4,967 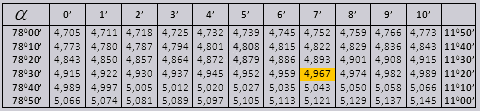
i ctg 20 0 13 min = 25,83 
Cóż, tutaj rozważyliśmy główne tabele trygonometryczne. Mamy nadzieję, że te informacje były dla Ciebie niezwykle przydatne. Twoje pytania na stołach, jeśli są, pisz w komentarzach!
Uwaga: Odbojnice ścienne - deska odbojowa do ochrony ścian. Skorzystaj z linku bezramowe błotniki bezścienne (http://www.spi-polymer.ru/otboyniki/) i dowiedz się więcej.
1. Funkcje trygonometryczne są funkcjami podstawowymi, których argumentem jest zastrzyk. Funkcje trygonometryczne opisują relacje między bokami i kątami ostrymi w trójkącie prostokątnym. Obszary zastosowań funkcji trygonometrycznych są niezwykle zróżnicowane. Na przykład dowolne procesy okresowe można przedstawić jako sumę funkcji trygonometrycznych (szereg Fouriera). Funkcje te często pojawiają się podczas rozwiązywania równań różniczkowych i funkcyjnych.
2. Funkcje trygonometryczne obejmują 6 następujących funkcji: Zatoka, cosinus, tangens,cotangens, sieczna oraz cosecant. Dla każdej z tych funkcji istnieje odwrotna funkcja trygonometryczna.
3. Wygodnie jest wprowadzić geometryczną definicję funkcji trygonometrycznych za pomocą koło jednostkowe. Poniższy rysunek przedstawia okrąg o promieniu r=1. Na okręgu zaznaczony jest punkt M(x,y). Kąt między wektorem promienia OM a dodatnim kierunkiem osi Ox wynosi α.
4. Zatoka kąt α jest stosunkiem rzędnej y punktu M(x,y) do promienia r:
sinα=y/r.
Ponieważ r=1, to sinus jest równy rzędnej punktu M(x,y).
5. cosinus kąt α jest stosunkiem odciętej x punktu M(x,y) do promienia r:
cosα=x/r
6. tangens kąt α jest stosunkiem rzędnej y punktu M(x,y) do jego odciętej x:
tanα=y/x,x≠0
7. Cotangens kąt α jest stosunkiem odciętej x punktu M(x,y) do jego rzędnej y:
cotα=x/y,y≠0
8. Sieczna kąt α jest stosunkiem promienia r do odciętej x punktu M(x,y):
sekα=r/x=1/x,x≠0
9. Cosecans kąt α jest stosunkiem promienia r do rzędnej y punktu M(x,y):
cscα=r/y=1/r,y≠0
10. W okręgu jednostkowym rzutu x, y punkty M(x,y) i promień r tworzą trójkąt prostokątny, w którym x,y to ramiona, a r to przeciwprostokątna. Dlatego powyższe definicje funkcji trygonometrycznych w odniesieniu do trójkąta prostokątnego są sformułowane w następujący sposób:
Zatoka kąt α to stosunek przeciwprostokątnej do przeciwprostokątnej.
cosinus kąt α to stosunek sąsiedniej nogi do przeciwprostokątnej.
tangens kąt α nazywany jest odnogą przeciwną do sąsiedniej.
Cotangens kąt α nazywany jest sąsiednią nogą do przeciwnej.
Sieczna kąt α to stosunek przeciwprostokątnej do sąsiedniej nogi.
Cosecans kąt α to stosunek przeciwprostokątnej do przeciwległej nogi.
11. wykres funkcji sinus
y=sinx, domena: x∈R, domena: −1≤sinx≤1
12. Wykres funkcji cosinus
y=cosx, dziedzina: x∈R, zakres: −1≤cosx≤1
13. wykres funkcji stycznej 14. Wykres funkcji cotangens 15. Wykres funkcji siecznej
y=tanx, dziedzina: x∈R,x≠(2k+1)π/2, dziedzina: −∞ 
y=cotx, dziedzina: x∈R,x≠kπ, dziedzina: −∞ 
y=secx, dziedzina: x∈R,x≠(2k+1)π/2, dziedzina: secx∈(−∞,−1]∪∪)