Sformułowanie definicji kąta między prostą a płaszczyzną. Kąt między linią prostą a płaszczyzną: definicja, przykłady znajdowania

Twoja prywatność jest dla nas ważna. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Przeczytaj naszą politykę prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które mogą posłużyć do identyfikacji konkretnej osoby lub do skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie, gdy się z nami skontaktujesz.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić oraz sposobu, w jaki możemy z nich korzystać.

Jakie dane osobowe zbieramy:

• Kiedy przesyłasz wniosek na stronie, możemy zbierać różne informacje, w tym imię i nazwisko, numer telefonu, adres E-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

• Zebrane przez nas informacje osobiste pozwala nam kontaktować się z Tobą i informować o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
• Od czasu do czasu możemy wykorzystywać Twoje dane osobowe, aby wysyłać Ci ważne powiadomienia i komunikaty.
• Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak audyt, analiza danych i różne studia w celu ulepszenia świadczonych przez nas usług i przedstawiania rekomendacji dotyczących naszych usług.
• Jeśli weźmiesz udział w losowaniu nagród, konkursie lub podobnym programie motywacyjnym, możemy wykorzystać podane przez Ciebie informacje do administrowania takimi programami.

Ujawnianie osobom trzecim

Nie ujawniamy informacji otrzymanych od Ciebie stronom trzecim.

Wyjątki:

• W razie potrzeby - zgodnie z prawem, nakaz sądowy, w spór, i/lub na podstawie publicznych próśb lub próśb z agencje rządowe na terytorium Federacji Rosyjskiej - ujawniać swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli ustalimy, że takie ujawnienie jest konieczne lub odpowiednie dla bezpieczeństwa, egzekwowania prawa lub innych publicznych ważne okazje.
• W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane przez nas dane osobowe odpowiedniemu następcy strony trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – w celu ochrony Twoich danych osobowych przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także przed nieautoryzowanym dostępem, ujawnieniem, zmianą i zniszczeniem.

Zachowanie prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo danych osobowych, informujemy naszych pracowników o praktykach dotyczących prywatności i bezpieczeństwa oraz ściśle egzekwujemy praktyki dotyczące prywatności.

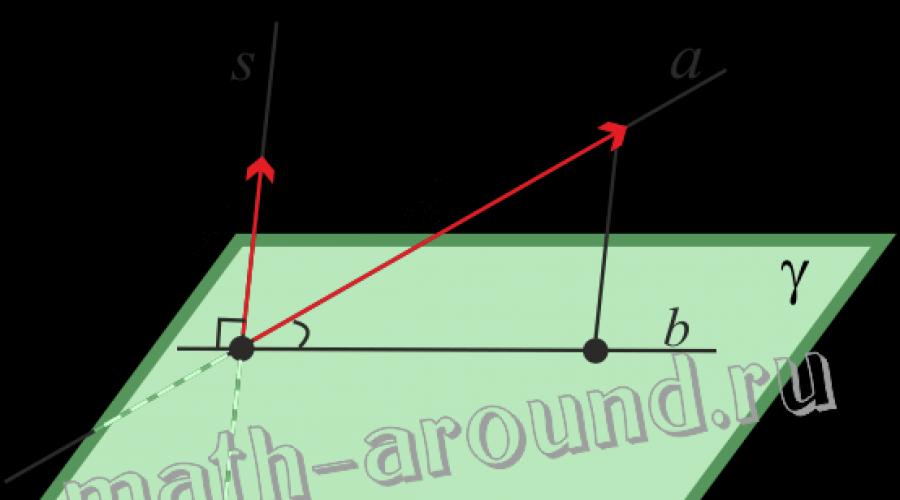
Powtórzmy definicję kąta między linią a płaszczyzną.

Definicja. Kąt między linią a płaszczyzną, która przecina tę linię i nie jest do niej prostopadła, to kąt między linią a jej rzutem na płaszczyznę.

Niech zostanie podana płaszczyzna γ i prosta a, które przecinają tę płaszczyznę i nie są do niej prostopadłe.

Skonstruujmy kąt między prostą a a płaszczyzną γ:

1. Z dowolnego dogodnego dla nas punktu linii prostej opuszczamy prostopadłą do płaszczyzny γ;
2. Przez punkty podstawy ukośnej i prostopadłej narysuj linię b. Prosta b - rzut prostej a na płaszczyznę γ;
3. Kąt ostry między liniami a i b to kąt między linią a i płaszczyzną γ, ​​tj. ∠(a;b)= ∠(a;γ) , gdzie ∠(a;b) jest kątem między liniami a i b; ∠(a;γ) - kąt między prostą a płaszczyzną γ.

Aby rozwiązać problemy metodą współrzędnych, musimy pamiętać o następujących kwestiach:

3. Jeżeli znane są współrzędne wektora kierunkowego ( a 1 ; b 1 ; c 1 ) i wektora normalnego
(a; b; c), to kąt między prostą a i płaszczyzną γ jest obliczany ze wzoru, który teraz wyprowadzimy.

Znamy wzór na znalezienie kąta między liniami:

; (1)
∠(s; a) = 90°-∠(a; b), wtedy cos∠(s;a)=cos (90°-∠(a;b))=sin ∠(a;b); (2)
Od (1) i (2) => ; (3)
, gdzie jest kątem między wektorami m i n; (cztery)
Podstawiamy (4) do (3) i ponieważ ∠(a;b)= ∠(a;γ), to otrzymujemy:

4. Jeśli współrzędne wektora normalnego są nieznane, musimy znać równanie płaszczyzny.

Dowolną płaszczyznę w prostokątnym układzie współrzędnych można podać równaniem

ax + przez + cz + d = 0,

gdzie co najmniej jeden ze współczynników a, b, c jest różny od zera. Te współczynniki będą współrzędnymi wektora normalnego, tj. (a; b; c).

Algorytm rozwiązywania problemów wyznaczania kąta między prostą a płaszczyzną metodą współrzędnych:

1. Wykonujemy rysunek, na którym zaznaczamy linię prostą i płaszczyznę;
2. Wprowadzamy prostokątny układ współrzędnych;
3. Współrzędne wektora kierunku znajdujemy na podstawie współrzędnych jego początku i końca;
4. Znajdujemy współrzędne wektora normalnego do płaszczyzny;
5. Otrzymane dane podstawiamy do wzoru na sinus kąta między linią a płaszczyzną;
6. Znajdź wartość samego kąta.

Rozważ problem:
1. W sześcianie ABCDA 1 B 1 C 1 D 1 znajdź styczną kąta między prostą AC 1 a płaszczyzną BDD 1.
Rozwiązanie:

1. Wprowadźmy prostokątny układ współrzędnych z początkiem w punkcie D.
2. Znajdź współrzędne wektora kierunkowego AC 1 . Aby to zrobić, najpierw określ współrzędne punktów A i C 1:
A(0; 1; 0);
C1 (1; 0; 1).
{1; -1; 1}.
3. Znajdź współrzędne wektora normalnego do płaszczyzny BB 1 D 1 . Aby to zrobić, znajdujemy współrzędne trzech punktów płaszczyzny, które nie leżą na jednej linii prostej i układamy równanie płaszczyzny:
D(0; 0; 0);
D1 (0; 0; 1);
B(1; 1; 0);
D: a⋅0+b⋅0+c⋅0+d=0;
D 1: a⋅0+b⋅0+c⋅1+d=0;
B: a⋅1+b⋅1+c⋅0+d=0.

Podstaw do równania: a⋅x+(-a)⋅y+0⋅z+0 = 0;
a⋅x-a⋅y = 0; |:a
x-y = 0.
Zatem wektor normalny do płaszczyzny BDD 1 ma współrzędne:
{1;-1; 0}.
4. Znajdź sinus pomiędzy linią prostą AC 1 a płaszczyzną BDD 1:

5. Wykorzystajmy podstawową tożsamość trygonometryczną i znajdźmy cosinus kąta między prostą AC 1 a płaszczyzną BDD 1:

6. Znajdź styczną kąta pomiędzy prostą AC 1 a płaszczyzną BDD 1:

Odpowiadać: .

2. W regularnej piramidzie czworokątnej SABCD, której wszystkie krawędzie są równe 1, znajdź sinus kąta między prostą BD a płaszczyzną SBC.

Rozwiązanie:

1. Wprowadźmy prostokątny układ współrzędnych z początkiem w punkcie B.
2. Znajdź współrzędne wektora kierunkowego BD . Aby to zrobić, najpierw określ współrzędne punktów B i D:

3. Znajdź współrzędne wektora normalnego do płaszczyzny SBC. Aby to zrobić, znajdujemy współrzędne trzech punktów płaszczyzny, które nie leżą na jednej linii prostej i układamy równanie płaszczyzny SBC:

Jak uzyskałeś współrzędne punktu S?

Od punktu S obniżono prostopadłą do płaszczyzny podstawy ABC. Punkt przecięcia oznaczono jako O. Punkt O jest rzutem punktu S na płaszczyznę ABC. Jego współrzędne x i y będą pierwszymi dwoma współrzędnymi punktu S.

Poznawszy wartość wysokości piramidy, znaleźliśmy trzecią współrzędną punktu S (wzdłuż osi z)

Trójkąt SOB jest więc trójkątem prostokątnym, zgodnie z twierdzeniem Pitagorasa:

Równanie płaszczyzny ma postać ax+by+cz+d=0. Podstaw współrzędne punktów do tego równania:

Otrzymaliśmy układ trzech równań:

Podstaw do równania:

Zatem wektor normalny do płaszczyzny SBD ma współrzędne:

.
4. Znajdź sinus między linią BD a płaszczyzną SBD.

Pojęcie rzutu figury na płaszczyznę

Aby wprowadzić pojęcie kąta między prostą a płaszczyzną, należy najpierw zrozumieć takie pojęcie jak rzut dowolnej figury na płaszczyznę.

Definicja 1

Daj nam dowolny punkt $A$. Punkt $A_1$ nazywamy rzutem punktu $A$ na płaszczyznę $\alpha $ jeśli jest podstawą prostopadłej narysowanej z punktu $A$ na płaszczyznę $\alpha $ (rys. 1).

Rysunek 1. Rzut punktu na płaszczyznę

Definicja 2

Dajmy nam dowolną liczbę $F$. Figura $F_1$ nazywana jest rzutem figury $F$ na płaszczyznę $\alpha $, złożoną z rzutów wszystkich punktów figury $F$ na płaszczyznę $\alpha $ (rys. 2).

Rysunek 2. Rzut figury na płaszczyznę

Twierdzenie 1

Rzut linii prostej nie prostopadłej do płaszczyzny jest linią prostą.

Dowód.

Dajmy płaszczyznę $\alpha $ i prostą $d$, która ją przecina i nie jest do niej prostopadła. Wybieramy punkt $M$ na prostej $d$ i rysujemy jego rzut $H$ na płaszczyznę $\alpha $. Narysuj płaszczyznę $\beta $ przez prostą $(MH)$. Oczywiście ta płaszczyzna będzie prostopadła do płaszczyzny $\alpha $. Niech przecinają się wzdłuż linii $m$. Rozważ dowolny punkt $M_1$ prostej $d$ i poprowadź przez niego prostą $(M_1H_1$) równolegle do prostej $(MH)$ (rys. 3).

Rysunek 3

Ponieważ płaszczyzna $\beta $ jest prostopadła do płaszczyzny $\alpha $, to $M_1H_1$ jest prostopadła do prostej $m$, czyli punkt $H_1$ jest rzutem punktu $M_1$ na płaszczyznę $\alfa $. Ponieważ wybór punktu $M_1$ jest dowolny, wszystkie punkty prostej $d$ rzutowane są na prostą $m$.

Argumentując podobnie. W odwrotnej kolejności otrzymamy, że każdy punkt linii $m$ jest rzutem jakiegoś punktu linii $d$.

Stąd linia $d$ jest rzutowana na linię $m$.

Twierdzenie zostało udowodnione.

Pojęcie kąta między linią a płaszczyzną

Definicja 3

Kąt pomiędzy linią prostą przecinającą płaszczyznę a jej rzutem na tę płaszczyznę nazywamy kątem pomiędzy linią prostą a płaszczyzną (rys. 4).

Rysunek 4. Kąt między linią a płaszczyzną

Zwracamy tutaj uwagę na kilka uwag.

Uwaga 1

Jeśli linia jest prostopadła do płaszczyzny. Wtedy kąt pomiędzy linią a płaszczyzną wynosi $90^\circ$.

Uwaga 2

Jeśli linia jest równoległa lub leży w płaszczyźnie. Wtedy kąt pomiędzy prostą a płaszczyzną jest równy $0^\circ$.

Przykłady zadań

Przykład 1

Dajmy równoległobok $ABCD$ i punkt $M$, który nie leży w płaszczyźnie równoległoboku. Wykazać, że trójkąty $AMB$ i $MBC$ są prostokątne, jeśli punkt $B$ jest rzutem punktu $M$ na płaszczyznę równoległoboku.

Dowód.

Przedstawmy stan problemu na rysunku (ryc. 5).

Rysunek 5

Ponieważ punkt $B$ jest rzutem punktu $M$ na płaszczyznę $(ABC)$, prosta $(MB)$ jest prostopadła do płaszczyzny $(ABC)$. Z uwagi 1 otrzymujemy, że kąt pomiędzy prostą $(MB)$ a płaszczyzną $(ABC)$ jest równy $90^\circ$. w konsekwencji

\[\angle MBC=MBA=(90)^0\]

Stąd trójkąty $AMB$ i $MBC$ są prostokątne.

Przykład 2

Podano płaszczyznę $\alpha $. Do tej płaszczyzny rysowany jest odcinek pod kątem $\varphi $, którego początek leży w danej płaszczyźnie. Rzut tego segmentu jest dwa razy mniejszy niż sam segment. Znajdź wartość $\varphi $.

Rozwiązanie.

Rozważ rysunek 6.

Rysunek 6

Z założenia mamy

Ponieważ trójkąt $BCD$ jest trójkątem prostokątnym, to z definicji cosinusa

\ \[\varphi =arccos\frac(1)(2)=(60)^0\]

Kurs wideo „Zdobądź piątkę” zawiera wszystkie tematy niezbędne do osiągnięcia sukcesu zdanie egzaminu z matematyki za 60-65 punktów. Całkowicie wszystkie zadania 1-13 z profilu USE w matematyce. Nadaje się również do zaliczenia podstawowego USE w matematyce. Jeśli chcesz zdać egzamin na 90-100 punktów, musisz rozwiązać część 1 w 30 minut i bez błędów!

Kurs przygotowujący do egzaminu dla klas 10-11, a także dla nauczycieli. Wszystko, czego potrzebujesz do rozwiązania części 1 egzaminu z matematyki (12 pierwszych zadań) i zadania 13 (trygonometria). A to ponad 70 punktów na Zjednoczonym Egzaminu Państwowym i ani stupunktowy student, ani humanista nie mogą się bez nich obejść.

Cała niezbędna teoria. Szybkie sposoby rozwiązania, pułapki i tajemnice egzaminu. Przeanalizowano wszystkie istotne zadania części 1 z zadań Banku FIPI. Kurs w pełni zgodny z wymaganiami USE-2018.

Kurs zawiera 5 duże tematy, 2,5 godziny każdy. Każdy temat podany jest od podstaw, prosto i przejrzyście.

Setki zadań egzaminacyjnych. Problemy tekstowe i teoria prawdopodobieństwa. Proste i łatwe do zapamiętania algorytmy rozwiązywania problemów. Geometria. Teoria, materiał referencyjny, analiza wszystkich typów zadań USE. Stereometria. Podstępne sztuczki rozwiązania, przydatne ściągawki, rozwój wyobraźni przestrzennej. Trygonometria od podstaw - do zadania 13. Zrozumienie zamiast wkuwania. Wizualne wyjaśnienie złożonych pojęć. Algebra. Pierwiastki, potęgi i logarytmy, funkcja i pochodna. Podstawa rozwiązania wymagające zadania 2 części egzaminu.

Artykuł zaczyna się od definicji kąta między linią a płaszczyzną. W tym artykule pokażemy, jak znaleźć kąt między linią prostą a płaszczyzną za pomocą metody współrzędnych. Rozwiązanie przykładów i zadań zostanie szczegółowo omówione.

Yandex.RTB R-A-339285-1

Po pierwsze, konieczne jest powtórzenie koncepcji linii prostej w przestrzeni i koncepcji płaszczyzny. Aby określić kąt między linią a płaszczyzną, potrzebnych jest kilka definicji pomocniczych. Rozważmy szczegółowo te definicje.

Definicja 1

Linia i płaszczyzna przecinają się kiedy mają jeden wspólny punkt, czyli jest to punkt przecięcia linii i płaszczyzny.

Linia przecinająca płaszczyznę może być prostopadła do płaszczyzny.

Definicja 2

Linia jest prostopadła do płaszczyzny gdy jest prostopadła do dowolnej linii na tej płaszczyźnie.

Definicja 3

Rzut punktu M na płaszczyznęγ jest samym punktem, jeśli leży w dany samolot, lub jest punktem przecięcia płaszczyzny z prostą prostopadłą do płaszczyzny γ przechodzącą przez punkt M , pod warunkiem że nie należy do płaszczyzny γ .

Definicja 4

Rzut prostej a na płaszczyznęγ to zbiór rzutów wszystkich punktów danej prostej na płaszczyznę.

Z tego otrzymujemy, że rzut prostej prostopadłej do płaszczyzny γ ma punkt przecięcia. Otrzymujemy, że rzut prostej a jest prostą należącą do płaszczyzny γ i przechodzącą przez punkt przecięcia prostej a i płaszczyzny. Rozważ poniższy rysunek.

Na ten moment mamy wszystkie niezbędne informacje i dane do sformułowania definicji kąta między prostą a płaszczyzną

Definicja 5

Kąt między linią a płaszczyzną nazywamy kątem między tą linią a jej rzutem na tę płaszczyznę, a linia nie jest do niej prostopadła.

Podana powyżej definicja kąta pozwala stwierdzić, że kąt między prostą a płaszczyzną jest kątem między dwiema przecinającymi się liniami, czyli daną linią wraz z jej rzutem na płaszczyznę. Oznacza to, że kąt między nimi zawsze będzie ostry. Spójrzmy na poniższy obrazek.

Kąt pomiędzy linią prostą a płaszczyzną jest uważany za prosty, czyli równy 90 stopni, a kąt leżący pomiędzy liniami równoległymi nie jest zdefiniowany. Zdarzają się przypadki, gdy jego wartość jest równa zeru.

Zadania, w których konieczne jest znalezienie kąta między linią prostą a płaszczyzną, mają wiele wariantów rozwiązania. Sam przebieg rozwiązania zależy od dostępnych danych o stanie. Częstymi towarzyszami rozwiązania są znaki podobieństwa lub równości liczb, cosinusów, sinusów, stycznych kątów. Znalezienie kąta jest możliwe przy użyciu metody współrzędnych. Rozważmy to bardziej szczegółowo.

Jeżeli w trójwymiarowej przestrzeni O x y z wprowadzimy prostokątny układ współrzędnych, to ustawia się w nim linię prostą a przecinającą płaszczyznę γ w punkcie M i nie jest ona prostopadła do płaszczyzny. Konieczne jest znalezienie kąta α znajdującego się między daną linią prostą a płaszczyzną.

Najpierw musisz zastosować definicję kąta między linią a płaszczyzną za pomocą metody współrzędnych. Następnie otrzymujemy następujące.

W układzie współrzędnych O x y z określona jest prosta a, której odpowiadają równania prostej w przestrzeni i wektor kierujący przestrzeni bezpośredniej, dla płaszczyzny γ odpowiada równanie płaszczyzny i wektor normalny samolot. Wtedy a → = (a x , a y , a z) jest wektorem kierunkowym danej prostej a , a n → (n x , n y , n z) jest wektorem normalnym płaszczyzny γ . Jeśli wyobrazimy sobie, że mamy współrzędne wektora kierującego prostej a i wektora normalnego płaszczyzny γ, to ich równania są znane, to znaczy są podane przez warunek, wtedy można wyznaczyć wektory a → i n → , na podstawie równania.

Aby obliczyć kąt, musisz przekształcić formułę, która pozwala uzyskać wartość tego kąta za pomocą dostępnych współrzędnych wektora kierunkowego wektora prostego i normalnego.

Należy odroczyć wektory a → i n → , zaczynając od punktu przecięcia prostej a z płaszczyzną γ . Istnieją 4 opcje lokalizacji tych wektorów względem podanych linii i płaszczyzny. Rozważ poniższy obrazek, który ma wszystkie 4 warianty.

Stąd otrzymujemy, że kąt między wektorami a → i n → ma oznaczenie a → , n → ^ i jest ostry, to żądany kąt α leżący między prostą a płaszczyzną jest uzupełniony, czyli otrzymujemy wyrażenie forma a → , n → ^ = 90 ° - α . Gdy warunek a → , n → ^ > 90 ° , wtedy mamy a → , n → ^ = 90 ° + α .

Stąd mamy, że cosinusy równe kąty są równe, to ostatnie równości są zapisywane jako system

cos a → , n → ^ = cos 90 ° - α , a → , n → ^< 90 ° cos a → , n → ^ = cos 90 ° + α , a → , n → ^ >90°

Aby uprościć wyrażenia, należy użyć formuł rzutowania. Następnie otrzymujemy równości postaci cos a → , n → ^ = sin α , a → , n → ^< 90 ° cos a → , n → ^ = - s i n α , a → , n → ^ >90°.

Po przekształceniach układ przyjmuje postać sin α = cos a → , n → ^ , a → , n → ^< 90 ° sin α = - cos a → , n → ^ , a → , n → ^ >90 ° ⇔ sin α = cos a → , n → ^ , a → , n → ^ > 0 sin α = - cos a → , n → ^ , a → , n → ^< 0 ⇔ ⇔ sin α = cos a → , n → ^

Z tego otrzymujemy, że sinus kąta między prostą a płaszczyzną jest równy modułowi cosinusa kąta między wektorem kierunkowym prostej a wektorem normalnym danej płaszczyzny.

Sekcja dotycząca znajdowania kąta utworzonego przez dwa wektory wykazała, że ​​kąt ten przyjmuje wartość iloczynu skalarnego wektorów i iloczynu tych długości. Proces obliczania sinusa kąta uzyskanego przez przecięcie linii prostej i płaszczyzny odbywa się za pomocą wzoru

sin α = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2

Oznacza to, że wzór na obliczenie kąta pomiędzy prostą a płaszczyzną ze współrzędnymi wektora kierunkowego prostej i wektora normalnego płaszczyzny po transformacji okazuje się być

α = a r c sin a → , n → ^ a → n → = a r c sin a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2

Znalezienie cosinusa ze znanym sinusem jest dopuszczalne przez zastosowanie podstawowego tożsamość trygonometryczna. Forma przecięcia linii i płaszczyzny ostry róg. Sugeruje to, że jego wartość będzie liczbą dodatnią, a jej obliczenie odbywa się ze wzoru cos α = 1 - sin α .

Rozwiążmy kilka podobnych przykładów, aby skonsolidować materiał.

Przykład 1

Znajdź kąt, sinus, cosinus kąta utworzonego przez prostą x 3 = y + 1 - 2 = z - 11 6 i płaszczyznę 2 x + z - 1 = 0 .

Rozwiązanie

Aby uzyskać współrzędne wektora kierującego, konieczne jest uwzględnienie równań kanonicznych linii prostej w przestrzeni. Wtedy otrzymujemy, że a → = (3, - 2, 6) jest wektorem kierunkowym prostej x 3 = y + 1 - 2 = z - 11 6 .

Aby znaleźć współrzędne wektora normalnego, należy wziąć pod uwagę ogólne równanie płaszczyzny, ponieważ ich obecność jest określona przez współczynniki dostępne przed zmienne równania. Wtedy otrzymujemy, że dla płaszczyzny 2 x + z - 1 = 0 wektor normalny ma postać n → = (2 , 0 , 1 ).

Konieczne jest przystąpienie do obliczenia sinusa kąta między linią a płaszczyzną. Aby to zrobić, konieczne jest podstawienie współrzędnych wektorów a → i b → do podanej formuły. Dostajemy wyrażenie jak

sin α = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2 = = 3 2 + (- 2 ) 0 + 6 1 3 2 + (- 2) 2 + 6 2 2 2 + 0 2 + 1 2 = 12 7 5

Stąd znajdujemy wartość cosinusa i wartość samego kąta. Otrzymujemy:

cos α = 1 - sin α = 1 - 12 7 5 2 = 101 7 5

Odpowiadać: sin α = 12 7 5 , cos α = 101 7 5 , α = a r c cos 101 7 5 = a r c sin 12 7 5 .

Przykład 2

Istnieje piramida zbudowana z wartości wektorów A B → = 1 , 0 , 2 , A C → = ( ​​- 1 , 3 , 0 ) , A D → = 4 , 1 , 1 . Znajdź kąt między linią A D a płaszczyzną A B C.

Rozwiązanie

Aby obliczyć pożądany kąt, konieczne jest posiadanie wartości współrzędnych wektora kierującego linii i wektora normalnego płaszczyzny. dla prostej AD wektor kierunkowy ma współrzędne AD → = 4 , 1 , 1 .

Wektor normalny n → należący do płaszczyzny A B C jest prostopadły do ​​wektora A B → i A C → . Oznacza to, że można wziąć pod uwagę wektor normalny płaszczyzny A B C produkt wektorowy wektory A B → i A C → . Obliczamy to według wzoru i otrzymujemy:

n → = A B → × A C → = i → j → k → 1 0 2 - 1 3 0 = - 6 i → - 2 j → + 3 k → ⇔ n → = (- 6 , - 2 , 3 )

Konieczne jest podstawienie współrzędnych wektorów, aby obliczyć żądany kąt utworzony przez przecięcie prostej i płaszczyzny. otrzymujemy wyrażenie takie jak:

α = a r c sin A D → , n → ^ A D → n → = a r c sin 4 - 6 + 1 - 2 + 1 3 4 2 + 1 2 + 1 2 - 6 2 + - 2 2 + 3 2 = a r c sin 23 21 2

Odpowiadać: a r c sin 23 21 2 .

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter