Tabela redukcji trygonometrii. Podstawowa tożsamość trygonometryczna
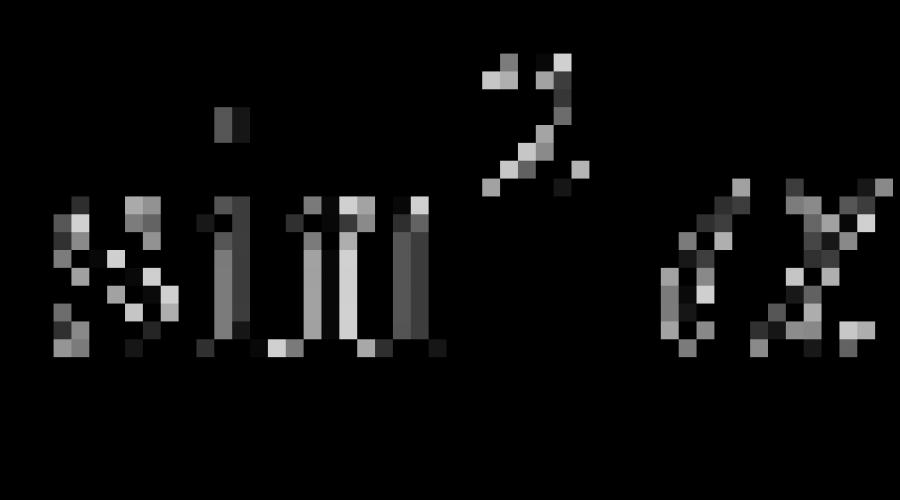
Przeczytaj także
W tym artykule przyjrzymy się kompleksowo . Podstawowe tożsamości trygonometryczne to równości, które ustalają związek między sinusem, cosinusem, tangensem i cotangensem jednego kąta i umożliwiają znalezienie dowolnej z tych funkcji trygonometrycznych poprzez znaną inną.
Natychmiast wymieniamy główne tożsamości trygonometryczne, które przeanalizujemy w tym artykule. Zapisujemy je w tabeli, a poniżej podajemy wyprowadzenie tych formuł i podajemy niezbędne wyjaśnienia.
Nawigacja po stronach.
Związek między sinusem i cosinusem jednego kąta
Czasami mówią nie o głównych tożsamościach trygonometrycznych wymienionych w powyższej tabeli, ale o jednej pojedynczej podstawowa tożsamość trygonometryczna uprzejmy ![]() . Wyjaśnienie tego faktu jest dość proste: równości uzyskuje się z podstawowego tożsamość trygonometryczna po podzieleniu obu jego części przez i odpowiednio oraz równości
. Wyjaśnienie tego faktu jest dość proste: równości uzyskuje się z podstawowego tożsamość trygonometryczna po podzieleniu obu jego części przez i odpowiednio oraz równości  oraz
oraz ![]() wynikają z definicji sinusa, cosinusa, tangensa i cotangensa. Omówimy to bardziej szczegółowo w kolejnych akapitach.
wynikają z definicji sinusa, cosinusa, tangensa i cotangensa. Omówimy to bardziej szczegółowo w kolejnych akapitach.
Oznacza to, że szczególnie interesująca jest równość, której nadano nazwę głównej tożsamości trygonometrycznej.
Zanim udowodnimy podstawową tożsamość trygonometryczną, podajemy jej sformułowanie: suma kwadratów sinusa i cosinusa jednego kąta jest identycznie równa jeden. Teraz udowodnijmy to.
Podstawowa tożsamość trygonometryczna jest bardzo często używana w transformacja wyrażeń trygonometrycznych. Pozwala to na zastąpienie sumy kwadratów sinusa i cosinusa jednego kąta przez jeden. Nie rzadziej podstawową tożsamość trygonometryczną stosuje się w odwrotnej kolejności: jednostkę zastępuje suma kwadratów sinusa i cosinusa dowolnego kąta.
Tangens i cotangens przez sinus i cosinus
Tożsamości łączące tangens i cotangens z sinusem i cosinusem jednego kąta formy i ![]() wynikają bezpośrednio z definicji sinusa, cosinusa, tangensa i cotangensa. Rzeczywiście, z definicji sinus jest rzędną y, cosinus jest odciętą x, tangens jest stosunkiem rzędnej do odciętej, czyli
wynikają bezpośrednio z definicji sinusa, cosinusa, tangensa i cotangensa. Rzeczywiście, z definicji sinus jest rzędną y, cosinus jest odciętą x, tangens jest stosunkiem rzędnej do odciętej, czyli ![]() , a cotangens to stosunek odciętej do rzędnej, czyli
, a cotangens to stosunek odciętej do rzędnej, czyli ![]() .
.
Ze względu na tę oczywistość tożsamości i ![]() często definicje tangensa i cotangensa podaje się nie poprzez stosunek odciętej do rzędnej, ale poprzez stosunek sinusa do cosinusa. Więc tangens kąta jest stosunkiem sinusa do cosinusa tego kąta, a cotangens jest stosunkiem cosinusa do sinusa.
często definicje tangensa i cotangensa podaje się nie poprzez stosunek odciętej do rzędnej, ale poprzez stosunek sinusa do cosinusa. Więc tangens kąta jest stosunkiem sinusa do cosinusa tego kąta, a cotangens jest stosunkiem cosinusa do sinusa.
Na zakończenie tej sekcji należy zauważyć, że tożsamości i ![]() trzymaj się wszystkich takich kątów, dla których zawarte w nich funkcje trygonometryczne mają sens. Czyli wzór obowiązuje dla każdego innego niż (w przeciwnym razie mianownik będzie wynosił zero, a nie zdefiniowaliśmy dzielenia przez zero) i wzór
trzymaj się wszystkich takich kątów, dla których zawarte w nich funkcje trygonometryczne mają sens. Czyli wzór obowiązuje dla każdego innego niż (w przeciwnym razie mianownik będzie wynosił zero, a nie zdefiniowaliśmy dzielenia przez zero) i wzór ![]() - dla wszystkich , różne od , gdzie z jest dowolnym .
- dla wszystkich , różne od , gdzie z jest dowolnym .
Związek między styczną i cotangens
Jeszcze bardziej oczywistą tożsamością trygonometryczną niż dwie poprzednie jest tożsamość łącząca styczną i cotangens jednego kąta formy ![]() . Oczywiste jest, że ma to miejsce dla dowolnych kątów innych niż , w przeciwnym razie tangens lub cotangens nie są zdefiniowane.
. Oczywiste jest, że ma to miejsce dla dowolnych kątów innych niż , w przeciwnym razie tangens lub cotangens nie są zdefiniowane.
Dowód formuły ![]() bardzo prosta. Z definicji i skąd
bardzo prosta. Z definicji i skąd  . Dowód mógł zostać przeprowadzony w nieco inny sposób. Od i
. Dowód mógł zostać przeprowadzony w nieco inny sposób. Od i ![]() , następnie
, następnie  .
.
Tak więc tangens i cotangens jednego kąta, pod którym mają sens, to.
To jest ostatni i najbardziej główna lekcja wymagane do rozwiązywania problemów B11. Wiemy już, jak zamieniać kąty z miary w radianach na miary w stopniach (patrz lekcja „Miara kąta w radianach i stopniach”), a także wiemy, jak wyznaczyć znak funkcji trygonometrycznej, koncentrując się na ćwiartkach współrzędnych (patrz lekcja „ Znaki funkcji trygonometrycznych”).
Sprawa pozostaje niewielka: obliczyć wartość samej funkcji - tę samą liczbę, która jest zapisana w odpowiedzi. Tutaj z pomocą przychodzi podstawowa tożsamość trygonometryczna.
Podstawowa tożsamość trygonometryczna. Dla dowolnego kąta α stwierdzenie jest prawdziwe:
sin 2 α + cos 2 α = 1.
Ten wzór odnosi się do sinusa i cosinusa jednego kąta. Teraz, znając sinus, możemy łatwo znaleźć cosinus - i na odwrót. Wystarczy wyciągnąć pierwiastek kwadratowy:
Zwróć uwagę na znak „±” przed korzeniami. Faktem jest, że z podstawowej tożsamości trygonometrycznej nie jest jasne, jaki był pierwotny sinus i cosinus: dodatni czy ujemny. W końcu kwadratura nawet funkcja, który „wypala” wszystkie minusy (jeśli występują).
Dlatego we wszystkich zadaniach B11, które znajdują się w USE w matematyce, koniecznie są dodatkowe warunki, które pomagają pozbyć się niepewności ze znakami. Zwykle jest to wskazanie ćwiartki współrzędnych, za pomocą której można określić znak.
Uważny czytelnik z pewnością zapyta: „A co z tangensem i cotangensem?” Niemożliwe jest bezpośrednie obliczenie tych funkcji z powyższych wzorów. Jednak są ważne implikacje z podstawowej tożsamości trygonometrycznej, która zawiera już styczne i kotangensy. Mianowicie:
Ważny wniosek: dla dowolnego kąta α podstawową tożsamość trygonometryczną można przepisać w następujący sposób:
Równania te łatwo wyprowadzić z podstawowej identyczności - wystarczy podzielić obie strony przez cos 2 α (aby otrzymać tangens) lub przez sin 2 α (dla cotangensa).
Rzućmy okiem na to wszystko konkretne przykłady. Poniżej znajdują się prawdziwe problemy z B11, które zostały zaczerpnięte z procesu UŻYJ opcji w matematyce 2012.
Znamy cosinus, ale nie znamy sinusa. Główna tożsamość trygonometryczna (w swojej „czystej” postaci) łączy właśnie te funkcje, więc będziemy z nią pracować. Mamy:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Aby rozwiązać problem, pozostaje znaleźć znak sinusa. Ponieważ kąt α ∈ (π /2; π ), to w mierze stopni zapisujemy go następująco: α ∈ (90°; 180°).
Dlatego kąt α leży w ćwiartce współrzędnej II - wszystkie tam sinusy są dodatnie. Dlatego sin α = 0,1.
Znamy więc sinus, ale musimy znaleźć cosinus. Obie te funkcje znajdują się w podstawowej tożsamości trygonometrycznej. Zastępujemy:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Pozostaje zająć się znakiem przed frakcją. Co wybrać: plus czy minus? Warunkiem jest, że kąt α należy do przedziału (π 3π /2). Przekształćmy kąty z miary w radianach na miarę stopni - otrzymujemy: α ∈ (180°; 270°).
Oczywiście jest to trzecia ćwiartka współrzędnych, w której wszystkie cosinusy są ujemne. Dlatego cosα = -0,5.
Zadanie. Znajdź tg α, jeśli znasz następujące elementy:
Tangens i cosinus są powiązane równaniem wynikającym z podstawowej tożsamości trygonometrycznej:
Otrzymujemy: tg α = ±3. Znak stycznej jest określony przez kąt α. Wiadomo, że α ∈ (3π /2; 2π ). Przekształćmy kąty z miary w radianach na miarę stopni - otrzymujemy α ∈ (270°; 360°).
Oczywiście jest to ćwiartka współrzędnych IV, w której wszystkie styczne są ujemne. Dlatego tgα = -3.
Zadanie. Znajdź cos α, jeśli znasz:
Ponownie sinus jest znany, a cosinus nieznany. Zapisujemy główną tożsamość trygonometryczną:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Znak jest określony przez kąt. Mamy: α ∈ (3π /2; 2π ). Przekształćmy kąty ze stopni na radiany: α ∈ (270°; 360°) to ćwiartka współrzędnych IV, tam cosinusy są dodatnie. Dlatego cos α = 0,6.
Zadanie. Znajdź sin α, jeśli wiesz, co następuje:
Napiszmy wzór, który wynika z podstawowej tożsamości trygonometrycznej i bezpośrednio łączy sinus i cotangens:
Stąd otrzymujemy, że sin 2 α = 1/25, tj. sin α = ±1/5 = ±0,2. Wiadomo, że kąt α ∈ (0; π/2). W stopniach jest to zapisane w następujący sposób: α ∈ (0°; 90°) - I współrzędna ćwiartka.
Zatem kąt znajduje się w ćwiartce współrzędnych I - wszystkie funkcje trygonometryczne są tam dodatnie, dlatego sin α \u003d 0,2.
Definicja. Formuły redukcyjne nazywane są formułami, które umożliwiają przejście od funkcji trygonometrycznych formularza do funkcji argumentów. Za ich pomocą sinus, cosinus, tangens i cotangens dowolnego kąta można sprowadzić do sinusa, cosinusa, tangensa i cotangensa kąta od 0 do 90 stopni (od 0 do radianów). Zatem formuły redukcyjne pozwalają nam przejść do pracy z kątami w granicach 90 stopni, co jest niewątpliwie bardzo wygodne.
Formuły odlewów:

Istnieją dwie zasady korzystania z formuł rzutowania.
1. Jeśli kąt można przedstawić jako (π/2 ±a) lub (3*π/2 ±a), to zmiana nazwy funkcji grzech do Kos, cos do grzechu, tg do ctg, ctg do tg. Jeśli kąt można przedstawić jako (π ±a) lub (2*π ±a), to nazwa funkcji pozostaje niezmieniona.
Spójrz na poniższy rysunek, który schematycznie pokazuje, kiedy znak powinien zostać zmieniony, a kiedy nie.

2. Zredukowany znak funkcyjny pozostaje takie samo. Jeśli pierwotna funkcja miała znak plus, to zredukowana funkcja również ma znak plus. Jeśli oryginalna funkcja miała znak minus, to funkcja zredukowana również ma znak minus.
Poniższy rysunek przedstawia znaki głównych funkcji trygonometrycznych w zależności od ćwiartki.

Przykład:
Oblicz
Wykorzystajmy formuły redukcyjne:
Grzech(150˚) jest w drugiej ćwiartce, z rysunku widać, że znak grzechu w tej ćwiartce jest równy „+”. Oznacza to, że powyższa funkcja będzie miała również znak „+”. Zastosowaliśmy drugą zasadę.
Teraz 150˚ = 90˚ +60˚. 90˚ to π/2. Oznacza to, że mamy do czynienia z przypadkiem π/2 + 60, dlatego zgodnie z pierwszą zasadą zmieniamy funkcję z sin na cos. W rezultacie otrzymujemy Sin(150˚) = cos(60˚) = ½.
Wzory redukcyjne to współczynniki, które pozwalają przejść od sinusa, cosinusa, tangensa i cotangensa z kątami `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi) 2 \pm \alpha`, `2\pi \pm \alpha` do tych samych funkcji kąta `\alpha`, który znajduje się w pierwszej ćwiartce okręgu jednostkowego. Zatem formuły redukcyjne „prowadzą” nas do pracy z kątami w zakresie od 0 do 90 stopni, co jest bardzo wygodne.
W sumie dostępne są 32 formuły redukcyjne. Niewątpliwie przydadzą się na egzaminie, egzaminach, sprawdzianach. Ale od razu ostrzeżemy, że nie ma potrzeby ich zapamiętywania! Musisz poświęcić trochę czasu i zrozumieć algorytm ich zastosowania, wtedy nie będzie ci trudno właściwy moment uzyskać niezbędną równość.
Najpierw zapiszmy wszystkie formuły redukcyjne:
Dla kąta (`\frac (\pi)2 \pm \alpha`) lub (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
Dla kąta (`\pi \pm \alpha`) lub (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Dla kąta (`\frac (3\pi)2 \pm \alpha`) lub (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 - \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 - \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
Dla kąta (`2\pi \pm \alpha`) lub (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Często można znaleźć wzory redukcyjne w postaci tabeli, w której kąty zapisywane są w radianach:
Aby z niego skorzystać, należy wybrać wiersz z potrzebną nam funkcją oraz kolumnę z żądanym argumentem. Na przykład, aby użyć tabeli do ustalenia, czym będzie ` sin(\pi + \alpha)`, wystarczy znaleźć odpowiedź na przecięciu wiersza ` sin \beta` i kolumny ` \pi + \ alfa”. Otrzymujemy ` sin(\pi + \alpha)=-sin \ \alpha`.
I druga, podobna tabela, w której kąty zapisane są w stopniach:

Mnemoniczna zasada rzutowania formuł, czyli jak je zapamiętywać
Jak już wspomnieliśmy, nie jest konieczne zapamiętywanie wszystkich powyższych wskaźników. Jeśli przyjrzałeś się im uważnie, prawdopodobnie zauważyłeś pewne wzory. Pozwalają nam na sformułowanie reguły mnemonicznej (mnemonik – zapamiętywanie), dzięki której w prosty sposób można uzyskać dowolne formuły redukcyjne.
Od razu zauważamy, że aby zastosować tę zasadę, trzeba dobrze umieć określić (lub zapamiętać) znaki funkcji trygonometrycznych w różnych ćwiartkach okręgu jednostkowego.  Sam przeszczep składa się z 3 etapów:
Sam przeszczep składa się z 3 etapów:
- Argument funkcji musi mieć postać `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, z `\alpha` wymagane ostry róg(od 0 do 90 stopni).
- Dla argumentów `\frac (\pi)2 \pm \alpha`, `\frac (3\pi)2 \pm \alpha` funkcja trygonometryczna przekształconego wyrażenia zmienia się na kofunkcję, czyli odwrotnie (sinus na cosinus, tangens na cotangens i vice versa). Dla argumentów `\pi \pm \alpha`, `2\pi \pm \alpha` funkcja nie zmienia się.
- Określa się znak pierwotnej funkcji. Wynikowa funkcja po prawej stronie będzie miała ten sam znak.
Aby zobaczyć, jak można zastosować tę zasadę w praktyce, przekształćmy kilka wyrażeń:
1. `cos(\pi + \alfa)`.
Funkcja nie jest odwrócona. Kąt ` \pi + \alpha` znajduje się w trzeciej ćwiartce, cosinus w tym kwadrancie ma znak „-”, więc przekonwertowana funkcja również będzie miała znak „-”.
Odpowiedź: ` cos(\pi + \alpha)= - cos \alpha`
2. `sin(\frac (3\pi)2 - \alfa)`.
Zgodnie z zasadą mnemoniczną funkcja zostanie odwrócona. Kąt `\frac (3\pi)2 - \alpha` znajduje się w trzeciej ćwiartce, tutaj sinus ma znak "-", więc wynik będzie również ze znakiem "-".
Odpowiedź: `sin(\frac (3\pi)2 - \alpha)= - cos \alpha`
3. `cos(\frac (7\pi)2 - \alfa)`.
`cos(\frac (7\pi)2 - \alpha)=cos(\frac (6\pi)2+\frac (\pi)2-\alpha)=cos (3\pi+(\frac(\pi )2-\alfa))". Reprezentujmy `3\pi` jako `2\pi+\pi`. `2\pi` to okres funkcji.
Ważne: Funkcje `cos \alpha` i `sin \alpha` mają kropkę `2\pi` lub `360^\circ`, ich wartości nie zmienią się, jeśli argument zostanie zwiększony lub zmniejszony o te wartości.
Na tej podstawie nasze wyrażenie można zapisać w następujący sposób: `cos (\pi+(\frac(\pi)2-\alpha)`. Stosując dwukrotnie regułę mnemoniczną, otrzymujemy: `cos (\pi+(\frac(\ pi) 2-\alpha)= - cos (\frac(\pi)2-\alpha)= - grzech \alpha`.
Odpowiedź: `cos(\frac (7\pi)2 - \alpha)=- sin \alpha`.
koń rządzi
Drugi punkt powyższej reguły mnemonicznej jest również nazywany regułą konia formuł redukcyjnych. Zastanawiam się, dlaczego konie?
Mamy więc funkcje z argumentami `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, punkty `\frac (\pi)2`, `\pi`, `\frac (3\pi)2`, `2\pi` są kluczowymi punktami, znajdują się na osiach współrzędnych. `\pi` i `2\pi` na poziomej osi X oraz `\frac (\pi)2` i `\frac (3\pi)2` na Oś pionowa rzędna
Zadajemy sobie pytanie: „Czy funkcja zamienia się w kofunkcję?”. Aby odpowiedzieć na to pytanie, musisz przesunąć głowę wzdłuż osi, na której znajduje się kluczowy punkt.
Oznacza to, że na argumenty, w których kluczowe punkty znajdują się na osi poziomej, odpowiadamy „nie”, kręcąc głową na boki. A w przypadku narożników z kluczowymi punktami na osi pionowej odpowiadamy „tak” kiwając głową od góry do dołu, jak koń 🙂
Polecamy obejrzeć film instruktażowy, w którym autor szczegółowo wyjaśnia, jak zapamiętywać formuły redukcyjne bez ich zapamiętywania.
Praktyczne przykłady wykorzystania formuł odlewniczych
Stosowanie formuł redukcyjnych zaczyna się w 9 i 10 klasie. Do egzaminu zgłaszanych jest wiele zadań z ich użyciem. Oto niektóre z zadań, w których będziesz musiał zastosować te formuły:
- zadania do rozwiązania trójkąta prostokątnego;
- konwersja liczbowych i alfabetycznych wyrażeń trygonometrycznych, obliczanie ich wartości;
- problemy stereometryczne.
Przykład 1. Użyj formuł redukcyjnych do obliczenia a) `sin 600^\circ`, b) `tg 480^\circ`, c) `cos 330^\circ`, d) `sin 240^\circ`.
Rozwiązanie: a) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
b) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac(\sqrt 3)3`;
c) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac(\sqrt 3)2`;
d) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac(\sqrt 3)2`.
Przykład 2. Po wyrażeniu cosinusa przez sinus za pomocą formuł redukcyjnych porównaj liczby: 1) `sin \frac (9\pi)8` i `cos \frac (9\pi)8`; 2) `sin \frac (\pi)8` i `cos \frac (3\pi)10`.
Rozwiązanie: 1)`sin \frac (9\pi)8=sin (\pi+\frac (\pi)8)=-sin \frac (\pi)8`
`cos \frac (9\pi)8=cos (\pi+\frac (\pi)8)=-cos \frac (\pi)8=-sin \frac (3\pi)8`
`-sin \frac (\pi)8> -sin \frac (3\pi)8`
`sin \frac (9\pi)8>cos \frac (9\pi)8`.
2) `cos \frac (3\pi)10=cos (\frac (\pi)2-\frac (\pi)5)=sin \frac (\pi)5`
„grzech \frac (\pi)8 „grzech \frac (\pi)8 Najpierw udowodnimy dwie formuły na sinus i cosinus argumentu `\frac (\pi)2 + \alpha`: ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha` i ` cos( \frac (\ pi)2 + \alpha)=-sin \\alpha`. Reszta pochodzi od nich. Weź okrąg jednostkowy i umieść na nim punkt A o współrzędnych (1,0). Niech po włączeniu Z definicji tangensa i cotangensa otrzymujemy ` tg(\frac (\pi)2 + \alpha)=\frac (sin(\frac (\pi)2 + \alpha))(cos(\frac (\pi )2 + \alpha))=\frac (cos \alpha)(-sin \alpha)=-ctg \alpha` i ` ctg(\frac (\pi)2 + \alpha)=\frac (cos(\frac (\ pi)2 + \alpha))(sin(\frac (\pi)2 + \alpha))=\frac (-sin \alpha)(cos \alpha)=-tg \alpha`, co świadczy o redukcji wzory na tangens i cotangens kąta `\frac (\pi)2 + \alpha`. Aby udowodnić formuły argumentem `\frac (\pi)2 - \alpha`, wystarczy przedstawić go jako `\frac (\pi)2 + (-\alpha)` i podążać tą samą ścieżką jak powyżej. Na przykład `cos(\frac (\pi)2 - \alpha)=cos(\frac (\pi)2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`. Kąty `\pi + \alpha` i `\pi - \alpha` można przedstawić jako `\frac (\pi)2 +(\frac (\pi)2+\alpha)` i `\frac (\pi ) 2 +(\frac (\pi)2-\alpha)` odpowiednio. Oraz `\frac (3\pi)2 + \alpha` i `\frac (3\pi)2 - \alpha` jako `\pi +(\frac (\pi)2+\alpha)` i `\pi +(\frac (\pi)2-\alpha)`. narożnik `\alpha` dojedzie do punktu `A_1(x, y)`, a po skręcie o kąt `\frac (\pi)2 + \alpha` do punktu `A_2(-y,x)` . Upuszczając prostopadłe z tych punktów do prostej OX, widzimy, że trójkąty `OA_1H_1` i `OA_2H_2` są równe, ponieważ ich przeciwprostokątne i przyległe kąty są równe. Następnie na podstawie definicji sinusa i cosinusa możemy napisać `sin \alpha=y`, `cos \alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\ pi)2 + \alpha)=-y`. Jak można napisać, że ` sin(\frac (\pi)2 + \alpha)=cos \alpha` i ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, co świadczy o redukcji wzory na sinus i cosinus kąta `\frac (\pi)2 + \alpha`.
narożnik `\alpha` dojedzie do punktu `A_1(x, y)`, a po skręcie o kąt `\frac (\pi)2 + \alpha` do punktu `A_2(-y,x)` . Upuszczając prostopadłe z tych punktów do prostej OX, widzimy, że trójkąty `OA_1H_1` i `OA_2H_2` są równe, ponieważ ich przeciwprostokątne i przyległe kąty są równe. Następnie na podstawie definicji sinusa i cosinusa możemy napisać `sin \alpha=y`, `cos \alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\ pi)2 + \alpha)=-y`. Jak można napisać, że ` sin(\frac (\pi)2 + \alpha)=cos \alpha` i ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, co świadczy o redukcji wzory na sinus i cosinus kąta `\frac (\pi)2 + \alpha`.