Kąt ABC to kąt wpisany. Opiera się na łuku AC, zamkniętym między jego bokami (ryc. 330).

Twierdzenie. Kąt wpisany jest mierzony przez połowę łuku, który przecina.

Należy to rozumieć w następujący sposób: kąt wpisany zawiera tyle stopni kątowych, minut i sekund, ile stopni kątowych, minut i sekund zawiera połowa łuku, na którym się opiera.

Dowodząc tego twierdzenia, musimy rozważyć trzy przypadki.

Pierwszy przypadek. Środek koła leży po stronie kąta wpisanego (ryc. 331).

Niech ∠ABC będzie kątem wpisanym, a środek okręgu O leży na boku BC. Wymagane jest udowodnienie, że mierzy się ją o połowę łuku AC.

Połącz punkt A ze środkiem okręgu. Otrzymujemy równoramienne \(\Delta\)AOB, w których AO = OB, jako promienie tego samego okręgu. Dlatego ∠A = ∠B.

∠AOC jest zewnętrzne względem trójkąta AOB, więc ∠AOC = ∠A + ∠B, a ponieważ kąty A i B są równe, ∠B wynosi 1/2 ∠AOC.

Ale ∠AOC jest mierzone przez łuk AC, dlatego ∠B jest mierzone przez połowę łuku AC.

Na przykład, jeśli \(\breve(AC)\) zawiera 60°18', to ∠B zawiera 30°9'.

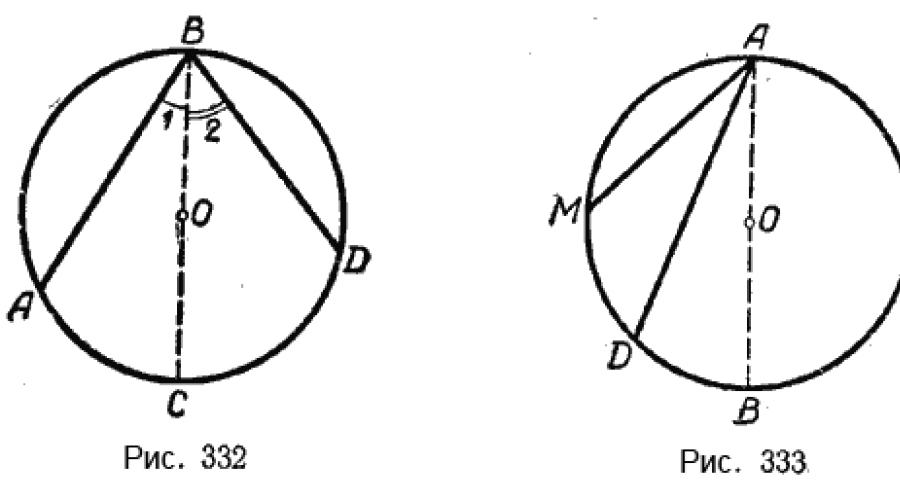
Drugi przypadek. Środek koła leży między bokami wpisanego kąta (ryc. 332).

Niech ∠ABD będzie kątem wpisanym. Środek koła O leży pomiędzy jego bokami. Należy wykazać, że ∠ABD jest mierzone przez połowę AD łuku.

Aby to udowodnić, narysujmy średnicę BC. Kąt ABD podzielony na dwa kąty: ∠1 i ∠2.

∠1 jest mierzone przez połowę łuku AC, a ∠2 jest mierzone przez połowę łuku CD, dlatego całe ∠ABD jest mierzone jako 1/2 \(\breve(AC)\) + 1/2 \( \breve(CD)\), czyli połowa łuku AD.

Na przykład, jeśli \(\breve(AD)\) zawiera 124°, to ∠B zawiera 62°.

Trzeci przypadek. Środek koła leży poza wpisanym kątem (ryc. 333).

Niech ∠MAD będzie kątem wpisanym. Środek okręgu O znajduje się poza rogiem. Wymagane jest wykazanie, że ∠MAD jest mierzone przez połowę MD łuku.

Aby to udowodnić, narysujmy średnicę AB. ∠MAD = ∠MAB - ∠DAB. Ale ∠MAB mierzy 1/2 \(\breve(MB)\), a ∠DAB mierzy 1/2 \(\breve(DB)\).

Dlatego ∠MAD mierzy 1/2 (\(\breve(MB) - \breve(DB))\), czyli 1/2 \(\breve(MD)\).

Na przykład, jeśli \(\breve(MD)\) zawiera 48° 38", to ∠MAD zawiera 24° 19' 8".

Konsekwencje
1. Wszystkie kąty wpisane na tym samym łuku są sobie równe, ponieważ są mierzone przez połowę tego samego łuku (ryc. 334, a).

2. Kąt wpisany oparty na średnicy jest kątem prostym, ponieważ opiera się na pół okręgu. Połowa koła zawiera 180 stopni łukowych, co oznacza, że ​​kąt oparty na średnicy zawiera 90 stopni kątowych (ryc. 334, b).

Pojęcie kąta wpisanego i środkowego

Najpierw wprowadźmy pojęcie kąta środkowego.

Uwaga 1

Zauważ, że miara stopnia kąta środkowego jest równa mierze stopnia łuku, który przecina.

Wprowadzamy teraz pojęcie kąta wpisanego.

Definicja 2

Kąt, którego wierzchołek leży na okręgu i którego boki przecinają ten sam okrąg, nazywany jest kątem wpisanym (rys. 2).

Rysunek 2. Kąt wpisany

Twierdzenie o kątach wpisanych

Twierdzenie 1

Miara kąta wpisanego jest połową miary łuku, który przecina.

Dowód.

Daj nam okrąg o środku w punkcie $O$. Oznacz kąt wpisany $ACB$ (rys. 2). Możliwe są następujące trzy przypadki:

• Promień $CO$ pokrywa się z pewną stroną kąta. Niech to będzie strona $CB$ (rys. 3).

Rysunek 3

W tym przypadku łuk $AB$ jest mniejszy niż $(180)^(()^\circ )$, stąd centralny róg$AOB$ jest równa łukowi $AB$. Ponieważ $AO=OC=r$, trójkąt $AOC$ jest równoramienny. Stąd kąty bazowe $CAO$ i $ACO$ są równe. Zgodnie z twierdzeniem o kącie zewnętrznym trójkąta mamy:

• Belka $CO$ dzieli wewnętrzny narożnik do dwóch rogów. Niech przecina okrąg w punkcie $D$ (rys. 4).

Rysunek 4

dostajemy

• Promień $CO$ nie dzieli kąta wewnętrznego na dwa kąty i nie pokrywa się z żadnym z jego boków (rys. 5).

Rysunek 5

Rozważ oddzielnie kąty $ACD$ i $DCB$. Na podstawie tego, co zostało udowodnione w punkcie 1, otrzymujemy

dostajemy

Twierdzenie zostało udowodnione.

Przynieśmy konsekwencje z tego twierdzenia.

Wniosek 1: Wpisane kąty przecinające ten sam łuk są równe.

Konsekwencja 2: Kąt wpisany, który przecina średnicę, jest kątem prostym.

Instrukcja

Jeśli znany jest promień (R) okręgu i długość łuku (L) odpowiadająca pożądanemu kątowi środkowemu (θ), można go obliczyć zarówno w stopniach, jak iw radianach. Suma jest określona wzorem 2 * π * R i odpowiada kątowi środkowemu 360 ° lub dwóm liczbom pi, jeśli zamiast stopni stosuje się radiany. Dlatego wyjdź z proporcji 2*π*R/L = 360°/θ = 2*π/θ. Wyraź z niego kąt środkowy w radianach θ = 2*π/(2*π*R/L) = L/R lub stopnie θ = 360°/(2*π*R/L) = 180*L/(π * R) i obliczyć zgodnie z otrzymanym wzorem.

Zgodnie z długością cięciwy (m) łączącej punkty określające kąt środkowy (θ), jego wartość można również obliczyć, jeśli znany jest promień (R) okręgu. Aby to zrobić, rozważ trójkąt utworzony przez dwa promienie i . To jest Trójkąt równoramienny, wszystkie są znane, ale musisz znaleźć kąt, który leży naprzeciw podstawy. Zatoka jego połowy jest równy stosunkowi długość podstawy - cięciwy - do dwukrotnej długości boku bocznego - promień. Dlatego do obliczeń użyj funkcji odwrotnego sinusa - arcus sinus: θ \u003d 2 * arcsin (½ * m / R).

Kąt środkowy można również określić w ułamkach obrotu lub w pełnym kącie. Na przykład, jeśli chcesz znaleźć kąt środkowy odpowiadający jednej czwartej pełnego obrotu, podziel 360° przez cztery: θ = 360°/4 = 90°. Ta sama wartość w radianach powinna wynosić 2*π/4 3,14/2 ≈ 1,57. Rozwinięty kąt jest równy połowie pełnego obrotu, więc na przykład kąt środkowy odpowiadający jednej czwartej będzie równy połowie wartości obliczonych powyżej, zarówno w stopniach, jak i radianach.

Funkcja trygonometryczna odwrotnego sinusa nosi nazwę arcus sinus. Może przyjmować wartości mieszczące się w granicach połowy liczby pi, zarówno dodatnie, jak i ujemne. zła strona mierzone w radianach. Mierzone w stopniach wartości te będą mieściły się odpowiednio w zakresie od -90° do +90°.

Instrukcja

Niektóre „okrągłe” wartości nie muszą być obliczane, łatwiej je zapamiętać. Na przykład: - jeśli argumentem funkcji jest zero, to wartość arcsinus od niej również wynosi zero, - od 1/2 to 30 ° lub 1/6 Pi, jeśli zmierzono, - arcus sinus od -1/2 jest równy do -30° lub -1/6 pi w ;- arcsinus 1 to 90° lub 1/2 pi w radianach;- arcsinus -1 to -90° lub -1/2 pi w radianach;

Aby zmierzyć wartości tej funkcji z innych argumentów, najłatwiej jest użyć standardowego kalkulatora Windows, jeśli masz . Aby rozpocząć, otwórz menu główne na przycisku „Start” (lub naciskając klawisz WIN), przejdź do sekcji „Wszystkie programy”, a następnie do podsekcji „Akcesoria” i kliknij element „Kalkulator”.

Przełącz interfejs kalkulatora w tryb pracy, który pozwala na obliczenia funkcje trygonometryczne. W tym celu otwórz sekcję „Widok” w jej menu i wybierz pozycję „Inżynieria” lub „Naukowa” (w zależności od system operacyjny).

Wprowadź wartość argumentu, na podstawie którego ma zostać obliczony łuk styczny. Można to zrobić, klikając myszą przyciski interfejsu kalkulatora lub naciskając klawisze na , albo kopiując wartość (CTRL + C), a następnie wklejając ją (CTRL + V) do pola wejściowego kalkulatora.

Wybierz jednostki, w których chcesz otrzymać wynik obliczenia funkcji. Poniżej pola wprowadzania znajdują się trzy opcje, z których należy wybrać (klikając myszą) jedną - , radiany lub rady.

Zaznacz pole wyboru, które odwraca funkcje wskazane na przyciskach interfejsu kalkulatora. Obok znajduje się krótki napis Inv.

Kliknij przycisk grzechu. Kalkulator odwróci dołączoną do niego funkcję, wykona obliczenia i przedstawi wynik w podanych jednostkach.

Powiązane wideo

Jednym z typowych problemów geometrycznych jest obliczanie powierzchni odcinka kołowego - części koła ograniczonej cięciwą i łukiem kołowym odpowiadającym cięciwie.

Powierzchnia segmentu kołowego jest równa różnicy między polem odpowiedniego sektora kołowego a polem trójkąta utworzonego przez promienie sektora odpowiadającego segmentowi i cięciwę ograniczającą segment.

Przykład 1

Długość cięciwy podległej okręgowi jest równa a. Miara stopnia łuku odpowiadającego cięciwie wynosi 60°. Znajdź obszar segmentu kołowego.

Decyzja

Trójkąt utworzony przez dwa promienie i cięciwę jest równoramienny, więc wysokość narysowana od wierzchołka kąta środkowego do boku trójkąta utworzonego przez cięciwę będzie również dwusieczną kąta środkowego, dzieląc go na pół i środkową , dzieląc akord na pół. Wiedząc, że sinus kąta β jest równy stosunkowi przeciwnej odnogi do przeciwprostokątnej, możemy obliczyć wartość promienia:

Grzech 30°= a/2:R = 1/2;

Sc = πR²/360°*60° = πa²/6

S▲=1/2*ah, gdzie h jest wysokością narysowaną od góry kąta środkowego do cięciwy. Według twierdzenia Pitagorasa h=√(R²-a²/4)= √3*a/2.

W związku z tym S▲=√3/4*a².

Powierzchnia segmentu, obliczona jako Sceg = Sc - S▲, jest równa:

Sseg \u003d πa² / 6 - √3 / 4 * a²

Podstawiając wartość liczbową do wartości a, możesz łatwo obliczyć wartość liczbową obszaru segmentu.

Przykład 2

Promień okręgu jest równy a. Miara stopnia łuku odpowiadającego segmentowi wynosi 60°. Znajdź obszar segmentu kołowego.

Decyzja:

Obszar sektora odpowiadający danemu kątowi można obliczyć za pomocą następującego wzoru:

Sc = πа²/360°*60° = πa²/6,

Pole trójkąta odpowiadające sektorowi oblicza się w następujący sposób:

S▲=1/2*ah, gdzie h jest wysokością narysowaną od góry kąta środkowego do cięciwy. Według twierdzenia Pitagorasa h=√(a²-a²/4)= √3*a/2.

W związku z tym S▲=√3/4*a².

I wreszcie powierzchnia segmentu, obliczona jako Sceg = Sc - S▲, jest równa:

Sseg \u003d πa² / 6 - √3 / 4 * a².

Rozwiązania w obu przypadkach są prawie identyczne. Możemy więc stwierdzić, że w najprostszym przypadku do obliczenia pola powierzchni odcinka wystarczy znać wartość kąta odpowiadającego łukowi odcinka oraz jeden z dwóch parametrów - albo promień odcinka. okrąg lub długość cięciwy leżącej na łuku okręgu tworzącego odcinek.

Źródła:

• Segment — geometria

Średni poziom

Okrąg i wpisany kąt. wizualny przewodnik (2019)

Podstawowe warunki.

Jak dobrze pamiętasz wszystkie nazwiska związane z kręgiem? Na wszelki wypadek przypomnimy sobie - spójrz na zdjęcia - odśwież swoją wiedzę.

Po pierwsze - Środek okręgu to punkt, od którego wszystkie punkty na okręgu znajdują się w tej samej odległości.

Po drugie - promień - segment linii łączący środek i punkt na okręgu.

Promieni jest dużo (tyle, ile jest punktów na okręgu), ale wszystkie promienie mają tę samą długość.

Czasami na krótko promień oni to nazywają długość segmentu„środek to punkt na okręgu”, a nie sam odcinek.

A oto co się dzieje jeśli połączysz dwa punkty na okręgu? Również cięcie?

Tak więc ten segment nazywa się "akord".

Podobnie jak w przypadku promienia, średnicę często nazywa się długością odcinka łączącego dwa punkty na okręgu i przechodzącego przez środek. Przy okazji, jak są powiązane średnica i promień? Przypatrz się. Oczywiście, promień to połowa średnicy.

Oprócz akordów są też sieczna.

Pamiętasz najprostsze?

Kąt środkowy to kąt pomiędzy dwoma promieniami.

A teraz wpisany kąt

Kąt wpisany to kąt między dwoma cięciwami, które przecinają się w punkcie na okręgu.

W tym przypadku mówią, że kąt wpisany opiera się na łuku (lub cięciwie).

Zobacz zdjęcie:

Pomiar łuków i kątów.

Obwód. Łuki i kąty są mierzone w stopniach i radianach. Najpierw o stopniach. Nie ma problemów z kątami - trzeba nauczyć się mierzyć łuk w stopniach.

Miara stopnia (wartość łuku) to wartość (w stopniach) odpowiedniego kąta środkowego

Co oznacza tutaj słowo „odpowiadający”? Przyjrzyjmy się uważnie:

Widzisz dwa łuki i dwa środkowe kąty? Cóż, większy łuk odpowiada większemu kątowi (i dobrze, że jest większy), a mniejszy łuk odpowiada mniejszemu kątowi.

Więc zgodziliśmy się: łuk zawiera taką samą liczbę stopni, jak odpowiadający mu kąt centralny.

A teraz o okropnościach - o radianach!

Jakim zwierzęciem jest ten „radian”?

Wyobraź to sobie: radiany to sposób pomiaru kąta... w promieniach!

Kąt w radianach to kąt środkowy, którego długość łuku jest równa promieniowi okręgu.

Wtedy pojawia się pytanie - ile radianów znajduje się pod kątem wyprostowanym?

Innymi słowy: ile promieni „pasuje” w pół okręgu? Albo inaczej: ile razy długość pół okręgu jest większa niż promień?

To pytanie zadawali naukowcy w starożytnej Grecji.

I tak po długich poszukiwaniach stwierdzili, że stosunek obwodu do promienia nie chce być wyrażony w liczbach „ludzkich”, takich jak itp.

I nie da się nawet wyrazić tej postawy przez korzenie. To znaczy, okazuje się, że nie można powiedzieć, że połowa koła to dwukrotność lub krotność promienia! Czy możesz sobie wyobrazić, jak niesamowite było odkrywanie ludzi po raz pierwszy?! Dla stosunku długości półkola do promienia wystarczyły „normalne” liczby. Musiałem wpisać list.

Jest to więc liczba wyrażająca stosunek długości półokręgu do promienia.

Teraz możemy odpowiedzieć na pytanie: ile radianów jest pod kątem prostym? Ma radian. Właśnie dlatego, że połowa koła to dwukrotność promienia.

Starożytni (i nie tacy) ludzie na przestrzeni wieków (!) próbowali dokładniej obliczyć tę tajemniczą liczbę, aby lepiej wyrazić ją (przynajmniej w przybliżeniu) za pomocą „zwykłych” liczb. A teraz jesteśmy niemożliwie leniwi - wystarczą nam dwa znaki po zajęciu, jesteśmy do tego przyzwyczajeni

Pomyśl o tym, oznacza to na przykład, że y koła o promieniu jednego ma w przybliżeniu taką samą długość, a zapisanie tej długości za pomocą liczby „ludzkiej” jest po prostu niemożliwe - potrzebujesz litery. A wtedy ten obwód będzie równy. I oczywiście obwód promienia jest równy.

Wróćmy do radianów.

Dowiedzieliśmy się już, że kąt prosty zawiera radian.

Co mamy:

Tak się cieszę, że się cieszę. W ten sam sposób uzyskuje się płytę o najpopularniejszych kątach.

Stosunek wartości kątów wpisanych i środkowych.

Jest niesamowity fakt:

Wartość kąta wpisanego jest o połowę mniejsza od odpowiedniego kąta centralnego.

Zobacz, jak wygląda to stwierdzenie na zdjęciu. „Odpowiadający” kąt środkowy to taki, w którym końce pokrywają się z końcami kąta wpisanego, a wierzchołek znajduje się pośrodku. Jednocześnie „odpowiadający” kąt środkowy musi „wyglądać” na ten sam cięciw () co kąt wpisany.

Dlaczego tak? Spójrzmy najpierw na prosty przypadek. Niech jeden z akordów przejdzie przez środek. W końcu to się czasem zdarza, prawda?

co się tutaj stało? Rozważać. W końcu są równoramienne i są promieniami. Tak więc (oznaczono je).

Teraz spójrzmy. To jest zewnętrzny róg! Przypominamy, że kąt zewnętrzny jest równy sumie dwóch kątów wewnętrznych, które z nim nie sąsiadują i piszemy:

Tj! Nieoczekiwany efekt. Ale jest też kąt środkowy dla wpisanego.

Tak więc w tym przypadku udowodniliśmy, że kąt środkowy jest dwukrotnie większy niż kąt wpisany. Ale to boli szczególny przypadek: czy to prawda, że ​​akord nie zawsze przechodzi prosto przez środek? Ale nic, teraz ten szczególny przypadek bardzo nam pomoże. Patrz: przypadek drugi: niech centrum leży w środku.

Zróbmy to: narysuj średnicę. A potem… widzimy dwa zdjęcia, które zostały już przeanalizowane w pierwszym przypadku. Dlatego już mamy

Więc (na rysunku a)

Cóż, pozostaje ostatni przypadek: środek jest poza rogiem.

Robimy to samo: narysuj średnicę przez punkt. Wszystko jest takie samo, ale zamiast sumy - różnica.

To wszystko!

Stwórzmy teraz dwa główne i bardzo ważne konsekwencje ze stwierdzenia, że ​​kąt wpisany jest połową kąta środkowego.

Następstwo 1

Wszystkie wpisane kąty przecinające ten sam łuk są równe.

Ilustrujemy:

Istnieje niezliczona ilość kątów wpisanych opartych na tym samym łuku (my mamy ten łuk), mogą wyglądać zupełnie inaczej, ale wszystkie mają ten sam kąt środkowy (), co oznacza, że ​​wszystkie te kąty wpisane są między sobą równe.

Konsekwencja 2

Kąt oparty na średnicy jest kątem prostym.

Spójrz: który róg jest centralny?

Na pewno, . Ale jest równy! No właśnie dlatego (a także wiele kątów wpisanych na podstawie) i jest równy.

Kąt między dwoma cięciwami i siecznymi

A co jeśli kąt, który nas interesuje, NIE jest wpisany i NIE jest centralny, ale np. tak:

czy tak?

Czy da się to jakoś wyrazić poprzez jakieś centralne kąty? Okazuje się, że możesz. Posłuchaj, jesteśmy zainteresowani.

a) (jako narożnik zewnętrzny). Ale - wpisany, oparty na łuku - . - wpisany, oparty na łuku - .

Dla urody mówią:

Kąt między akordami to połowa sumy wartości kątowełuki zawarte w tym rogu.

Jest to napisane dla zwięzłości, ale oczywiście używając tego wzoru, musisz pamiętać o kątach środkowych

b) A teraz - „na zewnątrz”! Jak być? Tak, prawie to samo! Tylko teraz (ponownie zastosuj właściwość narożnik zewnętrzny dla). To jest teraz.

I to oznacza, że ​​. Wprowadźmy piękno i zwięzłość do zapisów i sformułowań:

Kąt między siecznymi jest równy połowie różnicy wartości kątowych łuków zawartych w tym kącie.

Cóż, teraz jesteś uzbrojony w całą podstawową wiedzę na temat kątów związanych z kołem. Naprzód, do szturmu zadań!

OKRĄG I KĄT WPISANY. ŚREDNI POZIOM

Co to jest koło, nawet pięcioletnie dziecko wie, prawda? Matematycy, jak zawsze, mają na ten temat zawiłą definicję, ale nie podamy jej (patrz), ale raczej pamiętaj, jak nazywają się punkty, linie i kąty związane z okręgiem.

Ważne warunki

Po pierwsze:

Po drugie:

Jest tu inne akceptowane wyrażenie: „akord ściąga łuk”. Na przykład tutaj, na rysunku, akord kurczy łuk. A jeśli akord nagle przechodzi przez środek, ma specjalną nazwę: „średnica”.

Przy okazji, jak są powiązane średnica i promień? Przypatrz się. Oczywiście,

A teraz - nazwy rogów.

Oczywiście, prawda? Boki narożnika wychodzą ze środka, co oznacza, że ​​narożnik jest centralny.

Tutaj czasami pojawiają się trudności. Zwróć uwagę - ŻADNY kąt wewnątrz koła nie jest wpisany, ale tylko taki, którego wierzchołek „siedzi” na samym okręgu.

Zobaczmy różnicę na zdjęciach:

Mówią też inaczej:

Jest tutaj jeden trudny punkt. Co to jest „odpowiadający” lub „własny” kąt środkowy? Tylko kąt, którego wierzchołek znajduje się w środku okręgu i kończy się na końcach łuku? Nie na pewno w ten sposób. Zobacz zdjęcie.

Jeden z nich jednak nawet nie wygląda jak narożnik – jest większy. Ale w trójkącie nie może być więcej kątów, ale w kole - może dobrze! A więc: mniejszy łuk AB odpowiada mniejszemu kątowi (pomarańczowy), a większy większemu. Tak jak, prawda?

Związek między kątami wpisanymi i centralnymi

Zapamiętaj bardzo ważne stwierdzenie:

W podręcznikach lubią pisać ten sam fakt w ten sposób:

To prawda, że ​​przy kącie centralnym sformułowanie jest prostsze?

Ale mimo to znajdźmy zgodność między tymi dwoma sformułowaniami, a jednocześnie nauczmy się znajdować na rysunkach „odpowiadający” kąt środkowy i łuk, na którym wpisany kąt „opiera się”.

Spójrz, tutaj jest okrąg i wpisany kąt:

Gdzie jest jego „odpowiadający” kąt środkowy?

Spójrzmy jeszcze raz:

Jaka jest zasada?

Ale! W tym przypadku ważne jest, aby kąty wpisany i środkowy „wyglądały” po tej samej stronie łuku. Na przykład:

Co dziwne, niebieski! Ponieważ łuk jest długi, dłuższy niż połowa okręgu! Więc nigdy się nie pomyl!

Jakie konsekwencje można wywnioskować z „połowowości” wpisanego kąta?

A tutaj np.:

Kąt na podstawie średnicy

Czy zauważyłeś już, że matematycy bardzo lubią mówić o tej samej rzeczy różnymi słowami? Dlaczego to dla nich? Widzisz, chociaż język matematyki jest formalny, jest żywy i dlatego, tak jak w języku potocznym, za każdym razem, gdy chcesz to powiedzieć w wygodniejszy sposób. Cóż, już widzieliśmy, czym jest „kąt opiera się na łuku”. I wyobraź sobie, ten sam obrazek nazywa się „kąt opiera się na cięciwie”. Na czym? Tak, oczywiście, na tym, który ciągnie ten łuk!

Kiedy wygodniej jest polegać na cięciwie niż na łuku?

Cóż, w szczególności, gdy ten akord jest średnicą.

W takiej sytuacji istnieje zdumiewająco proste, piękne i przydatne stwierdzenie!

Spójrz: tutaj jest okrąg, średnica i kąt, na którym się opiera.

OKRĄG I KĄT WPISANY. KRÓTKO O GŁÓWNYM

1. Podstawowe pojęcia.

3. Pomiary łuków i kątów.

Kąt w radianach to kąt środkowy, którego długość łuku jest równa promieniowi okręgu.

Jest to liczba wyrażająca stosunek długości półokręgu do promienia.

Obwód promienia jest równy.

4. Stosunek wartości kątów wpisanych i środkowych.

centralny róg jest kątem utworzonym przez dwa promienie kręgi. Przykładem kąta środkowego jest kąt AOB, BOC, COE i tak dalej.

O centralny róg oraz łuk zawarte między jej stronami, mówią, że korespondować wzajemnie.

1. jeśli rogi środkowe łuki są równe.

2. jeśli rogi środkowe nie są równe, to większy z nich odpowiada większemu łuk.

Niech AOB i COD będą równe dwóm rogi środkowe, równe lub nierówne. Obróć sektor AOB wokół środka w kierunku wskazanym przez strzałkę tak, aby promień OA pokrywał się z OC. Następnie, jeśli kąty środkowe są równe, to promień OA pokrywa się z OD, a łuk AB pokrywa się z łukiem CD.

Więc te łuki będą równe.

Jeśli rogi środkowe nie są równe, to promień OB nie będzie przebiegał wzdłuż OD, ale wzdłuż jakiegoś innego kierunku, na przykład wzdłuż OE lub OF. W obu przypadkach większy kąt oczywiście odpowiada większemu łukowi.

Twierdzenie, które udowodniliśmy dla jednego koła, pozostaje prawdziwe dla równe koła, ponieważ takie kręgi nie różnią się od siebie, z wyjątkiem ich położenia.

Oferty odwrotne też będzie prawdziwe . W jednym kręgu lub równe koła:

1. jeśli łuki są równe, to odpowiadające rogi środkowe są równe.

2. jeśli łuki nie są równe, to większy z nich odpowiada większemu centralny róg.

W tym samym okręgu lub w równych okręgach kąty środkowe są powiązane jako odpowiadające im łuki. Albo parafrazując, otrzymujemy kąt środkowy proporcjonalny odpowiadający mu łuk.