Rozwiązywanie równań różniczkowych za pomocą przekształcenia Laplace'a. Operacyjna metoda rozwiązywania liniowych równań różniczkowych i ich układów. §jeden. Oryginały i obrazy funkcji według Laplace'a

07.10.2020

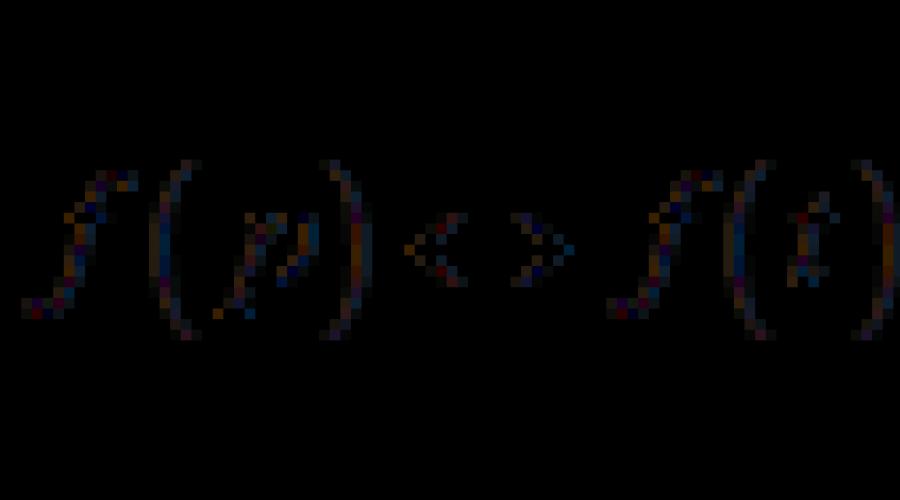
Przeczytaj także

Niezwykłe prezenty noworoczne, które możesz zrobić własnymi rękami

Przegląd recenzji na temat psychicznego rytuału Arina Evdokimova dla spełnienia pragnienia

Tatiana: dzień anioła, imieniny

Marilyn Kerro - biografia i życie osobiste estońskiej wiedźmy

Co to znaczy widzieć karaluchy we śnie - interpretacja dla kobiet

Rozmiar: piks

Rozpocznij wyświetlanie od strony:

transkrypcja

1 Rozwiązywanie równań różniczkowych za pomocą transformaty Laplace'a (metoda operacyjna) Rachunek operacyjny jest jedną z najbardziej ekonomicznych metod całkowania równań różniczkowych liniowych o stałych współczynnikach i jest bardzo popularny wśród inżynierów. Metodę zaproponował słynny amerykański inżynier elektryk i fizyk O. Heaviside (892). Zaproponował formalne zasady postępowania z operatorem d dx i niektórymi funkcjami tego operatora, za pomocą których rozwiązał szereg najważniejszych problemów elektrodynamiki. Rachunek operacyjny nie uzyskał jednak matematycznego uzasadnienia w pracach O. Heaviside'a („jego matematyka powstała w kontekście fizycznym, z którego nie było łatwo wyodrębnić” [, s. 8]), wiele jego wyników pozostało niesprawdzone. Dopiero w II latach XX wieku metoda ta znalazła uzasadnienie w pracach Bromwicha (T.J.I A. Bromwich) i Carsona (J.R. Carson) 2 .. Koncepcja oryginału i obrazu według definicji Laplace'a. Oryginalna funkcja to dowolna funkcja o wartości zespolonej f(x) rzeczywistego argumentu x, która spełnia następujące warunki: f(x) jest ciągła w x, być może z wyjątkiem skończonej liczby punktów nieciągłości -tego rodzaju; 2) dla wszystkich x< f(x) = ; 3) существуют такие постоянные M >oraz a > dla których f(x) M e ax dla x. () Równania różniczkowe i całkowe: podręcznik dla studentów Wydziału Fizyki i Techniki: za 3 godz. : N. Yu Svetova, E. E. Siemionowa. Pietrozawodsk: Wydawnictwo PetrSU, Próby rygorystycznego uzasadnienia i „matematycznie akceptowalnej” prezentacji rachunku różniczkowego przypominały „ogólny atak” Angielski matematyk Bromwich (96), amerykański inżynier Carson (925), holenderski inżynier elektryk Van der Pol () przyciągnął wyniki różnych teorii, wiązał rachunek Heaviside'a z transformatą Laplace'a, z teorią funkcji zmiennej zespolonej.

2 2 Dolna granica a wszystkich liczb a, dla których nierówność () jest prawdziwa nazywana jest tempem wzrostu funkcji f(x). Zauważ, że dla dowolnej funkcji ograniczonej, tempo wzrostu a =. Najprostszym oryginałem jest funkcja Heaviside'a (, x ; χ(x) =, x<. Очевидно, для любой функции ϕ(x) { ϕ(x), x, ϕ(x) χ(x) =, x <. Если при x функция ϕ(x) удовлетворяет условиям и 3 определения, то функция ϕ(x)χ(x) является оригиналом. В дальнейшем для сокращения записи будем, как правило, записывать ϕ(x) вместо ϕ(x)χ(x), считая, что рассматриваемые нами функции продолжены нулем для отрицательных значений аргумента x. Определение 2. Функция F (p) комплексного переменного p (p C), определяемая интегралом F (p) = e px f(x) dx, () называется преобразованием Лапласа, или изображением по Лапласу 3, функции f(x). Для указания соответствия между оригиналом и изображением будем использовать следующую запись 4: f(x) F (p). 3 В мемуарах П. Лапласа (782 82) современные оригинал и изображение именуются fonction determinant и fonction generatrice «определяющая функция» и «производящая». Эти названия, хотя и признанные неудачными, сохранились до XX в. Хевисайд употреблял названия «подоператорная функция» (892). Оператор он обозначал буквой p, которая употребляется в современном исчислении . 4 Названия original и image и знак предложил Ван дер Поль в статьях гг. В русской литературе термин изображение и символ, по-видимому, впервые появились в книге харьковских математиков А. М. Эфроса и А. М. Данилевского «Операционное исчисление и контурные интегралы» (937), а термин оригинал только в 953 г. . Используются и другие варианты записи соответствия между оригиналами и изображениями. Например, f(x) F (p) или L{f(x)} = F (p).

3 Dla dowolnego oryginalnego f(x), jego obraz F(p) jest zdefiniowany w półpłaszczyźnie Re p > a (a jest tempem wzrostu funkcji f(x)), gdzie niewłaściwa całka () jest zbieżna. Przykład. Korzystając z definicji, znajdź obraz funkcji f(x) = sin 3x. Decyzja. Dla funkcji f(x) = sin 3x mamy a =. Zatem obraz F(p) zostanie zdefiniowany w półpłaszczyźnie Re p >. Zastosujmy wzór () do danej funkcji, korzystając z zasady całkowania przez części i ograniczenia zbioru wartości zmiennej p, co zapewnia zbieżność całki: F(p) = + e px sin 3x dx = = p e px sin 3x x= = 3 p p e px cos 3x = 3 p 2 9 p 2 ). F (p) = 3 p 2 9 p 2 F (p). F (p) = 3 p Tak więc obowiązuje następująca korespondencja: sin 3x 3 p 2, Re p >. + 9 e px sin 3x dx = 3

4 4 2. Własności transformaty Laplace'a W praktyce przy konstruowaniu obrazów stosuje się różne techniki oparte na własnościach transformaty Laplace'a. Wymieniamy główne właściwości, których ważność można łatwo ustalić za pomocą definicji obrazu i oryginału.Właściwość liniowości. Jeśli f(x) F(p), g(x) G(p), to dla dowolnego α, β C αf(x) + βg(x) αf (p) + βg(p), Re p > max( a, b). Tutaj i poniżej, a i b są szybkościami wzrostu odpowiednio funkcji f(x) i g(x). 2. Twierdzenie o podobieństwie. Jeśli f(x) F (p), to dla dowolnego α > f(αx) α F (p α), Re p > αa. 3. Twierdzenie o przemieszczeniu. Jeśli f(x) F (p), to dla dowolnego λ C e λx f(x) F (p λ), Re p > a + Re λ. 4. Zróżnicowanie oryginału. Niech funkcja f(x) będzie n razy różniczkowalna. Wtedy f (x) pf (p) f(+), f (x) p 2 F (p) pf(+) f (+), f (n) (x) p n F (p) p n f(+). .. pf (n 2) (+) f (n) (+), gdzie f (k) (+) = lim x + f (k) (x), k =, n. Komentarz. Podczas konstruowania obrazów pochodnych funkcji ciągłych na zero znak plusa jest pomijany w zapisie argumentu funkcji i jej pochodnych. 5. Zróżnicowanie obrazu. Jeśli f(x) F (p), to W szczególności dla n = mamy F(n) (p) (x) n f(x), Re p >. F(p)xf(x).

5 5 6. Integracja oryginału. Jeśli f(x) F (p), to x f(ξ) dξ F (p) p, Re p > α. 7. Integracja obrazu. Jeżeli całka i F(p) f(x), to p F(p) dp f(x) x, Re p > α. p F (p) dp jest zbieżny 8. Twierdzenie o mnożeniu obrazu (twierdzenie o splocie) Jeśli f(x) F (p), g(x) G(p), to F (p)g(p) x f(t) g( x t) dt = x f(x t)g(t) dt gdy Re p > max(a, b). Całki po prawej stronie korespondencji nazywane są splotem funkcji f(x) i g(x). 9. Twierdzenie o opóźnieniu. Jeśli f(x) F (p), to dla każdego ξ > f(x ξ)χ(x ξ) e ξp F (p), Re p > α. Oryginał jest odtwarzany z obrazu w unikalny sposób, aż do wartości w punktach przerwania. W praktyce zwykle wykorzystuje się gotowe tabele oryginałów i obrazów 5. W tabeli wymieniono główne oryginały i obrazy, które często znajdują się w aplikacjach. Przykład 2. Korzystając z właściwości transformaty Laplace'a oraz tablicy podstawowych oryginałów i obrazów, znajdź obrazy następujących funkcji:) f(x) = e 4x sin 3x cos 2x; 3) f(x) = x 2 e 3x; 2) f (x) \u003d e (x 2) grzech (x 2); 4) f(x) = sin2 x x. 5 Ditkin V. A., Prudnikov A. P. Podręcznik rachunku operacyjnego. M., 965.

6 6 Tabela. Główne oryginały i obrazy Obraz oryginalny Obraz oryginalny p cos ωx p p 2 + ω 2 x n n! p n+ e λx p + λ sin ωx x cos ωx x n e λx n! (p + λ) n+ x sin ωx ω p 2 + ω 2 p 2 ω 2 (p 2 + ω 2) 2 2pω (p 2 + ω 2) 2 Rozwiązanie.) Przekształcamy wyrażenie na funkcję f (x) w następujący sposób: f(x) = e 4x grzech 3x cos 2x = 2 e 4x (sin 5x + sin x) = = 2 e 4x grzech 5x + 2 e 4x grzech x. Ponieważ sin x 5 p 2 i sin 5x + p , to korzystając z własności liniowości i twierdzenia o przemieszczeniu, dla obrazu funkcji f (x) będziemy mieli: F (p) = () 5 2 (p + 4 ) (p + 4 )) Ponieważ sin x p 2 +, ex sin x (p) 2 +, to korzystając z twierdzenia o opóźnieniu, będziemy mieli f (x) = e x 2 sin (x 2) F (p) = e 2p (p)) Czyli jako x 2 2 p 3, to z twierdzenia o przemieszczeniu mamy: f(x) = x 2 e 3x F (p) = 2 (p 3) 3.

7 Dla porównania przedstawiamy metodę konstruowania obrazu funkcji f(x) = x 2 e 3x z wykorzystaniem własności różnicowania obrazu: Otrzymaliśmy ten sam wynik. 4) Ponieważ e 3x p 3 ; xe 3x d () = dp p 3 (p 3) 2 ; x 2 e 3x d () 2 dp (p 3) 2 = (p 3) 3. sin 2 x = 2 2 cos 2x 2p 2 p p 2 + 4, to korzystając z całkowania obrazu, otrzymamy: sin 2 x ( x 2p) 2 p p 2 dp = + 4 p (= 4 ln p2) 4 ln(p2 + 4) = p 4 ln p 2 p p = 4 ln p2 + 4 p właściwy ułamek wymierny (jest funkcją wymierną). Jeśli ułamek zostanie rozłożony na sumę najprostszych (elementarnych) ułamków, wówczas dla każdego z nich odpowiedni oryginał można znaleźć za pomocą właściwości transformacji Laplace'a oraz tabeli oryginałów i ich obrazów. Rzeczywiście, A p a A eax ; A (p a) n A (n)! xn a tok.

8 8 Po wykonaniu przekształceń ułamkowych Ap + B A(p a) + aa + B A(p a) (p a) 2 = + b2 (p a) 2 + b 2 = (p a) 2 + b 2 + aa + B (p a) 2 + b 2, otrzymujemy Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sin bx. b Aby skonstruować oryginał odpowiadający ułamkowi Ap + B ((p a) 2 + b 2) n, możesz użyć twierdzenia o mnożeniu. Na przykład dla n = 2 mamy Ap + B ((p a) 2 + b 2) 2 = Ap + B (p a) 2 + b 2 (p a) 2 + b 2. Od tego momentu Dla n = 3: Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sin bx = h (x) b (p a) 2 + b 2 b eax sin bx = g(x), Ap + B ((p a) 2 + b 2) 2 = x Ap + B ((p a) 2 + b 2) 2 (p a) 2 + b 2 g(x t) h (t) dt = h 2 (t). x g(x t) h 2 (t) dt Jeśli ma k różnych zer p i, i =, k, to rozszerzając

9 mianownik przez czynniki (p p i), odpowiedni oryginał dla Y (p) można znaleźć za pomocą wzoru: y(x) = k (Y (p)(p p i)e px) p=pi. (2) i= iloczyn Y(p)(p p i) daje funkcję wymierną, której mianownik nie zawiera czynnika (p p i), a obliczony przy p = p i określa współczynnik, z jakim ułamek wchodzi w rozwinięcie funkcji p p i Y (p) na sumę ułamków elementarnych. Przykład 3. Znajdź oryginał pasujący do obrazu: Y (p) = p 3 p. Decyzja. Rozszerzając dany obrazek do sumy ułamków elementarnych: p 3 p = p(p)(p +) = p + 2(p) + 2(p +), znajdujemy oryginalną Odpowiedź: y(x) = + ch x. y(x) = + 2 ex + 2 e x = + ch x. Przykład 4. Znajdź oryginał obrazu: Y (p) = p(p 2 +). Decyzja. Skoro p 2 sin x, to stosując całkowanie oryginału, + otrzymujemy: p(p 2 +) x Odpowiedź: y(x) = cos x. sin t dt = cos t x = cos x. Przykład 5. Znajdź oryginał pasujący do obrazu: Y (p) = (p 2 + 4) 2. 9

10 Decyzja. Używając własności obrazu splotu, mamy: Y (p) = (p 2 + 4) 2 = p p x sin 2(x t) sin 2t dt. Po obliczeniu całki otrzymujemy pożądane wyrażenie dla oryginału. Odpowiedź: y(x) = 6 sin 2x x cos 2x. 8 Przykład 6. Znajdź oryginał pasujący do obrazu: Y (p) = p p 3 p 2 6p. Decyzja. Ponieważ p 3 p 2 6p \u003d p (p 3) (p + 2), to mianownik ułamka Y (p) ma trzy proste pierwiastki: p \u003d, p 2 \u003d 3 i p 3 \u003d 2. Odpowiedni oryginał konstruujemy za pomocą wzoru (2): y(x) = (p2 + 2)e px (p 3)(p + 2) + (p2 + 2)e px p= p(p + 2) + (p2 + 2)e px p =3 p(p 3) = p= 2 = e3x e 2x. Przykład 7. Znajdź oryginał pasujący do obrazu: Y (p) = e p 2 p(p +)(p 2 + 4). Decyzja. Przedstawmy ułamek zawarty w wyrażeniu w postaci ułamków prostych: p(p +)(p 2 + 4) = A p + B p + + Cp + D p Stosując metodę nieokreślonych współczynników do rozwinięcia, otrzymujemy : ; B=D=5; C \u003d 2. Y (p) \u003d e p 2 4 p 5 e p 2 p + pe p 2 2 p e p 2 5 p (a)

11 Wykorzystując zależności: p χ(x), p + e x χ(x), p p cos 2x χ(x), p sin 2x χ(x) 2 i uwzględniając twierdzenie o opóźnieniu otrzymujemy żądany oryginał dla obraz (a). Odpowiedź: y(x) = (4 5 e (x 2) cos (2x) sin (2x) 2) χ (x) Rozwiązanie problemu Cauchy'ego dla równania różniczkowego o stałych współczynnikach Metoda rozwiązywania różnych klas równań za pomocą transformata Laplace'a nazywana jest metodą operacyjną. Właściwość różniczkowania transformaty Laplace'a oryginału pozwala zredukować rozwiązanie liniowych równań różniczkowych o stałych współczynnikach do rozwiązania równań algebraicznych. Rozważ problem Cauchy'ego dla niejednorodnego równania z warunkami początkowymi y (n) + a y (n) a n y + a n y = f(x) (3) y() = y, y() = y,..., y (n ) ( ) = rz. (4) Niech funkcja f(x) i pożądane rozwiązanie spełniają warunki istnienia transformaty Laplace'a. Oznaczmy przez Y (p) obraz nieznanej funkcji (pierwotnej) y(x), a przez F (p) obraz prawej strony f(x): y(x) Y (p), f(x ) F (p). Zgodnie z regułą różniczkowania oryginału mamy y (x) py (p) y, y (x) p 2 Y (p) py y, y (n) (x) p n Y (p) p n y p n 2 y.. t n.

12 2 Następnie, ze względu na właściwość liniowości transformaty Laplace'a, po zastosowaniu jej do lewej i prawej części równania (3) otrzymujemy równanie operatorowe M(p)Y (p) N(p) = F (p ), (5) gdzie M(p) wielomian charakterystyczny równania (3): M(p) = p n + a p n a n p + a n y, wielomian N(p) zawierający dane początkowe problemu Cauchy'ego (znika, gdy dane początkowe wynoszą zero ): N(p) = y (p n + a p n a n) + + y (p n 2 + a p n a n 2) y n 2 (p + a) + y n, F (p) obraz funkcji f(x). Rozwiązując równanie operatora (5), otrzymujemy obraz Laplace'a Y(p) pożądanego rozwiązania y(x) w postaci Y(p) = F(p) + N(p). M(p) Przywracając oryginał dla Y(p), znajdujemy rozwiązanie równania (3), które spełnia warunki początkowe (4). Przykład 8. Znajdź rozwiązanie równania różniczkowego: y(x) + y(x) = e x spełniające warunek: y() =. Decyzja. Niech y(x) Y (p). Ponieważ y (x) py (p) y() = py (p), e x p +, to stosując transformatę Laplace'a do danego równania, korzystając z własności liniowości, otrzymujemy równanie algebraiczne względem Y (p): py (p) + Y (p) = p +. Gdzie znajdujemy wyrażenie na Y (p):

13 Od tego czasu mamy Y (p) = p + e x, (p +) 2 + p +. (p +) 2 xe x, Y (p) y(x) = e x x + e x. Weryfikacja: Pokażmy, że znaleziona funkcja jest rzeczywiście rozwiązaniem problemu Cauchy'ego. Podstawimy wyrażenie na funkcję y(x) i jej pochodną do podanego równania: y(x) = e x x + e x e x = e x x e x x + e x x + e x = e x. Po skróceniu podobnych wyrazów po lewej stronie równania otrzymujemy poprawną tożsamość: e x e x. Tak więc skonstruowana funkcja jest rozwiązaniem równania. Sprawdźmy, czy spełnia warunek początkowy y() = : y() = e + e =. Dlatego znaleziona funkcja jest rozwiązaniem problemu Cauchy'ego. Odpowiedź: y(x) = e x x + e x. Przykład 9. Rozwiąż problem Cauchy'ego y + y =, y() =, y() =. Decyzja. Niech y(x) Y (p). Skoro 3 y (x) p 2 Y (p) py() y (), /p, to stosując do równania transformatę Laplace'a, biorąc pod uwagę warunki początkowe, otrzymujemy (p 2 +)Y (p) = p = Y ( p) = p(p 2 +). Rozłóżmy ułamek na proste ułamki: Y (p) = p Zgodnie z tabelą znajdujemy y(x) = cos x. s p 2 +.

14 4 Oryginał można również przywrócić z obrazu, stosując oryginalną właściwość integracji (patrz przykład 4). Odpowiedź: y(x) = cosx. Przykład. Rozwiąż problem Cauchy'ego y +3y = e 3x, y() =, y() =. Decyzja. Niech y(x) Y (p). Ponieważ y py (p) y(), y (x) p 2 Y (p) py() y () oraz e 3x p + 3, to biorąc pod uwagę warunki początkowe, otrzymujemy równanie operatora (p 2 + 3p) Y (p) + = p + 2 = Y (p) = p + 3 (p + 3) 2 p. Rozwińmy funkcję wymierną na proste ułamki: p + 2 (p + 3) 2 p = A p + B p C (p + 3) 2 = A(p2 + 6p + 9) + B(p 2 + 3p) + Cp p (p + 3) 2. Ułóż układ równań do znalezienia współczynników A, B i C: A + B =, 6A + 3B + C =, 9A = 2, rozwiązując, który znajdziemy A = 2/9 , B = 2/9, C = /3. Zatem Y (p) = 2 9 p p (p + 3) 2. Korzystając z tabeli otrzymujemy odpowiedź. Odpowiedź: y(x) = e 3x 3 xe 3x. Przykład. Znajdź rozwiązanie równania różniczkowego: y (x) + 2y (x) + 5y (x) = spełniające warunki: y() =, y() = 2, y() =. Decyzja. Niech y(x) Y (p). Ponieważ przy danych warunkach mamy y (x) p Y (p) y() = py (p) () = py (p) +, y (x) p 2 Y (p) p y() y ( ) = = p 2 Y (p) p () 2 = p 2 Y (p) + p 2, y (x) p 3 Y (p) p 2 y() p y () y () = = p 3 Y ( p) p 2 () p 2 = p 3 Y (p) + p 2 2p,

15 następnie po zastosowaniu transformaty Laplace'a do danego równania otrzymujemy następujące równanie operatora: p 3 Y (p) + p 2 2p + 2p 2 Y (p) + 2p 4 + 5pY (p) + 5 = lub po przekształceniach : Y (p) (p 3 + 2p 2 + 5p) = p 2. Rozwiązując to równanie dla Y (p), otrzymujemy Y (p) = p 2 p(p 2 + 2p + 5). Rozszerzamy wynikowe wyrażenie na proste ułamki: p 2 p (p 2 + 2p + 5) = A p + Bp + C p 2 + 2p + 5. Stosując metodę nieokreślonych współczynników znajdujemy A, B, C. To zrób to, sprowadzamy ułamki do wspólnego mianownika i zrównujemy współczynniki o równych potęgach p: p 2 p(p 2 + 2p + 5) = Ap2 + 2Ap + 5A + Bp 2 + Cp p(p p + 5) Otrzymujemy układ równań algebraicznych dla A, B, C: przez rozwiązanie, które będzie: A + B =, 2A + C =, 5A =, A = 5, B = 4 5, C = 2 5. Wtedy Y(p) = 5p + 5 4p + 2p 2 + 2p + 5. Aby znaleźć oryginał drugiego ułamka, wybierz pełny kwadrat w jego mianowniku: p 2 + 2p + 5 = (p +) 2 + 4, a następnie wybierz wyraz p+ w liczniku: 4p+2 = 4(p+)+6 i rozwiń ułamek do sumy dwóch ułamków: 5 4p + 2 p 2 + 2p + 5 = 4 5 p + (p +) (p +) Odpowiedź: y(x) = e x cos 2x e x sin 2x.

16 6 Ogólne rozwiązanie równania (3) można również skonstruować metodą operacyjną. Aby to zrobić, określone wartości y, y,..., y (n) warunków początkowych należy zastąpić dowolnymi stałymi C, C 2,..., C n. Bibliografia. Alexandrova N. V. Historia terminów matematycznych, pojęć, oznaczeń: Słownik-podręcznik. M.: Wydawnictwo ŁKI, s. 2. Vasilyeva A. B., Miedwiediew G. N., Tichonow N. A., Urazgildina T. A. Równania różniczkowe i całkowe, rachunek wariacji w przykładach i problemach. M.: FIZ-MATLIT, s. 3. Sidorov Yu V. Wykłady z teorii funkcji zmiennej zespolonej / Yu. V. Sidorov, M. V. Fedoryuk, M. I. Shabunin. M.: Nauka, 989.

RACHUNEK OPERACYJNY Rachunek operacyjny jest rachunkiem symbolicznym opartym na konstrukcji analizy matematycznej jako systemu operacji formalnych na

Lekcja 18 Oryginały i ich obrazy Rachunek operacyjny jest jedną z metod analizy matematycznej, którą zastosujemy do rozwiązywania równań i układów różniczkowych. Istota tej metody

Równania fizyki matematycznej Zbiór przykładów i ćwiczeń Pietrozawodsk 1 Państwowy Uniwersytet w Pietrozawodsku Wydział Matematyki Równania fizyki matematycznej Zbiór przykładów i ćwiczeń

Tytuł Wprowadzenie. Podstawowe pojęcia... 4 1. Równania całkowe Volterry... 5 Zadania domowe.... 8 2. Rozwiązywanie równania całkowego Volterry. 10 opcji pracy domowej .... 11

1 Temat 4. Metoda operatorowa rozwiązywania równań i układów różniczkowych liniowych 4.1 Transformata Laplace'a Oryginałem jest dowolna funkcja f(t) zmiennej rzeczywistej t, która spełnia następujące

ELEMENTY OBLICZENIA OPERACYJNEGO WYDAWNICTWO TGTU MINISTERSTWO EDUKACJI I NAUKI FEDERACJI ROSYJSKIEJ GOU VPO "Tambow State Technical University" ELEMENTY OBLICZENIA OPERACYJNEGO

Analiza matematyczna Sekcja: Rachunek operacyjny Temat: Transformata Laplace'a i jej własności Prowadzący Pakhovova E.G. 2011 11. Oryginał i wizerunek. Twierdzenie o inwersji DEFINICJA 1. Niech: R C. Funkcja

Liczby zespolone, funkcje i operacje na nich y moduł R część rzeczywista liczba rzeczywista, yim część urojona liczba rzeczywista iy zapis algebraiczny liczby zespolonej Główna wartość argumentu

Rozwiązanie standardowych opcji pracy sterowania na temat Całki funkcji jednej zmiennej Wytyczne UDC 517.91 Wytyczne zawierają szczegółowe rozwiązania standardowych opcji pracy sterowania

Rozdział 1 Rachunek Operacyjny. 1. Definicja przekształcenia Laplace'a. Przekształcenie Laplace'a wiąże funkcję f(t) ze zmienną rzeczywistą t z funkcją F() zmiennej zespolonej = x + iy

MINISTERSTWO TRANSPORTU FEDERACJI ROSYJSKIEJ BUDŻET PAŃSTWA SZKOLNICTWA WYŻSZEGO INSTYTUCJA SZKOLNICTWA WYŻSZEGO „ROSYJSKA UNIWERSYTET TRANSPORTOWY (MIIT)”

FEDERALNA PAŃSTWOWA BUDŻETOWA INSTYTUCJA SZKOLNICTWA WYŻSZEGO „MOSKWA PAŃSTWOWA UNIWERSYTET KOMUNIKACJI IM. IM. MIKOŁAJA II” Wydział „Matematyki Wyższej i Obliczeniowej”

82 4. Sekcja 4. Szeregi funkcjonalne i mocy 4.2. Lekcja 3 4.2. Lekcja 3 4.2.. Rozwinięcie funkcji Taylora DEFINICJA 4.2.. Niech funkcja y = f(x) będzie nieskończenie różniczkowalna w pewnym otoczeniu

Wykład CAŁKOWANIE Ułamków wymiernych Ułamki wymierne Całkowanie prostych ułamków wymiernych Rozkład ułamka wymiernego na ułamki proste Całkowanie ułamków wymiernych Wymierne

TEMAT 5 Liniowe równanie Volterry-tego rodzaju Podstawowe definicje i twierdzenia Równanie y = λ K(,) y() d+ f(), [, lub w postaci operatorowej y = λ By+ f, nazywa się równaniem Volterry miły niech

Wykład 6 Rachunek operacyjny Transformacja Laplace'a Obrazy prostych funkcji Podstawowe własności transformacji Laplace'a Obraz pochodnej oryginału Rachunek operacyjny Transformacja Laplace'a

Lekcja 19 Rozwiązywanie równań i układów różniczkowych metodą operacyjną 19.1 Rozwiązywanie równań różniczkowych liniowych o stałych współczynnikach Niech będzie wymagane znalezienie konkretnego rozwiązania

2.2. Operatorska metoda obliczania procesów przejściowych. Informacje teoretyczne. Obliczanie procesów przejściowych w złożonych obwodach metodą klasyczną jest bardzo często trudne do znalezienia stałych całkowania.

DOROKHOV VM PRZEWODNIK ROZWIĄZYWANIA PROBLEMÓW Z RACHUNKU OPERACYJNEGO MOSKWA, 4 PRZEDMOWA Podręcznik ten przedstawia teoretyczne podstawy rachunku operacyjnego Metody rozwiązywania problemów

Ministerstwo Edukacji i Nauki Federacji Rosyjskiej Federalna Państwowa Budżetowa Instytucja Edukacyjna Wyższego Szkolnictwa Zawodowego „Rosyjski Uniwersytet Technologii Chemicznej im. DI Mendelejewa” Instytut Nowomoskowski (oddział) Test 8 z matematyki (operacyjny

UDC 53.7 DOTYCZĄCA JEDNEJ METODY WYSZUKIWANIA POSZCZEGÓLNEGO ROZWIĄZANIA LINIOWYCH RÓWNAŃ RÓŻNICZKOWYCH O STAŁYCH WSPÓŁCZYNNIKACH Zhanybekova A.A., [e-mail chroniony] Kazasko-Brytyjski Uniwersytet Techniczny,

INTEGRAL CALCULUS NIEPEWNY INTEGRAL Funkcja pierwotna i całka nieoznaczona funkcji pierwotnej Lemat Funkcja F(jest nazywana funkcją pierwotną dla funkcji f(na przedziale X, jeśli F (= f(Funkcja X,

Równania pierwszego rzędu nierozwiązane ze względu na pochodną Rozważymy równania pierwszego rzędu, które nie są rozwiązane ze względu na pochodną: F (x, y, y) = 0, (1)

II RÓWNANIA RÓŻNICZKOWE Równania różniczkowe pierwszego rzędu Definicja Zależności, w których nieznane zmienne i ich funkcje znajdują się pod znakiem pochodnej lub różniczkowej, nazywamy

ELEMENTY TEORII FUNKCJI ZŁOŻONEGO RACHUNKU OPERACYJNEGO ZMIENNEJ

Ministerstwo Edukacji i Nauki Federacji Rosyjskiej „MATI” Rosyjski Państwowy Uniwersytet Technologiczny. K.E. Ciołkowski Wydział Matematyki Wyższej Liczby zespolone i rachunek operacyjny

1 Temat 3. Liniowe równania różniczkowe o stałych współczynnikach 3.1 Liniowe równanie jednorodne Równanie różniczkowe postaci y (n) + a n 1 y (n 1) +... + a 1 y + a 0 y = 0, (3.1) gdzie a

NIEOKREŚLONE CAŁKOWITE. Całka pierwotna i nieoznaczona Głównym zadaniem rachunku różniczkowego jest znalezienie pochodnej (lub różniczki) danej funkcji. Rachunek całkowy

Ministerstwo Edukacji i Nauki Federacji Rosyjskiej Achinsk Oddział Federalnej Państwowej Autonomicznej Instytucji Edukacyjnej Wyższego Szkolnictwa Zawodowego „Syberyjski Uniwersytet Federalny” MATEMATYKA

Granica funkcji. Trafność studiowania tematu Teoria granic odgrywa fundamentalną rolę w analizie matematycznej, pozwala określić charakter zachowania funkcji dla danej zmiany argumentacji. Przez

Całka pierwotna i nieoznaczona Podstawowe pojęcia i wzory 1. Definicja całki pierwotnej i nieoznaczonej. Definicja. Funkcja F(x) nazywana jest funkcją pierwotną dla funkcji f(x) na przedziale

Rozdział 1 Równania różniczkowe 1.1 Pojęcie równania różniczkowego 1.1.1 Problemy prowadzące do równań różniczkowych. W fizyce klasycznej każda wielkość fizyczna jest przypisana

ZWYKŁE RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU Podstawowe pojęcia Równania różniczkowe ze zmiennymi separowalnymi Wiele problemów w nauce i technice sprowadza się do równań różniczkowych Rozważmy

Rozwój metodyczny Rozwiązywanie problemów na TFKP Liczby zespolone Działania na liczbach zespolonych Płaszczyzna zespolona Liczbę zespoloną można przedstawić w postaci wykładniczej algebraicznej i trygonometrycznej

Wykład 3 Szeregi Taylora i Maclaurina Zastosowanie szeregów potęgowych Rozwijanie funkcji w szeregi potęgowe Szeregi Taylora i Maclaurina Dla zastosowań ważna jest umiejętność rozwinięcia danej funkcji w szereg potęgowy, te funkcje

Typowy wariant "Liczby zespolone Wielomiany i ułamki wymierne" Zadanie Mając dwie liczby zespolone i cos sn Znajdź i zapisz wynik w postaci algebraicznej zapisz wynik w postaci trygonometrycznej

Federalna Agencja ds. Edukacji Federalna Państwowa Instytucja Edukacyjna Wyższego Szkolnictwa Zawodowego POŁUDNIOWY UNIWERSYTET FEDERALNY R. M. Gavrilova, G. S. Kostetskaya Metodyczny

SP PREOBRAZHENSKY, SR TIKHOMIROV INTEGRACJA RÓWNAŃ RÓŻNICZKOWYCH Z WYKORZYSTANIEM MOCY SERII 987 SPIS TREŚCI

Analiza matematyczna Sekcja: Całka nieoznaczona Temat: Całkowanie ułamków wymiernych Prowadzący Pakhovova E.G. 0 5. Całkowanie ułamków wymiernych DEFINICJA. Ułamek wymierny nazywa się

Ministerstwo Transportu Federacji Rosyjskiej BUDŻETOWA INSTYTUCJA SZKOLNICTWA WYŻSZEGO „ROSYJSKA UNIWERSYTET TRANSPORTOWY (MIIT)” Instytut Ekonomiczno-Finansowy

RACHUNEK OPERACYJNY Transformata Laplace'a i wzór inwersji Niech w przedziale Dirichleta, a mianowicie: Całka Fouriera (l l) a) jest ograniczona na tym przedziale; funkcja spełnia warunki b) jest odcinkowo ciągła

Ministerstwo Edukacji Federacji Rosyjskiej Rosyjski Państwowy Uniwersytet Nafty i Gazu im. Gubkina VI Iwanow Wytyczne dotyczące badania tematu „RÓWNANIA RÓŻNICZKOWE” (dla studentów

57 Rozważmy całkowanie najprostszego ułamka wymiernego czwartego typu (M N) d () p q p Dokonajmy zmiany zmiennej przez ustawienie d. gdzie p q. Wtedy całka M N d p p p q q a, M p N Mp q d M (p q) p

Równanie różniczkowe n-tego rzędu nazywamy liniowym, jeśli jest pierwszego stopnia względem funkcji y i jej pochodnych y...,y(n), czyli ma postać a 0 y (n) + a 1 y (n 1) +... + a ny = f(x), gdzie

Analiza matematyczna Sekcja: Całka nieoznaczona Temat: Całkowanie ułamków wymiernych Wykładowca Rozhkova S.V. 0 5. Całkowanie ułamków wymiernych DEFINICJA. Ułamek wymierny nazywa się

Ministerstwo Telekomunikacji i Komunikacji Masowej Federacji Rosyjskiej Państwowa Instytucja Edukacyjna Wyższego Szkolnictwa Zawodowego WOŁGA PAŃSTWOWY UNIWERSYTET TELEKOMUNIKACYJNY

Równania różniczkowe pierwszego rzędu rozwiązane względem pochodnej Twierdzenie o istnieniu i jednoznaczności rozwiązania W ogólnym przypadku równanie różniczkowe pierwszego rzędu ma postać F ()

T A Matveeva V B vetlichnaya D K Agisheva A Zotova

INTEGRAL CALCULUS UNDEFINITE INTEGRAL Funkcja pierwotna i całka nieoznaczona funkcji pierwotnej Funkcja F() jest nazywana funkcją pierwotną dla funkcji f() na przedziale X, jeśli F / () = f() X.

5. 4 Podstawowe metody integracji Integracja bezpośrednia. Obliczanie całek na podstawie doprowadzenia całki do postaci tabelarycznej i wykorzystania własności nieoznaczonego

Wykład 3 Opis matematyczny układów sterowania W teorii sterowania w analizie i syntezie układów sterowania zajmują się ich modelem matematycznym.Model matematyczny SKP jest równaniem

Całkowanie układu równań różniczkowych przez eliminację zmiennych Jedną z głównych metod całkowania układu równań różniczkowych jest: z równań normalnych

Równania różniczkowe cząstkowe pierwszego rzędu Niektóre zagadnienia mechaniki klasycznej, mechaniki ośrodków ciągłych, akustyki, optyki, hydrodynamiki, przenoszenia promieniowania sprowadzają się do równań różniczkowych cząstkowych

Najprostsze całki nieoznaczone Przykłady rozwiązywania problemów Poniższe całki sprowadza się do tabelarycznych przez identyczne przekształcenie całki. 1. dx = dx = 2x 2/3 /3 + 2x 1/2 + C. >2.

ĆWICZENIE PRAKTYCZNE Całkowanie ułamków wymiernych Ułamek wymierny to ułamek postaci P Q, gdzie P i Q są wielomianami Ułamek wymierny nazywamy właściwym, jeśli stopień wielomianu P jest mniejszy niż stopień

[F] Filippov AV Zbiór problemów dotyczących równań różniczkowych Moskwa-Iżewsk: Centrum Badawcze „Regular and Chaotic Dynamics” 00 URL: http://librarbsaz/kitablar/846pf [M] Matveev NM Zbiór problemów i ćwiczeń dotyczących

Zawód E. rzędy Taylora. Podsumowanie serii mocy Mat. analiza, aplikacja. Matematyka, 3 semestr Znajdź rozwinięcie funkcji w szereg potęgowy, oblicz promień zbieżności szeregu potęgowego: A f()

Zadanie 1.1. Znajdź rozwiązania y = y(x) równania różniczkowego, które są nieidentycznie zerowe we wskazanym obszarze i spełniają podane warunki brzegowe (problem Sturma-Liouville'a) Rozwiązanie: Rozważ

9. Całka pierwotna i nieoznaczona 9.. Niech funkcja f() będzie dana na przedziale I R. Funkcja F() nazywana jest funkcją pierwotną f() na przedziale I, jeśli F() = f() dla dowolnego I, a funkcja pierwotna

~ ~ Całki nieoznaczone i oznaczone Pojęcie całki pierwotnej i nieoznaczonej. Definicja: Funkcja F jest nazywana funkcją pierwotną w odniesieniu do funkcji f, jeśli te funkcje są powiązane w następujący sposób:

Wykład 5 7 Twierdzenie Hilberta-Schmidta Rozważymy operator całkowy A, którego jądro K(spełnia warunki: K(s) jest symetryczne, ciągłe w zbiorze zmiennych na [, ]

Ministerstwo Edukacji Republiki Białorusi Białoruski Uniwersytet Państwowy Wydział Fizyki Wydział Matematyki Wyższej i Fizyki Matematycznej O A Kononova, N I Ilyinkova, N K Filippova Linear

Temat 9 Szereg potęgowy Szereg potęgowy jest szeregiem funkcjonalnym postaci, natomiast liczby … są współczynnikami szeregu, a punkt rozwinięcia szeregu., …, … R … nazywa się centrum Szereg potęgowy Ogólny termin szeregu potęgowego

UKŁADY LINIOWYCH RÓWNAŃ RÓŻNICZKOWYCH O STAŁYCH WSPÓŁCZYNNIKACH Redukcja do pojedynczego równania rzędu-go Z praktycznego punktu widzenia układy liniowe o stałych współczynnikach są bardzo ważne

Całki i równania różniczkowe Moduł 1. Całka nieoznaczona Wykład 1.2 Streszczenie Ułamki wymierne. Rozkład właściwego ułamka wymiernego na sumę ułamków prostych. Integracja pierwotniaków

Formuła ekspansji Heaviside

Niech obraz funkcji będzie ułamkową funkcją wymierną.

Twierdzenie. Niech, gdzie i bądź funkcjami różniczkowalnymi. Przedstawmy oba bieguny funkcji, tj. pierwiastki (zera) jego mianownika. Wtedy, jeśli otrzymamy wzór Heaviside'a:

Dowód przeprowadzimy dla przypadku, gdy i są wielomianami stopni t oraz P odpowiednio, podczas gdy t P. Następnie jest właściwy ułamek wymierny. Przedstawmy to jako sumę prostych ułamków:

Stąd znajdujemy współczynniki z tożsamości (17.2), przepisując je w postaci

Mnożymy obie strony ostatniej równości przez i przechodzimy do granicy przy. Biorąc to pod uwagę i otrzymujemy

skąd następuje (17.1). Twierdzenie zostało udowodnione.

Uwaga 1. Jeśli współczynniki wielomianów i są rzeczywiste, to złożone pierwiastki wielomianu są sprzężone parami. W związku z tym we wzorze (17.1) złożone ilości sprzężone będą terminami odpowiadającymi złożonym sprzężonym pierwiastkom wielomianu, a formuła Heaviside'a przyjmie postać

gdzie pierwsza suma jest rozszerzona na wszystkie rzeczywiste pierwiastki wielomianu, druga - na wszystkie złożone pierwiastki z dodatnimi częściami urojonymi.

Uwaga 2. Każdy członek wzoru (17.1) jest oscylacją zapisaną w postaci złożonej, gdzie. Zatem pierwiastki rzeczywiste () odpowiadają oscylacjom aperiodycznym, pierwiastki złożone z ujemnymi częściami rzeczywistymi - oscylacje tłumione, pierwiastki czysto urojone - oscylacje harmoniczne nietłumione.

Jeśli mianownik nie ma pierwiastków z dodatnimi częściami rzeczywistymi, to dla wystarczająco dużych wartości uzyskujemy stan stacjonarny:

Czysto urojone pierwiastki wielomianu z dodatnimi częściami urojonymi.

Oscylacje odpowiadające pierwiastkom z ujemnymi częściami rzeczywistymi zanikają wykładniczo i dlatego nie wchodzą w stan ustalony.

Przykład 1 Znajdź oryginalny obraz

Decyzja. Mamy. Wypisujemy pierwiastki wielomianu: .

Według wzoru (17.1)

Tutaj, ponieważ liczby są pierwiastkami równania. Stąd,

Przykład 2 Znajdź oryginalny obraz

gdzie a 0; .

Decyzja. Tutaj funkcja oprócz oczywistego pierwiastka ma nieskończenie wiele pierwiastków, które są zerami funkcji. Rozwiązując równanie, dostajemy gdzie

Zatem pierwiastki mianownika mają formę i gdzie

Według wzoru (17.3) znajdujemy oryginał

Metoda operatorowa rozwiązywania równań różniczkowych

Równania różniczkowe. Rozważ problem Cauchy'ego dla liniowego równania różniczkowego

(tutaj) z warunkami początkowymi

Przechodząc do obrazów w (18.1), ze względu na liniowość transformaty Laplace'a mamy

Obrazy pochodnych, korzystając z Twierdzenia 3 z § 16 i warunków początkowych (18.2), piszemy w formie

Podstawiając (18.4) do (18.3), po prostych przekształceniach otrzymujemy równanie operatorowe

gdzie (wielomian charakterystyczny); .

Z równania (18.5) znajdujemy rozwiązanie operatorowe

Rozwiązanie problemu Cauchy'ego (18.1), (18.2) jest oryginalnym rozwiązaniem operatorowym (18.6):

Dla problemu Cauchy'ego w przyjętym zapisie możemy napisać

Równanie operatora ma postać

Rozłóżmy rozwiązanie operatorowe na proste ułamki:

Korzystając ze wzorów uzyskanych w § 15 uzyskujemy oryginały:

Zatem rozwiązanie problemu Cauchy'ego będzie miało postać

Przykład 1 Rozwiąż problem Cauchy'ego dla równania różniczkowego z warunkami początkowymi, gdzie.

Decyzja.

Jego rozwiązanie wygląda na

Korzystając z twierdzenia 2 z § 16, znajdujemy kolejno:

Przykład 2 Rozwiąż problem Cauchy'ego dla równania różniczkowego z zerowymi warunkami początkowymi, gdzie jest funkcją impulsu skokowego.

Decyzja. Napiszmy równanie operatora

i jego decyzja

Twierdzenie 2 z § 16 implikuje

zgodnie z twierdzeniem o lagach (§ 15)

Wreszcie,

Przykład 3 do punktu masy t sztywność przymocowana do sprężyny z i znajduje się na gładkiej płaszczyźnie poziomej, działa okresowo zmieniająca się siła. W tym momencie punkt został poddany uderzeniu niosącemu impuls. Zaniedbując opór, znajdź prawo ruchu punktu, jeśli w początkowym momencie znajdował się w spoczynku w punkcie początkowym.

Decyzja. Równanie ruchu zapisujemy w postaci

gdzie jest siła sprężystości; jest funkcją Diraca. Rozwiążmy równanie operatora

Jeśli (przypadek rezonansu), to

Zgodnie z twierdzeniem o opóźnieniu

Wreszcie,

Całka (wzór) Duhamela. Rozważ problem Cauchy'ego dla równania (18.1) w warunkach początkowych. Rozwiązanie operatorskie w tym przypadku ma postać

Niech funkcja wagi będzie oryginałem. następnie przez Twierdzenie 1 z § 16 otrzymujemy

Relacja (18,7) nazywana jest całką Duhamela (wzór).

Komentarz. W niezerowych warunkach początkowych wzór Duhamela nie ma bezpośredniego zastosowania. W takim przypadku konieczne jest najpierw przekształcenie pierwotnego problemu w problem z jednorodnymi (zerowymi) warunkami początkowymi. W tym celu wprowadzamy nową funkcję, ustawienie

gdzie są początkowe wartości pożądanego rozwiązania.

Jak łatwo zauważyć, a zatem .

Zatem funkcja jest rozwiązaniem równania (18.1) z prawą stroną otrzymaną przez podstawienie (18.8) do (18.1), z zerowymi danymi początkowymi.

Używając (18,7) znajdujemy i.

Przykład 4 Użyj całki Duhamela, aby znaleźć rozwiązanie problemu Cauchy'ego

z warunkami początkowymi.

Decyzja. Początkowe dane są niezerowe. Zakładamy, zgodnie z (18.8), . Następnie dla definicji otrzymujemy równanie o jednorodnych warunkach początkowych.

Dla rozważanego problemu wielomian charakterystyczny, funkcja wagi. Zgodnie ze wzorem Duhamela

Wreszcie,

Układy równań różniczkowych liniowych o stałych współczynnikach. Problem Cauchy'ego dla układu równań różniczkowych liniowych w notacji macierzowej ma postać

gdzie jest wektor pożądanych funkcji; - wektor właściwych części; - macierz współczynników; - wektor danych początkowych.

Rachunek operacyjny stał się obecnie jednym z najważniejszych rozdziałów praktycznej analizy matematycznej. Metoda operacyjna jest bezpośrednio wykorzystywana do rozwiązywania równań różniczkowych zwyczajnych i układów takich równań; może być również używany do rozwiązywania równań różniczkowych cząstkowych.

Założycielami rachunku symbolicznego (operacyjnego) są rosyjscy naukowcy M. E. Vashchenko-Zacharchenko i A. V. Letnikov.

Rachunek operacyjny zwrócił na siebie uwagę po tym, jak angielski inżynier elektryk Heaviside, posługując się rachunkiem symbolicznym, uzyskał szereg ważnych wyników. Ale nieufność do rachunku symbolicznego utrzymywała się, dopóki Georgi, Bromwich, Carson, A.M. Efros, A.I. Lurie, V.A.Ditkin i inni nie ustalili związku między rachunkiem operacyjnym a transformacjami całkowymi.

Pomysł rozwiązania równania różniczkowego metodą operacyjną polega na tym, że z równania różniczkowego w odniesieniu do pożądanej funkcji-pierwotnej f ( t ) przejdź do równania dla innej funkcji F ( p ), nazwany obrazem f ( t ) . Wynikowe (operacyjne) równanie jest zwykle już algebraiczne (co oznacza, że jest prostsze niż pierwotne). Rozwiązywanie go w odniesieniu do obrazu F ( p ) a następnie przechodząc do odpowiedniego oryginału, znajdują pożądane rozwiązanie tego równania różniczkowego.

Operacyjną metodę rozwiązywania równań różniczkowych można porównać z obliczaniem różnych wyrażeń za pomocą logarytmów, gdy na przykład podczas mnożenia obliczenia wykonywane są nie na samych liczbach, ale na ich logarytmach, co prowadzi do zastąpienia mnożenia przez prostsza obsługa - dodawanie.

Podobnie jak w przypadku logarytmu, stosując metodę operacyjną potrzebne są:

1) spis oryginałów i odpowiadających im obrazów;

2) znajomość zasad wykonywania operacji na obrazie odpowiadających czynnościom wykonywanym na oryginale.

§jeden. Oryginały i obrazy funkcji według Laplace'a

Definicja 1.Będziemy prawdziwą funkcją rzeczywistego argumentu f (t) połączenie oryginał, jeśli spełnia trzy wymagania:

1) f (t) 0 , w t 0

2) f ( t ) wzrasta nie szybciej niż jakaś funkcja wykładnicza

, w t0 , gdzie M 0, s00 - niektóre stałe rzeczywiste, s 0 nazywa wskaźnik wzrostu funkcji f(t) .

3) Na dowolnym odcinku skończonym  a , bdodatnia półoś Od funkcjonować f (t) spełnia warunki Dirichleta, tj.

limitowany,

b) jest albo ciągły, albo ma tylko skończoną liczbę punktów nieciągłości pierwszego rodzaju,

c) ma skończoną liczbę ekstremów.

Funkcje, które spełniają te trzy wymagania, są wywoływane w rachunku operacyjnym grana przez Laplacea lub oryginały .

Najprostszym oryginałem jest funkcja tożsamości Heaviside

Jeśli funkcja

spełnia warunek 2, a nie spełnia warunek 1, to produkt spełni również warunek 1, tj. będzie oryginalny. Aby uprościć notację, z reguły będziemy używać mnożnika H (t) należy pominąć, zakładając, że wszystkie rozważane funkcje są równe zeru dla wartości ujemnych t .

Całka Laplace'a za oryginał f (t) nazywamy całką niewłaściwą postaci