Fórmulas de seno cosseno tangente cotangente. Seno, cosseno, tangente, cotangente de um ângulo agudo. Funções trigonométricas
Leia também
A trigonometria é um ramo da matemática que estuda as funções trigonométricas e seu uso na geometria. O desenvolvimento da trigonometria começou na época Grécia antiga. Durante a Idade Média, cientistas do Oriente Médio e da Índia deram uma importante contribuição para o desenvolvimento dessa ciência.
Esse artigo é sobre Conceitos Básicos e definições de trigonometria. Discute as definições das principais funções trigonométricas: seno, cosseno, tangente e cotangente. Seu significado no contexto da geometria é explicado e ilustrado.
Yandex.RTB R-A-339285-1
Inicialmente, as definições das funções trigonométricas, cujo argumento é um ângulo, foram expressas através da razão dos lados de um triângulo retângulo.
Definições de funções trigonométricas
O seno de um ângulo (sen α) é a razão entre o cateto oposto a esse ângulo e a hipotenusa.
O cosseno do ângulo (cos α) é a razão entre o cateto adjacente e a hipotenusa.
A tangente do ângulo (t g α) é a razão entre a perna oposta e a adjacente.
A cotangente do ângulo (c t g α) é a razão entre a perna adjacente e a oposta.
Estas definições são dadas para ângulo agudo triângulo retângulo!
Vamos dar uma ilustração.
No triângulo ABC com ângulo reto C, o seno do ângulo A é igual à razão perna BC à hipotenusa AB.
As definições de seno, cosseno, tangente e cotangente permitem calcular os valores dessas funções a partir dos comprimentos conhecidos dos lados de um triângulo.
Importante lembrar!
O intervalo de valores de seno e cosseno: de -1 a 1. Em outras palavras, seno e cosseno assumem valores de -1 a 1. O intervalo de valores de tangente e cotangente é a reta numérica inteira, ou seja, estes funções podem assumir qualquer valor.
As definições dadas acima referem-se a ângulos agudos. Na trigonometria, introduz-se o conceito de ângulo de rotação, cujo valor, ao contrário de um ângulo agudo, não é limitado por quadros de 0 a 90 graus. O ângulo de rotação em graus ou radianos é expresso por qualquer número real de - ∞ a + ∞.
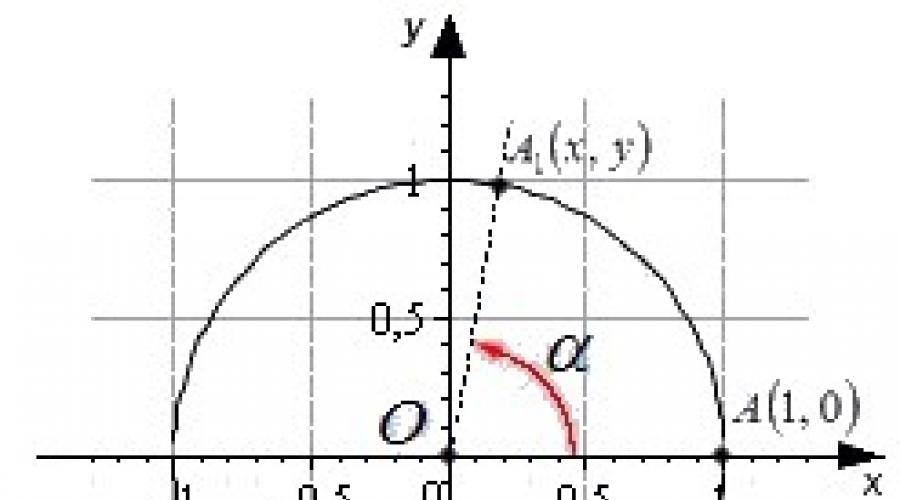
Neste contexto, pode-se definir o seno, cosseno, tangente e cotangente de um ângulo de magnitude arbitrária. Imagine um círculo unitário centrado na origem do sistema de coordenadas cartesianas.

O ponto inicial A com coordenadas (1 , 0) gira em torno do centro do círculo unitário por algum ângulo α e vai para o ponto A 1 . A definição é dada pelas coordenadas do ponto A 1 (x, y).
Seno (sen) do ângulo de rotação
O seno do ângulo de rotação α é a ordenada do ponto A 1 (x, y). sinα = y
Cosseno (cos) do ângulo de rotação
O cosseno do ângulo de rotação α é a abcissa do ponto A 1 (x, y). cosα = x
Tangente (tg) do ângulo de rotação
A tangente do ângulo de rotação α é a razão entre a ordenada do ponto A 1 (x, y) e sua abcissa. tgα = yx
Cotangente (ctg) do ângulo de rotação
A cotangente do ângulo de rotação α é a razão entre a abcissa do ponto A 1 (x, y) e sua ordenada. c t g α = x y
Seno e cosseno são definidos para qualquer ângulo de rotação. Isso é lógico, porque a abcissa e a ordenada do ponto após a rotação podem ser determinadas em qualquer ângulo. A situação é diferente com tangente e cotangente. A tangente não é definida quando o ponto após a rotação vai para o ponto com abcissa zero (0 , 1) e (0 , - 1). Nesses casos, a expressão para a tangente t g α = y x simplesmente não faz sentido, pois contém divisão por zero. A situação é semelhante com a cotangente. A diferença é que a cotangente não é definida nos casos em que a ordenada do ponto se anula.
Importante lembrar!
Seno e cosseno são definidos para quaisquer ângulos α.
A tangente é definida para todos os ângulos exceto α = 90° + 180° k , k ∈ Z (α = π 2 + π k , k ∈ Z)
A cotangente é definida para todos os ângulos exceto α = 180° k, k ∈ Z (α = π k, k ∈ Z)
Ao decidir exemplos práticos não diga "seno do ângulo de rotação α". As palavras "ângulo de rotação" são simplesmente omitidas, implicando que pelo contexto já está claro o que está em jogo.
Números
E a definição do seno, cosseno, tangente e cotangente de um número, e não o ângulo de rotação?
Seno, cosseno, tangente, cotangente de um número
Seno, cosseno, tangente e cotangente de um número t um número é chamado, que é respectivamente igual ao seno, cosseno, tangente e cotangente em t radiano.
Por exemplo, o seno de 10 π igual ao senoângulo de rotação de 10 π rad.
Há outra abordagem para a definição do seno, cosseno, tangente e cotangente de um número. Vamos considerá-lo com mais detalhes.
Qualquer número real t um ponto no círculo unitário é colocado em correspondência com o centro na origem do sistema retangular de coordenadas cartesianas. Seno, cosseno, tangente e cotangente são definidos em função das coordenadas deste ponto.
O ponto inicial no círculo é o ponto A com coordenadas (1 , 0).
número positivo t
Número negativo t corresponde ao ponto para o qual o ponto inicial se moverá se ele se mover no sentido anti-horário ao longo do círculo e vai passar o caminho t.
Agora que a conexão entre o número e o ponto no círculo foi estabelecida, passamos à definição de seno, cosseno, tangente e cotangente.
Seno (sen) do número t
Seno de um número t- ordenada do ponto do círculo unitário correspondente ao número t. sen t = y
Cosseno (cos) de t
Cosseno de um número t- abcissa do ponto do círculo unitário correspondente ao número t. cost = x
Tangente (tg) de t
Tangente de um número t- a razão entre a ordenada e a abcissa do ponto do círculo unitário correspondente ao número t. t g t = y x = sen t cos t
As últimas definições são consistentes e não contradizem a definição dada no início desta seção. Ponto em um círculo correspondente a um número t, coincide com o ponto para o qual passa o ponto de partida depois de girar o ângulo t radiano.
Funções trigonométricas de argumento angular e numérico
Cada valor do ângulo α corresponde a um determinado valor do seno e cosseno desse ângulo. Assim como todos os ângulos α diferentes de α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) corresponde a um determinado valor da tangente. A cotangente, como mencionado acima, é definida para todos os α, exceto para α = 180 ° k , k ∈ Z (α = π k , k ∈ Z).
Podemos dizer que sen α , cos α , t g α , c t g α são funções do ângulo alfa, ou funções do argumento angular.
Da mesma forma, pode-se falar de seno, cosseno, tangente e cotangente como funções de um argumento numérico. Cada número real t corresponde a um valor específico do seno ou cosseno de um número t. Todos os números, exceto π 2 + π · k , k ∈ Z, correspondem ao valor da tangente. A cotangente é definida similarmente para todos os números exceto π · k , k ∈ Z.
Funções básicas da trigonometria
Seno, cosseno, tangente e cotangente são as funções trigonométricas básicas.
A partir do contexto, geralmente fica claro com qual argumento da função trigonométrica ( argumento angular ou um argumento numérico) com o qual estamos lidando.
Vamos voltar aos dados bem no início das definições e ao ângulo alfa, que fica no intervalo de 0 a 90 graus. Definições trigonométricas seno, cosseno, tangente e cotangente são totalmente consistentes com definições geométricas, dado pelas razões dos lados de um triângulo retângulo. Vamos mostrar.

Pegue um círculo unitário centrado em um sistema de coordenadas cartesianas retangular. Vamos girar o ponto inicial A (1, 0) em um ângulo de até 90 graus e desenhar a partir do ponto resultante A 1 (x, y) perpendicular ao eixo x. No triângulo retângulo resultante, o ângulo A 1 O H igual ao ângulo volta α, o comprimento da perna O H é igual à abcissa do ponto A 1 (x, y) . O comprimento do cateto oposto ao canto é igual à ordenada do ponto A 1 (x, y), e o comprimento da hipotenusa é igual a um, pois é o raio do círculo unitário.
De acordo com a definição da geometria, o seno do ângulo α é igual à razão entre o cateto oposto e a hipotenusa.
sin α \u003d A 1 H O A 1 \u003d y 1 \u003d y
Isso significa que a definição do seno de um ângulo agudo em um triângulo retângulo pela razão de aspecto é equivalente à definição do seno do ângulo de rotação α, com alfa no intervalo de 0 a 90 graus.
Da mesma forma, a correspondência de definições pode ser mostrada para cosseno, tangente e cotangente.

Se você notar um erro no texto, destaque-o e pressione Ctrl+Enter
Onde foram consideradas as tarefas para resolver um triângulo retângulo, prometi apresentar uma técnica para memorizar as definições de seno e cosseno. Usando-o, você sempre lembrará rapidamente qual perna pertence à hipotenusa (adjacente ou oposta). Decidi não adiar indefinidamente, material necessário abaixo, veja
O fato é que tenho observado repetidamente como os alunos do 10º ao 11º ano têm dificuldade em lembrar essas definições. Eles se lembram muito bem que a perna se refere à hipotenusa, mas qual delas- esquece e confuso. O preço de um erro, como você sabe no exame, é uma pontuação perdida.
A informação que apresentarei diretamente à matemática não tem nada a ver. Ela está associada a pensamento figurativo, e com os métodos de conexão verbal-lógica. Isso mesmo, eu mesmo, de uma vez por todas me lembreidados de definição. Se você ainda os esquecer, com a ajuda das técnicas apresentadas, é sempre fácil lembrar.
Deixe-me lembrá-lo das definições de seno e cosseno em um triângulo retângulo:
Cossenoângulo agudo em um triângulo retângulo é a razão do cateto adjacente para a hipotenusa:

Seioângulo agudo em um triângulo retângulo é a razão entre o cateto oposto e a hipotenusa:

Então, que associações a palavra cosseno evoca em você?
Provavelmente cada um tem o seuLembre-se do link:
Assim, você terá imediatamente uma expressão em sua memória -
«… razão entre a perna ADJACENTE e a hipotenusa».
O problema com a definição de cosseno está resolvido.
Se você precisar se lembrar da definição do seno em um triângulo retângulo, lembrando-se da definição do cosseno, poderá estabelecer facilmente que o seno de um ângulo agudo em um triângulo retângulo é a razão entre o cateto oposto e a hipotenusa. Afinal, existem apenas duas pernas, se a perna adjacente é “ocupada” pelo cosseno, então apenas o lado oposto permanece para o seno.
E a tangente e a cotangente? Mesma confusão. Os alunos sabem que esta é a proporção de pernas, mas o problema é lembrar qual delas se refere a qual - ou oposta ao adjacente ou vice-versa.
Definições:
Tangente um ângulo agudo em um triângulo retângulo é a razão da perna oposta para a adjacente:

Co-tangenteângulo agudo em um triângulo retângulo é a razão da perna adjacente para o oposto:

Como lembrar? Existem duas maneiras. Um também usa uma conexão lógica-verbal, o outro - matemático.
MÉTODO MATEMÁTICO
Existe tal definição - a tangente de um ângulo agudo é a razão entre o seno de um ângulo e seu cosseno:

* Lembrando a fórmula, você sempre pode determinar que a tangente de um ângulo agudo em um triângulo retângulo é a razão entre a perna oposta e a adjacente.
Da mesma maneira.A cotangente de um ângulo agudo é a razão entre o cosseno de um ângulo e seu seno:

Então! Lembrando essas fórmulas, você sempre pode determinar que:
- a tangente de um ângulo agudo em um triângulo retângulo é a razão entre a perna oposta e a adjacente
- a cotangente de um ângulo agudo em um triângulo retângulo é a razão entre o cateto adjacente e o oposto.
MÉTODO VERBAL-LÓGICO
Sobre tangente. Lembre-se do link:

Ou seja, se você precisar lembrar a definição da tangente, usando essa conexão lógica, poderá lembrar facilmente o que é
"... a proporção da perna oposta para a adjacente"
Se se trata de cotangente, lembrando a definição de tangente, você pode facilmente expressar a definição de cotangente -
"... a proporção da perna adjacente para o oposto"
Existe uma técnica interessante para memorizar tangente e cotangente no site " Conjunto matemático " , olhar.
MÉTODO UNIVERSAL
Você pode apenas triturar.Mas, como mostra a prática, graças às conexões lógico-verbais, uma pessoa se lembra de informações por um longo tempo, e não apenas matemática.
Espero que o material tenha sido útil para você.
Atenciosamente, Alexander Krutitskikh
P.S: Agradeceria se você falasse sobre o site nas redes sociais.
Como encontrar o seno?



O estudo da geometria ajuda a desenvolver o pensamento. Este assunto está incluído no currículo. Na vida, o conhecimento desse assunto pode ser útil - por exemplo, ao planejar um apartamento.
Da história
Como parte do curso de geometria, também é estudada a trigonometria, que explora as funções trigonométricas. Na trigonometria, estudamos os senos, cossenos, tangentes e cotangentes de um ângulo.
Mas em este momento Vamos começar com o mais simples - seno. Vamos dar uma olhada no primeiro conceito - o seno de um ângulo na geometria. O que é um seno e como encontrá-lo?
O conceito de "seno do ângulo" e sinusóides
O seno de um ângulo é a razão entre os valores do cateto oposto e a hipotenusa de um triângulo retângulo. Esta é uma função trigonométrica direta, que é escrita por escrito como "sen (x)", onde (x) é o ângulo do triângulo.
No gráfico, o seno de um ângulo é indicado por uma senóide com características próprias. Uma senóide se parece com uma linha ondulada contínua que fica dentro de certos limites no plano de coordenadas. A função é ímpar, portanto é simétrica em relação a 0 no plano de coordenadas (deixa a origem das coordenadas).
O domínio desta função está na faixa de -1 a +1 no sistema de coordenadas cartesianas. O período da função ângulo seno é 2 Pi. Isso significa que a cada 2 Pi o padrão se repete e a onda senoidal passa por um ciclo completo.
Equação senoidal
- sen x = a/c
- onde a é o cateto oposto ao ângulo do triângulo
- c - hipotenusa de um triângulo retângulo
Propriedades do seno de um ângulo
- sen(x) = - sen(x). Esse recurso demonstra que a função é simétrica e, se os valores x e (-x) forem colocados de lado no sistema de coordenadas em ambas as direções, as ordenadas desses pontos serão opostas. Eles estarão a uma distância igual um do outro.
- Outra característica desta função é que o gráfico da função aumenta no segmento [- P / 2 + 2 Pn]; [P/2 + 2Pn], onde n é qualquer número inteiro. Uma diminuição no gráfico do seno do ângulo será observada no segmento: [P / 2 + 2 Pn]; [3P/2 + 2Pn].
- sin (x) > 0 quando x está no intervalo (2Pn, P + 2Pn)
- (x)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
Os valores dos senos do ângulo são determinados por tabelas especiais. Tais tabelas foram criadas para facilitar o processo de contagem. fórmulas complexas e equações. É fácil de usar e contém valores não só funções sin(x), mas também os valores de outras funções.
Além disso, uma tabela de valores padrão para essas funções está incluída no estudo obrigatório para memória, como uma tabuada de multiplicação. Isto é especialmente verdadeiro para aulas com um viés físico e matemático. Na tabela você pode ver os valores dos principais ângulos usados na trigonometria: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 e 360 graus.
Há também uma tabela que define os valores das funções trigonométricas de ângulos não padronizados. Tirando vantagem mesas diferentes, você pode calcular facilmente o seno, cosseno, tangente e cotangente de alguns ângulos.
As equações são feitas com funções trigonométricas. Resolver essas equações é fácil se você souber o simples identidades trigonométricas e reduções de funções, por exemplo, como sen (P/2 + x) = cos (x) e outras. Uma tabela separada também foi compilada para esses lançamentos.
Como encontrar o seno de um ângulo
Quando a tarefa é encontrar o seno de um ângulo e, por condição, temos apenas o cosseno, tangente ou cotangente do ângulo, podemos calcular facilmente o que precisamos usando identidades trigonométricas.
- sen 2 x + cos 2 x = 1
A partir desta equação, podemos encontrar seno e cosseno, dependendo de qual valor é desconhecido. Nós vamos ter sucesso equação trigonométrica com um desconhecido:
- sen 2 x = 1 - cos 2 x
- sen x = ± √ 1 - cos 2 x
- ctg 2 x + 1 = 1 / sin 2 x
A partir desta equação, você pode encontrar o valor do seno, conhecendo o valor da cotangente do ângulo. Para simplificar, substitua sen 2 x = y, e então você tem uma equação simples. Por exemplo, o valor da cotangente é 1, então:
- 1 + 1 = 1/ano
- 2 = 1 / ano
- 2a = 1
- y = 1/2
Agora realizamos a substituição inversa do player:
- sen 2 x = ½
- sen x = 1 / √2
Como pegamos o valor da cotangente para o ângulo padrão (45 0), os valores obtidos podem ser verificados na tabela.
Se você tiver um valor tangente, mas precisar encontrar o seno, outra identidade trigonométrica ajudará:
- tg x * ctg x = 1
Segue que:
- ctg x = 1 / tg x
Para encontrar o seno de um ângulo não padrão, por exemplo, 240 0, você precisa usar as fórmulas de redução de ângulo. Sabemos que π corresponde a 180 0 para nós. Assim, vamos expressar nossa igualdade usando ângulos padrão por expansão.
- 240 0 = 180 0 + 60 0
Precisamos encontrar o seguinte: sin (180 0 + 60 0). Em trigonometria, existem fórmulas de redução que, em este caso vir a calhar. Esta é a fórmula:
- sen (π + x) = - sen (x)
Assim, o seno de um ângulo de 240 graus é:
- sin (180 0 + 60 0) = - sin (60 0) = - √3/2
No nosso caso, x = 60 e P, respectivamente, 180 graus. Encontramos o valor (-√3/2) da tabela de valores das funções dos ângulos padrão.
Assim é possível decompor ângulos não padronizados, por exemplo: 210 = 180 + 30.
Os conceitos de seno (), cosseno (), tangente (), cotangente () estão inextricavelmente ligados ao conceito de ângulo. Para entender bem esses conceitos, à primeira vista, complexos (que causam um estado de horror em muitos escolares), e ter certeza de que “o diabo não é tão assustador quanto é pintado”, vamos começar do início e entender o conceito de ângulo.
O conceito de ângulo: radiano, grau
Vamos olhar para a imagem. O vetor "virou" em relação ao ponto por uma certa quantidade. Então a medida dessa rotação em relação à posição inicial será injeção.
O que mais você precisa saber sobre o conceito de ângulo? Bem, unidades de ângulo, é claro!
O ângulo, tanto em geometria quanto em trigonometria, pode ser medido em graus e radianos.
O ângulo em (um grau) é o ângulo central no círculo, baseado em um arco circular igual à parte do círculo. Assim, todo o círculo consiste em "pedaços" de arcos circulares, ou seja, o ângulo descrito pelo círculo é igual.

Ou seja, a figura acima mostra um ângulo que é igual, ou seja, esse ângulo é baseado em um arco circular do tamanho da circunferência.
Um ângulo em radianos é chamado de ângulo central em um círculo, com base em um arco circular, cujo comprimento é igual ao raio do círculo. Bem, você entendeu? Se não, então vamos olhar para a imagem.

Assim, a figura mostra um ângulo igual a um radiano, ou seja, esse ângulo é baseado em um arco circular, cujo comprimento é igual ao raio do círculo (o comprimento é igual ao comprimento ou raio igual ao comprimento arcos). Assim, o comprimento do arco é calculado pela fórmula:
Onde é o ângulo central em radianos.
Bem, sabendo disso, você pode responder quantos radianos contém um ângulo descrito por um círculo? Sim, para isso você precisa se lembrar da fórmula da circunferência de um círculo. Aqui está ela:
Bem, agora vamos correlacionar essas duas fórmulas e fazer com que o ângulo descrito pelo círculo seja igual. Ou seja, correlacionando o valor em graus e radianos, obtemos isso. Respectivamente, . Como você pode ver, ao contrário de "graus", a palavra "radiano" é omitida, pois a unidade de medida geralmente é clara no contexto.
Quantos radianos são? Está certo!
Entendi? Em seguida, aperte para a frente:
Alguma dificuldade? Então veja respostas:
Triângulo retângulo: seno, cosseno, tangente, cotangente de um ângulo
Então, com o conceito de ângulo descoberto. Mas o que é o seno, cosseno, tangente, cotangente de um ângulo? Vamos descobrir. Para isso, um triângulo retângulo nos ajudará.

Como se chamam os lados de um triângulo retângulo? Isso mesmo, a hipotenusa e os catetos: a hipotenusa é o lado oposto ângulo certo(no nosso exemplo, este é o lado); as pernas são os dois lados restantes e (aqueles que são adjacentes ao ângulo reto), além disso, se considerarmos as pernas em relação ao ângulo, então a perna é a perna adjacente e a perna é a oposta. Então, agora vamos responder a pergunta: quais são o seno, cosseno, tangente e cotangente de um ângulo?
Seno de um ânguloé a razão da perna oposta (distante) para a hipotenusa.
em nosso triângulo.
Cosseno de um ângulo- esta é a razão da perna adjacente (próxima) para a hipotenusa.
em nosso triângulo.
Ângulo tangente- esta é a proporção da perna oposta (distante) para a adjacente (perto).
em nosso triângulo.
Cotangente de um ângulo- esta é a proporção da perna adjacente (próxima) para a oposta (distante).
em nosso triângulo.
Essas definições são necessárias lembrar! Para tornar mais fácil lembrar qual perna dividir por qual, você precisa entender claramente que em tangente e co-tangente apenas as pernas ficam sentadas, e a hipotenusa aparece apenas em seio e cosseno. E então você pode criar uma cadeia de associações. Por exemplo, este:
cosseno→toque→toque→adjacente;
Cotangente→toque→toque→adjacente.
Antes de tudo, é necessário lembrar que o seno, cosseno, tangente e cotangente como razões dos lados de um triângulo não dependem dos comprimentos desses lados (em um ângulo). Não acredite? Então certifique-se olhando para a imagem:

Considere, por exemplo, o cosseno de um ângulo. Por definição, a partir de um triângulo: , mas podemos calcular o cosseno de um ângulo a partir de um triângulo: . Você vê, os comprimentos dos lados são diferentes, mas o valor do cosseno de um ângulo é o mesmo. Assim, os valores de seno, cosseno, tangente e cotangente dependem apenas da magnitude do ângulo.
Se você entende as definições, vá em frente e corrija-as!
Para o triângulo mostrado na figura abaixo, encontramos.

Bem, você conseguiu? Então tente você mesmo: calcule o mesmo para o canto.
Círculo unitário (trigonométrico)
Entendendo os conceitos de graus e radianos, consideramos um círculo com um raio igual a. Tal círculo é chamado solteiro. É muito útil no estudo da trigonometria. Portanto, nos debruçamos sobre isso com um pouco mais de detalhes.

Como você pode ver, este círculo é construído no sistema de coordenadas cartesianas. O raio do círculo é igual a um, enquanto o centro do círculo está na origem, a posição inicial do vetor de raio é fixada ao longo da direção positiva do eixo (no nosso exemplo, este é o raio).
Cada ponto do círculo corresponde a dois números: a coordenada ao longo do eixo e a coordenada ao longo do eixo. Quais são esses números de coordenadas? E, em geral, o que eles têm a ver com o tema em questão? Para fazer isso, lembre-se do triângulo retângulo considerado. Na figura acima, você pode ver dois triângulos retângulos inteiros. Considere um triângulo. É retangular porque é perpendicular ao eixo.
O que é igual a de um triângulo? Está certo. Além disso, sabemos que é o raio do círculo unitário e, portanto, . Substitua esse valor em nossa fórmula de cosseno. Aqui está o que acontece:
E o que é igual a de um triângulo? Bem, claro, ! Substitua o valor do raio nesta fórmula e obtenha:
Então, você pode dizer quais coordenadas um ponto tem, pertencente ao círculo? Bem, de jeito nenhum? E se você perceber isso e são apenas números? A que coordenada corresponde? Bem, é claro, a coordenada! A que coordenada corresponde? Isso mesmo, coordenar! Assim, o ponto.

E o que então são iguais e? Isso mesmo, vamos usar as definições apropriadas de tangente e cotangente e obter isso, a.
E se o ângulo for maior? Aqui, por exemplo, como nesta imagem:

O que mudou neste exemplo? Vamos descobrir. Para fazer isso, voltamos novamente para um triângulo retângulo. Considere um triângulo retângulo: um ângulo (como adjacente a um ângulo). Qual é o valor do seno, cosseno, tangente e cotangente de um ângulo? Isso mesmo, aderimos às definições correspondentes das funções trigonométricas:
Bem, como você pode ver, o valor do seno do ângulo ainda corresponde à coordenada; o valor do cosseno do ângulo - a coordenada; e os valores de tangente e cotangente às razões correspondentes. Assim, essas relações são aplicáveis a quaisquer rotações do vetor raio.
Já foi mencionado que a posição inicial do vetor raio é ao longo da direção positiva do eixo. Até agora, giramos esse vetor no sentido anti-horário, mas o que acontece se o girarmos no sentido horário? Nada de extraordinário, você também obterá um ângulo de um determinado tamanho, mas apenas negativo. Assim, ao girar o vetor raio no sentido anti-horário, obtemos ângulos positivos, e ao girar no sentido horário - negativo.
Então, sabemos que toda uma revolução do vetor raio ao redor do círculo é ou. É possível girar o vetor raio por ou por? Bem, claro que você pode! No primeiro caso, portanto, o vetor raio fará uma revolução completa e parará na posição ou.
No segundo caso, ou seja, o raio vetor fará três voltas completas e parará na posição ou.
Assim, a partir dos exemplos acima, podemos concluir que os ângulos que diferem por ou (onde é qualquer número inteiro) correspondem à mesma posição do vetor raio.
A figura abaixo mostra um ângulo. A mesma imagem corresponde ao canto, e assim por diante. Esta lista pode ser continuada indefinidamente. Todos esses ângulos podem ser escritos com a fórmula geral ou (onde é qualquer número inteiro)

Agora, conhecendo as definições das funções trigonométricas básicas e usando o círculo unitário, tente responder a quais valores são iguais:
Aqui está um círculo unitário para ajudá-lo:

Alguma dificuldade? Então vamos descobrir. Então sabemos que:
A partir daqui, determinamos as coordenadas dos pontos correspondentes a certas medidas do ângulo. Bem, vamos começar pela ordem: o canto em corresponde a um ponto com coordenadas, portanto:
Não existe;
Além disso, seguindo a mesma lógica, descobrimos que os cantos em correspondem a pontos com coordenadas, respectivamente. Sabendo disso, é fácil determinar os valores das funções trigonométricas nos pontos correspondentes. Tente você mesmo primeiro, depois verifique as respostas.
Respostas:
Não existe
Não existe
Não existe
Não existe
Assim, podemos fazer a seguinte tabela:

Não há necessidade de lembrar todos esses valores. Basta lembrar a correspondência entre as coordenadas dos pontos no círculo unitário e os valores das funções trigonométricas:
Mas os valores das funções trigonométricas dos ângulos e, dados na tabela abaixo, deve ser lembrado:

Não tenha medo, agora vamos mostrar um dos exemplos memorização bastante simples dos valores correspondentes:
Para usar este método, é vital lembrar os valores do seno para todas as três medidas do ângulo (), bem como o valor da tangente do ângulo em. Conhecendo esses valores, é bastante fácil restaurar toda a tabela - os valores de cosseno são transferidos de acordo com as setas, ou seja:
Sabendo disso, você pode restaurar os valores para. O numerador " " corresponderá e o denominador " " corresponderá. Os valores cotangentes são transferidos de acordo com as setas mostradas na figura. Se você entender isso e se lembrar do diagrama com setas, será suficiente lembrar o valor inteiro da tabela.
Coordenadas de um ponto em um círculo
É possível encontrar um ponto (suas coordenadas) em um círculo, conhecendo as coordenadas do centro do círculo, seu raio e ângulo de rotação?
Bem, claro que você pode! Vamos trazer para fora Fórmula geral encontrar as coordenadas de um ponto.
Aqui, por exemplo, temos esse círculo:

Nos é dado que o ponto é o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas girando o ponto em graus.
Como pode ser visto na figura, a coordenada do ponto corresponde ao comprimento do segmento. O comprimento do segmento corresponde à coordenada do centro do círculo, ou seja, é igual a. O comprimento de um segmento pode ser expresso usando a definição de cosseno:
Então temos que para o ponto a coordenada.
Pela mesma lógica, encontramos o valor da coordenada y para o ponto. Por isso,
Então em visão geral as coordenadas do ponto são determinadas pelas fórmulas:
Coordenadas do centro do círculo,
raio do círculo,
Ângulo de rotação do vetor raio.
Como você pode ver, para o círculo unitário que estamos considerando, essas fórmulas são significativamente reduzidas, pois as coordenadas do centro são zero e o raio é igual a um:
Bem, vamos tentar essas fórmulas para dar um gostinho, praticando encontrar pontos em um círculo?
1. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
2. Encontre as coordenadas de um ponto em um círculo unitário obtido pela rotação de um ponto.
3. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
4. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
5. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
Tendo problemas para encontrar as coordenadas de um ponto em um círculo?
Resolva esses cinco exemplos (ou entenda bem a solução) e você aprenderá como encontrá-los!
1.
Pode ser visto que. E sabemos o que corresponde a uma volta completa do ponto de partida. Assim, o ponto desejado estará na mesma posição que ao virar. Sabendo disso, encontramos as coordenadas desejadas do ponto:
2. O círculo é uma unidade com centro em um ponto, o que significa que podemos usar fórmulas simplificadas:
Pode ser visto que. Sabemos o que corresponde a duas rotações completas do ponto de partida. Assim, o ponto desejado estará na mesma posição que ao virar. Sabendo disso, encontramos as coordenadas desejadas do ponto:
Seno e cosseno são valores da tabela. Lembramos seus valores e obtemos:
Assim, o ponto desejado tem coordenadas.
3. O círculo é uma unidade com centro em um ponto, o que significa que podemos usar fórmulas simplificadas:
Pode ser visto que. Vamos descrever o exemplo considerado na figura:

O raio faz ângulos com o eixo igual a e. Sabendo que os valores tabulares do cosseno e do seno são iguais, e tendo determinado que o cosseno aqui assume um valor negativo e o seno é positivo, temos:
Exemplos semelhantes são analisados com mais detalhes ao estudar as fórmulas para reduzir funções trigonométricas no tópico.
Assim, o ponto desejado tem coordenadas.
4.
Ângulo de rotação do vetor de raio (por condição)
Para determinar os sinais correspondentes de seno e cosseno, construímos um círculo unitário e um ângulo:

Como você pode ver, o valor, ou seja, é positivo, e o valor, ou seja, é negativo. Conhecendo os valores tabulares das funções trigonométricas correspondentes, obtemos que:
Vamos substituir os valores obtidos em nossa fórmula e encontrar as coordenadas:
Assim, o ponto desejado tem coordenadas.
5. Para resolver este problema, usamos fórmulas na forma geral, onde
As coordenadas do centro do círculo (no nosso exemplo,
Raio do círculo (por condição)
Ângulo de rotação do vetor raio (por condição).
Substitua todos os valores na fórmula e obtenha:
e - valores da tabela. Lembramos e os substituímos na fórmula:
Assim, o ponto desejado tem coordenadas.
RESUMO E FÓRMULA BÁSICA
O seno de um ângulo é a razão entre o cateto oposto (distante) e a hipotenusa.
O cosseno de um ângulo é a razão entre o cateto adjacente (próximo) e a hipotenusa.
A tangente de um ângulo é a razão entre a perna oposta (distante) e a adjacente (próxima).
A cotangente de um ângulo é a razão entre a perna adjacente (próxima) e a oposta (distante).
Instrução
Use a função arcsine para calcular o valor de um ângulo em graus se você souber o valor desse ângulo. Se um injeção denotada pela letra α, em termos gerais, a solução pode ser escrita da seguinte forma: α = arcsin(sin(α)).
Se você tiver a oportunidade de usar um computador, é mais fácil usar o sistema operacional integrado para cálculos práticos. Nas duas versões mais recentes do Windows, você pode iniciá-lo assim: pressione a tecla Win, digite "ka" e pressione Enter. Em versões anteriores deste SO, procure o link "Calculadora" na subseção "Padrão" da seção "Todos os Programas" do menu principal do sistema.
Depois de iniciar o aplicativo, alterne-o para um modo que permita trabalhar com funções trigonométricas. Isso pode ser feito selecionando a linha "Engenharia" na seção "Visualizar" do menu da calculadora ou pressionando Alt + 2.
Insira um valor de seno. Por padrão, a interface da calculadora não possui um botão para calcular o arco-seno. Para poder usar esta função, você precisa inverter os valores padrão do botão - clique no botão Inv na janela do programa. Em mais versões anteriores este botão é substituído por uma caixa de seleção com a mesma designação - marque-a.
Você pode usar nos cálculos e vários serviços, que são mais que suficientes na Internet. Por exemplo, vá para a página http://planetcalc.com/326/, role um pouco para baixo e no campo Input insira o valor do seno. Para iniciar o procedimento de cálculo, existe um botão chamado Calcular - clique nele. Você encontrará o resultado dos cálculos na primeira linha da tabela sob este botão. Além do arco seno, ele exibe os valores e o arco tangente do valor inserido.
A função trigonométrica seno inversa é chamada arco-seno. Pode levar valores que estão dentro da metade do número de pi, tanto positivos quanto negativos. lado negativo quando medido em radianos. Quando medidos em graus, esses valores estarão, respectivamente, na faixa de -90° a +90°.
Instrução
Alguns valores "redondos" não precisam ser calculados, são mais fáceis de lembrar. Por exemplo: - se o argumento da função é zero, então o valor do arco seno dele também é zero; - de 1/2 é 30 ° ou 1/6 Pi, se medido; - o arco seno de -1/2 é igual para -30° ou -1/6 de pi em ;- arco-seno de 1 é 90° ou 1/2 de pi em radianos;- arco-seno de -1 é -90° ou -1/2 de pi em radianos;
Para medir os valores dessa função a partir de outros argumentos, a maneira mais fácil é usar a calculadora padrão do Windows, se você tiver . Para iniciar, abra o menu principal no botão "Iniciar" (ou pressionando a tecla WIN), vá para a seção "Todos os Programas" e depois para a subseção "Acessórios" e clique no item "Calculadora".
Mude a interface da calculadora para o modo de operação que permite calcular funções trigonométricas. Para isso, abra a seção "Visualizar" em seu menu e selecione o item "Engenharia" ou "Científico" (dependendo do sistema operacional utilizado).
Insira o valor do argumento a partir do qual calcular a tangente do arco. Isso pode ser feito clicando nos botões da interface da calculadora com o mouse, ou pressionando as teclas , ou copiando o valor (CTRL + C) e colando-o (CTRL + V) no campo de entrada da calculadora.
Selecione as unidades nas quais deseja obter o resultado do cálculo da função. Abaixo do campo de entrada estão três opções, das quais você precisa selecionar (clicando nele com o mouse) um - , radianos ou rads.
Marque a caixa de seleção que inverte as funções indicadas nos botões da interface da calculadora. Ao lado há uma pequena inscrição Inv.
Clique no botão pecado. A calculadora inverterá a função anexada a ela, realizará o cálculo e apresentará o resultado nas unidades fornecidas.
Vídeos relacionados
Em um triângulo retângulo, como o mais simples dos polígonos, vários cientistas aprimoraram seus conhecimentos no campo da trigonometria naqueles dias em que ninguém chamava essa área da matemática por essa palavra. Portanto, indique o autor que identificou padrões na proporção dos comprimentos dos lados e os valores dos ângulos neste plano figura geométrica hoje não é possível. Tais relações são chamadas de funções trigonométricas e são divididas em vários grupos, sendo os principais convencionalmente considerados funções "diretas". Apenas duas funções são atribuídas a este grupo, e uma delas é seno.

Instrução
Por definição, em um triângulo retângulo um dos ângulos é 90°, e devido ao fato de que a soma de seus ângulos na geometria euclidiana deve ser igual a 180°, os outros dois ângulos são (ou seja, 90°). As regularidades das razões precisamente desses ângulos e comprimentos dos lados descrevem funções trigonométricas.
A função, chamada de seno de um ângulo agudo, determina a razão entre os comprimentos de dois lados de um triângulo retângulo, um dos quais fica oposto a esse ângulo agudo e o outro é adjacente a ele e fica oposto ao ângulo reto. Como o lado oposto ao ângulo reto em tal triângulo é chamado de hipotenusa, e os outros dois são os catetos, as funções seno podem ser formuladas como a razão entre os comprimentos do cateto e a hipotenusa.
Além de uma definição tão simples desta função trigonométrica, existem outras mais complexas: através de um círculo em coordenadas cartesianas, através de séries, através de equações diferenciais e funcionais. Essa função é contínua, ou seja, seus argumentos ("domínio de definições") podem ser qualquer número - de infinitamente negativo a infinitamente positivo. E os valores máximos desta função são limitados pelo intervalo de -1 a +1 - este é o “intervalo de seus valores”. Valor mínimo o seno toma um ângulo de 270°, que corresponde a 3/Pi, e o máximo é obtido em 90° (½ de Pi). Os valores da função tornam-se zero em 0°, 180°, 360°, etc. De tudo isso, segue-se que o seno é uma função periódica e seu período é igual a 360 ° ou duas vezes o número Pi.
Para cálculos práticos dos valores dessa função a partir de um determinado argumento, você pode usar - a grande maioria deles (incluindo a calculadora de software incorporada sistema operacional seu computador) tem a opção correspondente.
Vídeos relacionados
Seio e cosseno- são funções trigonométricas diretas para as quais existem várias definições - através de um círculo no sistema de coordenadas cartesianas, através de soluções equação diferencial, através de ângulos agudos em um triângulo retângulo. Cada uma dessas definições permite deduzir a relação entre essas duas funções. O seguinte é talvez a maneira mais simples de expressar cosseno através do seno - através de suas definições para ângulos agudos de um triângulo retângulo.

Instrução
Expresse o seno de um ângulo agudo de um triângulo retângulo em termos dos comprimentos dos lados desta figura. De acordo com a definição, o seno do ângulo (α) deve ser a razão entre o comprimento do lado (a) oposto a ele - a perna - para o comprimento do lado (c) oposto ao ângulo reto - a hipotenusa: sin (α) = a/c.
Encontre uma fórmula semelhante para cosseno mas o mesmo ângulo. Por definição, esse valor deve ser expresso como a razão entre o comprimento do lado (b) adjacente a esse canto (a segunda perna) e o comprimento do lado (c) oposto ao ângulo reto: cos (a) \u003d a/c.
Reescreva a equação seguinte do teorema de Pitágoras de tal forma que use as relações entre os catetos e a hipotenusa derivadas nas duas etapas anteriores. Para fazer isso, primeiro divida ambos os originais deste teorema (a² + b² = c²) pelo quadrado da hipotenusa (a² / c² + b² / c² = 1), e então reescreva a igualdade resultante desta forma: (a /c)² + (b/c)² = 1.
Substitua na expressão resultante a razão dos comprimentos dos catetos e da hipotenusa por funções trigonométricas, com base nas fórmulas do primeiro e segundo passos: sen² (a) + cos² (a) \u003d 1. Expresse cosseno da igualdade resultante: cos(a) = √(1 - sin²(a)). Este problema pode ser resolvido de uma forma geral.
Se, além do resultado geral, você precisar obter um resultado numérico, use, por exemplo, uma calculadora embutida na sala de cirurgia Sistema Windows. Um link para seu lançamento na subseção "Padrão" da seção "Todos os Programas" do menu do SO. Este link é redigido de forma concisa - "Calculadora". Para poder calcular funções trigonométricas a partir deste programa, ative sua interface de "engenharia" - pressione a combinação de teclas Alt + 2.
Insira o valor do seno do ângulo nas condições e clique no botão da interface com a designação x² - isso elevará o valor original ao quadrado. Em seguida, digite *-1 no teclado, pressione Enter, digite +1 e pressione Enter novamente - desta forma, você subtrairá o quadrado do seno da unidade. Clique na tecla do ícone radical para extrair o quadrado e obter o resultado final.
O estudo dos triângulos tem sido realizado por matemáticos há vários milênios. A ciência dos triângulos - trigonometria - usa quantidades especiais: seno e cosseno.

Triângulo reto
Inicialmente, seno e cosseno surgiram devido à necessidade de calcular quantidades em triângulos retângulos. Percebeu-se que se o valor da medida em grau dos ângulos em um triângulo retângulo não for alterado, então a razão de aspecto, não importa o quanto esses lados mudem de comprimento, permanece sempre a mesma.
Foi assim que os conceitos de seno e cosseno foram introduzidos. O seno de um ângulo agudo em um triângulo retângulo é a razão entre o cateto oposto e a hipotenusa, e o cosseno é a razão entre o cateto adjacente e a hipotenusa.
Teoremas de cossenos e senos
Mas cossenos e senos podem ser usados não apenas em triângulos retângulos. Para encontrar o valor de um ângulo obtuso ou agudo, o lado de qualquer triângulo, basta aplicar o teorema do cosseno e do seno.
O teorema do cosseno é bastante simples: "O quadrado de um lado de um triângulo é igual à soma dos quadrados dos outros dois lados menos duas vezes o produto desses lados pelo cosseno do ângulo entre eles".
Existem duas interpretações do teorema do seno: pequena e estendida. De acordo com o pequeno: "Em um triângulo, os ângulos são proporcionais aos lados opostos." Este teorema é muitas vezes estendido devido à propriedade do círculo circunscrito em torno de um triângulo: "Em um triângulo, os ângulos são proporcionais aos lados opostos e sua razão é igual ao diâmetro do círculo circunscrito".
Derivativos
Uma derivada é uma ferramenta matemática que mostra a rapidez com que uma função muda em relação a uma mudança em seu argumento. As derivadas são usadas em geometria e em várias disciplinas técnicas.
Ao resolver problemas, você precisa conhecer os valores tabulares das derivadas das funções trigonométricas: seno e cosseno. A derivada do seno é o cosseno, e a derivada do cosseno é o seno, mas com sinal negativo.
Aplicação em matemática
Especialmente senos e cossenos são usados na resolução de triângulos retângulos e tarefas associadas a eles.
A conveniência de senos e cossenos também se reflete na tecnologia. Ângulos e lados eram fáceis de avaliar usando os teoremas do cosseno e do seno, quebrando formas e objetos complexos em triângulos "simples". Engenheiros e, muitas vezes lidando com cálculos de proporção e medidas de grau, gastaram muito tempo e esforço calculando cossenos e senos de ângulos que não são de mesa.
Então as tabelas Bradis vieram em socorro, contendo milhares de valoresde senos, cossenos, tangentes e cotangentes ângulos diferentes. Nos tempos soviéticos, alguns professores forçavam seus alunos a memorizar as páginas das tabelas Bradis.
Radiano - magnitude angular arcos, longitudinalmente igual ao raio ou 57,295779513 graus.
Grau (em geometria) - 1/360 de um círculo ou 1/90 de um ângulo reto.
π = 3,141592653589793238462… (valor aproximado de pi).
Tabela de cossenos para ângulos: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Ângulo x (em graus) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ângulo x (em radianos) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3xπ/4 | 5xπ/6 | π | 7xπ/6 | 5xπ/4 | 4xπ/3 | 3xπ/2 | 5xπ/3 | 7xπ/4 | 11xπ/6 | 2xπ |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |