Funções trigonométricas da lição de argumento angular. Funções trigonométricas de argumento numérico e angular. Linhas de senos, cossenos, tangentes e cotangentes

24.11.2019

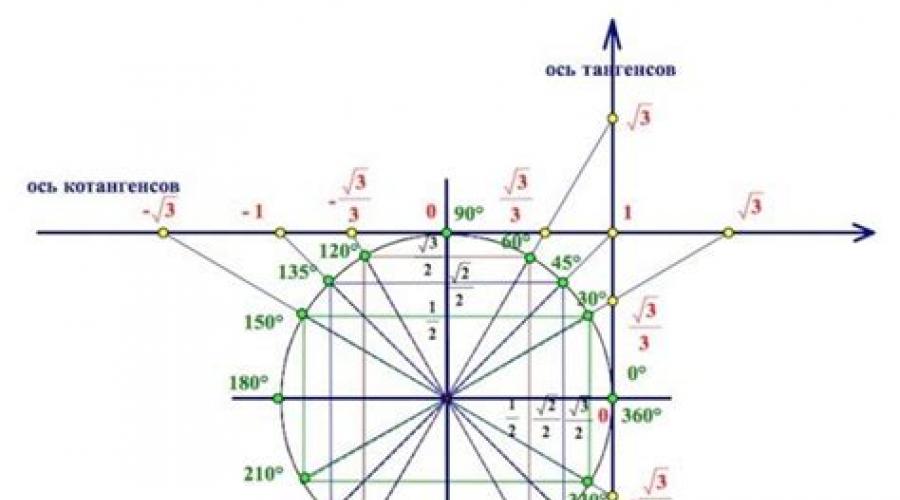
Linhas de senos, cossenos, tangentes e cotangentes

Nunca esqueça isso o eixo y é a linha senoidal, o eixo x é a linha dos cossenos! Os pontos obtidos do círculo são marcados nesses eixos.

MAS as linhas de tangentes e cotangentes são paralelas a elas e passam pelos pontos (1; 0) e (0; 1) respectivamente.

Qualquer que seja o número real t, pode ser atribuído a ele um número definido exclusivamente sin t. É verdade que a regra da correspondência é bastante complicada; como vimos acima, consiste no seguinte.

Para encontrar o valor de sen t pelo número t, você precisa:

1) posicione o círculo numérico no plano de coordenadas de modo que o centro do círculo coincida com a origem das coordenadas, e o ponto inicial A do círculo atinja o ponto (1; 0);

2) encontre um ponto no círculo correspondente ao número t;

3) encontre a ordenada deste ponto.

Esta ordenada é sen t.

Na verdade, estamos falando da função u = sin t, onde t é qualquer número real.

Todas essas funções são chamadas funções trigonométricas do argumento numérico t.

Existem várias relações conectando os valores de várias funções trigonométricas, já recebemos algumas dessas relações:

sen 2 t + cos 2 t = 1

Das duas últimas fórmulas, é fácil obter uma relação conectando tg t e ctg t:

Todas essas fórmulas são usadas nos casos em que, conhecendo o valor de qualquer função trigonométrica, é necessário calcular os valores das funções trigonométricas restantes.

Os termos "seno", "coseno", "tangente" e "cotangente" eram na verdade familiares, no entanto, ainda eram usados em uma interpretação um pouco diferente: em geometria e física, consideravam seno, cosseno, tangente e cotangente gl a(mas não

números, como foi nos parágrafos anteriores).

Sabe-se da geometria que o seno (cosseno) de um ângulo agudo é a razão entre os catetos de um triângulo retângulo e sua hipotenusa, e a tangente (cotangente) de um ângulo é a razão dos catetos de um triângulo retângulo. Uma abordagem diferente dos conceitos de seno, cosseno, tangente e cotangente foi desenvolvida nos parágrafos anteriores. Na verdade, essas abordagens estão inter-relacionadas.

Vamos pegar um ângulo com uma medida de grau b o e organizá-lo no modelo "círculo numérico em um sistema de coordenadas retangulares" como mostrado na Fig. quatorze

topo de canto compatível com centro

círculos (com a origem do sistema de coordenadas),

e um lado do canto é compatível com

raio positivo do eixo x. apontar

interseção do outro lado do ângulo com

o círculo será denotado pela letra M. Ordina-

Figura 14 b o , e a abcissa deste ponto é o cosseno do ângulo b o .

Para encontrar o seno ou cosseno do ângulo b o não é necessário fazer essas construções muito complexas a cada vez.

Basta notar que o arco AM é a mesma parte do comprimento do círculo numérico que o ângulo b o é do ângulo de 360°. Se o comprimento do arco AM é denotado pela letra t, então temos:

Por isso,

Por exemplo,

Acredita-se que 30° é uma medida em graus de um ângulo, e é uma medida em radianos do mesmo ângulo: 30° = rad. Geralmente:

Em particular, estou feliz de onde, por sua vez, chegamos.

Então, o que é 1 radiano? Existem várias medidas de comprimentos de segmentos: centímetros, metros, jardas, etc. Existem também várias medidas para indicar a magnitude dos ângulos. Consideramos os ângulos centrais do círculo unitário. Um ângulo de 1° é um ângulo central baseado em um arco que faz parte de um círculo. Um ângulo de 1 radiano é um ângulo central baseado em um arco de comprimento 1, ou seja, em um arco cujo comprimento é igual ao raio do círculo. Da fórmula, obtemos 1 rad \u003d 57,3 °.

Considerando a função u = sin t (ou qualquer outra função trigonométrica), podemos considerar a variável independente t como um argumento numérico, como foi o caso nos parágrafos anteriores, mas também podemos considerar essa variável como uma medida do ângulo, ou seja argumento angular. Portanto, falando de uma função trigonométrica, em certo sentido é indiferente considerá-la uma função de um argumento numérico ou angular.

A videoaula "Funções trigonométricas do argumento angular" é um material visual para a realização de uma aula de matemática sobre o tema relevante. O vídeo é composto de tal forma que o material estudado é apresentado da maneira mais conveniente possível para os alunos entenderem, é fácil de lembrar, revela bem a conexão entre as informações disponíveis sobre funções trigonométricas da seção sobre estudo de triângulos e sua definição usando um círculo unitário. Pode tornar-se uma parte independente da lição, pois abrange totalmente este tópico, complementado por comentários importantes durante a pontuação.

Os efeitos de animação são usados para demonstrar visualmente a relação entre as diferentes definições de funções trigonométricas. Destacar o texto em cores, construções claras e compreensíveis, complementando com comentários ajuda a dominar rapidamente, lembrar do material e atingir os objetivos da lição mais rapidamente. A conexão entre as definições de funções trigonométricas é claramente demonstrada por meio de efeitos de animação e realce de cores, contribuindo para a compreensão e memorização do material. O manual visa melhorar a eficácia do treinamento.

A lição começa com uma introdução ao tópico. Em seguida, as definições de seno, cosseno, tangente e cotangente de um ângulo agudo de um triângulo retângulo são lembradas. A definição destacada no quadro lembra que o seno e o cosseno são formados pela razão entre o cateto e a hipotenusa, a tangente e a cotangente são formadas pela razão dos catetos. Os alunos também são lembrados do material recentemente estudado que, ao considerar um ponto pertencente a um círculo unitário, a abcissa do ponto é o cosseno e a ordenada é o seno do número correspondente a esse ponto. A conexão desses conceitos é demonstrada por meio de construção. Um círculo unitário é exibido na tela, colocado de forma que seu centro coincida com a origem. Um raio é construído a partir da origem das coordenadas, fazendo um ângulo α com o semi-eixo positivo da abcissa. Este raio intercepta o círculo unitário no ponto O. As perpendiculares descem do ponto até a abcissa e o eixo y, demonstrando que as coordenadas deste ponto determinam o cosseno e o seno do ângulo α. Note-se que o comprimento do arco AO do ponto de intersecção do círculo unitário com a direção positiva do eixo das abcissas até o ponto O é a mesma parte de todo o arco que o ângulo α de 360°. Isso permite que você faça a proporção α/360=t/2π, que é exibida logo ali e destacada em vermelho para memorização. O valor t=πα/180° é derivado desta proporção. Levando isso em consideração, determina-se a relação entre as definições de seno e cosseno senα°= sint= senπα/180, cosα°=custo=cosπα/180. Por exemplo, encontrar sin60 ° é dado. Substituindo a medida em graus do ângulo na fórmula, obtemos sen π 60°/180°. Reduzindo a fração por 60, obtemos sen π/3, que é igual a √3/2. Note-se que se 60° é a medida em graus de um ângulo, então π/3 é chamado de medida em radianos do ângulo. Existem dois registros possíveis da razão da medida em graus do ângulo para o radiano: 60°=π/3 e 60°=π/3 rad.

O conceito de ângulo de um grau é definido como um ângulo central baseado em um arco cujo comprimento 1/360 representa parte da circunferência. A definição a seguir revela o conceito de um ângulo de um radiano - um ângulo central baseado em um arco de comprimento um, ou igual ao raio de um círculo. As definições são marcadas como importantes e destacadas para memorização.

Para converter a medida de um grau de um ângulo em radiano e vice-versa, é usada a fórmula α ° \u003d πα / 180 rad. Esta fórmula é destacada em um quadro na tela. Desta fórmula segue que 1°=π/180 rad. Neste caso, um radiano corresponde a um ângulo de 180°/π≈57,3°. Note-se que, ao encontrar os valores das funções trigonométricas da variável independente t, ela pode ser considerada tanto um argumento numérico quanto angular.

Além disso, são demonstrados exemplos de uso do conhecimento adquirido no curso de resolução de problemas matemáticos. No exemplo 1, é necessário converter valores de graus para radianos 135° e 905°. No lado direito da tela, há uma fórmula que mostra a relação entre um grau e um radiano. Depois de substituir o valor na fórmula, obtemos (π/180) 135. Após reduzir esta fração em 45, obtemos o valor 135°=3π/4. Para converter um ângulo de 905° para radianos, a mesma fórmula é usada. Depois de substituir o valor nele, fica (π / 180) 905 \u003d 181π / 36 rad.

No segundo exemplo, o problema inverso é resolvido - a medida em graus dos ângulos expressos em radianos π/12, -21π/20, 2,4π é encontrada. No lado direito da tela, é recuperada a fórmula estudada para a relação entre o grau e a medida em radianos do ângulo 1 rad \u003d 180 ° / π. Cada exemplo é resolvido substituindo a medida em radianos na fórmula. Substituindo π/12, obtemos (180°/π)·(π/12)=15°. Da mesma forma, os valores dos ângulos restantes -21π/20=-189° e 2,4π=432° são encontrados.

A videoaula "Funções trigonométricas do argumento angular" é recomendada para ser usada em aulas de matemática tradicional para aumentar a eficácia do aprendizado. O material ajudará a proporcionar a visualização do aprendizado durante o ensino a distância sobre este tema. Uma explicação detalhada e compreensível do tópico, resolvendo problemas sobre ele, pode ajudar o aluno a dominar o material por conta própria.

INTERPRETAÇÃO DO TEXTO:

"Funções trigonométricas de argumento angular".

Já sabemos da geometria que o seno (cosseno) de um ângulo agudo de um triângulo retângulo é a razão entre o cateto e a hipotenusa, e a tangente (cotangente) é a razão dos catetos. E em álgebra, chamamos a abcissa de um ponto no círculo unitário de cosseno, e a ordenada desse ponto de seno. Garantiremos que tudo isso esteja intimamente interligado.

Vamos colocar um ângulo com uma medida de grau α° (graus alfa), como mostrado na Figura 1: o vértice do ângulo é compatível com o centro do círculo unitário (com a origem do sistema de coordenadas), e um lado do ângulo é compatível com o raio positivo do eixo x. O segundo lado do ângulo intercepta o círculo no ponto O. A ordenada do ponto O é o seno do ângulo alfa, e a abcissa deste ponto é o cosseno de alfa.

Observe que o arco AO é a mesma parte do comprimento do círculo unitário que o ângulo alfa é do ângulo de trezentos e sessenta graus. Vamos denotar o comprimento do arco AO através de t(te), então vamos fazer a proporção =

(alfa refere-se a trusts de sessenta como te para dois pi) Daqui encontramos te: t = = (te é igual a pi alfa dividido por cento e oitenta).

Assim, para encontrar o seno ou cosseno do ângulo alfa graus, você pode usar a fórmula:

sin α ° \u003d sint \u003d sin (o seno de graus alfa é igual ao seno de te e é igual ao seno de pi privado alfa para cento e oitenta),

cosα° \u003d custo \u003d cos (o cosseno de alfa graus é igual ao cosseno de te e é igual ao cosseno de pi privado alfa para cento e oitenta).

Por exemplo, sin 60 ° \u003d sin \u003d sin \u003d (o seno de sessenta graus é igual ao seno de pi por três, de acordo com a tabela de valores básicosde senos, é igual à raiz de três por dois).

Acredita-se que 60° é uma medida em graus de um ângulo, e (pi por três) é uma medida em radianos do mesmo ângulo, ou seja, 60° = alegre(sessenta graus é igual a pi vezes três radianos). Por brevidade, concordamos com a notação alegre omitir, ou seja, a seguinte notação é permitida: 60°= (mostrar abreviaturas radiano medida = rad.)

Um ângulo de um grau é um ângulo central que é suportado por um arco que é (um trecentésimo sexagésimo) parte do arco. Um ângulo de um radiano é um ângulo central que repousa sobre um arco de comprimento um, isto é, sobre um arco cujo comprimento é igual ao raio de um círculo (consideramos os ângulos centrais de um círculo unitário para mostrar um ângulo em pi radianos em um círculo).

Vamos lembrar a importante fórmula para converter uma medida de grau em radiano:

α° = alegre. (alfa é igual a pi alfa dividido por cento e oitenta radianos) Em particular, 1° = alegre(um grau é igual a pi dividido por cento e oitenta radianos).

A partir disso, podemos descobrir que um radiano é igual à razão de cento e oitenta graus para pi e é aproximadamente igual a cinquenta e sete vírgula três décimos de grau: 1 alegre= ≈ 57,3°.

Do exposto: quando falamos de qualquer função trigonométrica, por exemplo, sobre a função s \u003d sint (es é igual a sinus te), a variável independente t (te) pode ser considerada tanto um argumento numérico quanto um argumento angular.

Considere exemplos.

EXEMPLO 1. Converter de graus para radianos: a) 135°; b) 905°.

Decisão. Vamos usar a fórmula para converter graus em radianos:

a) 135° = 1° ∙ 135 = alegre ∙ 135 = alegre

(cento e trinta e cinco graus é igual a pi vezes cento e oitenta radianos vezes cento e trinta e cinco, e após a redução é três pi vezes quatro radianos)

b) Da mesma forma, usando a fórmula para converter uma medida de grau em radiano, obtemos

905° = alegre ∙ 905 = alegre.

(novecentos e cinco graus é igual a cento e oitenta e um pi vezes trinta e seis radianos).

EXEMPLO 2. Expresse em graus: a) ; b) -; c) 2,4π

(pi vezes doze; menos vinte e um pi vezes vinte; dois vírgula quatro décimos de um pi).

Decisão. a) Expresse em graus pi por doze, use a fórmula para traduzir a medida em radianos do ângulo para a medida em graus em 1 alegre=, obtemos

alegre = 1 alegre∙ = ∙ = 15°

Da mesma forma b) - = 1 alegre∙ (-) \u003d ∙ (-) \u003d - 189 ° (menos vinte e um pi por vinte é igual a menos cento e oitenta e nove graus),

c) 2,4π = 1 alegre∙ 2,4π = ∙ 2,4π = 432° (dois vírgula quatro de pi é igual a quatrocentos e trinta e dois graus).

Aula e apresentação sobre o tema: "A função trigonométrica do argumento angular, a medida de grau do ângulo e radianos"

Materiais adicionais
Caros usuários, não se esqueça de deixar seus comentários, comentários, sugestões. Todos os materiais são verificados por um programa antivírus.

Manuais e simuladores na loja online "Integral" para o grau 10 de 1C
Resolvemos problemas de geometria. Tarefas interativas de construção
Resolvemos problemas de geometria. Tarefas interativas para construir no espaço

O que vamos estudar:
1. Vamos lembrar da geometria.
2. Definição do argumento angular.
3. Medida em grau de um ângulo.
4. Medida em radianos de um ângulo.
5. O que é um radiano?
6. Exemplos e tarefas para solução independente.

Repetição de geometria

Pessoal, em nossas funções:

y= sin(t), y= cos(t), y= tg(t), y= ctg(t)

A variável t pode assumir não apenas valores numéricos, ou seja, ser um argumento numérico, mas também pode ser considerada uma medida de um ângulo - um argumento angular.

Vamos relembrar a geometria!
Como definimos seno, cosseno, tangente, cotangente aí?

O seno de um ângulo é a razão entre o cateto oposto e a hipotenusa

Cosseno de um ângulo - a razão entre o cateto adjacente e a hipotenusa

A tangente de um ângulo é a razão entre a perna oposta e a adjacente.

A cotangente de um ângulo é a razão entre a perna adjacente e a oposta.

Definição da função trigonométrica do argumento angular

Vamos definir funções trigonométricas como funções de um argumento de ângulo em um círculo numérico:
Com a ajuda de um círculo numérico e um sistema de coordenadas, sempre podemos encontrar facilmente o seno, o cosseno, a tangente e a cotangente de um ângulo:

Colocamos o vértice do nosso ângulo α no centro do círculo, ou seja. ao centro do eixo de coordenadas e posicione um dos lados de modo que coincida com a direção positiva do eixo x (OA)
Então o segundo lado intercepta o círculo numérico no ponto M.

Ordenar pontos M: seno do ângulo α
Abscissa pontos M: cosseno do ângulo α

Observe que o comprimento do arco AM é a mesma parte do círculo unitário que nosso ângulo α de 360 graus: onde t é o comprimento do arco AM.

Medida em grau de um ângulo

1) Pessoal, temos uma fórmula para determinar a medida em grau de um ângulo através do comprimento de um arco de um círculo numérico, vamos dar uma olhada mais de perto:

Em seguida, escrevemos as funções trigonométricas na forma:

Por exemplo:

Medida em radianos de ângulos

Ao calcular a medida em graus ou radianos de um ângulo, lembre-se! :
Por exemplo:

A propósito! Designação rad. você pode soltar!

O que é um radiano?

Caros amigos, nos deparamos com um novo conceito - Radiano. Então o que é?

Existem várias medidas de comprimento, tempo, peso, por exemplo: metro, quilômetro, segundo, hora, grama, quilograma e outros. Portanto, o radiano é uma das medidas do ângulo. Vale a pena considerar os ângulos centrais, ou seja, localizados no centro do círculo numérico.
Um ângulo de 1 grau é um ângulo central baseado em um arco igual a 1/360 da circunferência.

Um ângulo de 1 radiano é um ângulo central baseado em um arco igual a 1 em um círculo unitário e em um círculo arbitrário em um arco igual ao raio do círculo.

Exemplos: