Resolução de equações diferenciais usando a transformada de Laplace. Método operacional de resolução de equações diferenciais lineares e seus sistemas. §1. Originais e imagens de funções de acordo com Laplace
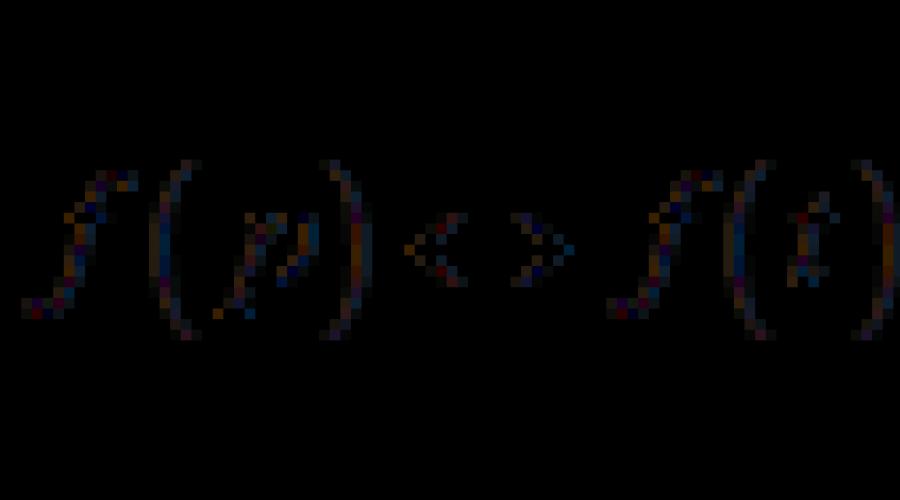
Tamanho: px
Iniciar impressão da página:
transcrição
1 Resolvendo equações diferenciais usando a transformada de Laplace (método operacional) O cálculo operacional é um dos métodos mais econômicos para integrar equações diferenciais lineares com coeficientes constantes e é muito popular entre os engenheiros. O método foi proposto pelo famoso engenheiro elétrico e físico americano O. Heaviside (892). Ele propôs regras formais para lidar com o operador d dx e algumas funções deste operador, usando as quais resolveu vários dos problemas mais importantes da eletrodinâmica. No entanto, o cálculo operacional não recebeu uma justificativa matemática nos trabalhos de O. Heaviside (“sua matemática surgiu em um contexto físico do qual não era fácil destacar” [, p. 8]), muitos de seus resultados permaneceram não comprovado. Somente nos 2º anos do século XX o método foi justificado nas obras de Bromwich (T. J. I A. Bromwich) e Carson (J. R. Carson) 2 .. O conceito de original e a imagem segundo a definição de Laplace. Uma função original é qualquer função de valor complexo f(x) de um argumento real x que satisfaça as seguintes condições: f(x) é contínua em x, exceto, talvez, por um número finito de pontos de descontinuidade do tipo -th; 2) para todo x< f(x) = ; 3) существуют такие постоянные M >e a > para o qual f(x) M e ax para x. () Equações diferenciais e integrais: um livro didático para alunos da Faculdade de Física e Tecnologia: em 3 horas Parte 2 / comp. : N. Yu. Svetova, E. E. Semyonova. Petrozavodsk: PetrSU Publishing House, Tentativas de justificar rigorosamente e apresentação "matematicamente aceitável" do cálculo se assemelhavam a um "ataque geral" O matemático inglês Bromwich (96), o engenheiro americano Carson (925), o engenheiro elétrico holandês Van der Pol () atraiu os resultados de várias teorias, conectou o cálculo de Heaviside com a transformada de Laplace, com a teoria das funções de uma variável complexa.
2 2 O ínfimo a de todos os números a para os quais a desigualdade () é verdadeira é chamada de taxa de crescimento da função f(x). Observe que para qualquer função limitada, a taxa de crescimento a =. A original mais simples é a função Heaviside (, x ; χ(x) =, x<. Очевидно, для любой функции ϕ(x) { ϕ(x), x, ϕ(x) χ(x) =, x <. Если при x функция ϕ(x) удовлетворяет условиям и 3 определения, то функция ϕ(x)χ(x) является оригиналом. В дальнейшем для сокращения записи будем, как правило, записывать ϕ(x) вместо ϕ(x)χ(x), считая, что рассматриваемые нами функции продолжены нулем для отрицательных значений аргумента x. Определение 2. Функция F (p) комплексного переменного p (p C), определяемая интегралом F (p) = e px f(x) dx, () называется преобразованием Лапласа, или изображением по Лапласу 3, функции f(x). Для указания соответствия между оригиналом и изображением будем использовать следующую запись 4: f(x) F (p). 3 В мемуарах П. Лапласа (782 82) современные оригинал и изображение именуются fonction determinant и fonction generatrice «определяющая функция» и «производящая». Эти названия, хотя и признанные неудачными, сохранились до XX в. Хевисайд употреблял названия «подоператорная функция» (892). Оператор он обозначал буквой p, которая употребляется в современном исчислении . 4 Названия original и image и знак предложил Ван дер Поль в статьях гг. В русской литературе термин изображение и символ, по-видимому, впервые появились в книге харьковских математиков А. М. Эфроса и А. М. Данилевского «Операционное исчисление и контурные интегралы» (937), а термин оригинал только в 953 г. . Используются и другие варианты записи соответствия между оригиналами и изображениями. Например, f(x) F (p) или L{f(x)} = F (p).
3 Para qualquer original f(x), sua imagem F(p) é definida no semiplano Re p > a (a é a taxa de crescimento da função f(x)), onde a integral imprópria () converge. Exemplo. Usando a definição, encontre a imagem da função f(x) = sin 3x. Decisão. Para a função f(x) = sen 3x temos a =. Portanto, a imagem F (p) será definida no semiplano Re p >. Vamos aplicar a fórmula () à função dada, usando a regra de integração por partes e a restrição no conjunto de valores da variável p, que garante a convergência da integral: F(p) = + e px sen 3x dx = = p e px sen 3x x= = 3 p p e px cos 3x = 3 p 2 9 p 2 ). F (p) = 3 p 2 9 p 2 F (p). F (p) = 3 p Assim, a seguinte correspondência é válida: sen 3x 3 p 2, Re p >. + 9 e px sen 3x dx = 3
4 4 2. Propriedades da transformada de Laplace Na prática, na construção de imagens, são utilizadas várias técnicas baseadas nas propriedades da transformada de Laplace. Listamos as principais propriedades, cuja validade é fácil de estabelecer usando as definições da imagem e do original.Propriedade da linearidade. Se f(x) F (p), g(x) G(p), então para qualquer α, β C αf(x) + βg(x) αf (p) + βg(p), Re p > max( a, b). Aqui e abaixo, aeb são as taxas de crescimento das funções f(x) eg(x), respectivamente. 2. Teorema da similaridade. Se f(x) F (p), então para qualquer α > f(αx) α F (p α), Re p > αa. 3. O teorema do deslocamento. Se f(x) F (p), então para qualquer λ C e λx f(x) F (p λ), Re p > a + Re λ. 4. Diferenciação do original. Seja a função f(x) n vezes diferenciável. Então f (x) pf (p) f(+), f (x) p 2 F (p) pf(+) f (+), f (n) (x) p n F (p) p n f(+). .. pf (n 2) (+) f (n) (+), onde f (k) (+) = lim x + f (k) (x), k =, n. Comente. Ao construir imagens de derivadas de funções contínuas em zero, o sinal de mais é omitido na notação do argumento da função e suas derivadas. 5. Diferenciação de imagens. Se f(x) F (p), então Em particular, para n = temos F (n) (p) (x) n f(x), Re p >. F(p)xf(x).
5 5 6. Integração do original. Se f(x) F (p), então x f(ξ) dξ F (p) p, Re p > α. 7. Integração de imagens. Se a integral e F (p) f(x), então p F (p) dp f(x) x, Re p > α. p F (p) dp converge 8. Teorema da multiplicação de imagens (teorema da convolução) Se f(x) F (p), g(x) G(p), então F (p)g(p) x f(t) g( x t) dt = x f(x t)g(t) dt quando Re p > max(a, b). As integrais do lado direito da correspondência são chamadas de convolução das funções f(x) eg(x). 9. Teorema do atraso. Se f(x) F (p), então para qualquer ξ > f(x ξ)χ(x ξ) e ξp F (p), Re p > α. O original é restaurado a partir da imagem de forma única, até os valores nos pontos de quebra. Na prática, geralmente são utilizadas tabelas prontas de originais e imagens 5. A tabela lista os principais originais e imagens que são frequentemente encontrados nos aplicativos. Exemplo 2. Usando as propriedades da transformada de Laplace e a tabela de originais e imagens básicas, encontre imagens das seguintes funções:) f(x) = e 4x sen 3x cos 2x; 3) f(x) = x 2 e 3x; 2) f (x) \u003d e (x 2) sen (x 2); 4) f(x) = sen2 x x. 5 Ditkin V. A., Prudnikov A. P. Manual de Cálculo Operacional. M., 965.
6 6 Tabela. Principais originais e imagens Imagem original Imagem original p cos ωx p p 2 + ω 2 x n n! p n+ e λx p + λ sen ωx x cos ωx x n e λx n! (p + λ) n+ x sen ωx ω p 2 + ω 2 p 2 ω 2 (p 2 + ω 2) 2 2pω (p 2 + ω 2) 2 Solução.) Transformamos a expressão para a função f (x) da seguinte forma: f(x) = e 4x sen 3x cos 2x = 2 e 4x (sen 5x + sen x) = = 2 e 4x sen 5x + 2 e 4x sen x. Como sen x 5 p 2 e sen 5x + p , então, usando a propriedade da linearidade e o teorema do deslocamento, para a imagem da função f (x) teremos: F (p) = () 5 2 (p + 4) ) (p + 4 )) Como sen x p 2 +, ex sen x (p) 2 +, então, usando o teorema do atraso, teremos f (x) = e x 2 sen (x 2) F (p) = e 2p (p)) Então como x 2 2 p 3, então pelo teorema do deslocamento temos: f(x) = x 2 e 3x F (p) = 2 (p 3) 3.
7 Para comparação, apresentamos um método para construir uma imagem da função f(x) = x 2 e 3x usando a propriedade de diferenciação de imagem: Obtivemos o mesmo resultado. 4) Desde e 3x p 3 ; xe 3x d() = dp p 3 (p 3) 2 ; x 2 e 3x d() 2 dp (p 3) 2 = (p 3) 3. sin 2 x = 2 2 cos 2x 2p 2 p p 2 + 4, então, usando a propriedade de integração da imagem, teremos: sin 2 x ( x 2p) 2 p p 2 dp = + 4 p (= 4 ln p2) 4 ln(p2 + 4) = p 4 ln p 2 p p = 4 ln p2 + 4 p fração racional própria (é uma função racional). Se a fração é decomposta na soma das frações mais simples (elementares), então para cada uma delas o original correspondente pode ser encontrado usando as propriedades da transformada de Laplace e a tabela de originais e suas imagens. De fato, A p a A eax ; A (p a) n A (n)! xn e ax.
8 8 Após realizar transformações de fração Ap + B A(p a) + aa + B A(p a) (p a) 2 = + b2 (p a) 2 + b 2 = (p a) 2 + b 2 + aa + B (p a) 2 + b 2, obtemos Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sin bx. b Para construir o original correspondente à fração Ap + B ((p a) 2 + b 2) n, pode-se usar o teorema da multiplicação. Por exemplo, para n = 2 temos Ap + B ((p a) 2 + b 2) 2 = Ap + B (p a) 2 + b 2 (p a) 2 + b 2. Desde então Para n = 3: Ap + B (p a) 2 + b 2 A eax cos bx + aa + B e ax sen bx = h (x) b (p a) 2 + b 2 b eax sen bx = g(x), Ap + B ((p a) 2 + b 2) 2 = x Ap + B ((p a) 2 + b 2) 2 (p a) 2 + b 2 g(x t) h (t) dt = h 2 (t). x g(x t) h 2 (t) dt Se tem k zeros diferentes p i, i =, k, então, expandindo
9 o denominador por fatores (p p i), o original correspondente para Y (p) pode ser encontrado pela fórmula: y(x) = k (Y (p)(p p i)e px) p=pi. (2) i= O produto de Y (p)(p p i) dá uma função racional cujo denominador não contém o fator (p p i), e calculado em p = p i determina o coeficiente com o qual a fração entra na expansão p p i da função Y (p) na soma de frações elementares. Exemplo 3. Encontre o original que corresponde à imagem: Y (p) = p 3 p. Decisão. Expandindo a imagem dada na soma de frações elementares: p 3 p = p(p)(p +) = p + 2(p) + 2(p +), encontramos a resposta original: y(x) = + ch x. y(x) = + 2 ex + 2 e x = + ch x. Exemplo 4. Encontre o original para a imagem: Y (p) = p(p 2 +). Decisão. Como p 2 sen x, então, aplicando a propriedade de integração do original, + obtemos: p(p 2 +) x Resposta: y(x) = cos x. sen t dt = cos t x = cos x. Exemplo 5. Encontre o original que corresponde à imagem: Y (p) = (p 2 + 4) 2. 9
10 Decisão. Usando a propriedade da imagem de convolução, temos: Y (p) = (p 2 + 4) 2 = p p x sen 2(x t) sen 2t dt. Tendo calculado a integral, obtemos a expressão desejada para o original. Resposta: y(x) = 6 sen 2x x cos 2x. 8 Exemplo 6. Encontre o original que corresponde à imagem: Y (p) = p p 3 p 2 6p. Decisão. Como p 3 p 2 6p \u003d p (p 3) (p + 2), o denominador da fração Y (p) tem três raízes simples: p \u003d, p 2 \u003d 3 e p 3 \u003d 2. Construímos o original correspondente usando a fórmula (2): y(x) = (p2 + 2)e px (p 3)(p + 2) + (p2 + 2)e px p= p(p + 2) + (p2 + 2)e px p =3 p(p 3) = p= 2 = e3x e 2x. Exemplo 7. Encontre o original que corresponde à imagem: Y (p) = e p 2 p(p +)(p 2 + 4). Decisão. Vamos representar a fração incluída na expressão na forma de frações simples: p(p +)(p 2 + 4) = A p + B p + + Cp + D p Aplicando o método dos coeficientes indefinidos à expansão, obtemos : ; B=D=5; C \u003d 2. Y (p) \u003d e p 2 4 p 5 e p 2 p + pe p 2 2 p e p 2 5 p (a)
11 Usando as relações: p χ(x), p + e x χ(x), p p cos 2x χ(x), p sin 2x χ(x) 2 e levando em consideração o teorema do atraso, obtemos o original desejado para o imagem (a). Resposta: y(x) = (4 5 e (x 2) cos (2x) sin (2x) 2) χ (x) Solução do problema de Cauchy para uma equação diferencial com coeficientes constantes O método de resolver várias classes de equações usando a transformada de Laplace é chamada de método operacional. A propriedade da diferenciação da transformada de Laplace do original permite reduzir a solução de equações diferenciais lineares com coeficientes constantes à solução de equações algébricas. Considere o problema de Cauchy para uma equação não homogênea com condições iniciais y (n) + a y (n) a n y + a n y = f(x) (3) y() = y, y () = y,..., y (n ) ( ) = yn. (4) Deixe que a função f(x) e a solução desejada satisfaçam as condições para a existência da transformada de Laplace. Denote por Y (p) a imagem da função desconhecida (original) y(x), e por F (p) a imagem do lado direito de f(x): y(x) Y (p), f(x) ) F (p). Pela regra de diferenciação do original, temos y (x) py (p) y, y (x) p 2 Y (p) py y, y (n) (x) p n Y (p) p n y p n 2 y.. . s n.
12 2 Então, devido à propriedade de linearidade da transformada de Laplace, após aplicá-la nas partes esquerda e direita da equação (3), obtemos a equação do operador M(p)Y (p) N(p) = F (p ), (5) onde M(p) polinômio característico da equação (3): M(p) = p n + a p n a n p + a n y, N(p) polinômio contendo os dados iniciais do problema de Cauchy (desaparece quando os dados iniciais são zero ): N(p) = y (p n + a p n a n) + + y (p n 2 + a p n a n 2) y n 2 (p + a) + y n, F (p) imagem da função f(x). Resolvendo a equação do operador (5), obtemos a imagem de Laplace Y (p) da solução desejada y(x) na forma Y (p) = F (p) + N(p). M(p) Restaurando o original para Y (p), encontramos uma solução para a equação (3) que satisfaz as condições iniciais (4). Exemplo 8. Encontre uma solução para a equação diferencial: y (x) + y(x) = e x que satisfaça a condição: y() =. Decisão. Seja y(x)Y(p). Como y (x) py (p) y() = py (p), e x p +, então, aplicando a transformada de Laplace à equação dada, usando a propriedade de linearidade, obtemos uma equação algébrica para Y (p): py ( p) + Y (p) = p +. Onde encontramos a expressão para Y (p):
13 Desde então temos Y (p) = p + e x, (p +) 2 + p +. (p +) 2 x x, Y (p) y(x) = e x x + e x. Verificação: Vamos mostrar que a função encontrada é de fato uma solução para o problema de Cauchy. Substituímos a expressão para a função y(x) e sua derivada na equação dada: y (x) = e x x + e x e x = e x x e x x + e x x + e x = e x. Após reduzir termos semelhantes no lado esquerdo da equação, obtemos a identidade correta: e x e x. Assim, a função construída é uma solução para a equação. Vamos verificar se ele satisfaz a condição inicial y() = : y() = e + e =. Portanto, a função encontrada é uma solução para o problema de Cauchy. Resposta: y(x) = e x x + e x. Exemplo 9. Resolva o problema de Cauchy y + y =, y() =, y() =. Decisão. Seja y(x)Y(p). Como 3 y (x) p 2 Y (p) py() y (), /p, então, aplicando a transformada de Laplace à equação, levando em conta as condições iniciais, obtemos (p 2 +)Y (p) = p = Y (p) = p(p 2 +). Vamos decompor a fração em frações simples: Y (p) = p De acordo com a tabela, encontramos y(x) = cos x. pp 2 +.
14 4 Você também pode restaurar o original da imagem aplicando a propriedade de integração original (veja o exemplo 4). Resposta: y(x) = cosx. Exemplo. Resolva o problema de Cauchy y +3y = e 3x, y() =, y() =. Decisão. Seja y(x)Y(p). Como y py (p) y(), y (x) p 2 Y (p) py() y (), e e 3x p + 3, então, dadas as condições iniciais, obtemos a equação do operador (p 2 + 3p) Y (p) + = p + 2 = Y (p) = p + 3 (p + 3) 2 p. Vamos expandir a função racional em frações simples: p + 2 (p + 3) 2 p = A p + B p C (p + 3) 2 = A(p2 + 6p + 9) + B(p 2 + 3p) + Cp p (p + 3) 2. Componha um sistema de equações para encontrar os coeficientes A, B e C: A + B =, 6A + 3B + C =, 9A = 2, resolvendo que encontramos A = 2/9 , B = 2/9, C = /3. Portanto, Y (p) = 2 9 p p (p + 3) 2. Usando a tabela, obtemos a resposta. Resposta: y(x) = e 3x 3 xe 3x. Exemplo. Encontre uma solução para a equação diferencial: y (x) + 2y (x) + 5y (x) = satisfazendo as condições: y() =, y () = 2, y () =. Decisão. Seja y(x)Y(p). Uma vez que, dadas as condições dadas, temos y (x) p Y (p) y() = py (p) () = py (p) +, y (x) p 2 Y (p) p y() y ( ) = = p 2 Y (p) p () 2 = p 2 Y (p) + p 2, y (x) p 3 Y (p) p 2 y() p y () y () = = p 3 Y (p) p 2 () p 2 = p 3 Y (p) + p 2 2p,
15 então depois de aplicar a transformada de Laplace à equação dada, obtemos a seguinte equação de operador: p 3 Y (p) + p 2 2p + 2p 2 Y (p) + 2p 4 + 5pY (p) + 5 = ou após transformações : Y (p) (p 3 + 2p 2 + 5p) = p 2. Resolvendo esta equação para Y (p), obtemos Y (p) = p 2 p(p 2 + 2p + 5). Expandimos a expressão resultante em frações simples: p 2 p (p 2 + 2p + 5) = A p + Bp + C p 2 + 2p + 5. Usando o método dos coeficientes indefinidos, encontramos A, B, C. Para fazer isso, reduzimos as frações a um denominador comum e igualamos os coeficientes em potências iguais p: p 2 p(p 2 + 2p + 5) = Ap2 + 2Ap + 5A + Bp 2 + Cp p(p p + 5) Obtemos um sistema de equações algébricas para A, B, C: resolvendo que será: A + B =, 2A + C =, 5A =, A = 5, B = 4 5, C = 2 5. Então Y(p) = 5p + 5 4p + 2p 2 + 2p + 5. Para encontrar o original da segunda fração, selecione o quadrado completo em seu denominador: p 2 + 2p + 5 = (p +) 2 + 4, então selecione o termo p+ no numerador: 4p+2 = 4(p+)+6 e expanda a fração na soma de duas frações: 5 4p + 2 p 2 + 2p + 5 = 4 5 p + (p +) (p +) Resposta: y(x) = e x cos 2x e x sen 2x.
16 6 A solução geral da Eq. (3) também pode ser construída pelo método operacional. Para fazer isso, os valores específicos y, y,..., y (n) das condições iniciais devem ser substituídos por constantes arbitrárias C, C 2,..., C n. Bibliografia. Alexandrova N. V. História de termos matemáticos, conceitos, designações: livro de referência de dicionário. M.: Editora LKI, p. 2. Vasilyeva A. B., Medvedev G. N., Tikhonov N. A., Urazgildina T. A. Equações diferenciais e integrais, cálculo de variações em exemplos e problemas. M.: FIZ-MATLIT, p. 3. Sidorov Yu. V. Palestras sobre a teoria das funções de uma variável complexa / Yu. V. Sidorov, M. V. Fedoryuk, M. I. Shabunin. M.: Nauka, 989.
CÁLCULO OPERACIONAL O cálculo operacional é um cálculo simbólico baseado na construção da análise matemática como um sistema de operações formais sobre
Lição 18 Originais e suas imagens O cálculo operacional é um dos métodos de análise matemática que aplicaremos à solução de equações e sistemas diferenciais. A essência deste método
Equações de Física Matemática Coleção de Exemplos e Exercícios Petrozavodsk 1 Universidade Estadual de Petrozavodsk Faculdade de Matemática Equações de Física Matemática Coleção de Exemplos e Exercícios
Título Introdução. Conceitos básicos.... 4 1. Equações integrais de Volterra... 5 Opções de trabalhos de casa.... 8 2. Resolvente da equação integral de Volterra. 10 opções de trabalhos de casa.... 11
1 Tópico 4. Método de operador para resolver equações diferenciais lineares e sistemas 4.1 Transformada de Laplace Um original é qualquer função f(t) de uma variável real t que satisfaça o seguinte
ELEMENTOS DE CÁLCULO OPERACIONAL EDITORA TGTU MINISTÉRIO DA EDUCAÇÃO E CIÊNCIA DA FEDERAÇÃO RUSSA SEI HPE "Tambov State Technical University" ELEMENTOS DE CÁLCULO OPERACIONAL
Análise matemática Seção: cálculo operacional Tópico: Transformada de Laplace e suas propriedades Palestrante Pakhomova E.G. 2011 11. Original e imagem. Teorema de inversão DEFINIÇÃO 1. Seja: R C. Função
Números complexos, funções e operações neles y módulo R parte real número real, yim parte imaginária número real iy notação algébrica do número complexo O valor principal do argumento
A solução de opções padrão para trabalho de controle no tópico Integrais de uma função de uma variável Diretrizes UDC 517.91 As diretrizes contêm soluções detalhadas para opções padrão para trabalho de controle
Capítulo 1 Cálculo Operacional. 1. Definição da transformada de Laplace. A transformada de Laplace associa a função f(t) com a variável real t com a função F() da variável complexa = x + iy
MINISTÉRIO DOS TRANSPORTES DA FEDERAÇÃO RUSSA ORÇAMENTO DO ESTADO FEDERAL INSTITUIÇÃO EDUCACIONAL DE ENSINO SUPERIOR "UNIVERSIDADE RUSSA DE TRANSPORTES (MIIT)"
INSTITUIÇÃO EDUCACIONAL ORÇAMENTAL DO ESTADO FEDERAL DE ENSINO SUPERIOR "UNIVERSIDADE ESTADUAL DE COMUNICAÇÃO DE MOSCOU IMPERADOR NICHOLAS II" Departamento "Matemática Superior e Computacional"
82 4. Seção 4. Séries funcionais e de potência 4.2. Lição 3 4.2. Lição 3 4.2.. Expansão de Taylor de uma função DEFINIÇÃO 4.2.. Seja a função y = f(x) infinitamente diferenciável em alguma vizinhança
Aula INTEGRAÇÃO DE FRAÇÃO RACIONAL Frações racionais Integração de frações racionais simples Decomposição de uma fração racional em frações simples Integração de frações racionais Racional
TÓPICO 5 Equação de Volterra linear do º tipo Definições básicas e teoremas A equação y = λ K(,) y() d+ f(), [, ou na forma de operador y = λ By+ f, é chamada de equação de Volterra do º tipo Let
Aula 6 Cálculo operacional Transformada de Laplace Imagens de funções simples Propriedades básicas da transformada de Laplace Imagem da derivada do cálculo operacional original Transformada de Laplace
Lição 19 Resolvendo equações diferenciais e sistemas usando o método operacional 19.1 Resolvendo equações diferenciais lineares com coeficientes constantes Seja necessário encontrar uma solução particular de um problema linear
2.2. Método do operador para calcular processos transitórios. Informações teóricas. O cálculo de processos transitórios em circuitos complexos pelo método clássico é muitas vezes difícil de encontrar as constantes de integração.
DOROKHOV VM GUIA PARA RESOLVER PROBLEMAS DE CÁLCULO OPERACIONAL MOSCOU, 4 PREFÁCIO Este livro descreve os fundamentos teóricos do cálculo operacional Métodos para resolver problemas
Ministério da Educação e Ciência da Federação Russa Orçamento do Estado Federal Instituição Educacional de Ensino Profissional Superior "Universidade Russa de Tecnologia Química em homenagem a DI Mendeleev" Instituto Novomoskovsk (filial) Teste 8 em matemática (Operacional
UDC 53.7 EM UM MÉTODO PARA ENCONTRAR UMA SOLUÇÃO ESPECÍFICA DE EQUAÇÕES DIFERENCIAIS LINEARES COM COEFICIENTES CONSTANTES Zhanybekova A.A., [e-mail protegido] Universidade Técnica Cazaque-Britânica,
CÁLCULO INTEGRAL INTEGRAL INCERTO Função antiderivada e integral indefinida da antiderivada Lema A função F(é chamada de antiderivada para a função f(no intervalo X, se F (= f(Função X,
Equações de primeira ordem não resolvidas em relação à derivada Consideraremos equações de primeira ordem que não são resolvidas em relação à derivada: F (x, y, y) = 0, (1)
II EQUAÇÕES DIFERENCIAIS Equações Diferenciais de Primeira Ordem Definição Relações nas quais variáveis desconhecidas e suas funções estão sob o sinal derivativo ou diferencial são chamadas
ELEMENTOS DA TEORIA DAS FUNÇÕES DE UM CÁLCULO OPERACIONAL COMPLEXO DE VARIÁVEIS
Ministério da Educação e Ciência da Federação Russa "MATI" Universidade Tecnológica Estatal Russa. K.E. Tsiolkovsky Departamento de Matemática Superior Números complexos e cálculo operacional
1 Tópico 3. Equações diferenciais lineares com coeficientes constantes 3.1 Equação homogênea linear Equação diferencial da forma y (n) + a n 1 y (n 1) +... + a 1 y + a 0 y = 0, (3.1) onde uma
INTEGRAL INDEFINIDA. Antiderivada e integral indefinida A principal tarefa do cálculo diferencial é encontrar a derivada (ou diferencial) de uma dada função. Cálculo integral
Ministério da Educação e Ciência da Federação Russa Filial de Achinsk da Instituição Educacional Autônoma do Estado Federal de Educação Profissional Superior "Universidade Federal da Sibéria" MATEMÁTICA
Limite de função. A relevância de estudar o tema A teoria dos limites desempenha um papel fundamental na análise matemática, pois permite determinar a natureza do comportamento de uma função para uma determinada mudança no argumento. Através da
Antiderivada e integral indefinida Conceitos básicos e fórmulas 1. Definição de antiderivada e integral indefinida. Definição. A função F(x) é chamada de antiderivada para a função f(x) no intervalo
Capítulo 1 Equações Diferenciais 1.1 O conceito de uma equação diferencial 1.1.1 Problemas que levam a equações diferenciais. Na física clássica, cada quantidade física é atribuída
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE PRIMEIRA ORDEM Conceitos básicos Equações diferenciais separáveis Muitos problemas em ciência e tecnologia são reduzidos a equações diferenciais Considere
Desenvolvimento metodológico Resolvendo problemas em TFKP Números complexos Operações em números complexos Plano complexo Um número complexo pode ser representado em exponencial algébrica e trigonométrica
Aula 3 Séries de Taylor e Maclaurin Aplicação de séries de potências Expansão de funções em séries de potências Séries de Taylor e Maclaurin Para aplicações, é importante ser capaz de expandir uma determinada função em uma série de potências, essas funções
Variante típica "Números complexos Polinômios e frações racionais" Tarefa Dados dois números complexos e cos sn Encontre e escreva o resultado na forma algébrica escreva o resultado na forma trigonométrica
Agência Federal de Educação Instituição Educacional Estadual Federal de Educação Profissional Superior UNIVERSIDADE FEDERAL DO SUL R. M. Gavrilova, G. S. Kostetskaya Metodológico
S P PREOBRAZHENSKY, SR TIKHOMIROV INTEGRAÇÃO DE EQUAÇÕES DIFERENCIAIS USANDO POWER SÉRIE 987 CONTEÚDO
Análise matemática Seção: Integral indefinido Tópico: Integração de frações racionais Palestrante Pakhomova E.G. 0 5. Integração de frações racionais DEFINIÇÃO. A fração racional é chamada
Ministério dos Transportes da Federação Russa INSTITUIÇÃO EDUCACIONAL ORÇAMENTAL DO ESTADO FEDERAL DE ENSINO SUPERIOR "UNIVERSIDADE RUSSA DE TRANSPORTES (MIIT)" Instituto de Economia e Finanças
CÁLCULO OPERACIONAL Fórmula de transformação e inversão de Laplace Deixe no intervalo de Dirichlet a saber: A integral de Fourier (l l) a) é limitada neste intervalo; a função satisfaz as condições b) é contínua por partes
Ministério da Educação da Federação Russa Gubkin Universidade Estatal Russa de Petróleo e Gás VI Ivanov Diretrizes para o estudo do tópico "EQUAÇÕES DIFERENCIAIS" (para estudantes
57 Considere a integração da fração racional mais simples do quarto tipo (M N) d () p q p Vamos fazer uma mudança de variável configurando d. onde p q. Então a integral M N d p p p q q a, M p N Mp q d M (p q) p
Uma equação diferencial de ordem n é dita linear se for de primeiro grau em relação à função y e suas derivadas y..., y (n), ou seja, tem a forma a 0 y (n) + a 1 y (n 1) +. .. + a ny = f(x), onde
Análise matemática Seção: Integral indefinido Tópico: Integração de frações racionais Palestrante Rozhkova S.V. 0 5. Integração de frações racionais DEFINIÇÃO. A fração racional é chamada
Ministério das Telecomunicações e Comunicações de Massa da Federação Russa Instituição Educacional Estatal de Ensino Superior Profissional UNIVERSIDADE ESTADUAL DE TELECOMUNICAÇÕES DE VOLGA
Equações diferenciais de primeira ordem resolvidas em relação à derivada Teorema de existência e unicidade para uma solução No caso geral, uma equação diferencial de primeira ordem tem a forma F ()
T A Matveeva V B vetlichnaya D K Agisheva A Zotova
CÁLCULO INTEGRAL INTEGRAL INDEFINITO Uma função antiderivada e uma integral indefinida de uma antiderivada A função F() é chamada de antiderivada para a função f() no intervalo X, se F / () = f() X.
5. 4 Métodos básicos de integração Integração direta. Cálculo de integrais baseado em trazer o integrando para uma forma tabular e usando as propriedades do indefinido
Aula 3 Descrição matemática de sistemas de controle Na teoria de controle, na análise e síntese de sistemas de controle, eles lidam com seu modelo matemático.O modelo matemático do ACS é uma equação
Integração de um sistema de equações diferenciais eliminando variáveis Um dos principais métodos de integração de um sistema de equações diferenciais é o seguinte: a partir das equações da normal
Equações diferenciais parciais de primeira ordem Alguns problemas de mecânica clássica, mecânica do contínuo, acústica, óptica, hidrodinâmica, transferência de radiação são reduzidos a equações diferenciais parciais
As Integrais Indefinidas Mais Simples Exemplos de Resolução de Problemas As seguintes integrais são reduzidas a tabulares pela transformação idêntica do integrando. 1. dx = dx = 2x 2/3/3 + 2x 1/2 + C. >2.
ATIVIDADE PRÁTICA Integração de frações racionais Uma fração racional é uma fração da forma P Q, onde P e Q são polinômios Uma fração racional é dita própria se o grau do polinômio P for menor que o grau
[F] Filippov AV Coleção de problemas sobre equações diferenciais Moscou-Izhevsk: Centro de Pesquisa "Dinâmica Regular e Caótica" 00 URL: http://librarbsaz/kitablar/846pf [M] Matveev NM Coleção de problemas e exercícios sobre
E ocupação. Linhas de Taylor. Soma de séries de potências Mat. análise, ap. Matemática, 3º semestre Encontre a expansão de uma função em uma série de potências em potências, calcule o raio de convergência da série de potências: A f()
Tarefa 1.1. Encontre soluções y = y(x) da equação diferencial que não são idênticas a zero na área indicada e satisfaçam as condições de contorno dadas (o problema de Sturm-Liouville) Solução: Considere
9. Antiderivada e integral indefinida 9.. Seja a função f() dada no intervalo I R. A função F() é chamada de antiderivada f() no intervalo I, se F() = f() para qualquer I, e a antiderivada
~ ~ Integrais indefinidas e definidas O conceito de antiderivada e integral indefinida. Definição: Uma função F é chamada de antiderivada em relação a uma função f se essas funções estiverem relacionadas da seguinte forma
Aula 5 7 Teorema de Hilbert-Schmidt Consideraremos um operador integral A, cujo núcleo K(satisfaz as seguintes condições: K(s) é simétrico, contínuo no conjunto de variáveis em [, ]
Ministério da Educação da República da Bielorrússia Universidade Estatal da Bielorrússia Faculdade de Física Departamento de Matemática Superior e Física Matemática O A Kononova, N I Ilyinkova, N K Filippova Linear
Tópico 9 Série de potências Uma série de potências é uma série funcional da forma, enquanto os números ... são os coeficientes da série e o ponto de expansão da série., ..., ... R ... é chamado o centro Série de potências O termo geral da série de potências
SISTEMAS DE EQUAÇÕES DIFERENCIAIS LINEARES COM COEFICIENTES CONSTANTES Redução a uma única equação de ª ordem Do ponto de vista prático, sistemas lineares com coeficientes constantes são muito importantes
Integrais e equações diferenciais Módulo 1. Integrais indefinidos Aula 1.2 Resumo Frações racionais. Decomposição de uma fração racional própria em uma soma de frações simples. Integração de protozoários
Fórmula de expansão Heaviside
Seja a imagem da função uma função racional fracionária.
Teorema. Let, onde e ser funções diferenciáveis. Vamos introduzir ambos os pólos da função, ou seja, raízes (zeros) do seu denominador. Então, se obtivermos a fórmula de Heaviside:
Faremos a prova para o caso em que e são polinômios de graus t e P em conformidade, enquanto t P. Então é uma fração racional própria. Vamos representá-lo como uma soma de frações simples:
A partir daqui encontramos os coeficientes de identidade (17.2), reescrevendo-o na forma
Multiplicamos ambos os lados da última igualdade por e passamos para o limite em. Levando em conta isso e, obtemos
de onde segue (17.1). O teorema foi provado.
Observação 1. Se os coeficientes dos polinômios e são reais, então as raízes complexas do polinômio são conjugadas aos pares. Conseqüentemente, na fórmula (17.1), as quantidades conjugadas complexas serão os termos correspondentes às raízes conjugadas complexas do polinômio, e a fórmula de Heaviside terá a forma
onde a primeira soma é estendida a todas as raízes reais do polinômio, a segunda - a todas as suas raízes complexas com partes imaginárias positivas.
Observação 2. Cada membro da fórmula (17.1) é uma oscilação escrita na forma complexa, onde. Assim, raízes reais () correspondem a oscilações aperiódicas, raízes complexas com partes reais negativas - oscilações amortecidas, raízes puramente imaginárias - oscilações harmônicas não amortecidas.
Se o denominador não tiver raízes com partes reais positivas, então, para valores suficientemente grandes, obtemos um estado estacionário:
Raízes puramente imaginárias de um polinômio com partes imaginárias positivas.
As oscilações correspondentes a raízes com partes reais negativas decaem exponencialmente em e, portanto, não entram no estado estacionário.
Exemplo 1 Encontrar imagem original
Decisão. Nós temos. Escrevemos as raízes do polinômio: .
Pela fórmula (17.1)
Aqui, já que os números são as raízes da equação. Conseqüentemente,
Exemplo 2 Encontrar imagem original
Onde uma 0; .
Decisão. Aqui, a função, além da raiz óbvia, tem infinitas raízes, que são zeros da função. Resolvendo a equação, chegamos onde
Assim, as raízes do denominador têm a forma e, onde
Pela fórmula (17.3) encontramos o original
Método do operador para resolver equações diferenciais
Equações diferenciais. Considere o problema de Cauchy para a equação diferencial linear
(aqui) com condições iniciais
Passando às imagens em (18.1), devido à linearidade da transformada de Laplace, temos
Imagens de derivadas, usando o Teorema 3 do § 16 e condições iniciais (18.2), escrevemos na forma
Substituindo (18.4) em (18.3), após transformações simples, obtemos a equação do operador
onde (polinômio característico); .
Da equação (18.5) encontramos a solução do operador
A solução do problema de Cauchy (18.1), (18.2) é a solução original do operador (18.6):
Para o problema de Cauchy, na notação aceita, podemos escrever
A equação do operador tem a forma
Vamos decompor a solução do operador em frações simples:
Usando as fórmulas obtidas no § 15, obtemos os originais:
Assim, a solução do problema de Cauchy terá a forma
Exemplo 1 Resolva o problema de Cauchy para uma equação diferencial com condições iniciais, onde.
Decisão.
A solução dele parece
Usando o Teorema 2 do § 16, encontramos sucessivamente:
Exemplo 2 Resolva o problema de Cauchy para uma equação diferencial com condições iniciais nulas, onde é uma função de impulso em degrau.
Decisão. Vamos escrever a equação do operador
e sua solução
O Teorema 2 do § 16 implica
de acordo com o teorema do atraso (§ 15)
Finalmente,
Exemplo 3 a um ponto de massa t preso à mola por rigidez com e localizada em um plano horizontal suave, atua uma força que muda periodicamente. No momento, o ponto foi submetido a um impacto de impulso. Desprezando a resistência, encontre a lei do movimento de um ponto se no momento inicial ele estava em repouso na origem.
Decisão. Escrevemos a equação do movimento na forma
onde é a força elástica; é a função de Dirac. Vamos resolver a equação do operador
Se (caso de ressonância), então
De acordo com o teorema do atraso
Finalmente,

Integral (fórmula) de Duhamel. Considere o problema de Cauchy para a equação (18.1) sob condições iniciais. A solução do operador neste caso tem a forma
Seja a função peso o original para. então pelo Teorema 1 do § 16 obtemos
A relação (18.7) é chamada de integral de Duhamel (fórmula).
Comente. Sob condições iniciais diferentes de zero, a fórmula de Duhamel não é diretamente aplicável. Neste caso, é necessário primeiro transformar o problema original em um problema com condições iniciais homogêneas (zero). Para isso, introduzimos uma nova função, configurando
onde estão os valores iniciais da solução desejada.
Como é fácil de ver e, portanto, .
Assim, a função é a solução da equação (18.1) com o lado direito obtido substituindo (18.8) em (18.1), com dados iniciais zero.
Usando (18.7), encontramos e.
Exemplo 4 Use a integral de Duhamel para encontrar uma solução para o problema de Cauchy
com condições iniciais.
Decisão. Os dados iniciais são diferentes de zero. Assumimos, de acordo com (18.8), . Então, e para a definição, obtemos uma equação com condições iniciais homogêneas.
Para o problema em consideração, o polinômio característico, a função peso. Pela fórmula de Duhamel
Finalmente,
Sistemas de equações diferenciais lineares com coeficientes constantes. O problema de Cauchy para um sistema de equações diferenciais lineares em notação matricial tem a forma
onde é o vetor das funções desejadas; - vetor de partes direitas; - matriz de coeficientes; - vetor de dados iniciais.
O cálculo operacional tornou-se agora um dos capítulos mais importantes da análise matemática prática. O método operacional é usado diretamente na resolução de equações diferenciais ordinárias e sistemas de tais equações; também pode ser usado na resolução de equações diferenciais parciais.
Os fundadores do cálculo simbólico (operacional) são os cientistas russos M. E. Vashchenko-Zakharchenko e A. V. Letnikov.
O cálculo operacional chamou a atenção depois que o engenheiro eletricista inglês Heaviside, usando o cálculo simbólico, obteve uma série de resultados importantes. Mas a desconfiança do cálculo simbólico persistiu até que Georgi, Bromwich, Carson, A. M. Efros, A. I. Lurie, V. A. Ditkin e outros estabeleceram a conexão entre cálculo operacional e transformações integrais.
A ideia de resolver uma equação diferencial pelo método operacional é aquela a partir da equação diferencial em relação à função-original desejada f ( t ) vá para a equação para outra função F ( p ), chamado de imagem f ( t ) . A equação resultante (operacional) geralmente já é algébrica (o que significa que é mais simples que a original). Resolvendo com relação à imagem F ( p ) e então procedendo ao original correspondente, eles encontram a solução desejada desta equação diferencial.
O método operacional para resolver equações diferenciais pode ser comparado com o cálculo de várias expressões usando logaritmos, quando, por exemplo, ao multiplicar, os cálculos são realizados não nos próprios números, mas em seus logaritmos, o que leva à substituição da multiplicação por um operação mais simples - adição.
Assim como no logaritmo, ao usar o método operacional, você precisa:
1) uma tabela de originais e suas imagens correspondentes;
2) conhecimento das regras para realizar operações na imagem, correspondentes às ações realizadas no original.
§1. Originais e imagens de funções de acordo com Laplace
Definição 1.Seremos a função real do argumento real f (t) ligar original, se satisfizer três requisitos:
1) f (t) 0 , no t 0
2) f ( t ) não aumenta mais rápido do que alguma função exponencial
, no t0 , onde M 0, s00 - algumas constantes reais, s 0 chamado indicador de crescimento da função f(t) .3) Em qualquer segmento finito uma , bsemi-eixo positivo A partir de função f (t) satisfaz as condições de Dirichlet, ou seja,
uma limitada,
b) é contínuo ou tem apenas um número finito de pontos de descontinuidade do primeiro tipo,
c) tem um número finito de extremos.
As funções que satisfazem esses três requisitos são chamadas no cálculo operacional retratado por Laplace ou originais .
O original mais simples é a função identidade de Heaviside
Se a função
satisfaça a condição 2 e não satisfaça a condição 1, então o produto também satisfará a condição 1, ou seja, será original. Para simplificar a notação, vamos, via de regra, usar o multiplicador H (t) ser omitido, assumindo que todas as funções consideradas são iguais a zero para valores negativos t .integral de Laplace para o original f (t) é chamada de integral imprópria da forma
 , é um parâmetro complexo.
, é um parâmetro complexo. Teorema.
A integral de Laplace converge absolutamente no semiplano
(ou seja, imagem F (p) é definitivamente definido para ), onde s 0 - taxa de crescimento f (t). , mas pelas propriedades dos módulos
, mas pelas propriedades dos módulos  .
.
Observe que, por definição do original

 .
.
Vamos calcular essa integral:
Ou seja, obtemos F (p) existe em
Comente . A seguinte estimativa segue da prova do teorema:

Definição 2 . Imagem de acordo com Laplace funções f (t) é chamada de função da variável complexa p = s + iσ determinado pela relação
 (1)
(1)
O fato de a função F (t) é uma imagem do original f (t), simbolicamente está escrito assim:
§2. Teoremas básicos de cálculo operacional
2.1 Dobrar originais.
Coleção de originais
e a função é chamada .
.
Funções f (t) e g (t) são chamados componentes de convolução .
Vamos encontrar, por exemplo, a convolução de um original arbitrário
e a função identidade Temos . enquanto
. enquanto  . (2.1.1)
. (2.1.1)
Teorema 1. Se um