Formulação da definição do ângulo entre uma linha e um plano. O ângulo entre uma linha reta e um plano: definição, exemplos de encontrar

10.10.2019

Coleta e uso de informações pessoais

Informações pessoais referem-se a dados que podem ser usados para identificar ou contatar uma pessoa específica.

Você pode ser solicitado a fornecer suas informações pessoais a qualquer momento quando entrar em contato conosco.

A seguir estão alguns exemplos dos tipos de informações pessoais que podemos coletar e como podemos usar essas informações.

Quais informações pessoais coletamos:

Quando você envia uma inscrição no site, podemos coletar várias informações, incluindo seu nome, número de telefone, endereço E-mail etc.

Como usamos suas informações pessoais:

Recolhido por nós informação pessoal nos permite entrar em contato com você e informá-lo sobre ofertas exclusivas, promoções e outros eventos e eventos futuros.
De tempos em tempos, podemos usar suas informações pessoais para enviar avisos e mensagens importantes.
Também podemos usar informações pessoais para fins internos, como auditoria, análise de dados e vários estudos para melhorar os serviços que prestamos e para lhe fornecer recomendações sobre os nossos serviços.
Se você participar de um sorteio, concurso ou incentivo semelhante, poderemos usar as informações fornecidas para administrar tais programas.

Divulgação a terceiros

Não divulgamos informações recebidas de você a terceiros.

Exceções:

Se necessário - de acordo com a lei, ordem judicial, dentro litígio, e/ou com base em solicitações públicas ou solicitações de agências governamentais no território da Federação Russa - divulgue suas informações pessoais. Também podemos divulgar informações sobre você se determinarmos que tal divulgação é necessária ou apropriada para segurança, aplicação da lei ou outras ocasiões importantes.
No caso de uma reorganização, fusão ou venda, podemos transferir as informações pessoais que coletamos para o sucessor terceirizado relevante.

Proteção de informações pessoais

Tomamos precauções - incluindo administrativas, técnicas e físicas - para proteger suas informações pessoais contra perda, roubo e uso indevido, bem como de acesso, divulgação, alteração e destruição não autorizados.

Mantendo sua privacidade no nível da empresa

Para garantir que suas informações pessoais estejam seguras, comunicamos práticas de privacidade e segurança aos nossos funcionários e aplicamos rigorosamente as práticas de privacidade.

Vamos repetir a definição do ângulo entre uma linha e um plano.

Definição. O ângulo entre uma linha e um plano que intercepta esta linha e não é perpendicular a ela, é o ângulo entre a linha e sua projeção no plano.

Seja dado um plano γ e uma reta a que interceptam este plano e não são perpendiculares a ele.

Vamos construir o ângulo entre a linha a e o plano γ:

De qualquer ponto da reta a conveniente para nós, soltamos a perpendicular ao plano γ;
Através dos pontos das bases da oblíqua e perpendicular trace uma linha b. Linha b - projeção da linha a no plano γ;
O ângulo agudo entre as linhas a e b é o ângulo entre a linha a e o plano γ, ou seja. ∠(a;b)= ∠(a;γ) , onde ∠(a;b) é o ângulo entre as linhas aeb; ∠(a;γ) - ângulo entre a reta a e o plano γ.

Para resolver problemas usando o método de coordenadas, precisamos lembrar o seguinte:

3. Se as coordenadas do vetor de direção ( a 1 ; b 1 ; c 1 ) e do vetor normal são conhecidas
(a; b; c), então o ângulo entre a linha a e o plano γ é calculado pela fórmula que derivaremos agora.

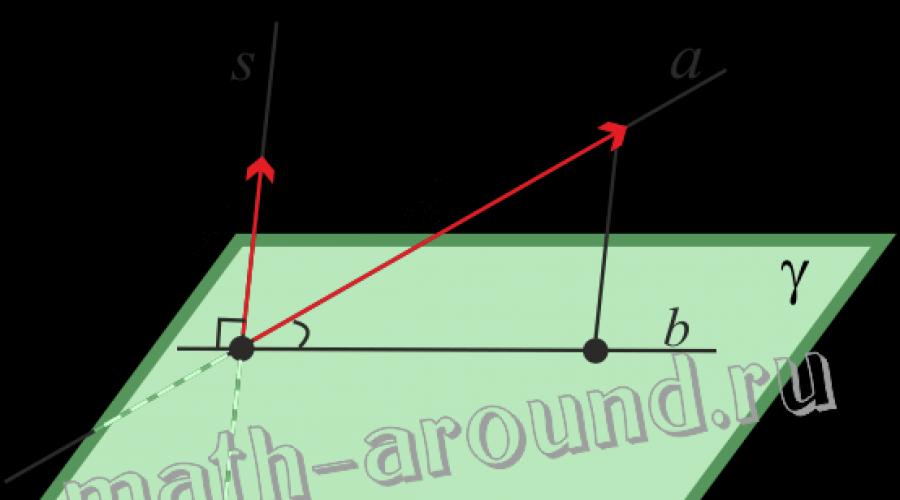
Conhecemos a fórmula para encontrar o ângulo entre as linhas:

; (1)
∠(s; a) = 90°-∠(a; b), então cos∠(s;a)=cos(90°-∠(a;b))=sen ∠(a;b); (2)
De (1) e (2) => ; (3)
, onde é o ângulo entre os vetores m e n; (quatro)
Substituímos (4) em (3) e como ∠(a;b)= ∠(a;γ), então temos:

4. Se as coordenadas do vetor normal são desconhecidas, então precisamos conhecer a equação do plano.

Qualquer plano em um sistema de coordenadas retangulares pode ser dado pela equação

ax + por + cz + d = 0,

onde pelo menos um dos coeficientes a, b, c é diferente de zero. Esses coeficientes serão as coordenadas do vetor normal, ou seja, (a; b; c).

Algoritmo para resolver problemas de encontrar o ângulo entre uma linha reta e um plano usando o método de coordenadas:

Fazemos um desenho no qual marcamos uma linha reta e um plano;
Introduzimos um sistema de coordenadas retangulares;
Encontramos as coordenadas do vetor de direção pelas coordenadas de seu início e fim;
Encontramos as coordenadas do vetor normal ao plano;
Substituímos os dados obtidos na fórmula do seno do ângulo entre a reta e o plano;
Encontre o valor do ângulo em si.

Considere o problema:
1. No cubo ABCDA 1 B 1 C 1 D 1 encontre a tangente do ângulo entre a linha AC 1 e o plano BDD 1.
Solução:

1. Vamos introduzir um sistema de coordenadas retangulares com origem no ponto D.
2. Encontre as coordenadas do vetor diretor AC 1 . Para fazer isso, primeiro determine as coordenadas dos pontos A e C 1:
A(0; 1; 0);
C1 (1; 0; 1).
{1; -1; 1}.
3. Encontre as coordenadas do vetor normal ao plano BB 1 D 1 . Para fazer isso, encontramos as coordenadas de três pontos do plano que não estão em uma linha reta e compomos a equação do plano:
D(0; 0; 0);
D1 (0; 0; 1);
B(1; 1; 0);
D: a⋅0+b⋅0+c⋅0+d=0;
D1: a⋅0+b⋅0+c⋅1+d=0;
B: a⋅1+b⋅1+c⋅0+d=0.

Substituir na equação: a⋅x+(-a)⋅y+0⋅z+0 = 0;
a⋅x-a⋅y = 0; |:a
x-y = 0.
Assim, o vetor normal ao plano BDD 1 tem as coordenadas:
{1;-1; 0}.
4. Encontre o seno entre a reta AC 1 e o plano BDD 1:

5. Vamos usar a identidade trigonométrica básica e encontrar o cosseno do ângulo entre a reta AC 1 e o plano BDD 1:

6. Encontre a tangente do ângulo entre a reta AC 1 e o plano BDD 1:

Responda: .

2. Em uma pirâmide quadrangular regular SABCD, cujas arestas são iguais a 1, encontre o seno do ângulo entre a linha BD e o plano SBC.

Solução:

1. Vamos introduzir um sistema de coordenadas retangulares com origem no ponto B.
2. Encontre as coordenadas do vetor de direção BD . Para fazer isso, primeiro determine as coordenadas dos pontos B e D:

3. Encontre as coordenadas do vetor normal ao plano SBC. Para fazer isso, encontramos as coordenadas de três pontos do plano que não estão em uma linha reta e compomos a equação do plano SBC:

Como você conseguiu as coordenadas do ponto S?

A partir do ponto S, desceu-se uma perpendicular ao plano da base ABC. O ponto de interseção foi designado por O. O ponto O é a projeção do ponto S no plano ABC. Suas coordenadas x e y serão as duas primeiras coordenadas do ponto S.

Tendo aprendido o valor da altura da pirâmide, encontramos a terceira coordenada do ponto S (ao longo do eixo z)

O triângulo SOB é um triângulo retângulo, portanto, de acordo com o teorema de Pitágoras:

A equação do plano tem a forma ax+by+cz+d=0. Substitua as coordenadas dos pontos nesta equação:

Temos um sistema de três equações:

Substituindo na equação:

Assim, o vetor normal ao plano SBD tem coordenadas:

.
4. Encontre o seno entre a linha BD e o plano SBD.

O conceito da projeção de uma figura em um plano

Para introduzir o conceito de ângulo entre uma linha reta e um plano, primeiro é necessário entender um conceito como a projeção de uma figura arbitrária em um plano.

Definição 1

Seja-nos dado um ponto arbitrário $A$. O ponto $A_1$ chama-se projeção do ponto $A$ sobre o plano $\alpha $ se for a base da perpendicular traçada do ponto $A$ ao plano $\alpha $ (Fig. 1).

Figura 1. Projeção de um ponto em um plano

Definição 2

Seja dado um valor arbitrário $F$. A figura $F_1$ é chamada de projeção da figura $F$ sobre o plano $\alpha $, composta pelas projeções de todos os pontos da figura $F$ sobre o plano $\alpha $ (Fig. 2).

Figura 2. Projeção de uma figura em um plano

Teorema 1

A projeção de uma linha reta não perpendicular ao plano é uma linha reta.

Prova.

Seja dado um plano $\alpha $ e uma reta $d$ que o intercepta e não é perpendicular a ele. Escolhemos um ponto $M$ na reta $d$ e desenhamos sua projeção $H$ no plano $\alpha $. Desenhe o plano $\beta $ pela reta $(MH)$. Obviamente, este plano será perpendicular ao plano $\alpha $. Deixe que eles se cruzem ao longo da linha $m$. Considere um ponto arbitrário $M_1$ da linha $d$ e desenhe a linha $(M_1H_1$) através dele paralela à linha $(MH)$ (Fig. 3).

Figura 3

Como o plano $\beta $ é perpendicular ao plano $\alpha $, então $M_1H_1$ é perpendicular à reta $m$, ou seja, o ponto $H_1$ é a projeção do ponto $M_1$ no plano $\alfa $. Como a escolha do ponto $M_1$ é arbitrária, todos os pontos da reta $d$ são projetados na reta $m$.

Argumentando da mesma forma. Na ordem inversa, obteremos que cada ponto da reta $m$ é uma projeção de algum ponto da reta $d$.

Assim, a linha $d$ é projetada na linha $m$.

O teorema foi provado.

O conceito do ângulo entre uma linha e um plano

Definição 3

O ângulo entre uma linha reta que intercepta um plano e sua projeção neste plano é chamado de ângulo entre a linha reta e o plano (Fig. 4).

Figura 4. Ângulo entre uma linha e um plano

Registramos aqui algumas observações.

Observação 1

Se a linha é perpendicular ao plano. Então o ângulo entre a linha e o plano é $90^\circ$.

Observação 2

Se a linha é paralela ou está em um plano. Então o ângulo entre a linha e o plano é igual a $0^\circ$.

Exemplos de tarefas

Exemplo 1

Seja-nos dado um paralelogramo $ABCD$ e um ponto $M$ que não está no plano do paralelogramo. Prove que os triângulos $AMB$ e $MBC$ são retângulos se o ponto $B$ é a projeção do ponto $M$ no plano do paralelogramo.

Prova.

Vamos descrever a condição do problema na figura (Fig. 5).

Figura 5

Como o ponto $B$ é a projeção do ponto $M$ no plano $(ABC)$, a reta $(MB)$ é perpendicular ao plano $(ABC)$. Pela Observação 1, obtemos que o ângulo entre a reta $(MB)$ e o plano $(ABC)$ é igual a $90^\circ$. Consequentemente

\[\angle MBC=MBA=(90)^0\]

Portanto, os triângulos $AMB$ e $MBC$ são retângulos.

Exemplo 2

Plano $\alpha $ é dado. Um segmento é desenhado em um ângulo $\varphi $ com este plano, cujo início está no plano dado. A projeção deste segmento é duas vezes menor que o próprio segmento. Encontre o valor de $\varphi $.

Solução.

Considere a Figura 6.

Figura 6

Por suposição, temos

Como o triângulo $BCD$ é retângulo, então, pela definição do cosseno

\ \[\varphi =arccos\frac(1)(2)=(60)^0\]

O curso em vídeo "Get an A" inclui todos os tópicos necessários para um sucesso passando no exame em matemática para 60-65 pontos. Completamente todas as tarefas 1-13 do Perfil USE em matemática. Também adequado para passar o Basic USE em matemática. Se você quer passar no exame com 90-100 pontos, você precisa resolver a parte 1 em 30 minutos e sem erros!

Curso de preparação para o exame do 10º ao 11º ano, bem como para professores. Tudo o que você precisa para resolver a parte 1 do exame de matemática (os primeiros 12 problemas) e o problema 13 (trigonometria). E isso são mais de 70 pontos no Exame Estadual Unificado, e nem um estudante de cem pontos nem um humanista podem prescindir deles.

Toda a teoria necessária. Maneiras Rápidas soluções, armadilhas e segredos do exame. Todas as tarefas relevantes da parte 1 das tarefas do Banco de FIPI foram analisadas. O curso está em total conformidade com os requisitos do USE-2018.

O curso contém 5 grandes tópicos, 2,5 horas cada. Cada tópico é dado do zero, de forma simples e clara.

Centenas de tarefas de exame. Problemas de texto e teoria das probabilidades. Algoritmos de resolução de problemas simples e fáceis de lembrar. Geometria. Teoria, material de referência, análise de todos os tipos de tarefas de USE. Estereometria. Truques complicados soluções, dicas úteis, desenvolvimento da imaginação espacial. Trigonometria do zero - à tarefa 13. Compreender em vez de estudar. Explicação visual de conceitos complexos. Álgebra. Raízes, potências e logaritmos, função e derivada. Base para solução Tarefas desafiantes 2 partes do exame.

O artigo começa com a definição do ângulo entre uma linha e um plano. Este artigo mostrará como encontrar o ângulo entre uma linha reta e um plano usando o método de coordenadas. A solução de exemplos e tarefas será considerada em detalhe.

Yandex.RTB R-A-339285-1

Em primeiro lugar, é necessário repetir o conceito de linha reta no espaço e o conceito de plano. Para determinar o ângulo entre uma linha e um plano, várias definições auxiliares são necessárias. Vamos considerar essas definições em detalhes.

Definição 1

Linha e plano se cruzam quando eles tiverem um ponto comum, ou seja, é o ponto de intersecção da linha e do plano.

Uma linha que cruza um plano pode ser perpendicular ao plano.

Definição 2

A linha é perpendicular ao plano quando é perpendicular a qualquer linha nesse plano.

Definição 3

Projeção do ponto M em um planoγ é o próprio ponto se estiver em dado avião, ou é o ponto de intersecção do plano com uma reta perpendicular ao plano γ que passa pelo ponto M, desde que não pertença ao plano γ.

Definição 4

Projeção de uma linha reta a em um planoγ é o conjunto de projeções de todos os pontos da linha dada no plano.

Disso obtemos que a projeção de uma reta perpendicular ao plano γ tem um ponto de interseção. Obtemos que a projeção da reta a é uma reta pertencente ao plano γ e que passa pelo ponto de interseção da reta a com o plano. Considere a figura abaixo.

No este momento temos todas as informações e dados necessários para formular a definição do ângulo entre uma linha reta e um plano

Definição 5

Ângulo entre a linha e o plano chamado de ângulo entre esta linha e sua projeção neste plano, e a linha não é perpendicular a ela.

A definição do ângulo dada acima ajuda a concluir que o ângulo entre uma linha e um plano é o ângulo entre duas linhas que se cruzam, ou seja, uma dada linha juntamente com sua projeção no plano. Isso significa que o ângulo entre eles será sempre agudo. Vejamos a imagem abaixo.

O ângulo localizado entre uma linha e um plano é considerado reto, ou seja, igual a 90 graus, e o ângulo localizado entre linhas paralelas não é definido. Há casos em que seu valor é tomado igual a zero.

Tarefas onde é necessário encontrar o ângulo entre uma linha reta e um plano possuem muitas variações da solução. O curso da solução em si depende dos dados disponíveis sobre a condição. Companheiros freqüentes da solução são sinais de semelhança ou igualdade de figuras, cossenos, senos, tangentes de ângulos. Encontrar o ângulo é possível usando o método de coordenadas. Vamos considerá-lo com mais detalhes.

Se um sistema de coordenadas retangular é introduzido no espaço tridimensional sobre x y z, então uma linha reta a é definida nele, cruzando o plano γ no ponto M, e não é perpendicular ao plano. É necessário encontrar o ângulo α localizado entre a reta dada e o plano.

Primeiro você precisa aplicar a definição do ângulo entre a linha e o plano usando o método de coordenadas. Então obtemos o seguinte.

No sistema de coordenadas O x y z, especifica-se uma reta a, à qual correspondem as equações da reta no espaço e o vetor diretor do espaço direto, para o plano γ corresponde a equação do plano e o vetor normal de o avião. Então a → = (a x , a y , a z) é o vetor direcional da reta dada a , e n → (n x , n y , n z) é o vetor normal para o plano γ . Se imaginarmos que temos as coordenadas do vetor diretor da reta a e do vetor normal do plano γ, então suas equações são conhecidas, ou seja, são dadas por condição, então é possível determinar os vetores a → e n → , com base na equação.

Para calcular o ângulo, você precisa transformar a fórmula que permite obter o valor desse ângulo usando as coordenadas disponíveis do vetor diretor do vetor direto e normal.

É necessário adiar os vetores a → e n → , partindo do ponto de interseção da reta a com o plano γ . Existem 4 opções para a localização desses vetores em relação às linhas e planos fornecidos. Considere a imagem abaixo, que tem todas as 4 variações.

A partir daqui temos que o ângulo entre os vetores a → e n → tem a designação a → , n → ^ e é agudo, então o ângulo desejado αlocalizado entre a linha e o plano é complementado, ou seja, obtemos uma expressão de a forma a → , n → ^ = 90 ° - α . Quando pela condição a → , n → ^ > 90 ° , então temos a → , n → ^ = 90 ° + α .

Portanto, temos que os cossenos ângulos iguais são iguais, então as últimas igualdades são escritas como um sistema

cos a → , n → ^ = cos 90 ° - α , a → , n → ^< 90 ° cos a → , n → ^ = cos 90 ° + α , a → , n → ^ >90°

Você deve usar fórmulas de conversão para simplificar expressões. Então obtemos igualdades da forma cos a → , n → ^ = sin α , a → , n → ^< 90 ° cos a → , n → ^ = - s i n α , a → , n → ^ >90°.

Após as transformações, o sistema assume a forma sen α = cos a → , n → ^ , a → , n → ^< 90 ° sin α = - cos a → , n → ^ , a → , n → ^ >90 ° ⇔ sen α = cos a → , n → ^ , a → , n → ^ > 0 sen α = -cos a → , n → ^ , a → , n → ^< 0 ⇔ ⇔ sin α = cos a → , n → ^

Disto obtemos que o seno do ângulo entre a reta e o plano é igual ao módulo do cosseno do ângulo entre o vetor diretor da reta e o vetor normal do plano dado.

A seção sobre encontrar o ângulo formado por dois vetores revelou que esse ângulo assume o valor do produto escalar dos vetores e o produto desses comprimentos. O processo de cálculo do seno do ângulo obtido pela interseção de uma linha reta e um plano é realizado pela fórmula

sin α = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2

Isso significa que a fórmula para calcular o ângulo entre uma linha e um plano com as coordenadas do vetor diretor da linha e o vetor normal do plano após a transformação acaba sendo

α = a r c sen a → , n → ^ a → n → = a r c sen a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2

Encontrar o cosseno com um seno conhecido é permitido aplicando o básico identidade trigonométrica. A interseção de uma linha e um plano forma canto afiado. Isso sugere que seu valor será um número positivo e seu cálculo é feito a partir da fórmula cos α \u003d 1 - sin α.

Vamos resolver vários exemplos semelhantes para consolidar o material.

Exemplo 1

Encontre o ângulo, seno, cosseno do ângulo formado pela linha reta x 3 = y + 1 - 2 = z - 11 6 e o plano 2 x + z - 1 = 0 .

Solução

Para obter as coordenadas do vetor diretor, é necessário considerar as equações canônicas da reta no espaço. Então temos que a → = (3, - 2, 6) é o vetor diretor da linha x 3 = y + 1 - 2 = z - 11 6 .

Para encontrar as coordenadas do vetor normal, é necessário considerar a equação geral do plano, pois sua presença é determinada pelos coeficientes disponíveis na frente de variáveis de equação. Então temos que para o plano 2 x + z - 1 = 0 o vetor normal tem a forma n → = (2 , 0 , 1) .

É necessário proceder ao cálculo do seno do ângulo entre a linha e o plano. Para fazer isso, é necessário substituir as coordenadas dos vetores a → e b → na fórmula dada. Obtemos uma expressão como

sen α = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2 = = 3 2 + (- 2 ) 0 + 6 1 3 2 + (- 2) 2 + 6 2 2 2 + 0 2 + 1 2 = 12 7 5

A partir daqui encontramos o valor do cosseno e o valor do próprio ângulo. Nós temos:

cos α = 1 - sin α = 1 - 12 7 5 2 = 101 7 5

Responda: sen α = 12 7 5 , cos α = 101 7 5 , α = a r c cos 101 7 5 = a r c sen 12 7 5 .

Exemplo 2

Existe uma pirâmide construída usando os valores dos vetores A B → = 1 , 0 , 2 , A C → = (- 1 , 3 , 0) , A D → = 4 , 1 , 1 . Encontre o ângulo entre a linha A D e o plano A B C.

Solução

Para calcular o ângulo desejado, é necessário ter os valores das coordenadas do vetor diretor da linha e do vetor normal do plano. para a reta A D o vetor de direção tem coordenadas A D → = 4 , 1 , 1 .

O vetor normal n → pertencente ao plano A B C é perpendicular ao vetor A B → e A C → . Isso implica que o vetor normal do plano A B C pode ser considerado produto vetorial vetores A B → e A C → . Calculamos isso pela fórmula e obtemos:

n → = A B → × A C → = i → j → k → 1 0 2 - 1 3 0 = - 6 i → - 2 j → + 3 k → ⇔ n → = (- 6 , - 2 , 3 )

É necessário substituir as coordenadas dos vetores para calcular o ângulo desejado formado pela interseção da linha e do plano. obtemos uma expressão como:

α = a r c sen A D → , n → ^ A D → n → = a r c sen 4 - 6 + 1 - 2 + 1 3 4 2 + 1 2 + 1 2 - 6 2 + - 2 2 + 3 2 = a r c sin 23 21 2

Responda: a r c sin 23 21 2 .

Se você notar um erro no texto, destaque-o e pressione Ctrl+Enter