Boletim Científico do Estudante Internacional. Problemas de expansão de funções em série de Fourier e sua solução. Encontre os pontos zero do seno

20.09.2019

Revisão de comentários sobre o ritual psíquico Arina Evdokimova para a realização do desejo

Marilyn Kerro - biografia e vida pessoal de uma bruxa estoniana

O que significa ver baratas em um sonho - interpretação para mulheres

Em muitos casos, a tarefa de obter (calcular) o espectro do sinal é a seguinte. Existe um ADC, que com uma frequência de amostragem Fd converte um sinal contínuo que chega à sua entrada durante o tempo T, em leituras digitais - N peças. Em seguida, a matriz de leituras é alimentada em um determinado programa que fornece N / 2 de alguns valores numéricos (o programador que retirado da internet escreveu um programa, afirma que faz a transformada de Fourier).

Para verificar se o programa está funcionando corretamente, formaremos um array de leituras como a soma de duas senoides sin(10*2*pi*x)+0,5*sin(5*2*pi*x) e o colocaremos no programa. O programa desenhou o seguinte:

fig.1 Gráfico da função tempo do sinal

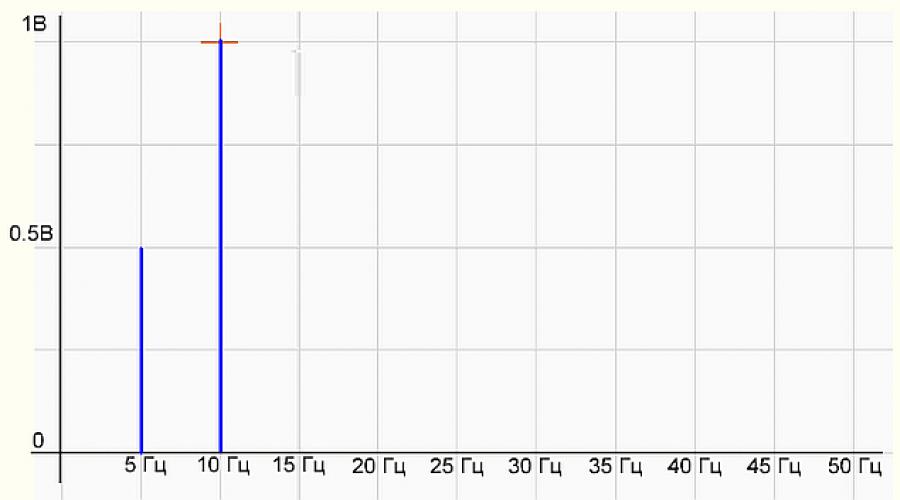
fig.2 Gráfico do espectro do sinal

No gráfico do espectro há dois bastões (harmônicos) de 5 Hz com amplitude de 0,5 V e 10 Hz - com amplitude de 1 V, tudo como na fórmula do sinal original. Está tudo bem, programador bem feito! O programa está funcionando corretamente.

Isso significa que, se aplicarmos um sinal real de uma mistura de duas senoides à entrada do ADC, obteremos um espectro semelhante composto por dois harmônicos.

Total, nosso real sinal medido, duração 5 seg, digitalizado pelo ADC, ou seja, representado discreto conta, tem discreto não periódico alcance.

Do ponto de vista matemático, quantos erros há nessa frase?

Agora as autoridades decidiram que 5 segundos é muito longo, vamos medir o sinal em 0,5 segundos.

fig.3 Gráfico da função sin(10*2*pi*x)+0,5*sin(5*2*pi*x) para um período de medição de 0,5 segundos

fig.4 Espectro da função

Algo não está certo! O harmônico de 10 Hz é desenhado normalmente, mas em vez de um bastão de 5 Hz, vários harmônicos incompreensíveis apareceram. Procuramos na Internet, o que e como ...

Em, eles dizem que zeros devem ser adicionados ao final da amostra e o espectro será desenhado normal.

fig.5 Zeros finalizados até 5 segundos

fig.6 Temos o espectro

Ainda não o que era em 5 segundos. Você tem que lidar com a teoria. Vamos para Wikipédia- fonte de conhecimento.

2. Uma função contínua e sua representação por uma série de Fourier

Matematicamente, nosso sinal com duração de T segundos é alguma função f(x) definida no segmento (0, T) (X em este caso- Tempo). Tal função sempre pode ser representada como uma soma de funções harmônicas (seno ou cosseno) da forma:

(1), onde:

K - número da função trigonométrica (número do componente harmônico, número harmônico)
T - segmento onde a função é definida (duração do sinal)
Ak - amplitude do k-ésimo componente harmônico,
θk - fase inicial da k-ésima componente harmônica

O que significa "representar uma função como a soma de uma série"? Isso significa que somando os valores das componentes harmônicas da série de Fourier em cada ponto, obteremos o valor da nossa função neste ponto.

(Mais estritamente, o desvio padrão da série da função f(x) tenderá a zero, mas apesar da convergência padrão, a série de Fourier da função, em geral, não precisa convergir pontualmente para ela. Veja https: //ru.wikipedia.org/wiki/Fourier_Series .)

Esta série também pode ser escrita como:

(2),
Onde , k-ésimo complexo amplitude.

A relação entre os coeficientes (1) e (3) é expressa pelas seguintes fórmulas:

Observe que todas essas três representações da série de Fourier são completamente equivalentes. Às vezes, ao trabalhar com séries de Fourier, é mais conveniente usar os expoentes do argumento imaginário em vez de senos e cossenos, ou seja, usar a transformada de Fourier na forma complexa. Mas é conveniente usarmos a fórmula (1), onde a série de Fourier é representada como uma soma de ondas cosseno com as amplitudes e fases correspondentes. De qualquer forma, é incorreto dizer que o resultado da transformada de Fourier do sinal real serão as amplitudes complexas dos harmônicos. Como o wiki diz corretamente, "A transformada de Fourier (ℱ) é uma operação que mapeia uma função de uma variável real para outra função, também de uma variável real".

Total:
A base matemática da análise espectral de sinais é a transformada de Fourier.

A transformada de Fourier nos permite representar uma função contínua f(x) (sinal) definida no intervalo (0, T) como a soma de um número infinito (uma série infinita) funções trigonométricas(ondas sinusóides e/ou cosseno) com certas amplitudes e fases, também consideradas no segmento (0, T). Tal série é chamada de série de Fourier.

Há mais alguns pontos que precisam ser entendidos para aplicação correta Transformadas de Fourier para análise de sinal. Se considerarmos a série de Fourier (a soma das senoides) em todo o eixo X, podemos ver que fora do segmento (0, T), a função representada pela série de Fourier repetirá periodicamente nossa função.

Por exemplo, no gráfico da Fig. 7, a função original é definida no segmento (-T \ 2, + T \ 2), e a série de Fourier representa uma função periódica definida em todo o eixo x.

Isso ocorre porque as próprias senoides são funções periódicas, respectivamente, e sua soma será uma função periódica.

fig.7 Representação de uma função original não periódica por uma série de Fourier

Por isso:

Nossa função original é contínua, não periódica, definida em algum intervalo de comprimento T.
O espectro desta função é discreto, ou seja, apresenta-se como uma série infinita de componentes harmônicos - a série de Fourier.
De fato, a série de Fourier define alguns função periódica, coincidindo com a nossa no segmento (0, T), mas para nós essa periodicidade não é essencial.

Os períodos das componentes harmônicas são múltiplos do segmento (0, T) no qual a função original f(x) é definida. Em outras palavras, os períodos harmônicos são múltiplos da duração da medição do sinal. Por exemplo, o período do primeiro harmônico da série de Fourier é igual ao intervalo T no qual a função f(x) é definida. O período do segundo harmônico da série de Fourier é igual ao intervalo T/2. E assim por diante (ver Fig. 8).

fig.8 Períodos (frequências) das componentes harmônicas da série de Fourier (aqui T=2π)

Assim, as frequências dos componentes harmônicos são múltiplos de 1/T. Ou seja, as frequências das componentes harmônicas Fk são iguais a Fk= k\T, onde k varia de 0 a ∞, por exemplo, k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (na frequência zero - componente constante).

Seja nossa função original um sinal gravado para T=1 seg. Então o período do primeiro harmônico será igual à duração do nosso sinal T1=T=1 seg e a frequência do harmônico é 1 Hz. O período do segundo harmônico será igual à duração do sinal dividido por 2 (T2=T/2=0,5 seg) e a frequência é de 2 Hz. Para o terceiro harmônico T3=T/3 seg e a frequência é de 3 Hz. etc.

O passo entre harmônicos neste caso é de 1 Hz.

Assim, um sinal com duração de 1 segundo pode ser decomposto em componentes harmônicos (para obter um espectro) com resolução de frequência de 1 Hz.
Para aumentar a resolução em 2 vezes para 0,5 Hz, é necessário aumentar a duração da medição em 2 vezes - até 2 segundos. Um sinal com duração de 10 segundos pode ser decomposto em componentes harmônicos (para obter um espectro) com resolução de frequência de 0,1 Hz. Não há outras maneiras de aumentar a resolução de frequência.

Existe uma maneira de aumentar artificialmente a duração do sinal adicionando zeros ao conjunto de amostras. Mas não aumenta a resolução de frequência real.

3. Sinais discretos e transformada discreta de Fourier

Com desenvolvimento tecnologia digital as formas de armazenamento de dados de medição (sinais) também mudaram. Se antes o sinal podia ser gravado em um gravador e armazenado em fita de forma analógica, agora os sinais são digitalizados e armazenados em arquivos na memória do computador como um conjunto de números (contagens).

O esquema usual para medir e digitalizar um sinal é o seguinte.

fig.9 Esquema do canal de medição

O sinal do transdutor de medição chega ao ADC durante um período de tempo T. As amostras de sinal (amostra) obtidas durante o tempo T são transferidas para o computador e armazenadas na memória.

fig.10 Sinal digitalizado - N leituras recebidas no tempo T

Quais são os requisitos para os parâmetros de digitalização de sinal? Um dispositivo que converte a entrada sinal analógico em um código discreto ( sinal digital) é chamado de conversor analógico-digital (ADC) (Wiki).

Um dos principais parâmetros do ADC é a taxa de amostragem máxima (ou taxa de amostragem, taxa de amostragem inglesa) - a frequência de coleta de amostras de um sinal contínuo no tempo durante sua amostragem. Medido em hertz. ((Wiki))

De acordo com o teorema de Kotelnikov, se um sinal contínuo tem um espectro limitado pela frequência Fmax, então ele pode ser restaurado completa e exclusivamente de suas amostras discretas tomadas em intervalos de tempo. , ou seja com frequência Fd ≥ 2*Fmax, onde Fd - taxa de amostragem; Fmax - frequência máxima do espectro do sinal. Em outras palavras, a taxa de amostragem do sinal (taxa de amostragem ADC) deve ser pelo menos 2 vezes a frequência máxima do sinal que queremos medir.

E o que acontecerá se fizermos leituras com uma frequência menor do que a exigida pelo teorema de Kotelnikov?

Nesse caso, ocorre o efeito de "aliasing" (também conhecido como efeito estroboscópico, efeito moiré), em que o sinal de alta frequência após a digitalização se transforma em um sinal de baixa frequência que na verdade não existe. Na fig. 11 onda senoidal vermelha de alta frequência é o sinal real. A onda senoidal azul de baixa frequência é um sinal fictício resultante do fato de que mais da metade do período de um sinal de alta frequência tem tempo para passar durante o tempo de amostragem.

Arroz. 11. O aparecimento de um sinal falso de baixa frequência quando a taxa de amostragem não é alta o suficiente

Para evitar o efeito de aliasing, um filtro anti-aliasing especial é colocado na frente do ADC - LPF (filtro passa-baixa), que passa frequências abaixo da metade da frequência de amostragem do ADC e corta as frequências mais altas.

Para calcular o espectro de um sinal a partir de suas amostras discretas, é utilizada a transformada discreta de Fourier (DFT). Notamos mais uma vez que o espectro de um sinal discreto é "por definição" limitado pela frequência Fmax, que é menos da metade da frequência de amostragem Fd. Portanto, o espectro de um sinal discreto pode ser representado pela soma de um número finito de harmônicos, em contraste com a soma infinita para a série de Fourier de um sinal contínuo, cujo espectro pode ser ilimitado. De acordo com o teorema de Kotelnikov, a frequência harmônica máxima deve ser tal que seja responsável por pelo menos duas amostras, de modo que o número de harmônicos seja igual à metade do número de amostras do sinal discreto. Ou seja, se houver N amostras na amostra, então o número de harmônicos no espectro será igual a N/2.

Considere agora a transformada discreta de Fourier (DFT).

Comparando com a série de Fourier

Vemos que eles coincidem, exceto que o tempo na DFT é discreto e o número de harmônicos é limitado a N/2 - metade do número de amostras.

As fórmulas DFT são escritas em variáveis inteiras adimensionais k, s, onde k são os números de amostras de sinal, s são os números de componentes espectrais.
O valor de s mostra o número de oscilações completas do harmônico no período T (a duração da medição do sinal). A transformada discreta de Fourier é usada para encontrar as amplitudes e fases dos harmônicos numericamente, ou seja, "no computador"

Voltando aos resultados obtidos no início. Como mencionado acima, ao expandir uma função não periódica (nosso sinal) em uma série de Fourier, a série de Fourier resultante na verdade corresponde a uma função periódica com período T. (Fig. 12).

fig.12 Função periódica f(x) com período Т0, com período de medição Т>T0

Como pode ser visto na Fig. 12, a função f(x) é periódica com período Т0. No entanto, devido ao fato de que a duração da amostra de medição T não coincide com o período da função T0, a função obtida como uma série de Fourier tem uma descontinuidade no ponto T. Como resultado, o espectro desta função será contém um grande número de harmônicos de alta frequência. Se a duração da amostra de medição T coincidisse com o período da função T0, então apenas o primeiro harmônico (uma senóide com período igual à duração da amostra) estaria presente no espectro obtido após a transformada de Fourier, pois a função f (x) é uma senóide.

Em outras palavras, o programa DFT "não sabe" que nosso sinal é um "pedaço de uma onda senoidal", mas está tentando representar uma função periódica como uma série, que tem uma lacuna devido à inconsistência dos pedaços individuais de a onda senoidal.

Como resultado, aparecem harmônicos no espectro, que no total devem representar a forma da função, incluindo essa descontinuidade.

Assim, para obter o espectro "correto" do sinal, que é a soma de várias senoides com diferentes períodos, é necessário que um número inteiro de períodos de cada senóide caiba no período de medição do sinal. Na prática, esta condição pode ser satisfeita por uma duração suficientemente longa da medição do sinal.

Fig.13 Um exemplo da função e espectro do sinal do erro cinemático da caixa de engrenagens

Com uma duração mais curta, a imagem ficará "pior":

Fig.14 Um exemplo da função e espectro do sinal de vibração do rotor

Na prática, pode ser difícil entender onde estão os “componentes reais” e onde estão os “artefatos” causados pela não multiplicidade dos períodos dos componentes e a duração da amostra de sinal ou os “saltos e quebras” de a forma de onda. É claro que as palavras "componentes reais" e "artefatos" não são citadas em vão. A presença de muitos harmônicos no gráfico do espectro não significa que nosso sinal realmente “consiste” deles. É como pensar que o número 7 "consiste" nos números 3 e 4. O número 7 pode ser representado como a soma dos números 3 e 4 - isso está correto.

Assim é o nosso sinal... ou melhor, nem mesmo “nosso sinal”, mas uma função periódica compilada pela repetição do nosso sinal (amostragem) pode ser representada como uma soma de harmônicos (senoides) com certas amplitudes e fases. Mas em muitos casos importantes para a prática (veja as figuras acima), é realmente possível relacionar os harmônicos obtidos no espectro a processos reais, que são de natureza cíclica e contribuem significativamente para a forma do sinal.

Alguns resultados

1. O sinal real medido, duração T s, digitalizado pelo ADC, ou seja, representado por um conjunto de amostras discretas (N peças), possui um espectro não periódico discreto, representado por um conjunto de harmônicos (N/2 peças ).

2. O sinal é representado por um conjunto de valores reais e seu espectro é representado por um conjunto de valores reais. As frequências harmônicas são positivas. O fato de ser mais conveniente para os matemáticos representar o espectro de forma complexa usando frequências negativas não significa que “está certo” e “deve ser feito sempre assim”.

3. O sinal medido no intervalo de tempo T é determinado apenas no intervalo de tempo T. O que aconteceu antes de começarmos a medir o sinal e o que acontecerá depois disso - isso é desconhecido para a ciência. E no nosso caso - não é interessante. A DFT de um sinal de tempo limitado fornece seu espectro "real", no sentido de que, sob certas condições, permite calcular a amplitude e a frequência de seus componentes.

Materiais usados e outros materiais úteis.

Acima, vemos que a expansão das funções em séries de potências possibilita calcular os valores aproximados dessas funções com a precisão necessária. Mas existem muitas funções que não se expandem em séries de potências (séries de Taylor ou Maclaurin), porque os requisitos para funções são bastante estritos (a função deve ser infinitamente diferenciável, etc.). Portanto, outros tipos de séries funcionais também são usados, cujas condições de expansão são menos onerosas. Essas linhas incluem série trigonométrica.

Definição: série trigonométrica série funcional da forma:, (1)

onde existem números constantes chamados:

Os coeficientes da série trigonométrica.

Todos os termos da série (1) são funcionais não periódicos e têm um período mínimo comum 2p. Isso implica que, se a função f(x) for expandida em uma série trigonométrica (1), ou seja, é a soma desta série, então esta função deve ser a soma da série (1) apenas em algum intervalo de comprimento 2p.

As principais propriedades da série trigonométrica decorrem da propriedade principal do sistema de funções trigonométricas. Stochala uma definição.

Definição: Um sistema infinito de funções j1(x),j2(x),...,j3(x)... definido no segmento é chamado ortogonal neste segmento se as seguintes condições forem atendidas:
para m¹n;

para qualquer n.

Teorema: O sistema de funções trigonométricas é ortogonal no intervalo [-p,p].

Prova: Precisamos verificar as condições 1) e 2) da definição anterior.

1) Considere as integrais:

Vamos aplicar fórmulas trigonométricas:

Obviamente, com a ajuda deles, todas as integrais anteriores são reduzidas a integrais da forma:
e

Vamos calculá-los.

;

Assim, o primeiro requisito de ortogonalidade será cumprido.

2)
;

e o segundo requisito é cumprido h., etc.

Série trigonométrica de Fourier.

Seja uma função f(x) periódica com período 2p ser representada como a soma de uma série trigonométrica
(1).

para todo x de algum intervalo de comprimento 2p. Mas a soma da série S(x) é uma função periódica com período 2p. Portanto, o valor de f(x) e S(x) coincidem em toda a reta numérica (-¥, +¥). Portanto, basta estudar a igualdade (1) em algum intervalo de comprimento 2p, geralmente [-p,p] .

Então, seja f(x) a soma da série (1) em [-p,p] e, além disso, suponha que ela possa ser integrada termo a termo, portanto, um segmento. Isso, por exemplo, é possível se a série numérica dos coeficientes da série (1) convergir absolutamente, ou seja, série converge

(2).

Neste caso, os termos da série funcional (1) não excedem os termos correspondentes da série (2) em valor absoluto, o que implica a convergência uniforme da série (1), e, portanto, a possibilidade de sua não integração de -term sobre [-p,p].

Usamos isso para calcular o coeficiente a 0 . Integramos termo a termo ambas as partes da desigualdade (1) sobre [-p,p]:

Todas as integrais à direita, de acordo com a propriedade de ortogonalidade das funções trigonométricas, são iguais a zero, exceto a primeira. Então:
, Onde
(3).

Para calcular a até /k¹0/ multiplicamos ambos os lados de (1) por coskx. A série resultante também convergirá uniformemente em [-p,p], pois ½coskx1£1 e pode ser integrado termo a termo sobre [-p,p].

Pela mesma propriedade de ortogonalidade, todas as integrais à direita são iguais a zero, exceto a que contém um k.

Então
. Onde

(4).

Multiplicando ambos os lados de (1) por sen kx e integrando a igualdade resultante por , obtemos
. Onde

(5).

Os coeficientes calculados pelas fórmulas (3)-(5) são chamados

Coeficientes de Fourier para a função f(x), e a série trigonométrica (1) com esses coeficientes - ao lado da função de Fourier (x).

Note-se que nem sempre é possível integrar a série (1) termo a termo. Portanto, é formalmente possível calcular os coeficientes de Fourier, para compor a série de Fourier (1), mas não se pode garantir que essa série seja convergente; e se converge, então sua soma é uma função de f(x). Nesses casos, concordamos em vez de igualdade (1) “correspondência”:

funções. Essa transformação tem grande importância porque pode ser usado para resolver muitos problemas práticos. As séries de Fourier são usadas não apenas por matemáticos, mas também por especialistas em outras ciências.

A expansão de funções em uma série de Fourier é uma técnica matemática que pode ser observada na natureza se você usar um instrumento que detecte funções senoidais.

Este processo ocorre quando uma pessoa ouve um som. O ouvido humano é projetado de tal forma que pode sentir flutuações senoidais individuais na pressão do ar de diferentes frequências, o que, por sua vez, permite que uma pessoa reconheça a fala e ouça música.

O ouvido humano não percebe o som como um todo, mas através dos componentes de sua série de Fourier. cordas instrumento musical produz sons que são oscilações senoidais de várias frequências. A realidade da decomposição da luz em uma série de Fourier é representada por um arco-íris. A visão humana percebe a luz através de alguns de seus componentes de diferentes frequências de oscilações eletromagnéticas.

A transformada de Fourier é uma função que descreve a fase e a amplitude de senoides de uma determinada frequência. Essa transformação é usada para resolver equações que descrevem processos dinâmicos que ocorrem sob a ação da energia. As séries de Fourier resolvem o problema de extrair componentes constantes em sinais oscilatórios complexos, o que permitiu interpretar corretamente os dados obtidos em experimentos, observações em medicina, química e astronomia.

A descoberta desta transformação pertence ao matemático francês Jean Baptiste Joseph Fourier. Em homenagem a quem mais tarde foi nomeado perto de Fourier. Inicialmente, o cientista encontrou a aplicação de seu método no estudo e explicação dos mecanismos de condução de calor. Assumiu-se que a distribuição irregular inicial de calor pode ser representada na forma das senóides mais simples. Para cada um dos quais a temperatura mínima, máxima e fase serão determinadas. A função que descreve os picos superior e inferior da curva, a fase de cada harmônico, é chamada de transformada de Fourier da expressão de distribuição de temperatura. O autor da transformação propôs um método de decomposição função complexa como uma soma de funções cosseno periódicas, seno.

mirar trabalho de conclusão de cursoé o estudo da série de Fourier e a relevância da aplicação prática desta transformação.

Para atingir este objetivo, foram formuladas as seguintes tarefas:

1) dê o conceito de série trigonométrica de Fourier;

2) determinar as condições para a expansão de uma função em uma série de Fourier;

3) considere a expansão em série de Fourier de funções pares e ímpares;

4) considere a expansão em série de Fourier de uma função não periódica;

5) revelam a aplicação prática da série de Fourier.

Objeto de estudo: expansão de funções em uma série de Fourier.

Objeto de estudo: Série de Fourier.

Métodos de investigação: análise, síntese, comparação, método axiomático.

1.5. Série de Fourier para funções pares e ímpares

Considere a integral simétrica

onde é contínuo ou contínuo por partes. Fazemos uma mudança na primeira integral. Acreditamos. Então

Portanto, se uma função par, então (ou seja, o gráfico de uma função par é simétrico em torno do eixo e

Se é uma função ímpar, então (ou seja, o gráfico de uma função ímpar é simétrico em relação à origem) e

Aqueles. a integral simétrica de uma função par é igual a duas vezes a integral sobre metade do intervalo de integração, e a integral simétrica de uma função ímpar é zero.

Observe as duas propriedades a seguir de funções pares e ímpares:

1) o produto de uma função par por uma ímpar é uma função ímpar;

2) o produto de duas funções pares (ímpares) é uma função par.

Seja uma função par dada e expandindo neste segmento em uma série trigonométrica de Fourier. Usando os resultados obtidos acima, obtemos que os coeficientes desta série se parecerão com:

Se for uma função ímpar dada em um segmento e expandida neste segmento em uma série trigonométrica de Fourier, então os coeficientes desta série terão a seguinte aparência:

Portanto, a série trigonométrica de Fourier no segmento terá a forma

para uma função par:

(16)

para uma função ímpar:

A série (16) não contém os senos de múltiplos ângulos, ou seja, a série de Fourier de uma função par inclui apenas funções pares e um termo livre. A série (17) não contém cossenos de múltiplos ângulos, ou seja, a série de Fourier de uma função ímpar inclui apenas funções ímpares.

Definição. fileiras
são partes Gama completa Fourier e são chamados de incompletossérie trigonométrica de Fourier.

Se uma função é expandida em uma série trigonométrica incompleta (16) (ou (17)), então diz-se que elaexpande em uma série trigonométrica de Fourier em cossenos (ou senos).

1.6. Expansão de Fourier de uma função não periódica

1.6.1. Expansão em série de Fourier de funções em

Seja uma função dada em um intervalo e satisfaça as condições do teorema de Dirichlet nesse intervalo. Vamos mudar a variável. Deixe onde escolhemos para que a função argumento resultante seja definida. Por isso, consideramos que

A função resultante pode ser expandida em uma série de Fourier:

Onde

Vamos fazer uma substituição inversa⇒ Obter

Onde

(19)

Série (18) - Série de Fourier no principal sistema trigonométrico de funções

Assim, obtivemos que se uma função é dada em um segmento e satisfaz as condições do teorema de Dirichlet neste segmento, então ela pode ser expandida em uma série trigonométrica de Fourier (18) de acordo com o sistema trigonométrico de funções (20) .

A série trigonométrica de Fourier para uma função par dada em terá a forma

Onde

para uma função ímpar

Onde

Comente! Em alguns problemas, é necessário expandir uma função em uma série trigonométrica de Fourier em termos do sistema de funções (20) não em um segmento, mas em um segmento. Neste caso, basta alterar os limites de integração nas fórmulas (19) ((15), se, ou seja, neste caso

(23)

ou se

(24)

A soma da série trigonométrica de Fourier é uma função periódica com um período, que é uma continuação periódica determinada função. E para uma função periódica, a igualdade (4) é válida.

1.6.2. Expansão em série de Fourier de funções em

Seja uma função dada e satisfaça as condições do teorema de Dirichlet neste intervalo. Tal função também pode ser expandida em uma série de Fourier. Para fazer isso, a função deve ser estendida ao intervalo e a função resultante expandida em uma série de Fourier no segmento. Nesse caso, a série resultante deve ser considerada apenas no segmento em que a função é dada. Para conveniência dos cálculos, estendemos a definição da função de maneira par e ímpar.

1) Continuamos a função no intervalo de maneira par, ou seja, construímos uma nova função par, coincidindo no segmento com a função. Portanto, o gráfico dessa função é simétrico em relação ao eixo e coincide com o gráfico do segmento. Usando as fórmulas (21), encontramos os coeficientes da série de Fourier para a função e escrevemos a própria série de Fourier. A soma da série de Fourier para é uma função periódica, com um período. Irá coincidir com a função ligada em todos os pontos de continuidade.

2) Vamos estender a função no intervalo de maneira ímpar, ou seja, construir uma nova Função estranha, coincidindo com a função. O gráfico de tal função é simétrico em relação à origem das coordenadas e coincide com o gráfico do segmento. Usando as fórmulas (22), encontramos os coeficientes da série de Fourier para a função e escrevemos a própria série de Fourier. A soma da série de Fourier para é uma função periódica com um período. Irá coincidir com a função ligada em todos os pontos de continuidade.

Observações!

1) Da mesma forma, podemos expandir em uma série de Fourier uma função definida no segmento

2) Como a expansão de uma função em um segmento implica sua extensão ao segmento de forma arbitrária, então a série de Fourier para a função não será única.

1.6.3. Expansão em série de Fourier de funções em

Seja a função dada em um segmento arbitrário de comprimento e satisfaça as condições do teorema de Dirichlet sobre ele.

Então esta função pode ser expandida em uma série de Fourier. Para fazer isso, a função deve ser estendida periodicamente (com um ponto) para toda a reta numérica e a função resultante expandida em uma série de Fourier, que deve ser considerada apenas em um segmento. Devido à propriedade (3) das funções periódicas, temos

Portanto, os coeficientes de Fourier para a continuação obtida da função podem ser encontrados pelas fórmulas

(25)

2. Uso pratico Séries de Fourier

2.1. Problemas para a expansão de funções em uma série de Fourier e sua solução

Em uma série trigonométrica de Fourier, é necessário expandir uma função que é uma continuação periódica de uma função dada em um segmento. Para isso, é necessário utilizar um algoritmo de expansão de uma função periódica em uma série de Fourier.

Algoritmo para expandir uma função periódica em uma série de Fourier:

1) Construir um gráfico de uma dada função e sua continuação periódica;

2) Defina o período da função dada;

3) Determine a função par, ímpar ou visão geral;

4) Verificar a viabilidade das condições do teorema de Dirichlet;

5) Faça um registro formal da série de Fourier gerada por esta função;

6) Calcule os coeficientes de Fourier;

7) Escreva a série de Fourier para a função dada usando os coeficientes da série de Fourier (item 4).

Exemplo 1 Expanda a função em uma série de Fourier no intervalo.

Decisão:

1) Vamos construir um gráfico de uma dada função e sua continuação periódica.

2) O período de expansão da função.

3) A função é ímpar.

4) A função é contínua e monotônica ligada, ou seja, a função satisfaz as condições de Dirichlet.

5) Calcule os coeficientes da série de Fourier.

6) Escrevemos a série de Fourier substituindo os coeficientes de Fourier na fórmula

Responda:

Exemplo 2 Expandimos uma função com um período arbitrário em uma série de Fourier.

Solução: a função é definida no meio intervalo (-3; 3]. O período de expansão da função, meio período. Vamos expandir a função em uma série de Fourier

Na origem, a função é descontínua, então cada coeficiente de Fourier será representado como a soma de duas integrais.

Escrevemos a série de Fourier substituindo os coeficientes encontrados da série de Fourier na fórmula.

Exemplo 3 Expandir funçãoentreem uma série de Fourier em cossenos. Trace a soma da série.

Solução: continuamos a função no intervalo de forma par, ou seja, construímos uma nova função par que coincide com a função no segmento. Encontre os coeficientes da série de Fourier para a função e escreva a série de Fourier. A soma da série de Fourier para é uma função periódica, com um período. Irá coincidir com a função ligada em todos os pontos de continuidade.

A série trigonométrica de Fourier para a função se parecerá com

Encontre os coeficientes da série de Fourier

Assim, quando os coeficientes são encontrados, pode-se escrever a série de Fourier

Vamos traçar a soma da série

Exemplo 4 Dada uma função definida no segmento . Descubra se a função pode ser expandida em uma série de Fourier. Escreva a expansão da função em uma série de Fourier.

Decisão:

1) traçar um gráfico de função em .

2) a função é contínua e monotônica em , ou seja, de acordo com o teorema de Dirichlet, ela se expande em uma série trigonométrica de Fourier.

3) calcule os coeficientes de Fourier usando as fórmulas (1.19).

4) escreva a série de Fourier usando os coeficientes encontrados.

2.2. Exemplos da aplicação da série de Fourier em vários campos da atividade humana

A matemática é uma das ciências que ampla aplicação na prática. Qualquer processo produtivo e tecnológico é baseado em leis matemáticas. Inscrição várias ferramentas aparato matemático permite projetar dispositivos e unidades automatizadas capazes de realizar operações, cálculos complexos e cálculos no projeto de edifícios, estruturas.

As séries de Fourier são usadas por matemáticos em geometria pararesolução de problemas em geometria esférica; em mfísica matemática emresolução de problemas de pequenas oscilações de meios elásticos. Mas além da matemática, as séries de Fourier encontraram sua aplicação em outras áreas da ciência.

Todos os dias as pessoas usam vários dispositivos. E muitas vezes esses dispositivos não funcionam corretamente. Por exemplo, o som é difícil de distinguir devido ao alto ruído ou a imagem enviada por fax não é nítida. Uma pessoa pode determinar a causa do mau funcionamento pelo som. O computador também pode diagnosticar danos ao dispositivo. Ruído excessivo pode ser removido usando processamento de sinal de computador. O sinal é representado como uma sequência de valores digitais, que são então inseridos em um computador. Depois de completar certos cálculos, obtenha os coeficientes da série de Fourier.

Alterar o espectro do sinal permite limpar a gravação de ruído, compensar a distorção do sinal por vários dispositivos de gravação de som, alterar os timbres dos instrumentos e concentrar a atenção dos ouvintes em partes individuais.

No processamento digital de imagens, o uso da série Fourier permite os seguintes efeitos: desfoque, aprimoramento de bordas, restauração de imagem, efeitos artísticos (embossing)

A expansão em série de Fourier é usada em arquitetura no estudo de processos oscilatórios. Por exemplo, ao criar um projeto tipo diferente estruturas calculam a resistência, rigidez e estabilidade dos elementos estruturais.

Na medicina, para realizar um exame médico usando cardiogramas, máquinas de ultrassom, é usado um aparato matemático, baseado na teoria da série de Fourier.

Problemas computacionais volumétricos de estimativa das características estatísticas de sinais e filtragem de ruído surgem durante o registro e processamento de dados contínuos do fundo do mar. Ao fazer medições e registrá-las, os métodos holográficos usando séries de Fourier são promissores. Ou seja, as séries de Fourier também são usadas em uma ciência como a oceanologia.

Elementos de matemática são encontrados na produção em quase todas as etapas, por isso é importante que os especialistas conheçam e naveguem brilhantemente no campo de aplicação de certas ferramentas de análise e cálculo..

Conclusão

O tema do trabalho do curso é dedicado ao estudo da série de Fourier. Uma função arbitrária pode ser decomposta em outras mais simples, ou seja, pode ser decomposta em uma série de Fourier. O volume do trabalho do curso não permite divulgar em detalhes todos os aspectos da expansão da função em uma série. No entanto, a partir do conjunto de tarefas, foi possível revelar a teoria básica das séries de Fourier.

O trabalho de conclusão de curso divulgou o conceito de uma série trigonométrica de Fourier. As condições para a expansão de uma função em uma série de Fourier são determinadas. Expansões em série de Fourier de funções pares e ímpares são consideradas; funções não periódicas.

No segundo capítulo, são dados apenas alguns exemplos da expansão de funções dadas em diferentes intervalos em uma série de Fourier. São descritos os campos da ciência onde esta transformação é utilizada.

Há também uma forma complexa de representação da série de Fourier, que não poderia ser considerada, pois o volume do trabalho do curso não permite. forma complexa série é algebricamente simples. Portanto, é frequentemente usado em física e cálculos aplicados.

A importância do tema do trabalho do curso se deve ao fato de ser amplamente utilizado não só na matemática, mas em outras ciências: física, mecânica, medicina, química e muitas outras.

Bibliografia

1. Bari, N. K. Série trigonométrica. [texto] / N. K. Bari. - Moscou, 1961. - 936 segundos.

2. Bermant, A. F. Curso de curta duração analise matemática: livro didático para universidades[texto]/ A. F. Bermant, I. G. Aramanovich. - 11ª edição, Sr. - São Petersburgo: Editora "Lan", 2005. - 736 p.

3. Bugrov, Ya. S. Higher Mathematics: A Textbook for Universities: In 3 vols.[texto]/ Ya. S. Bugrov, S. M. Nikolsky; Ed. V. A. Sadovnichy. - 6ª ed., estereótipo. - M.: Abetarda, 2004. -512 p.

4. Vinogradova, I. A. Problemas e exercícios de análise matemática: um guia para universidades, ped. Universidades: às 14h[texto]/ I. A. Vinogradova, S. N. Olehnik, V. A. Sadovnichy; ed. V.A. Sadovnichy. - 3ª edição, Rev. – M.: Abetarda, 2001. – 712 p.

5. Gusak, A.A. Matemática Superior. Em 2 vols. T. 2. Um livro para estudantes universitários.[texto]/ A. A. Gusak.– 5ª edição. – Minsk: TetraSystems, 2004.

6. Danko, P.E. Matemática superior em exercícios e tarefas: livro didático para universidades: 2 horas.[texto]/ EDUCAÇAO FISICA. Danko, A. G. Popov, T.Ya. Kozhevnikov. Moscou: ONIKS: Mundo e educação, 2003. - 306 p.

7. Lukin, A. Introdução à processamento digital sinais (fundamentos matemáticos) [texto] / A. Lukin. - M., 2007. - 54 p.

8. Piskunov, N. S. Cálculo diferencial e integral para instituições de ensino superior, vol. 2: Tutorial para universidades.[texto]/ N. S. Piskunov. - 13ª ed. - M.: Nauka, 1985. - 432 p.

9. Rudin, U. Fundamentos da Análise Matemática.[texto]/ W. Rudin. - 2ª ed., Pe. do inglês. .- M.: Mir, 1976 .- 206 p.

10. Fikhtengol'ts, G. M. Fundamentos da Análise Matemática. Parte 2.[texto]/ G. M. Fikhtengolts. -6ª ed., ester. - São Petersburgo: Editora "Lan", 2005. - 464 p.

Oremburgo, 2015

A possibilidade de aproximar a série de Fourier no caso de um sinal linear pode ser necessária para construir funções no caso de um sinal descontínuo. elementos periódicos. Possibilidades de uso este método para construí-los e decompô-los usando somas finitas Série de Fourier usada na resolução de muitos problemas de várias ciências, como física, sismologia e assim por diante. Os processos das marés oceânicas, a atividade solar são considerados como processos de expansão dos processos oscilatórios, funções descritas por essas transformações. Com desenvolvimento tecnologia de computador A série de Fourier começou a ser usada cada vez mais Tarefas desafiantes, e também graças a isso, tornou-se possível usar essas transformações em ciências indiretas, como medicina, química. A transformada de Fourier é descrita na forma real e complexa, a segunda distribuição possibilitou um avanço no estudo espaço sideral. O resultado deste trabalho é a aplicação da série de Fourier à linearização função descontínua e seleção do número de coeficientes da série para uma imposição mais precisa da série sobre a função. Além disso, ao usar a expansão em uma série de Fourier, determinada função deixa de ser descontínuo e já suficientemente pequeno, realiza-se uma boa aproximação da função utilizada.

Séries de Fourier

transformada de Fourier

espectro de fase.

1. Alasheeva E.A., Rogova N.V. Método numérico para resolver o problema de eletrodinâmica na aproximação de fios finos. Ciência e Paz. Internacional Revista Ciência, No. 8(12), 2014. Volume 1. Volgograd. pp.17-19.

2. Vorobyov N.N. Teoria das linhas. Ed. Nauka, edição principal da literatura física e matemática, M., 1979, -408 p.

3. Kalinina V.N., Pankin V.F. Estatísticas matemáticas. - M.: pós-graduação, 2001.

4. Série de R. Edwards Fourier em apresentação moderna. Ed. Mundo. Em 2 volumes. Volume 1. 1985. 362 páginas

5. Sigorsky V.P. Aparelho matemático de um engenheiro. Ed. 2º estereótipo. "Técnica", 1997. – 768 p.

A representação de uma função tomada arbitrariamente com um período específico como uma série é chamada de série de Fourier. Uma expansão em uma base ortogonal é chamada de esta decisão em geral. A expansão de funções em uma série de Fourier é uma ferramenta bastante poderosa para resolver vários problemas. Porque as propriedades desta transformação são bem conhecidas e estudadas ao integrar, diferenciar, bem como deslocar a expressão em relação ao argumento e convolução. Uma pessoa não familiarizada matemática superior, assim como com os trabalhos do cientista francês Fourier, muito provavelmente, não entenderá o que são essas “séries” e para que servem. Essa transformada de Fourier tornou-se uma parte muito densa de nossas vidas. Ele é usado não apenas por matemáticos, mas também por físicos, químicos, médicos, astrônomos, sismólogos, oceanógrafos e muitos outros.

As séries de Fourier são usadas na resolução de muitos problemas aplicados. A transformada de Fourier pode ser realizada por métodos analíticos, numéricos e outros. Processos como marés oceânicas e ondas de luz até ciclos de atividade solar referem-se ao método numérico de expansão de quaisquer processos oscilatórios em uma série de Fourier. Usando essas técnicas matemáticas, é possível analisar funções, representando quaisquer processos oscilatórios como uma série de componentes senoidais que vão do mínimo ao máximo e vice-versa. A transformada de Fourier é uma função que descreve a fase e a amplitude das senoides correspondentes a uma frequência específica. Esta transformação é usada para resolver um problema muito equações complexas, que descrevem processos dinâmicos que ocorrem sob a ação de calor, luz ou energia elétrica. Além disso, as séries de Fourier permitem isolar os componentes constantes em sinais oscilatórios complexos, o que permitiu interpretar corretamente as observações experimentais obtidas em medicina, química e astronomia.

Com o crescimento da tecnologia, ou seja, surgimento e desenvolvimento do computador, trouxe a transformada de Fourier para novo nível. Esta técnica firmemente enraizado em quase todas as áreas da ciência e tecnologia. Um exemplo é um sinal de áudio e vídeo digital. O que se tornou uma clara percepção do crescimento processo científico e aplicação da série de Fourier. Assim, a série de Fourier em uma forma complexa tornou possível fazer um avanço no estudo do espaço sideral. Além disso, influenciou o estudo da física materiais semicondutores e plasma, acústica de microondas, oceanografia, radar, sismologia.

Considere que o espectro de fase de um sinal periódico é determinado a partir da seguinte expressão:

onde os símbolos e respectivamente denotam as partes imaginária e real do valor entre colchetes.

Se multiplicado por um valor constante real K, então a expansão em uma série de Fourier tem a seguinte forma:

Segue-se da expressão (1) que o espectro de Fourier de fase tem as seguintes propriedades:

1) é uma função, ou seja, diferentemente do espectro de potência, que não depende de , , muda quando o sinal é deslocado ao longo do eixo do tempo;

2) não depende de K, ou seja, é invariante à amplificação ou atenuação do sinal, enquanto o espectro de potência é função de K.

3) ou seja, é uma função ímpar de n.

Observação. Dada a interpretação geométrica do raciocínio acima, ele pode ser expresso em termos do espectro de potência e do espectro de fase da seguinte forma:

Na medida em que

então de (2) e (3) segue que ele pode ser recuperado unicamente se a amplitude (ou espectro de potência) e os espectros de fase forem conhecidos.

Considere um exemplo. Nos é dada uma função entre

Visão geral da série de Fourier:

Substitua nossos valores e obtenha:

Substitua seus valores e obtenha.

funções. Essa transformação é de grande importância, pois pode ser usada para resolver muitos problemas práticos. As séries de Fourier são usadas não apenas por matemáticos, mas também por especialistas em outras ciências.

A expansão de funções em uma série de Fourier é uma técnica matemática que pode ser observada na natureza se você usar um instrumento que detecte funções senoidais.

O ouvido humano não percebe o som como um todo, mas através dos componentes de sua série de Fourier. As cordas de um instrumento musical produzem sons que são vibrações senoidais de várias frequências. A realidade da decomposição da luz em uma série de Fourier é representada por um arco-íris. A visão humana percebe a luz através de alguns de seus componentes de diferentes frequências de oscilações eletromagnéticas.

A descoberta desta transformação pertence ao matemático francês Jean Baptiste Joseph Fourier. Em homenagem a quem mais tarde foi nomeado perto de Fourier. Inicialmente, o cientista encontrou a aplicação de seu método no estudo e explicação dos mecanismos de condução de calor. Assumiu-se que a distribuição irregular inicial de calor pode ser representada na forma das senóides mais simples. Para cada um dos quais a temperatura mínima, máxima e fase serão determinadas. A função que descreve os picos superior e inferior da curva, a fase de cada harmônico, é chamada de transformada de Fourier da expressão de distribuição de temperatura. O autor da transformação propôs um método para expandir uma função complexa como uma soma de funções periódicas de cosseno, seno.

O objetivo do trabalho do curso é estudar a série de Fourier e a relevância da aplicação prática dessa transformação.