1 x par ou ímpar. Funções pares e ímpares. Funções periódicas

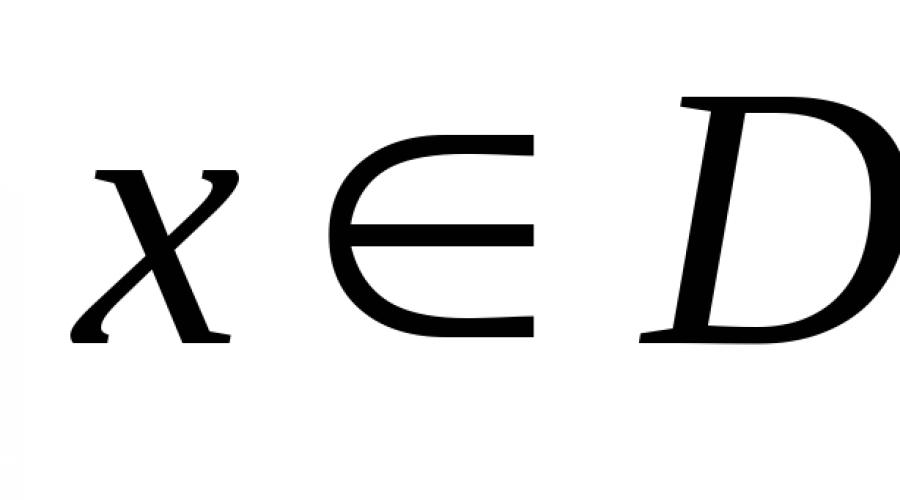
Gráficos de pares e não função par possuem as seguintes características:

Se uma função é par, então seu gráfico é simétrico em relação ao eixo y. Se uma função é ímpar, então seu gráfico é simétrico em relação à origem.

Decisão. Considere a função: \(f\left(x \right)=\left|x \right|\) e substitua \(x \) pelo oposto \(-x \). Como resultado de transformações simples, obtemos: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ In outras palavras, se substituir o argumento pelo sinal oposto, a função não será alterada.

Isso significa que essa função é par e seu gráfico será simétrico em relação ao eixo y ( eixo vertical). O gráfico desta função é mostrado na figura à esquerda. Isso significa que, ao traçar um gráfico, você pode construir apenas metade e a segunda parte (à esquerda do eixo vertical, desenhe já simetricamente para o lado direito). Ao determinar a simetria de uma função antes de começar a traçar seu gráfico, você pode simplificar bastante o processo de construção ou estudo de uma função. Se for difícil realizar uma verificação de forma geral, você pode fazê-lo mais facilmente: substitua os mesmos valores de sinais diferentes na equação. Por exemplo -5 e 5. Se os valores da função forem iguais, podemos esperar que a função seja par. Do ponto de vista matemático, essa abordagem não é totalmente correta, mas do ponto de vista prático, é conveniente. Para aumentar a confiabilidade do resultado, você pode substituir vários pares desses valores opostos.

Decisão. Vamos verificar o mesmo que no exemplo anterior: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right ) $$ Isso significa que a função original é ímpar (o sinal da função é invertido).

Conclusão: a função é simétrica em relação à origem. Você pode construir apenas uma metade e desenhar a outra metade simetricamente. Essa simetria é mais difícil de desenhar. Isso significa que você está olhando para o gráfico do outro lado da folha, e até mesmo virado de cabeça para baixo. E você também pode fazer isso: pegue a parte desenhada e gire-a em torno da origem em 180 graus no sentido anti-horário.

Decisão. Vamos realizar a mesma verificação de mudança de sinal dos dois exemplos anteriores. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ $$f\left( -x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ O que significa que a função não é nem par nem ímpar .

Conclusão: a função não é simétrica nem em relação à origem nem em relação ao centro do sistema de coordenadas. Isso aconteceu porque é a soma de duas funções: par e ímpar. A mesma situação será se você subtrair duas funções diferentes. Mas a multiplicação ou divisão levará a um resultado diferente. Por exemplo, o produto de uma função par por uma função ímpar dá uma função ímpar. Ou o quociente de dois ímpares leva a uma função par.

A paridade e a estranheza de uma função são uma de suas principais propriedades, e a paridade ocupa uma parte impressionante curso escolar matemática. Ele determina em grande parte a natureza do comportamento da função e facilita muito a construção do gráfico correspondente.

Vamos definir a paridade da função. De um modo geral, a função em estudo é considerada mesmo que para valores opostos da variável independente (x) localizada em seu domínio, os valores correspondentes de y (função) sejam iguais.

Vamos dar uma definição mais rigorosa. Considere alguma função f(x), que é definida no domínio D. Será mesmo se para qualquer ponto x localizado no domínio de definição:

• -x (ponto oposto) também está no escopo fornecido,

• f(-x) = f(x).

Da definição acima segue a condição necessária para o domínio de definição de tal função, a saber, a simetria em relação ao ponto O, que é a origem das coordenadas, pois se algum ponto b está contido no domínio de definição de uma função função par, então o ponto correspondente - b também está neste domínio. Do exposto, portanto, segue-se a conclusão: uma função par tem uma forma que é simétrica em relação ao eixo das ordenadas (Oy).

Como determinar a paridade de uma função na prática?

Seja dado usando a fórmula h(x)=11^x+11^(-x). Seguindo o algoritmo que segue diretamente da definição, primeiro estudamos seu domínio de definição. Obviamente, ele é definido para todos os valores do argumento, ou seja, a primeira condição é satisfeita.

O próximo passo é substituir o argumento (x) pelo seu valor oposto (-x).
Nós temos:
h(-x) = 11^(-x) + 11^x.
Como a adição satisfaz a lei comutativa (deslocamento), é óbvio que h(-x) = h(x) e o dado dependência funcional- mesmo.

Vamos verificar a equidade da função h(x)=11^x-11^(-x). Seguindo o mesmo algoritmo, obtemos h(-x) = 11^(-x) -11^x. Tirando o menos, como resultado, temos
h(-x)=-(11^x-11^(-x))=- h(x). Portanto, h(x) é ímpar.

A propósito, deve-se lembrar que existem funções que não podem ser classificadas de acordo com esses critérios, elas são chamadas nem pares nem ímpares.

Até mesmo funções têm várias propriedades interessantes:

• como resultado da adição de funções semelhantes, obtém-se uma par;
• como resultado da subtração de tais funções, obtém-se um par;
• mesmo, também mesmo;
• como resultado da multiplicação de duas dessas funções, obtém-se uma par;
• como resultado da multiplicação de funções ímpares e pares, obtém-se uma ímpar;
• como resultado da divisão das funções ímpares e pares, obtém-se uma ímpar;
• a derivada de tal função é ímpar;
• Se elevarmos ao quadrado uma função ímpar, obtemos uma função par.

A paridade de uma função pode ser usada na resolução de equações.

Para resolver uma equação como g(x) = 0, onde lado esquerdo equação é uma função par, será suficiente encontrar suas soluções para valores não negativos da variável. As raízes obtidas da equação devem ser combinadas com números opostos. Um deles está sujeito a verificação.

O mesmo tem sido usado com sucesso para resolver tarefas não padronizadas com um parâmetro.

Por exemplo, existe algum valor para o parâmetro a que faria a equação 2x^6-x^4-ax^2=1 ter três raízes?

Se levarmos em conta que a variável entra na equação em potências pares, fica claro que substituir x por - x dada equação não vai mudar. Segue-se que se um certo número é sua raiz, então o número oposto também é. A conclusão é óbvia: as raízes da equação, diferentes de zero, estão incluídas no conjunto de suas soluções em “pares”.

É claro que o próprio número 0 não é, ou seja, o número de raízes de tal equação só pode ser par e, naturalmente, para qualquer valor do parâmetro não pode ter três raízes.

Mas o número de raízes da equação 2^x+ 2^(-x)=ax^4+2x^2+2 pode ser ímpar, e para qualquer valor do parâmetro. De fato, é fácil verificar que o conjunto de raízes de uma dada equação contém soluções em “pares”. Vamos verificar se 0 é uma raiz. Ao substituí-lo na equação, obtemos 2 = 2. Assim, além de "emparelhado" 0 também é uma raiz, o que comprova seu número ímpar.

Definição 1. A função é chamada até (ímpar ) se junto com cada valor da variável
significado - X também pertence
e a igualdade

Assim, uma função só pode ser par ou ímpar quando seu domínio de definição é simétrico em relação à origem das coordenadas na reta real (números X e - X pertencem simultaneamente
). Por exemplo, a função
não é nem par nem ímpar, pois seu domínio de definição
não simétrica em relação à origem.

Função
até porque
simétrico em relação à origem das coordenadas e.

Função
estranho porque
e
.

Função
não é par nem ímpar, pois embora
e é simétrica em relação à origem, as igualdades (11.1) não são satisfeitas. Por exemplo,.

O gráfico de uma função par é simétrico em relação ao eixo UO, pois se o ponto

também pertence ao gráfico. O gráfico de uma função ímpar é simétrico em relação à origem, porque se
pertence ao gráfico, então o ponto
também pertence ao gráfico.

Ao provar se uma função é par ou ímpar, as instruções a seguir são úteis.

Teorema 1. a) A soma de duas funções pares (ímpares) é uma função par (ímpar).

b) O produto de duas funções pares (ímpares) é uma função par.

c) O produto de uma função par por uma função ímpar é uma função ímpar.

d) Se fé uma função par no conjunto X, e a função g definido no set
, então a função
- mesmo.

e) Se fé uma função ímpar no conjunto X, e a função g definido no set
e par (ímpar), então a função
- par ou ímpar).

Prova. Vamos provar, por exemplo, b) e d).

b) Deixe
e
são funções pares. Então, portanto. O caso de funções ímpares é considerado de forma semelhante
e
.

d) Deixe f é uma função par. Então.

As outras asserções do teorema são provadas de forma semelhante. O teorema foi provado.

Teorema 2. Qualquer função
, definido no conjunto X, que é simétrica em relação à origem, pode ser representada como a soma de uma função par e de uma função ímpar.

Prova. Função
pode ser escrito na forma

.

Função
é par, pois
, e a função
é estranho porque. Por isso,
, Onde
- mesmo, e
é uma função ímpar. O teorema foi provado.

Definição 2. Função
chamado periódico se houver um número
, tal que para qualquer
números
e
também pertencem ao domínio da definição
e as igualdades

tal número T chamado período funções
.

A definição 1 implica que se T- período de função
, então o número T também é o período da função
(porque ao substituir T no - T igualdade é mantida). Usando o método de indução matemática, pode-se mostrar que se T- período de função f, então e
, também é um período. Segue-se que se uma função tem um período, então ela tem infinitos períodos.

Definição 3. O menor dos períodos positivos de uma função é chamado de seu a Principal período.

Teorema 3. Se Té o período principal da função f, então os períodos restantes são múltiplos dele.

Prova. Suponha o oposto, ou seja, que existe um período funções f (>0), não múltiplo T. Em seguida, dividindo no T com o restante, obtemos
, Onde
. então

ou seja - período de função f, e
, o que contradiz o fato de que Té o período principal da função f. A asserção do teorema decorre da contradição obtida. O teorema foi provado.

Sabe-se que as funções trigonométricas são periódicas. Período principal
e
é igual a
,
e
. Encontre o período da função
. Deixe ser
é o período desta função. Então

(como
.

ororor
.

Significado T, determinado a partir da primeira igualdade, não pode ser um período, pois depende de X, ou seja é uma função de X, não um número constante. O período é determinado a partir da segunda igualdade:
. Existem infinitos períodos
o menor período positivo é obtido quando
:
. Este é o período principal da função
.

Um exemplo de uma função periódica mais complexa é a função de Dirichlet

Observe que se Té um número racional, então
e
são números racionais sob racionais X e irracional quando irracional X. então

para qualquer número racional T. Portanto, qualquer número racional Té o período da função de Dirichlet. É claro que esta função não tem período principal, uma vez que existem números racionais arbitrariamente próximo de zero (por exemplo, um número racional pode ser feito escolhendo-se n arbitrariamente próximo de zero).

Teorema 4. Se funcionar f definido no conjunto X e tem um período T, e a função g definido no conjunto
, então a função complexa
também tem um período T.

Prova. Temos portanto

isto é, a asserção do teorema está provada.

Por exemplo, desde porque x tem um período
, então as funções
ter um período
.

Definição 4. As funções que não são periódicas são chamadas não periódico .

Funçãoé um dos conceitos matemáticos mais importantes. Função - dependência de variável no de uma variável x, se cada valor X corresponde a um único valor no. variável X chamada de variável independente ou argumento. variável no chamada de variável dependente. Todos os valores da variável independente (variável x) formam o domínio da função. Todos os valores que a variável dependente assume (variável y), formam o intervalo da função.

Gráfico de funções eles chamam o conjunto de todos os pontos do plano coordenado, cujas abcissas são iguais aos valores do argumento, e as ordenadas são iguais aos valores correspondentes da função, ou seja, os valores de a variável é plotada ao longo da abcissa x, e os valores da variável são plotados ao longo do eixo y y. Para plotar uma função, você precisa conhecer as propriedades da função. As principais propriedades da função serão discutidas abaixo!

Para traçar um gráfico de função, recomendamos usar nosso programa - Graphing Functions Online. Se você tiver alguma dúvida enquanto estuda o material desta página, você sempre pode perguntar em nosso fórum. Também no fórum você será ajudado a resolver problemas de matemática, química, geometria, teoria das probabilidades e muitos outros assuntos!

Propriedades básicas das funções.

1) Escopo de função e faixa de função.

O escopo de uma função é o conjunto de todos os valores válidos válidos do argumento x(variável x) para o qual a função y = f(x) definiram.
A imagem de uma função é o conjunto de todos os valores reais y que a função aceita.

NO matemática elementar funções são estudadas apenas no conjunto dos números reais.

2) Zeros de função.

Valores X, em qual y=0, é chamado função zeros. Estas são as abcissas dos pontos de intersecção do gráfico da função com o eixo x.

3) Intervalos de constância de sinal de uma função.

Os intervalos de constância de sinal de uma função são tais intervalos de valores x, em que os valores da função y ou apenas positivo ou apenas negativo são chamados intervalos de constância de sinal da função.

4) Monotonicidade da função.

Função crescente (em algum intervalo) - uma função para a qual maior valor um argumento deste intervalo corresponde a um valor maior da função.

Função decrescente (em algum intervalo) - uma função na qual um valor maior do argumento desse intervalo corresponde a um valor menor da função.

5) Funções pares (ímpares).

Uma função par é uma função cujo domínio de definição é simétrico em relação à origem e para qualquer X f(-x) = f(x). O gráfico de uma função par é simétrico em relação ao eixo y.

Uma função ímpar é uma função cujo domínio de definição é simétrico em relação à origem e para qualquer X do domínio da definição a igualdade f(-x) = - f(x). O gráfico de uma função ímpar é simétrico em relação à origem.

Função par
1) O domínio de definição é simétrico em relação ao ponto (0; 0), ou seja, se o ponto uma pertence ao domínio da definição, então o ponto -uma também pertence ao domínio da definição.
2) Para qualquer valor x f(-x)=f(x)
3) O gráfico de uma função par é simétrico em relação ao eixo Oy.

Função estranha tem as seguintes propriedades:
1) O domínio de definição é simétrico em relação ao ponto (0; 0).
2) para qualquer valor x, que pertence ao domínio de definição, a igualdade f(-x)=-f(x)
3) O gráfico de uma função ímpar é simétrico em relação à origem (0; 0).

Nem toda função é par ou ímpar. Funções visão geral não são pares nem ímpares.

6) Funções limitadas e ilimitadas.

Uma função é dita limitada se existir um número M positivo tal que |f(x)| ≤ M para todos os valores de x . Se não houver tal número, então a função é ilimitada.

7) Periodicidade da função.

Uma função f(x) é periódica se existe um número T diferente de zero tal que para qualquer x do domínio da função, f(x+T) = f(x). Tal menor númeroé chamado de período da função. Tudo funções trigonométricas são periódicas. (Fórmulas trigonométricas).

Função fé chamado periódico se existe um número tal que para qualquer x do domínio da definição a igualdade f(x)=f(x-T)=f(x+T). Té o período da função.

Toda função periódica tem conjunto infinito períodos. Na prática, geralmente é considerado o menor período positivo.

Os valores da função periódica são repetidos após um intervalo igual ao período. Isso é usado ao plotar gráficos.

A dependência da variável y da variável x, na qual cada valor de x corresponde a um único valor de y, é chamada de função. A notação é y=f(x). Cada função tem uma série de propriedades básicas, como monotonicidade, paridade, periodicidade e outras.

Considere a propriedade de paridade com mais detalhes.

Uma função y=f(x) é chamada mesmo que satisfaça as duas condições a seguir:

2. O valor da função no ponto x pertencente ao escopo da função deve ser igual ao valor da função no ponto -x. Ou seja, para qualquer ponto x, do domínio da função, a seguinte igualdade f (x) \u003d f (-x) deve ser verdadeira.

Gráfico de uma função par

Se você construir um gráfico de uma função par, ela será simétrica em relação ao eixo y.

Por exemplo, a função y=x^2 é par. Vamos verificar. O domínio de definição é todo o eixo numérico, o que significa que é simétrico em relação ao ponto O.

Tome um x = 3 arbitrário. f(x)=3^2=9.

f(-x)=(-3)^2=9. Portanto, f(x) = f(-x). Assim, ambas as condições são satisfeitas para nós, o que significa que a função é par. Abaixo está um gráfico da função y=x^2.

A figura mostra que o gráfico é simétrico em relação ao eixo y.

Gráfico de uma função ímpar

Uma função y=f(x) é dita ímpar se satisfaz as duas condições a seguir:

1. O domínio da função dada deve ser simétrico em relação ao ponto O. Ou seja, se algum ponto a pertence ao domínio da função, então o ponto correspondente -a também deve pertencer ao domínio da função dada.

2. Para qualquer ponto x, do domínio da função, a seguinte igualdade f (x) \u003d -f (x) deve ser satisfeita.

O gráfico de uma função ímpar é simétrico em relação ao ponto O - a origem. Por exemplo, a função y=x^3 é ímpar. Vamos verificar. O domínio de definição é todo o eixo numérico, o que significa que é simétrico em relação ao ponto O.

Tome um x = 2 arbitrário. f(x)=2^3=8.

f(-x)=(-2)^3=-8. Portanto f(x) = -f(x). Assim, ambas as condições são satisfeitas para nós, o que significa que a função é ímpar. Abaixo está um gráfico da função y=x^3.

A figura mostra claramente que a função ímpar y=x^3 é simétrica em relação à origem.