Confira a solução do maior e do menor do segmento. O maior e o menor valor da função. Tarefa B15 (2014)

Vamos ver como explorar uma função usando um gráfico. Acontece que olhando para o gráfico, você pode descobrir tudo o que nos interessa, a saber:

• escopo da função
• intervalo de funções
• função zeros
• períodos de aumento e diminuição
• pontos altos e baixos
• o maior e o menor valor da função no segmento.

Vamos esclarecer a terminologia:

Abscissaé a coordenada horizontal do ponto.
Ordenar- coordenada vertical.
abscissa- o eixo horizontal, mais frequentemente chamado de eixo.
Eixo Y - eixo vertical, ou eixo .

Argumentoé uma variável independente da qual dependem os valores da função. Na maioria das vezes indicado.
Em outras palavras, nós mesmos escolhemos , substituímos na fórmula da função e obtemos .

Domínio funções - o conjunto daqueles (e somente aqueles) valores do argumento para o qual a função existe.
Denotado: ou .

Em nossa figura, o domínio da função é um segmento. É neste segmento que se desenha o gráfico da função. Só aqui determinada função existe.

Faixa de funçõesé o conjunto de valores que a variável assume. Em nossa figura, este é um segmento - do menor ao maior valor.

Zeros de função- pontos onde o valor da função é igual a zero, ou seja . Em nossa figura, esses são os pontos e .

Os valores da função são positivos Onde . Em nossa figura, esses são os intervalos e .
Os valores da função são negativos Onde . Temos esse intervalo (ou intervalo) de até.

Os conceitos mais importantes - funções crescentes e decrescentes em algum conjunto. Como um conjunto, você pode pegar um segmento, um intervalo, uma união de intervalos ou a reta numérica inteira.

Função aumenta

Ou seja, quanto mais , mais , ou seja, o gráfico vai para a direita e para cima.

Função diminuindo no conjunto se para qualquer e pertencendo ao conjunto a desigualdade implica a desigualdade .

Para uma função decrescente, um valor maior corresponde a um valor menor. O gráfico vai para a direita e para baixo.

Em nossa figura, a função aumenta no intervalo e diminui nos intervalos e .

Vamos definir o que é pontos de máximo e mínimo da função.

Ponto máximo- este é um ponto interno do domínio de definição, tal que o valor da função nele é maior do que em todos os pontos suficientemente próximos a ele.
Em outras palavras, o ponto máximo é tal ponto, o valor da função em que mais do que nas vizinhas. Esta é uma "colina" local no gráfico.

Em nossa figura - o ponto máximo.

Ponto baixo- um ponto interno do domínio de definição, tal que o valor da função nele seja menor do que em todos os pontos suficientemente próximos a ele.
Ou seja, o ponto mínimo é tal que o valor da função nele é menor do que nas vizinhas. No gráfico, este é um “buraco” local.

Em nossa figura - o ponto mínimo.

O ponto é o limite. Não é um ponto interior do domínio de definição e, portanto, não se enquadra na definição de ponto máximo. Afinal, ela não tem vizinhos à esquerda. Da mesma forma, não pode haver ponto mínimo em nosso gráfico.

Os pontos máximo e mínimo são chamados coletivamente pontos extremos da função. No nosso caso, isso é e .

Mas e se você precisar encontrar, por exemplo, função mínima no corte? NO este caso responda: . Porque função mínimaé o seu valor no ponto mínimo.

Da mesma forma, o máximo de nossa função é . É alcançado no ponto .

Podemos dizer que os extremos da função são iguais a e .

Às vezes, em tarefas, você precisa encontrar os maiores e menores valores da função em um determinado segmento. Eles não coincidem necessariamente com os extremos.

No nosso caso menor valor de função no intervalo é igual e coincide com o mínimo da função. Mas seu maior valor neste segmento é igual a . Ele é alcançado na extremidade esquerda do segmento.

De qualquer forma, os maiores e menores valores de uma função contínua em um segmento são alcançados nos pontos extremos ou nas extremidades do segmento.

pequeno e bonito tarefa simples da categoria daqueles que servem de tábua de salvação para um aluno flutuante. Na natureza, o reino sonolento de meados de julho, então é hora de se acomodar com um laptop na praia. De manhã cedo, um raio de sol da teoria tocou para logo se concentrar na prática, que, apesar de sua declarada leveza, contém cacos de vidro na areia. A este respeito, recomendo considerar conscientemente alguns exemplos desta página. Para resolver tarefas práticas, você precisa ser capaz de encontrar derivadas e entender o material do artigo Intervalos de monotonicidade e extremos de uma função.

Primeiro, brevemente sobre a coisa principal. Em uma aula sobre continuidade de função Dei a definição de continuidade em um ponto e continuidade em um intervalo. O comportamento exemplar de uma função em um segmento é formulado de maneira semelhante. Uma função é contínua em um segmento se:

1) é contínua no intervalo ;
2) contínua em um ponto na direita e no ponto deixei.

O segundo parágrafo trata do chamado continuidade unilateral funções em um ponto. Existem várias abordagens para sua definição, mas vou me ater à linha iniciada anteriormente:

A função é contínua em um ponto na direita, se for definido em um determinado ponto e seu limite à direita coincidir com o valor da função em um determinado ponto: . é contínua no ponto deixei, se definido em um determinado ponto e seu limite esquerdo é igual ao valor nesse ponto:

Imagine que os pontos verdes são os pregos nos quais o elástico mágico está preso:

Mentalmente, pegue a linha vermelha em suas mãos. Obviamente, não importa o quanto estiquemos o gráfico para cima e para baixo (ao longo do eixo), a função ainda permanecerá limitado- uma cerca viva acima, uma cerca viva abaixo, e nosso produto pasta em um piquete. Nesse caminho, uma função contínua em um segmento é limitada por ele. No curso da análise matemática, este fato aparentemente simples é declarado e rigorosamente comprovado Primeiro teorema de Weierstrass.… Muitas pessoas se incomodam com o fato de afirmações elementares serem tediosas em matemática, mas isso tem um significado importante. Suponha que um certo habitante da Idade Média tenha puxado o gráfico para o céu além dos limites da visibilidade, isso foi inserido. Antes da invenção do telescópio, a função limitada no espaço não era nada óbvia! De fato, como você sabe o que nos espera além do horizonte? Afinal, uma vez que a Terra era considerada plana, hoje até o teletransporte comum exige comprovação =)

De acordo com segundo teorema de Weierstrass, contínuo no segmentofunção atinge seu borda superior exata e ele borda inferior exata .

O número também é chamado o valor máximo da função no segmento e denotado por , e o número - o valor mínimo da função no segmento com aviso.

No nosso caso:

Observação : em teoria, os registros são comuns .

A grosso modo, valor mais alto está localizado onde o ponto mais alto do gráfico e o menor - onde o ponto mais baixo.

Importante! Como já foi apontado no artigo sobre extremo da função, o maior valor da função e menor valor de função – NÃO É O MESMO, o que função máxima e função mínima. Portanto, neste exemplo, o número é o mínimo da função, mas não o valor mínimo.

Aliás, o que acontece fora do segmento? Sim, mesmo a inundação, no contexto do problema em apreço, isso não nos interessa em nada. A tarefa envolve apenas encontrar dois números e é isso!

Além disso, a solução é puramente analítica, portanto, não precisa desenhar!

O algoritmo está na superfície e sugere-se a partir da figura acima:

1) Encontre os valores da função em Pontos críticos, que pertencem a este segmento.

Pegue mais uma guloseima: não há necessidade de verificar uma condição suficiente para um extremo, pois, como mostrado, a presença de um mínimo ou máximo ainda não garantido qual é o valor mínimo ou máximo. A função de demonstração atinge seu máximo e, por vontade do destino, o mesmo número é o maior valor da função no intervalo . Mas, é claro, essa coincidência nem sempre ocorre.

Assim, na primeira etapa, fica mais rápido e fácil calcular os valores da função em pontos críticos pertencentes ao segmento, sem se preocupar se eles possuem extremos ou não.

2) Calculamos os valores da função nas extremidades do segmento.

3) Dentre os valores da função encontrados nos 1º e 2º parágrafos, selecionamos os menores e mais grande número, anote a resposta.

Sentamos na margem do mar azul e batemos os calcanhares em águas rasas:

Exemplo 1

Encontre os maiores e menores valores de uma função em um segmento

Solução:
1) Calcule os valores da função em pontos críticos pertencentes a este segmento:

Vamos calcular o valor da função no segundo ponto crítico:

2) Calcule os valores da função nas extremidades do segmento:

3) Obtiveram-se resultados "negritos" com exponenciais e logaritmos, o que dificulta significativamente sua comparação. Por isso, vamos nos armar com uma calculadora ou Excel e calcular os valores aproximados, não esquecendo que:

Agora tudo está claro.

Responda:

Instância fracional-racional para decisão independente:

Exemplo 6

Encontre o máximo e valor mínimo funções no intervalo

O processo de encontrar os menores e maiores valores de uma função em um segmento lembra um voo fascinante em torno de um objeto (o gráfico de uma função) em um helicóptero com disparo de um canhão de longo alcance em determinados pontos e escolha entre estes pontos pontos muito especiais para tiros de controle. Os pontos são selecionados de uma certa maneira e de acordo com certas regras. Por quais regras? Falaremos sobre isso mais adiante.

Se a função y = f(x) contínua no segmento [ uma, b] , então atinge este segmento ao menos e valores mais altos . Isso pode acontecer tanto em pontos extremos ou nas extremidades do segmento. Portanto, para encontrar ao menos e os maiores valores da função , contínua no intervalo [ uma, b] , você precisa calcular seus valores em todos Pontos críticos e nas extremidades do segmento e, em seguida, escolha o menor e o maior deles.

Seja, por exemplo, necessário determinar o valor máximo da função f(x) no segmento [ uma, b] . Para fazer isso, encontre todos os seus pontos críticos sobre [ uma, b] .

ponto crítico é chamado de ponto em que função definida, e ela derivadoé zero ou não existe. Então você deve calcular os valores da função em pontos críticos. E, por fim, deve-se comparar os valores da função nos pontos críticos e nas extremidades do segmento ( f(uma) e f(b)). O maior desses números será o maior valor da função no intervalo [uma, b] .

O problema de encontrar os menores valores da função .

Estamos procurando os menores e maiores valores da função juntos

Exemplo 1. Encontre os menores e maiores valores de uma função no segmento [-1, 2] .

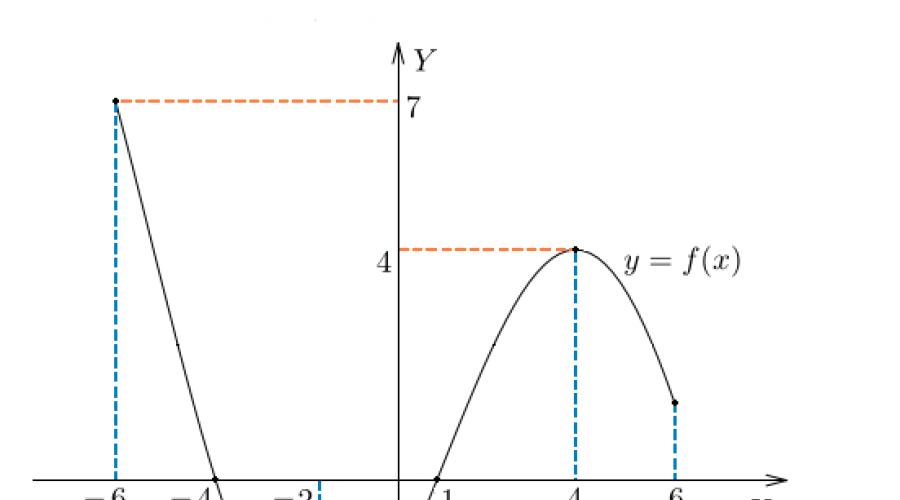
Solução. Encontramos a derivada desta função. Iguale a derivada a zero () e obtenha dois pontos críticos: e . Para encontrar os menores e maiores valores de uma função em um determinado segmento, basta calcular seus valores nas extremidades do segmento e no ponto , pois o ponto não pertence ao segmento [-1, 2] . Esses valores de função são os seguintes: , , . Segue que menor valor de função(marcado em vermelho no gráfico abaixo), igual a -7, é alcançado na extremidade direita do segmento - no ponto , e o melhor(também vermelho no gráfico), é igual a 9, - no ponto crítico .

Se a função é contínua em um determinado intervalo e esse intervalo não é um segmento (mas é, por exemplo, um intervalo; a diferença entre um intervalo e um segmento: os pontos de fronteira do intervalo não estão incluídos no intervalo, mas o pontos de limite do segmento estão incluídos no segmento), então entre os valores da função pode não haver o menor e o maior. Assim, por exemplo, a função representada na figura abaixo é contínua em ]-∞, +∞[ e não possui o maior valor.

No entanto, para qualquer intervalo (fechado, aberto ou infinito), vale a seguinte propriedade de funções contínuas.

Exemplo 4. Encontre os menores e maiores valores de uma função no segmento [-1, 3] .

Solução. Encontramos a derivada desta função como a derivada do quociente:

.

Igualamos a derivada a zero, o que nos dá um ponto crítico: . Pertence ao intervalo [-1, 3] . Para encontrar os menores e maiores valores de uma função em um determinado segmento, encontramos seus valores nas extremidades do segmento e no ponto crítico encontrado:

Vamos comparar esses valores. Conclusão: igual a -5/13, no ponto e o maior valor igual a 1 no ponto .

Continuamos a procurar os menores e maiores valores da função juntos

Há professores que, no tópico de encontrar os menores e maiores valores de uma função, não dão aos alunos exemplos mais complicados do que os que acabamos de considerar, ou seja, aqueles em que a função é um polinômio ou uma fração, o numerador e denominador são polinômios. Mas não nos limitaremos a tais exemplos, pois entre os professores há amantes de fazer os alunos pensarem por completo (tabela de derivadas). Portanto, o logaritmo e a função trigonométrica serão usados.

Exemplo 6. Encontre os menores e maiores valores de uma função no segmento .

Solução. Encontramos a derivada desta função como derivado do produto :

Igualamos a derivada a zero, o que dá um ponto crítico: . Pertence ao segmento. Para encontrar os menores e maiores valores de uma função em um determinado segmento, encontramos seus valores nas extremidades do segmento e no ponto crítico encontrado:

O resultado de todas as ações: a função atinge seu valor mínimo, igual a 0, em um ponto e em um ponto e o maior valor igual a e², no ponto.

Exemplo 7. Encontre os menores e maiores valores de uma função no segmento .

Solução. Encontramos a derivada desta função:

Igualando a derivada a zero:

O único ponto crítico pertence ao segmento. Para encontrar os menores e maiores valores de uma função em um determinado segmento, encontramos seus valores nas extremidades do segmento e no ponto crítico encontrado:

Conclusão: a função atinge seu valor mínimo, igual a , no ponto e o maior valor, igual a , no ponto .

Em problemas extremos aplicados, encontrar os menores (maiores) valores da função, via de regra, é reduzido a encontrar o mínimo (máximo). Mas não são os mínimos ou máximos em si que têm maior interesse prático, mas os valores do argumento em que são alcançados. Ao resolver problemas aplicados, surge uma dificuldade adicional - a compilação de funções que descrevem o fenômeno ou processo em consideração.

Exemplo 8 Deve ser estanhado um tanque com capacidade para 4, em forma de paralelepípedo com base quadrada e aberto na parte superior. Quais devem ser as dimensões do tanque para cobri-lo com a menor quantidade de material?

Solução. Deixar x- lado da base h- altura do tanque, S- sua superfície sem cobertura, V- seu volume. A área de superfície do tanque é expressa pela fórmula , ou seja, é uma função de duas variáveis. Para expressar S como função de uma variável, usamos o fato de que , de onde . Substituindo a expressão encontrada h na fórmula de S:

Vamos examinar esta função para um extremo. É definido e diferenciável em todos os lugares em ]0, +∞[ , e

.

Igualamos a derivada a zero () e encontramos o ponto crítico. Além disso, em , a derivada não existe, mas esse valor não está incluído no domínio de definição e, portanto, não pode ser um ponto extremo. Então, - o único ponto crítico. Vamos verificar a presença de um extremo usando o segundo sinal suficiente. Vamos encontrar a segunda derivada. Quando a segunda derivada é maior que zero (). Isso significa que quando a função atinge um mínimo . Porque isso mínimo - o único extremo desta função, é o seu menor valor. Portanto, o lado da base do tanque deve ser igual a 2 m e sua altura.

Exemplo 9 Do parágrafo UMA, localizado na linha férrea, até o ponto A PARTIR DE, a uma distância dele eu, as mercadorias devem ser transportadas. O custo de transporte de uma unidade de peso por unidade de distância por via férrea é igual a , e por rodovia é igual a . Até que ponto M linhas estrada de ferro uma rodovia deve ser construída para que o transporte de mercadorias MAS dentro A PARTIR DE foi o mais econômico AB ferrovia é considerada reta)?

Na prática, é bastante comum usar a derivada para calcular o maior e o menor valor de uma função. Realizamos essa ação quando descobrimos como minimizar custos, aumentar lucros, calcular carga ideal para produção, etc., ou seja, nos casos em que é necessário determinar valor ideal qualquer parâmetro. Para resolver esses problemas corretamente, é preciso ter um bom entendimento do que são o maior e o menor valor de uma função.

Yandex.RTB R-A-339285-1

Normalmente definimos esses valores dentro de algum intervalo x , que por sua vez pode corresponder a todo o escopo da função ou parte dela. Pode ser um segmento [ a ; b ] , e intervalo aberto (a ; b ), (a ; b ] , [ a ; b) , intervalo infinito (a ; b) , (a ; b ] , [ a ; b ) ou intervalo infinito - ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .

Neste artigo, explicaremos como os valores maiores e menores são calculados explicitamente. determinada função com uma variável y=f(x) y = f (x) .

Definições básicas

Começamos, como sempre, pela formulação das principais definições.

Definição 1

O maior valor da função y = f (x) em algum intervalo x é o valor m a x y = f (x 0) x ∈ X , que, para qualquer valor x x ∈ X , x ≠ x 0, faz a desigualdade f (x ) ≤ f (x 0) .

Definição 2

O menor valor da função y = f (x) em algum intervalo x é o valor m i n x ∈ X y = f (x 0) , que, para qualquer valor x ∈ X , x ≠ x 0, faz a desigualdade f(X f(x) ≥ f(x0) .

Essas definições são bastante óbvias. Ainda mais fácil, você pode dizer o seguinte: o maior valor de uma função é o seu valor mais grande importância em um intervalo conhecido na abscissa x 0 , e o menor é o menor valor aceito no mesmo intervalo em x 0 .

Definição 3

Pontos estacionários são tais valores do argumento da função em que sua derivada se torna 0.

Por que precisamos saber o que são pontos estacionários? Para responder a esta pergunta, precisamos lembrar o teorema de Fermat. Segue-se que um ponto estacionário é um ponto no qual o extremo de uma função diferenciável está localizado (ou seja, seu mínimo ou máximo local). Consequentemente, a função assumirá o menor ou o maior valor em um determinado intervalo exatamente em um dos pontos estacionários.

Outra função pode assumir o maior ou menor valor naqueles pontos em que a própria função é definida e sua primeira derivada não existe.

A primeira pergunta que surge ao estudar este tópico é: em todos os casos, podemos determinar o valor máximo ou mínimo de uma função em um determinado intervalo? Não, não podemos fazer isso quando os limites do intervalo dado coincidem com os limites do domínio de definição, ou se estamos lidando com um intervalo infinito. Acontece também que uma função em um dado intervalo ou no infinito tomará infinitesimal ou infinito grandes valores. Nestes casos, não é possível determinar o maior e/ou menor valor.

Esses momentos ficarão mais compreensíveis após a imagem nos gráficos:

A primeira figura nos mostra uma função que assume os maiores e menores valores (m a x y e m i n y) em pontos estacionários localizados no intervalo [ - 6 ; 6].

Vamos examinar em detalhes o caso indicado no segundo gráfico. Vamos alterar o valor do segmento para [ 1 ; 6] e obtemos que o maior valor da função será alcançado no ponto com a abcissa no limite direito do intervalo e o menor - no ponto estacionário.

Na terceira figura, as abcissas dos pontos representam os pontos limites do segmento [ - 3 ; 2]. Eles correspondem ao maior e menor valor da função dada.

Agora vamos olhar para a quarta foto. Nela, a função toma m a x y (o maior valor) e m i n y (o menor valor) em pontos estacionários no intervalo aberto (- 6 ; 6) .

Se tomarmos o intervalo [ 1 ; 6) , então podemos dizer que o menor valor da função sobre ela será alcançado em um ponto estacionário. Não saberemos o valor máximo. A função poderia ter o maior valor em x igual a 6 se x = 6 pertencesse ao intervalo. É este caso que é mostrado na Figura 5.

No gráfico 6, esta função adquire o menor valor na borda direita do intervalo (- 3 ; 2 ] , e não podemos tirar conclusões definitivas sobre o maior valor.

Na figura 7, vemos que a função terá m a x y no ponto estacionário, tendo uma abcissa igual a 1 . A função atinge seu valor mínimo no limite do intervalo no lado direito. No infinito menos, os valores da função se aproximarão assintoticamente de y = 3 .

Se tomarmos um intervalo x ∈ 2 ; + ∞ , então veremos que a função dada não assumirá nem o menor nem o maior valor. Se x tende a 2, então os valores da função tenderão a menos infinito, pois a linha reta x = 2 é uma assíntota vertical. Se a abcissa tende a mais infinito, então os valores da função se aproximarão assintoticamente de y = 3. Este é o caso mostrado na Figura 8.

Neste parágrafo, daremos uma sequência de ações que devem ser executadas para encontrar o maior ou o menor valor de uma função em um determinado intervalo.

1. Primeiro, vamos encontrar o domínio da função. Vamos verificar se o segmento especificado na condição está incluído nela.
2. Agora vamos calcular os pontos contidos neste segmento em que a primeira derivada não existe. Na maioria das vezes eles podem ser encontrados em funções cujo argumento é escrito sob o sinal de módulo, ou em funções de energia, cujo expoente é um número fracionalmente racional.
3. Em seguida, descobrimos quais pontos estacionários caem em um determinado segmento. Para fazer isso, você precisa calcular a derivada da função, igualá-la a 0 e resolver a equação resultante e, em seguida, escolher as raízes apropriadas. Se não obtivermos um único ponto estacionário ou eles não se enquadrarem em um determinado segmento, prosseguimos para a próxima etapa.
4. Vamos determinar quais valores a função assumirá nos pontos estacionários fornecidos (se houver), ou naqueles pontos onde a primeira derivada não existe (se houver), ou calculamos os valores para x = a e x = b.
5. 5. Temos uma série de valores de função, dos quais agora precisamos escolher o maior e o menor. Este será o maior e o menor valor da função que precisamos encontrar.

Vamos ver como aplicar este algoritmo corretamente ao resolver problemas.

Exemplo 1

Doença: a função y = x 3 + 4 x 2 é dada. Determine seu maior e menor valor nos segmentos [ 1 ; 4] e [-4; - 1 ] .

Solução:

Vamos começar encontrando o domínio desta função. Nesse caso, será o conjunto de todos os números reais, exceto 0 . Em outras palavras, D(y) : x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . Ambos os segmentos especificados na condição estarão dentro da área de definição.

Agora calculamos a derivada da função de acordo com a regra de diferenciação de uma fração:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x 3

Aprendemos que a derivada da função existirá em todos os pontos dos segmentos [ 1 ; 4] e [-4; - 1 ] .

Agora precisamos determinar os pontos estacionários da função. Vamos fazer isso com a equação x 3 - 8 x 3 = 0. Ele tem apenas uma raiz real, que é 2. Será um ponto estacionário da função e cairá no primeiro segmento [ 1 ; quatro].

Vamos calcular os valores da função nas extremidades do primeiro segmento e no ponto dado, ou seja, para x = 1 , x = 2 e x = 4:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Obtivemos que o maior valor da função m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 será alcançado em x = 1 , e o menor m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – em x = 2 .

O segundo segmento não inclui nenhum ponto estacionário, portanto, precisamos calcular os valores da função apenas nas extremidades do segmento fornecido:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Assim, m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Responda: Para o segmento [ 1 ; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , para o segmento [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Ver foto:

Antes de estudar Por aqui, recomendamos que você repita como calcular corretamente o limite unilateral e o limite no infinito, além de aprender os métodos básicos para encontrá-los. Para encontrar o maior e/ou menor valor de uma função em um intervalo aberto ou infinito, realizamos os seguintes passos em sequência.

1. Primeiro você precisa verificar se o intervalo dado será um subconjunto do domínio da função dada.
2. Vamos determinar todos os pontos que estão contidos no intervalo requerido e nos quais a primeira derivada não existe. Geralmente eles são para funções onde o argumento está dentro do sinal de módulo e para funções de potência com indicador racional. Se esses pontos estiverem ausentes, você poderá prosseguir para a próxima etapa.
3. Agora determinamos quais pontos estacionários caem em um determinado intervalo. Primeiro, igualamos a derivada a 0, resolvemos a equação e encontramos raízes adequadas. Se não temos um único ponto estacionário ou eles não caem em um determinado intervalo, então vamos imediatamente para ação posterior. Eles são determinados pelo tipo de intervalo.

• Se o intervalo se parece com [ a ; b) , então precisamos calcular o valor da função no ponto x = a e o limite unilateral lim x → b - 0 f (x) .
• Se o intervalo tem a forma (a ; b ] , então precisamos calcular o valor da função no ponto x = b e o limite unilateral lim x → a + 0 f (x) .
• Se o intervalo tem a forma (a ; b) , então precisamos calcular os limites laterais lim x → b - 0 f (x) , lim x → a + 0 f (x) .
• Se o intervalo se parece com [ a ; + ∞) , então é necessário calcular o valor no ponto x = a e o limite para mais infinito lim x → + ∞ f (x) .
• Se o intervalo se parece com (- ∞ ; b ] , calculamos o valor no ponto x = b e o limite em menos infinito lim x → - ∞ f (x) .
• Se - ∞ ; b , então consideramos o limite unilateral lim x → b - 0 f (x) e o limite no infinito menos lim x → - ∞ f (x)
• Se - ∞ ; + ∞ , então consideramos os limites para menos e mais infinito lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. Ao final, você precisa tirar uma conclusão com base nos valores obtidos​​da função e nos limites. Há muitas opções aqui. Assim, se o limite unilateral é igual a menos infinito ou mais infinito, fica imediatamente claro que nada pode ser dito sobre o menor e o maior valor da função. Abaixo vamos considerar um exemplo típico. Descrições detalhadas ajudá-lo a entender o que é o quê. Se necessário, você pode retornar às figuras 4 - 8 na primeira parte do material.

Condição: dada uma função y = 3 e 1 x 2 + x - 6 - 4 . Calcule seu maior e menor valor nos intervalos - ∞ ; - 4 , - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2 ), [ 1 ; 2 ), 2 ; + ∞ , [ 4 ; +∞) .

Solução

Em primeiro lugar, encontramos o domínio da função. O denominador da fração é trinômio quadrado, que não deve se transformar em 0:

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y): x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Obtivemos o escopo da função, à qual pertencem todos os intervalos especificados na condição.

Agora vamos derivar a função e obter:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

Consequentemente, as derivadas de uma função existem em todo o domínio de sua definição.

Vamos passar para encontrar pontos estacionários. A derivada da função torna-se 0 em x = - 1 2 . Este é um ponto estacionário que está nos intervalos (- 3 ; 1 ] e (- 3 ; 2) .

Vamos calcular o valor da função em x = - 4 para o intervalo (- ∞ ; - 4 ] , bem como o limite em menos infinito:

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

Como 3 e 1 6 - 4 > - 1 , então m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. Isso não nos permite determinar exclusivamente o menor valor da função. Podemos apenas concluir que existe um limite abaixo de - 1 , pois é desse valor que a função se aproxima assintoticamente em menos infinito.

Uma característica do segundo intervalo é que ele não possui um único ponto estacionário e nem um único limite estrito. Portanto, não podemos calcular o maior ou o menor valor da função. Ao definir o limite em menos infinito e como o argumento tende a -3 no lado esquerdo, obtemos apenas o intervalo de valores:

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Isso significa que os valores da função estarão localizados no intervalo - 1; +∞

Para encontrar o valor máximo da função no terceiro intervalo, determinamos seu valor no ponto estacionário x = - 1 2 se x = 1 . Também precisamos saber o limite unilateral para o caso em que o argumento tende a - 3 no lado direito:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 anos (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Descobriu-se que a função terá o maior valor em um ponto estacionário m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4. Quanto ao menor valor, não podemos determiná-lo. saber , é a presença de um limite inferior a - 4 .

Para o intervalo (- 3 ; 2), vamos pegar os resultados do cálculo anterior e mais uma vez calcular a que o limite unilateral é igual quando tende a 2 do lado esquerdo:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Assim, m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 , e o menor valor não pode ser determinado, e os valores da função são limitados a partir de baixo pelo número - 4 .

Com base no que fizemos nos dois cálculos anteriores, podemos afirmar que no intervalo [ 1 ; 2) a função terá o maior valor em x = 1, e é impossível encontrar o menor.

No intervalo (2 ; + ∞), a função não atingirá nem o maior nem o menor valor, ou seja. levará valores do intervalo - 1; +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Tendo calculado qual será o valor da função em x = 4 , descobrimos que m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , e a função dada em mais infinito se aproximará assintoticamente da reta y = - 1 .

Vamos comparar o que obtivemos em cada cálculo com o gráfico da função dada. Na figura, as assíntotas são mostradas por linhas pontilhadas.

Isso é tudo o que queríamos falar sobre encontrar o maior e o menor valor de uma função. Essas sequências de ações que fornecemos ajudarão você a fazer os cálculos necessários da maneira mais rápida e simples possível. Mas lembre-se de que muitas vezes é útil descobrir primeiro em quais intervalos a função diminuirá e em quais intervalos ela aumentará, após o que outras conclusões podem ser tiradas. Assim, você pode determinar com mais precisão o maior e o menor valor da função e justificar os resultados.

Se você notar um erro no texto, destaque-o e pressione Ctrl+Enter