Fórmulas de raízes do enésimo grau. Função de potência e raízes - definição, propriedades e fórmulas
Leia também
Vídeo aula 2: Propriedades da raiz do grau n > 1
Palestra: Raiz do grau n > 1 e suas propriedades
Raiz
Suponha que você tenha uma equação como:
Decisão dada equação será x 1 = 2 e x 2 = (-2). Ambas as soluções são adequadas como resposta, pois números com módulos iguais, quando elevados a uma potência par, dão o mesmo resultado.
Este foi um exemplo simples, no entanto, o que podemos fazer se, por exemplo,
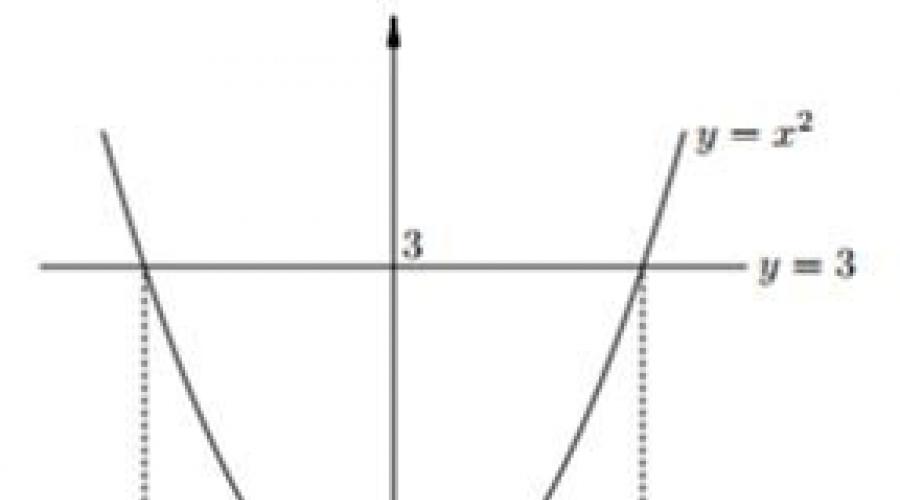
Vamos tentar representar graficamente a função y=x 2 . Seu gráfico é uma parábola:

No gráfico, você precisa encontrar pontos que correspondam ao valor y \u003d 3. Esses pontos são:
![]()
Isso significa que esse valor não pode ser chamado de inteiro, mas pode ser representado como uma raiz quadrada.
Qualquer raiz é Número irracional. Os números irracionais incluem raízes, frações infinitas não periódicas.
Raiz quadradaé um número não negativo "a", cuja expressão radical é igual ao número dado "a" ao quadrado.
Por exemplo,
Ou seja, como resultado, obteremos apenas um valor positivo. No entanto, como solução para uma equação quadrática da forma
A solução será x 1 = 4, x 2 = (-4).
Propriedades da raiz quadrada
1. Qualquer que seja o valor de x, esta expressão é verdadeira em qualquer caso:
![]()
2. Comparação de números contendo uma raiz quadrada. Para comparar esses números, é necessário inserir um e o segundo número sob o sinal da raiz. Esse número será maior cuja expressão radical é maior.
Entramos no número 2 sob o sinal da raiz
![]()
Agora vamos colocar o número 4 sob o sinal da raiz. Como resultado disso, obtemos
E só agora as duas expressões resultantes podem ser comparadas:
3. Removendo o multiplicador debaixo da raiz.
Se a expressão radical pode ser decomposta em dois fatores, um dos quais pode ser retirado do subsinal da raiz, então esta regra deve ser usada.
4. Existe uma propriedade inversa a isso - introduzir um multiplicador sob a raiz. Obviamente, usamos essa propriedade na segunda propriedade.
Sua privacidade é importante para nós. Por esse motivo, desenvolvemos uma Política de Privacidade que descreve como usamos e armazenamos suas informações. Por favor, leia nossa política de privacidade e deixe-nos saber se você tiver alguma dúvida.
Coleta e uso de informações pessoais
Informações pessoais referem-se a dados que podem ser usados para identificar ou contatar uma pessoa específica.
Você pode ser solicitado a fornecer suas informações pessoais a qualquer momento quando entrar em contato conosco.
A seguir estão alguns exemplos dos tipos de informações pessoais que podemos coletar e como podemos usar essas informações.
Quais informações pessoais coletamos:
- Quando você envia uma inscrição no site, podemos coletar várias informações, incluindo seu nome, número de telefone, endereço E-mail etc.
Como usamos suas informações pessoais:
- Recolhido por nós informação pessoal nos permite entrar em contato com você e informá-lo sobre ofertas exclusivas, promoções e outros eventos e eventos futuros.
- De tempos em tempos, podemos usar suas informações pessoais para enviar avisos e mensagens importantes.
- Também podemos usar informações pessoais para fins internos, como auditoria, análise de dados e vários estudos para melhorar os serviços que prestamos e para lhe fornecer recomendações sobre os nossos serviços.
- Se você participar de um sorteio, concurso ou incentivo semelhante, poderemos usar as informações fornecidas para administrar tais programas.
Divulgação a terceiros
Não divulgamos informações recebidas de você a terceiros.
Exceções:
- Se necessário - de acordo com a lei, ordem judicial, dentro litígio, e/ou com base em solicitações públicas ou solicitações de agências governamentais no território da Federação Russa - divulgue suas informações pessoais. Também podemos divulgar informações sobre você se determinarmos que tal divulgação é necessária ou apropriada para segurança, aplicação da lei ou outras ocasiões importantes.
- No caso de uma reorganização, fusão ou venda, podemos transferir as informações pessoais que coletamos para o sucessor terceirizado relevante.
Proteção de informações pessoais
Tomamos precauções - incluindo administrativas, técnicas e físicas - para proteger suas informações pessoais contra perda, roubo e uso indevido, bem como de acesso, divulgação, alteração e destruição não autorizados.
Mantendo sua privacidade no nível da empresa
Para garantir que suas informações pessoais estejam seguras, comunicamos práticas de privacidade e segurança aos nossos funcionários e aplicamos rigorosamente as práticas de privacidade.
Aula e apresentação sobre o tema: "Propriedades da raiz do grau n. Teoremas"
Materiais adicionais
Caros usuários, não se esqueça de deixar seus comentários, comentários, sugestões! Todos os materiais são verificados por um programa antivírus.
Material didático e simuladores na loja online "Integral" para o 11º ano
Manual interativo para graus 9-11 "Trigonometria"
Manual interativo para graus 10-11 "Logaritmos"
Propriedades da raiz do enésimo grau. Teoremas
Pessoal, continuamos estudando as raízes do enésimo grau de um número real. Como quase todos os objetos matemáticos, as raízes do grau n possuem algumas propriedades, hoje vamos estudá-las.Todas as propriedades que consideramos são formuladas e provadas apenas para valores não negativos das variáveis contidas sob o sinal da raiz.
No caso de um expoente de raiz ímpar, eles também valem para variáveis negativas.
Teorema 1. A raiz n do produto de dois números não negativos é igual ao produto das raízes n desses números: $\sqrt[n](a*b)=\sqrt[n](a)*\ sqrt[n](b) $ .
Vamos provar o teorema.
Prova. Pessoal, para provar o teorema, vamos introduzir novas variáveis, denotar:
$\sqrt[n](a*b)=x$.
$\sqrt[n](a)=y$.
$\sqrt[n](b)=z$.
Precisamos provar que $x=y*z$.
Observe que as seguintes identidades também são válidas:
$a*b=x^n$.
$a=y^n$.
$b=z^n$.
Então a seguinte identidade também vale: $x^n=y^n*z^n=(y*z)^n$.
Os graus de dois números não negativos e seus expoentes são iguais, então as bases dos próprios graus são iguais. Portanto, $x=y*z$, que é o que precisava ser provado.
Teorema 2. Se $a≥0$, $b>0$ e n - número natural, que é maior que 1, a seguinte igualdade é válida: $\sqrt[n](\frac(a)(b))=\frac(\sqrt[n](a))(\sqrt[n](b) ))$.
Ou seja, a n-ésima raiz do quociente é igual ao quociente das n-ésimas raízes.
Prova.
Para provar isso, usamos um esquema simplificado na forma de uma tabela:
Exemplos de cálculo da raiz n
Exemplo.Calcule: $\sqrt(16*81*256)$.
Solução. Vamos usar o Teorema 1: $\sqrt(16*81*256)=\sqrt(16)*\sqrt(81)*\sqrt(256)=2*3*4=24$.
Exemplo.
Calcule: $\sqrt(7\frac(19)(32))$.
Solução. Representamos a expressão radical na forma Fração imprópria: $7\frac(19)(32)=\frac(7*32+19)(32)=\frac(243)(32)$.
Vamos usar o Teorema 2: $\sqrt(\frac(243)(32))=\frac(\sqrt(243))(\sqrt(32))=\frac(3)(2)=1\frac(1 ) (2)$.
Exemplo.
Calcular:
a) $\sqrt(24)*\sqrt(54)$.
b) $\frac(\sqrt(256))(\sqrt(4))$.
Solução:
a) $\sqrt(24)*\sqrt(54)=\sqrt(24*54)=\sqrt(8*3*2*27)=\sqrt(16*81)=\sqrt(16)*\ sqrt(81)=2*3=6$.
b) $\frac(\sqrt(256))(\sqrt(4))=\sqrt(\frac(256)(4))=\sqrt(64)=24$.
Teorema 3. Se $a≥0$, ke n são números naturais maiores que 1, então a igualdade é verdadeira: $(\sqrt[n](a))^k=\sqrt[n](a^k)$.
Para erguer uma raiz a uma potência natural, basta elevar a expressão radical a essa potência.
Prova.
vamos considerar caso especial para $k=3$. Vamos usar o Teorema 1.
$(\sqrt[n](a))^k=\sqrt[n](a)*\sqrt[n](a)*\sqrt[n](a)=\sqrt[n](a*a *a)=\sqrt[n](a^3)$.
O mesmo pode ser provado para qualquer outro caso. Pessoal, provem vocês mesmos para o caso em que $k=4$ e $k=6$.
Teorema 4. Se $a≥0$ b n,k são números naturais maiores que 1, então vale a seguinte igualdade: $\sqrt[n](\sqrt[k](a))=\sqrt(a)$.
Para extrair uma raiz de uma raiz, basta multiplicar os expoentes das raízes.
Prova.
Vamos provar novamente brevemente usando a tabela. Para provar isso, usamos um esquema simplificado na forma de uma tabela: 
Exemplo.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.
Teorema 5. Se os índices da raiz e a expressão da raiz forem multiplicados pelo mesmo número natural, então o valor da raiz não mudará: $\sqrt(a^(kp))=\sqrt[n](a) $.
Prova.
O princípio da prova do nosso teorema é o mesmo dos outros exemplos. Vamos introduzir novas variáveis:
$\sqrt(a^(k*p))=x=>a^(k*p)=x^(n*p)$ (por definição).
$\sqrt[n](a^k)=y=>y^n=a^k$ (por definição).
Elevamos a última igualdade à potência p
$(y^n)^p=y^(n*p)=(a^k)^p=a^(k*p)$.
Pegou:
$y^(n*p)=a^(k*p)=x^(n*p)=>x=y$.
Ou seja, $\sqrt(a^(k*p))=\sqrt[n](a^k)$, que deveria ser provado.
Exemplos:
$\sqrt(a^5)=\sqrt(a)$ (dividido por 5).
$\sqrt(a^(22))=\sqrt(a^(11))$ (dividido por 2).
$\sqrt(a^4)=\sqrt(a^(12))$ (multiplicado por 3).
Exemplo.
Executar ações: $\sqrt(a)*\sqrt(a)$.
Solução.
Os expoentes raiz são números diferentes, então não podemos usar o Teorema 1, mas aplicando o Teorema 5 podemos obter expoentes iguais.
$\sqrt(a)=\sqrt(a^3)$ (multiplicado por 3).
$\sqrt(a)=\sqrt(a^4)$ (multiplicado por 4).
$\sqrt(a)*\sqrt(a)=\sqrt(a^3)*\sqrt(a^4)=\sqrt(a^3*a^4)=\sqrt(a^7)$.
Tarefas para solução independente
1. Calcule: $\sqrt(32*243*1024)$.2. Calcule: $\sqrt(7\frac(58)(81))$.
3. Calcule:
a) $\sqrt(81)*\sqrt(72)$.
b) $\frac(\sqrt(1215))(\sqrt(5))$.
4. Simplifique:
a) $\sqrt(\sqrt(a))$.
b) $\sqrt(\sqrt(a))$.
c) $\sqrt(\sqrt(a))$.
5. Execute as ações: $\sqrt(a^2)*\sqrt(a^4)$.
Exemplos:
\(\sqrt(16)=2\) porque \(2^4=16\)
\(\sqrt(-\frac(1)(125))\) \(=\) \(-\frac(1)(5)\) ,porque \((-\frac(1)(5)) ) ^3\) \(=\) \(-\frac(1)(125)\)
Como calcular a raiz do enésimo grau?
Para calcular a raiz \(n\)-th, você precisa se perguntar: que número ao grau \(n\)-th dará sob a raiz?
Por exemplo. Calcule a raiz \(n\)th: a)\(\sqrt(16)\); b) \(\sqrt(-64)\); c) \(\sqrt(0,00001)\); d)\(\sqrt(8000)\); e) \(\sqrt(\frac(1)(81))\).
a) Que número elevado a \(4\)ésima potência dará \(16\)? Obviamente, \(2\). É por isso:
b) Que número elevado à \(3\)ésima potência dará \(-64\)?
\(\sqrt(-64)=-4\)
c) Qual número elevado à \(5\)ésima potência, dará \(0,00001\)?
\(\sqrt(0,00001)=0,1\)
d) Que número elevado a \(3\)-ésimo grau dará \(8000\)?
\(\sqrt(8000)=20\)
e) Qual número elevado à \(4\)ésima potência dará \(\frac(1)(81)\)?
\(\sqrt(\frac(1)(81))=\frac(1)(3)\)
Nós revisamos os mais exemplos simples com uma raiz \(n\)º grau. Para resolver mais Tarefas desafiantes com \(n\)-th raízes - é vital conhecê-las.
Exemplo. Calcular:
|
\(\sqrt 3\cdot \sqrt(-3) \cdot \sqrt(27) \cdot \sqrt(9) -\) \(=\) |
NO este momento nenhuma das raízes pode ser calculada. Portanto, aplicamos as propriedades da raiz \(n\)-ésimo grau e transformamos a expressão. |
|
|
\(=\sqrt(3)\cdot \sqrt(-3)\cdot \sqrt(27)\cdot \sqrt(9)-\sqrt(-32)=\) |
Vamos reorganizar os fatores no primeiro termo para que a raiz quadrada e a raiz do \(n\)º grau fiquem lado a lado. Isso facilitará a aplicação das propriedades. a maioria das propriedades de raízes \(n\)th funcionam apenas com raízes do mesmo grau. |
|
|
\(=\sqrt(3) \cdot \sqrt(27) \cdot \sqrt(-3)\cdot \sqrt(9)-(-5)=\) |
Aplique a propriedade \(\sqrt[n](a)\cdot \sqrt[n](b)=\sqrt[n](a\cdot b)\) e expanda o colchete |
|
|
\(=\sqrt(81)\cdot \sqrt(-27)+5=\) |
Calcular \(\sqrt(81)\) e \(\sqrt(-27)\) |
|
|
\(=9\cdot(-3)+5=-27+5=-22\) |
|
A raiz n e a raiz quadrada estão relacionadas?
De qualquer forma, qualquer raiz de qualquer grau é apenas um número, embora escrito de uma forma incomum para você.
Singularidade da raiz n
Uma raiz \(n\)-ésima com \(n\) ímpar pode ser obtida de qualquer número, mesmo negativo (veja exemplos no início). Mas se \(n\) for par (\(\sqrt(a)\), \(\sqrt(a)\),\(\sqrt(a)\)…), então tal raiz será extraída somente se \( a ≥ 0\) (a propósito, a raiz quadrada tem o mesmo). Isso se deve ao fato de que extrair uma raiz é o oposto da exponenciação.

E elevar a uma potência par torna até um número negativo positivo. De fato, \((-2)^6=(-2) \cdot (-2) \cdot (-2) \cdot (-2) \cdot (-2) \cdot (-2)=64\). Portanto, não podemos obter um número negativo sob a raiz de um grau par. Isso significa que não podemos extrair tal raiz de um número negativo.

Uma potência ímpar não tem tais restrições - um número negativo elevado a uma potência ímpar permanecerá negativo: \((-2)^5=(-2) \cdot (-2) \cdot (-2) \cdot (-2) ) \cdot(-2)=-32\). Portanto, sob a raiz de um grau ímpar, você pode obter um número negativo. Isso significa que também é possível extraí-lo de um número negativo.

Raizn-º grau e suas propriedades
O que é uma raiznº grau? Como extrair a raiz?
Na oitava série, você já conseguiu se familiarizar com raiz quadrada. Decidido exemplos típicos com raízes, aplicando certas propriedades das raízes. Também decidiu equações quadráticas , onde sem extrair a raiz quadrada - de jeito nenhum. Mas a raiz quadrada é apenas um caso especial de mais conceito amplo – raiz n º grau . Além do quadrado, há, por exemplo, uma raiz cúbica, a raiz da quarta, quinta e mais altos graus. E para trabalho de sucesso com essas raízes, ainda seria bom começar com “você” com raízes quadradas.) Portanto, para aqueles que têm problemas com elas, recomendo fortemente repetir.
Extrair uma raiz é uma das operações inversas da exponenciação.) Por que "um de"? Porque, extraindo a raiz, procuramos base de acordo com famosos grau e indicador. E há outra operação inversa - encontrar indicador de acordo com famosos grau e base. Essa operação é chamada de encontrar logaritmo.É mais complexo do que extrair a raiz e é estudado no ensino médio.)
Então vamos nos conhecer!
Primeiro, a designação. A raiz quadrada, como já sabemos, é denotada assim:. Este ícone é chamado de forma muito bonita e científica - radical. E quais são as raízes de outros graus? É muito simples: acima da "cauda" do radical, eles também escrevem um indicador do grau cuja raiz está sendo procurada. Se você estiver procurando por uma raiz cúbica, escreva um triplo: . Se a raiz do quarto grau, então, respectivamente, . E assim por diante.) visão geral raiz enésimo grau está marcado assim:
Onde .
Númerouma , como em raízes quadradas, é chamado expressão radical e aqui está o númeron isso é novo para nós. E chamou indicador de raiz .
Como extrair raízes de qualquer grau? Assim como os quadrados - descubra qual número elevado à enésima potência nos dá um númerouma .)
Como, por exemplo, extrair a raiz cúbica de 8? Aquilo é ? E que número ao cubo nos dará 8? Deuce, é claro.) Então eles escrevem:
Ou . Qual é o número elevado à quarta potência de 81? Três.) Então,
E a raiz décima de 1? Bem, é óbvio que uma unidade para qualquer potência (incluindo a décima) é igual a um.) Ou seja:
E de um modo geral.
Com zero, a mesma história: zero para qualquer poder natural é igual a zero. Aquilo é, .
Como você pode ver, em comparação com as raízes quadradas, já é mais difícil descobrir qual número nos dá o número da raiz em um grau ou outrouma . Mais difícil pegar responda e verifique se está correto por exponenciaçãon . A situação é muito facilitada se você souber pessoalmente o grau de números populares. Então agora estamos treinando. :) Reconhecemos os graus!)
Respostas (em desordem):
Sim Sim! Há mais respostas do que tarefas.) Porque, por exemplo, 2 8 , 4 4 e 16 2 são todos o mesmo número 256.
Treinado? Em seguida, consideramos exemplos:

Respostas (também em desordem): 6; 2; 3; 2; 3; 5.
Ocorrido? Fabuloso! Vamos continuar.)
Restrições de raiz. raiz aritmética nº grau.
NO raízes do enésimo graus, assim como em quadrados, também têm suas limitações e suas fichas. Em essência, eles não são diferentes daquelas restrições para raízes quadradas.
Não é escolhido, não é? O que é 3, o que é -3 à quarta potência será +81. :) E com qualquer raiz até grau de um número negativo será a mesma música. E isso significa que é impossível extrair raízes pares de números negativos . Esta é uma ação proibida em matemática. Tão proibido quanto dividir por zero. Portanto, expressões como , e similares - não faz sentido.
Mas as raízes ímpar graus de números negativos - por favor!
Por exemplo, ; ![]() , e assim por diante.)
, e assim por diante.)
E de números positivos, você pode extrair com segurança qualquer raiz, qualquer grau:
![]()
Em geral, é compreensível, eu acho.) E, a propósito, a raiz não precisa ser extraída exatamente. Estes são apenas exemplos, puramente para compreensão.) Acontece que no processo de resolução (por exemplo, equações) surgem raízes bastante ruins. Algo como . Do oito, a raiz cúbica é extraída perfeitamente, e aqui o sete está sob a raiz. O que fazer? Tudo bem. Tudo é exatamente igual.- este é o número que, ao cubo, nos dará 7. Só que o número é muito feio e desgrenhado. Aqui está:
Além disso, esse número nunca termina e não tem ponto final: os números seguem de forma completamente aleatória. É irracional ... Nesses casos, a resposta é deixada na forma de uma raiz.) Mas se a raiz for extraída puramente (por exemplo), então, naturalmente, a raiz deve ser calculada e escrita:
![]()
Novamente, pegamos nosso número experimental 81 e extraímos a raiz quarta dele:
Porque três na quarta será 81. Bem, que bom! Mas também menos três o quarto também será 81!
Há uma ambiguidade:
E, para eliminá-lo, assim como nas raízes quadradas, foi introduzido um termo especial: raiz aritméticanº grau entre uma - é assim não negativo número,n-º grau do qual é igual a uma .
E a resposta com mais ou menos é chamada de forma diferente - raiz algébricanº grau. Para qualquer potência par, a raiz algébrica será dois números opostos. Na escola, eles trabalham apenas com raízes aritméticas. É por isso números negativos em raízes aritméticas são simplesmente descartadas. Por exemplo, eles escrevem: O positivo em si, é claro, não está escrito: ele implicar.
Tudo, ao que parece, é simples, mas ... Mas e as raízes de um grau ímpar de números negativos? Afinal, sempre há um número negativo ao extrair! Como qualquer número negativo em grau ímpar também dá um número negativo. E a raiz aritmética só funciona com números não negativos! É por isso que é aritmética.)
Em tais raízes, eles fazem isso: eles tiram um menos de baixo da raiz e o colocam na frente da raiz. Assim:
![]()
Nesses casos, diz-se que expresso em termos de uma raiz aritmética (ou seja, já não negativa) .
Mas há uma coisa que pode ser confusa - esta é a solução de equações simples com potências. Por exemplo, aqui está uma equação:
Escrevemos a resposta: Na verdade, esta resposta é apenas uma notação abreviada duas respostas:
![]()
![]()
O mal-entendido aqui é que eu já escrevi um pouco mais alto que apenas raízes não negativas (ou seja, aritméticas) são consideradas na escola. E aqui está uma das respostas com menos... Como ser? De jeito nenhum! Os sinais aqui são o resultado da resolução da equação. MAS a própria raiz- o valor ainda não é negativo! Veja por si mesmo:
Bem, está mais claro agora? com colchetes?)
Com um grau ímpar, tudo é muito mais simples - sempre acontece 1 raiz. Mais ou menos. Por exemplo:
Então se nós simplesmente extraímos a raiz (de grau par) do número, então sempre obtemos 1 resultado não negativo. Porque é uma raiz aritmética. Agora, se decidirmos a equação com um grau par, obtemos duas raízes opostas, já que este é solução da equação.
Com raízes de graus ímpares (cúbico, quinto grau, etc.) não há problemas. Extraímos a nós mesmos e não nos banhamos com signos. Plus sob a raiz significa o resultado da extração com um plus. Menos significa menos.
E agora é hora de conhecer propriedades da raiz. Alguns já nos serão familiares de raízes quadradas, mas alguns novos serão adicionados. Vai!
Propriedades da raiz. A raiz do trabalho.
Esta propriedade já nos é familiar de raízes quadradas. Para raízes de outros graus, tudo é semelhante:
![]()
Aquilo é, a raiz do produto é igual ao produto das raízes de cada fator separadamente.
Se o indicadorn par, então ambos os números radicaisuma eb deve, é claro, ser não negativo, caso contrário a fórmula não tem significado. No caso de um indicador ímpar, não há restrições: tiramos os menos abaixo das raízes e depois trabalhamos com raízes aritméticas.)
Como nas raízes quadradas, aqui esta fórmula é igualmente útil tanto da esquerda para a direita quanto da direita para a esquerda. Aplicar a fórmula da esquerda para a direita permite extrair as raízes do trabalho. Por exemplo:
Essa fórmula, aliás, é válida não apenas para dois, mas para qualquer número de fatores. Por exemplo:
Além disso, usando essa fórmula, você pode extrair raízes de números grandes: para isso, o número sob a raiz é decomposto em fatores menores e, em seguida, as raízes são extraídas separadamente de cada fator.
Por exemplo, tal tarefa:
O número é grande o suficiente. Faz raiz? suave- também sem uma calculadora não é claro. Seria bom fatorar isso. Por que exatamente o número 3375 é divisível? Por 5, parece: o último dígito é cinco.) Divida:
![]()
Ah, divisível por 5 novamente! 675:5 = 135. E 135 é novamente dividido por cinco. Sim, quando vai acabar?
135:5 = 27. Com o número 27, tudo já está claro - este é um três em um cubo. Significa,
Então:
Eles tiraram a raiz pedaço por pedaço, bem, tudo bem.)
Ou este exemplo:
Novamente, fatoramos de acordo com os sinais de divisibilidade. O que? Em 4, porque o último par de números 40 é divisível por 4. E por 10, porque o último dígito é zero. Então, você pode dividir de uma só vez por 40 de uma só vez:
![]()
Sobre o número 216, já sabemos que este é um seis ao cubo. Aquilo é,
E 40, por sua vez, pode ser decomposto como . Então
E então finalmente obtemos:
Não funcionou de forma limpa para extrair a raiz, bem, tudo bem. De qualquer forma, simplificamos a expressão: sabemos que sob a raiz (pelo menos quadrado, pelo menos cúbico - qualquer) é costume deixar o mais número pequeno possível.) Neste exemplo, fizemos uma operação muito útil, também já familiar para nós de raízes quadradas. Você reconhece? Sim! Nós suportou fatores de baixo da raiz. Neste exemplo, tiramos um dois e um seis, ou seja, número 12.
Como tirar o fator do sinal da raiz?
É muito fácil eliminar o fator (ou fatores) além do sinal da raiz. Decompomos a expressão raiz em fatores e extraímos o que é extraído.) E o que não é extraído, deixamos na raiz. Ver:
Decompomos o número 9072 em fatores. Como temos uma raiz do quarto grau, primeiro tentamos decompor em fatores que são as quartas potências dos números naturais - 16, 81, etc.
Vamos tentar dividir 9072 por 16:
Compartilhado!
Mas 567 parece ser divisível por 81:
Significa, .
Então
Propriedades da raiz. Multiplicação de raízes.
Considere agora a aplicação inversa da fórmula - da direita para a esquerda:
![]()
À primeira vista, nada de novo, mas as aparências enganam.) Aplicação reversa fórmula expande muito nossas capacidades. Por exemplo:
Hmm, então o que há de errado com isso? Multiplicaram tudo. Realmente não há nada de especial aqui. A multiplicação usual de raízes. E aqui está um exemplo!
Separadamente, as raízes não são puramente extraídas dos fatores. Mas o resultado é excelente.)
Novamente, a fórmula é válida para qualquer número de fatores. Por exemplo, você precisa calcular a seguinte expressão:
O principal aqui é a atenção. O exemplo contém vários as raízes são cúbicas e de quarto grau. E nenhum deles é definitivamente extraído ...
E a fórmula do produto de raízes é aplicável apenas a raízes com o mesmo indicadores. Então vamos agrupá-los em um grupo separado. raízes cúbicas e separadamente - o quarto grau. E lá, você vê, tudo vai crescer junto.))
E eu não precisava de uma calculadora.
Como adicionar um multiplicador sob o sinal de raiz?
Próximo coisa útil – digitando um número sob a raiz. Por exemplo:
É possível remover o triplo dentro da raiz? Elementar! Se o triplo for transformado em raiz, então a fórmula do produto das raízes funcionará. Então, transformamos o três em uma raiz. Como temos uma raiz do quarto grau, também a transformaremos em uma raiz do quarto grau.) Assim:
![]()
Então
A raiz, a propósito, pode ser feita a partir de qualquer número não negativo. E na medida em que queremos (tudo desde estudo de caso depende). Esta será a raiz da enésima potência deste mesmo número:
![]()
E agora - Atenção! Fonte de erros muito grosseiros! Eu não disse nada aqui por nada não negativo números. A raiz aritmética funciona apenas com tal. Se tivermos um número negativo em algum lugar da tarefa, deixamos o menos na frente da raiz (se estiver fora) ou nos livramos do menos abaixo da raiz, se estiver dentro. Eu te lembro se sob a raiz até grau acaba por ser um número negativo, então a expressão não faz sentido.
Por exemplo, tal tarefa. Insira um multiplicador sob o sinal de raiz:
Se agora rootearmos menos dois, então estaremos cruelmente enganados:
O que está errado aqui? E o fato de que o quarto grau, devido à sua paridade, “comeu” com segurança esse menos, como resultado do qual um número deliberadamente negativo se transformou em positivo. A solução correta é assim:
Nas raízes de graus ímpares, o menos não é “comido”, mas também é melhor deixá-lo de fora:
Aqui a raiz de um grau ímpar é cúbica, e temos todo o direito de colocar o menos sob a raiz também. Mas é preferível em tais exemplos deixar também o menos de fora e escrever a resposta expressa através da raiz aritmética (não negativa), pois a raiz, embora tenha direito à vida, mas não é aritmética.
Assim, com a introdução de um número sob a raiz, tudo também fica claro, espero.) Vamos passar para a próxima propriedade.
Propriedades da raiz. A raiz da fração. Divisão de raízes.
Essa propriedade também repete completamente a das raízes quadradas. Só agora estendemos para raízes de qualquer grau:
A raiz da fração igual a raiz do numerador dividido pela raiz do denominador.
Se n é par, então o númerouma deve ser não negativo, e o númerob - estritamente positivo (você não pode dividir por zero). No caso de um expoente ímpar, a única restrição será .
Esta propriedade permite extrair raízes de frações de forma fácil e rápida:


A ideia é clara, eu acho. Em vez de trabalhar com a fração inteira, passamos a trabalhar separadamente com o numerador e separadamente com o denominador.) Se a fração for decimal ou, oh horror, número misto, então passamos primeiro para frações ordinárias:


Agora vamos ver como essa fórmula funciona da direita para a esquerda. Aqui também são reveladas possibilidades muito úteis. Por exemplo, este exemplo:

As raízes não são exatamente extraídas do numerador e do denominador, mas da fração inteira, tudo bem.) Você pode resolver este exemplo de uma maneira diferente - retire o fator no numerador de baixo da raiz, seguido pela redução:

Como quiser. A resposta é sempre a mesma - a correta. Se você não cometer erros ao longo do caminho.)
Então, descobrimos a multiplicação/divisão das raízes. Subimos para o próximo passo e consideramos a terceira propriedade - raiz em grau e raiz do grau .
Raiz em grau. Raiz do grau.
Como elevar uma raiz a uma potência? Por exemplo, digamos que temos um número . Este número pode ser elevado a uma potência? Em um cubo, por exemplo? É claro! Multiplique a raiz por ela mesma três vezes e - de acordo com a fórmula do produto das raízes:
Aqui está a raiz e o grau Até parece mutuamente cancelados ou compensados. De fato, se elevarmos um número que, ao cubo, nos dará um triplo, aumentarmos para esse mesmo cubo, então o que obteremos? Três e obter, é claro! E assim será para qualquer número não negativo. No geral:
Se os expoentes e a raiz forem diferentes, também não há problema. Se você conhece as propriedades dos graus.)
![]()
Se o expoente for menor que o expoente da raiz, simplesmente direcionamos o expoente sob a raiz:
![]()
Em geral será:
![]()
A ideia é clara: elevamos a expressão radical a uma potência e, em seguida, a simplificamos retirando fatores da raiz, se possível. Se umn direto, entãouma deve ser não negativo. Por que é compreensível, eu acho.) E sen estranho, então não há restrições sobreuma Já foi:
Vamos tratar agora raiz do grau . Isto é, não a própria raiz será elevada a um poder, mas expressão radical. Também não há nada complicado aqui, mas há muito mais espaço para erros. Por quê? Porque os números negativos entram em jogo, o que pode confundir os sinais. Por enquanto, vamos começar com as raízes das potências ímpares - elas são muito mais simples.
Digamos que temos o número 2. Podemos cubá-lo? É claro!
E agora - de volta, extraia a raiz cúbica dos oito:
![]()
Eles começaram com um deuce e voltaram para um deuce.) Não é de admirar: aumentar para um cubo foi compensado pela operação inversa - extrair a raiz cúbica.
Outro exemplo:
Aqui, também, tudo está no caminho certo. O grau e a raiz um do outro compensaram. Em geral, para as raízes de graus ímpares, podemos escrever a seguinte fórmula:
![]()
Esta fórmula é válida para qualquer número realuma . Seja positivo ou negativo.
Ou seja, um grau ímpar e uma raiz de mesmo grau sempre se compensam e uma expressão radical é obtida. :)
Mas com até grau, esse foco pode não passar mais. Veja por si mesmo:
![]()
Ainda não há nada de especial aqui. O quarto grau e a raiz do quarto grau também se equilibraram e resultou apenas um deuce, ou seja, expressão enraizada. E para qualquer um não negativo os números serão os mesmos. E agora nós apenas substituímos dois nesta raiz por menos dois. Então vamos criar uma raiz assim:
O menos do deuce "queimado" com segurança devido ao quarto grau. E como resultado da extração da raiz (aritmética!) positivo número. Era menos dois, tornou-se mais dois).
![]()
Qual é o maior erro, sim.
Portanto, para até A fórmula para a raiz do expoente é assim:
Aqui, o sinal do módulo, não amado por muitos, foi adicionado, mas não há nada de terrível nele: graças a ele, a fórmula também funciona para qualquer número realuma. E o módulo simplesmente elimina os contras:
![]()
![]()
Somente nas raízes do enésimo grau apareceu uma distinção adicional entre graus pares e ímpares. Até os graus, como vemos, são mais caprichosos, sim.)
E agora vamos considerar uma nova propriedade útil e muito interessante, já característica das raízes do enésimo grau: se o expoente raiz e o expoente da expressão raiz forem multiplicados (divididos) pelo mesmo número natural, então o valor da raiz não mudará.
![]()
Algo que lembra a propriedade básica de uma fração, não é? Em frações, também podemos multiplicar (dividir) o numerador e o denominador pelo mesmo número (exceto zero). De fato, essa propriedade das raízes também é consequência da propriedade básica da fração. Quando conhecemos grau com indicador racional então tudo ficará claro. O que, como e onde.)
A aplicação direta desta fórmula nos permite simplificar absolutamente quaisquer raízes de qualquer grau. Inclusive, se os expoentes da expressão raiz e a própria raiz vários. Por exemplo, vamos simplificar a seguinte expressão:
Agimos com simplicidade. Para começar, separamos o quarto grau do décimo abaixo da raiz e - vá em frente! Como? Pelas propriedades dos graus, é claro! Retiramos o fator de baixo da raiz ou trabalhamos de acordo com a fórmula da raiz do grau.
Mas vamos simplificar, usando apenas esta propriedade. Para fazer isso, representamos os quatro sob a raiz como:
E agora - o mais interessante - nós reduzimos mentalmente o indicador sob a raiz (dois) com o indicador de raiz (quatro)! E obtemos: