Linha reta. Equação de uma linha reta. Equação de uma reta que passa por dois pontos Dados 2 pontos encontre a equação de uma reta
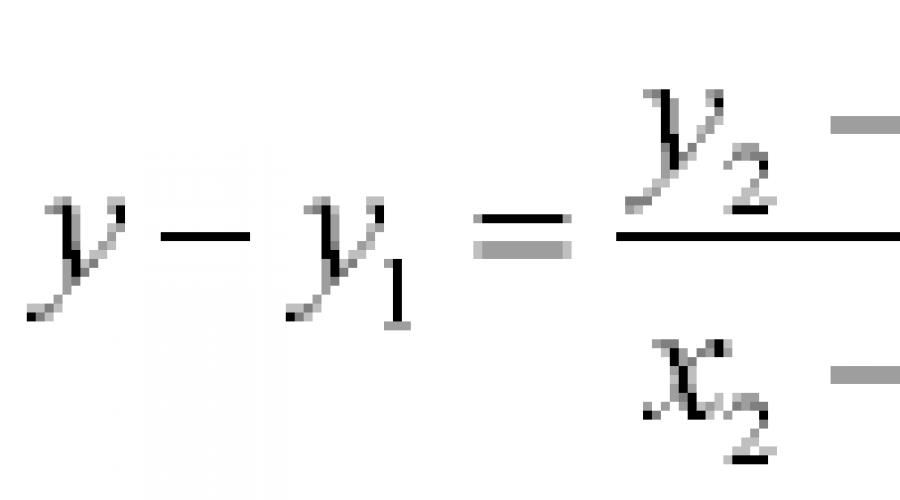
Leia também
Propriedades de uma reta na geometria euclidiana.
Existem infinitas linhas que podem ser traçadas através de qualquer ponto.
Por quaisquer dois pontos não coincidentes, há apenas uma linha reta.
Duas linhas não coincidentes no plano se cruzam em um único ponto ou são
paralelo (segue do anterior).
No espaço tridimensional, existem três opções para a posição relativa de duas linhas:
- linhas se cruzam;
- linhas retas são paralelas;
- linhas retas se cruzam.
Em linha reta linha- curva algébrica de primeira ordem: no sistema de coordenadas cartesianas, uma linha reta
é dado no plano por uma equação de primeiro grau (equação linear).
Equação geral de uma reta.
Definição. Qualquer linha no plano pode ser dada por uma equação de primeira ordem
Ah + Wu + C = 0,
e constante A, B não é igual a zero ao mesmo tempo. Essa equação de primeira ordem é chamada em geral
equação da reta. Dependendo dos valores das constantes A, B e Com Os seguintes casos especiais são possíveis:
. C = 0, A ≠ 0, B ≠ 0- a linha passa pela origem
. A = 0, B ≠0, C ≠0 (Por + C = 0)- linha reta paralela ao eixo Oh
. B = 0, A ≠ 0, C ≠ 0 (Ax + C = 0)- linha reta paralela ao eixo UO
. B = C = 0, A ≠ 0- a linha coincide com o eixo UO
. A = C = 0, B ≠ 0- a linha coincide com o eixo Oh
A equação de uma linha reta pode ser representada de várias formas, dependendo de qualquer
condições iniciais.
Equação de uma reta por um ponto e um vetor normal.
Definição. Em um sistema de coordenadas retangulares cartesianas, um vetor com componentes (A, B)
perpendicular à reta dada pela equação
Ah + Wu + C = 0.
Exemplo. Encontre a equação de uma reta que passa por um ponto A(1, 2) perpendicular ao vetor (3, -1).
Decisão. Vamos compor em A \u003d 3 e B \u003d -1 a equação da linha reta: 3x - y + C \u003d 0. Para encontrar o coeficiente C
substituimos as coordenadas do ponto A dado na expressão resultante. Obtemos: 3 - 2 + C = 0, portanto
C = -1. Total: a equação desejada: 3x - y - 1 \u003d 0.
Equação de uma linha reta que passa por dois pontos.
Sejam dados dois pontos no espaço M 1 (x 1 , y 1 , z 1) e M2 (x 2, y 2 , z 2), então equação de linha reta,
passando por estes pontos:
Se algum dos denominadores for igual a zero, o numerador correspondente deve ser igual a zero. No
plano, a equação de uma linha reta escrita acima é simplificada:

E se x 1 ≠ x 2 e x = x 1, E se x 1 = x 2 .
Fração = k chamado fator de inclinação Em linha reta.
Exemplo. Encontre a equação de uma linha reta que passa pelos pontos A(1, 2) e B(3, 4).
Decisão. Aplicando a fórmula acima, obtemos:

Equação de uma linha reta por um ponto e uma inclinação.
Se a equação geral de uma reta Ah + Wu + C = 0 trazer para o formulário:

e designar  , então a equação resultante é chamada
, então a equação resultante é chamada
equação de uma linha reta com inclinação k.
A equação de uma linha reta em um ponto e um vetor diretor.
Por analogia com o ponto considerando a equação de uma linha reta através do vetor normal, você pode entrar na tarefa
uma linha reta que passa por um ponto e um vetor direcional de uma linha reta.
Definição. Todo vetor diferente de zero (α 1 , α 2), cujos componentes satisfazem a condição
Aα 1 + Bα 2 = 0 chamado vetor de direção da reta.
Ah + Wu + C = 0.
Exemplo. Encontre a equação de uma linha reta com vetor de direção (1, -1) e passando pelo ponto A(1, 2).
Decisão. Vamos procurar a equação da linha reta desejada na forma: Ax + Por + C = 0. De acordo com a definição,
os coeficientes devem satisfazer as condições:
1 * A + (-1) * B = 0, ou seja A = B
Então a equação de uma reta tem a forma: Ax + Ay + C = 0, ou x + y + C / A = 0.
no x=1, y=2 Nós temos C/A = -3, ou seja equação desejada:
x + y - 3 = 0
Equação de uma linha reta em segmentos.
Se na equação geral da reta Ah + Wu + C = 0 C≠0, então, dividindo por -C, obtemos:
 ou onde
ou onde

O significado geométrico dos coeficientes é que o coeficiente a é a coordenada do ponto de interseção
reta com eixo Oh, uma b- a coordenada do ponto de intersecção da linha com o eixo UO.
Exemplo. A equação geral de uma reta é dada x - y + 1 = 0. Encontre a equação desta linha reta em segmentos.
C \u003d 1, , a \u003d -1, b \u003d 1.
Equação normal de uma reta.
Se ambos os lados da equação Ah + Wu + C = 0 dividir por número  , que é chamado
, que é chamado
fator de normalização, então obtemos
xcosφ + ysinφ - p = 0 -equação normal de uma reta.
O sinal ± do fator de normalização deve ser escolhido de modo que µ * C< 0.
R- o comprimento da perpendicular baixada da origem até a linha,
uma φ - o ângulo formado por esta perpendicular com a direção positiva do eixo Oh.
Exemplo. Dada a equação geral de uma linha reta 12x - 5a - 65 = 0. Necessário para escrever vários tipos de equações
esta linha reta.
A equação desta linha reta em segmentos:

A equação desta linha com inclinação: (dividir por 5)

Equação de uma reta:

cos φ = 12/13; sen φ= -5/13; p=5.
Deve-se notar que nem toda linha reta pode ser representada por uma equação em segmentos, por exemplo, linhas retas,
paralelas aos eixos ou passando pela origem.
Ângulo entre linhas em um plano.
Definição. Se duas linhas são dadas y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, então o ângulo agudo entre essas linhas
será definido como

Duas retas são paralelas se k 1 = k 2. Duas retas são perpendiculares
E se k 1 \u003d -1 / k 2 .
Teorema.
Direto Ah + Wu + C = 0 e A 1 x + B 1 y + C 1 \u003d 0 são paralelos quando os coeficientes são proporcionais
A 1 \u003d λA, B 1 \u003d λB. Se também С 1 \u003d λС, então as linhas coincidem. Coordenadas do ponto de intersecção de duas linhas
são encontrados como uma solução para o sistema de equações dessas linhas.
A equação de uma reta que passa por um ponto dado é perpendicular a uma reta dada.
Definição. Uma linha que passa por um ponto M 1 (x 1, y 1) e perpendicular à linha y = kx + b
representado pela equação:

A distância de um ponto a uma linha.
Teorema. Se for dado um ponto M(x 0, y 0), então a distância até a linha Ah + Wu + C = 0 definido como:

Prova. Deixe o ponto M 1 (x 1, y 1)- a base da perpendicular caiu do ponto M para um dado
direto. Então a distância entre os pontos M e M 1:
![]() (1)
(1)
Coordenadas x 1 e 1 pode ser encontrada como uma solução para o sistema de equações:

A segunda equação do sistema é a equação de uma linha reta que passa por um ponto dado M 0 perpendicularmente
dada linha. Se transformarmos a primeira equação do sistema na forma:
A(x - x 0) + B(y - y 0) + Ax 0 + Por 0 + C = 0,
então, resolvendo, temos:

Substituindo essas expressões na equação (1), encontramos:

O teorema foi provado.
Sejam dados dois pontos M 1 (x 1, y 1) e M 2 (x 2, y 2). Escrevemos a equação de uma linha reta na forma (5), onde k coeficiente ainda desconhecido:
Desde o ponto M 2 pertence a uma dada linha, então suas coordenadas satisfazem a equação (5): . Expressando a partir daqui e substituindo na equação (5), obtemos a equação desejada:
![]()
Se um ![]() Esta equação pode ser reescrita de uma forma que seja mais fácil de lembrar:
Esta equação pode ser reescrita de uma forma que seja mais fácil de lembrar:
![]() (6)
(6)
Exemplo. Escreva a equação de uma linha reta que passa pelos pontos M 1 (1,2) e M 2 (-2,3)
Decisão. ![]() . Usando a propriedade da proporção, e realizando as transformações necessárias, obtemos a equação geral de uma reta:
. Usando a propriedade da proporção, e realizando as transformações necessárias, obtemos a equação geral de uma reta:
Ângulo entre duas linhas
Considere duas linhas l 1 e l 2:
l 1: , , e
l 2: , ,
φ é o ângulo entre eles (). A Figura 4 mostra: .
 |
Daqui ![]() , ou
, ou
Usando a fórmula (7), um dos ângulos entre as linhas pode ser determinado. O segundo ângulo é .
Exemplo. Duas retas são dadas pelas equações y=2x+3 ey=-3x+2. encontre o ângulo entre essas linhas.
Decisão. Pode ser visto nas equações que k 1 \u003d 2 e k 2 \u003d-3. substituindo esses valores na fórmula (7), encontramos
![]() . Portanto, o ângulo entre essas linhas é .
. Portanto, o ângulo entre essas linhas é .
Condições para paralelismo e perpendicularidade de duas linhas
Se em linha reta l 1 e l 2 são paralelas, então φ=0 e tgφ=0. da fórmula (7) segue que , de onde k 2 \u003d k 1. Assim, a condição para que duas retas sejam paralelas é a igualdade de suas inclinações.
Se em linha reta l 1 e l 2 perpendicular, então φ=π/2, α 2 = π/2+ α 1 . ![]() . Assim, a condição para que duas retas sejam perpendiculares é que suas inclinações sejam recíprocas em magnitude e opostas em sinal.
. Assim, a condição para que duas retas sejam perpendiculares é que suas inclinações sejam recíprocas em magnitude e opostas em sinal.
Distância do ponto à linha
Teorema. Se um ponto M(x 0, y 0) for fornecido, a distância até a linha Ax + Vy + C \u003d 0 será definida como
Prova. Seja o ponto M 1 (x 1, y 1) a base da perpendicular baixada do ponto M até a reta dada. Então a distância entre os pontos M e M 1:
As coordenadas x 1 e y 1 podem ser encontradas como uma solução para o sistema de equações:
A segunda equação do sistema é a equação de uma linha reta que passa por um ponto dado M 0 perpendicular a uma linha reta dada.
Se transformarmos a primeira equação do sistema na forma:
A(x - x 0) + B(y - y 0) + Ax 0 + Por 0 + C = 0,
então, resolvendo, temos:
Substituindo essas expressões na equação (1), encontramos:
O teorema foi provado.
Exemplo. Determine o ângulo entre as linhas: y = -3x + 7; y = 2x + 1.
k 1 \u003d -3; k2 = 2tgj= ; j = p/4.
Exemplo. Mostre que as retas 3x - 5y + 7 = 0 e 10x + 6y - 3 = 0 são perpendiculares.
Encontramos: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 k 2 \u003d -1, portanto, as linhas são perpendiculares.
Exemplo. Os vértices do triângulo A(0; 1), B(6; 5), C(12; -1) são dados. Encontre a equação para a altura tirada do vértice C.
Encontramos a equação do lado AB: ; 4x = 6a - 6;
2x - 3y + 3 = 0;
A equação de altura desejada é: Ax + By + C = 0 ou y = kx + b.
k= . Então y = . Porque altura passa pelo ponto C, então suas coordenadas satisfazem esta equação: de onde b \u003d 17. Total: .
Resposta: 3x + 2y - 34 = 0.
A distância de um ponto a uma linha é determinada pelo comprimento da perpendicular baixada do ponto à linha.
Se a linha é paralela ao plano de projeção (h | | P 1), então para determinar a distância do ponto MAS para em linha reta hé necessário soltar uma perpendicular do ponto MAS para a horizontal h.
Consideremos um exemplo mais complicado, quando a linha ocupa uma posição geral. Seja necessário determinar a distância do ponto M para em linha reta uma posição geral.
Tarefa de definição distâncias entre linhas paralelas resolvido da mesma forma que o anterior. Um ponto é tomado em uma linha, e uma perpendicular é traçada a partir dele para outra linha. O comprimento da perpendicular é igual à distância entre as linhas paralelas.
Curva de segunda ordemé uma linha definida por uma equação do segundo grau em relação às coordenadas cartesianas atuais. No caso geral, Ax 2 + 2Bxy + Su 2 + 2Dx + 2Ey + F \u003d 0,
onde A, B, C, D, E, F são números reais e pelo menos um dos números A 2 + B 2 + C 2 ≠0.
Círculo
Centro do círculo- este é o lugar geométrico dos pontos no plano equidistantes do ponto do plano C (a, b).
A circunferência é dada pela seguinte equação:
Onde x, y são as coordenadas de um ponto arbitrário no círculo, R é o raio do círculo.
Sinal da equação do círculo
1. Não há termo com x, y
2. Coeficientes em x 2 e y 2 são iguais
Elipse
Elipse o lugar geométrico dos pontos em um plano é chamado, a soma das distâncias de cada um dos quais de dois pontos dados deste plano é chamada de focos (um valor constante).
Equação canônica de uma elipse:
X e y pertencem a uma elipse.
a é o semieixo maior da elipse
b é o semieixo menor da elipse
A elipse tem 2 eixos de simetria OX e OY. Os eixos de simetria da elipse são seus eixos, o ponto de sua interseção é o centro da elipse. O eixo no qual os focos estão localizados é chamado eixo focal. O ponto de intersecção da elipse com os eixos é o vértice da elipse.
Relação de compressão (alongamento): ε = c/a- excentricidade (caracteriza a forma da elipse), quanto menor, menos a elipse se estende ao longo do eixo focal.
Se os centros da elipse não estiverem no centro С(α, β)

Hipérbole
Hipérbole chamado lugar geométrico dos pontos em um plano, o valor absoluto da diferença de distâncias, cada um dos quais de dois pontos dados desse plano, chamados focos, é um valor constante diferente de zero.
Equação canônica de uma hipérbole
Uma hipérbole tem 2 eixos de simetria:
a - semieixo real de simetria
b - semieixo imaginário de simetria
Assíntotas de uma hipérbole:

Parábola
parábolaé o lugar geométrico dos pontos de um plano equidistantes de um dado ponto F, chamado foco, e de uma dada reta, chamada diretriz.
Equação da parábola canônica:
Y 2 \u003d 2px, onde p é a distância do foco até a diretriz (parâmetro de parábola)
Se o vértice da parábola é C (α, β), então a equação da parábola (y-β) 2 \u003d 2p (x-α)
Se o eixo focal for considerado o eixo y, a equação da parábola terá a forma: x 2 \u003d 2qy
Considere como escrever a equação de uma linha reta que passa por dois pontos, usando exemplos.
Exemplo 1
Escreva a equação de uma reta que passa pelos pontos A(-3; 9) e B(2;-1).
1 via - vamos compor a equação de uma linha reta com inclinação.
A equação de uma linha reta com uma inclinação tem a forma . Substituindo as coordenadas dos pontos A e B na equação de uma reta (x= -3 e y=9 - no primeiro caso, x=2 e y= -1 - no segundo), obtemos um sistema de equações , a partir do qual encontramos os valores de k e b:
Somando termo a termo as 1ª e 2ª equações, obtemos: -10=5k, de onde k= -2. Substituindo k= -2 na segunda equação, encontramos b: -1=2 (-2)+b, b=3.
Assim, y= -2x+3 é a equação desejada.
2 vias - vamos compor a equação geral de uma linha reta.
A equação geral de uma reta tem a forma . Substituindo as coordenadas dos pontos A e B na equação, obtemos o sistema:
Como o número de incógnitas é maior que o número de equações, o sistema não é solúvel. Mas é possível expressar todas as variáveis através de uma. Por exemplo, através de b.
Multiplicando a primeira equação do sistema por -1 e somando termo a termo à segunda:
obtemos: 5a-10b=0. Portanto, a = 2b.
Vamos substituir a expressão recebida na segunda equação: 2·2b -b+c=0; 3b+c=0; c=-3b.
Substitua a=2b, c= -3b na equação ax+by+c=0:
2bx+por-3b=0. Resta dividir ambas as partes por b:
A equação geral de uma linha reta é facilmente reduzida à equação de uma linha reta com inclinação:
3 vias - vamos compor a equação de uma reta passando por 2 pontos.
A equação de uma reta que passa por dois pontos é:
![]()
Substitua nesta equação as coordenadas dos pontos A(-3; 9) e B(2;-1)
(ou seja, x 1 = -3, y 1 =9, x 2 =2, y 2 = -1):
![]()
e simplificar:
onde 2x+y-3=0.
No curso escolar, a equação de uma linha reta com um coeficiente de inclinação é mais frequentemente usada. Mas a maneira mais fácil é derivar e usar a fórmula para a equação de uma linha reta que passa por dois pontos.
Comente.
Se, ao substituir as coordenadas de pontos dados, um dos denominadores da equação
![]()
for igual a zero, então a equação desejada é obtida igualando o numerador correspondente a zero.
Exemplo 2
Escreva a equação de uma reta que passa por dois pontos C(5; -2) e D(7; -2).
Substitua na equação de uma reta que passa por 2 pontos as coordenadas dos pontos C e D.
Sejam dados dois pontos M(X 1 ,No 1) e N(X 2,y 2). Vamos encontrar a equação da reta que passa por esses pontos.
Como esta linha passa pelo ponto M, então de acordo com a fórmula (1.13) sua equação tem a forma
No – S 1 = K(X-x 1),
Onde Ké a inclinação desconhecida.
O valor deste coeficiente é determinado a partir da condição de que a linha reta desejada passe pelo ponto N, o que significa que suas coordenadas satisfazem a equação (1.13)
S 2 – S 1 = K(X 2 – X 1),
A partir daqui você pode encontrar a inclinação desta linha:
![]() ,
,
Ou após a conversão
![]() (1.14)
(1.14)
A fórmula (1.14) define Equação de uma reta que passa por dois pontos M(X 1, S 1) e N(X 2, S 2).
No caso particular em que os pontos M(UMA, 0), N(0, B), MAS ¹ 0, B¹ 0, encontra-se nos eixos coordenados, a equação (1.14) assume uma forma mais simples
Equação (1,15) chamado Equação de uma linha reta em segmentos, aqui MAS e B denotam segmentos cortados por uma linha reta nos eixos (Figura 1.6).

Figura 1.6
Exemplo 1.10. Escreva a equação de uma reta que passa pelos pontos M(1, 2) e B(3, –1).
. De acordo com (1.14), a equação da reta desejada tem a forma
![]()
2(S – 2) = -3(X – 1).
Transferindo todos os termos para o lado esquerdo, finalmente obtemos a equação desejada
3X + 2S – 7 = 0.
Exemplo 1.11. Escreva uma equação para uma reta que passa por um ponto M(2, 1) e o ponto de intersecção das linhas X+ S- 1 = 0, X - y+ 2 = 0.
. Encontramos as coordenadas do ponto de intersecção das linhas resolvendo essas equações em conjunto
Se somarmos essas equações termo a termo, obtemos 2 X+ 1 = 0, de onde . Substituindo o valor encontrado em qualquer equação, encontramos o valor da ordenada No:
Agora vamos escrever a equação de uma linha reta que passa pelos pontos (2, 1) e :
 ou .
ou .
Daí ou -5( S – 1) = X – 2.
Finalmente, obtemos a equação da reta desejada na forma X + 5S – 7 = 0.
Exemplo 1.12. Encontre a equação de uma linha reta que passa por pontos M(2.1) e N(2,3).
Usando a fórmula (1.14), obtemos a equação
Não faz sentido porque o segundo denominador é zero. Pode-se ver a partir da condição do problema que as abcissas de ambos os pontos têm o mesmo valor. Portanto, a linha necessária é paralela ao eixo OY e sua equação é: x = 2.
Comente . Se, ao escrever a equação de uma linha reta de acordo com a fórmula (1.14), um dos denominadores for igual a zero, a equação desejada pode ser obtida igualando o numerador correspondente a zero.
Vamos considerar outras maneiras de definir uma linha reta em um plano.
1. Seja um vetor diferente de zero perpendicular a uma determinada linha eu, e o ponto M 0(X 0, S 0) encontra-se nesta linha (Figura 1.7).

Figura 1.7
Indicar M(X, S) um ponto arbitrário na linha eu. Vetores e ![]() Ortogonal. Usando as condições de ortogonalidade para esses vetores, obtemos ou MAS(X – X 0) + B(S – S 0) = 0.
Ortogonal. Usando as condições de ortogonalidade para esses vetores, obtemos ou MAS(X – X 0) + B(S – S 0) = 0.
Obtivemos a equação de uma reta que passa por um ponto M 0 é perpendicular ao vetor . Esse vetor é chamado Vetor normal para uma linha reta eu. A equação resultante pode ser reescrita como
Oh + Wu + Com= 0, onde Com = –(MASX 0 + De 0), (1.16),
Onde MAS e NO são as coordenadas do vetor normal.
Obtemos a equação geral de uma linha reta de forma paramétrica.
2. Uma linha em um plano pode ser definida da seguinte forma: seja um vetor diferente de zero paralelo a uma dada linha eu e ponto M 0(X 0, S 0) encontra-se nesta linha. Novamente, tome um ponto arbitrário M(X, y) em linha reta (Figura 1.8).

Figura 1.8
Vetores e ![]() colinear.
colinear.
Vamos escrever a condição de colinearidade desses vetores: , onde Té um número arbitrário, chamado de parâmetro. Vamos escrever essa igualdade em coordenadas:
Essas equações são chamadas Equações paramétricas Em linha reta. Vamos excluir dessas equações o parâmetro T:
Essas equações podem ser escritas na forma
![]() . (1.18)
. (1.18)
A equação resultante é chamada A equação canônica de uma linha reta. Chamada vetorial Vetor de direção reto .
Comente . É fácil ver que se é o vetor normal à linha eu, então seu vetor de direção pode ser o vetor , já que , ou seja, .
Exemplo 1.13. Escreva a equação de uma reta que passa por um ponto M 0(1, 1) paralelo à linha 3 X + 2No– 8 = 0.
Decisão . O vetor é o vetor normal às linhas dadas e desejadas. Vamos usar a equação de uma linha reta que passa por um ponto M 0 com um determinado vetor normal 3( X –1) + 2(No– 1) = 0 ou 3 X + 2 anos- 5 \u003d 0. Obtemos a equação da linha reta desejada.