Fórmulas de funções complexas. derivadas complexas. Derivada logarítmica. Derivada da função exponencial
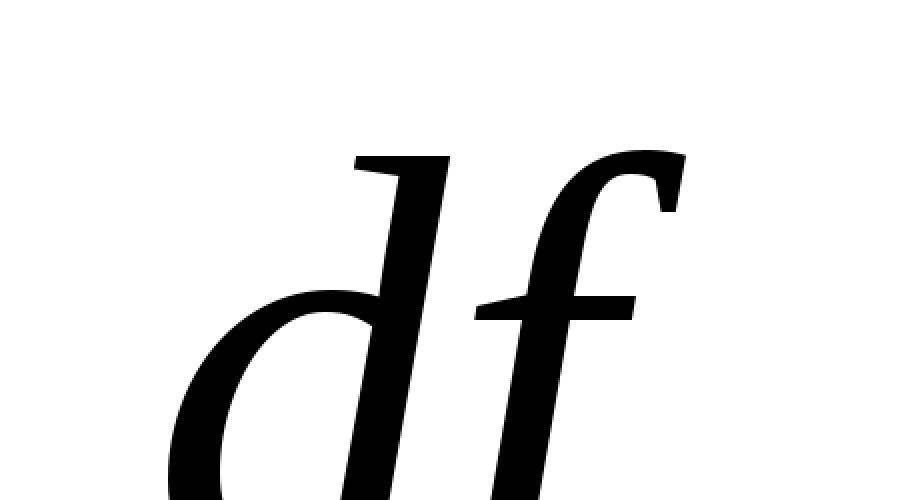
Nos livros didáticos "antigos", também é chamada de regra da "cadeia". Então se y \u003d f (u), e u \u003d φ (x), ou seja
y \u003d f (φ (x))
complexo - função composta (composição de funções) então
Onde  , após o cálculo ser considerado em u = φ (x).
, após o cálculo ser considerado em u = φ (x).


Observe que aqui tomamos composições "diferentes" das mesmas funções, e o resultado da diferenciação naturalmente se mostrou dependente da ordem da "mistura".
A regra da cadeia se estende naturalmente à composição de três ou mais funções. Nesse caso, haverá três ou mais “elos” na “cadeia” que compõe a derivada, respectivamente. Aqui está uma analogia com a multiplicação: “temos” - uma tabela de derivadas; "lá" - tabuada de multiplicação; “com a gente” é uma regra da cadeia e “há” é uma regra de multiplicação com uma “coluna”. Ao calcular tais derivadas “complexas”, é claro, nenhum argumento auxiliar (u¸v, etc.) a ordem indicada.
 . Aqui, são realizadas cinco operações com "x" para obter o valor de "y", ou seja, ocorre uma composição de cinco funções: "externa" (a última delas) - exponencial - e ; então na ordem inversa é uma lei de potência. (♦) 2 ; pecado trigonométrico(); potência. () 3 e finalmente o logarítmico ln.(). então
. Aqui, são realizadas cinco operações com "x" para obter o valor de "y", ou seja, ocorre uma composição de cinco funções: "externa" (a última delas) - exponencial - e ; então na ordem inversa é uma lei de potência. (♦) 2 ; pecado trigonométrico(); potência. () 3 e finalmente o logarítmico ln.(). então
Os exemplos a seguir vão “matar pares de pássaros com uma cajadada só”: vamos praticar a diferenciação de funções complexas e complementar a tabela de derivadas de funções elementares. Então:
4. Para uma função de potência - y \u003d x α - reescrevendo-a usando o conhecido "básico identidade logarítmica» - b=e ln b - na forma x α = x α ln x obtemos
5. Para uma função exponencial arbitrária, usando a mesma técnica, teremos
6. Para uma função logarítmica arbitrária, usando a conhecida fórmula de transição para uma nova base, obtemos sucessivamente
 .
.
7. Para diferenciar a tangente (cotangente), usamos a regra de diferenciação do quociente:
Para obter derivadas de funções trigonométricas inversas, usamos a relação que é satisfeita pelas derivadas de duas funções mutuamente inversas, ou seja, as funções φ (x) ef (x) conectadas pelas relações:
Aqui está a proporção

É a partir desta fórmula para funções mutuamente inversas
 e
e  ,
,
No final, resumimos essas e algumas outras derivadas, de fácil obtenção, na tabela a seguir.
|
|
|
||
|
|
|
||
|
|
Desde que você chegou aqui, provavelmente já conseguiu ver essa fórmula no livro didático
e faça uma cara assim:
Amigo, não se preocupe! Na verdade, tudo é simples de desgraçar. Com certeza você vai entender tudo. Apenas um pedido - leia o artigo devagar tente entender cada passo. Eu escrevi da forma mais simples e clara possível, mas você ainda precisa se aprofundar na ideia. E certifique-se de resolver as tarefas do artigo.
O que é uma função complexa?
Imagine que você está se mudando para outro apartamento e, portanto, está empacotando coisas em caixas grandes. Vamos coletar alguns pequenos itens como papelaria escolar. Se você apenas jogá-los em uma caixa enorme, eles se perderão entre outras coisas. Para evitar isso, você os coloca primeiro, por exemplo, em um saco, que depois coloca em uma caixa grande, depois o sela. Este processo "mais difícil" é mostrado no diagrama abaixo:

Parece, de onde vem a matemática? Além disso, uma função complexa é formada EXATAMENTE DA MESMA maneira! Apenas “embalamos” não cadernos e canetas, mas \(x\), enquanto diferentes “pacotes” e “caixas” servem.
Por exemplo, vamos pegar x e "empacotar" em uma função:

Como resultado, obtemos, é claro, \(\cosx\). Este é o nosso "saco de coisas". E agora nós o colocamos em uma "caixa" - nós o empacotamos, por exemplo, em uma função cúbica.

O que vai acontecer no final? Sim, isso mesmo, haverá um "pacote com coisas em uma caixa", ou seja, "cosseno de x ao cubo".

A construção resultante é uma função complexa. Difere do simples porque VÁRIOS “impactos” (pacotes) são aplicados a um X seguido e acontece, por assim dizer, “uma função de uma função” - “um pacote em um pacote”.
NO curso escolar existem muito poucos tipos desses mesmos “pacotes”, apenas quatro:

Vamos agora "empacotar" x primeiro em função exponencial com base 7, e depois em uma função trigonométrica. Nós temos:
\(x → 7^x → tg(7^x)\)
E agora vamos "empacotar" x duas vezes funções trigonométricas, primeiro em , e depois em :
\(x → senx → ctg (senx)\)
Simples, certo?
Agora escreva as funções você mesmo, onde x:
- primeiro é “empacotado” em um cosseno e depois em uma função exponencial com base \(3\);
- primeiro à quinta potência e depois à tangente;
- primeiro para o logaritmo base \(4\)
, então à potência \(-2\).
Veja as respostas para essa pergunta no final do artigo.
Mas podemos "empacotar" x não duas, mas três vezes? Sem problemas! E quatro, e cinco, e vinte e cinco vezes. Aqui, por exemplo, está uma função na qual x é "empacotado" \(4\) vezes:
\(y=5^(\log_2(\sin(x^4)))\)
Mas tais fórmulas não serão encontradas na prática escolar (os alunos são mais afortunados - podem ser mais difíceis☺).
"Desempacotando" uma função complexa
Olhe para a função anterior novamente. Você consegue descobrir a sequência de "empacotar"? O que X foi colocado primeiro, o que depois, e assim por diante até o final. Ou seja, qual função está aninhada em qual? Pegue um pedaço de papel e escreva o que você pensa. Você pode fazer isso com uma cadeia de flechas, como escrevemos acima, ou de qualquer outra forma.
Agora a resposta correta é: primeiro x foi “empacotado” na potência \(4\), então o resultado foi empacotado no seno, ele, por sua vez, foi colocado na base do logaritmo \(2\), e em no final, toda a construção foi empurrada para os cincos poderosos.
Ou seja, é necessário desenrolar a sequência NA ORDEM INVERSA. E aqui está uma dica de como fazer isso mais fácil: basta olhar para o X - você tem que dançar com ele. Vejamos alguns exemplos.
Por exemplo, aqui está uma função: \(y=tg(\log_2x)\). Nós olhamos para X - o que acontece com ele primeiro? Tirado dele. E então? A tangente do resultado é tomada. E a sequência será a mesma:
\(x → \log_2x → tg(\log_2x)\)
Outro exemplo: \(y=\cos((x^3))\). Analisamos - primeiro x foi cubado e, em seguida, o cosseno foi retirado do resultado. Então a sequência será: \(x → x^3 → \cos((x^3))\). Preste atenção, a função parece ser semelhante à primeira (onde com fotos). Mas esta é uma função completamente diferente: aqui no cubo x (ou seja, \(\cos((x x x)))\), e lá no cubo o cosseno \(x\) (ou seja, \(\ cos x·\cosx·\cosx\)). Esta diferença surge de diferentes sequências de "empacotamento".
O último exemplo (com informação importante nele): \(y=\sin((2x+5))\). É claro que aqui primeiro realizamos operações aritméticas com x, então o seno foi retirado do resultado: \(x → 2x+5 → \sin((2x+5))\). E isto ponto importante: apesar de as operações aritméticas não serem funções em si mesmas, aqui elas também atuam como uma forma de "empacotar". Vamos nos aprofundar um pouco mais nessa sutileza.
Como eu disse acima, em funções simples x é "empacotado" uma vez e em funções complexas - duas ou mais. Além disso, qualquer combinação de funções simples (isto é, sua soma, diferença, multiplicação ou divisão) também é função simples. Por exemplo, \(x^7\) é uma função simples, assim como \(ctg x\). Portanto, todas as suas combinações são funções simples:
\(x^7+ ctg x\) - simples,
\(x^7 ctg x\) é simples,
\(\frac(x^7)(ctg x)\) é simples e assim por diante.
No entanto, se mais uma função for aplicada a tal combinação, já será uma função complexa, pois haverá dois “pacotes”. Veja diagrama:

Ok, vamos continuar com isso agora. Escreva a sequência de funções de "empacotamento":
\(y=cos((senx))\)
\(y=5^(x^7)\)
\(y=arctg(11^x)\)
\(y=log_2(1+x)\)
As respostas estão novamente no final do artigo.
Funções internas e externas
Por que precisamos entender o aninhamento de funções? O que isso nos dá? O ponto é que sem tal análise não seremos capazes de encontrar de forma confiável as derivadas das funções discutidas acima.
E para seguir em frente, precisaremos de mais dois conceitos: funções internas e externas. Isto é muito coisa simples, além disso, de fato, já os analisamos acima: se lembrarmos nossa analogia no início, a função interna é o “pacote” e a externa é a “caixa”. Aqueles. o que X é “embrulhado” primeiro é uma função interna, e o que o interno é “embrulhado” já é externo. Bem, é compreensível o porquê - está do lado de fora, significa externo.
Aqui neste exemplo: \(y=tg(log_2x)\), a função \(\log_2x\) é interna, e  - externo.
- externo.
E neste: \(y=\cos((x^3+2x+1))\), \(x^3+2x+1\) é interno, e  - externo.
- externo.
Realize a última prática de análise de funções complexas e, finalmente, vamos para o ponto em que tudo foi iniciado - encontraremos derivadas de funções complexas:
Preencha as lacunas da tabela:
Derivada de uma função composta
Bravo para nós, ainda chegamos ao "chefe" deste tópico - na verdade, um derivado função complexa, e especificamente, para aquela fórmula terrível desde o início do artigo.☺
\((f(g(x)))"=f"(g(x))\cdot g"(x)\)
Esta fórmula fica assim:
A derivada de uma função complexa é igual ao produto da derivada da função externa em relação à função interna constante e a derivada da função interna.
E imediatamente olhe para o esquema de análise, de acordo com as palavras, para entender com o que se relacionar:

Espero que os termos "derivado" e "produto" não causem dificuldades. "Função complexa" - já desmontamos. O problema está na "derivada da função externa em relação à constante interna". O que é isso?
Resposta: esta é a derivada usual da função externa, na qual apenas a função externa muda, enquanto a interna permanece a mesma. Ainda não está claro? Ok, vamos dar um exemplo.
Digamos que temos uma função \(y=\sin(x^3)\). É claro que a função interna aqui é \(x^3\), e a externa  . Vamos agora encontrar a derivada do externo em relação à constante interna.
. Vamos agora encontrar a derivada do externo em relação à constante interna.
Após a preparação preliminar da artilharia, os exemplos com 3-4-5 anexos de funções serão menos assustadores. Talvez os dois exemplos a seguir pareçam complicados para alguns, mas se forem entendidos (alguém sofrerá), quase todo o resto será cálculo diferencial vai parecer brincadeira de criança.
Exemplo 2
Encontre a derivada de uma função
Como já observado, ao encontrar a derivada de uma função complexa, em primeiro lugar, é necessário direita ENTENDA OS INVESTIMENTOS. Nos casos de dúvida, relembro técnica útil: tomamos o valor experimental "x", por exemplo, e tentamos (mentalmente ou em um rascunho) substituir esse valor na "expressão terrível".
1) Primeiro precisamos calcular a expressão, então a soma é o aninhamento mais profundo.
2) Então você precisa calcular o logaritmo:
4) Cubra o cosseno:
5) Na quinta etapa, a diferença:
6) E, finalmente, a função mais externa é a raiz quadrada: ![]()
Fórmula de Diferenciação de Função Complexa ![]() são aplicados na ordem inversa, da função mais externa para a mais interna. Nós decidimos:
são aplicados na ordem inversa, da função mais externa para a mais interna. Nós decidimos:

Parece estar livre de erros:
1) Derivamos a raiz quadrada.
2) Derivamos a diferença usando a regra ![]()
3) A derivada do triplo é igual a zero. No segundo termo, tomamos a derivada do grau (cubo).
4) Derivamos o cosseno.
6) E, finalmente, tomamos a derivada do aninhamento mais profundo.
Pode parecer muito difícil, mas este não é o exemplo mais brutal. Tomemos, por exemplo, a coleção de Kuznetsov e você apreciará todo o charme e simplicidade da derivada analisada. Percebi que eles gostam de dar uma coisa parecida na prova para verificar se o aluno entende como encontrar a derivada de uma função complexa, ou não entende.
O próximo exemplo para decisão independente.
Exemplo 3
Encontre a derivada de uma função
Dica: Primeiro aplicamos as regras de linearidade e a regra de diferenciação do produto
Solução completa e resposta no final da lição.
É hora de passar para algo mais compacto e mais bonito.
Não é incomum para um exemplo dar um produto de não dois, mas três funções. Como encontrar a derivada do produto de três fatores?
Exemplo 4
Encontre a derivada de uma função ![]()
Primeiro, olhamos, mas é possível transformar o produto de três funções em um produto de duas funções? Por exemplo, se tivéssemos dois polinômios no produto, poderíamos abrir os colchetes. Mas neste exemplo, todas as funções são diferentes: grau, expoente e logaritmo.
Nesses casos, é necessário sucessivamente aplicar a regra de diferenciação do produto ![]() duas vezes
duas vezes
O truque é que para "y" denotamos o produto de duas funções: , e para "ve" - o logaritmo:. Por que isso pode ser feito? É isso ![]() - isso não é produto de dois fatores e a regra não funciona?! Não há nada complicado:
- isso não é produto de dois fatores e a regra não funciona?! Não há nada complicado:
Agora resta aplicar a regra uma segunda vez ![]() para colchete:
para colchete:
Você ainda pode perverter e tirar algo dos parênteses, mas em este casoé melhor deixar a resposta neste formulário - será mais fácil verificar.
O exemplo acima pode ser resolvido da segunda maneira:

Ambas as soluções são absolutamente equivalentes.
Exemplo 5
Encontre a derivada de uma função
Este é um exemplo para uma solução independente, na amostra ela é resolvida da primeira maneira.
Considere exemplos semelhantes com frações.
Exemplo 6
Encontre a derivada de uma função ![]()
Aqui você pode ir de várias maneiras:
Ou assim:
Mas a solução pode ser escrita de forma mais compacta se, antes de tudo, usarmos a regra de diferenciação do quociente  , tomando para o numerador inteiro:
, tomando para o numerador inteiro:

Em princípio, o exemplo está resolvido e, se for deixado dessa forma, não será um erro. Mas se você tiver tempo, é sempre aconselhável verificar um rascunho, mas é possível simplificar a resposta?
Trazemos a expressão do numerador para denominador comum e se livrar da fração de três andares:

A desvantagem de simplificações adicionais é que existe o risco de errar não ao encontrar uma derivada, mas ao banalizar as transformações escolares. Por outro lado, os professores muitas vezes rejeitam a tarefa e pedem para “lembrar” a derivada.
Um exemplo mais simples para uma solução faça você mesmo:
Exemplo 7
Encontre a derivada de uma função
Continuamos a dominar as técnicas para encontrar a derivada, e agora vamos considerar um caso típico em que um logaritmo “terrível” é proposto para a diferenciação
É absolutamente impossível resolver problemas físicos ou exemplos em matemática sem conhecimento sobre a derivada e os métodos para calculá-la. Derivada é um dos conceitos mais importantes analise matemática. Decidimos dedicar o artigo de hoje a este tema fundamental. O que é um derivado, qual é o seu aspecto físico e significado geométrico como calcular a derivada de uma função? Todas essas questões podem ser combinadas em uma: como entender a derivada?
Significado geométrico e físico da derivada
Seja uma função f(x) , dado em algum intervalo (a, b) . Os pontos x e x0 pertencem a este intervalo. Quando x muda, a própria função muda. Mudança de argumento - diferença de seus valores x-x0 . Essa diferença é escrita como delta x e é chamado de incremento de argumento. A mudança ou incremento de uma função é a diferença entre os valores da função em dois pontos. Definição derivada:
A derivada de uma função em um ponto é o limite da razão entre o incremento da função em um dado ponto e o incremento do argumento quando este tende a zero.
Caso contrário, pode ser escrito assim:

Qual é o ponto em encontrar tal limite? Mas qual deles:
a derivada de uma função em um ponto é igual à tangente do ângulo entre o eixo OX e a tangente ao gráfico da função em um determinado ponto.

O significado físico da derivada: a derivada temporal da trajetória é igual à velocidade do movimento retilíneo.
De fato, desde os tempos de escola, todos sabem que a velocidade é um caminho particular. x=f(t) e tempo t . velocidade média por algum tempo:

Para descobrir a velocidade do movimento de cada vez t0 você precisa calcular o limite:

Regra um: tire a constante
A constante pode ser retirada do sinal da derivada. Além disso, deve ser feito. Ao resolver exemplos em matemática, tome como regra - se você pode simplificar a expressão, certifique-se de simplificar .
Exemplo. Vamos calcular a derivada:

Regra dois: derivada da soma de funções
A derivada da soma de duas funções é igual à soma das derivadas dessas funções. O mesmo vale para a derivada da diferença de funções.

Não daremos uma demonstração deste teorema, mas consideraremos um exemplo prático.
Encontre a derivada de uma função:


Regra três: a derivada do produto de funções
A derivada do produto de duas funções diferenciáveis é calculada pela fórmula:

Exemplo: encontre a derivada de uma função:

Decisão: 
Aqui é importante dizer sobre o cálculo de derivadas de funções complexas. A derivada de uma função complexa é igual ao produto da derivada desta função em relação ao argumento intermediário pela derivada do argumento intermediário em relação à variável independente.
NO o exemplo acima encontramos a expressão:

Nesse caso, o argumento intermediário é 8x elevado à quinta potência. Para calcular a derivada de tal expressão, primeiro consideramos a derivada da função externa em relação ao argumento intermediário e, em seguida, multiplicamos pela derivada do próprio argumento intermediário em relação à variável independente.
Regra Quatro: A derivada do quociente de duas funções
Fórmula para determinar a derivada de um quociente de duas funções:



Tentamos falar sobre derivativos para manequins do zero. Este tópico não é tão simples quanto parece, então esteja avisado: muitas vezes há armadilhas nos exemplos, então tenha cuidado ao calcular as derivadas.
Com qualquer dúvida sobre este e outros temas, você pode entrar em contato com o atendimento ao aluno. Atras do curto prazo vamos ajudá-lo a resolver o teste mais difícil e lidar com tarefas, mesmo que você nunca tenha lidado com o cálculo de derivativos antes.
Funções tipo complexo nem sempre se encaixam na definição de uma função complexa. Se houver uma função da forma y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, ela não pode ser considerada complexa, ao contrário de y \u003d sin 2 x.
Este artigo mostrará o conceito de função complexa e sua identificação. Vamos trabalhar com fórmulas para encontrar a derivada com exemplos de soluções na conclusão. O uso da tabela de derivadas e as regras de diferenciação reduzem significativamente o tempo para encontrar a derivada.
Yandex.RTB R-A-339285-1
Definições básicas
Definição 1Uma função complexa é uma função cujo argumento também é uma função.
É denotado desta forma: f (g (x)) . Temos que a função g (x) é considerada um argumento f (g (x)) .
Definição 2
Se existe uma função f e é uma função cotangente, então g(x) = ln x é a função logarítmica natural. Obtemos que a função complexa f (g (x)) será escrita como arctg (lnx). Ou uma função f, que é uma função elevada à 4ª potência, onde g (x) \u003d x 2 + 2 x - 3 é considerada uma função racional inteira, obtemos que f (g (x)) \u003d (x 2 + 2 x - 3) 4 .
Obviamente g(x) pode ser complicado. A partir do exemplo y \u003d sin 2 x + 1 x 3 - 5, pode-se ver que o valor de g tem raiz cúbica com fração. Esta expressão pode ser denotada como y = f (f 1 (f 2 (x))) . De onde temos que f é uma função seno, e f 1 é uma função localizada sob raiz quadrada, f 2 (x) = 2 x + 1 x 3 - 5 - função racional fracionária.
Definição 3
O grau de aninhamento é definido por qualquer número natural e é escrito como y = f (f 1 (f 2 (f 3 (. . . (f n (x))))))) .
Definição 4
O conceito de composição de funções refere-se ao número de funções aninhadas de acordo com o enunciado do problema. Para a solução, a fórmula para encontrar a derivada de uma função complexa da forma
(f(g(x)))"=f"(g(x)) g"(x)
Exemplos
Exemplo 1Encontre a derivada de uma função complexa da forma y = (2 x + 1) 2 .
Decisão
Por convenção, f é uma função quadrada e g(x) = 2 x + 1 é considerada uma função linear.
Aplicamos a fórmula da derivada para uma função complexa e escrevemos:
f "(g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g "(x) = (2x + 1)" = (2x)" + 1" = 2 x" + 0 = 2 1 x 1 - 1 = 2 ⇒ (f(g(x))) "=f" ( g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4
É necessário encontrar uma derivada com uma forma inicial simplificada da função. Nós temos:
y = (2x + 1) 2 = 4x2 + 4x + 1
Daí temos que
y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8x + 4
Os resultados combinaram.
Ao resolver problemas desse tipo, é importante entender onde a função da forma f e g (x) estará localizada.
Exemplo 2
Você deve encontrar as derivadas de funções complexas da forma y \u003d sin 2 x e y \u003d sin x 2.
Decisão
A primeira entrada da função diz que f é a função quadrática e g(x) é a função seno. Então obtemos isso
y "= (sen 2 x)" = 2 sen 2 - 1 x (sen x)" = 2 sen x cos x
A segunda entrada mostra que f é uma função seno, e g (x) = x 2 denota Função liga-desliga. Segue que o produto de uma função complexa pode ser escrito como
y " \u003d (sen x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)
A fórmula para a derivada y \u003d f (f 1 (f 2 (f 3 (. . . (f n (x))))))) será escrita como y "= f" (f 1 (f 2 (f 3) (. . . (f n (x)))))) f 1 "(f 2 (f 3 (. . . (f n (x))))) f 2 " (f 3 (. . . (f n (x) )))). . . f n "(x)
Exemplo 3
Encontre a derivada da função y = sin (ln 3 a r c t g (2 x)) .
Decisão
Este exemplo mostra a complexidade de escrever e determinar a localização das funções. Então y \u003d f (f 1 (f 2 (f 3 (f 4 (x)))))) denota, onde f , f 1 , f 2 , f 3 , f 4 (x) é a função seno, a função de elevar a 3 graus, uma função com logaritmo e base e, uma função do arco tangente e uma função linear.
Da fórmula para a definição de uma função complexa, temos que
y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f) 4 (x))) f 3 "(f 4 (x)) f 4" (x)
Obtendo o que encontrar
- f "(f 1 (f 2 (f 3 (f 4 (x))))) como a derivada do seno na tabela de derivadas, então f "(f 1 (f 2 (f 3 (f 4 (x) ))))) ) = cos (ln 3 a r c t g (2 x)) .
- f 1 "(f 2 (f 3 (f 4 (x)))) como uma derivada de uma função de potência, então f 1 "(f 2 (f 3 (f 4 (x))))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
- f 2 "(f 3 (f 4 (x))) como uma derivada logarítmica, então f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 "(f 4 (x)) como uma derivada do arco tangente, então f 3 "(f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
- Ao encontrar a derivada f 4 (x) \u003d 2 x, tire 2 do sinal da derivada usando a fórmula para a derivada da função potência com um expoente que é 1, então f 4 "(x) \u003d ( 2 x)" \u003d 2 x "\u003d 2 · 1 · x 1 - 1 = 2 .
Combinamos os resultados intermediários e obtemos que
y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f) 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)
A análise de tais funções assemelha-se a bonecas aninhadas. As regras de diferenciação nem sempre podem ser aplicadas explicitamente usando uma tabela derivada. Muitas vezes você precisa aplicar a fórmula para encontrar derivadas de funções complexas.
Existem algumas diferenças entre uma visão complexa e uma função complexa. Com uma capacidade clara de distinguir isso, encontrar derivativos será especialmente fácil.
Exemplo 4
É necessário considerar em trazer tal exemplo. Se existe uma função da forma y = t g 2 x + 3 t g x + 1 , então ela pode ser considerada como uma função complexa da forma g (x) = t g x , f (g) = g 2 + 3 g + 1 . Obviamente, é necessário aplicar a fórmula para a derivada complexa:
f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1) " \u003d (g 2 (x)) " + (3 g (x)) " + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 t g x + 3; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) 1 cos 2 x = 2 t g x + 3 cos 2 x
Uma função da forma y = t g x 2 + 3 t g x + 1 não é considerada complexa, pois tem a soma t g x 2 , 3 t g x e 1 . No entanto, t g x 2 é considerada uma função complexa, então obtemos uma função de potência da forma g (x) \u003d x 2 e f, que é uma função da tangente. Para fazer isso, você precisa diferenciar pelo valor. Nós entendemos isso
y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 cos 2 x
Vamos passar para encontrar a derivada de uma função complexa (t g x 2) ":
f "(g (x)) = (t g (g (x)))" = 1 cos 2 g (x) = 1 cos 2 (x 2) g "(x) = (x 2)" = 2 x 2 - 1 \u003d 2 x ⇒ (t g x 2) " \u003d f " (g (x)) g " (x) \u003d 2 x cos 2 (x 2)
Obtemos que y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Funções complexas podem ser incluídas em funções complexas, e as próprias funções complexas podem ser funções compostas da forma complexa.
Exemplo 5
Por exemplo, considere uma função complexa da forma y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)
Esta função pode ser representada como y = f (g (x)) , onde o valor de f é uma função do logaritmo de base 3, e g (x) é considerado a soma de duas funções da forma h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 ek (x) = ln 2 x (x 2 + 1) . Obviamente, y = f (h (x) + k (x)) .
Considere a função h(x) . Esta é a razão de l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 para m (x) = e x 2 + 3 3
Temos que l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) é a soma de duas funções n (x) = x 2 + 7 e p ( x) \u003d 3 cos 3 (2 x + 1) , onde p (x) \u003d 3 p 1 (p 2 (p 3 (x))) é uma função complexa com um coeficiente numérico de 3 e p 1 é uma função cubo, p 2 função cosseno, p 3 (x) = 2 x + 1 - função linear.
Descobrimos que m (x) = e x 2 + 3 3 = q (x) + r (x) é a soma de duas funções q (x) = e x 2 e r (x) = 3 3 , onde q (x) = q 1 (q 2 (x)) é uma função complexa, q 1 é uma função com um expoente, q 2 (x) = x 2 é uma função de potência.
Isso mostra que h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3) (x))) q 1 (q 2 (x)) + r (x)
Ao passar para uma expressão da forma k (x) \u003d ln 2 x (x 2 + 1) \u003d s (x) t (x), fica claro que a função é representada como um complexo s (x) \ u003d ln 2 x \u003d s 1 ( s 2 (x)) com inteiro racional t (x) = x 2 + 1, onde s 1 é a função quadrática e s 2 (x) = ln x é logarítmico com base e .
Segue-se que a expressão terá a forma k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .
Então obtemos isso
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)
De acordo com as estruturas da função, ficou claro como e quais fórmulas devem ser aplicadas para simplificar a expressão quando ela é diferenciada. Para se familiarizar com tais problemas e entender sua solução, é necessário referir-se ao ponto de diferenciação de uma função, ou seja, encontrar sua derivada.
Se você notar um erro no texto, destaque-o e pressione Ctrl+Enter




