Faça um estudo completo das funções da calculadora online. Investigue a função \(y=\frac(x3)(1-x)\) usando os métodos de cálculo diferencial, construa seu gráfico

16.10.2019

Investigue uma função e um enredo: exemplos e soluções online

Preparamos para você muitos estudos de recursos prontos, pagos no livro de soluções e gratuitos na seção Exemplos de pesquisa de recursos. Com base nessas tarefas resolvidas, você poderá se familiarizar em detalhes com a metodologia para realizar tais tarefas, por analogia, realizar sua própria pesquisa.

Nós oferecemos exemplos prontos pesquisa completa e plotagem do gráfico de funções dos tipos mais comuns: polinômios, fracionário-racionais, irracionais, exponenciais, logarítmicos, funções trigonométricas. Cada problema resolvido é acompanhado por um gráfico pronto com pontos-chave selecionados, assíntotas, máximos e mínimos, a solução é realizada de acordo com o algoritmo para estudar a função.

Os exemplos resolvidos, em qualquer caso, se tornarão para você boa ajuda, pois cobrem os tipos mais populares de funções. Oferecemos centenas de problemas já resolvidos, mas, como você sabe, há um número infinito de funções matemáticas no mundo, e os professores são grandes especialistas em inventar tarefas cada vez mais complexas para alunos pobres. Então, queridos alunos, ajuda qualificada não vai incomodá-lo.

Resolvendo problemas para o estudo de uma função de ordem

Nesse caso, nossos parceiros oferecerão outro serviço - estudo completo recursos online pedir. A tarefa será concluída para você em conformidade com todos os requisitos do algoritmo para resolver esses problemas, o que agradará muito seu professor.

Faremos um estudo completo da função para você: encontraremos o domínio de definição e o intervalo de valores, examinaremos a continuidade e a descontinuidade, estabeleceremos a paridade, verificaremos a periodicidade da função, encontrar pontos intersecções com eixos coordenados. E, claro, ainda mais com a ajuda do cálculo diferencial: encontraremos assíntotas, calcularemos extremos, pontos de inflexão e construiremos o próprio gráfico.

Sua privacidade é importante para nós. Por esse motivo, desenvolvemos uma Política de Privacidade que descreve como usamos e armazenamos suas informações. Por favor, leia nossa política de privacidade e deixe-nos saber se você tiver alguma dúvida.

Coleta e uso de informações pessoais

Informações pessoais referem-se a dados que podem ser usados para identificar uma pessoa específica ou contatá-la.

Você pode ser solicitado a fornecer suas informações pessoais a qualquer momento quando entrar em contato conosco.

A seguir estão alguns exemplos dos tipos de informações pessoais que podemos coletar e como podemos usar essas informações.

Quais informações pessoais coletamos:

Quando você envia uma inscrição no site, podemos coletar várias informações, incluindo seu nome, número de telefone, endereço E-mail etc.

Como usamos suas informações pessoais:

Recolhido por nós informação pessoal nos permite entrar em contato com você e informá-lo sobre ofertas exclusivas, promoções e outros eventos e eventos futuros.
De tempos em tempos, podemos usar suas informações pessoais para enviar avisos e mensagens importantes.
Também podemos usar informações pessoais para fins internos, como auditoria, análise de dados e vários estudos para melhorar os serviços que prestamos e para lhe fornecer recomendações sobre os nossos serviços.
Se você participar de um sorteio, concurso ou incentivo semelhante, poderemos usar as informações fornecidas para administrar tais programas.

Divulgação a terceiros

Não divulgamos informações recebidas de você a terceiros.

Exceções:

Se necessário - de acordo com a lei, ordem judicial, dentro litígio, e/ou com base em solicitações públicas ou solicitações de agências governamentais no território da Federação Russa - divulgue suas informações pessoais. Também podemos divulgar informações sobre você se determinarmos que tal divulgação é necessária ou apropriada para segurança, aplicação da lei ou outras ocasiões importantes.
No caso de uma reorganização, fusão ou venda, podemos transferir as informações pessoais que coletamos para o sucessor terceirizado relevante.

Proteção de informações pessoais

Tomamos precauções - incluindo administrativas, técnicas e físicas - para proteger suas informações pessoais contra perda, roubo e uso indevido, bem como de acesso, divulgação, alteração e destruição não autorizados.

Mantendo sua privacidade no nível da empresa

Para garantir que suas informações pessoais estejam seguras, comunicamos práticas de privacidade e segurança aos nossos funcionários e aplicamos rigorosamente as práticas de privacidade.

Se no problema for necessário realizar um estudo completo da função f (x) \u003d x 2 4 x 2 - 1 com a construção de seu gráfico, consideraremos esse princípio em detalhes.

Para resolver o problema deste tipo deve usar as propriedades e gráficos dos principais funções elementares. O algoritmo de pesquisa inclui as seguintes etapas:

Yandex.RTB R-A-339285-1

Encontrando o domínio de definição

Como a pesquisa é realizada no domínio da função, é necessário começar com esta etapa.

Exemplo 1

O exemplo dado envolve encontrar os zeros do denominador para excluí-los do DPV.

4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞ ; - 1 2 ∪ - 1 2 ; 1 2 ∪ 1 2 ; +∞

Como resultado, você pode obter raízes, logaritmos e assim por diante. Então a ODZ pode ser procurada por uma raiz par do tipo g (x) 4 pela desigualdade g (x) ≥ 0 , para o logaritmo log a g (x) pela desigualdade g (x) > 0 .

Investigação dos limites da ODZ e encontrar assíntotas verticais

Existem assíntotas verticais nos limites da função, quando os limites laterais em tais pontos são infinitos.

Exemplo 2

Por exemplo, considere os pontos de fronteira iguais a x = ± 1 2 .

Então é necessário estudar a função para encontrar o limite unilateral. Então temos que: lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (- 2) - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) 2 = - ∞ lim x → 1 2 - 0 f (x) = limite x → 1 2 - 0 x 2 4 x 2 - 1 = = limite x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0) 2 = + ∞

Isso mostra que os limites laterais são infinitos, o que significa que as linhas x = ± 1 2 são as assíntotas verticais do gráfico.

Investigação da função e para par ou ímpar

Quando a condição y (- x) = y (x) é satisfeita, a função é considerada par. Isso sugere que o gráfico está localizado simetricamente em relação a O y. Quando a condição y (- x) = - y (x) é satisfeita, a função é considerada ímpar. Isso significa que a simetria vai em relação à origem das coordenadas. Se pelo menos uma desigualdade falhar, obtemos uma função de forma geral.

O cumprimento da igualdade y (- x) = y (x) indica que a função é par. Ao construir, é necessário levar em conta que haverá simetria em relação a O y.

Para resolver a desigualdade, são usados intervalos de aumento e diminuição com as condições f "(x) ≥ 0 ef" (x) ≤ 0, respectivamente.

Definição 1

Pontos estacionários são pontos que transformam a derivada em zero.

Pontos críticos são pontos interiores do domínio onde a derivada da função é igual a zero ou não existe.

Ao tomar uma decisão, os seguintes pontos devem ser levados em consideração:

para os intervalos existentes de aumento e diminuição da desigualdade da forma f"(x) > 0, os pontos críticos não estão incluídos na solução;
pontos nos quais a função é definida sem uma derivada finita devem ser incluídos nos intervalos de aumento e diminuição (por exemplo, y \u003d x 3, onde o ponto x \u003d 0 torna a função definida, a derivada tem o valor de infinito neste ponto, y " \u003d 1 3 x 2 3 , y " (0) = 1 0 = ∞ , x = 0 é incluído no intervalo de aumento);
para evitar divergências, recomenda-se o uso da literatura matemática, que é recomendada pelo Ministério da Educação.

A inclusão de pontos críticos nos intervalos crescentes e decrescentes caso satisfaçam o domínio da função.

Definição 2

Por determinando os intervalos de aumento e diminuição da função, é necessário encontrar:

derivado;
Pontos críticos;
quebrar o domínio de definição com a ajuda de pontos críticos em intervalos;
determine o sinal da derivada em cada um dos intervalos, onde + é um aumento e - é uma diminuição.

Exemplo 3

Encontre a derivada no domínio f "(x) = x 2" (4 x 2 - 1) - x 2 4 x 2 - 1 "(4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .

Solução

Para resolver você precisa:

encontre pontos estacionários, este exemplo tem x = 0 ;
encontre os zeros do denominador, o exemplo assume o valor zero em x = ± 1 2 .

Expomos pontos no eixo numérico para determinar a derivada em cada intervalo. Para fazer isso, basta pegar qualquer ponto do intervalo e realizar o cálculo. Se o resultado for positivo, desenhamos + no gráfico, o que significa um aumento na função e - significa sua diminuição.

Por exemplo, f "(- 1) \u003d - 2 (- 1) 4 - 1 2 - 1 2 \u003d 2 9\u003e 0, o que significa que o primeiro intervalo à esquerda tem um sinal +. Considere o número linha.

Responda:

há um aumento da função no intervalo - ∞ ; - 1 2 e (- 1 2 ; 0 ] ;
há uma diminuição no intervalo [ 0 ; 1 2) e 1 2 ; +∞ .

No diagrama, usando + e -, a positividade e a negatividade da função são representadas, e as setas indicam decrescente e crescente.

Os pontos extremos de uma função são os pontos onde a função é definida e através dos quais a derivada muda de sinal.

Exemplo 4

Se considerarmos um exemplo em que x \u003d 0, então o valor da função nele é f (0) \u003d 0 2 4 0 2 - 1 \u003d 0. Quando o sinal da derivada muda de + para - e passa pelo ponto x \u003d 0, o ponto com coordenadas (0; 0) é considerado o ponto máximo. Quando o sinal é alterado de - para +, obtemos o ponto mínimo.

A convexidade e a concavidade são determinadas resolvendo as desigualdades da forma f "" (x) ≥ 0 ef "" (x) ≤ 0 . Com menos frequência, eles usam o nome protuberância para baixo em vez de concavidade e protuberância para cima em vez de protuberância.

Definição 3

Por determinando as lacunas de concavidade e convexidade necessário:

encontre a segunda derivada;
encontre os zeros da função da segunda derivada;
quebrar o domínio de definição pelos pontos que aparecem em intervalos;
determinar o sinal da lacuna.

Exemplo 5

Encontre a segunda derivada do domínio de definição.

Solução

f "" (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) " (4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 " (4 x 2) - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3

Encontramos os zeros do numerador e denominador, onde, usando nosso exemplo, temos que os zeros do denominador x = ± 1 2

Agora você precisa colocar pontos na reta numérica e determinar o sinal da segunda derivada de cada intervalo. Nós entendemos isso

Responda:

a função é convexa do intervalo - 1 2 ; 12;
a função é côncava das lacunas - ∞ ; - 1 2 e 1 2 ; +∞ .

Definição 4

ponto de inflexãoé um ponto da forma x 0 ; f(x0). Quando ela tem uma tangente ao gráfico da função, então quando ela passa por x 0, a função muda de sinal para o oposto.

Em outras palavras, este é um ponto pelo qual a segunda derivada passa e muda de sinal, e nos próprios pontos é igual a zero ou não existe. Todos os pontos são considerados domínio da função.

No exemplo, foi visto que não há pontos de inflexão, pois a segunda derivada muda de sinal ao passar pelos pontos x = ± 1 2 . Eles, por sua vez, não estão incluídos no domínio da definição.

Encontrar assíntotas horizontais e oblíquas

Ao definir uma função no infinito, deve-se procurar assíntotas horizontais e oblíquas.

Definição 5

Assíntotas oblíquas representado por linhas retas dado pela equação y = k x + b , onde k = lim x → ∞ f (x) x e b = lim x → ∞ f (x) - k x .

Para k = 0 e b não igual ao infinito, descobrimos que a assíntota oblíqua se torna horizontal.

Em outras palavras, as assíntotas são as linhas que o gráfico da função se aproxima no infinito. Isso contribui para a construção rápida do gráfico da função.

Se não houver assíntotas, mas a função estiver definida em ambos os infinitos, é necessário calcular o limite da função nesses infinitos para entender como o gráfico da função se comportará.

Exemplo 6

Como exemplo, considere que

k = limite x → ∞ f (x) x = limite x → ∞ x 2 4 x 2 - 1 x = 0 b = limite x → ∞ (f (x) - k x) = limite x → ∞ x 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4

é uma assíntota horizontal. Depois de pesquisar a função, você pode começar a construí-la.

Calculando o valor de uma função em pontos intermediários

Para tornar a plotagem mais precisa, é recomendável encontrar vários valores da função em pontos intermediários.

Exemplo 7

A partir do exemplo que consideramos, é necessário encontrar os valores da função nos pontos x \u003d - 2, x \u003d - 1, x \u003d - 3 4, x \u003d - 1 4. Como a função é par, conseguimos que os valores coincidam com os valores nesses pontos, ou seja, obtemos x \u003d 2, x \u003d 1, x \u003d 3 4, x \u003d 1 4.

Vamos escrever e resolver:

F (- 2) = f (2) = 2 2 4 2 2 - 1 = 4 15 ≈ 0, 27 f (- 1) - f (1) = 1 2 4 1 2 - 1 = 1 3 ≈ 0 , 33 f - 3 4 = f 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 f - 1 4 = f 1 4 = 1 4 2 4 1 4 2 - 1 = - 1 12 ≈ - 0,08

Para determinar os máximos e mínimos da função, pontos de inflexão, pontos intermediários, é necessário construir assíntotas. Para designação conveniente, os intervalos de aumento, diminuição, convexidade e concavidade são fixos. Considere a figura abaixo.

É necessário traçar linhas do gráfico através dos pontos marcados, o que permitirá que você se aproxime das assíntotas, seguindo as setas.

Isso conclui o estudo completo da função. Há casos de construção de algumas funções elementares para as quais são utilizadas transformações geométricas.

Se você notar um erro no texto, destaque-o e pressione Ctrl+Enter

Um de tarefas críticas cálculo diferencial é o desenvolvimento exemplos comuns estudos do comportamento das funções.

Se a função y \u003d f (x) for contínua no intervalo e sua derivada for positiva ou igual a 0 no intervalo (a, b), então y \u003d f (x) aumentará em (f "(x) 0). Se a função y \u003d f (x) for contínua no segmento , e sua derivada for negativa ou igual a 0 no intervalo (a,b), então y=f(x) diminuirá em (f"( x)0)

Os intervalos em que a função não diminui ou aumenta são chamados de intervalos de monotonicidade da função. A natureza da monotonicidade de uma função pode mudar apenas naqueles pontos de seu domínio de definição, em que o sinal da primeira derivada muda. Os pontos em que a primeira derivada de uma função desaparece ou quebra são chamados de pontos críticos.

Teorema 1 (1ª condição suficiente para a existência de um extremo).

Seja a função y=f(x) definida no ponto x 0 e seja uma vizinhança δ>0 tal que a função seja contínua no segmento , diferenciável no intervalo (x 0 -δ, x 0)u( x 0 , x 0 + δ) , e sua derivada mantém um sinal constante em cada um desses intervalos. Então se em x 0 -δ, x 0) e (x 0, x 0 + δ) os sinais da derivada são diferentes, então x 0 é um ponto extremo, e se eles combinam, então x 0 não é um ponto extremo . Além disso, se, ao passar pelo ponto x0, a derivada muda de sinal de mais para menos (à esquerda de x 0, f "(x)> 0 é executado, então x 0 é o ponto de máximo; se a derivada muda de sinal de menos para mais (à direita de x 0 é executado por f"(x)<0, то х 0 - точка минимума.

Os pontos de máximo e mínimo são chamados de pontos extremos da função, e os máximos e mínimos da função são chamados de seus valores extremos.

Teorema 2 (critério necessário para um extremo local).

Se a função y=f(x) tem um extremo na corrente x=x 0, então f'(x 0)=0 ou f'(x 0) não existe.
Nos pontos extremos de uma função diferenciável, a tangente ao seu gráfico é paralela ao eixo Ox.

Algoritmo para estudar uma função para um extremo:

1) Encontre a derivada da função.
2) Encontre pontos críticos, ou seja, pontos onde a função é contínua e a derivada é zero ou não existe.
3) Considere a vizinhança de cada um dos pontos e examine o sinal da derivada à esquerda e à direita deste ponto.
4) Determine as coordenadas dos pontos extremos, para este valor dos pontos críticos, substitua nesta função. Usando condições extremas suficientes, tire as conclusões apropriadas.

Exemplo 18. Investigue a função y=x 3 -9x 2 +24x

Solução.
1) y"=3x 2 -18x+24=3(x-2)(x-4).
2) Igualando a derivada a zero, encontramos x 1 =2, x 2 =4. Nesse caso, a derivada é definida em todos os lugares; portanto, além dos dois pontos encontrados, não há outros pontos críticos.
3) O sinal da derivada y "=3(x-2)(x-4) muda dependendo do intervalo conforme mostrado na Figura 1. Ao passar pelo ponto x=2, a derivada muda de sinal de mais para menos, e ao passar pelo ponto x=4 - de menos para mais.
4) No ponto x=2, a função tem um máximo y max =20, e no ponto x=4 - um mínimo y min =16.

Teorema 3. (2ª condição suficiente para a existência de um extremo).

Seja f "(x 0) ef "" (x 0) existir no ponto x 0. Então se f "" (x 0)> 0, então x 0 é o ponto mínimo, e se f "" (x 0 )<0, то х 0 – точка максимума функции y=f(x).

No segmento, a função y \u003d f (x) pode atingir o menor (pelo menos) ou o maior (no máximo) valor nos pontos críticos da função situada no intervalo (a; b) ou nas extremidades do segmento.

O algoritmo para encontrar os maiores e menores valores de uma função contínua y=f(x) no segmento:

1) Encontre f "(x).
2) Encontre os pontos em que f "(x) = 0 ou f" (x) - não existe e selecione deles aqueles que estão dentro do segmento.
3) Calcule o valor da função y \u003d f (x) nos pontos obtidos no parágrafo 2), bem como nas extremidades do segmento e escolha o maior e o menor deles: eles são, respectivamente, os maiores ( para o maior) e o menor (para o menor) valores de função no intervalo .

Exemplo 19. Encontre o maior valor de uma função contínua y=x 3 -3x 2 -45+225 no segmento .

1) Temos y "=3x 2 -6x-45 no segmento
2) A derivada y" existe para todo x. Vamos encontrar os pontos onde y"=0; Nós temos:
3x2 -6x-45=0
x 2 -2x-15=0
x 1 \u003d -3; x2=5
3) Calcule o valor da função nos pontos x=0 y=225, x=5 y=50, x=6 y=63
Apenas o ponto x=5 pertence ao segmento. O maior dos valores encontrados da função é 225, e o menor é o número 50. Então, no max = 225, no max = 50.

Investigação de uma função na convexidade

A figura mostra os gráficos de duas funções. O primeiro deles é virado com uma protuberância para cima, o segundo - com uma protuberância para baixo.

A função y=f(x) é contínua em um segmento e diferenciável no intervalo (a;b), é chamada convexa para cima (para baixo) nesse segmento se, para axb, seu gráfico não for superior (não inferior) ao tangente desenhada em qualquer ponto M 0 (x 0 ;f(x 0)), onde axb.

Teorema 4. Seja a função y=f(x) uma segunda derivada em qualquer ponto interno x do segmento e contínua nas extremidades deste segmento. Então, se a desigualdade f""(x)0 é satisfeita no intervalo (a;b), então a função é convexa para baixo no segmento ; se a desigualdade f""(x)0 for satisfeita no intervalo (à;b), então a função é convexa para cima em .

Teorema 5. Se a função y \u003d f (x) tiver uma segunda derivada no intervalo (a; b) e se mudar de sinal ao passar pelo ponto x 0, então M (x 0 ; f (x 0)) é um ponto de inflexão.

Regra para encontrar pontos de inflexão:

1) Encontre pontos onde f""(x) não existe ou desaparece.
2) Examine o sinal f""(x) à esquerda e à direita de cada ponto encontrado no primeiro passo.
3) Com base no Teorema 4, tire uma conclusão.

Exemplo 20. Encontre pontos extremos e pontos de inflexão do gráfico da função y=3x 4 -8x 3 +6x 2 +12.

Temos f"(x)=12x 3 -24x 2 +12x=12x(x-1) 2. Obviamente, f"(x)=0 para x 1 =0, x 2 =1. A derivada, ao passar pelo ponto x=0, muda de sinal de menos para mais, e ao passar pelo ponto x=1, não muda de sinal. Isso significa que x=0 é o ponto mínimo (y min =12), e não há extremo no ponto x=1. A seguir, encontramos . A segunda derivada se anula nos pontos x 1 = 1, x 2 = 1/3. Os sinais da segunda derivada mudam da seguinte forma: Na reta (-∞;) temos f""(x)>0, no intervalo (;1) temos f""(x)<0, на луче (1;+∞) имеем f""(x)>0. Portanto, x= é o ponto de inflexão do gráfico da função (transição da convexidade para baixo para convexidade para cima) e x=1 também é um ponto de inflexão (transição da convexidade para cima para convexidade para baixo). Se x=, então y=; se, então x=1, y=13.

Um algoritmo para encontrar a assíntota de um grafo

I. Se y=f(x) como x → a , então x=a é uma assíntota vertical.
II. Se y=f(x) como x → ∞ ou x → -∞ então y=A é a assíntota horizontal.
III. Para encontrar a assíntota oblíqua, usamos o seguinte algoritmo:
1) Calcule. Se o limite existe e é igual a b, então y=b é a assíntota horizontal; se , então vá para a segunda etapa.
2) Calcule. Se esse limite não existir, então não há assíntota; se existir e for igual a k, então vá para a terceira etapa.
3) Calcule. Se esse limite não existir, então não há assíntota; se existir e for igual a b, então vá para a quarta etapa.
4) Escreva a equação da assíntota oblíqua y=kx+b.

Exemplo 21: Encontre uma assíntota para uma função

1)
2)
3)
4) A equação assíntota oblíqua tem a forma

O esquema do estudo da função e a construção de seu gráfico

I. Encontre o domínio da função.
II. Encontre os pontos de intersecção do gráfico da função com os eixos coordenados.
III. Encontre assíntotas.
4. Encontre pontos de possível extremo.
V. Encontre pontos críticos.
VI. Usando o desenho auxiliar, investigue o sinal da primeira e da segunda derivada. Determine as áreas de aumento e diminuição da função, encontre a direção da convexidade do gráfico, pontos extremos e pontos de inflexão.
VII. Construa um gráfico, levando em consideração o estudo realizado nos parágrafos 1-6.

Exemplo 22: Plote um gráfico de função de acordo com o esquema acima

Solução.
I. O domínio da função é o conjunto de todos os números reais, exceto x=1.
II. Como a equação x 2 +1=0 não tem raízes reais, então o gráfico da função não tem pontos de interseção com o eixo Ox, mas intercepta o eixo Oy no ponto (0; -1).
III. Esclareçamos a questão da existência de assíntotas. Investigamos o comportamento da função próximo ao ponto de descontinuidade x=1. Como y → ∞ para x → -∞, y → +∞ para x → 1+, então a reta x=1 é uma assíntota vertical do gráfico da função.
Se x → +∞(x → -∞), então y → +∞(y → -∞); portanto, o gráfico não tem uma assíntota horizontal. Além disso, da existência de limites

Resolvendo a equação x 2 -2x-1=0, obtemos dois pontos de um possível extremo:
x 1 =1-√2 e x 2 =1+√2

V. Para encontrar os pontos críticos, calculamos a segunda derivada:

Como f""(x) não desaparece, não há pontos críticos.
VI. Investigamos o sinal da primeira e segunda derivadas. Possíveis pontos extremos a serem considerados: x 1 =1-√2 e x 2 =1+√2, dividir a área de existência da função em intervalos (-∞;1-√2),(1-√2 ;1+√2) e (1+√2;+∞).

Em cada um desses intervalos, a derivada mantém seu sinal: no primeiro - mais, no segundo - menos, no terceiro - mais. A sequência de sinais da primeira derivada será escrita da seguinte forma: +, -, +.
Obtemos que a função em (-∞;1-√2) aumenta, em (1-√2;1+√2) diminui e em (1+√2;+∞) aumenta novamente. Pontos extremos: máximo em x=1-√2, além disso f(1-√2)=2-2√2 mínimo em x=1+√2, além disso f(1+√2)=2+2√2. Em (-∞;1) o gráfico é convexo para cima, e em (1;+∞) - para baixo.
VII Vamos fazer uma tabela dos valores obtidos

VIII Com base nos dados obtidos, construímos um esboço do gráfico da função

Neste artigo, consideraremos um esquema para estudar uma função e também daremos exemplos de estudo de extremos, monotonicidade e assíntotas de uma determinada função.

Esquema

O domínio de existência (ODZ) de uma função.
Interseção de função (se houver) com eixos de coordenadas, sinais de função, paridade, periodicidade.
Pontos de interrupção (seu tipo). Continuidade. Assíntotas são verticais.
Monotonicidade e pontos extremos.
Pontos de inflexão. Convexo.
Investigação de uma função no infinito, para assíntotas: horizontal e oblíqua.
Construindo um gráfico.

Estudo para monotonicidade

Teorema. Se a função g contínuo em , diferenciado por (a; b) e g'(x) ≥ 0 (g'(x) ≤0), xє(а; b), então g aumentando (diminuindo) .

Exemplo:

y = 1: 3x 3 - 6: 2x 2 + 5x.

ODZ: хєR

y' = x 2 + 6x + 5.

Encontrar intervalos de sinais constantes você. Porque o vocêé uma função elementar, então ela pode mudar de sinal apenas nos pontos em que se torna zero ou não existe. Seu ODZ: хєR.

Vamos encontrar os pontos onde a derivada é igual a 0 (zero):

y' = 0;

x = -1; -5.

Então, y crescendo em (-∞; -5] e em [-1; +∞), y descendo em .

Pesquisa para extremos

T. x0é chamado de ponto máximo (max) no conjunto MAS funções g quando o valor máximo é tomado neste ponto pela função g(x 0) ≥ g(x), xєA.

T. x0é chamado de ponto mínimo (min) da função g no set MAS quando o menor valor é tomado pela função neste ponto g(x 0) ≤ g(x), xєА.

No set MAS os pontos máximo (max) e mínimo (min) são chamados de pontos extremos g. Tais extremos também são chamados de extremos absolutos no conjunto .

Se um x0- ponto extremo da função g em algum distrito, então x0é chamado de ponto de extremo local ou local (máximo ou mínimo) da função g.

Teorema (condição necessária). Se um x0- ponto extremo da função (local) g, então a derivada não existe ou é igual a 0 (zero) neste ponto.

Definição. Pontos com derivada inexistente ou igual a 0 (zero) são chamados de críticos. São esses pontos que são suspeitos para um extremo.

Teorema (condição suficiente nº 1). Se a função gé contínua em algum distrito. x0 e o sinal muda através deste ponto quando a derivada passa, então este ponto é o ponto de extremo g.

Teorema (condição suficiente nº 2). Seja a função duas vezes diferenciável em alguma vizinhança do ponto e g' = 0 e g'' > 0 (g''< 0) , então este ponto é o ponto de máximo (max) ou mínimo (min) da função.

Teste de convexidade

A função é chamada de convexa para baixo (ou côncava) no intervalo (a, b) quando o gráfico da função não está localizado acima da secante no intervalo para qualquer x com (a, b) que passa por esses pontos .

A função será convexa estritamente para baixo em (a, b), se - o gráfico está abaixo da secante no intervalo.

A função é chamada de convexa ascendente (convexa) no intervalo (a, b), se para qualquer t pontos Com (a, b) o gráfico da função no intervalo não fica abaixo da secante que passa pelas abcissas nesses pontos .

A função será estritamente convexa para cima em (a, b), se - o gráfico no intervalo estiver acima da secante.

Se a função está em alguma vizinhança do ponto contínuo e através t. x 0 durante a transição, a função muda sua convexidade, então esse ponto é chamado de ponto de inflexão da função.

Estudo para assíntotas

Definição. A reta é chamada de assíntota g(x), se a uma distância infinita da origem, o ponto do gráfico da função se aproxima dela: d(M,l).

As assíntotas podem ser verticais, horizontais ou oblíquas.

Linha vertical com equação x = x 0 será a assíntota do gráfico vertical da função g , se o ponto x 0 tem uma descontinuidade infinita, então há pelo menos um limite esquerdo ou direito neste ponto - infinito.

Investigação de uma função em um segmento para o valor do menor e do maior

Se a função for contínua em , então de acordo com o teorema de Weierstrass, existe o maior valor e o menor valor neste segmento, ou seja, existem t óculos que pertencem de tal modo que g(x 1) ≤ g(x)< g(x 2), x 2 є . A partir de teoremas sobre monotonicidade e extremos, obtemos o seguinte esquema para estudar uma função em um segmento para os menores e maiores valores.

Plano

Encontrar derivada g'(x).
Consultar o valor de uma função g nesses pontos e nas extremidades do segmento.
Compare os valores encontrados e escolha o menor e o maior.

Comente. Se você precisa estudar uma função em um intervalo finito (a, b), ou em um infinito (-∞; b); (-∞; +∞) nos valores máximo e mínimo, então no plano, em vez dos valores da função nas extremidades do intervalo, eles procuram os limites unilaterais correspondentes: em vez de f(a) procurando por f(a+) = limf(x), ao invés de f(b) procurando por f(-b). Portanto, você pode encontrar a função ODZ no intervalo, porque os extremos absolutos não existem necessariamente neste caso.

Aplicação da derivada à solução de problemas aplicados para o extremo de algumas grandezas

Expresse esse valor em termos de outras grandezas da condição do problema para que seja função de apenas uma variável (se possível).
O intervalo de mudança desta variável é determinado.
Faça um estudo da função no intervalo para os valores máximo e mínimo.

Uma tarefa.É necessário construir uma plataforma retangular, usando uma malha, perto da parede, de modo que de um lado fique adjacente à parede e, nos outros três, seja cercada com uma malha. Em que proporção a área de tal site será a maior?

S=xyé uma função de 2 variáveis.

S = x(a - 2x)- função da 1ª variável ; x .

S = ax - 2x2; S" = a - 4x = 0, xєR, x = a: 4.

S(a: 4) = a 2: 8- o valor mais alto;

S(0)=0.

Encontre o outro lado do retângulo: no = a: 2.

Proporção da tela: y:x=2.

Responda. A maior área será um 2/8 se o lado paralelo à parede for 2 vezes o outro lado.

Pesquisa de função. Exemplos

Exemplo 1

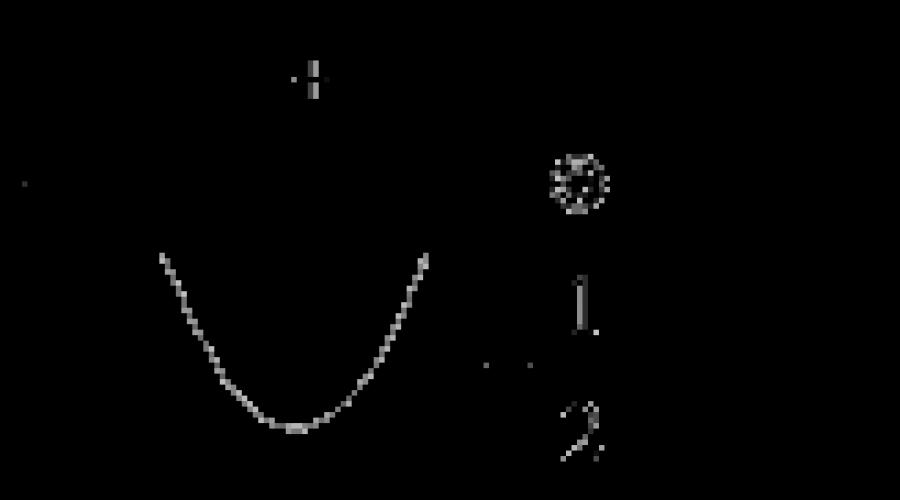
Disponível y=x 3: (1-x) 2 . Faça pesquisas.

ODZ: хє(-∞; 1) U (1; ∞).
Uma função geral (nem par nem ímpar) não é simétrica em relação ao ponto 0 (zero).
Sinais de função. A função é elementar, portanto só pode mudar de sinal nos pontos em que é igual a 0 (zero), ou não existe.
A função é elementar, portanto contínua na ODZ: (-∞; 1) U (1; ∞).

Lacuna: x = 1;

limite 3: (1- x) 2 = ∞- Descontinuidade do 2º tipo (infinito), portanto existe uma assíntota vertical no ponto 1;

x = 1- a equação da assíntota vertical.

5. y' = x 2 (3 - x): (1 - x) 3 ;

ODZ (y'): x ≠ 1;

x = 1é um ponto crítico.

y' = 0;

0; 3 são pontos críticos.

6. y'' = 6x: (1 - x) 4 ;

Crítico t.: 1, 0;

x= 0 - ponto de inflexão, y(0) = 0.

7. limite 3: (1 - 2x + x 2) = ∞- não há assíntota horizontal, mas pode ser oblíqua.

k = 1- número;

b = 2- número.

Portanto, existe uma assíntota oblíqua y=x+2 para + ∞ e para - ∞.

Exemplo 2

Dado y = (x 2 + 1): (x - 1). Produzir e investigação. Construir um gráfico.

1. A área de existência é toda a reta numérica, exceto a chamada. x=1.

2. y cruza OY (se possível) incl. (0;g(0)). Nós achamos y(0) = -1 - ponto de interseção OY .

Pontos de intersecção do gráfico com BOI encontre resolvendo a equação y=0. A equação não tem raízes reais, então esta função não intercepta BOI.

3. A função não é periódica. Considere a expressão

g(-x) ≠ g(x), e g(-x) ≠ -g(x). Isso significa que é uma função genérica (nem par nem ímpar).

4. T. x=1 a descontinuidade é do segundo tipo. Em todos os outros pontos, a função é contínua.

5. Estudo da função para um extremo:

(x 2 - 2x - 1): (x - 1)2=s"

e resolva a equação y" = 0.

Então, 1 - √2, 1 + √2, 1 - pontos críticos ou pontos de possível extremo. Esses pontos dividem a reta numérica em quatro intervalos .

Em cada intervalo, a derivada tem um certo sinal, que pode ser definido pelo método dos intervalos ou calculando os valores da derivada em pontos individuais. Nos intervalos (-∞; 1 - √2 ) você (1 + √2 ; ∞) , uma derivada positiva, o que significa que a função está crescendo; E se xє(1 - √2 ; 1) U(1; 1 + √2 ) , então a função é decrescente, porque a derivada é negativa nesses intervalos. Através. x 1 durante a transição (o movimento segue da esquerda para a direita), a derivada muda de sinal de "+" para "-", portanto, neste ponto há um máximo local, encontramos

y máximo = 2 - 2 √2 .

Ao passar por x2 altera o sinal da derivada de "-" para "+", portanto, há um mínimo local neste ponto, e

y mistura = 2 + 2√2.

T. x=1 não tão extremo.

6.4: (x - 1) 3 = y"".

No (-∞; 1 ) 0 > você"" , consequentemente, a curva é convexa nesse intervalo; se xє (1 ; ∞) - a curva é côncava. Em t ponto 1 nenhuma função é definida, então este ponto não é um ponto de inflexão.

7. Decorre dos resultados do parágrafo 4 que x=1é a assíntota vertical da curva.

Não há assíntotas horizontais.

x + 1 = y é a assíntota da inclinação desta curva. Não há outras assíntotas.

8. Tendo em conta os estudos realizados, construímos um gráfico (ver figura acima).