O significado da derivada. Função derivada. O significado geométrico da derivada

10.10.2019

O que é um derivado?
Definição e significado da derivada de uma função

Muitos ficarão surpresos com a localização inesperada deste artigo no curso do meu autor sobre a derivada de uma função de uma variável e suas aplicações. Afinal, como era na escola: um livro-texto padrão, antes de tudo, dá uma definição de derivada, seu significado geométrico, mecânico. Em seguida, os alunos encontram derivadas de funções por definição e, de fato, só então a técnica de diferenciação é aperfeiçoada usando tabelas derivadas.

Mas do meu ponto de vista, a seguinte abordagem é mais pragmática: antes de tudo, é aconselhável ENTENDER BEM limite de função, e especialmente infinitesimais. O fato é que a definição da derivada é baseada no conceito de limite, que é mal considerado curso escolar. É por isso que uma parte significativa dos jovens consumidores de conhecimento do granito penetra mal na própria essência do derivado. Assim, se você está mal orientado em cálculo diferencial ou um cérebro sábio para longos anos descartou com sucesso esta bagagem, por favor, comece de limites de função. Ao mesmo tempo, domine / lembre-se de sua decisão.

O mesmo sentido prático sugere que é lucrativo primeiro Aprenda a encontrar derivadas, Incluindo derivadas de funções complexas. A teoria é uma teoria, mas, como dizem, você sempre quer diferenciar. A este respeito, é melhor trabalhar as lições básicas listadas e talvez tornar-se mestre de diferenciação sem sequer perceber a essência de suas ações.

Eu recomendo iniciar os materiais nesta página depois de ler o artigo. Os problemas mais simples com uma derivada, onde, em particular, é considerado o problema da tangente ao gráfico de uma função. Mas pode demorar. O fato é que muitas aplicações da derivada não requerem seu entendimento, e não é de se estranhar que a lição teórica tenha surgido bem tarde - quando precisei explicar encontrar intervalos de aumento/diminuição e extremos funções. Além disso, ele estava no assunto por um bom tempo " Funções e gráficos”, até que decidi colocar mais cedo.

Portanto, queridos bules, não se apressem em absorver a essência do derivado, como animais famintos, porque a saturação será insípida e incompleta.

O conceito de crescente, decrescente, máximo, mínimo de uma função

Muitos guias de estudo levar ao conceito de derivada com a ajuda de alguns problemas práticos, e também exemplo interessante. Imagine que temos que viajar para uma cidade que pode ser alcançada de diferentes maneiras. Descartamos imediatamente os caminhos sinuosos curvos e consideraremos apenas linhas retas. No entanto, as direções em linha reta também são diferentes: a cidade pode ser alcançada em uma autoestrada plana. Ou em uma estrada montanhosa - para cima e para baixo, para cima e para baixo. Outra estrada só sobe, e outra desce o tempo todo. Os caçadores de emoções escolherão uma rota pelo desfiladeiro com um penhasco íngreme e uma subida íngreme.

Mas quaisquer que sejam as suas preferências, é aconselhável conhecer a zona, ou pelo menos localizá-la. mapa topográfico. E se não houver essa informação? Afinal, você pode escolher, por exemplo, um caminho plano, mas, como resultado, tropeçar em uma pista de esqui com finlandeses engraçados. Não o fato de que o navegador e até mesmo uma imagem de satélite fornecerão dados confiáveis. Portanto, seria bom formalizar o relevo do caminho por meio da matemática.

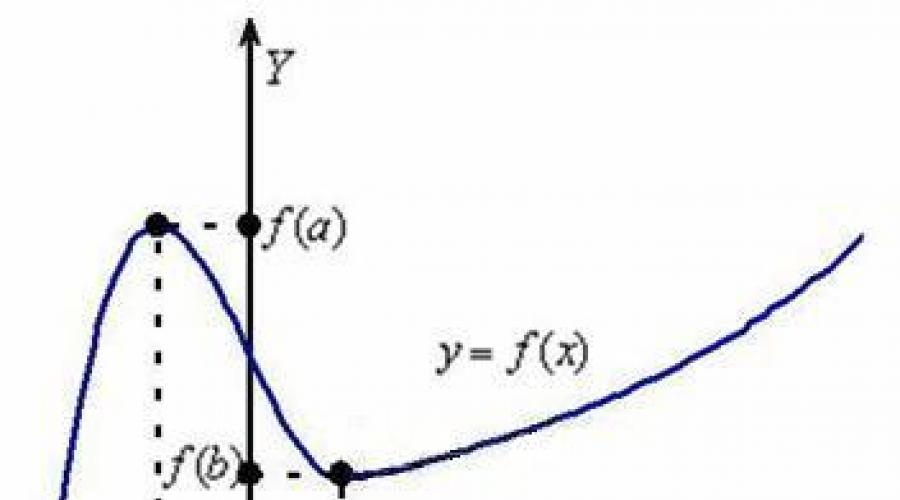
Considere alguma estrada (vista lateral):

Por precaução, lembro-lhe um fato elementar: a viagem acontece da esquerda para a direita. Por simplicidade, assumimos que a função contínuo na área considerada.

Quais são as características deste gráfico?

Nos intervalos função aumenta, ou seja, cada um de seus próximos valores mais o anterior. Grosso modo, o cronograma vai para cima(subimos o morro). E no intervalo a função diminuindo- cada próximo valor menos o anterior, e nossa agenda vai careca(descendo a ladeira).

Também prestamos atenção pontos especiais. No ponto em que chegamos máximo, isso é existe tal seção do caminho em que o valor será o maior (mais alto). No mesmo ponto, mínimo, e existe tal sua vizinhança, em que o valor é o menor (menor).

Terminologia e definições mais rigorosas serão consideradas na lição. sobre os extremos da função enquanto estudamos mais um característica importante: entre a função é crescente, mas é crescente Com velocidade diferente . E a primeira coisa que chama sua atenção é que o gráfico sobe no intervalo muito mais legal do que no intervalo. É possível medir a inclinação da estrada usando ferramentas matemáticas?

Taxa de alteração de função

A ideia é esta: tirar algum valor (leia "delta x"), que chamaremos incremento de argumento, e vamos começar a "experimentar" em vários pontos do nosso caminho:

1) Vejamos o ponto mais à esquerda: contornando a distância , subimos a encosta até uma altura (linha verde). O valor é chamado incremento de função, e em este caso este incremento é positivo (a diferença de valores ao longo do eixo é maior que zero). Vamos fazer a relação , que será a medida da inclinação da nossa estrada. Obviamente, é um número muito específico, e como ambos os incrementos são positivos, então .

Atenção! A designação é 1 símbolo, ou seja, você não pode “arrancar” o “delta” do “x” e considerar essas letras separadamente. Claro, o comentário também se aplica ao símbolo de incremento da função.

Vamos explorar a natureza da fração resultante mais significativa. Suponha que inicialmente estamos a uma altura de 20 metros (no ponto preto à esquerda). Vencida a distância de metros (linha vermelha à esquerda), estaremos a uma altura de 60 metros. Então o incremento da função será metros (linha verde) e: . Nesse caminho, em cada metro este troço da estrada altura aumenta média por 4 metros… você esqueceu seu equipamento de escalada? =) Em outras palavras, a razão construída caracteriza a TAXA MÉDIA DE VARIAÇÃO (neste caso, crescimento) da função.

Observação : Os valores numéricos do exemplo em questão correspondem às proporções do desenho apenas aproximadamente.

2) Agora vamos percorrer a mesma distância do ponto preto mais à direita. Aqui o aumento é mais suave, então o incremento (linha carmesim) é relativamente pequeno, e a relação em relação ao caso anterior será bastante modesta. Relativamente falando, metros e taxa de crescimento da funçãoé . Ou seja, aqui para cada metro de estrada há média meio metro de altura.

3) Uma pequena aventura na montanha. Vamos olhar para cima Ponto preto localizado no eixo y. Vamos supor que esta seja uma marca de 50 metros. Mais uma vez superamos a distância, pelo que nos encontramos mais baixos - no nível de 30 metros. Desde que o movimento foi feito careca(na direção "oposta" do eixo), então o final o incremento da função (altura) será negativo: metros (linha marrom no desenho). E neste caso estamos falando de taxa de decaimento recursos: , ou seja, para cada metro do trajeto deste trecho, a altura diminui média por 2 metros. Cuide das roupas no quinto ponto.

Agora vamos fazer a pergunta: qual é o melhor valor de "padrão de medição" a ser usado? É claro que 10 metros é muito difícil. Uma boa dúzia de solavancos pode caber facilmente neles. Por que existem solavancos, pode haver um desfiladeiro profundo abaixo e depois de alguns metros - seu outro lado com uma subida ainda mais íngreme. Assim, com um de dez metros, não obteremos uma característica inteligível de tais seções do caminho através da razão.

Da discussão acima, segue a seguinte conclusão: Como as menos valor , mais precisamente descreveremos o relevo da estrada. Além disso, os seguintes fatos são verdadeiros:

– Para qualquer pontos de elevação você pode escolher um valor (ainda que muito pequeno) que se encaixe nos limites de um ou outro aumento. E isso significa que o incremento de altura correspondente será garantido como positivo, e a desigualdade indicará corretamente o crescimento da função em cada ponto desses intervalos.

- Da mesma maneira, para qualquer ponto de inclinação, existe um valor que caberá completamente nesta inclinação. Portanto, o aumento correspondente na altura é inequivocamente negativo, e a desigualdade mostrará corretamente a diminuição da função em cada ponto do intervalo dado.

– De particular interesse é o caso em que a taxa de variação da função é zero: . Primeiro, um incremento de altura zero () é um sinal de um caminho par. E em segundo lugar, existem outras situações curiosas, cujos exemplos você vê na figura. Imagine que o destino nos levou ao topo de uma colina com águias voando ou ao fundo de uma ravina com sapos coaxando. Se você der um pequeno passo em qualquer direção, a mudança na altura será desprezível e podemos dizer que a taxa de mudança da função é realmente zero. O mesmo padrão é observado em pontos.

Assim, nos aproximamos de uma oportunidade incrível para caracterizar com precisão a taxa de variação de uma função. Afinal, a análise matemática nos permite direcionar o incremento do argumento para zero: ou seja, torná-lo infinitesimal.

Como resultado, surge outra questão lógica: é possível encontrar para a estrada e seu horário outra função, que nos diria sobre todos os planos, subidas, descidas, picos, planícies, bem como a taxa de aumento/diminuição em cada ponto do caminho?

O que é um derivado? Definição de um derivado.
O significado geométrico da derivada e diferencial

Por favor, leia com atenção e não muito rapidamente - o material é simples e acessível a todos! Tudo bem se em alguns lugares algo não parecer muito claro, você sempre pode retornar ao artigo mais tarde. Direi mais, é útil estudar a teoria várias vezes para entender qualitativamente todos os pontos (o conselho é especialmente relevante para estudantes “técnicos” que matemática superior desempenha um papel importante no processo educacional).

Naturalmente, na própria definição da derivada em um ponto, vamos substituí-la por:

A que chegamos? E chegamos à conclusão de que para uma função de acordo com a lei está alinhado outra função, que é chamado função derivada(ou simplesmente derivado).

A derivada caracteriza taxa de variação funções . Como? O pensamento vai como um fio vermelho desde o início do artigo. Considere algum ponto domínios funções . Seja a função diferenciável em um dado ponto. Então:

1) Se , então a função aumenta no ponto . E obviamente existe intervalo(mesmo que muito pequeno) contendo o ponto em que a função cresce, e seu gráfico vai “de baixo para cima”.

2) Se , então a função diminui no ponto . E há um intervalo contendo um ponto no qual a função diminui (o gráfico vai “de cima para baixo”).

3) Se , então infinitamente perto próximo ao ponto, a função mantém sua velocidade constante. Isso acontece, como observado, para uma constante de função e em pontos críticos da função, em particular nos pontos mínimo e máximo.

Alguma semântica. O que em sentido amplo O que significa o verbo "diferenciar"? Diferenciar significa destacar uma característica. Diferenciando a função , "selecionamos" a taxa de sua variação na forma de uma derivada da função . E o que, a propósito, significa a palavra "derivada"? Função ocorrido da função.

Os termos interpretam com muito sucesso o significado mecânico da derivada :
Vamos considerar a lei da mudança das coordenadas do corpo, que depende do tempo, e a função da velocidade de movimento do corpo dado. A função caracteriza a taxa de variação da coordenada do corpo, portanto é a primeira derivada da função em relação ao tempo: . Se o conceito de “movimento do corpo” não existisse na natureza, então não existiria derivado conceito de "velocidade".

A aceleração de um corpo é a taxa de variação da velocidade, portanto: . Se os conceitos originais de “movimento do corpo” e “velocidade de movimento do corpo” não existissem na natureza, então não haveria derivado o conceito de aceleração de um corpo.

Ao decidir várias tarefas geometria, mecânica, física e outros ramos do conhecimento, tornou-se necessário utilizar o mesmo processo analítico a partir de uma determinada função y=f(x) obter uma nova função chamada função derivada(ou simplesmente derivada) desta função f(x) e são simbolizados

O processo pelo qual uma determinada função f(x) obter uma nova função f"(x), chamado diferenciação e consiste nos três passos seguintes: 1) damos o argumento x incremento  x e determine o incremento correspondente da função  y = f(x+ x)-f(x); 2) faça a relação

3) contagem x permanente, e  x0, encontramos
, que é denotado por f"(x), como se enfatizasse que a função resultante depende apenas do valor x, no qual passamos ao limite. Definição: Derivada y "=f" (x) dada função y=f(x) dado xé chamado de limite da razão entre o incremento da função e o incremento do argumento, desde que o incremento do argumento tenda a zero, se, é claro, esse limite existir, ou seja, finito. Nesse caminho,
, ou

Observe que se para algum valor x, por exemplo, quando x=a, relação
no  x0 não tende a um limite finito, então neste caso dizemos que a função f(x) no x=a(ou no ponto x=a) não tem derivada ou não é diferenciável em um ponto x=a.

2. O significado geométrico da derivada.

Considere o gráfico da função y \u003d f (x), diferenciável na vizinhança do ponto x 0

f(x)

Considere uma linha arbitrária passando pelo ponto do gráfico da função - o ponto A (x 0, f (x 0)) e cruzando o gráfico em algum ponto B (x; f (x)). Essa linha reta (AB) é chamada de secante. De ∆ABC: AC = ∆x; BC \u003d ∆y; tgβ=∆y/∆x.

Desde AC || Ox, então ALO = BAC = β (como correspondente em paralelo). Mas ALO é o ângulo de inclinação da secante AB para a direção positiva do eixo Ox. Portanto, tgβ = k - declive AB direto.

Agora vamos diminuir ∆x, ou seja. ∆x→ 0. Neste caso, o ponto B se aproximará do ponto A conforme o gráfico, e a secante AB irá girar. A posição limite da secante AB em ∆x → 0 será a linha reta (a), chamada de tangente ao gráfico da função y \u003d f (x) no ponto A.

Se passarmos ao limite como ∆х → 0 na igualdade tgβ =∆y/∆x, então obtemos
ou tg \u003d f "(x 0), já que
-ângulo de inclinação da tangente à direção positiva do eixo Ox
, por definição de uma derivada. Mas tg \u003d k é a inclinação da tangente, o que significa que k \u003d tg \u003d f "(x 0).

Assim, o significado geométrico da derivada é o seguinte:

Derivada de uma função em um ponto x 0 igual à inclinação da tangente ao gráfico da função desenhada no ponto com a abcissa x 0 .

3. Significado físico da derivada.

Considere o movimento de um ponto ao longo de uma linha reta. Seja a coordenada de um ponto em qualquer instante x(t). Sabe-se (do curso de física) que a velocidade média durante um período de tempo é igual à razão entre a distância percorrida durante esse período de tempo e o tempo, ou seja,

Vav = ∆x/∆t. Passemos ao limite na última igualdade como ∆t → 0.

lim Vav (t) = (t 0) - velocidade instantânea no tempo t 0, ∆t → 0.

e lim = ∆x/∆t = x "(t 0) (pela definição de uma derivada).

Então, (t) = x"(t).

O significado físico da derivada é o seguinte: a derivada da funçãoy = f(x) no pontox 0 é a taxa de variação da funçãof(x) no pontox 0

A derivada é usada na física para encontrar a velocidade de uma função conhecida de coordenadas do tempo, aceleração de uma função conhecida de velocidade do tempo.

 (t) \u003d x "(t) - velocidade,

a(f) = "(t) - aceleração, ou

Se a lei do movimento de um ponto material ao longo de um círculo é conhecida, então é possível encontrar a velocidade angular e a aceleração angular durante o movimento de rotação:

φ = φ(t) - mudança no ângulo com o tempo,

ω \u003d φ "(t) - velocidade angular,

ε = φ"(t) - aceleração angular, ou ε = φ"(t).

Se a lei de distribuição para a massa de uma haste não homogênea for conhecida, então a densidade linear da haste não homogênea pode ser encontrada:

m \u003d m (x) - massa,

x  , l - comprimento da haste,

p \u003d m "(x) - densidade linear.

Com a ajuda da derivada, os problemas da teoria da elasticidade e das vibrações harmônicas são resolvidos. Sim, de acordo com a lei de Hooke

F = -kx, x – coordenada variável, k – coeficiente de elasticidade da mola. Colocando ω 2 \u003d k / m, obtemos a equação diferencial do pêndulo da mola x "(t) + ω 2 x (t) \u003d 0,

onde ω = √k/√m é a frequência de oscilação (l/c), k é a taxa de mola (H/m).

Uma equação da forma y "+ ω 2 y \u003d 0 é chamada de equação de oscilações harmônicas (mecânicas, elétricas, eletromagnéticas). A solução para tais equações é a função

y = Asin(ωt + φ 0) ou y = Acos(ωt + φ 0), onde

A - amplitude de oscilação, ω - frequência cíclica,

φ 0 - fase inicial.

(\large\bf Função derivada)

Considere a função y=f(x), dado no intervalo (a, b). Deixar x- qualquer intervalo de ponto fixo (a, b), uma Δx- um número arbitrário, tal que o valor x+Δx também pertence ao intervalo (a, b). Este número Δxé chamado de incremento de argumento.

Definição. Incremento de função y=f(x) no ponto x, correspondente ao incremento do argumento Δx, vamos ligar para o número

Δy = f(x+Δx) - f(x).

Acreditamos que Δx ≠ 0. Considere em um dado ponto fixo x a razão do incremento da função naquele ponto para o incremento correspondente do argumento Δx

Essa relação será chamada de relação de diferença. Já que o valor x consideramos fixo, a relação de diferença é uma função do argumento Δx. Esta função é definida para todos os valores de argumento Δx, pertencente a alguma vizinhança suficientemente pequena do ponto ∆x=0, exceto o ponto ∆x=0. Assim, temos o direito de considerar a questão da existência de um limite da função especificada para ∆x → 0.

Definição. Função derivada y=f(x) em um determinado ponto fixo xé chamado de limite ∆x → 0 relação diferencial, ou seja,

Desde que este limite exista.

Designação. y (x) ou f′(x).

O significado geométrico da derivada: Derivada de função f(x) neste ponto x igual à tangente do ângulo entre o eixo Boi e uma tangente ao gráfico desta função no ponto correspondente:

f′(x 0) = \tgα.

O significado mecânico da derivada: A derivada do caminho em relação ao tempo é igual à velocidade do movimento retilíneo do ponto:

Equação da tangente da linha y=f(x) no ponto M0 (x0,y0) toma a forma

y-y 0 = f (x 0) (x-x 0).

A normal à curva em algum ponto é a perpendicular à tangente no mesmo ponto. Se um f′(x 0)≠ 0, então a equação da normal à linha y=f(x) no ponto M0 (x0,y0) está escrito assim:

O conceito de diferenciabilidade de uma função

Deixe a função y=f(x) definido em algum intervalo (a, b), x- algum valor fixo do argumento deste intervalo, Δx- qualquer incremento do argumento tal que o valor do argumento x+Δx ∈ (a, b).

Definição. Função y=f(x)é chamado de diferenciável em um dado ponto x se incrementar Δy esta função no ponto x, correspondente ao incremento do argumento Δx, pode ser representado como

Δy = A Δx +αΔx,

Onde UMAé algum número independente de Δx, uma α - função argumento Δx, que é infinitamente pequeno em ∆x → 0.

Como o produto de duas funções infinitesimais αΔxé uma ordem infinitesimal superior a Δx(propriedade 3 de funções infinitesimais), podemos escrever:

∆y = A ∆x +o(∆x).

Teorema. Para a função y=f(x) era diferenciável em um determinado ponto x, é necessário e suficiente que tenha uma derivada finita neste ponto. Em que A=f'(x), isso é

Δy = f′(x) Δx +o(Δx).

A operação de encontrar a derivada é geralmente chamada de diferenciação.

Teorema. Se a função y=f(x) x, então ela é contínua nesse ponto.

Comente. Da continuidade da função y=f(x) neste ponto x, de modo geral, não se segue que a função seja diferenciável f(x) neste ponto. Por exemplo, a função y=|x|- contínua em um ponto x=0, mas não tem derivada.

O conceito de uma função diferencial

Definição. diferencial de função y=f(x)é chamado o produto da derivada desta função e o incremento da variável independente x:

dy = y′ ∆x, df(x) = f′(x) ∆x.

Para função y=x Nós temos dy=dx=x'Δx = 1 Δx= Δx, isso é dx=Δx- o diferencial de uma variável independente é igual ao incremento dessa variável.

Assim, podemos escrever

dy = y′dx, df(x) = f′(x)dx

Diferencial dy e incrementar Δy funções y=f(x) neste ponto x, ambos correspondendo ao mesmo incremento do argumento Δx são, em geral, não iguais entre si.

O significado geométrico do diferencial: O diferencial de uma função é igual ao incremento da ordenada da tangente ao gráfico da função dada quando o argumento é incrementado Δx.

Regras de diferenciação

Teorema. Se cada uma das funções u(x) e v(x) diferenciável em um dado ponto x, então a soma, diferença, produto e quociente dessas funções (quociente desde que v(x)≠ 0) também são diferenciáveis neste ponto, e as seguintes fórmulas são válidas:

Considere uma função complexa y=f(φ(x))≡ F(x), Onde y=f(u), u=φ(x). Nesse caso você chamado argumento intermediário, x - variável independente.

Teorema. Se um y=f(u) e u=φ(x) são funções diferenciáveis de seus argumentos, então a derivada função complexa y=f(φ(x)) existe e é igual ao produto desta função em relação ao argumento intermediário e a derivada do argumento intermediário em relação à variável independente, ou seja,

Comente. Para uma função complexa que é uma superposição de três funções y=F(f(φ(x)))), a regra de diferenciação tem a forma

y′ x = y′ u u′ v v′ x,

onde funciona v=φ(x), u=f(v) e y=F(u) são funções diferenciáveis de seus argumentos.

Teorema. Deixe a função y=f(x)é crescente (ou decrescente) e contínua em alguma vizinhança do ponto x0. Seja, além disso, esta função diferenciável no ponto indicado x0 e sua derivada neste ponto f′(x 0) ≠ 0. Então em alguma vizinhança do ponto correspondente y0=f(x0) o inverso para y=f(x) função x=f-1 (y), e o especificado função inversa diferenciável no ponto correspondente y0=f(x0) e para sua derivada neste ponto y a fórmula é válida

Tabela de derivativos

Invariância da forma do primeiro diferencial

Considere a diferencial de uma função complexa. Se um y=f(x), x=φ(t) são funções diferenciáveis de seus argumentos, então a derivada da função y=f(φ(t))é expresso pela fórmula

y′t = y′ x x′t.

Por definição dy = você dt, então obtemos

dy = y′ t dt = y′ x x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y′ x dx.

Então, nós provamos

Propriedade da invariância da forma da primeira diferencial de uma função: como no caso em que o argumento xé uma variável independente, e no caso em que o argumento xé em si uma função diferenciável da nova variável, o diferencial dy funções y=f(x)é igual à derivada desta função, multiplicada pela diferencial do argumento dx.

Aplicação do diferencial em cálculos aproximados

Mostramos que o diferencial dy funções y=f(x), em geral, não é igual ao incremento Δy esta função. No entanto, até uma função infinitamente pequena de uma ordem de pequenez mais alta do que Δx, a igualdade aproximada

∆y ≈ dy.

A razão é chamada de erro relativo da igualdade dessa igualdade. Porque ∆y-dy=o(∆x), então erro relativo desta igualdade torna-se arbitrariamente pequena à medida que |Δх|.

Dado que Δy=f(x+δx)-f(x), dy=f′(x)Δx, Nós temos f(x+δx)-f(x) ≈ f′(x)Δx ou

f(x+δx) ≈ f(x) + f′(x)Δx.

Esta igualdade aproximada permite com um erro o(Δx) substituir função f(x) em uma pequena vizinhança de um ponto x(ou seja, para valores pequenos Δx) Função linear argumento Δx de pé do lado direito.

Derivados de ordens superiores

Definição. A segunda derivada (ou derivada de segunda ordem) da função y=f(x)é chamada de derivada de sua primeira derivada.

Notação para a segunda derivada de uma função y=f(x):

Significado mecânico da segunda derivada. Se a função y=f(x) descreve a lei do movimento ponto material em uma linha reta, então a segunda derivada f″(x)é igual à aceleração do ponto em movimento no tempo x.

A terceira e quarta derivadas são definidas de forma semelhante.

Definição. n-ª derivada (ou derivada nª ordem) funções y=f(x) chamado de derivada dele n-1-ª derivada:

y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.

Designações: y″′, e IV, y V etc.

O Problema B9 fornece um gráfico de uma função ou derivada, a partir do qual é necessário determinar uma das seguintes quantidades:

O valor da derivada em algum ponto x 0,
Pontos altos ou baixos (pontos extremos),
Intervalos de funções crescentes e decrescentes (intervalos de monotonicidade).

As funções e derivadas apresentadas neste problema são sempre contínuas, o que simplifica bastante a solução. Apesar do fato de que a tarefa pertence à seção analise matemática, está ao alcance mesmo dos alunos mais fracos, já que nenhum conhecimento teórico profundo é necessário aqui.

Para encontrar o valor da derivada, pontos extremos e intervalos de monotonicidade, existem algoritmos simples e universais - todos eles serão discutidos abaixo.

Leia atentamente a condição do problema B9 para não cometer erros estúpidos: às vezes, textos bastante volumosos aparecem, mas condições importantes, que afetam o curso da solução, são poucos.

Cálculo do valor da derivada. Método de dois pontos

Se o problema recebe um gráfico da função f(x), tangente a este gráfico em algum ponto x 0 , e é necessário encontrar o valor da derivada neste ponto, o seguinte algoritmo é aplicado:

Encontre dois pontos "adequados" no gráfico tangente: suas coordenadas devem ser inteiras. Vamos denotar esses pontos como A (x 1 ; y 1) e B (x 2 ; y 2). Escreva corretamente as coordenadas - isso é momento chave soluções, e qualquer erro aqui leva à resposta errada.
Conhecendo as coordenadas, é fácil calcular o incremento do argumento Δx = x 2 − x 1 e o incremento da função Δy = y 2 − y 1 .
Finalmente, encontramos o valor da derivada D = Δy/Δx. Em outras palavras, você precisa dividir o incremento da função pelo incremento do argumento - e esta será a resposta.

Mais uma vez, notamos: os pontos A e B devem ser procurados precisamente na tangente, e não no gráfico da função f(x), como é frequentemente o caso. A tangente necessariamente conterá pelo menos dois desses pontos, caso contrário o problema é formulado incorretamente.

Considere os pontos A (−3; 2) e B (−1; 6) e encontre os incrementos:
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Vamos encontrar o valor da derivada: D = Δy/Δx = 4/2 = 2.

Uma tarefa. A figura mostra o gráfico da função y \u003d f (x) e a tangente a ela no ponto com a abcissa x 0. Encontre o valor da derivada da função f(x) no ponto x 0 .

Considere os pontos A (0; 3) e B (3; 0), encontre incrementos:
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

Agora encontramos o valor da derivada: D = Δy/Δx = −3/3 = −1.

Uma tarefa. A figura mostra o gráfico da função y \u003d f (x) e a tangente a ela no ponto com a abcissa x 0. Encontre o valor da derivada da função f(x) no ponto x 0 .

Considere os pontos A (0; 2) e B (5; 2) e encontre incrementos:
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.

Resta encontrar o valor da derivada: D = Δy/Δx = 0/5 = 0.

A partir do último exemplo, podemos formular a regra: se a tangente é paralela ao eixo OX, a derivada da função no ponto de contato é igual a zero. Nesse caso, você nem precisa calcular nada - basta olhar para o gráfico.

Cálculo de pontos altos e baixos

Às vezes, em vez de um gráfico de uma função no problema B9, um gráfico de derivada é fornecido e é necessário encontrar o ponto máximo ou mínimo da função. Nesse cenário, o método de dois pontos é inútil, mas existe outro algoritmo ainda mais simples. Primeiro, vamos definir a terminologia:

O ponto x 0 é chamado de ponto máximo da função f(x) se a seguinte desigualdade vale em alguma vizinhança deste ponto: f(x 0) ≥ f(x).
O ponto x 0 é chamado de ponto mínimo da função f(x) se a seguinte desigualdade vale em alguma vizinhança deste ponto: f(x 0) ≤ f(x).

Para encontrar os pontos de máximo e mínimo no gráfico da derivada, basta realizar os seguintes passos:

Redesenhe o gráfico da derivada, removendo todas as informações desnecessárias. Como mostra a prática, dados extras apenas interferem na decisão. Por isso, marcamos eixo coordenado zeros da derivada - e é isso.
Descubra os sinais da derivada nos intervalos entre zeros. Se para algum ponto x 0 se sabe que f'(x 0) ≠ 0, então apenas duas opções são possíveis: f'(x 0) ≥ 0 ou f'(x 0) ≤ 0. O sinal da derivada é fácil de determinar a partir do desenho original: se o gráfico da derivada estiver acima do eixo OX, então f'(x) ≥ 0. Por outro lado, se o gráfico da derivada estiver abaixo do eixo OX, então f'(x) ≤ 0.
Verificamos novamente os zeros e sinais da derivada. Onde o sinal muda de menos para mais, há um ponto mínimo. Por outro lado, se o sinal da derivada mudar de mais para menos, este é o ponto máximo. A contagem é sempre feita da esquerda para a direita.

Este esquema funciona apenas para funções contínuas - não há outros no problema B9.

Uma tarefa. A figura mostra um gráfico da derivada da função f(x) definida no intervalo [−5; 5]. Encontre o ponto mínimo da função f(x) neste segmento.

Vamos nos livrar informação extra— deixe apenas os limites [−5; 5] e os zeros da derivada x = −3 ex = 2,5. Observe também os sinais:

Obviamente, no ponto x = −3, o sinal da derivada muda de menos para mais. Este é o ponto mínimo.

Uma tarefa. A figura mostra um gráfico da derivada da função f(x) definida no intervalo [−3; 7]. Encontre o ponto de máximo da função f(x) neste segmento.

Vamos redesenhar o gráfico, deixando apenas os limites [−3; 7] e os zeros da derivada x = −1,7 ex = 5. Observe os sinais da derivada no gráfico resultante. Nós temos:

Obviamente, no ponto x = 5, o sinal da derivada muda de mais para menos - este é o ponto máximo.

Uma tarefa. A figura mostra um gráfico da derivada da função f(x) definida no intervalo [−6; quatro]. Encontre o número de pontos máximos da função f(x) que pertencem ao intervalo [−4; 3].

Segue das condições do problema que é suficiente considerar apenas a parte do grafo limitada pelo segmento [−4; 3]. Portanto, construímos um novo grafo, no qual marcamos apenas os limites [−4; 3] e os zeros da derivada dentro dela. Ou seja, os pontos x = −3,5 e x = 2. Obtemos:

Nesse gráfico, há apenas um ponto de máximo x = 2. É nele que o sinal da derivada muda de mais para menos.

Uma pequena nota sobre pontos com coordenadas não inteiras. Por exemplo, no último problema, o ponto x = −3,5 foi considerado, mas com o mesmo sucesso podemos tomar x = −3,4. Se o problema for formulado corretamente, tais mudanças não devem afetar a resposta, pois os pontos "sem residência fixa" não estão diretamente envolvidos na solução do problema. É claro que, com pontos inteiros, esse truque não funcionará.

Encontrar intervalos de aumento e diminuição de uma função

Em tal problema, como os pontos de máximo e mínimo, propõe-se encontrar áreas nas quais a própria função aumenta ou diminui a partir do gráfico da derivada. Primeiro, vamos definir o que são ascendentes e descendentes:

Uma função f(x) é chamada crescente em um segmento se para quaisquer dois pontos x 1 e x 2 deste segmento a afirmação for verdadeira: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Em outras palavras, quanto maior o valor do argumento, maior o valor da função.
Uma função f(x) é chamada decrescente em um segmento se para quaisquer dois pontos x 1 e x 2 deste segmento a afirmação for verdadeira: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Aqueles. maior valor argumento corresponde ao menor valor da função.

Formulamos condições suficientes para aumentar e diminuir:

Para que uma função contínua f(x) cresça no segmento , é suficiente que sua derivada dentro do segmento seja positiva, ou seja. f'(x) ≥ 0.
Para uma função contínua f(x) diminuir no segmento , é suficiente que sua derivada dentro do segmento seja negativa, ou seja. f'(x) ≤ 0.

Aceitamos essas afirmações sem provas. Assim, obtemos um esquema para encontrar intervalos de aumento e diminuição, que é em muitos aspectos semelhante ao algoritmo para calcular pontos extremos:

Remova todas as informações redundantes. No gráfico original da derivada, estamos principalmente interessados nos zeros da função, então deixamos apenas eles.
Marque os sinais da derivada nos intervalos entre zeros. Onde f'(x) ≥ 0, a função aumenta, e onde f'(x) ≤ 0, ela diminui. Se o problema tiver restrições na variável x, também as marcamos no novo gráfico.
Agora que conhecemos o comportamento da função e a restrição, resta calcular o valor requerido no problema.

Uma tarefa. A figura mostra um gráfico da derivada da função f(x) definida no intervalo [−3; 7.5]. Encontre os intervalos da função decrescente f(x). Em sua resposta, escreva a soma dos inteiros incluídos nesses intervalos.

Como de costume, redesenhamos o gráfico e marcamos os limites [−3; 7.5], bem como os zeros da derivada x = −1,5 ex = 5,3. Em seguida, marcamos os sinais da derivada. Nós temos:

Como a derivada é negativa no intervalo (− 1,5), este é o intervalo da função decrescente. Resta somar todos os inteiros que estão dentro desse intervalo:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Uma tarefa. A figura mostra um gráfico da derivada da função f(x) definida no segmento [−10; quatro]. Encontre os intervalos da função crescente f(x). Em sua resposta, escreva o comprimento do maior deles.

Vamos nos livrar de informações redundantes. Deixamos apenas os limites [−10; 4] e zeros da derivada, que desta vez resultou em quatro: x = −8, x = −6, x = −3 e x = 2. Observe os sinais da derivada e obtenha a seguinte figura:

Estamos interessados nos intervalos de função crescente, ou seja, onde f'(x) ≥ 0. Existem dois desses intervalos no gráfico: (−8; −6) e (−3; 2). Vamos calcular seus comprimentos:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Como é necessário encontrar o comprimento do maior dos intervalos, escrevemos o valor l 2 = 5 em resposta.

Derivada de uma função de uma variável.

Introdução.

Real desenvolvimentos metodológicos destinado aos alunos da Faculdade de Engenharia Industrial e Civil. Eles são compilados em relação ao programa do curso de matemática na seção "Cálculo diferencial de funções de uma variável".

Os desenvolvimentos representam um único guia metodológico, que inclui: breves informações teóricas; tarefas e exercícios "típicos" com soluções detalhadas e explicações para essas soluções; opções de controle.

Exercícios adicionais no final de cada parágrafo. Essa estrutura de desenvolvimentos os torna adequados para o domínio independente da seção com o mínimo de assistência do professor.

§1. Definição de um derivado.

Significado mecânico e geométrico

derivado.

O conceito de derivada é um dos conceitos mais importantes da análise matemática, surgindo já no século XVII. A formação do conceito de derivada está historicamente associada a dois problemas: o problema da velocidade do movimento variável e o problema da tangente a uma curva.

Essas tarefas, apesar de seu conteúdo diferente, levam à mesma operação matemática que deve ser realizada em uma função, operação que recebeu um nome especial em matemática. É chamada de operação de diferenciação de uma função. O resultado de uma operação de diferenciação é chamado de derivada.

Então, a derivada da função y=f(x) no ponto x0 é o limite (se existir) da razão entre o incremento da função e o incremento do argumento
no
.

A derivada é geralmente denotada da seguinte forma:
.

Então por definição

Os símbolos também são usados para denotar a derivada
.

O significado mecânico da derivada.

Se s=s(t) é a lei do movimento retilíneo de um ponto material, então
é a velocidade desse ponto no instante t.

O significado geométrico da derivada.

Se a função y=f(x) tem uma derivada em um ponto , então a inclinação da tangente ao gráfico da função no ponto
é igual a
.

Exemplo.

Encontre a derivada de uma função
no ponto =2:

1) Vamos dar um ponto =2 incremento
. Notar que.

2) Encontre o incremento da função no ponto =2:

3) Componha a razão do incremento da função para o incremento do argumento:

Vamos encontrar o limite da relação em
:

Nesse caminho,
.

§ 2. Derivados de alguns

as funções mais simples.

O aluno precisa aprender a calcular as derivadas de funções específicas: y=x,y= e em geral y= .

Encontre a derivada da função y=x.

Essa. (x)′=1.

Vamos encontrar a derivada da função

Derivado

Deixar
então

É fácil notar um padrão nas expressões para derivadas de uma função potência
em n=1,2,3.

Consequentemente,

. (1)

Esta fórmula é válida para qualquer n real.

Em particular, usando a fórmula (1), temos:

;

Exemplo.

Encontre a derivada de uma função

Esta função é um caso especial de uma função da forma

no
.

Usando a fórmula (1), temos

Derivadas de funções y=sen x e y=cos x.

Seja y=senx.

Dividindo por ∆x, temos

Passando ao limite como ∆x→0, temos

Seja y=cosx.

Passando ao limite como ∆x→0, obtemos

;
. (2)

§3. Regras básicas de diferenciação.

Considere as regras de diferenciação.

Teorema1 . Se as funções u=u(x) e v=v(x) são diferenciáveis em um dado ponto x, então sua soma também é diferenciável neste ponto, e a derivada da soma é igual à soma dos termos derivados: (u+v)"=u"+v".(3)

Demonstração: considere a função y=f(x)=u(x)+v(x).

O incremento ∆x do argumento x corresponde aos incrementos ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) das funções u e v. Então a função y será incrementada

∆y=f(x+∆x)-f(x)=

=--=∆u+∆v.

Consequentemente,

Então, (u+v)"=u"+v".

Teorema2. Se as funções u=u(x) ev=v(x) são deriváveis em um dado ponto x, então seu produto também é derivável no mesmo ponto. Neste caso, a derivada do produto é encontrada pela seguinte fórmula : (uv) "=u" v + uv ". (quatro)

Prova: Seja y=uv, onde uev são algumas funções diferenciáveis de x. Seja x incrementado em ∆x, então u será incrementado em ∆u, v será incrementado em ∆v, e y será incrementado em ∆y.

Temos y+∆y=(u+∆u)(v+∆v), ou

y+∆y=uv+u∆v+v∆u+∆u∆v.

Portanto, ∆y=u∆v+v∆u+∆u∆v.

Daqui

Passando ao limite como ∆x→0 e levando em conta que u e v não dependem de ∆x, temos

Teorema 3. A derivada de um quociente de duas funções é igual a uma fração, cujo denominador é igual ao quadrado do divisor, e o numerador é a diferença entre o produto da derivada do dividendo pelo divisor e o produto do dividendo pela derivada do divisor, ou seja,

Se um
então
(5)