É um gráfico da função y kx b. Função linear

Instrução

Se o gráfico é uma linha reta passando pela origem e formando um ângulo α com o eixo OX (o ângulo de inclinação da linha reta para o semieixo OX positivo). A função que descreve esta linha será semelhante a y = kx. O fator de proporcionalidade k é igual a tg α. Se a linha passa pelos 2º e 4º quartos de coordenadas, então k< 0, и является убывающей, если через 1-ю и 3-ю, то k >0 e a função é crescente. Seja uma linha reta localizada de varias maneiras em relação aos eixos coordenados. Esta é uma função linear, e tem a forma y = kx + b, onde as variáveis ​​x e y estão na primeira potência, e k e b podem assumir valores positivos e negativos ou iguais a zero. A linha é paralela à linha y = kx e corta no eixo |b| unidades. Se a linha reta é paralela ao eixo das abcissas, então k = 0, se o eixo das ordenadas, então a equação tem a forma x = const.

Uma curva composta por dois ramos localizados em quadrantes diferentes e simétricos em relação à origem, uma hipérbole. Este gráfico relação inversa variável y de x e é descrita pela equação y = k/x. Aqui k ≠ 0 é o coeficiente de proporcionalidade. Além disso, se k > 0, a função diminui; se k< 0 - функция возрастает. Таким образом, областью определения функции является вся числовая прямая, кроме x = 0. Ветви приближаются к осям координат как к своим асимптотам. С уменьшением |k| ветки гиперболы все больше «вдавливаются» в ângulos coordenados.

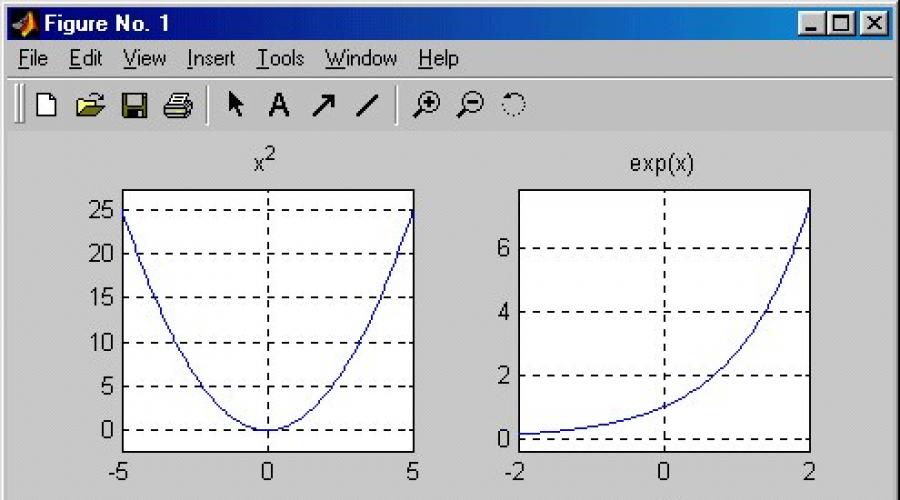
Uma função quadrática tem a forma y = ax2 + bx + c, onde a, b e c são constantes e a  0. Quando a condição b = c = 0 é atendida, a equação da função se parece com y = ax2 (o caso mais simples), e seu gráfico é uma parábola que passa pela origem. O gráfico da função y = ax2 + bx + c tem a mesma forma do caso mais simples da função, mas seu vértice (o ponto de interseção com o eixo OY) não está na origem.

Uma parábola também é o gráfico de uma função potência expressa pela equação y = xⁿ se n for qualquer número par. Se n é qualquer número ímpar, o gráfico de tal função de potência se parecerá com uma parábola cúbica.
Se n for qualquer , a equação da função assume a forma. O gráfico da função para n ímpar será uma hipérbole, e para n pares seus ramos serão simétricos em relação ao eixo do op-y.

Mesmo nos anos escolares, as funções são estudadas em detalhes e seus gráficos são construídos. Mas, infelizmente, eles praticamente não ensinam a ler o gráfico de uma função e encontrar seu tipo de acordo com o desenho apresentado. Na verdade, é bem simples se você se lembrar dos tipos básicos de funções.

Instrução

Se o gráfico apresentado for , que passa pela origem e com o eixo OX o ângulo α (que é o ângulo de inclinação da reta ao semieixo positivo), então a função que descreve tal reta será representada como y = kx. Neste caso, o coeficiente de proporcionalidade k igual a tangenteângulo α.

Se a linha dada passa pelo segundo e quarto quartos das coordenadas, então k é 0 e a função é crescente. Seja o gráfico apresentado uma linha reta localizada de qualquer maneira em relação aos eixos coordenados. Então a função de tal Artes gráficas será linear, que é representado pela forma y = kx + b, onde as variáveis ​​y e x estão no primeiro , e b e k podem assumir valores negativos e positivos ou .

Se a linha é paralela à linha com o gráfico y = kx e corta b unidades no eixo y, então a equação tem a forma x = const, se o gráfico é paralelo ao eixo x, então k = 0 .

Uma linha curva, que consiste em dois ramos, simétricos em relação à origem e localizados em diferentes quadrantes, uma hipérbole. Tal gráfico mostra a dependência inversa da variável y da variável x e é descrito por uma equação da forma y = k/x, onde k não deve ser igual a zero, pois é um coeficiente proporcionalidade inversa. Nesse caso, se o valor de k for maior que zero, a função diminui; se k for menor que zero, ela aumenta.

Se o gráfico proposto for uma parábola passando pela origem, sua função, se a condição de que b = c = 0 for atendida, será semelhante a y = ax2. Este é o caso mais simples função quadrática. O gráfico de uma função da forma y = ax2 + bx + c terá a mesma forma do caso mais simples, porém, o vértice (o ponto onde o gráfico intercepta o eixo y) não estará na origem. Em uma função quadrática representada pela forma y = ax2 + bx + c, os valores de a, b e c são constantes, enquanto a não é igual a zero.

Uma parábola também pode ser um gráfico de uma função de potência expressa por uma equação da forma y = xⁿ, somente se n for qualquer número par. Se o valor de n for um número ímpar, tal gráfico de uma função de potência será representado por uma parábola cúbica. Se a variável n for qualquer número negativo, a equação da função assume a forma .

Vídeos relacionados

A coordenada de absolutamente qualquer ponto no plano é determinada por seus dois valores: ao longo do eixo das abcissas e do eixo das ordenadas. O conjunto de muitos desses pontos é o gráfico da função. De acordo com ele, você pode ver como o valor de Y muda dependendo da mudança no valor de X. Você também pode determinar em qual seção (intervalo) a função aumenta e em qual ela diminui.

Instrução

O que pode ser dito sobre uma função se seu gráfico é uma linha reta? Veja se esta linha passa pela origem das coordenadas (ou seja, aquela onde os valores de X e Y são 0). Se passar, então tal função é descrita pela equação y = kx. É fácil entender que quanto maior o valor de k, mais próxima esta linha estará do eixo y. E o próprio eixo Y corresponde a infinitamente grande importância k.

Neste artigo, veremos Função linear, o gráfico de uma função linear e suas propriedades. E, como de costume, resolveremos vários problemas sobre esse tópico.

Função linearé chamada de função da forma

Na equação da função, o número pelo qual multiplicamos é chamado de fator de inclinação.

Por exemplo, na equação da função ;

na equação da função;

na equação da função;

na equação da função.

O gráfico de uma função linear é uma linha reta.

1 . Para plotar uma função, precisamos das coordenadas de dois pontos pertencentes ao gráfico da função. Para encontrá-los, você precisa pegar dois valores de x, substituí-los na equação da função e calcular os valores de y correspondentes a partir deles.

Por exemplo, para plotar a função , é conveniente tomar e , então as ordenadas desses pontos serão iguais a e .

Obtemos os pontos A(0;2) e B(3;3). Vamos conectá-los e obter o gráfico da função:

2 . Na equação da função, o coeficiente é responsável pela inclinação do gráfico da função:

Title="(!LANG:k>0">!}

O coeficiente é responsável por deslocar o gráfico ao longo do eixo:

Title="(!LANG:b>0">!}

A figura abaixo mostra os gráficos das funções; ;

Observe que em todas essas funções o coeficiente Acima de zero direita. Além disso, do que mais valor, mais íngreme a linha reta vai.

Em todas as funções - e vemos que todos os gráficos interceptam o eixo OY no ponto (0;3)

Agora considere os gráficos das funções; ;

Desta vez em todas as funções o coeficiente menos que zero, e todos os gráficos de função são assimétricos Para a esquerda.

Observe que quanto maior |k|, mais inclinada será a linha. O coeficiente b é o mesmo, b=3, e os gráficos, como no caso anterior, cruzam o eixo OY no ponto (0;3)

Considere os gráficos de funções; ;

Agora em todas as equações de funções os coeficientes são iguais. E nós temos três linhas paralelas.

Mas os coeficientes b são diferentes, e esses gráficos cruzam o eixo OY em pontos diferentes:

O gráfico da função (b=3) cruza o eixo OY no ponto (0;3)

O gráfico da função (b=0) cruza o eixo OY no ponto (0;0) - a origem.

O gráfico da função (b=-2) cruza o eixo OY no ponto (0;-2)

Então, se conhecemos os sinais dos coeficientes k e b, podemos imaginar imediatamente como é o gráfico da função.

Se um k<0 и b>0 , então o gráfico da função fica assim:

Se um k>0 eb>0, então o gráfico da função fica assim:

Se um k>0 e b<0 , então o gráfico da função fica assim:

Se um k<0 и b<0 , então o gráfico da função fica assim:

Se um k=0 , então a função se transforma em uma função e seu gráfico se parece com:

As ordenadas de todos os pontos do gráfico da função são iguais

Se um b=0, então o gráfico da função passa pela origem:

Isso é gráfico de proporcionalidade direta.

3 . Separadamente, observo o gráfico da equação. O gráfico desta equação é uma linha reta paralela ao eixo, todos os pontos dos quais têm uma abcissa.

Por exemplo, o gráfico de equação se parece com isso:

Atenção! A equação não é uma função, pois valores diferentes do argumento correspondem ao mesmo valor da função, que não corresponde a .

4 . Condição para paralelismo de duas linhas:

Gráfico de funções paralelo ao gráfico da função, E se

5. A condição de perpendicularidade de duas linhas:

Gráfico de funções perpendicular ao gráfico da função se ou

6. Pontos de intersecção do gráfico da função com os eixos coordenados.

com eixo OY. A abcissa de qualquer ponto pertencente ao eixo OY é igual a zero. Portanto, para encontrar o ponto de interseção com o eixo OY, você precisa substituir zero em vez de x na equação da função. Obtemos y=b. Ou seja, o ponto de intersecção com o eixo OY tem coordenadas (0;b).

Com eixo OX: A ordenada de qualquer ponto pertencente ao eixo OX é zero. Portanto, para encontrar o ponto de interseção com o eixo OX, você precisa substituir zero em vez de y na equação da função. Obtemos 0=kx+b. Daqui. Ou seja, o ponto de intersecção com o eixo OX possui coordenadas (; 0):

Considere a resolução de problemas.

1 . Construa um gráfico da função se souber que ela passa pelo ponto A (-3; 2) e é paralela à linha y \u003d -4x.

Existem dois parâmetros desconhecidos na equação da função: ke b. Portanto, no texto do problema deve haver duas condições que caracterizam o gráfico da função.

a) Do fato de o gráfico da função ser paralelo à reta y=-4x, segue-se que k=-4. Ou seja, a equação da função tem a forma

b) Resta-nos encontrar b. Sabe-se que o gráfico da função passa pelo ponto A (-3; 2). Se um ponto pertence ao gráfico de uma função, ao substituir suas coordenadas na equação da função, obtemos a igualdade correta:

portanto b = -10

Assim, precisamos traçar a função

O ponto A(-3;2) é conhecido por nós, pegue o ponto B(0;-10)

Vamos colocar esses pontos no plano de coordenadas e conectá-los com uma linha reta:

2. Escreva a equação de uma reta que passa pelos pontos A(1;1); B(2;4).

Se a linha passa por pontos com coordenadas dadas, então as coordenadas dos pontos satisfazem a equação da linha. Ou seja, se substituirmos as coordenadas dos pontos na equação de uma reta, obteremos a igualdade correta.

Substitua as coordenadas de cada ponto na equação e obtenha o sistema equações lineares.

Subtraímos a primeira equação da segunda equação do sistema e obtemos . Substitua o valor de k na primeira equação do sistema e obtenha b=-2.

Então, a equação de uma linha reta.

3 . Equação do gráfico

Para descobrir em quais valores da incógnita o produto de vários fatores é igual a zero, você precisa igualar cada fator a zero e levar em consideração cada multiplicador.

Esta equação não tem restrições em ODZ. Vamos fatorar o segundo colchete e igualar cada fator a zero. Obtemos um conjunto de equações:

Construímos gráficos de todas as equações do conjunto em um plano coordenado. Este é o gráfico da equação :

4 . Construa um gráfico da função se ela for perpendicular à reta e passar pelo ponto M (-1; 2)

Não vamos construir um gráfico, vamos apenas encontrar a equação de uma reta.

a) Desde o gráfico da função, se é perpendicular à reta, portanto, daqui. Ou seja, a equação da função tem a forma

b) Sabemos que o gráfico da função passa pelo ponto M (-1; 2). Substitua suas coordenadas na equação da função. Nós temos:

Daqui.

Portanto, nossa função se parece com: .

5 . Plote a função

Vamos simplificar a expressão do lado direito da equação da função.

Importante! Antes de simplificar a expressão, vamos encontrar sua ODZ.

O denominador de uma fração não pode ser zero, então title="(!LANG:x1">, title="x-1">.!}

Então nossa função se torna:

Title="(!LANG:delim(lbrace)(matrix(3)(1)((y=x+2) (x1) (x-1)))( )">!}

Ou seja, precisamos construir um gráfico de função e destacar dois pontos nele: com abcissas x=1 e x=-1:

"Pontos críticos da função" - Pontos críticos. Entre os pontos críticos estão os pontos extremos. Condição necessaria extremo. Resposta: 2. Definição. Mas, se f "(x0) = 0, então não é necessário que o ponto x0 seja um ponto extremo. Pontos extremos (repetição). Pontos críticos da função. Pontos extremos.

"Plano coordenado 6º ano" - Matemática 6º ano. 1. X. 1. Encontre e anote as coordenadas pontos A, B, C, D: -6. Plano coordenado. O.-3. 7. W.

"Funções e seus gráficos" - Continuidade. O maior e menor valor funções. conceito função inversa. Linear. Logarítmico. Monótono. Se k > 0, então o ângulo formado é agudo, se k< 0, то угол тупой. В самой точке x = a функция может существовать, а может и не существовать. Х1, х2, х3 – нули функции у = f(x).

"Funções Grau 9" - Operações aritméticas permitidas em funções. [+] - adição, [-] - subtração, [*] - multiplicação, [:] - divisão. Nesses casos, fala-se tarefa gráfica funções. Educação de classe funções elementares. Função liga-desliga y=x0,5. Iovlev Maxim Nikolaevich, aluno do 9º ano da escola RIOU Raduhskaya.

"Equação da Tangente da Lição" - 1. Esclarecer o conceito de tangente a um gráfico de função. Leibniz considerou o problema de traçar uma tangente a uma curva arbitrária. ALGORITMO PARA COMPOSIÇÃO DA EQUAÇÃO DA FUNÇÃO tangente ao GRÁFICO y=f(x). Tópico da lição: Teste: encontre a derivada de uma função. Equação tangente. Fluxão. Grau 10. Decifre como Isaac Newton chamou a derivada de uma função.

"Construir um gráfico da função" - A função y=3cosx é fornecida. Gráfico da função y=m*sen x. Trace o gráfico da função. Conteúdo: Dada uma função: y=sen (x+?/2). Esticando o gráfico y=cosx ao longo do eixo y. Para continuar pressione L. Botão do mouse. A função y=cosx+1 é dada. Deslocamentos do gráfico y=sinx verticalmente. A função y=3sinx é dada. Deslocamento do gráfico y=cosx horizontalmente.

São 25 apresentações no total sobre o tema

Instrução

Existem várias maneiras de resolver funções lineares. Vamos dar uma olhada na maioria deles. Mais comumente usado método passo a passo substituições. Em uma das equações, é necessário expressar uma variável em função de outra e substituí-la em outra equação. E assim sucessivamente até que apenas uma variável permaneça em uma das equações. Para resolvê-lo, você precisa deixar a variável de um lado do sinal de igual (pode ser com um coeficiente), e do outro lado do sinal de igual todos os dados numéricos, não esquecendo de alterar o sinal do número para o oposto ao transferir. Tendo calculado uma variável, substitua-a em outras expressões, continue os cálculos de acordo com o mesmo algoritmo.

Por exemplo, tome um sistema linear funções, que consiste em duas equações:
2x+y-7=0;
x-y-2=0.
A partir da segunda equação é conveniente expressar x:
x=y+2.
Como você pode ver, ao transferir de uma parte da igualdade para outra, o sinal de e as variáveis ​​mudaram, conforme descrito acima.
Substituímos a expressão resultante na primeira equação, excluindo assim a variável x dela:
2*(y+2)+y-7=0.
Expandindo os colchetes:
2a+4+a-7=0.
Compomos variáveis ​​e números, adicionamos:
3a-3=0.
Transferimos para o lado direito da equação, mudamos o sinal:
3a=3.
Dividido por proporção geral, Nós temos:
y=1.
Substitua o valor resultante na primeira expressão:
x=y+2.
Obtemos x = 3.

Outra maneira de resolver semelhantes é usar duas equações termo a termo para obter uma nova com uma variável. A equação pode ser multiplicada por um certo coeficiente, o principal é multiplicar cada termo da equação e não esquecer e depois adicionar ou subtrair uma equação. Este método economiza muito ao encontrar um linear funções.

Vamos pegar o já familiar sistema de equações com duas variáveis:
2x+y-7=0;
x-y-2=0.
É fácil ver que o coeficiente da variável y é idêntico na primeira e na segunda equações e difere apenas no sinal. Isso significa que ao somarmos essas duas equações termo a termo, obtemos uma nova, mas com uma variável.
2x+x+y-y-7-2=0;
3x-9=0.
Transferimos os dados numéricos para o lado direito da equação, enquanto alteramos o sinal:
3x=9.
Encontrando o fator comum igual ao coeficiente estando em x e divida ambos os lados da equação por ele:
x=3.
O resultado pode ser substituído em qualquer uma das equações do sistema para calcular y:
x-y-2=0;
3-y-2=0;
-y+1=0;
-y=-1;
y=1.

Você também pode calcular dados traçando um gráfico preciso. Para fazer isso, você precisa encontrar os zeros funções. Se uma das variáveis ​​for igual a zero, essa função é chamada de homogênea. Ao resolver essas equações, você obterá dois pontos necessários e suficientes para construir uma linha reta - um deles estará localizado no eixo x, o outro no eixo y.

Pegamos qualquer equação do sistema e substituímos o valor x \u003d 0 lá:
2*0+y-7=0;
Obtemos y = 7. Assim, o primeiro ponto, vamos chamá-lo de A, terá as coordenadas A (0; 7).
Para calcular um ponto no eixo x, é conveniente substituir o valor y \u003d 0 na segunda equação do sistema:
x-0-2=0;
x=2.
O segundo ponto (B) terá as coordenadas B (2;0).
Marcamos os pontos obtidos na grade de coordenadas e traçamos uma linha reta através deles. Se você construí-lo com bastante precisão, outros valores x e y podem ser calculados diretamente a partir dele.