Método de coordenadas para encontrar o ângulo entre as linhas. Método de coordenadas no espaço: fórmulas e comentários do tutor

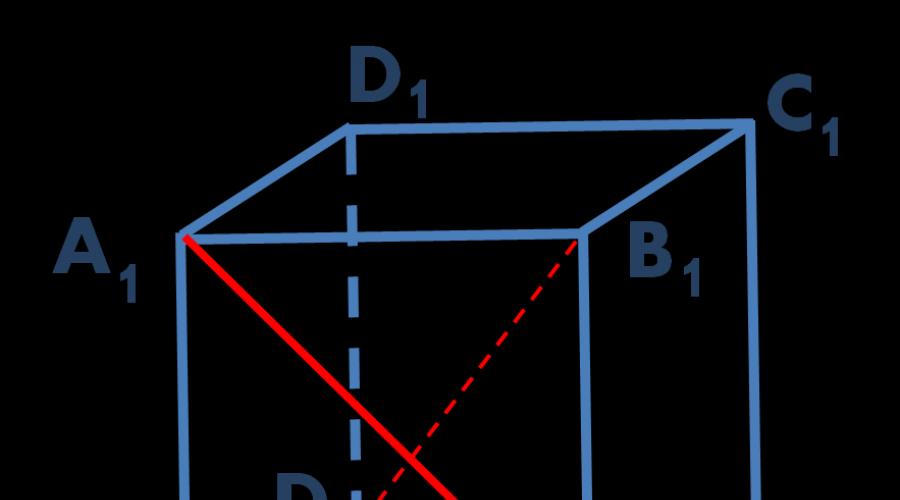
Neste artigo, usando o exemplo de resolução do problema C2 do Unified State Examination, é analisado o método de encontrar coordenadas usando o método. Lembre-se de que as linhas são enviesadas se não estiverem no mesmo plano. Em particular, se uma linha estiver em um plano e a segunda linha cruzar esse plano em um ponto que não está na primeira linha, essas linhas são enviesadas (veja a figura).

Para encontrar distâncias entre linhas que se cruzam necessário:

1. Desenhe um plano através de uma das linhas de inclinação que é paralela à outra linha de inclinação.
2. Solte uma perpendicular de qualquer ponto da segunda linha reta até o plano resultante. O comprimento desta perpendicular será a distância desejada entre as linhas.

Vamos analisar esse algoritmo com mais detalhes usando o exemplo de resolução do problema C2 do Exame de Estado Unificado em matemática.

Distância entre linhas no espaço

Uma tarefa. em um único cubo ABCDA 1 B 1 C 1 D 1 encontrar a distância entre as linhas BA 1 e D.B. 1 .

Arroz. 1. Desenho para a tarefa

Solução. Pelo ponto médio da diagonal do cubo D.B. 1 (ponto O) traçar uma linha paralela à linha UMA 1 B. Pontos de intersecção de uma determinada linha com arestas BC e UMA 1 D 1 denotam respectivamente N e M. Em linha reta MN fica no avião MNB 1 e paralela à linha UMA 1 B, que não está neste plano. Isso significa que o direto UMA 1 B paralelo ao plano MNB 1 com base no paralelismo de uma linha reta e um plano (Fig. 2).

Arroz. 2. A distância desejada entre as linhas de cruzamento é igual à distância de qualquer ponto da linha selecionada até o plano representado

Agora estamos procurando a distância de algum ponto na linha reta UMA 1 B até o avião MNB 1 . Essa distância, por definição, será a distância desejada entre as linhas inclinadas.

Para encontrar essa distância, usamos o método das coordenadas. Introduzimos um sistema de coordenadas cartesianas retangular para que sua origem coincida com o ponto B, o eixo X foi direcionado ao longo da borda BA, eixo S- ao longo da costela BC, eixo Z- ao longo da costela BB 1 (Fig. 3).

Arroz. 3. Escolhemos um sistema de coordenadas cartesianas retangular como mostrado na figura

Encontramos a equação do plano MNB 1 neste sistema de coordenadas. Para fazer isso, primeiro determinamos as coordenadas dos pontos M, N e B 1: Substituímos as coordenadas obtidas na equação geral de uma linha reta e obtemos o seguinte sistema de equações:

Da segunda equação do sistema, obtemos da terceira, e depois da primeira obtemos. Substituímos os valores obtidos na equação geral da reta:

Observe que, caso contrário, o plano MNB 1 passaria pela origem. Dividimos ambos os lados desta equação por e obtemos:

A distância de um ponto a um plano é determinada pela fórmula.

Usando o método de coordenadas ao calcular um ângulo

entre aviões

A maioria método geral encontrar um ânguloentre planos - o método de coordenadas (às vezes - com o envolvimento de vetores). Ele pode ser usado quando todos os outros foram tentados. Mas há situações em que faz sentido aplicar o método de coordenadas imediatamente, ou seja, quando o sistema de coordenadas está naturalmente relacionado ao poliedro especificado no enunciado do problema, ou seja, três linhas perpendiculares aos pares são claramente visíveis, nas quais os eixos de coordenadas podem ser definidos. Tais poliedros são cubóide e uma pirâmide quadrangular regular. No primeiro caso, o sistema de coordenadas pode ser definido pelas arestas que emergem de um vértice (Fig. 1), no segundo - pela altura e diagonais da base (Fig. 2)

A aplicação do método de coordenadas é a seguinte.

Um sistema de coordenadas retangulares é introduzido no espaço. É desejável apresentá-lo de maneira "natural" - "anexá-lo" a um triplo de linhas perpendiculares aos pares que têm um ponto comum.

Para cada um dos planos, cujo ângulo entre os quais se busca, elabora-se uma equação. A maneira mais fácil de escrever tal equação é conhecer as coordenadas de três pontos no plano que não estão em uma linha reta.

Equação do plano em visão geral tem a forma Ax + By + Cz + D = 0.

Coeficientes A, B, C nesta equação são as coordenadas do vetor normal do plano (o vetor perpendicular ao plano). Em seguida, determinamos os comprimentos e o produto escalar de vetores normais aos planos, cujo ângulo entre os quais se busca. Se as coordenadas desses vetores(A 1, B 1; C 1) e (A 2; B 2; C 2 ), então o ângulo desejadocalculado pela fórmula

Comente. Deve-se lembrar que o ângulo entre vetores (em oposição ao ângulo entre planos) pode ser obtuso e, para evitar possíveis incertezas, o módulo está no numerador do lado direito da fórmula.

Resolva o seguinte problema usando o método de coordenadas.

Problema 1. Um cubo ABCDA 1 B 1 C 1 D 1 é dado. O ponto K é o ponto médio da aresta AD, o ponto L é o ponto médio da aresta CD. Qual é o ângulo entre os planos A 1 KL e A 1 AD?

Solução . Seja a origem do sistema de coordenadas no ponto MAS, e os eixos coordenados vão ao longo dos raios AD, AB, AA 1 (Fig. 3). Tomamos a aresta do cubo igual a 2 (é conveniente dividir ao meio). Então as coordenadas dos pontos A 1 , K, L são: A 1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).

Arroz. 3

Escrevemos a equação do plano A 1 KL no geral. Em seguida, substituímos as coordenadas dos pontos selecionados deste plano nele. Obtemos um sistema de três equações com quatro incógnitas:

Expressamos os coeficientes A, B, C a D e vamos à equação

Dividindo ambas as partes em D (por que D = 0?) e multiplicando por -2, obtemos a equação do plano A 1 KL: 2x - 2 y + z - 2 = 0. Então o vetor normal a este plano tem coordenadas (2: -2; 1) . Equação do plano A 1 AD é: y=0, e as coordenadas do vetor normal a ele, por exemplo, (0; 2: 0) . De acordo com a fórmula acima para o cosseno do ângulo entre os planos, temos:

Na tarefa C2 em matemática, na maioria das vezes você precisa resolver um problema no qual precisa determinar:

1. Distância entre dois pontos
2. Distância do ponto à linha
3. Distância do ponto ao plano
4. Distância entre linhas de interseção
5. Ângulo entre duas linhas
6. Ângulo entre a linha e o plano
7. Ângulo entre planos

As tarefas são elementares, se você seguir o algoritmo para resolver C2 e se lembrar das principais propriedades trigonométricas, como as propriedades das diagonais ou a área da superfície de um poliedro. As tarefas de suporte ajudarão você a lembrar dessas propriedades básicas.

Agora vamos para os algoritmos.

1. Para determinar a distância entre dois pontos A e B, usamos um dos dois métodos:

• Incluímos AB em algum triângulo e encontramos seu comprimento como o lado do triângulo
• De acordo com a fórmula

Além disso, o método das coordenadas, na minha opinião, é o mais simples, só é necessário determinar com precisão as coordenadas de cada ponto.

2. Para determinar a distância de um ponto a uma linha, calcule

• como o comprimento de um segmento perpendicular, se for possível incluir este segmento em algum triângulo como uma das alturas

usando o método de coordenadas usando fórmulas para calcular a área, em que a distância necessária será a altura e

3. A distância de um ponto a um plano é

• o comprimento da perpendicular caiu deste ponto para o plano. Para fazer isso, construa cuidadosamente uma seção perpendicular ao plano e passe por dado ponto. A distância desejada será igual à altura do novo poliedro resultante.
• Usando o método de coordenadas

A equação é encontrada substituindo as coordenadas de três pontos pertencentes a este plano

• Usando o método vetorial

Para fazer isso, você precisa se lembrar das regras para adicionar e subtrair vetores, que o produto de vetores perpendiculares é igual a zero.

• Usando o método do volume, se houver uma pirâmide ABCM, a distância do ponto M ao plano que contém o triângulo ABC é calculada pela fórmula

• Pelo método de problemas de referência, que pode ser visto

4. A distância entre as linhas de cruzamento pode ser resolvida usando

4.1. Método computacional passo a passo:

• construa uma perpendicular comum de duas linhas que se cruzam e encontre seu comprimento;
• construir um plano contendo uma das linhas e paralela à outra. Então a distância desejada será igual à distância do ponto à reta construída no plano;
• coloque as linhas dadas em planos paralelos passando pelas linhas de interseção dadas, encontre a distância entre esses planos
• construir um plano perpendicular a uma dessas linhas e construir uma projeção ortogonal da segunda linha

4.2. Método de coordenadas vetoriais

• Encontre as coordenadas das extremidades de um segmento que é uma perpendicular comum de duas linhas que se cruzam
• Encontrar a distância entre dois pontos

4.3. método vetorial
Reduzimos o problema a determinar o comprimento de um vetor pertencente a uma perpendicular que é uma perpendicular comum de duas linhas que se cruzam

6. Ângulo entre a linha e o plano determinado ao incluí-lo em triângulo retângulo como um dos cantos afiados, ou pelo método do coordenador vetorial

Como o ângulo entre os planos é determinado será considerado na próxima lição. Esses algoritmos para resolver C2 contribuem para uma compreensão abrangente do método para resolver o problema. "Para ajudar a revista estudantil para os alunos e seus pais." Leia mais: http://education-club.ru/#ixzz2IXf5GOJU

7. Ângulo entre planos(método geométrico)

• 1. Encontre a linha ao longo da qual os planos se cruzam.
• 2. Escolha um ponto nesta linha e desenhe duas perpendiculares a ele, situadas nesses planos. Ou desenhe um plano perpendicular à linha de interseção dos planos.
• 3. Encontre a função trigonométrica do ângulo formado pelas perpendiculares à linha de intersecção dos planos. Como regra, fazemos isso através de um triângulo, que inclui o ângulo desejado.
• 4. Na resposta, anote o valor do ângulo, ou função trigonométricaângulo.

Ângulo entre planos. método coordenado. Tarefa C2

Dois planos que se cruzam formam dois pares de ângulos diedros iguais:

O valor do ângulo diedro é medido pelo valor do ângulo linear correspondente.

Para construir um ângulo linear de um ângulo diedro, você precisa pegar um ponto arbitrário na linha de interseção dos planos e, em cada plano, desenhar um raio para esse ponto perpendicular à linha de interseção dos planos. O ângulo formado por esses raios é o ângulo linear do ângulo diedro:

O valor do ângulo entre os planos é o valor do ângulo diedro inferior a um ano.

Sejam nossos planos e dados pelas equações:

O cosseno do ângulo entre os planos é encontrado pela seguinte fórmula:

Na resposta, escrevemos , pois o valor do ângulo entre os planos é o valor do menor ângulo diedro.

Na direita prisma quadrangular com um lado da base de 12 e uma altura de 21, um ponto M é tomado na borda de modo que . Ponto K é tomado na borda de modo que . Encontre o ângulo entre o plano e o plano.

Vamos fazer um desenho. Como vamos usar o método de coordenadas, vamos introduzir imediatamente o sistema de coordenadas: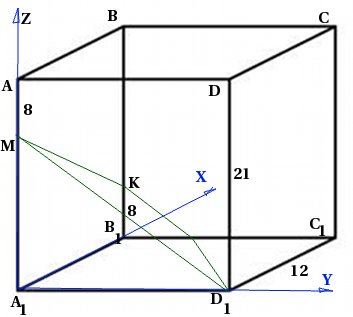

Agora estamos diante da tarefa de escrever as equações do plano e do plano.

Descrevi um algoritmo detalhado para encontrar a equação de um plano usando três pontos.

Depois de encontrarmos os coeficientes no plano e nas equações do plano, nós os substituímos na fórmula para encontrar o cosseno do ângulo entre os planos e encontrar o ângulo.

Sugiro que você assista a uma solução detalhada em vídeo para esse problema:

Outra tarefa de Inna Vladimirovna Feldman

Aulas em vídeo "Método de coordenação para resolução de problemas c-2"

Lição 2 http://youtu.be/dKQWG8OZRGo
lição 3 http://youtu.be/ddgr0PnbFno
lição 4 http://youtu.be/n6yx2pQC0Lo
lição 5 http://youtu.be/JkWbxAw1YLI
lição 6 http://youtu.be/gybIqCMKBiI
lição 7 http://youtu.be/_LpARpYxp5g
lição 8 http://youtu.be/XJhyZQoofD8

O método de coordenadas é muito eficiente e maneira universal encontrar quaisquer ângulos ou distâncias entre objetos estereométricos no espaço. Se o seu professor de matemática é altamente qualificado, ele deve saber disso. Caso contrário, eu aconselharia a parte "C" a mudar o tutor. Minha preparação para o exame de matemática C1-C6 geralmente inclui uma análise dos algoritmos e fórmulas básicos descritos abaixo.

Ângulo entre as linhas a e b

O ângulo entre as linhas no espaço é o ângulo entre quaisquer linhas de interseção paralelas a elas. Este canto igual ao ângulo entre os vetores de direção dessas linhas (ou complementa a 180 graus).

Qual algoritmo o professor de matemática usa para encontrar o ângulo?

1) Escolha quaisquer vetores e tendo direções das linhas a e b (paralelas a elas).
2) Determinamos as coordenadas dos vetores e pelas coordenadas correspondentes de seus inícios e finais (as coordenadas do início devem ser subtraídas das coordenadas do final do vetor).
3) Substituímos as coordenadas encontradas na fórmula:
. Para encontrar o ângulo em si, você precisa encontrar o arco cosseno do resultado.

Normal ao plano

Uma normal a um plano é qualquer vetor perpendicular a esse plano.
Como encontrar o normal? Para encontrar as coordenadas da normal, basta conhecer as coordenadas de quaisquer três pontos M, N e K situados no plano dado. Usando essas coordenadas, encontramos as coordenadas dos vetores e e exigimos que as condições e sejam satisfeitas. Igualando o produto escalar de vetores a zero, compomos um sistema de equações com três variáveis, a partir das quais podemos encontrar as coordenadas da normal.

Nota do professor de matemática : Não é necessário resolver o sistema completamente, pois basta escolher pelo menos uma normal. Para fazer isso, você pode substituir qualquer número (por exemplo, um) em vez de qualquer uma de suas coordenadas desconhecidas e resolver um sistema de duas equações com as duas incógnitas restantes. Se não tiver soluções, isso significa que na família de normais não há ninguém que tenha uma unidade para a variável selecionada. Em seguida, substitua uma por outra variável (outra coordenada) e resolva novo sistema. Se você errar novamente, seu normal terá uma unidade na última coordenada e ficará paralelo a algum plano de coordenadas (neste caso, é fácil encontrá-lo sem um sistema).

Digamos que recebemos uma reta e um plano com as coordenadas do vetor de direção e da normal
O ângulo entre uma linha reta e um plano é calculado usando a seguinte fórmula:

Sejam e sejam quaisquer duas normais aos planos dados. Então o cosseno do ângulo entre os planos é igual ao módulo do cosseno do ângulo entre as normais:

Equação de um plano no espaço

Pontos que satisfazem a igualdade formam um plano com a normal. O coeficiente é responsável pela quantidade de desvio (deslocamento paralelo) entre dois planos com a mesma normal dada. Para escrever a equação de um plano, você deve primeiro encontrar sua normal (como descrito acima), e então substituir as coordenadas de qualquer ponto no plano, juntamente com as coordenadas da normal encontrada, na equação e encontrar o coeficiente .

MOU médio escola compreensiva №13

Método de Coordenadas

2008
Plano:

1. 
   Introdução
2. 
   
3. 
   A essência do método de coordenadas
4. 
   Sistemas de métodos de coordenadas
5. 
   Fórmulas básicas do método de coordenadas
6. 
   Tarefas de diferentes níveis de complexidade sobre o tema "Método de coordenadas"

(com soluções detalhadas)

1. 
   Conclusão
2. 
   Bibliografia

Introdução

Em geometria, aplique vários métodos a resolução de problemas é um método sintético (puramente geométrico), um método de transformações, um método vetorial, um método de coordenadas e outros. Eles ocupam posições diferentes na escola. O método principal é considerado sintético e, dos demais, o método das coordenadas ocupa a posição mais alta por estar intimamente relacionado à álgebra. A elegância do método sintético é alcançada com a ajuda da intuição, conjecturas, construções adicionais. O método coordenado não exige isso: a solução de problemas é amplamente algoritmizada, o que na maioria dos casos simplifica a busca e a solução do próprio problema.

Método de Coordenadas- uma maneira de determinar a posição de um ponto ou corpo usando números ou outros símbolos.

Sistema de coordenadas- um conjunto de definições que implementa o método de coordenadas, ou seja, uma maneira de definir a posição de um ponto ou corpo usando números ou outros símbolos.

Dando um caráter algébrico aos estudos geométricos, o método das coordenadas transfere para a geometria o mais característica importanteálgebra - a uniformidade de maneiras de resolver problemas. Se na geometria aritmética e elementar, em regra, se deve procurar uma maneira especial de resolver para cada problema, então na álgebra e na geometria analítica as soluções são realizadas de acordo com um plano comum a todos os problemas, facilmente adaptável a qualquer problema . A transferência para a geometria de métodos de resolução de problemas inerentes à álgebra e, portanto, de grande generalidade é o principal valor do método das coordenadas. Outra vantagem do método de coordenadas é que sua aplicação elimina a necessidade de recorrer a uma representação visual de imagens espaciais complexas.

Objetivos de estudar o método das coordenadas

Os seguintes objetivos para estudar o método de coordenadas em um curso de geometria escolar podem ser distinguidos:

• 
  dar aos alunos método eficaz resolver problemas e provar vários teoremas;
• 
  mostrar, com base neste método, a estreita ligação entre álgebra e geometria;
• 
  promover o desenvolvimento da cultura computacional e gráfica dos alunos.

A essência do método de coordenadas

A essência do método de coordenadas como método de resolução de problemas é que, ao definir figuras por equações e expressar várias relações geométricas em coordenadas, podemos resolver um problema geométrico por meio da álgebra. Por outro lado, usando coordenadas, pode-se interpretar relações e fatos algébricos e analíticos geometricamente e, assim, aplicar a geometria à solução de problemas algébricos.

O método de coordenadas é um método genérico.

Em um relacionamento curso escolar geometria, pode-se dizer que, em alguns casos, o método das coordenadas torna possível construir provas e resolver muitos problemas de forma mais racional e bela do que por métodos puramente geométricos. O método das coordenadas está associado, porém, a uma complexidade geométrica. Um mesmo problema recebe uma representação analítica diferente dependendo de uma ou outra escolha do sistema de coordenadas. E apenas a experiência suficiente permite que você escolha o sistema de coordenadas mais apropriado.

Sistemas coordenados:
1. Sistema de coordenadas retangulares (cartesianas) (Descartes René (1596-1650))

Nascido em Turim em uma família nobre rica. Alguns dias depois, sua mãe morreu de tuberculose, a enfermeira saiu e salvou sua vida. Aos 8 anos, René recebeu cuidados completos em um dos melhores colégios jesuítas. Desde a infância, Descartes adorava resolver problemas e tudo tempo livre dedicado ao estudo da matemática. Descartes estudou filosofia, matemática, física, astronomia e filologia. Descartes foi o primeiro a mostrar como a matemática pode ser aplicada à representação visual e analise matemática para uma ampla variedade de fenômenos naturais e sociais.

Primeira aparição em seu trabalho:

1. 
   variáveis
2. 
   leis estritas da geometria traduzidas para a linguagem algébrica
3. 
   foi proposto descrever as conexões entre fenômenos naturais com linhas curvas e escrevê-las com expressões algébricas
4. 
   letras latinas de constantes e variáveis, bem como a notação de graus

2.Sistema de coordenadas oblíquas difere de um retangular em que seus eixos não são perpendiculares. As coordenadas de ponto são definidas como em um sistema de coordenadas retangular ao longo de eixos paralelos retos.

3. Sistema de coordenadas polares . As coordenadas polares de um ponto são definidas da seguinte forma: um raio numérico OX é especificado no plano. O início do feixe, o ponto O, é chamado de pólo, e o eixo OX é chamado de eixo polar. Para determinar a posição do ponto M no sistema de coordenadas polares, indique a distância do pólo a este ponto e a direção em que está localizado. A distância de um ponto a um pólo é chamada de raio polar do ponto e é denotada pela letra (pronuncia-se “ro”).

A direção é definida pelo ângulo de rotação do feixe OX para o feixe OM

Método de Coordenadas

fórmulas

Comprimento de um vetor por suas coordenadas

Fórmula para encontrar as coordenadas do ponto médio de um segmento

Distância entre dois pontos

Equação do círculo,(centro do círculo
,raio r)

Equação de uma reta
, sob condição
(a equação de uma linha reta em um sistema de coordenadas retangulares é uma equação do primeiro grau)

Cada linha é dada por uma equação. Em que números a,b,c são determinados para cada linha reta exclusivamente até a proporcionalidade (se os multiplicarmos pelo mesmo número
, então a equação resultante
definirá a mesma linha).

Distância do ponto
para em linha reta m
,é igual a

Distância do ponto
até o avião
, é igual a

Derivação da fórmula
.

Descer do ponto
perpendicular AB ao plano , dado pela equação
.Deixar
- o ponto de intersecção desta perpendicular com o plano . Então
- distância do ponto
até o avião .Como o vetor é perpendicular ao plano , é colinear ao vetor
.Significa que
,E se
, ou
,E se
, isso é
.Vamos reescrever esta igualdade em coordenadas: .Mas o ponto
, é por isso
e
=
.
(Teorema de Stuart)

Dado o triângulo ABC e com base nisso o ponto D entre os pontos B e C, então a igualdade é verdadeira:

Prova:

Vamos escolher um sistema de coordenadas como mostrado na figura.

No sistema de coordenadas escolhido, os vértices do triângulo abc terá as seguintes coordenadas:

Machado 1 ;y 1 ), B(x 2 ;0), C(0;0) e ponto D(x 3 ;0) .

Calculamos todas as quantidades incluídas na igualdade:

Substitua todos esses valores em lado esquerdo igualdade:

Q.E.D.

Tarefa 1. Encontre a distância do ponto A(-1,3,0) ao plano , dado pela equação x -3y -2z +5=0.

Solução. De acordo com a fórmula
Nós temos:

.

Responda:
.

Tarefa 2. Vetores e são mutuamente perpendiculares, e o vetor forma um ângulo de 60˚ com cada um deles. Saber o que
, calcule o produto escalar

Solução. Pela propriedade do produto escalar, expandimos os colchetes:

=

Da definição do produto escalar, temos:
(Porque e perpendicular);

Substituindo esses valores na expressão
=, encontre o produto escalar:
=0 – 50+9 12 -120=-62

Responda:
=0 – 50+9 12 -120=-62
Tarefa 3.Dan quadrado ABCD com uma festa uma . Determine a distância entre o ponto médio do segmento SOU , Onde M - meio Sol , e ponto N no lado CD dividindo-o para que CN:ND=3:1 .

Solução:

Vamos escolher um sistema de coordenadas como mostrado na figura.

Então os pontos M e N , de acordo com a condição, terá coordenadas:

respectivamente.

Porque E - meio SOU , então suas coordenadas serão as seguintes:

Significa, E .

Encontre a distância entre os pontos E e N :

Resposta: PT =

Tarefa 4. Dado um cubo ABCDA1B1C1D1 com arestas de comprimento 1. O ponto E é tomado em sua aresta lateral AA 1 de modo que
.Na aresta BC, toma-se um ponto F tal que
Um plano passa pelo centro do cubo e pelos pontos E e F .Encontre a distância do vértice B ao plano .

Solução.

Introduzimos um sistema de coordenadas centrado no vértice B. Então
Vamos encontrar a equação do plano . Seja esta equação. notar que não passa pela origem, então
e a equação pode ser dividida por D; obtemos a seguinte equação:
ou ax + por + cz +1=0

Para determinar os coeficientes desconhecidos a, b e c, substituímos na equação ax + by + cz +1=0 as coordenadas dos três pontos E, F e O que satisfazem esta equação (já que esses pontos estão no plano ). Obtemos um sistema de equações:
Transformamos o sistema multiplicando a primeira equação por 3, a segunda por 4 e a terceira por -6 e somando a primeira equação à terceira, obtemos
,b=-4,
.Assim, a equação do plano tem a forma:

5x + 8y - 9z - 2 = 0. Agora encontramos a distância do ponto В1(0,0,1) ao plano
.

Responda:
.

Tarefa 5.base pirâmide triangular SABC é um triângulo equilátero ABC, cujo lado é 4. Sabe-se também que AS = BS =
, e CS = 3. Encontre a área da esfera circunscrita por esta pirâmide.