O ângulo ABC é um ângulo inscrito. Ele repousa sobre o arco AC, fechado entre seus lados (Fig. 330).

Teorema. Um ângulo inscrito é medido pela metade do arco que ele intercepta.

Isto deve ser entendido da seguinte forma: um ângulo inscrito contém tantos graus angulares, minutos e segundos quantos graus, minutos e segundos de arco estão contidos na metade do arco sobre o qual ele repousa.

Para provar este teorema, precisamos considerar três casos.

Primeiro caso. O centro do círculo fica do lado do ângulo inscrito (Fig. 331).

Seja ∠ABC um ângulo inscrito e o centro do círculo O esteja no lado BC. É necessário provar que é medido pela metade do arco AC.

Conecte o ponto A ao centro do círculo. Obtemos os isósceles \(\Delta\)AOB, em que AO = OB, como os raios do mesmo círculo. Portanto, ∠A = ∠B.

∠AOC é externo ao triângulo AOB, então ∠AOC = ∠A + ∠B, e como os ângulos A e B são iguais, ∠B é 1/2 ∠AOC.

Mas ∠AOC é medido pelo arco AC, portanto ∠B é medido pela metade do arco AC.

Por exemplo, se \(\breve(AC)\) contém 60°18', então ∠B contém 30°9'.

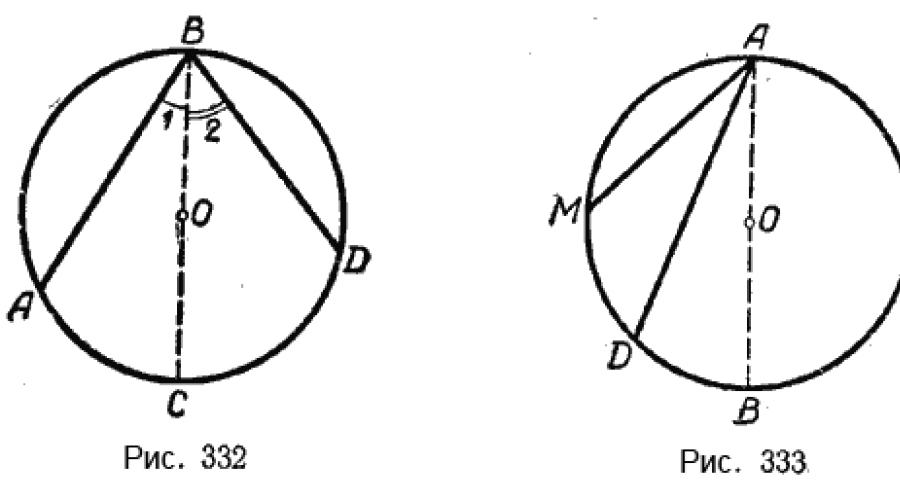
Segundo caso. O centro do círculo fica entre os lados do ângulo inscrito (Fig. 332).

Seja ∠ABD um ângulo inscrito. O centro do círculo O está entre seus lados. É necessário provar que ∠ABD é medido pela metade do arco AD.

Para provar isso, vamos desenhar o diâmetro BC. Ângulo ABD dividido em dois ângulos: ∠1 e ∠2.

∠1 é medido pela metade do arco AC, e ∠2 é medido pela metade do arco CD, portanto, todo o ∠ABD é medido por 1/2 \(\breve(AC)\) + 1/2 \( \breve(CD)\), ou seja, metade do arco AD.

Por exemplo, se \(\breve(AD)\) contém 124°, então ∠B contém 62°.

Terceiro caso. O centro do círculo fica fora do ângulo inscrito (Fig. 333).

Seja ∠MAD um ângulo inscrito. O centro do círculo O está fora do canto. É necessário provar que ∠MAD é medido pela metade do arco MD.

Para provar isso, vamos desenhar o diâmetro AB. ∠MAD = ∠MAB - ∠DAB. Mas ∠MAB mede 1/2 \(\breve(MB)\) e ∠DAB mede 1/2 \(\breve(DB)\).

Portanto, ∠MAD mede 1/2 (\(\breve(MB) - \breve(DB))\), ou seja, 1/2 \(\breve(MD)\).

Por exemplo, se \(\breve(MD)\) contém 48° 38", então ∠MAD contém 24° 19' 8".

Consequências
1. Todos os ângulos inscritos com base no mesmo arco são iguais entre si, pois são medidos pela metade do mesmo arco (Fig. 334, a).

2. Um ângulo inscrito com base em um diâmetro é um ângulo reto porque é baseado em meio círculo. Metade do círculo contém 180 graus de arco, o que significa que o ângulo baseado no diâmetro contém 90 graus angulares (Fig. 334, b).

Conceito de ângulo inscrito e central

Vamos primeiro introduzir o conceito de ângulo central.

Observação 1

Observe que a medida em graus de um ângulo central é igual à medida em graus do arco que ele intercepta.

Introduzimos agora o conceito de ângulo inscrito.

Definição 2

Um ângulo cujo vértice está em um círculo e cujos lados interceptam o mesmo círculo é chamado de ângulo inscrito (Fig. 2).

Figura 2. Ângulo inscrito

Teorema do ângulo inscrito

Teorema 1

A medida de um ângulo inscrito é metade da medida do arco que ele intercepta.

Prova.

Seja-nos dado um círculo centrado no ponto $O$. Denote o ângulo inscrito $ACB$ (Fig. 2). Os três casos a seguir são possíveis:

• O raio $CO$ coincide com algum lado do ângulo. Seja este o lado $CB$ (Fig. 3).

Figura 3

Neste caso, o arco $AB$ é menor que $(180)^(()^\circ )$, portanto canto central$AOB$ é igual ao arco $AB$. Como $AO=OC=r$, o triângulo $AOC$ é isósceles. Portanto, os ângulos da base $CAO$ e $ACO$ são iguais. De acordo com o teorema do ângulo externo de um triângulo, temos:

• Divida $CO$ do feixe canto interno para dois cantos. Deixe-o cruzar o círculo no ponto $D$ (Fig. 4).

Figura 4

Nós temos

• O raio $CO$ não divide um ângulo interno em dois ângulos e não coincide com nenhum de seus lados (Fig. 5).

Figura 5

Considere separadamente os ângulos $ACD$ e $DCB$. Pelo que foi provado no item 1, obtemos

Nós temos

O teorema foi provado.

Vamos trazer consequências deste teorema.

Corolário 1: Os ângulos inscritos que interceptam o mesmo arco são iguais.

Corolário 2: Um ângulo inscrito que intercepta um diâmetro é um ângulo reto.

Instrução

Se o raio (R) do círculo e o comprimento do arco (L) correspondente ao ângulo central desejado (θ) são conhecidos, ele pode ser calculado tanto em graus quanto em radianos. O total é determinado pela fórmula 2 * π * R e corresponde a um ângulo central de 360 ​​° ou dois números pi, se forem usados ​​radianos em vez de graus. Portanto, proceda da proporção 2*π*R/L = 360°/θ = 2*π/θ. Expresse a partir dele o ângulo central em radianos θ = 2*π/(2*π*R/L) = L/R ou graus θ = 360°/(2*π*R/L) = 180*L/(π * R) e calcule de acordo com a fórmula resultante.

De acordo com o comprimento da corda (m) que liga os pontos que definem o ângulo central (θ), seu valor também pode ser calculado se o raio (R) do círculo for conhecido. Para fazer isso, considere um triângulo formado por dois raios e . isto Triângulo isósceles, todos são conhecidos, mas você precisa encontrar o ângulo oposto à base. O seio de sua metade é igual à razão o comprimento da base - a corda - para duas vezes o comprimento do lado lateral - o raio. Portanto, use a função seno inversa para cálculos - o arco seno: θ \u003d 2 * arcsin (½ * m / R).

O ângulo central também pode ser especificado em frações de volta ou de um ângulo completo. Por exemplo, se você quiser encontrar o ângulo central que corresponde a um quarto de volta completa, divida 360° por quatro: θ = 360°/4 = 90°. O mesmo valor em radianos deve ser 2*π/4 ≈ 3,14/2 ≈ 1,57. O ângulo desenvolvido é igual a meia volta completa, então, por exemplo, o ângulo central correspondente a um quarto dela será metade dos valores calculados acima, tanto em graus quanto em radianos.

A função trigonométrica inversa do seno é chamada arco-seno. Pode levar valores que estão dentro da metade do número de pi, tanto positivos quanto negativos. lado negativo quando medido em radianos. Quando medidos em graus, esses valores estarão, respectivamente, na faixa de -90° a +90°.

Instrução

Alguns valores "redondos" não precisam ser calculados, são mais fáceis de lembrar. Por exemplo: - se o argumento da função é zero, então o valor do arco seno dele também é zero; - de 1/2 é 30 ° ou 1/6 Pi, se medido; - o arco seno de -1/2 é igual para -30° ou -1/6 de Pi em ;- arcsine de 1 é 90° ou 1/2 de Pi em radianos;- arcsine de -1 é -90° ou -1/2 de Pi em radianos;

Para medir os valores dessa função a partir de outros argumentos, a maneira mais fácil é usar a calculadora padrão do Windows, se você tiver . Para iniciar, abra o menu principal no botão "Iniciar" (ou pressionando a tecla WIN), vá para a seção "Todos os Programas" e depois para a subseção "Acessórios" e clique no item "Calculadora".

Mude a interface da calculadora para o modo de operação que permite calcular funções trigonométricas. Para isso, abra a seção “Visualizar” em seu menu e selecione o item “Engenharia” ou “Científico” (dependendo do sistema operacional).

Insira o valor do argumento a partir do qual calcular a tangente do arco. Isso pode ser feito clicando nos botões da interface da calculadora com o mouse, ou pressionando as teclas , ou copiando o valor (CTRL + C) e colando-o (CTRL + V) no campo de entrada da calculadora.

Selecione as unidades nas quais deseja obter o resultado do cálculo da função. Abaixo do campo de entrada estão três opções, das quais você precisa selecionar (clicando nele com o mouse) um - , radianos ou rads.

Marque a caixa de seleção que inverte as funções indicadas nos botões da interface da calculadora. Ao lado há uma pequena inscrição Inv.

Clique no botão pecado. A calculadora inverterá a função anexada a ela, realizará o cálculo e apresentará o resultado nas unidades fornecidas.

Vídeos relacionados

Um dos problemas geométricos comuns é o cálculo da área de um segmento circular - uma parte de um círculo delimitada por uma corda e um arco de círculo correspondente à corda.

A área de um segmento circular é igual à diferença entre a área do setor circular correspondente e a área do triângulo formado pelos raios do setor correspondente ao segmento e a corda que delimita o segmento.

Exemplo 1

O comprimento da corda que subtende o círculo é igual a a. A medida em grau do arco correspondente à corda é 60°. Encontre a área do segmento circular.

Solução

Um triângulo formado por dois raios e uma corda é isósceles, então a altura traçada do vértice do ângulo central ao lado do triângulo formado pela corda também será a bissetriz do ângulo central, dividindo-o ao meio, e a mediana, dividindo o acorde ao meio. Sabendo que o seno do ângulo β é igual à razão entre o cateto oposto e a hipotenusa, podemos calcular o valor do raio:

Sin 30°= a/2:R = 1/2;

Sc = πR²/360°*60° = πa²/6

S▲=1/2*ah, onde h é a altura traçada do topo do ângulo central até a corda. Pelo teorema de Pitágoras h=√(R²-a²/4)= √3*a/2.

Assim, S▲=√3/4*a².

A área do segmento, calculada como Sceg = Sc - S▲, é igual a:

Sseg \u003d πa² / 6 - √3 / 4 * a²

Ao substituir um valor numérico pelo valor a, você pode calcular facilmente o valor numérico da área do segmento.

Exemplo 2

O raio do círculo é igual a a. A medida em grau do arco correspondente ao segmento é 60°. Encontre a área do segmento circular.

Solução:

A área do setor correspondente a um determinado ângulo pode ser calculada usando a seguinte fórmula:

Sc = πа²/360°*60° = πa²/6,

A área do triângulo correspondente ao setor é calculada da seguinte forma:

S▲=1/2*ah, onde h é a altura traçada do topo do ângulo central até a corda. Pelo teorema de Pitágoras h=√(a²-a²/4)= √3*a/2.

Assim, S▲=√3/4*a².

E por fim, a área do segmento, calculada como Sceg = Sc - S▲, é igual a:

Sseg \u003d πa² / 6 - √3 / 4 * a².

As soluções em ambos os casos são quase idênticas. Assim, podemos concluir que no caso mais simples, para calcular a área de um segmento, basta saber o valor do ângulo correspondente ao arco do segmento e um dos dois parâmetros - seja o raio do círculo ou o comprimento da corda que subentende o arco do círculo que forma o segmento.

Fontes:

• Segmento - Geometria

Nível médio

Círculo e ângulo inscrito. guia visual (2019)

Termos básicos.

Quão bem você se lembra de todos os nomes associados ao círculo? Apenas no caso, lembramos - veja as fotos - atualize seu conhecimento.

Primeiramente - O centro de um círculo é um ponto a partir do qual todos os pontos do círculo estão à mesma distância.

Em segundo lugar - raio - um segmento de linha que liga o centro e um ponto no círculo.

Existem muitos raios (tantos quantos pontos existem em um círculo), mas todos os raios têm o mesmo comprimento.

Às vezes para breve raio eles chamam isso comprimento do segmento"o centro é um ponto no círculo", e não o próprio segmento.

E aqui está o que acontece se você conectar dois pontos em um círculo? Também um corte?

Então, esse segmento é chamado "acorde".

Assim como no caso do raio, o diâmetro é frequentemente chamado de comprimento de um segmento que conecta dois pontos em um círculo e passa pelo centro. A propósito, como o diâmetro e o raio estão relacionados? Olhe atentamente. É claro, o raio é metade do diâmetro.

Além dos acordes, há também secante.

Você se lembra do mais simples?

O ângulo central é o ângulo entre dois raios.

E agora o ângulo inscrito

Um ângulo inscrito é o ângulo entre duas cordas que se interceptam em um ponto de um círculo.

Neste caso, dizem que o ângulo inscrito depende de um arco (ou de uma corda).

Olha a foto:

Medição de arcos e ângulos.

Circunferência. Arcos e ângulos são medidos em graus e radianos. Primeiro, sobre graus. Não há problemas para ângulos - você precisa aprender a medir o arco em graus.

Medida de grau (valor do arco) é o valor (em graus) do ângulo central correspondente

O que significa a palavra "correspondente" aqui? Vejamos com atenção:

Vê os dois arcos e os dois ângulos centrais? Bem, um arco maior corresponde a um ângulo maior (e tudo bem que seja maior), e um arco menor corresponde a um ângulo menor.

Então, concordamos: o arco contém o mesmo número de graus que o ângulo central correspondente.

E agora sobre o terrível - sobre radianos!

Que tipo de animal é esse "radiano"?

Imagina isto: radianos são uma forma de medir um ângulo... em raios!

Um ângulo radiano é um ângulo central cujo comprimento do arco é igual ao raio do círculo.

Então surge a pergunta - quantos radianos estão em um ângulo reto?

Em outras palavras: quantos raios "se encaixam" em meio círculo? Ou de outra forma: quantas vezes o comprimento de meio círculo é maior que o raio?

Esta pergunta foi feita por cientistas na Grécia antiga.

E assim, depois de uma longa busca, eles descobriram que a razão entre a circunferência e o raio não quer ser expressa em números “humanos”, como, etc.

E nem é possível expressar essa atitude pelas raízes. Ou seja, acontece que não se pode dizer que metade do círculo é duas vezes ou vezes o raio! Você pode imaginar como foi incrível descobrir pessoas pela primeira vez?! Para a razão entre o comprimento de um semicírculo e o raio, os números “normais” eram suficientes. Eu tive que digitar uma letra.

Então, é um número que expressa a razão entre o comprimento de um semicírculo e o raio.

Agora podemos responder à pergunta: quantos radianos estão em um ângulo reto? Tem um radiano. Precisamente porque metade do círculo é o dobro do raio.

Pessoas antigas (e nem tanto) ao longo dos tempos (!) tentaram calcular esse número misterioso com mais precisão, para expressá-lo melhor (pelo menos aproximadamente) por meio de números "comuns". E agora estamos impossivelmente preguiçosos - dois sinais depois de ocupados são suficientes para nós, estamos acostumados a

Pense nisso, isso significa, por exemplo, que y de um círculo com um raio de um é aproximadamente igual em comprimento e é simplesmente impossível escrever esse comprimento com um número “humano” - você precisa de uma letra. E então essa circunferência será igual. E, claro, a circunferência do raio é igual.

Voltemos aos radianos.

Já descobrimos que um ângulo reto contém um radiano.

O que nós temos:

Tão feliz, isso é feliz. Da mesma forma, obtém-se uma placa com os ângulos mais populares.

A razão entre os valores dos ângulos inscritos e centrais.

Há um fato surpreendente:

O valor do ângulo inscrito é metade do valor do ângulo central correspondente.

Veja como esta afirmação fica na imagem. Um ângulo central "correspondente" é aquele em que as extremidades coincidem com as extremidades do ângulo inscrito e o vértice está no centro. E, ao mesmo tempo, o ângulo central “correspondente” deve “olhar” para a mesma corda () que o ângulo inscrito.

Por quê então? Vejamos primeiro um caso simples. Deixe um dos acordes passar pelo centro. Afinal, isso acontece às vezes, certo?

o que acontece aqui? Considerar. É isósceles - afinal, e são raios. Então, (denotou-os).

Agora vamos olhar. Este é o canto externo! Lembramos que um ângulo externo é igual à soma de dois internos que não são adjacentes a ele e escrevemos:

Aquilo é! Um efeito inesperado. Mas há também um ângulo central para o inscrito.

Então, para este caso, provamos que o ângulo central é o dobro do ângulo inscrito. Mas isso machuca caso especial: é verdade que o acorde nem sempre passa direto pelo centro? Mas nada, agora este caso especial vai nos ajudar muito. Veja: segundo caso: deixe o centro ficar dentro.

Vamos fazer isso: desenhe um diâmetro. E então... vemos duas fotos que já foram analisadas no primeiro caso. Portanto, já temos

Então (no desenho, a)

Bem, o último caso permanece: o centro está fora do canto.

Fazemos o mesmo: desenhamos um diâmetro através de um ponto. Tudo é o mesmo, mas em vez da soma - a diferença.

Isso é tudo!

Vamos agora formar dois principais e muito consequências importantes da afirmação de que um ângulo inscrito é metade do ângulo central.

Corolário 1

Todos os ângulos inscritos que interceptam o mesmo arco são iguais.

Ilustramos:

Existem inúmeros ângulos inscritos com base no mesmo arco (temos este arco), eles podem parecer completamente diferentes, mas todos têm o mesmo ângulo central (), o que significa que todos esses ângulos inscritos são iguais entre si.

Consequência 2

O ângulo baseado no diâmetro é um ângulo reto.

Veja: qual canto é central?

É claro, . Mas ele é igual! Bem, é por isso (assim como um monte de ângulos inscritos com base) e é igual a.

Ângulo entre duas cordas e secantes

Mas e se o ângulo em que estamos interessados ​​NÃO estiver inscrito e NÃO for central, mas, por exemplo, assim:

ou assim?

É possível expressá-lo de alguma forma através de alguns ângulos centrais? Acontece que você pode. Olha, estamos interessados.

a) (como canto externo para). Mas - inscrito, com base no arco - . - inscrito, baseado no arco - .

Para a beleza eles dizem:

O ângulo entre as cordas é metade da soma valores angulares arcos incluídos neste canto.

Isso foi escrito para ser breve, mas é claro que, ao usar esta fórmula, você precisa ter em mente os ângulos centrais

b) E agora - "fora"! Como ser? Sim, quase o mesmo! Só agora (novamente aplique a propriedade canto externo por). Isso é agora.

E isso significa. Vamos trazer beleza e brevidade nos registros e formulações:

O ângulo entre as secantes é igual à metade da diferença nos valores angulares dos arcos incluídos neste ângulo.

Bem, agora você está armado com todo o conhecimento básico sobre os ângulos associados a um círculo. Avante, ao assalto das tarefas!

CÍRCULO E ÂNGULO INCORDADO. NÍVEL MÉDIO

O que é um círculo, até uma criança de cinco anos sabe, né? Os matemáticos, como sempre, têm uma definição abstrusa sobre este assunto, mas não a daremos (veja), mas sim lembrar como são chamados os pontos, linhas e ângulos associados a um círculo.

Termos importantes

Primeiramente:

Em segundo lugar:

Há outra expressão aceita aqui: "o acorde contrai o arco". Aqui, aqui na figura, por exemplo, um acorde contrai um arco. E se o acorde de repente passar pelo centro, ele terá um nome especial: "diâmetro".

A propósito, como o diâmetro e o raio estão relacionados? Olhe atentamente. É claro,

E agora - os nomes dos cantos.

Naturalmente, não é? Os lados do canto saem do centro, o que significa que o canto é central.

É aqui que às vezes surgem as dificuldades. Prestar atenção - NEM QUALQUER ângulo dentro de um círculo é inscrito, mas apenas aquele cujo vértice "fica" no próprio círculo.

Vamos ver a diferença nas fotos:

Eles também dizem de forma diferente:

Há um ponto complicado aqui. O que é um ângulo central “correspondente” ou “próprio”? Apenas um ângulo com vértice no centro do círculo e termina nas extremidades do arco? Não certamente dessa maneira. Olha a foto.

Um deles, no entanto, nem parece um canto - é maior. Mas em um triângulo não pode haver mais ângulos, mas em um círculo - pode muito bem! Assim: um arco AB menor corresponde a um ângulo menor (laranja), e um arco maior a um ângulo maior. Assim como, não é?

Relação entre ângulos inscritos e centrais

Lembre-se de uma afirmação muito importante:

Nos livros didáticos, eles gostam de escrever o mesmo fato assim:

Verdade, com um ângulo central, a formulação é mais simples?

Mas, ainda assim, vamos encontrar uma correspondência entre as duas formulações e, ao mesmo tempo, aprender a encontrar nas figuras o ângulo central "correspondente" e o arco sobre o qual o ângulo inscrito "inclina".

Veja, aqui está um círculo e um ângulo inscrito:

Onde está seu ângulo central "correspondente"?

Vejamos novamente:

Qual é a regra?

Mas! Neste caso, é importante que os ângulos inscrito e central "olhem" do mesmo lado do arco. Por exemplo:

Curiosamente, azul! Porque o arco é longo, maior que a metade do círculo! Portanto, nunca se confunda!

Que consequência pode ser deduzida da "meia-meia" do ângulo inscrito?

E aqui, por exemplo:

Ângulo com base no diâmetro

Você já percebeu que os matemáticos gostam muito de falar sobre a mesma coisa com palavras diferentes? Por que é para eles? Veja bem, embora a linguagem da matemática seja formal, ela está viva e, portanto, como na linguagem comum, toda vez que você quiser dizê-la da maneira mais conveniente. Bem, já vimos o que é “o ângulo repousa sobre o arco”. E imagine, a mesma imagem é chamada de "o ângulo repousa sobre a corda". Em que? Sim, claro, naquele que puxa este arco!

Quando é mais conveniente confiar em um acorde do que em um arco?

Bem, em particular, quando esta corda é um diâmetro.

Há uma declaração incrivelmente simples, bonita e útil para tal situação!

Veja: aqui está um círculo, um diâmetro e um ângulo que repousa sobre ele.

CÍRCULO E ÂNGULO INCORDADO. BREVEMENTE SOBRE O PRINCIPAL

1. Conceitos básicos.

3. Medições de arcos e ângulos.

Um ângulo radiano é um ângulo central cujo comprimento do arco é igual ao raio do círculo.

Este é um número que expressa a razão entre o comprimento de um semicírculo e o raio.

A circunferência do raio é igual a.

4. A razão entre os valores dos ângulos inscritos e centrais.

canto centralé o ângulo formado por dois raios círculos. Um exemplo de ângulo central é o ângulo AOB, BOC, COE e assim por diante.

O canto central e arco celebrado entre as suas partes, dizem que corresponder uns aos outros.

1. se cantos centrais arcos são iguais.

2. se cantos centrais não são iguais, então o maior deles corresponde ao maior arco.

Seja AOB e COD dois cantos centrais, iguais ou desiguais. Girar o setor AOB em torno do centro na direção indicada pela seta para que o raio OA coincida com OC. Então, se os ângulos centrais são iguais, então o raio OA coincide com OD e o arco AB coincide com o arco CD.

Então esses arcos serão iguais.

Se cantos centrais não são iguais, então o raio OB não irá ao longo de OD, mas ao longo de alguma outra direção, por exemplo, ao longo de OE ou OF. Em ambos os casos, um ângulo maior obviamente corresponde a um arco maior.

O teorema que provamos para um círculo permanece verdadeiro para círculos iguais, porque tais círculos não diferem entre si, exceto por sua posição.

Reverter ofertas também será verdade . Em um círculo ou círculos iguais:

1. se arcos são iguais, então o correspondente cantos centrais são iguais.

2. se arcos não são iguais, então o maior deles corresponde ao maior canto central.

No mesmo círculo ou em círculos iguais, os ângulos centrais são relacionados como seus arcos correspondentes. Ou, parafraseando, temos que o ângulo central proporcional arco correspondente a ele.