1 aula por tópico

Realizado:

Telegina L. B.

O objetivo da lição:

1. repita todo o material estudado por função.
2. apresentar a definição de proporcionalidade inversa e ensinar como construir seu gráfico.
3. desenvolver o raciocínio lógico.
4. cultivar atenção, precisão, precisão.

Plano de aula:

1. Repetição.
2. Explicação do novo material.
3. Fizkultminutka.
4. Consolidação.

Equipamento: cartazes.

Durante as aulas:

1. A lição começa com repetição. Os alunos são convidados a resolver um jogo de palavras cruzadas (preparado com antecedência na folha grande papel).

Perguntas de palavras cruzadas:

1. Dependência entre variáveis, em que cada valor da variável independente corresponde a um único valor da variável dependente. [Função].

2. Variável independente. [Argumento].

3. O conjunto de pontos do plano de coordenadas da abcissa, que são iguais aos valores do argumento, e as ordenadas - aos valores da função. [Cronograma].

4. A função dada pela fórmula y=kx+b. [Linear].

5. Qual é o número chamado de coeficiente k na fórmula y=kx+b? [Angular].

6. O que serve como gráfico de uma função linear? [Em linha reta].

7. Se k≠0, então o gráfico y=kx+b intercepta este eixo, e se k=0, então é paralelo a ele. Qual é a letra desse eixo? [X].

8. A palavra no nome da função y=kx? [Proporcionalidade].

9. A função dada pela fórmula y=x 2. [Quadrático].

10. Título do gráfico função quadrática. [Parábola].

11. Uma letra do alfabeto latino, que muitas vezes denota uma função. [Yy].

12. Uma das maneiras de definir uma função. [Fórmula].

Professora : Quais são as principais formas de definir uma função que conhecemos?

(Um aluno recebe uma tarefa no quadro-negro: preencha a tabela de valores da função 12/x de acordo com os valores dados de seu argumento e, em seguida, construa os pontos correspondentes no plano de coordenadas).

O restante responde às perguntas do professor: (que são pré-gravadas no quadro)

1. Quais são os nomes das seguintes funções dadas pelas fórmulas: y=kx, y=kx+b, y=x 2, y=x3?

2. Especifique o escopo das seguintes funções: y=x 2 +8, y=1/x-7, y=4x-1/5, y=2x, y=7-5x, y=2/x, y=x 3, y=-10/x.

Em seguida, os alunos trabalham na mesa, respondendo às questões colocadas pelo professor:

1. Qual figura da tabela mostra os gráficos:

a) função linear;

b) proporcionalidade direta;

c) função quadrática;

d) funções da forma y=kx 3 ?

2. Qual é o sinal do coeficiente k nas fórmulas da forma y=kx+b, que correspondem aos gráficos das figuras 1, 2, 4, 5 da tabela?

3. Encontre gráficos na tabela funções lineares, cujos coeficientes de inclinação são:

a) são iguais;

b) são iguais em valor absoluto e opostos em sinal.

(Depois toda a turma verifica se o aluno chamado ao quadro preencheu corretamente a tabela e colocou os pontos no plano de coordenadas).

2. A explicação começa com a motivação.

Professora: Como você sabe, cada função descreve alguns processos que ocorrem no mundo ao nosso redor.

Considere, por exemplo, um retângulo com lados x e y e área 12cm 2 . Sabe-se que x*y=12, mas o que acontecerá se você começar a mudar um dos lados do retângulo, digamos que o lado seja longo x?

Comprimento lateral y pode ser encontrado pela fórmula y=12/x. Se um x aumentar em 2 vezes, então terá y = 12/2x, ou seja lado y diminuirá 2 vezes. Se o valor x aumentar em 3, 4, 5 ... vezes, então o valor y diminuirá na mesma proporção. Ao contrário, se x diminuir várias vezes y aumentará na mesma proporção. (Trabalhe na mesa).

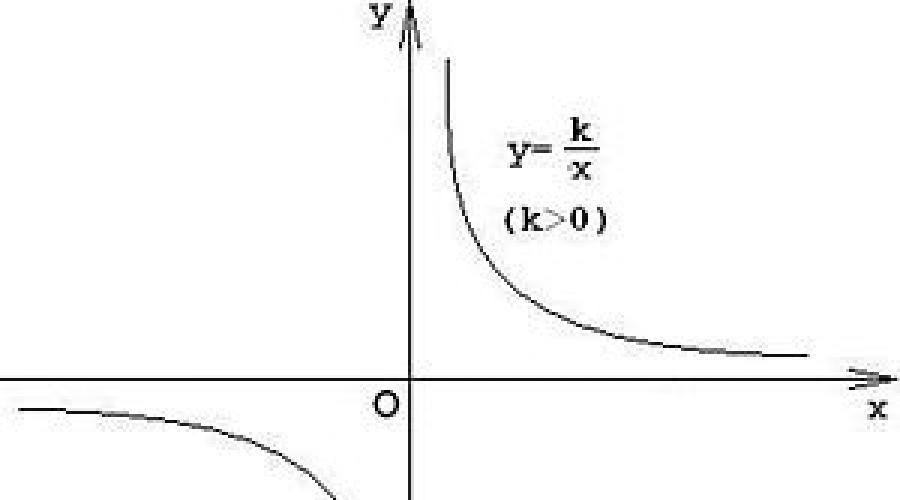
Portanto, uma função da forma y=12/x é chamada de proporcionalidade inversa. NO visão geralé escrito como y=k/x, onde k é uma constante e k≠0.

Este é o tema da lição de hoje, registrado em cadernos. Eu dou uma definição estrita. Para a função y=12/x, que é uma forma particular de proporcionalidade inversa, já escrevemos vários valores do argumento e da função na tabela e representaremos os pontos correspondentes no plano coordenado. Como é o gráfico dessa função? É difícil julgar o gráfico inteiro pelos pontos construídos, porque os pontos podem ser conectados de qualquer maneira. Vamos tentar juntos tirar conclusões sobre o gráfico da função decorrente da consideração da tabela e da fórmula.

Perguntas para a turma:

1. Qual é o escopo da função y=12/x?
2. Os valores de y são positivos ou negativos se

a) x

b) x>0?

3. Como o valor de uma variável muda y com alteração de valor x?

Então,

1. o ponto (0,0) não pertence ao gráfico, ou seja, não intercepta os eixos OX ou OY;
2. o gráfico está nos quartos das coordenadas Ι e ΙΙΙ;
3. aproxima-se suavemente dos eixos coordenados tanto no quarto de coordenadas Ι quanto no ΙΙΙ, e aproxima-se dos eixos o mais próximo desejado.

Com essas informações, já podemos ligar os pontos da figura (o próprio professor faz isso na lousa) e ver o gráfico da função y=12/x na íntegra. A curva resultante é chamada de hipérbole, que em grego significa "passar por algo". Esta curva foi descoberta por matemáticos da antiga escola grega por volta do século 4 aC. O termo hipérbole foi introduzido por Apolônio da cidade de Pérgamo (Ásia Menor), que viveu no ΙΙΙ-ΙΙ c. BC.

Agora, ao lado do gráfico da função y=12/x, vamos traçar o gráfico da função y=-12/x. (Os alunos fazem esta tarefa em cadernos e um aluno no quadro-negro).

Comparando os dois gráficos, os alunos notam que o segundo ocupa 2 e 4 quartos de coordenadas. Além disso, se o gráfico da função y=12/x for exibido simetricamente em relação ao eixo OS, então será obtido o gráfico da função y=-12/x.

Pergunta: Como a localização do gráfico da hipérbole y=k/x depende do sinal e do valor do coeficiente k?

Os alunos certificam-se de que se k>0, então o gráfico está localizado em Ι e ΙΙΙ coordenadas trimestres, e se k

1. A educação física é conduzida pelo professor.

1. A consolidação do estudado se dá ao realizar o nº 180, 185 do livro didático.

1. A lição é resumida, avaliações, dever de casa: item 8 nº 179, 184.

2 aulas sobre o tema

"A função de proporcionalidade inversa e seu gráfico".

Realizado:

Telegina L. B.

O objetivo da lição:

1. consolidar a habilidade de traçar um gráfico de uma função de proporcionalidade inversa;
2. desenvolver interesse pelo assunto, raciocínio lógico;
3. cultivar independência, atenção.

Plano de aula:

1. Verificação de execução trabalho de casa.
2. trabalho oral.
3. Solução de problemas.
4. Fizkultminutka.
5. Trabalho independente em vários níveis.
6. Resumindo, avaliação, lição de casa.

Equipamento: cartas.

Durante as aulas:

1. O professor anuncia o tema da aula, objetivos e plano de aula.

Em seguida, dois alunos completam os números 179, 184 atribuídos à casa no quadro.

1. Os restantes alunos trabalham frontalmente, respondendo às questões do professor.

Perguntas:

• Defina a função de proporcionalidade inversa.
• Qual é o gráfico da função proporcional inversa.
• Como a localização do gráfico da hipérbole y=k/x depende do valor do coeficiente k?

Tarefas:

1. Entre as funções dadas pelas fórmulas, nomeie as funções de proporcionalidade inversa:

a) y = x2 +5, b) y=1/x, c) y= 4x-1, d) y=2x, e) y=7-5x, f) y=-11/x, g) y=x 3, h) y=15/x-2.

2. Para funções de proporcionalidade inversa, nomeie o coeficiente e indique em quais quartos o gráfico se encontra.

3. Encontre o domínio de definição das funções de proporcionalidade inversa.

(Depois os alunos verificam os trabalhos de casa uns dos outros com um lápis de acordo com as soluções dos números assinalados pelo professor no quadro e dão uma nota).

Trabalho frontal no livro didático nº 190, 191, 192, 193 (oral).

1. Execução em cadernos e na lousa do livro didático nº 186 (b), 187 (b), 182.

4. Uma sessão de educação física é conduzida por um professor.

5. Trabalho independente dado em três opções de complexidade variada(distribuído em cartões).

Ι c. (leve).

Trace a função de proporcionalidade inversa y=-6/x usando a tabela:

Usando o gráfico, encontre:

a) o valor de y, se x = - 1,5; 2;

b) o valor de x, no qual y \u003d - 1; quatro.

ΙΙ c. (dificuldade média)

Trace a função de proporcionalidade inversa y=16/x preenchendo primeiro a tabela.

Usando o gráfico, encontre em quais valores xy > 0.

ΙΙΙ em. (aumento da dificuldade)

Trace a função de proporcionalidade inversa y=10/x-2 preenchendo a tabela primeiro.

Encontre o domínio da função dada.

(Os alunos entregam as folhas com os gráficos construídos para verificação).

6. A lição é resumida, avaliações, trabalhos de casa: nº 186 (a), 187 (a).

Hoje veremos quais quantidades são chamadas de inversamente proporcionais, como é o gráfico da proporcionalidade inversa e como tudo isso pode ser útil para você não apenas nas aulas de matemática, mas também fora dos muros da escola.

proporções tão diferentes

Proporcionalidade nomeie duas quantidades que são mutuamente dependentes uma da outra.

A dependência pode ser direta e reversa. Portanto, a relação entre quantidades descreve proporcionalidade direta e inversa.

Proporcionalidade direta- esta é uma relação entre duas quantidades, em que um aumento ou diminuição em uma delas leva a um aumento ou diminuição na outra. Aqueles. sua atitude não muda.

Por exemplo, quanto mais esforço você colocar na preparação para os exames, mais altas serão suas notas. Ou quanto mais coisas você leva com você em uma caminhada, mais difícil é carregar sua mochila. Aqueles. a quantidade de esforço gasto na preparação para os exames é diretamente proporcional às notas recebidas. E o número de coisas empacotadas em uma mochila é diretamente proporcional ao seu peso.

Proporcionalidade inversa - isto é dependência funcional, em que uma diminuição ou aumento em várias vezes de um valor independente (é chamado de argumento) causa um aumento ou diminuição proporcional (ou seja, na mesma quantidade) em um valor dependente (é chamado de função).

Ilustrar exemplo simples. Você quer comprar maçãs no mercado. As maçãs no balcão e a quantidade de dinheiro na carteira estão inversamente relacionadas. Aqueles. quanto mais maçãs você compra, menos dinheiro sobra.

Função e seu gráfico

A função de proporcionalidade inversa pode ser descrita como y = k/x. Em que x≠ 0 e k≠ 0.

Esta função tem as seguintes propriedades:

1. Seu domínio de definição é o conjunto de todos os números reais, exceto x = 0. D(y): (-∞; 0) U (0; +∞).
2. O intervalo são todos os números reais, exceto y= 0. E(s): (-∞; 0) você (0; +∞) .
3. Não possui valores máximos ou mínimos.
4. É ímpar e seu gráfico é simétrico em relação à origem.
5. Não periódico.
6. Seu gráfico não cruza os eixos coordenados.
7. Não tem zeros.
8. Se um k> 0 (ou seja, o argumento aumenta), a função diminui proporcionalmente em cada um de seus intervalos. Se um k< 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
9. À medida que o argumento aumenta ( k> 0) os valores negativos da função estão no intervalo (-∞; 0), e os valores positivos estão no intervalo (0; +∞). Quando o argumento está diminuindo ( k< 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

O gráfico da função de proporcionalidade inversa é chamado de hipérbole. Representado da seguinte forma:

Problemas proporcionais inversos

Para deixar mais claro, vamos ver algumas tarefas. Eles não são muito complicados, e sua solução ajudará você a visualizar o que é proporção inversa e como esse conhecimento pode ser útil em seu vida comum.

Tarefa número 1. O carro está se movendo a uma velocidade de 60 km/h. Ele levou 6 horas para chegar ao seu destino. Quanto tempo ele levará para percorrer a mesma distância se ele se mover com o dobro da velocidade?

Podemos começar escrevendo uma fórmula que descreve a relação entre tempo, distância e velocidade: t = S/V. Concordo, isso nos lembra muito a função de proporcionalidade inversa. E indica que o tempo que o carro passa na estrada e a velocidade com que se move são inversamente proporcionais.

Para verificar isso, vamos encontrar V 2, que, por condição, é 2 vezes maior: V 2 \u003d 60 * 2 \u003d 120 km / h. Em seguida, calculamos a distância usando a fórmula S = V * t = 60 * 6 = 360 km. Agora não é difícil descobrir o tempo t 2 que nos é exigido de acordo com a condição do problema: t 2 = 360/120 = 3 horas.

Como você pode ver, o tempo de viagem e a velocidade são de fato inversamente proporcionais: com uma velocidade 2 vezes maior que a original, o carro gastará 2 vezes menos tempo na estrada.

A solução para este problema também pode ser escrita como uma proporção. Por que criamos um diagrama como este:

↓ 60 km/h – 6 h

↓120 km/h – x h

As setas indicam uma relação inversa. E eles também sugerem que, ao elaborar a proporção, o lado direito do registro deve ser virado: 60/120 \u003d x / 6. Onde obtemos x \u003d 60 * 6/120 \u003d 3 horas.

Tarefa número 2. A oficina emprega 6 trabalhadores que lidam com uma determinada quantidade de trabalho em 4 horas. Se o número de trabalhadores for reduzido pela metade, quanto tempo levará para os trabalhadores restantes completarem a mesma quantidade de trabalho?

Escrevemos as condições do problema na forma esquema visual:

↓ 6 trabalhadores - 4 horas

↓ 3 trabalhadores - x h

Vamos escrever isso como uma proporção: 6/3 = x/4. E obtemos x \u003d 6 * 4/3 \u003d 8 horas. Se houver 2 vezes menos trabalhadores, o restante gastará 2 vezes mais tempo para concluir todo o trabalho.

Tarefa número 3. Dois tubos levam à piscina. Através de um tubo, a água entra a uma taxa de 2 l/s e enche a piscina em 45 minutos. Através de outra tubulação, a piscina será preenchida em 75 minutos. Com que velocidade a água entra na piscina através deste tubo?

Para começar, traremos todas as grandezas que nos são dadas de acordo com a condição do problema para as mesmas unidades de medida. Para fazer isso, expressamos a taxa de enchimento da piscina em litros por minuto: 2 l / s \u003d 2 * 60 \u003d 120 l / min.

Como decorre da condição de que a piscina seja enchida mais lentamente através do segundo tubo, isso significa que a taxa de entrada de água é menor. Na face da proporção inversa. Vamos expressar a velocidade desconhecida para nós em termos de x e esboçar o seguinte esquema:

↓ 120 l/min - 45 min

↓ x l/min – 75 min

E então faremos uma proporção: 120 / x \u003d 75/45, de onde x \u003d 120 * 45/75 \u003d 72 l / min.

No problema, a taxa de enchimento da piscina é expressa em litros por segundo, vamos trazer nossa resposta para a mesma forma: 72/60 = 1,2 l/s.

Tarefa número 4. Os cartões de visita são impressos em uma pequena gráfica particular. Um funcionário da gráfica trabalha a uma velocidade de 42 cartões de visita por hora e trabalha em período integral - 8 horas. Se ele trabalhasse mais rápido e imprimisse 48 cartões de visita por hora, quanto tempo antes ele poderia ir para casa?

Vamos de maneira comprovada e elaboramos um esquema de acordo com a condição do problema, denotando o valor desejado como x:

↓ 42 cartões de visita/h – 8h

↓ 48 cartões de visita/h – xh

Diante de nós está uma relação inversamente proporcional: quantas vezes mais cartões de visita um funcionário de uma gráfica imprime por hora, o mesmo tempo que ele levará para concluir o mesmo trabalho. Sabendo disso, podemos configurar a proporção:

42/48 \u003d x / 8, x \u003d 42 * 8/48 \u003d 7 horas.

Assim, tendo concluído o trabalho em 7 horas, o funcionário da gráfica poderia ir para casa uma hora mais cedo.

Conclusão

Parece-nos que esses problemas de proporcionalidade inversa são realmente simples. Esperamos que agora você também os considere assim. E o mais importante, esse conhecimento sobre as costas dependência proporcional valores podem realmente ser úteis para você mais de uma vez.

Não só nas aulas de matemática e exames. Mas mesmo assim, quando você vai viajar, fazer compras, decidir ganhar algum dinheiro durante as férias, etc.

Conte-nos nos comentários quais exemplos de proporcionalidade inversa e direta você percebe ao seu redor. Que isso seja um jogo. Você verá como é emocionante. Não se esqueça de compartilhar este artigo nas redes sociais para que seus amigos e colegas também possam jogar.

site, com cópia total ou parcial do material, é necessário um link para a fonte.

Primeiro nível

Relação inversa. Primeiro nível.

Agora vamos falar sobre relação inversa, ou em outras palavras - proporcionalidade inversa, como uma função. Você se lembra que uma função é um certo tipo de dependência? Se você ainda não leu o tópico, eu recomendo fortemente que você largue tudo e leia, porque você não pode estudar nenhuma função em particular sem entender o que é - uma função.

Também é muito útil antes de iniciar este tópico dominar mais dois funções simples: e . Lá você consolidará o conceito de função e aprenderá a trabalhar com coeficientes e gráficos.

E aí, você lembra o que é uma função?
Repetimos: uma função é uma regra segundo a qual cada elemento de um conjunto (argumento) está associado a algum ( o único!) um elemento de outro conjunto (conjunto de valores de função). Ou seja, se você tem uma função, significa que cada valor permitido uma variável (chamada de "argumento") corresponde a um valor de uma variável (chamada de "função"). O que significa "aceitável"? Se você não conseguir responder a esta pergunta, volte ao tópico “” novamente! É tudo sobre o conceito "domínio": para algumas funções, nem todos os argumentos são igualmente úteis podem ser substituídos em uma dependência. Por exemplo, para uma função, valores de argumentos negativos são inválidos.

Uma função que descreve a relação inversa

Esta é uma função da forma onde.

De outra forma, é chamada de proporcionalidade inversa: um aumento no argumento causa uma diminuição proporcional na função.
Vamos definir o escopo. O que pode ser igual? Ou, em outras palavras, a que não pode ser igual?

O único número que não pode ser dividido por é, portanto:

ou, o que é o mesmo,

(tal notação significa que pode ser qualquer número, exceto: o sinal "" denota o conjunto dos números reais, ou seja, todos os números possíveis; o sinal "" denota a exclusão de algo deste conjunto (análogo do sinal de menos ), e o número entre parênteses curly significa apenas um número; acontece que excluímos de todos os números possíveis).

O conjunto de valores da função, ao que parece, é exatamente o mesmo: afinal, se, então, não importa em que o dividamos, não funcionará:

Algumas variações da fórmula também são possíveis. Por exemplo, também é uma função que descreve uma relação inversa.
Defina você mesmo o escopo e o escopo desta função. Deve resultar:

Vejamos esta função: . É uma relação inversa?

À primeira vista, é difícil dizer: afinal, com um aumento, tanto o denominador da fração quanto o numerador aumentam, então não fica claro se a função diminuirá e, em caso afirmativo, diminuirá proporcionalmente? Para entender isso, precisamos transformar a expressão para que não haja variável no numerador:

De fato, obtivemos uma relação inversa, mas com uma ressalva: .

Aqui está outro exemplo: .

É mais complicado aqui: afinal, o numerador e o denominador agora certamente não são reduzidos. Mas ainda podemos tentar:

Você entende o que eu fiz? No numerador, somei e subtraí o mesmo número (), então não pareceu mudar nada, mas agora o numerador tem uma parte igual ao denominador. Agora vou dividir termo por termo, ou seja, vou quebrar essa fração na soma de duas frações:

(e é verdade, se você trouxer o que eu tenho denominador comum, nossa fração inicial resultará apenas uma vez):

Uau! Acontece novamente relação inversa, somente agora um número é adicionado a ele.
Este método será muito útil para nós mais tarde ao traçar gráficos.

E agora, independentemente, traga as expressões para a forma de uma relação inversa:

Respostas:

2. Aqui você precisa se lembrar de como trinômio quadradoé fatorado (isso é descrito em detalhes no tópico ""). Deixe-me lembrá-lo que para isso você precisa encontrar as raízes dos Equação quadrática: . Vou encontrá-los verbalmente usando o teorema de Vieta: , . Como isso é feito? Você pode aprender isso lendo o tópico.
Assim, obtemos: , portanto:

3. Você já tentou resolvê-lo sozinho? Qual é o problema? Certamente no fato de que no numerador temos e no denominador - apenas. Isso não é um problema. Precisaremos reduzir por, então o numerador deve ser retirado dos colchetes (para que fique entre colchetes sem um coeficiente):

Gráfico inverso

Como sempre, vamos começar com o caso mais simples: .
Vamos fazer uma tabela:

Desenhe pontos no plano de coordenadas:

Agora eles precisam ser conectados sem problemas, mas como? Pode-se ver que os pontos nas partes direita e esquerda formam linhas curvas aparentemente não relacionadas. Do jeito que está. O gráfico ficará assim:

Este gráfico é chamado "hipérbole"(há algo parecido com "parábola" neste nome, certo?). Como uma parábola, uma hipérbole tem dois ramos, só que eles não estão conectados um ao outro. Cada um deles tende a aproximar-se dos eixos com suas extremidades, mas nunca os alcança. Se você olhar para a mesma hipérbole de longe, terá a seguinte imagem:

É compreensível: já que o gráfico não pode cruzar o eixo. Mas também, para que o gráfico nunca toque o eixo.

Bem, agora vamos ver o que os coeficientes afetam. Considere estas funções:
:

Nossa, que beleza!
Todos os gráficos são construídos Cores diferentes para torná-lo mais fácil de diferenciá-los.

Então, em que devemos prestar atenção em primeiro lugar? Por exemplo, se a função tiver um menos antes da fração, o gráfico será invertido, ou seja, será exibido simetricamente em torno do eixo.

Segundo: quanto maior o número no denominador, mais o gráfico "se afasta" da origem.

Mas e se a função parecer mais complicada, por exemplo, ?

Nesse caso, a hipérbole será exatamente a mesma que a usual, só que se deslocará um pouco. Vamos pensar, onde?

O que não pode ser igual agora? Corretamente, . Isso significa que o gráfico nunca alcançará uma linha reta. O que não pode ser igual? Agora. Isso significa que agora o gráfico tenderá a uma linha reta, mas nunca a cruzará. Então, agora eles são heterossexuais e desempenham o mesmo papel que desempenham eixos de coordenadas para a função. Tais linhas são chamadas assíntotas(linhas para as quais o gráfico tende, mas não alcança):

Aprenderemos mais sobre como esses gráficos são construídos no tópico.

E agora tente resolver alguns exemplos para consolidar:

1. A figura mostra um gráfico de função. Determinar.

2. A figura mostra um gráfico de função. Determinar

3. A figura mostra um gráfico de função. Determinar.

4. A figura mostra um gráfico de função. Determinar.

5. A figura mostra os gráficos das funções e.

Escolha a proporção certa:

Respostas:

Relação inversa na vida

Onde encontramos tal função na prática? Existem muitos exemplos. O mais comum é o movimento: quanto maior a velocidade com que nos movemos, menos tempo precisamos para percorrer a mesma distância. De fato, vamos relembrar a fórmula da velocidade: , onde é a velocidade, é o tempo de viagem, é a distância (caminho).

A partir daqui podemos expressar o tempo:

Exemplo:

O homem vai trabalhar com velocidade média km/h, e chega em uma hora. Quantos minutos ele passará na mesma estrada se viajar a uma velocidade de km/h?

Solução:

Em geral, você já resolveu esses problemas na 5ª e 6ª séries. Você fez a proporção?

Ou seja, o conceito de proporcionalidade inversa já é exatamente familiar para você. Isso é o que eles se lembraram. E agora a mesma coisa, só que de forma adulta: através de uma função.

Função (ou seja, dependência) do tempo em minutos da velocidade:

Sabe-se que então:

Precisa encontrar:

Agora, apresente alguns exemplos da vida em que há uma proporcionalidade inversa.
Inventado? Bem feito se sim. Boa sorte!

DEPENDÊNCIA INVERSA. BREVEMENTE SOBRE O PRINCIPAL

1. Definição

Uma função que descreve a relação inversaé uma função da forma onde.

De outra forma, essa função é chamada de proporcionalidade inversa, pois um aumento no argumento causa uma diminuição proporcional na função.

ou, o que é o mesmo,

O gráfico de relação inversa é uma hipérbole.

2. Coeficientes e.

Responsável por "inclinação" e a direção do gráfico: quanto maior esse coeficiente, mais distante da origem a hipérbole está localizada e, portanto, “gira” menos acentuadamente (veja a figura). O sinal do coeficiente afeta os trimestres em que o gráfico está localizado:

• se, então os ramos da hipérbole estão localizados em e quartos;
• se, então em e.

x=a é assíntota vertical, isto é, a vertical para a qual o gráfico tende.

O número é responsável por deslocar o gráfico da função para cima em um valor se , e deslocar para baixo se .

Daí, é assíntota horizontal.

Vamos repetir a teoria sobre funções. Uma função é uma regra segundo a qual a cada elemento de um conjunto (argumento) é atribuído algum ( o único!) um elemento de outro conjunto (conjunto de valores de função). Ou seja, se existe uma função \(y = f(x)\), o que significa que para cada valor válido da variável \(x\)(que é chamado de "argumento") corresponde a um valor da variável \(s\)(chamada "função").

Uma função que descreve a relação inversa

Esta é uma função da forma \(y = \frac(k)(x)\) Onde \(k \ne 0.\)

De outra forma, é chamada de proporcionalidade inversa: um aumento no argumento causa uma diminuição proporcional na função.
Vamos definir o domínio de definição. A que \(x\) pode ser igual? Ou, em outras palavras, a que não pode ser igual?

O único número pelo qual você não pode dividir é 0, então \(x \ne 0.\):

\(D(y) = (- \infty ;0) \cup (0; + \infty)\)

ou, que é o mesmo:

\(D(y) = R\barra invertida \( 0\) .\)

Tal notação significa que \(x\) pode ser qualquer número exceto 0: o sinal "R" denota o conjunto dos números reais, ou seja, todos os números possíveis; o sinal "\" denota a exclusão de algo deste conjunto (análogo ao sinal "menos"), e o número 0 entre colchetes significa simplesmente o número 0; acontece que excluímos 0 de todos os números possíveis.

O conjunto de valores da função, ao que parece, é exatamente o mesmo: afinal, se \(k \ne 0.\) , não importa o que dividimos, 0 não funcionará:

\(E(y) = (- \infty ;0) \cup (0; + \infty)\)

ou \(E(y) = R\barra invertida \( 0\) .\)

Algumas variações da fórmula também são possíveis. \(y = \frac(k)(x)\). Por exemplo, \(y = \frac(k)((x + a))\)- também é uma função que descreve uma relação inversa. O escopo e o alcance desta função são os seguintes:

\(D(y) = (- \infty ; - a) \cup (- a; + \infty)\)

\(E(y) = (- \infty ;0) \cup (0; + \infty).\)

Considerar exemplo, traremos a expressão para a forma de uma relação inversa:

\(y = \frac((x + 2))((x - 3)).\)

\(y = \frac((x + 2))((x - 3)) = \frac((x - 3 + 3 + 2))((x - 3)) = \frac(((x - 3) ) + 5))((x - 3)).\)

Introduzimos artificialmente o valor 3 no numerador, e agora dividimos o numerador pelo denominador termo por termo, obtemos:

\(y = \frac(((x - 3) + 5))((x - 3)) = \frac((x - 3))((x - 3)) + \frac(5)((x) - 3)) = 1 + \frac(5)((x - 3)).\)

Temos uma relação inversa mais o número 1.

Gráfico inverso

Vamos começar com um caso simples \(y = \frac(1)(x).\)

Vamos fazer uma tabela de valores:

Desenhe pontos no plano de coordenadas:

Ligue os pontos, o gráfico ficará assim:

Este gráfico é chamado "hipérbole". Como uma parábola, uma hipérbole tem dois ramos, só que eles não estão conectados um ao outro. Cada um deles se esforça com suas extremidades para se aproximar dos eixos Boi e Oi mas nunca os alcança.

Vamos observar algumas características da função:

1. Se a função tiver um menos antes da fração, o gráfico é invertido, ou seja, é exibido simetricamente em torno do eixo Boi.
2. Quanto maior o número no denominador, mais o gráfico "se afasta" da origem.

Relação inversa na vida

Onde encontramos tal função na prática? Existem muitos exemplos. O mais comum é o movimento: quanto maior a velocidade com que nos movemos, menos tempo precisamos para percorrer a mesma distância. Vamos lembrar a fórmula da velocidade:

\(v = \frac(S)(t),\)

onde v - velocidade, t - tempo de viagem, S - distância (caminho).

A partir daqui podemos expressar o tempo: \(t = \frac(S)(v).\)