Área de Valor Aceitável (ODZ): teoria, exemplos, soluções. Como encontrar o escopo de uma função? Exemplos de soluções
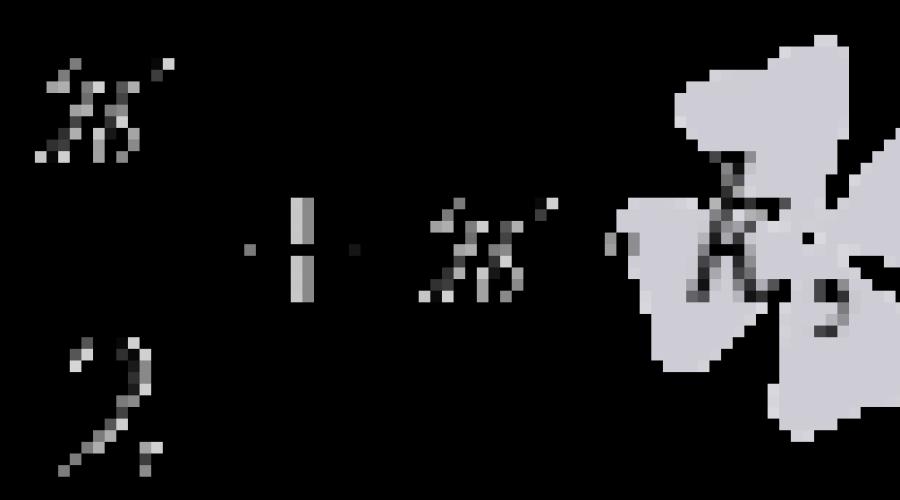
Leia também
Sua privacidade é importante para nós. Por esse motivo, desenvolvemos uma Política de Privacidade que descreve como usamos e armazenamos suas informações. Por favor, leia nossa política de privacidade e deixe-nos saber se você tiver alguma dúvida.
Coleta e uso de informações pessoais
Informações pessoais referem-se a dados que podem ser usados para identificar uma pessoa específica ou contatá-la.
Você pode ser solicitado a fornecer suas informações pessoais a qualquer momento quando entrar em contato conosco.
A seguir estão alguns exemplos dos tipos de informações pessoais que podemos coletar e como podemos usar essas informações.
Quais informações pessoais coletamos:
- Quando você envia uma inscrição no site, podemos coletar várias informações, incluindo seu nome, número de telefone, endereço E-mail etc.
Como usamos suas informações pessoais:
- Recolhido por nós informação pessoal nos permite entrar em contato com você e informá-lo sobre ofertas exclusivas, promoções e outros eventos e eventos futuros.
- De tempos em tempos, podemos usar suas informações pessoais para enviar avisos e mensagens importantes.
- Também podemos usar informações pessoais para fins internos, como auditoria, análise de dados e vários estudos para melhorar os serviços que prestamos e para lhe fornecer recomendações sobre os nossos serviços.
- Se você participar de um sorteio, concurso ou incentivo semelhante, poderemos usar as informações fornecidas para administrar tais programas.
Divulgação a terceiros
Não divulgamos informações recebidas de você a terceiros.
Exceções:
- Se necessário - de acordo com a lei, ordem judicial, dentro litígio, e/ou com base em solicitações públicas ou solicitações de agências governamentais no território da Federação Russa - divulgue suas informações pessoais. Também podemos divulgar informações sobre você se determinarmos que tal divulgação é necessária ou apropriada para segurança, aplicação da lei ou outras ocasiões importantes.
- No caso de uma reorganização, fusão ou venda, podemos transferir as informações pessoais que coletamos para o sucessor terceirizado relevante.
Proteção de informações pessoais
Tomamos precauções - incluindo administrativas, técnicas e físicas - para proteger suas informações pessoais contra perda, roubo e uso indevido, bem como de acesso, divulgação, alteração e destruição não autorizados.
Mantendo sua privacidade no nível da empresa
Para garantir que suas informações pessoais estejam seguras, comunicamos práticas de privacidade e segurança aos nossos funcionários e aplicamos rigorosamente as práticas de privacidade.
Vamos começar encontrando domínio de definição da soma de funções. É claro que tal função faz sentido para todos esses valores da variável para os quais todas as funções que compõem a soma fazem sentido. Portanto, não há dúvida sobre a validade da seguinte afirmação:
Se a função f é a soma de n funções f 1 , f 2 , …, f n , ou seja, a função f é dada pela fórmula y=f 1 (x)+f 2 (x)+…+f n (x ), então o domínio da função f é a interseção dos domínios das funções f 1 , f 2 , …, f n . Vamos escrever como .
Vamos concordar em continuar usando registros como o último, ou seja, escritos entre colchetes, ou o cumprimento simultâneo de quaisquer condições. Isso é conveniente e naturalmente ressoa com o significado de sistemas.
Exemplo.
Dada uma função y=x 7 +x+5+tgx , precisamos encontrar seu domínio.
Solução.
A função f é representada pela soma de quatro funções: f 1 é uma função de potência com um expoente de 7 , f 2 é uma função de potência com um expoente de 1 , f 3 é uma função constante e f 4 é uma função tangente.
Olhando para a tabela de áreas de definição dos principais funções elementares, descobrimos que D(f 1)=(−∞, +∞) , D(f 2)=(−∞, +∞) , D(f 3)=(−∞, +∞) , e o domínio de a tangente é o conjunto de todos os números reais, exceto os números ![]() .
.
O domínio da função f é a intersecção dos domínios das funções f 1 , f 2 , f 3 e f 4 . É bastante óbvio que este é o conjunto de todos os números reais, com exceção dos números ![]() .
.
Responda:
conjunto de todos os números reais, exceto ![]() .
.
Vamos seguir para encontrar domínios do produto de funções. Para este caso, uma regra semelhante vale:
Se a função f é o produto de n funções f 1 , f 2 , …, f n , ou seja, a função f é dada pela fórmula y=f 1 (x) f 2 (x) ... f n (x), então o domínio da função f é a interseção dos domínios das funções f 1 , f 2 , …, f n . Então, .
É compreensível, na área indicada todas as funções do produto são definidas e, portanto, a própria função f.
Exemplo.
Y=3 arctgx lnx.
Solução.
A estrutura do lado direito da fórmula que define a função pode ser considerada como f 1 (x) f 2 (x) f 3 (x) , onde f 1 é uma função constante, f 2 é a função arco tangente, e f 3 é a função logarítmica com base e.
Sabemos que D(f 1)=(−∞, +∞) , D(f 2)=(−∞, +∞) e D(f 3)=(0, +∞) . Então  .
.
Responda:
o domínio da função y=3 arctgx lnx é o conjunto de todos os números reais positivos.
Vamos nos deter separadamente em encontrar o domínio da função dada pela fórmula y=C·f(x) , onde C é algum número real. É fácil mostrar que o domínio desta função e o domínio da função f coincidem. De fato, a função y=C f(x) é o produto de uma função constante e uma função f . O domínio de uma função constante é o conjunto de todos os números reais, e o domínio da função f é D(f). Então o domínio da função y=C f(x) é  , que deveria ser mostrado.
, que deveria ser mostrado.
Assim, os domínios das funções y=f(x) e y=C·f(x) , onde С é algum número real, coincidem. Por exemplo, se o domínio da raiz é , fica claro que D(f) é o conjunto de todos os x do domínio da função f 2 para o qual f 2 (x) está incluído no domínio da função f 1 .
Nesse caminho, domínio de uma função complexa y=f 1 (f 2 (x)) é a intersecção de dois conjuntos: o conjunto de todos os x tais que x∈D(f 2) e o conjunto de todos os x tais que f 2 (x)∈D(f 1 ). Ou seja, em nossa notação  (este é essencialmente um sistema de desigualdades).
(este é essencialmente um sistema de desigualdades).
Vamos dar uma olhada em alguns exemplos. No processo, não descreveremos em detalhes, pois isso está além do escopo deste artigo.
Exemplo.
Encontre o domínio da função y=lnx 2 .
Solução.
A função original pode ser representada como y=f 1 (f 2 (x)) , onde f 1 é um logaritmo com base e, e f 2 é uma função de potência com expoente 2.
Voltando-se para áreas famosas definições de funções elementares básicas, temos D(f 1)=(0, +∞) e D(f 2)=(−∞, +∞) .
Então 
Então encontramos o domínio de definição da função que precisávamos, é o conjunto de todos os números reais, exceto o zero.
Responda:
(−∞, 0)∪(0, +∞) .
Exemplo.
Qual é o escopo da função ![]() ?
?
Solução.
Essa função é complexa, pode ser considerada como y \u003d f 1 (f 2 (x)) , onde f 1 é uma função de potência com expoente e f 2 é a função arcsine, e precisamos encontrar seu domínio.
Vamos ver o que sabemos: D(f 1)=(0, +∞) e D(f 2)=[−1, 1] . Resta encontrar a interseção de conjuntos de valores x tais que x∈D(f 2) ef 2 (x)∈D(f 1) : 
Para arcsinx>0, vamos recuperar as propriedades da função arcsine. O arcsine aumenta em todo o domínio [−1, 1] e desaparece em x=0 , portanto, arcsinx>0 para qualquer x do intervalo (0, 1] .
Voltemos ao sistema: 
Assim, o domínio desejado de definição da função é um meio-intervalo (0, 1] .
Responda:
(0, 1] .
Agora vamos passar para funções gerais complexas y=f 1 (f 2 (…f n (x)))) . O domínio da função f neste caso é encontrado como  .
.
Exemplo.
Encontrar o escopo de uma função ![]() .
.
Solução.
A função complexa dada pode ser escrita como y \u003d f 1 (f 2 (f 3 (x))), onde f 1 - sin, f 2 - função da raiz do quarto grau, f 3 - lg.
Sabemos que D(f 1)=(−∞, +∞) , D(f 2)=- ∞; +∞[.
Exemplo 1. Encontre o escopo de uma função y = 2 .
Solução. O escopo da função não é especificado, o que significa que, em virtude da definição acima, entende-se o domínio natural da definição. Expressão f(x) = 2 é definido para quaisquer valores reais x, Consequentemente, determinada função definido em todo o conjunto R numeros reais.

Portanto, no desenho acima, a reta numérica está sombreada desde menos infinito até mais infinito.
Escopo da raiz nº grau
No caso em que a função é dada pela fórmula e n- número natural:
Exemplo 2. Encontre o escopo de uma função .
Solução. Como segue da definição, a raiz de um grau par faz sentido se a expressão radical for não negativa, isto é, se - 1 ≤ x≤ 1 . Portanto, o escopo desta função é [- 1; 1] .

A área sombreada da reta numérica no desenho acima é a área de definição desta função.
Domínio da função de potência
Domínio de uma função potência com um expoente inteiro
E se uma- positivo, então o domínio da função é o conjunto de todos os números reais, ou seja, ]- ∞; + ∞[ ;
E se uma- negativo, então o domínio de definição da função é o conjunto ]- ∞; 0[ ∪ ]0 ;+ ∞[ , ou seja, toda a reta numérica exceto zero.

No desenho correspondente, toda a linha numérica é sombreada de cima e o ponto correspondente a zero é perfurado (não está incluído na área de definição da função).
Exemplo 3. Encontre o escopo de uma função .
Solução. O primeiro termo é uma potência inteira de x igual a 3, e a potência de x no segundo termo pode ser representada como uma unidade - também um inteiro. Portanto, o domínio desta função é a reta numérica inteira, ou seja, ]- ∞; +∞[.

Domínio de uma função potência com um expoente fracionário
No caso em que a função é dada pela fórmula:
se - for positivo, então o domínio da função é o conjunto 0; +∞[.
Exemplo 4. Encontre o escopo de uma função .
Solução. Ambos os termos na expressão da função - funções de energia com expoentes fracionários positivos. Portanto, o domínio desta função é o conjunto - ∞; +∞[.

Domínio de definição de funções exponenciais e logarítmicas
Domínio da função exponencial
No caso em que a função é dada pela fórmula, o domínio da função é a reta numérica inteira, ou seja, ]- ∞; +∞[.
O domínio da função logarítmica
A função logarítmica é definida sob a condição de que seu argumento seja positivo, ou seja, seu domínio de definição é o conjunto ]0; +∞[.
Encontre você mesmo o escopo da função e depois veja a solução
Domínio de definição de funções trigonométricas
Escopo da função y= cos( x) também é um conjunto R numeros reais.
Escopo da função y= tg( x) - vários R
números reais que não sejam números ![]() .
.
Escopo da função y=ctg( x) - vários R números reais que não sejam números.
Exemplo 8. Encontre o escopo de uma função .
Solução. A função externa é um logaritmo decimal e as condições de domínio se aplicam ao seu domínio de definição função logarítmica geralmente. Ou seja, seu argumento deve ser positivo. O argumento aqui é o seno de "x". Girando uma bússola imaginária em torno de um círculo, vemos que a condição sin x> 0 é violado quando "x" é igual a zero, "pi", dois, multiplicado por "pi" e geralmente igual ao produto do número "pi" e qualquer inteiro par ou ímpar.
Assim, o domínio de definição desta função é dado pela expressão
![]() ,
,
Onde ké um número inteiro.
Domínio das funções trigonométricas inversas
Escopo da função y= arcsin( x) - definir [-1; 1] .
Escopo da função y= arcos( x) - também o conjunto [-1; 1] .
Escopo da função y= arctan( x) - vários R numeros reais.
Escopo da função y= arcctg( x) também é um conjunto R numeros reais.
Exemplo 9. Encontre o escopo de uma função .
Solução. Vamos resolver a desigualdade:
Assim, obtemos o domínio de definição desta função - o segmento [- 4; quatro] .
Exemplo 10. Encontre o escopo de uma função
![]() .
.
Solução. Vamos resolver duas inequações:
Solução da primeira desigualdade:
Solução da segunda desigualdade:
Assim, obtemos o domínio de definição desta função - o segmento.
Domínio da fração
Se a função é dada por uma expressão fracionária na qual a variável está no denominador da fração, então o domínio da função é o conjunto R números reais, exceto x para o qual o denominador da fração se anula.
Exemplo 11. Encontre o escopo de uma função .
Solução. Resolvendo a igualdade a zero do denominador da fração, encontramos o domínio de definição desta função - o conjunto] - ∞; - 2[ ∪ ]- 2 ;+ ∞[ .