As propriedades da função são o maior e o menor valor. Como encontrar o menor valor de uma função
E para resolvê-lo, você precisa de conhecimento mínimo do tema. O próximo ano letivo está terminando, todos querem sair de férias e, para aproximar esse momento, vou imediatamente ao que interessa:
Vamos começar pela área. A área referida na condição é limitado fechado conjunto de pontos do plano. Por exemplo, um conjunto de pontos delimitados por um triângulo, incluindo o triângulo INTEIRO (se de fronteiras“Peça” pelo menos um ponto, então a área não será mais fechada). Na prática, também existem áreas de formato retangular, redondo e um pouco mais formas complexas. Vale lembrar que teoricamente analise matemática definições estritas são dadas limitações, isolamento, limites, etc., mas acho que todos estão cientes desses conceitos em um nível intuitivo, e não é necessário mais agora.
A área plana é denotada padrão pela letra , e, como regra, é dada analiticamente - por várias equações (não necessariamente linear); menos frequentemente desigualdades. Uma típica reviravolta verbal: "área fechada delimitada por linhas".
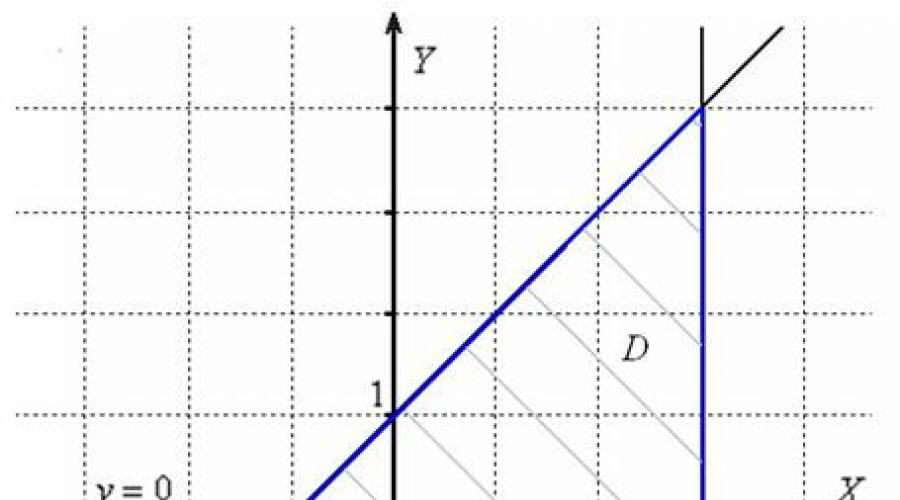
Uma parte integrante da tarefa em consideração é a construção da área no desenho. Como fazer isso? É necessário desenhar todas as linhas listadas (em este caso 3 direto) e analisar o que aconteceu. A área desejada geralmente é levemente hachurada e sua borda é destacada com uma linha em negrito: 
A mesma área pode ser definida desigualdades lineares: , que por algum motivo são mais frequentemente escritos como uma lista de enumeração, e não sistema.
Como a fronteira pertence à região, então todas as desigualdades, é claro, não estrito.
E agora o cerne da questão. Imagine que o eixo vai direto para você a partir da origem das coordenadas. Considere uma função que contínuo em cada ponto de área. O gráfico desta função é superfície, e a pequena felicidade é que, para resolver o problema de hoje, não precisamos saber como é essa superfície. Ele pode estar localizado acima, abaixo, cruzar o plano - tudo isso não é importante. E o seguinte é importante: de acordo com Teoremas de Weierstrass, contínuo dentro limitado fechadoárea, a função atinge seu máximo (do "mais alto") e menos (do "mais baixo") valores a serem encontrados. Esses valores são alcançados ou dentro pontos estacionários, pertencente à regiãoD , ou em pontos que se encontram no limite desta região. A partir do qual segue um algoritmo de solução simples e transparente:
Exemplo 1
Em uma área fechada limitada
Solução: Em primeiro lugar, você precisa representar a área no desenho. Infelizmente, é tecnicamente difícil para mim fazer um modelo interativo do problema e, portanto, darei imediatamente a ilustração final, que mostra todos os pontos "suspeitos" encontrados durante o estudo. Geralmente eles são colocados um após o outro à medida que são encontrados: 
Com base no preâmbulo, a decisão pode ser convenientemente dividida em dois pontos:
I) Vamos encontrar pontos estacionários. Esta é uma ação padrão que realizamos repetidamente na lição. sobre extremos de várias variáveis:
Ponto estacionário encontrado pertenceáreas: (marque no desenho), o que significa que devemos calcular o valor da função em um determinado ponto:
- como no artigo Os maiores e menores valores de uma função em um segmento, vou destacar os resultados importantes em negrito. Em um caderno, é conveniente circulá-los com um lápis.
Preste atenção à nossa segunda felicidade - não faz sentido verificar condição suficiente para um extremo. Por quê? Mesmo que no ponto em que a função atinja, por exemplo, mínimo local, isso NÃO SIGNIFICA que o valor resultante será mínimo em toda a região (veja o início da lição sobre extremos incondicionais) .
E se o ponto estacionário NÃO pertencer à área? Quase nada! Deve-se notar isso e ir para o próximo parágrafo.
II) Investigamos a fronteira da região.
Como a borda consiste nos lados de um triângulo, é conveniente dividir o estudo em 3 subparágrafos. Mas é melhor não fazê-lo de qualquer maneira. Do meu ponto de vista, é mais vantajoso considerar primeiro os segmentos paralelos aos eixos de coordenadas, e, em primeiro lugar, aqueles que estão nos próprios machados. Para pegar toda a sequência e lógica das ações, tente estudar o final "em uma respiração":
1) Vamos lidar com o lado inferior do triângulo. Para fazer isso, substituímos diretamente na função:
Alternativamente, você pode fazer assim: 
Geometricamente, isso significa que o plano de coordenadas (que também é dado pela equação)"cortar" de superfícies parábola "espacial", cujo topo cai imediatamente sob suspeita. Vamos descobrir onde ela está:
- o valor resultante "atingido" na área, e pode ser que no ponto (marca no desenho) a função atinge o maior ou menor valor em toda a área. De qualquer forma, vamos fazer os cálculos:
Outros "candidatos" são, claro, os extremos do segmento. Calcular os valores da função em pontos ![]() (marca no desenho):
(marca no desenho):
Aqui, a propósito, você pode realizar uma mini-verificação oral na versão "despojada": 
2) Para estudar o lado direito do triângulo, substituímos na função e “colocamos as coisas em ordem ali”:
Aqui realizamos imediatamente uma verificação aproximada, “tocando” o final do segmento já processado:
, perfeito.
A situação geométrica está relacionada com o ponto anterior:
- o valor resultante também “entrou no escopo de nossos interesses”, o que significa que precisamos calcular a que a função é igual no ponto que apareceu:
Vamos examinar a segunda extremidade do segmento:
Usando a função ![]() , vamos checar:
, vamos checar: 
3) Todo mundo provavelmente sabe como explorar o lado restante. Substituímos na função e realizamos simplificações:
A linha termina ![]() já foram investigados, mas no rascunho ainda verificamos se encontramos a função corretamente
já foram investigados, mas no rascunho ainda verificamos se encontramos a função corretamente ![]() :
:
– coincidiu com o resultado do 1º parágrafo;
– coincidiu com o resultado do 2º parágrafo.
Resta descobrir se há algo interessante dentro do segmento:
- há! Substituindo uma linha reta na equação, obtemos a ordenada desse “interesse”:
Marcamos um ponto no desenho e encontramos o valor correspondente da função:
Vamos controlar os cálculos de acordo com a versão "orçamento" ![]() :
:
, ordem.
E o passo final: CUIDADOSAMENTE examine todos os números "gordos", recomendo que até os iniciantes façam uma única lista: 
a partir do qual escolhemos o maior e o menor valor. Responda escreva no estilo do problema de encontrar os maiores e menores valores da função no intervalo:
Vou comentar novamente apenas no caso. sentido geométrico resultado:
– aqui é o ponto mais alto da superfície da região;
- aqui é o ponto mais baixo da superfície na área.
No problema analisado, encontramos 7 pontos “suspeitos”, mas seu número varia de tarefa para tarefa. Para uma região triangular, o "conjunto de exploração" mínimo consiste em três pontos. Isso acontece quando a função, por exemplo, define avião- é bastante claro que não há pontos estacionários, e a função pode atingir os valores máximos / mínimos apenas nos vértices do triângulo. Mas não existem exemplos assim uma, duas vezes - normalmente você tem que lidar com algum tipo de superfície de 2ª ordem.
Se você resolver um pouco essas tarefas, os triângulos podem fazer sua cabeça girar e, portanto, preparei para você exemplos incomuns para torná-lo quadrado :)
Exemplo 2
Encontre os maiores e menores valores de uma função ![]() em uma área fechada delimitada por linhas
em uma área fechada delimitada por linhas
Exemplo 3
Encontre os maiores e menores valores de uma função em uma área fechada limitada.
Atenção especial preste atenção à ordem racional e técnica de estudar o limite da área, bem como à cadeia de verificações intermediárias, o que evitará quase completamente erros computacionais. De um modo geral, você pode resolvê-lo como quiser, mas em alguns problemas, por exemplo, no mesmo Exemplo 2, há todas as chances de complicar significativamente sua vida. Amostra de Amostra terminar as tarefas no final da aula.
Sistematizamos o algoritmo de solução, caso contrário, com minha diligência de aranha, de alguma forma ele se perdeu em um longo fio de comentários do 1º exemplo:
- Na primeira etapa, construímos uma área, é desejável sombreá-la e destacar a borda com uma linha em negrito. Durante a solução, aparecerão pontos que precisam ser colocados no desenho.
– Encontre pontos estacionários e calcule os valores da função apenas naqueles, que pertencem à área . Os valores obtidos são destacados no texto (por exemplo, circulados com um lápis). Se o ponto estacionário NÃO pertence à área, marcamos esse fato com um ícone ou verbalmente. Se não houver pontos estacionários, tiramos uma conclusão por escrito de que eles estão ausentes. Em qualquer caso, este item não pode ser ignorado!
– Explorar a zona fronteiriça. Primeiro, é vantajoso lidar com linhas retas paralelas aos eixos coordenados (se houver algum). Os valores da função calculados em pontos "suspeitos" também são destacados. Muito foi dito sobre a técnica de solução acima e outra coisa será dita abaixo - leia, releia, mergulhe!
- Dos números selecionados, selecione os valores maiores e menores e dê uma resposta. Às vezes acontece que a função atinge esses valores em vários pontos ao mesmo tempo - nesse caso, todos esses pontos devem ser refletidos na resposta. Deixe, por exemplo, ![]() e aconteceu que menor valor. Então escrevemos que
e aconteceu que menor valor. Então escrevemos que
Os exemplos finais são dedicados a outros ideias úteisútil na prática:
Exemplo 4
Encontre os maiores e menores valores de uma função em uma área fechada ![]() .
.
Mantive a formulação do autor, na qual a área é dada como uma dupla desigualdade. Esta condição pode ser escrita em um sistema equivalente ou em uma forma mais tradicional para este problema: ![]()
Lembro-lhe que com não linear encontramos desigualdades em , e se você não entender o significado geométrico da entrada, por favor, não demore e esclareça a situação agora ;-)
Solução, como sempre, começa com a construção da área, que é uma espécie de “sola”: 
Hmm, às vezes você tem que roer não só o granito da ciência....
I) Encontre pontos estacionários: 
O sistema dos sonhos do idiota :) 
O ponto estacionário pertence à região, ou seja, encontra-se em seu limite.
E assim, não é nada ... a lição divertida foi - é isso que significa beber o chá certo =)
II) Investigamos a fronteira da região. Sem mais delongas, vamos começar com o eixo x:
1) Se , então
Descubra onde está o topo da parábola:
- Aprecie tais momentos - "acerte" direto ao ponto, a partir do qual tudo já está claro. Mas não deixe de conferir: ![]()
Vamos calcular os valores da função nas extremidades do segmento: 
2) C fundo Vamos descobrir as "solas" "de uma só vez" - sem nenhum complexo que substituímos na função, além disso, estaremos interessados apenas no segmento:
Ao controle:
Agora, isso já está trazendo algum renascimento ao passeio monótono em uma pista serrilhada. Vamos encontrar os pontos críticos:
Nós decidimos Equação quadrática você se lembra desse? ... No entanto, lembre-se, é claro, caso contrário você não leria essas linhas =) Se nos dois exemplos anteriores os cálculos fossem convenientes em frações decimais(que, aliás, é raro), então aqui estamos esperando o habitual frações comuns. Encontramos as raízes “x” e, usando a equação, determinamos as correspondentes coordenadas de “jogo” dos pontos “candidatos”: 
Vamos calcular os valores da função nos pontos encontrados: 
Verifique a função você mesmo.
Agora estudamos cuidadosamente os troféus ganhos e anotamos responda:
Aqui estão os "candidatos", portanto os "candidatos"!
Para uma solução autônoma:
Exemplo 5
Encontre os menores e maiores valores de uma função ![]() em uma área fechada
em uma área fechada ![]()
Uma entrada com chaves é assim: “um conjunto de pontos tal que”.
Às vezes, em tais exemplos, eles usam Método do multiplicador de Lagrange, mas necessidade realé improvável que seja usado. Assim, por exemplo, se uma função com a mesma área "de" for fornecida, após a substituição - com uma derivada sem dificuldades; além disso, tudo é traçado em “uma linha” (com sinais) sem a necessidade de considerar os semicírculos superior e inferior separadamente. Mas, claro, há mais casos difíceis, onde sem a função de Lagrange (onde , por exemplo, é a mesma equação do círculo)é difícil sobreviver - como é difícil sobreviver sem um bom descanso!
Tudo de bom para passar a sessão e até breve na próxima temporada!
Soluções e respostas:
Exemplo 2: Solução: desenhe a área no desenho:
Às vezes, nos problemas B15, existem funções "ruins" para as quais é difícil encontrar a derivada. Anteriormente, isso era apenas em testes, mas agora essas tarefas são tão comuns que não podem mais ser ignoradas na preparação para este exame.
Nesse caso, outros truques funcionam, um dos quais é - monótono.
A função f(x) é chamada monotonicamente crescente no segmento se para quaisquer pontos x 1 e x 2 deste segmento o seguinte for verdadeiro:
x 1< x 2 ⇒ f (x 1) < f (x2).
A função f(x) é chamada decrescente monotonicamente no segmento se para quaisquer pontos x 1 e x 2 deste segmento o seguinte for verdadeiro:
x 1< x 2 ⇒ f (x 1) > f ( x2).
Em outras palavras, para uma função crescente, quanto maior for x, maior será f(x). Para uma função decrescente, o oposto é verdadeiro: quanto mais x , menos f(x).
Por exemplo, o logaritmo aumenta monotonicamente se a base a > 1 e diminui monotonicamente se 0< a < 1. Не забывайте про область valores permitidos logaritmo: x > 0.
f (x) = log a x (a > 0; a ≠ 1; x > 0)
A raiz quadrada aritmética (e não apenas quadrada) aumenta monotonicamente em todo o domínio de definição:
A função exponencial se comporta de maneira semelhante ao logaritmo: aumenta para a > 1 e diminui para 0< a < 1. Но в отличие от логарифма, função exponencial definido para todos os números, não apenas x > 0:
f (x) = a x (a > 0)
Finalmente, graus com um expoente negativo. Você pode escrevê-los como uma fração. Eles têm um ponto de ruptura onde a monotonia é quebrada.
Todos esses recursos nunca são encontrados em forma pura. Polinômios, frações e outros absurdos são adicionados a eles, por causa dos quais se torna difícil calcular a derivada. O que acontece neste caso - agora vamos analisar.
Coordenadas do vértice da parábola
Na maioria das vezes, o argumento da função é substituído por trinômio quadrado da forma y = ax 2 + bx + c . Seu gráfico é uma parábola padrão, na qual estamos interessados em:
- Ramificações da parábola - podem subir (para a > 0) ou para baixo (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
- O vértice da parábola é o ponto extremo de uma função quadrática, no qual esta função toma seu menor (para a > 0) ou maior (a< 0) значение.
De maior interesse é topo de uma parábola, cuja abcissa é calculada pela fórmula:
Assim, encontramos o ponto extremo da função quadrática. Mas se a função original é monotônica, para ela o ponto x 0 também será um ponto extremo. Assim, formulamos a regra chave:
pontos extremos trinômio quadrado e função complexa, em que ele entra, são os mesmos. Portanto, você pode procurar x 0 para um trinômio quadrado e esquecer a função.
A partir do raciocínio acima, ainda não está claro que tipo de ponto chegamos: um máximo ou um mínimo. No entanto, as tarefas são projetadas especificamente para que isso não importe. Julgue por si mesmo:
- Não há segmento na condição do problema. Portanto, não é necessário calcular f(a) ef(b). Resta considerar apenas os pontos extremos;
- Mas existe apenas um ponto - este é o topo da parábola x 0, cujas coordenadas são calculadas literalmente oralmente e sem derivadas.
Assim, a solução do problema é bastante simplificada e reduzida a apenas duas etapas:
- Escreva a equação da parábola y = ax 2 + bx + c e encontre seu vértice usando a fórmula: x 0 = −b /2a;
- Encontre o valor da função original neste ponto: f (x 0). Se não houver condições adicionais, esta será a resposta.
À primeira vista, esse algoritmo e sua justificativa podem parecer complicados. Eu deliberadamente não publico um esquema de solução "nua", uma vez que a aplicação impensada de tais regras está repleta de erros.
Vamos considerar os problemas reais de exame experimental em matemática - é onde essa técnica ocorre com mais frequência. Ao mesmo tempo, garantiremos que muitos problemas de B15 se tornem quase verbais.
Sob a raiz está função quadrática y \u003d x 2 + 6x + 13. O gráfico desta função é uma parábola com ramificações para cima, já que o coeficiente a \u003d 1\u003e 0.
Parte superior da parábola:
x 0 \u003d -b / (2a) \u003d -6 / (2 1) \u003d -6 / 2 \u003d -3
Como os ramos da parábola são direcionados para cima, no ponto x 0 \u003d −3, a função y \u003d x 2 + 6x + 13 assume o menor valor.
A raiz é crescente monotonicamente, então x 0 é o ponto mínimo de toda a função. Nós temos:
Uma tarefa. Encontre o menor valor da função:
y = log 2 (x 2 + 2x + 9)
Sob o logaritmo está novamente uma função quadrática: y \u003d x 2 + 2x + 9. O gráfico é uma parábola com ramificações para cima, porque a = 1 > 0.
Parte superior da parábola:
x 0 \u003d -b / (2a) \u003d -2 / (2 1) \u003d -2/2 \u003d -1
Assim, no ponto x 0 = −1, a função quadrática assume o menor valor. Mas a função y = log 2 x é monótona, então:
y min = y (−1) = log 2 ((−1) 2 + 2 (−1) + 9) = ... = log 2 8 = 3
O expoente é uma função quadrática y = 1 − 4x − x 2 . Vamos reescrever na forma normal: y = −x 2 − 4x + 1.
Obviamente, o gráfico desta função é uma parábola, ramos para baixo (a = −1< 0). Поэтому вершина будет точкой максимума:
x 0 = −b /(2a ) = −(−4)/(2 (−1)) = 4/(−2) = −2
A função original é exponencial, é monotônica, então valor mais alto estará no ponto encontrado x 0 = −2:
Um leitor atento certamente notará que não escrevemos a área dos valores permitidos da raiz e do logaritmo. Mas isso não era necessário: dentro existem funções cujos valores são sempre positivos.
Consequências do escopo de uma função
Às vezes, para resolver o problema B15, não basta encontrar o vértice da parábola. O valor desejado pode estar no final do segmento, mas não no ponto extremo. Se a tarefa não especificar um segmento, veja faixa de tolerância função originária. Nomeadamente:
Preste atenção novamente: o zero pode estar abaixo da raiz, mas nunca no logaritmo ou no denominador de uma fração. Vamos ver como funciona com exemplos específicos:
Uma tarefa. Encontre o maior valor da função:
Sob a raiz está novamente uma função quadrática: y \u003d 3 - 2x - x 2. Seu gráfico é uma parábola, mas se ramifica desde a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Raiz quadrada de um número negativo não existe.
Escrevemos a área dos valores permitidos (ODZ):
3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]
Agora encontre o vértice da parábola:
x 0 = −b /(2a ) = −(−2)/(2 (−1)) = 2/(−2) = −1
O ponto x 0 = −1 pertence ao segmento ODZ - e isso é bom. Agora consideramos o valor da função no ponto x 0, bem como nas extremidades da ODZ:
y(−3) = y(1) = 0
Então, temos os números 2 e 0. Pedem-nos para encontrar o maior - este é o número 2.
Uma tarefa. Encontre o menor valor da função:
y = log 0,5 (6x - x 2 - 5)
Dentro do logaritmo existe uma função quadrática y = 6x − x 2 − 5. Esta é uma parábola com ramificações para baixo, mas no logaritmo não pode ser números negativos, então escrevemos a ODZ:
6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)
Observe: a desigualdade é estrita, portanto, as extremidades não pertencem à ODZ. Desta forma, o logaritmo difere da raiz, onde as extremidades do segmento nos convém muito bem.
Procurando o vértice da parábola:
x 0 = −b /(2a ) = −6/(2 (−1)) = −6/(−2) = 3
O topo da parábola se ajusta ao longo da ZOD: x 0 = 3 ∈ (1; 5). Mas como as extremidades do segmento não nos interessam, consideramos o valor da função apenas no ponto x 0:
y min = y (3) = log 0,5 (6 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2
A PARTIR DE ponto prático De maior interesse é o uso da derivada para encontrar os maiores e menores valores de uma função. Com o que está conectado? Maximizar lucros, minimizar custos, determinar a carga ótima dos equipamentos... Ou seja, em muitas áreas da vida, é preciso resolver o problema de otimizar alguns parâmetros. E este é o problema de encontrar os maiores e menores valores da função.
Deve-se notar que o maior e o menor valor de uma função geralmente é procurado em algum intervalo X , que é todo o domínio da função ou parte do domínio. O próprio intervalo X pode ser um segmento de linha, um intervalo aberto ![]() , um intervalo infinito.
, um intervalo infinito.
Neste artigo, falaremos sobre encontrar os maiores e menores valores explicitamente. determinada função uma variável y=f(x) .
Navegação da página.
O maior e o menor valor de uma função - definições, ilustrações.
Detenhamo-nos brevemente nas principais definições.
O maior valor da função ![]() , que para qualquer
, que para qualquer ![]() a desigualdade é verdadeira.
a desigualdade é verdadeira.
O menor valor da função y=f(x) no intervalo X é chamado de tal valor ![]() , que para qualquer
, que para qualquer ![]() a desigualdade é verdadeira.
a desigualdade é verdadeira.
Essas definições são intuitivas: o maior (menor) valor de uma função é o maior (menor) valor aceito no intervalo considerado com a abcissa.
Pontos estacionários são os valores do argumento em que a derivada da função desaparece.
Por que precisamos de pontos estacionários ao encontrar os maiores e menores valores? A resposta a esta questão é dada pelo teorema de Fermat. Segue-se deste teorema que se uma função diferenciável tem um extremo (mínimo local ou máximo local) em algum ponto, então este ponto é estacionário. Assim, a função geralmente assume seu valor máximo (menor) no intervalo X em um dos pontos estacionários desse intervalo.
Além disso, uma função geralmente pode assumir os maiores e menores valores em pontos onde a primeira derivada dessa função não existe e a própria função é definida.
Vamos responder imediatamente a uma das perguntas mais comuns sobre este tema: "É sempre possível determinar o maior (menor) valor de uma função"? Não nem sempre. Às vezes, os limites do intervalo X coincidem com os limites do domínio da função, ou o intervalo X é infinito. E algumas funções no infinito e nos limites do domínio de definição podem assumir valores infinitamente grandes e infinitamente pequenos. Nesses casos, nada pode ser dito sobre o maior e o menor valor da função.
Para maior clareza, damos uma ilustração gráfica. Olhe para as fotos - e muito ficará claro.
No segmento

Na primeira figura, a função assume os valores maior (max y ) e menor (min y ) em pontos estacionários dentro do segmento [-6;6] .
Considere o caso mostrado na segunda figura. Altere o segmento para . Neste exemplo, o menor valor da função é obtido em um ponto estacionário e o maior - em um ponto com uma abcissa correspondente ao limite direito do intervalo.
Na figura nº 3, os pontos de fronteira do segmento [-3; 2] são as abcissas dos pontos correspondentes ao maior e ao menor valor da função.
Na faixa aberta

Na quarta figura, a função assume os valores maior (max y ) e menor (min y ) em pontos estacionários dentro do intervalo aberto (-6;6) .
No intervalo , nenhuma conclusão pode ser tirada sobre o maior valor.
No infinito

No exemplo mostrado na sétima figura, a função toma o maior valor (max y ) em um ponto estacionário com a abcissa x=1 , e o menor valor (min y ) é alcançado no limite direito do intervalo. No infinito menos, os valores da função se aproximam assintoticamente de y=3 .
No intervalo, a função não atinge nem o menor nem o maior valor. Como x=2 tende para a direita, os valores da função tendem a menos infinito (a linha reta x=2 é uma assíntota vertical), e como a abcissa tende a mais infinito, os valores da função se aproximam assintoticamente de y=3 . Uma ilustração gráfica deste exemplo é mostrada na Figura 8.
Algoritmo para encontrar os maiores e menores valores de uma função contínua no segmento.
Escrevemos um algoritmo que nos permite encontrar o maior e o menor valor de uma função em um segmento.
- Encontramos o domínio da função e verificamos se ele contém o segmento inteiro.
- Encontramos todos os pontos nos quais a primeira derivada não existe e que estão contidos no segmento (geralmente tais pontos ocorrem em funções com um argumento sob o sinal do módulo e em funções de energia com um expoente racional fracionário). Se não houver tais pontos, vá para o próximo ponto.
- Determinamos todos os pontos estacionários que se enquadram no segmento. Para fazer isso, igualamos a zero, resolvemos a equação resultante e escolhemos as raízes apropriadas. Se não houver pontos estacionários ou nenhum deles cair no segmento, vá para a próxima etapa.
- Calculamos os valores da função nos pontos estacionários selecionados (se houver), em pontos onde a primeira derivada não existe (se houver), e também em x=a e x=b .
- A partir dos valores obtidos da função, selecionamos o maior e o menor - serão os valores máximo e menor desejados da função, respectivamente.
Vamos analisar o algoritmo ao resolver um exemplo para encontrar os maiores e menores valores de uma função em um segmento.
Exemplo.
Encontre o maior e o menor valor de uma função
- no segmento;
- no intervalo [-4;-1] .
Solução.
O domínio da função é todo o conjunto dos números reais, exceto o zero, ou seja, . Ambos os segmentos se enquadram no domínio da definição.
Encontramos a derivada da função em relação a: 
Obviamente, a derivada da função existe em todos os pontos dos segmentos e [-4;-1] .
Pontos estacionários são determinados a partir da equação. A única raiz real é x=2. Este ponto estacionário cai no primeiro segmento.
Para o primeiro caso, calculamos os valores da função nas extremidades do segmento e em um ponto estacionário, ou seja, para x=1 , x=2 e x=4 : 
Portanto, o maior valor da função ![]() é alcançado em x=1, e o menor valor
é alcançado em x=1, e o menor valor  – em x=2.
– em x=2.
Para o segundo caso, calculamos os valores da função apenas nas extremidades do segmento [-4;-1] (já que não contém um único ponto estacionário): 
Declaração do problema 2:
Dada uma função que é definida e contínua em algum intervalo . É necessário encontrar o maior (menor) valor da função nesse intervalo.
Base teórica.
Teorema (Segundo Teorema de Weierstrass):
Se uma função é definida e contínua em um intervalo fechado, ela atinge seus valores máximo e mínimo nesse intervalo.
A função pode atingir seus valores máximos e mínimos nos pontos internos do intervalo ou em seus limites. Vamos ilustrar tudo opções possíveis.
Explicação:
1) A função atinge seu valor máximo na borda esquerda do intervalo no ponto , e seu valor mínimo na borda direita do intervalo no ponto .
2) A função atinge seu valor máximo no ponto (este é o ponto máximo) e seu valor mínimo no limite direito do intervalo no ponto.
3) A função atinge seu valor máximo na borda esquerda do intervalo no ponto , e seu valor mínimo no ponto (este é o ponto mínimo).
4) A função é constante no intervalo, ou seja. atinge seus valores mínimo e máximo em qualquer ponto do intervalo, e os valores mínimo e máximo são iguais entre si.
5) A função atinge seu valor máximo no ponto , e seu valor mínimo no ponto (apesar de a função ter um máximo e um mínimo nesse intervalo).
6) A função atinge seu valor máximo em um ponto (este é o ponto máximo) e seu valor mínimo em um ponto (este é o ponto mínimo).
Comente:
"Máximo" e "valor máximo" são coisas diferentes. Isso decorre da definição do máximo e da compreensão intuitiva da frase "valor máximo".
Algoritmo para resolver o problema 2.
4) Escolha o maior (menor) dos valores obtidos e anote a resposta.
Exemplo 4:
Determine o maior e o menor valor de uma função ![]() no segmento.
no segmento.
Solução:
1) Encontre a derivada da função. ![]()
2) Encontre pontos estacionários (e pontos que suspeitem de um extremo) resolvendo a equação . Preste atenção aos pontos onde não há derivada finita bilateral. 
3) Calcule os valores da função em pontos estacionários e nos limites do intervalo.
4) Escolha o maior (menor) dos valores obtidos e anote a resposta.
A função neste segmento atinge seu valor máximo no ponto com coordenadas .
A função neste segmento atinge seu valor mínimo no ponto com coordenadas .
Você pode verificar a exatidão dos cálculos observando o gráfico da função em estudo. 
Comente: A função atinge seu valor máximo no ponto máximo e o valor mínimo no limite do segmento.
Caso especial.
Suponha que queremos encontrar o máximo e valor mínimo alguma função no intervalo. Após a execução do primeiro parágrafo do algoritmo, ou seja, cálculo do derivativo, fica claro que, por exemplo, leva apenas valores negativos em todo o segmento em consideração. Lembre-se que se a derivada for negativa, então a função é decrescente. Descobrimos que a função está diminuindo em todo o intervalo. Esta situação é mostrada no gráfico nº 1 no início do artigo.
A função diminui no intervalo, ou seja, não tem pontos extremos. Pode-se ver na imagem que a função terá o menor valor na borda direita do segmento e o maior valor na esquerda. se a derivada no intervalo for sempre positiva, então a função é crescente. O menor valor está na borda esquerda do segmento, o maior está à direita.
