Tabela de valores sin. Funções trigonométricas
Os conceitos de seno (), cosseno (), tangente (), cotangente () estão inextricavelmente ligados ao conceito de ângulo. Para entender bem esses conceitos, à primeira vista, complexos (que causam um estado de horror em muitos escolares), e ter certeza de que “o diabo não é tão assustador quanto é pintado”, vamos começar do início e entender o conceito de ângulo.
O conceito de ângulo: radiano, grau
Vamos olhar para a imagem. O vetor "virou" em relação ao ponto por uma certa quantidade. Então a medida dessa rotação em relação à posição inicial será canto.
O que mais você precisa saber sobre o conceito de ângulo? Bem, unidades de ângulo, é claro!
O ângulo, tanto em geometria quanto em trigonometria, pode ser medido em graus e radianos.
O ângulo em (um grau) é chamado de ângulo central no círculo, com base em um arco circular igual à parte do círculo. Assim, todo o círculo consiste em "pedaços" de arcos circulares, ou seja, o ângulo descrito pelo círculo é igual.

Ou seja, a figura acima mostra um ângulo que é igual, ou seja, esse ângulo é baseado em um arco circular do tamanho da circunferência.
Um ângulo em radianos é chamado de ângulo central em um círculo, com base em um arco circular, cujo comprimento é igual ao raio do círculo. Bem, você entendeu? Se não, então vamos olhar para a imagem.

Assim, a figura mostra um ângulo igual a um radiano, ou seja, esse ângulo é baseado em um arco circular, cujo comprimento é igual ao raio do círculo (o comprimento é igual ao comprimento ou o raio é igual a o comprimento do arco). Assim, o comprimento do arco é calculado pela fórmula:
Onde é o ângulo central em radianos.
Bem, sabendo disso, você pode responder quantos radianos contém um ângulo descrito por um círculo? Sim, para isso você precisa se lembrar da fórmula da circunferência de um círculo. Lá está ela:
Bem, agora vamos correlacionar essas duas fórmulas e fazer com que o ângulo descrito pelo círculo seja igual. Ou seja, correlacionando o valor em graus e radianos, obtemos isso. Respectivamente, . Como você pode ver, ao contrário de "graus", a palavra "radiano" é omitida, pois a unidade de medida geralmente é clara no contexto.
Quantos radianos são? Isso mesmo!
Entendi? Em seguida, aperte para a frente:
Alguma dificuldade? Então veja respostas:
Triângulo retângulo: seno, cosseno, tangente, cotangente de um ângulo
Então, com o conceito de ângulo descoberto. Mas o que é o seno, cosseno, tangente, cotangente de um ângulo? Vamos descobrir. Para isso, um triângulo retângulo nos ajudará.

Como se chamam os lados de um triângulo retângulo? Isso mesmo, a hipotenusa e os catetos: a hipotenusa é o lado oposto ao ângulo reto (no nosso exemplo, este é o lado); as pernas são os dois lados restantes e (aqueles que são adjacentes ao ângulo reto), além disso, se considerarmos as pernas em relação ao ângulo, então a perna é a perna adjacente e a perna é a oposta. Então, agora vamos responder a pergunta: quais são o seno, cosseno, tangente e cotangente de um ângulo?
Seno de um ânguloé a razão da perna oposta (distante) para a hipotenusa.
em nosso triângulo.
Cosseno de um ângulo- esta é a razão da perna adjacente (próxima) para a hipotenusa.
em nosso triângulo.
Ângulo tangente- esta é a proporção da perna oposta (distante) para a adjacente (perto).
em nosso triângulo.
Cotangente de um ângulo- esta é a proporção da perna adjacente (próxima) para a oposta (distante).
em nosso triângulo.
Essas definições são necessárias lembrar! Para tornar mais fácil lembrar qual perna dividir por qual, você precisa entender claramente que em tangente e co-tangente apenas as pernas ficam sentadas, e a hipotenusa aparece apenas em seio e cosseno. E então você pode criar uma cadeia de associações. Por exemplo, este:
cosseno→toque→toque→adjacente;
Cotangente→toque→toque→adjacente.
Antes de tudo, é necessário lembrar que o seno, cosseno, tangente e cotangente como razões dos lados de um triângulo não dependem dos comprimentos desses lados (em um ângulo). Não confie? Então certifique-se olhando para a imagem:

Considere, por exemplo, o cosseno de um ângulo. Por definição, a partir de um triângulo: , mas podemos calcular o cosseno de um ângulo a partir de um triângulo: . Você vê, os comprimentos dos lados são diferentes, mas o valor do cosseno de um ângulo é o mesmo. Assim, os valores de seno, cosseno, tangente e cotangente dependem apenas da magnitude do ângulo.
Se você entende as definições, vá em frente e corrija-as!
Para o triângulo mostrado na figura abaixo, encontramos.

Bem, você conseguiu? Então tente você mesmo: calcule o mesmo para o canto.
Círculo unitário (trigonométrico)
Entendendo os conceitos de graus e radianos, consideramos um círculo com um raio igual a. Tal círculo é chamado solteiro. É muito útil no estudo da trigonometria. Portanto, nos debruçamos sobre isso com um pouco mais de detalhes.

Como você pode ver, este círculo é construído no sistema de coordenadas cartesianas. O raio do círculo é igual a um, enquanto o centro do círculo está na origem, a posição inicial do vetor de raio é fixada ao longo da direção positiva do eixo (no nosso exemplo, este é o raio).
Cada ponto do círculo corresponde a dois números: a coordenada ao longo do eixo e a coordenada ao longo do eixo. Quais são esses números de coordenadas? E, em geral, o que eles têm a ver com o tema em questão? Para fazer isso, lembre-se do triângulo retângulo considerado. Na figura acima, você pode ver dois triângulos retângulos inteiros. Considere um triângulo. É retangular porque é perpendicular ao eixo.
O que é igual a de um triângulo? Isso mesmo. Além disso, sabemos que é o raio do círculo unitário e, portanto, . Substitua esse valor em nossa fórmula de cosseno. Aqui está o que acontece:
E o que é igual a de um triângulo? Bem, claro, ! Substitua o valor do raio nesta fórmula e obtenha:
Então, você pode me dizer quais são as coordenadas de um ponto que pertence ao círculo? Bem, de jeito nenhum? E se você perceber isso e são apenas números? A que coordenada corresponde? Bem, é claro, a coordenada! A que coordenada corresponde? Isso mesmo, coordenar! Assim, o ponto.

E o que então são iguais e? Isso mesmo, vamos usar as definições apropriadas de tangente e cotangente e obter isso, a.
E se o ângulo for maior? Aqui, por exemplo, como nesta imagem:

O que mudou neste exemplo? Vamos descobrir. Para fazer isso, voltamos novamente para um triângulo retângulo. Considere um triângulo retângulo: um ângulo (como adjacente a um ângulo). Qual é o valor do seno, cosseno, tangente e cotangente de um ângulo? Isso mesmo, aderimos às definições correspondentes das funções trigonométricas:
Bem, como você pode ver, o valor do seno do ângulo ainda corresponde à coordenada; o valor do cosseno do ângulo - a coordenada; e os valores de tangente e cotangente às razões correspondentes. Assim, essas relações são aplicáveis a quaisquer rotações do vetor raio.
Já foi mencionado que a posição inicial do vetor raio é ao longo da direção positiva do eixo. Até agora, giramos esse vetor no sentido anti-horário, mas o que acontece se o girarmos no sentido horário? Nada de extraordinário, você também obterá um ângulo de um determinado tamanho, mas apenas negativo. Assim, ao girar o vetor raio no sentido anti-horário, obtemos ângulos positivos, e ao girar no sentido horário - negativo.
Então, sabemos que toda uma revolução do vetor raio ao redor do círculo é ou. É possível girar o vetor raio por ou por? Bem, claro que você pode! No primeiro caso, portanto, o vetor raio fará uma revolução completa e parará na posição ou.
No segundo caso, ou seja, o raio vetor fará três voltas completas e parará na posição ou.
Assim, a partir dos exemplos acima, podemos concluir que os ângulos que diferem por ou (onde é qualquer número inteiro) correspondem à mesma posição do vetor raio.
A figura abaixo mostra um ângulo. A mesma imagem corresponde ao canto, e assim por diante. Esta lista pode ser continuada indefinidamente. Todos esses ângulos podem ser escritos com a fórmula geral ou (onde é qualquer número inteiro)

Agora, conhecendo as definições das funções trigonométricas básicas e usando o círculo unitário, tente responder a quais valores são iguais:
Aqui está um círculo unitário para ajudá-lo:

Alguma dificuldade? Então vamos descobrir. Então sabemos que:
A partir daqui, determinamos as coordenadas dos pontos correspondentes a certas medidas do ângulo. Bem, vamos começar pela ordem: o canto em corresponde a um ponto com coordenadas, portanto:
Não existe;
Além disso, seguindo a mesma lógica, descobrimos que os cantos em correspondem a pontos com coordenadas, respectivamente. Sabendo disso, é fácil determinar os valores das funções trigonométricas nos pontos correspondentes. Tente você mesmo primeiro, depois verifique as respostas.
Respostas:
Não existe
Não existe
Não existe
Não existe
Assim, podemos fazer a seguinte tabela:

Não há necessidade de lembrar todos esses valores. Basta lembrar a correspondência entre as coordenadas dos pontos no círculo unitário e os valores das funções trigonométricas:
Mas os valores das funções trigonométricas dos ângulos e, dados na tabela abaixo, deve ser lembrado:

Não tenha medo, agora vamos mostrar um dos exemplos memorização bastante simples dos valores correspondentes:
Para usar este método, é vital lembrar os valores do seno para todas as três medidas do ângulo (), bem como o valor da tangente do ângulo em. Conhecendo esses valores, é bastante fácil restaurar toda a tabela - os valores de cossenosão transferidos de acordo com as setas, ou seja:
Sabendo disso, você pode restaurar os valores para. O numerador " " corresponderá e o denominador " " corresponderá. Os valores cotangentes são transferidos de acordo com as setas mostradas na figura. Se você entender isso e se lembrar do diagrama com setas, será suficiente lembrar o valor inteiro da tabela.
Coordenadas de um ponto em um círculo
É possível encontrar um ponto (suas coordenadas) em um círculo, conhecendo as coordenadas do centro do círculo, seu raio e ângulo de rotação?
Bem, claro que você pode! Vamos trazer para fora fórmula geral para encontrar as coordenadas de um ponto.
Aqui, por exemplo, temos esse círculo:

Nos é dado que o ponto é o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas girando o ponto em graus.
Como pode ser visto na figura, a coordenada do ponto corresponde ao comprimento do segmento. O comprimento do segmento corresponde à coordenada do centro do círculo, ou seja, é igual a. O comprimento de um segmento pode ser expresso usando a definição de cosseno:
Então temos que para o ponto a coordenada.
Pela mesma lógica, encontramos o valor da coordenada y para o ponto. Nesse caminho,
Então, em termos gerais, as coordenadas dos pontos são determinadas pelas fórmulas:
Coordenadas do centro do círculo,
raio do círculo,
Ângulo de rotação do vetor raio.
Como você pode ver, para o círculo unitário que estamos considerando, essas fórmulas são significativamente reduzidas, pois as coordenadas do centro são zero e o raio é igual a um:
Bem, vamos tentar essas fórmulas para dar um gostinho, praticando encontrar pontos em um círculo?
1. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
2. Encontre as coordenadas de um ponto em um círculo unitário obtido pela rotação de um ponto.
3. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
4. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
5. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
Tendo problemas para encontrar as coordenadas de um ponto em um círculo?
Resolva esses cinco exemplos (ou entenda bem a solução) e você aprenderá como encontrá-los!
1.
Pode ser visto que. E sabemos o que corresponde a uma volta completa do ponto de partida. Assim, o ponto desejado estará na mesma posição que ao virar. Sabendo disso, encontramos as coordenadas desejadas do ponto:
2. O círculo é uma unidade com centro em um ponto, o que significa que podemos usar fórmulas simplificadas:
Pode ser visto que. Sabemos o que corresponde a duas rotações completas do ponto de partida. Assim, o ponto desejado estará na mesma posição que ao virar. Sabendo disso, encontramos as coordenadas desejadas do ponto:
Seno e cosseno são valores tabulares. Lembramos seus valores e obtemos:
Assim, o ponto desejado tem coordenadas.
3. O círculo é uma unidade com centro em um ponto, o que significa que podemos usar fórmulas simplificadas:
Pode ser visto que. Vamos descrever o exemplo considerado na figura:

O raio faz ângulos com o eixo igual a e. Sabendo que os valores tabulares do cosseno e do seno são iguais, e tendo determinado que o cosseno aqui assume um valor negativo e o seno é positivo, temos:
Exemplos semelhantes são analisados com mais detalhes ao estudar as fórmulas para reduzir funções trigonométricas no tópico.
Assim, o ponto desejado tem coordenadas.
4.
Ângulo de rotação do vetor de raio (por condição)
Para determinar os sinais correspondentes de seno e cosseno, construímos um círculo unitário e um ângulo:

Como você pode ver, o valor, ou seja, é positivo, e o valor, ou seja, é negativo. Conhecendo os valores tabulares das funções trigonométricas correspondentes, obtemos que:
Vamos substituir os valores obtidos em nossa fórmula e encontrar as coordenadas:
Assim, o ponto desejado tem coordenadas.
5. Para resolver este problema, usamos fórmulas na forma geral, onde
As coordenadas do centro do círculo (no nosso exemplo,
Raio do círculo (por condição)
Ângulo de rotação do vetor raio (por condição).
Substitua todos os valores na fórmula e obtenha:
e - valores da tabela. Lembramos e os substituímos na fórmula:
Assim, o ponto desejado tem coordenadas.
RESUMO E FÓRMULA BÁSICA
O seno de um ângulo é a razão entre o cateto oposto (distante) e a hipotenusa.
O cosseno de um ângulo é a razão entre o cateto adjacente (próximo) e a hipotenusa.
A tangente de um ângulo é a razão entre a perna oposta (distante) e a adjacente (próxima).
A cotangente de um ângulo é a razão entre a perna adjacente (próxima) e a oposta (distante).
Este artigo coletou tabelas de senos, cossenos, tangentes e cotangentes. Primeiro, damos uma tabela de valores básicosde funções trigonométricas, ou seja, uma tabela de senos, cossenos, tangentes e cotangentes de ângulos 0, 30, 45, 60, 90, ..., 360 graus ( 0, π/6, π/4, π/3, π/2, …, 2π radiano). Depois disso, daremos uma tabela de senos e cossenos, bem como uma tabela de tangentes e cotangentes de V. M. Bradis, e mostraremos como usar essas tabelas na hora de encontrar os valores das funções trigonométricas.
Navegação da página.
Tabela de senos, cossenos, tangentes e cotangentes para ângulos 0, 30, 45, 60, 90, ... graus
Bibliografia.
- Álgebra: Proc. para 9 células. média escola / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Iluminismo, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
- Bashmakov M.I.Álgebra e o início da análise: Proc. para 10-11 células. média escola - 3ª edição. - M.: Iluminismo, 1993. - 351 p.: ll. - ISBN 5-09-004617-4.
- Álgebra e o início da análise: Proc. para 10-11 células. Educação geral instituições / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn e outros; Ed. A. N. Kolmogorova.- 14ª ed.- M.: Iluminismo, 2004.- 384 p.: il.- ISBN 5-09-013651-3.
- Gusev V. A., Mordkovich A. G. Matemática (um manual para candidatos a escolas técnicas): Proc. subsídio.- M.; Mais alto escola, 1984.-351 p., ll.
- Bradis V.M. Tabelas matemáticas de quatro dígitos: Para educação geral. livro didático estabelecimentos. - 2ª edição. - M.: Abetarda, 1999.- 96 p.: il. ISBN 5-7107-2667-2
No artigo, entenderemos completamente como é tabela de valores trigonométricos, seno, cosseno, tangente e cotangente. Considere o valor básico das funções trigonométricas, de um ângulo de 0,30,45,60,90,...,360 graus. E vamos ver como usar essas tabelas no cálculo do valor das funções trigonométricas.
Primeiro considere tabela de cosseno, seno, tangente e cotangente de um ângulo de 0, 30, 45, 60, 90, .. graus. A definição dessas quantidades permite determinar o valor das funções dos ângulos de 0 e 90 graus:
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, a cotangente de 00 será indefinida
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, a tangente de 90 0 será indefinida
Se tomarmos triângulos retângulos cujos ângulos são de 30 a 90 graus. Nós temos:
sen 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sen 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sen 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Representamos todos os valores obtidos na forma tabela trigonométrica:
Tabela de senos, cossenos, tangentes e cotangentes!
Se usarmos a fórmula de redução, nossa tabela aumentará, valores para ângulos de até 360 graus serão adicionados. Será parecido com:

Além disso, com base nas propriedades da periodicidade, a tabela pode ser aumentada se substituirmos os ângulos por 0 0 +360 0 *z .... 330 0 +360 0 *z, em que z é um número inteiro. Nesta tabela, é possível calcular o valor de todos os ângulos correspondentes a pontos em um único círculo.

Vamos ver claramente como usar a tabela na solução.
Tudo é muito simples. Como o valor de que precisamos está no ponto de interseção das células de que precisamos. Por exemplo, vamos pegar cos de um ângulo de 60 graus, na tabela ficará assim:

Na tabela final dos principais valores das funções trigonométricas, agimos da mesma forma. Mas nesta tabela é possível descobrir quanto será a tangente de um ângulo de 1020 graus, ela = -√3 Vamos verificar 1020 0 = 300 0 +360 0 *2. Vamos encontrar a mesa.

Mesa Bradis. Para seno, cosseno, tangente e cotangente.
As tabelas de Bradys são divididas em várias partes, elas consistem em tabelas de cosseno e seno, tangente e cotangente - que é dividida em duas partes (tg de um ângulo de até 90 graus e ctg de pequenos ângulos).
Seno e cosseno


ângulo tg de 00 a 760, ângulo ctg de 140 a 900.


tg até 900 e ctg pequenos ângulos.
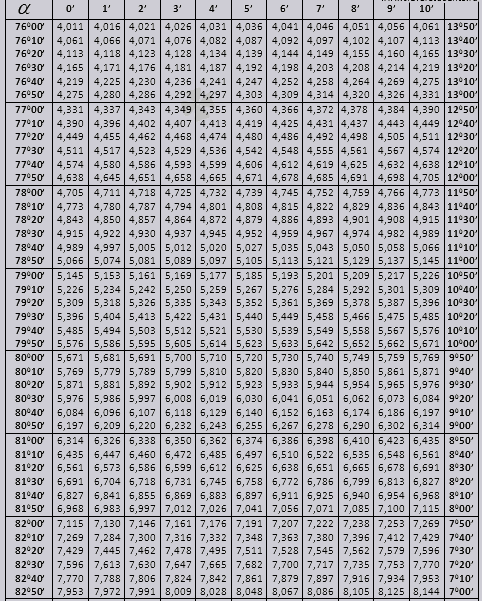

Vamos descobrir como usar as tabelas de Bradis na resolução de problemas.
Vamos encontrar a designação sin (a designação na coluna da borda esquerda) 42 minutos (a designação está na linha superior). Ao cruzar estamos procurando uma designação, é = 0,3040.
Os valores de minutos são indicados com um intervalo de seis minutos, e se o valor que precisamos estiver dentro desse intervalo. Vamos levar 44 minutos, e na tabela são apenas 42. Tomamos 42 como base e usamos as colunas adicionais do lado direito, pegamos a 2ª correção e somamos 0,3040 + 0,0006, obtemos 0,3046.
Com sen 47 min, tomamos 48 min como base e subtraímos 1 correção dele, ou seja, 0,3057 - 0,0003 = 0,3054
Ao calcular cos, trabalhamos de forma semelhante ao sin, apenas tomamos a linha inferior da tabela como base. Por exemplo, cos 20 0 = 0,9397
Os valores tg de um ângulo de até 90 0 e cot de um ângulo pequeno estão corretos e não há correções neles. Por exemplo, encontre tg 78 0 37min = 4,967 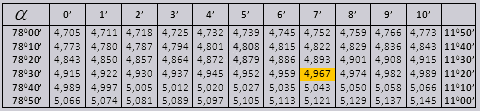
e ctg 20 0 13 min = 25,83 
Bem, aqui consideramos as principais tabelas trigonométricas. Esperamos que esta informação tenha sido extremamente útil para você. Suas dúvidas sobre as mesas, se houver, não deixe de escrever nos comentários!
Nota: Guarda-lamas de parede - uma placa de guarda-lamas para proteger as paredes. Siga o link para-lamas sem moldura (http://www.spi-polymer.ru/otboyniki/) e saiba mais.
1. Funções trigonométricas são funções elementares cujo argumento é canto. As funções trigonométricas descrevem a relação entre lados e ângulos agudos em um triângulo retângulo. As áreas de aplicação das funções trigonométricas são extremamente diversas. Assim, por exemplo, quaisquer processos periódicos podem ser representados como uma soma de funções trigonométricas (série de Fourier). Essas funções geralmente aparecem ao resolver equações diferenciais e funcionais.
2. As funções trigonométricas incluem as seguintes 6 funções: seio, cosseno, tangente,co-tangente, secante e cossecante. Para cada uma dessas funções, existe uma função trigonométrica inversa.
3. É conveniente introduzir a definição geométrica de funções trigonométricas usando círculo unitário. A figura abaixo mostra um círculo com raio r = 1. O ponto M(x,y) está marcado no círculo. O ângulo entre o vetor raio OM e a direção positiva do eixo Ox é α.
4. seio o ângulo α é a razão da ordenada y do ponto M(x,y) para o raio r:
sinα=s/r.
Como r=1, então o seno é igual à ordenada do ponto M(x,y).
5. cosseno o ângulo α é a razão da abcissa x do ponto M(x,y) para o raio r:
cosα=x/r
6. tangente o ângulo α é a razão da ordenada y do ponto M(x,y) para sua abcissa x:
tanα=y/x,x≠0
7. Co-tangente o ângulo α é a razão entre a abcissa x do ponto M(x,y) e sua ordenada y:
cotα=x/y,y≠0
8. Secanteângulo α é a razão do raio r para a abcissa x do ponto M(x,y):
secα=r/x=1/x,x≠0
9. Cossecanteângulo α é a razão do raio r para a ordenada y do ponto M(x,y):
cscα=r/y=1/y,y≠0
10. No círculo unitário da projeção x, y, os pontos M(x, y) e o raio r formam um triângulo retângulo, no qual x, y são os catetos e r é a hipotenusa. Portanto, as definições acima de funções trigonométricas aplicadas a um triângulo retângulo são formuladas da seguinte forma:
seio o ângulo α é a razão entre o cateto oposto e a hipotenusa.
cosseno o ângulo α é a razão entre o cateto adjacente e a hipotenusa.
tangenteângulo α é chamado de perna oposta à adjacente.
Co-tangente o ângulo α é chamado de cateto adjacente ao oposto.
Secante o ângulo α é a razão entre a hipotenusa e o cateto adjacente.
Cossecante o ângulo α é a razão entre a hipotenusa e o cateto oposto.
11. gráfico de função seno
y=sinx, domínio: x∈R, domínio: −1≤sinx≤1
12. Gráfico da função cosseno
y=cosx, domínio: x∈R, intervalo: −1≤cosx≤1
13. gráfico de função tangente 14. Gráfico da função cotangente 15. Gráfico da função secante
y=tanx, domínio: x∈R,x≠(2k+1)π/2, domínio: −∞ 
y=cotx, domínio: x∈R,x≠kπ, domínio: −∞ 
y=secx, domínio: x∈R,x≠(2k+1)π/2, domínio: secx∈(−∞,−1]∪∪)