Tabela de redução de trigonometria. Identidade trigonométrica básica
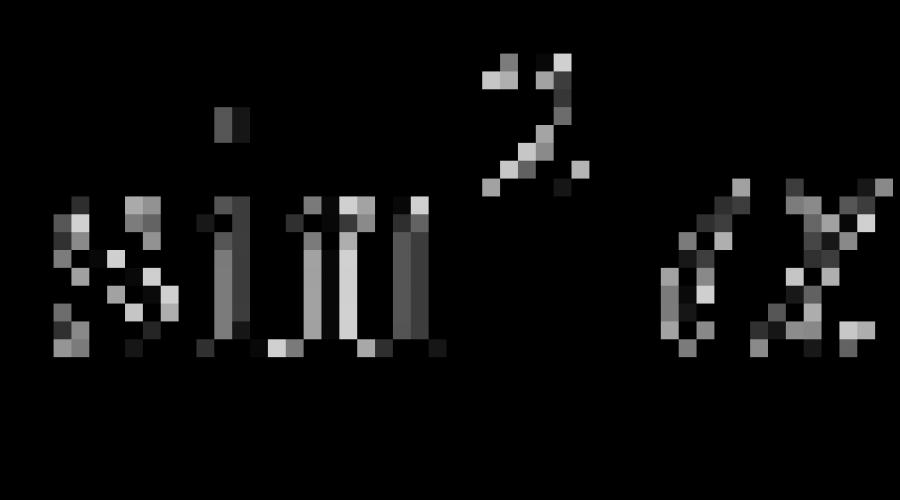
Neste artigo, vamos dar uma olhada abrangente no . As identidades trigonométricas básicas são igualdades que estabelecem uma relação entre o seno, o cosseno, a tangente e a cotangente de um ângulo, e permitem encontrar qualquer uma dessas funções trigonométricas através de uma outra conhecida.
Listamos imediatamente as principais identidades trigonométricas, que analisaremos neste artigo. Nós as escrevemos em uma tabela, e abaixo damos a derivação dessas fórmulas e damos as explicações necessárias.
Navegação da página.
Relação entre seno e cosseno de um ângulo
Às vezes eles não falam sobre as principais identidades trigonométricas listadas na tabela acima, mas sobre uma única identidade trigonométrica básica Gentil ![]() . A explicação para este fato é bastante simples: as igualdades são obtidas a partir do identidade trigonométrica depois de dividir ambas as suas partes por e respectivamente, e as igualdades
. A explicação para este fato é bastante simples: as igualdades são obtidas a partir do identidade trigonométrica depois de dividir ambas as suas partes por e respectivamente, e as igualdades  e
e ![]() seguem as definições de seno, cosseno, tangente e cotangente. Discutiremos isso com mais detalhes nos próximos parágrafos.
seguem as definições de seno, cosseno, tangente e cotangente. Discutiremos isso com mais detalhes nos próximos parágrafos.
Ou seja, é a igualdade que é de particular interesse, que recebeu o nome de identidade trigonométrica principal.
Antes de provar a identidade trigonométrica básica, damos sua formulação: a soma dos quadrados do seno e do cosseno de um ângulo é identicamente igual a um. Agora vamos provar.
A identidade trigonométrica básica é muito usada em transformação de expressões trigonométricas. Permite que a soma dos quadrados do seno e cosseno de um ângulo seja substituída por um. Não menos frequentemente, a identidade trigonométrica básica é usada na ordem inversa: a unidade é substituída pela soma dos quadrados do seno e cosseno de qualquer ângulo.
Tangente e cotangente através de seno e cosseno
Identidades conectando a tangente e a cotangente com o seno e o cosseno de um ângulo da forma e ![]() seguem imediatamente das definições de seno, cosseno, tangente e cotangente. De fato, por definição, o seno é a ordenada de y, o cosseno é a abcissa de x, a tangente é a razão entre a ordenada e a abcissa, ou seja,
seguem imediatamente das definições de seno, cosseno, tangente e cotangente. De fato, por definição, o seno é a ordenada de y, o cosseno é a abcissa de x, a tangente é a razão entre a ordenada e a abcissa, ou seja, ![]() , e a cotangente é a razão entre a abcissa e a ordenada, ou seja,
, e a cotangente é a razão entre a abcissa e a ordenada, ou seja, ![]() .
.
Devido a essa obviedade das identidades e ![]() muitas vezes as definições de tangente e cotangente são dadas não pela razão da abcissa e da ordenada, mas pela razão do seno e cosseno. Assim, a tangente de um ângulo é a razão do seno para o cosseno desse ângulo, e a cotangente é a razão do cosseno para o seno.
muitas vezes as definições de tangente e cotangente são dadas não pela razão da abcissa e da ordenada, mas pela razão do seno e cosseno. Assim, a tangente de um ângulo é a razão do seno para o cosseno desse ângulo, e a cotangente é a razão do cosseno para o seno.
Para concluir esta seção, deve-se notar que as identidades e ![]() vale para todos os ângulos para os quais as funções trigonométricas contidas neles fazem sentido. Portanto, a fórmula é válida para qualquer outra que não seja (caso contrário, o denominador será zero, e não definimos a divisão por zero), e a fórmula
vale para todos os ângulos para os quais as funções trigonométricas contidas neles fazem sentido. Portanto, a fórmula é válida para qualquer outra que não seja (caso contrário, o denominador será zero, e não definimos a divisão por zero), e a fórmula ![]() - for all , diferente de , onde z é qualquer .
- for all , diferente de , onde z é qualquer .
Relação entre tangente e cotangente
Uma identidade trigonométrica ainda mais óbvia do que as duas anteriores é a identidade que liga a tangente e a cotangente de um ângulo da forma ![]() . É claro que ocorre para quaisquer ângulos diferentes de , caso contrário, a tangente ou a cotangente não são definidas.
. É claro que ocorre para quaisquer ângulos diferentes de , caso contrário, a tangente ou a cotangente não são definidas.
Prova da fórmula ![]() muito simples. Por definição e de onde
muito simples. Por definição e de onde  . A prova poderia ter sido realizada de uma maneira ligeiramente diferente. Desde e
. A prova poderia ter sido realizada de uma maneira ligeiramente diferente. Desde e ![]() , então
, então  .
.
Então, a tangente e a cotangente de um ângulo, no qual elas fazem sentido, é.
Este é o último e mais lição principal necessários para resolver problemas B11. Já sabemos como converter ângulos de uma medida em radianos para uma medida em graus (veja a lição "Radianos e medidas em graus de um ângulo"), e também sabemos como determinar o sinal de uma função trigonométrica, focando em quartos de coordenadas (veja a lição "Sinais de funções trigonométricas").
A questão permanece pequena: calcular o valor da própria função - o próprio número que está escrito na resposta. Aqui a identidade trigonométrica básica vem em socorro.
Identidade trigonométrica básica. Para qualquer ângulo α, a afirmação é verdadeira:
sen 2 α + cos 2 α = 1.
Esta fórmula relaciona o seno e o cosseno de um ângulo. Agora, conhecendo o seno, podemos facilmente encontrar o cosseno - e vice-versa. Basta tirar a raiz quadrada:
Observe o sinal "±" na frente das raízes. O fato é que a partir da identidade trigonométrica básica não fica claro quais eram o seno e o cosseno originais: positivo ou negativo. Afinal, esquadrinhar função par, que "queima" todas as desvantagens (se houver).
É por isso que em todas as tarefas B11 encontradas no USE em matemática, existem necessariamente condições adicionais que ajudam a se livrar da incerteza com os sinais. Normalmente esta é uma indicação do quarto de coordenadas pelo qual o sinal pode ser determinado.
Um leitor atento certamente perguntará: “E a tangente e a cotangente?” É impossível calcular diretamente essas funções a partir das fórmulas acima. No entanto, existem implicações importantes da identidade trigonométrica básica, que já contém tangentes e cotangentes. Nomeadamente:
Um corolário importante: para qualquer ângulo α, a identidade trigonométrica básica pode ser reescrita da seguinte forma:
Essas equações são facilmente deduzidas da identidade básica - basta dividir ambos os lados por cos 2 α (para obter uma tangente) ou por sen 2 α (para uma cotangente).
Vamos dar uma olhada em tudo isso exemplos concretos. Abaixo estão os problemas reais do B11 que são retirados do teste Opções de USO em matemática 2012.
Sabemos o cosseno, mas não sabemos o seno. A identidade trigonométrica principal (em sua forma "pura") conecta apenas essas funções, então vamos trabalhar com ela. Nós temos:
sen 2 α + cos 2 α = 1 ⇒ sen 2 α + 99/100 = 1 ⇒ sen 2 α = 1/100 ⇒ sen α = ±1/10 = ±0,1.
Para resolver o problema, resta encontrar o sinal do seno. Como o ângulo α ∈ (π /2; π ), então em medida de grau escreve-se da seguinte forma: α ∈ (90°; 180°).
Portanto, o ângulo α está no quarto da coordenada II - todos os senos são positivos. Portanto sen α = 0,1.
Então, sabemos o seno, mas precisamos encontrar o cosseno. Ambas as funções estão na identidade trigonométrica básica. Substituímos:
sen 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Resta lidar com o sinal na frente da fração. O que escolher: mais ou menos? Por condição, o ângulo α pertence ao intervalo (π 3π /2). Vamos converter os ângulos da medida em radianos para a medida em graus - obtemos: α ∈ (180°; 270°).
Obviamente, este é o quarto coordenado III, onde todos os cossenos são negativos. Portanto cosα = −0,5.
Tarefa. Encontre tg α se você souber o seguinte:
A tangente e o cosseno estão relacionados por uma equação que segue da identidade trigonométrica básica:
Obtemos: tg α = ±3. O sinal da tangente é determinado pelo ângulo α. Sabe-se que α ∈ (3π /2; 2π ). Vamos converter os ângulos da medida em radianos para a medida em graus - obtemos α ∈ (270°; 360°).
Obviamente, este é o quarto da coordenada IV, onde todas as tangentes são negativas. Portanto, tgα = −3.
Tarefa. Encontre cos α se você souber o seguinte:
Novamente, o seno é conhecido e o cosseno é desconhecido. Escrevemos a identidade trigonométrica principal:
sen 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
O sinal é determinado pelo ângulo. Temos: α ∈ (3π /2; 2π ). Vamos converter os ângulos de graus para radianos: α ∈ (270°; 360°) é o quarto da coordenada IV, os cossenos são positivos ali. Portanto, cos α = 0,6.
Tarefa. Encontre sen α se você souber o seguinte:
Vamos escrever uma fórmula que segue da identidade trigonométrica básica e conecta diretamente o seno e a cotangente:
Daqui obtemos que sen 2 α = 1/25, ou seja. sin α = ±1/5 = ±0,2. Sabe-se que o ângulo α ∈ (0; π /2). Em graus, escreve-se da seguinte forma: α ∈ (0°; 90°) - I coordenado quarto.
Portanto, o ângulo está no quarto coordenado I - todas as funções trigonométricas são positivas lá, portanto, sin α \u003d 0,2.
Definição. As fórmulas de redução são chamadas de fórmulas que permitem passar de funções trigonométricas da forma para funções de argumento. Com a ajuda deles, o seno, cosseno, tangente e cotangente de um ângulo arbitrário podem ser reduzidos ao seno, cosseno, tangente e cotangente de um ângulo do intervalo de 0 a 90 graus (de 0 a radianos). Assim, as fórmulas de redução nos permitem passar a trabalhar com ângulos dentro de 90 graus, o que sem dúvida é muito conveniente.
Fórmulas de elenco:

Existem duas regras para usar fórmulas de conversão.
1. Se o ângulo pode ser representado como (π/2 ±a) ou (3*π/2 ±a), então alterações de nome de função pecado para cos, cos para pecado, tg para ctg, ctg para tg. Se o ângulo pode ser representado como (π ±a) ou (2*π ±a), então o nome da função permanece inalterado.
Observe a figura abaixo, ela mostra esquematicamente quando mudar o sinal e quando não

2. Sinal de função reduzida continua o mesmo. Se a função original tinha um sinal de mais, então a função reduzida também tem um sinal de mais. Se a função original tinha um sinal de menos, então a função reduzida também tem um sinal de menos.
A figura abaixo mostra os sinais das principais funções trigonométricas dependendo do trimestre.

Exemplo:
Calcular
Vamos usar as fórmulas de redução:
Sin(150˚) está no segundo trimestre, podemos ver pela figura que o sinal do sen neste trimestre é igual a "+". Isso significa que a função acima também terá um sinal “+”. Aplicamos a segunda regra.
Agora 150˚ = 90˚ +60˚. 90˚ é π/2. Ou seja, estamos lidando com o caso π / 2 + 60, portanto, de acordo com a primeira regra, alteramos a função de sen para cos. Como resultado, obtemos Sin(150˚) = cos(60˚) = ½.
As fórmulas de redução são razões que permitem ir de seno, cosseno, tangente e cotangente com ângulos `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi) 2 \pm \alpha`, `2\pi \pm \alpha` para as mesmas funções do ângulo `\alpha`, que está no primeiro quarto do círculo unitário. Assim, as fórmulas de redução nos "levam" a trabalhar com ângulos na faixa de 0 a 90 graus, o que é muito conveniente.
Ao todo são 32 fórmulas de redução. Eles, sem dúvida, serão úteis no exame, exames, testes. Mas avisaremos imediatamente que não há necessidade de memorizá-los! Você precisa gastar um pouco de tempo e entender o algoritmo para sua aplicação, então não será difícil para você momento certo obter a igualdade necessária.
Primeiro, vamos escrever todas as fórmulas de redução:
Para ângulo (`\frac (\pi)2 \pm \alpha`) ou (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
Para ângulo (`\pi \pm \alpha`) ou (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Para ângulo (`\frac (3\pi)2 \pm \alpha`) ou (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 - \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 - \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
Para ângulo (`2\pi \pm \alpha`) ou (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Muitas vezes você pode encontrar fórmulas de redução na forma de uma tabela, onde os ângulos são escritos em radianos:
Para usá-lo, você precisa selecionar a linha com a função que precisamos e a coluna com o argumento desejado. Por exemplo, para usar uma tabela para descobrir o que será ` sin(\pi + \alpha)`, basta encontrar a resposta na interseção da linha ` sin \beta` e a coluna ` \pi + \ alfa`. Obtemos ` sin(\pi + \alpha)=-sin \\alpha`.
E a segunda tabela semelhante, onde os ângulos são escritos em graus:

Regra mnemônica de fórmulas de lançamento ou como lembrá-las
Como já mencionamos, não é necessário memorizar todos os índices acima. Se você olhou atentamente para eles, provavelmente notou alguns padrões. Eles nos permitem formular uma regra mnemônica (mnemônica - memorizar), com a qual você pode obter facilmente qualquer uma das fórmulas de redução.
Observamos imediatamente que, para aplicar esta regra, é preciso ser bem capaz de determinar (ou lembrar) os sinais das funções trigonométricas em diferentes quadrantes do círculo unitário.  O enxerto em si contém 3 etapas:
O enxerto em si contém 3 etapas:
- O argumento da função deve estar no formato `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, com `\alpha` obrigatório canto afiado(de 0 a 90 graus).
- Para argumentos `\frac (\pi)2 \pm \alpha`, `\frac (3\pi)2 \pm \alpha` função trigonométrica da expressão convertida muda para uma cofunção, ou seja, o oposto (seno para cosseno, tangente para cotangente e vice-versa). Para argumentos `\pi \pm \alpha`, `2\pi \pm \alpha` a função não muda.
- O sinal da função original é determinado. A função resultante do lado direito terá o mesmo sinal.
Para ver como essa regra pode ser aplicada na prática, vamos transformar algumas expressões:
1. `cos(\pi + \alpha)`.
A função não é invertida. O ângulo ` \pi + \alpha` está no terceiro quadrante, o cosseno neste quadrante tem um sinal "-", então a função convertida também terá um sinal "-".
Resposta: ` cos(\pi + \alpha)= - cos \alpha`
2. `sin(\frac (3\pi)2 - \alpha)`.
De acordo com a regra mnemônica, a função será invertida. O ângulo `\frac (3\pi)2 - \alpha` está no terceiro quadrante, o seno aqui tem um sinal "-", então o resultado também estará com um sinal "-".
Resposta: `sin(\frac (3\pi)2 - \alpha)= - cos \alpha`
3. `cos(\frac (7\pi)2 - \alpha)`.
`cos(\frac (7\pi)2 - \alpha)=cos(\frac (6\pi)2+\frac (\pi)2-\alpha)=cos (3\pi+(\frac(\pi) )2-\alpha))`. Vamos representar `3\pi` como `2\pi+\pi`. `2\pi` é o período da função.
Importante: As funções `cos \alpha` e `sin \alpha` possuem um período de `2\pi` ou `360^\circ`, seus valores não serão alterados se o argumento for aumentado ou diminuído por esses valores.
Com base nisso, nossa expressão pode ser escrita da seguinte forma: `cos (\pi+(\frac(\pi)2-\alpha)`. Aplicando a regra mnemônica duas vezes, obtemos: `cos (\pi+(\frac(\ pi) 2-\alpha)= - cos (\frac(\pi)2-\alpha)= - sin \alpha`.
Resposta: `cos(\frac (7\pi)2 - \alpha)=- sin \alpha`.
regra do cavalo
O segundo ponto da regra mnemônica acima também é chamado de regra de cavalo das fórmulas de redução. Eu me pergunto por que cavalos?
Então temos funções com argumentos `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, pontos `\frac (\pi)2`, `\pi`, `\frac (3\pi)2`, `2\pi` são pontos chave, eles estão localizados nos eixos coordenados. `\pi` e `2\pi` no eixo x horizontal e `\frac (\pi)2` e `\frac (3\pi)2` no eixo vertical ordenado
Nós nos perguntamos: “A função se transforma em uma cofunção?”. Para responder a esta pergunta, você precisa mover a cabeça ao longo do eixo em que o ponto-chave está localizado.
Ou seja, para argumentos com pontos-chave localizados no eixo horizontal, respondemos “não” balançando a cabeça para os lados. E para cantos com pontos-chave localizados no eixo vertical, respondemos “sim” balançando a cabeça de cima para baixo, como um cavalo 🙂
Recomendamos assistir a um tutorial em vídeo no qual o autor explica detalhadamente como memorizar fórmulas de redução sem memorizá-las.
Exemplos práticos de uso de fórmulas de fundição
O uso de fórmulas de redução começa no 9º e 10º anos. Muitas tarefas com seu uso são submetidas ao exame. Aqui estão algumas das tarefas em que você precisará aplicar essas fórmulas:
- tarefas para resolver um triângulo retângulo;
- conversão de expressões trigonométricas numéricas e alfabéticas, cálculo de seus valores;
- problemas estereométricos.
Exemplo 1. Use as fórmulas de redução para calcular a) `sin 600^\circ`, b) `tg 480^\circ`, c) `cos 330^\circ`, d) `sin 240^\circ`.
Solução: a) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
b) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac(\sqrt 3)3`;
c) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac(\sqrt 3)2`;
d) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac(\sqrt 3)2`.
Exemplo 2. Tendo expressado o cosseno pelo seno usando as fórmulas de redução, compare os números: 1) `sin \frac (9\pi)8` e `cos \frac (9\pi)8`; 2) `sin \frac (\pi)8` e `cos \frac (3\pi)10`.
Solução: 1)`sin \frac (9\pi)8=sin (\pi+\frac (\pi)8)=-sin \frac (\pi)8`
`cos \frac (9\pi)8=cos (\pi+\frac (\pi)8)=-cos \frac (\pi)8=-sin \frac (3\pi)8`
`-sin \frac (\pi)8> -sin \frac (3\pi)8`
`sin \frac (9\pi)8>cos \frac (9\pi)8`.
2) `cos \frac (3\pi)10=cos (\frac (\pi)2-\frac (\pi)5)=sin \frac (\pi)5`
`sen\frac (\pi)8 `sen\frac (\pi)8 Primeiro provamos duas fórmulas para o seno e o cosseno do argumento `\frac (\pi)2 + \alpha`: ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha` e ` cos( \frac (\pi)2 + \alpha)=-sin \\alpha`. Os demais são derivados deles. Pegue um círculo unitário e ponto A nele com coordenadas (1,0). Deixe depois de ligar Da definição de tangente e cotangente, obtemos ` tg(\frac (\pi)2 + \alpha)=\frac (sin(\frac (\pi)2 + \alpha))(cos(\frac (\pi) )2 + \alpha))=\frac (cos \alpha)(-sin \alpha)=-ctg \alpha` e ` ctg(\frac (\pi)2 + \alpha)=\frac (cos(\frac (\ pi)2 + \alpha))(sin(\frac (\pi)2 + \alpha))=\frac (-sin \alpha)(cos \alpha)=-tg \alpha`, o que prova a redução fórmulas para a tangente e a cotangente do ângulo `\frac (\pi)2 + \alpha`. Para provar fórmulas com o argumento `\frac (\pi)2 - \alpha`, basta representá-lo como `\frac (\pi)2 + (-\alpha)` e seguir o mesmo caminho acima. Por exemplo, `cos(\frac (\pi)2 - \alpha)=cos(\frac (\pi)2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`. Os ângulos `\pi + \alpha` e `\pi - \alpha` podem ser representados como `\frac (\pi)2 +(\frac (\pi)2+\alpha)` e `\frac (\pi ) 2 +(\frac (\pi)2-\alpha)` respectivamente. E `\frac (3\pi)2 + \alpha` e `\frac (3\pi)2 - \alpha` como `\pi +(\frac (\pi)2+\alpha)` e `\pi +(\frac (\pi)2-\alpha)`. canto `\alpha` ele irá até o ponto `A_1(x,y)`, e depois de girar pelo ângulo `\frac (\pi)2 + \alpha` até o ponto `A_2(-y,x)` . Baixando as perpendiculares desses pontos até a reta OX, vemos que os triângulos `OA_1H_1` e `OA_2H_2` são iguais, pois suas hipotenusas e ângulos adjacentes são iguais. Então, com base nas definições de seno e cosseno, podemos escrever `sin \alpha=y`, `cos \alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\pi)2 + \alpha)=-y`. Como alguém pode escrever que ` sin(\frac (\pi)2 + \alpha)=cos \alpha` e ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, o que prova a redução fórmulas para o seno e cosseno do ângulo `\frac (\pi)2 + \alpha`.
canto `\alpha` ele irá até o ponto `A_1(x,y)`, e depois de girar pelo ângulo `\frac (\pi)2 + \alpha` até o ponto `A_2(-y,x)` . Baixando as perpendiculares desses pontos até a reta OX, vemos que os triângulos `OA_1H_1` e `OA_2H_2` são iguais, pois suas hipotenusas e ângulos adjacentes são iguais. Então, com base nas definições de seno e cosseno, podemos escrever `sin \alpha=y`, `cos \alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\pi)2 + \alpha)=-y`. Como alguém pode escrever que ` sin(\frac (\pi)2 + \alpha)=cos \alpha` e ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, o que prova a redução fórmulas para o seno e cosseno do ângulo `\frac (\pi)2 + \alpha`.