Właściwości funkcji to największa i najmniejsza wartość. Jak znaleźć najmniejszą wartość funkcji

Aby go rozwiązać, potrzebujesz minimalnej wiedzy na ten temat. Kończy się kolejny rok akademicki, wszyscy chcą wyjechać na wakacje, a żeby ten moment przybliżyć, od razu zabieram się do rzeczy:

Zacznijmy od obszaru. Obszar, o którym mowa w warunku to ograniczony Zamknięte zbiór punktów w płaszczyźnie. Na przykład zbiór punktów ograniczony trójkątem, w tym CAŁY trójkąt (jeśli z granice„Wysuń” co najmniej jeden punkt, wtedy obszar nie będzie już zamknięty). W praktyce są też obszary prostokątne, okrągłe i nieco więcej złożone kształty. Należy zauważyć, że teoretycznie Analiza matematyczna podane są ścisłe definicje ograniczenia, izolacja, granice itp., ale myślę, że wszyscy są świadomi tych pojęć na poziomie intuicyjnym i teraz nie potrzeba więcej.

Powierzchnia płaska jest standardowo oznaczana literą i z reguły jest podawana analitycznie - kilkoma równaniami (niekoniecznie liniowe); rzadziej nierówności. Typowy zwrot werbalny: „zamknięty obszar ograniczony liniami”.

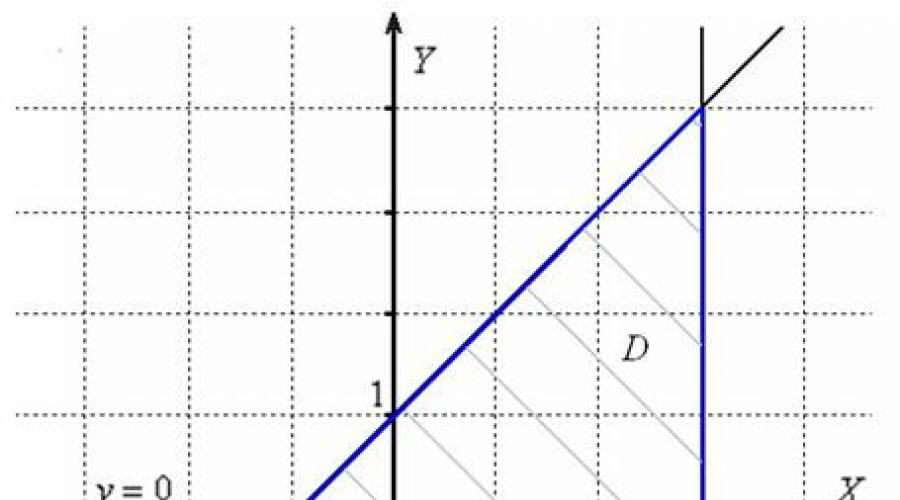
Integralną częścią rozważanego zadania jest budowa obszaru na rysunku. Jak to zrobić? Konieczne jest narysowanie wszystkich wymienionych linii (w ta sprawa 3 prosty) i przeanalizuj, co się stało. Pożądany obszar jest zwykle lekko kreskowany, a jego granica jest wyróżniona pogrubioną linią:


Można ustawić ten sam obszar nierówności liniowe: , które z jakiegoś powodu częściej zapisuje się jako wyliczenie, a nie system.
Skoro granica należy do regionu, to oczywiście wszelkie nierówności nieścisłe.

A teraz sedno sprawy. Wyobraź sobie, że oś idzie prosto do ciebie od początku współrzędnych. Rozważ funkcję, która ciągły w każdym punkt obszaru. Wykres tej funkcji to powierzchnia, a małym szczęściem jest to, że aby rozwiązać dzisiejszy problem, wcale nie musimy wiedzieć, jak ta powierzchnia wygląda. Może znajdować się powyżej, poniżej, przekroczyć płaszczyznę - wszystko to nie jest ważne. A ważne jest: według Twierdzenia Weierstrassa, ciągły w ograniczone zamknięte obszar, funkcja osiąga maksimum (z „najwyższego”) i najmniej (z „najniższego”) wartości do znalezienia. Te wartości są osiągane lub w punkty stacjonarne, należący do regionuD , lub w punktach leżących na granicy tego regionu. Z czego wynika prosty i przejrzysty algorytm rozwiązania:

Przykład 1

W ograniczonym, zamkniętym obszarze

Decyzja: Przede wszystkim musisz przedstawić obszar na rysunku. Niestety technicznie trudno jest mi zrobić interaktywny model problemu, dlatego od razu podam ostateczną ilustrację, która pokazuje wszystkie „podejrzane” punkty znalezione podczas badania. Zazwyczaj odkłada się je jeden po drugim w miarę ich znajdowania:

Na podstawie preambuły decyzję można wygodnie podzielić na dwa punkty:

I) Znajdźmy punkty stacjonarne. Jest to standardowa czynność, którą wielokrotnie wykonywaliśmy na lekcji. o ekstremach kilku zmiennych:

Znaleziono punkt stacjonarny należy obszary: (zaznacz to na rysunku), co oznacza, że ​​powinniśmy obliczyć wartość funkcji w danym punkcie:

- jak w artykule Największe i najmniejsze wartości funkcji na segmencie, ważne wyniki zaznaczę pogrubioną czcionką. W notatniku wygodnie jest zakreślić je ołówkiem.

Zwróć uwagę na nasze drugie szczęście – nie ma sensu sprawdzać warunek wystarczający dla ekstremum. Czemu? Nawet jeśli w punkcie funkcja osiągnie np. lokalne minimum, to NIE OZNACZA to, że otrzymana wartość będzie minimalny w całym regionie (patrz początek lekcji o bezwarunkowych skrajnościach) .

Co jeśli punkt stacjonarny NIE należy do obszaru? Prawie nic! Należy to zauważyć i przejść do następnego akapitu.

II) Badamy granicę regionu.

Ponieważ granica składa się z boków trójkąta, wygodnie jest podzielić badanie na 3 akapity. Ale lepiej tego nie robić. Z mojego punktu widzenia korzystniej jest najpierw rozważyć odcinki równoległe do osie współrzędnych, a przede wszystkim leżące na samych toporach. Aby uchwycić całą sekwencję i logikę działań, spróbuj przestudiować zakończenie „jednym oddechem”:

1) Zajmijmy się dolną stroną trójkąta. W tym celu podstawiamy bezpośrednio do funkcji:

Alternatywnie możesz to zrobić w ten sposób:

Geometrycznie oznacza to, że płaszczyzna współrzędnych (co jest również podane przez równanie)"wyciąć" z powierzchnie parabola „przestrzenna”, której wierzchołek natychmiast staje się podejrzany. Dowiedzmy Się gdzie ona jest:

- wynikowa wartość „trafił” w okolicy, a równie dobrze może być tak, że w punkcie (zaznacz na rysunku) funkcja osiąga największą lub najmniejszą wartość w całym obszarze. W każdym razie zróbmy obliczenia:

Inni „kandydaci” są oczywiście końcówkami segmentu. Oblicz wartości funkcji w punktach (zaznacz na rysunku):

Tutaj, przy okazji, możesz przeprowadzić ustny mini-test w wersji „okrojonej”:

2) Aby zbadać prawą stronę trójkąta, podstawiamy ją do funkcji i „uporządkuj tam”:

Tutaj natychmiast przeprowadzamy zgrubną kontrolę, „dzwoniąc” już przetworzony koniec segmentu:
, idealny.

Sytuacja geometryczna jest związana z poprzednim punktem:

- otrzymana wartość również „weszła w zakres naszych zainteresowań”, co oznacza, że ​​musimy obliczyć, jaka jest funkcja w punkcie, który się pojawił:

Zbadajmy drugi koniec segmentu:

Korzystanie z funkcji , Sprawdźmy:

3) Każdy prawdopodobnie wie, jak zbadać pozostałą stronę. Zastępujemy w funkcję i przeprowadzamy uproszczenia:

Linia się kończy zostały już zbadane, ale w wersji roboczej nadal sprawdzamy, czy znaleźliśmy funkcję poprawnie :
– zbiegł się z wynikiem w akapicie pierwszym;
– zbiegł się z wynikiem w akapicie drugim.

Pozostaje dowiedzieć się, czy w segmencie jest coś ciekawego:

- jest! Podstawiając do równania linię prostą otrzymujemy rzędną tej „ciekawości”:

Zaznaczamy punkt na rysunku i znajdujemy odpowiednią wartość funkcji:

Kontrolujmy obliczenia według wersji „budżetowej” :
, zamówienie.

I ostatni krok: UWAŻNIE przejrzyj wszystkie „grube” liczby, nawet początkującym polecam zrobić jedną listę:

z których wybieramy wartości największe i najmniejsze. Odpowiedź pisz w stylu problemu ze znalezieniem największe i najmniejsze wartości funkcji na segmencie:

Na wszelki wypadek jeszcze raz skomentuję. zmysł geometryczny wynik:
– tu znajduje się najwyższy punkt powierzchni w regionie;
- tutaj znajduje się najniższy punkt powierzchni w okolicy.

W analizowanym problemie znaleźliśmy 7 „podejrzanych” punktów, ale ich liczba jest różna w zależności od zadania. W przypadku regionu trójkątnego minimalny „zestaw eksploracji” składa się z trzy punkty. Dzieje się tak, gdy funkcja, na przykład, ustawia samolot- dość jasne jest, że nie ma punktów stacjonarnych, a funkcja może osiągać wartości maksymalne/minimalne tylko na wierzchołkach trójkąta. Ale nie ma takich przykładów raz, dwa razy - zwykle masz do czynienia z jakimś rodzajem powierzchnia II rzędu.

Jeśli trochę rozwiążesz takie zadania, to trójkąty mogą przyprawić o zawrót głowy, dlatego przygotowałem dla Ciebie niezwykłe przykłady zrobić kwadrat :)

Przykład 2

Znajdź największe i najmniejsze wartości funkcji w zamkniętym obszarze ograniczonym liniami

Przykład 3

Znajdź największe i najmniejsze wartości funkcji w ograniczonym obszarze zamkniętym.

Specjalna uwaga zwróć uwagę na racjonalny porządek i technikę badania granicy obszaru, a także na łańcuch kontroli pośrednich, co prawie całkowicie pozwoli uniknąć błędów obliczeniowych. Ogólnie rzecz biorąc, możesz to rozwiązać, jak chcesz, ale w niektórych problemach, na przykład w tym samym Przykładzie 2, są wszelkie szanse, aby znacznie skomplikować Ci życie. Próbka próbki kończące zadania na koniec lekcji.

Systematyzujemy algorytm rozwiązania, w przeciwnym razie z moją pajęczą starannością jakoś zgubił się on w długim wątku komentarzy pierwszego przykładu:

- W pierwszym kroku budujemy obszar, pożądane jest jego zacienienie i podkreślenie granicy pogrubioną linią. W trakcie rozwiązywania pojawią się punkty, które należy umieścić na rysunku.

– Znajdź punkty stacjonarne i oblicz wartości funkcji tylko w tych, które należą do pow . Uzyskane wartości są wyróżnione w tekście (na przykład zakreślone ołówkiem). Jeżeli punkt stacjonarny NIE należy do obszaru, to zaznaczamy ten fakt ikoną lub słownie. Jeśli w ogóle nie ma punktów stacjonarnych, to wyciągamy pisemny wniosek, że ich nie ma. W każdym razie tej pozycji nie można pominąć!

– Eksploracja pogranicza. Po pierwsze, korzystne jest radzenie sobie z liniami prostymi, które są równoległe do osi współrzędnych (Jeśli znajdują się jakiekolwiek). Podświetlane są również wartości funkcji obliczone w „podejrzanych” punktach. Wiele powiedziano o powyższej technice rozwiązywania problemów, a coś jeszcze zostanie powiedziane poniżej - czytaj, czytaj ponownie, zagłębiaj się!

- Z wybranych liczb wybierz największą i najmniejszą wartość i udziel odpowiedzi. Czasami zdarza się, że funkcja osiąga takie wartości w kilku punktach na raz – w takim przypadku wszystkie te punkty powinny znaleźć odzwierciedlenie w odpowiedzi. Niech na przykład i okazało się, że najmniejsza wartość. Potem piszemy, że

Ostateczne przykłady są dedykowane innym przydatne pomysły przydatne w praktyce:

Przykład 4

Znajdź największe i najmniejsze wartości funkcji w obszarze zamkniętym .

Zachowałem sformułowanie autora, w którym obszar jest podany jako podwójna nierówność. Warunek ten można zapisać w systemie równoważnym lub w bardziej tradycyjnej formie dla tego problemu:

Przypominam ci to z nieliniowy Napotkaliśmy nierówności na , a jeśli nie rozumiesz geometrycznego znaczenia wpisu, to proszę nie zwlekać i wyjaśnić sytuację już teraz ;-)

Decyzja, jak zawsze, zaczyna się od budowy terenu, który jest rodzajem „podeszwy”:

Hmm, czasem trzeba obgryzać nie tylko granit nauki....

I) Znajdź punkty stacjonarne:

System marzeń idioty :)

Punkt stacjonarny należy do regionu, a mianowicie leży na jego granicy.

I tak to nic ... fajna lekcja poszła - to znaczy pić odpowiednią herbatę =)

II) Badamy granicę regionu. Bez dalszych ceregieli zacznijmy od osi x:

1) Jeśli , to

Znajdź górną część paraboli:
- Doceń takie chwile - "uderz" prosto do punktu, z którego wszystko jest już jasne. Ale nie zapomnij sprawdzić:

Obliczmy wartości funkcji na końcach segmentu:

2) C na dole Pomyślmy o "podeszwach" "za jednym posiedzeniem" - bez kompleksów podstawiamy do funkcji, ponadto interesuje nas tylko segment:

Kontrola:

Teraz to już ożywia monotonną jazdę po moletowanym torze. Znajdźmy punkty krytyczne:

My decydujemy równanie kwadratowe pamiętasz ten? ... Pamiętaj jednak oczywiście, że inaczej nie przeczytałbyś tych wierszy =) Gdyby w dwóch poprzednich przykładach obliczenia były wygodne w ułamki dziesiętne(co, nawiasem mówiąc, jest rzadkością), to tutaj czekamy na zwykłe wspólne ułamki. Znajdujemy pierwiastki „x” i za pomocą równania określamy odpowiednie współrzędne „gry” punktów „kandydatów”:


Obliczmy wartości funkcji w znalezionych punktach:

Sprawdź sam funkcję.

Teraz dokładnie studiujemy zdobyte trofea i zapisujemy odpowiedź:

Oto „kandydaci”, czyli „kandydaci”!

Dla samodzielnego rozwiązania:

Przykład 5

Znajdź najmniejszą i największą wartość funkcji na terenie zamkniętym

Wpis z nawiasami klamrowymi brzmi tak: „zestaw takich punktów”.

Czasami w takich przykładach używają Metoda mnożnika Lagrange'a, ale prawdziwa potrzeba jest mało prawdopodobne, aby był używany. Czyli np. jeśli podana jest funkcja z tą samą dziedziną "de", to po podstawieniu do niej - z pochodną bez trudności; co więcej, wszystko jest narysowane w „jednej linii” (ze znakami) bez konieczności oddzielnego rozpatrywania górnego i dolnego półokręgu. Ale oczywiście jest ich więcej trudne przypadki, gdzie bez funkcji Lagrange (gdzie , na przykład, to to samo równanie okręgu) ciężko się obejść - jakże ciężko obejść się bez dobrego wypoczynku!

Wszystkiego najlepszego, aby zaliczyć sesję i do zobaczenia wkrótce w przyszłym sezonie!

Rozwiązania i odpowiedzi:

Przykład 2: Decyzja: narysuj obszar na rysunku:

Czasami w problemach B15 występują "złe" funkcje, dla których trudno znaleźć pochodną. Wcześniej było to tylko na sondach, ale teraz te zadania są tak powszechne, że nie można ich już ignorować podczas przygotowań do tego egzaminu.

W tym przypadku działają inne sztuczki, z których jedna to - monotonia.

Funkcję f(x) nazywamy monotonicznie rosnącą na odcinku, jeśli dla dowolnych punktów x 1 i x 2 tego odcinka jest prawdziwe:

x 1< x 2 ⇒ f (x 1) < f (x2).

Funkcję f(x) nazywamy monotonicznie malejącą na odcinku, jeśli dla dowolnych punktów x 1 i x 2 tego odcinka jest prawdziwe:

x 1< x 2 ⇒ f (x 1) > f ( x2).

Innymi słowy, dla funkcji rosnącej im większe jest x, tym większe jest f(x). Dla funkcji malejącej jest odwrotnie: im więcej x , tym mniejszy f(x).

Na przykład logarytm rośnie monotonicznie, jeśli podstawa a > 1 i maleje monotonicznie, jeśli 0< a < 1. Не забывайте про область dozwolone wartości logarytm: x > 0.

f (x) = log a x (a > 0; a ≠ 1; x > 0)

Pierwiastek arytmetyczny (i nie tylko kwadratowy) rośnie monotonicznie w całej dziedzinie definicji:

Funkcja wykładnicza zachowuje się podobnie jak logarytm: rośnie dla a > 1 i maleje dla 0< a < 1. Но в отличие от логарифма, funkcja wykładnicza zdefiniowany dla wszystkich liczb, nie tylko x > 0:

f (x) = a x (a > 0)

Wreszcie stopnie z ujemnym wykładnikiem. Możesz zapisać je jako ułamek. Mają punkt załamania, w którym załamuje się monotonia.

Wszystkie te cechy nigdy nie znajdują się w czysta forma. Dodawane są do nich wielomiany, ułamki i inne bzdury, przez co trudno jest obliczyć pochodną. Co dzieje się w tym przypadku - teraz przeanalizujemy.

Współrzędne wierzchołka paraboli

Najczęściej argument funkcji jest zastępowany przez trójmian kwadratowy postaci y = ax 2 + bx + c . Jej wykres to standardowa parabola, która nas interesuje:

1. Gałęzie paraboli - mogą iść w górę (dla a > 0) lub w dół (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Wierzchołek paraboli to ekstremum funkcji kwadratowej, w którym funkcja ta przyjmuje najmniejszą (dla a > 0) lub największą (a< 0) значение.

Największym zainteresowaniem jest szczyt paraboli, którego odcięta jest obliczana według wzoru:

Tak więc znaleźliśmy punkt skrajny funkcji kwadratowej. Ale jeśli pierwotna funkcja jest monotoniczna, dla niej punkt x 0 będzie również punktem ekstremum. W ten sposób formułujemy kluczową zasadę:

punkty ekstremalne trójmian kwadratowy oraz złożona funkcja, w którym wchodzi, są takie same. Dlatego możesz poszukać x 0 dla trójmianu kwadratowego i zapomnieć o funkcji.

Z powyższego rozumowania nie jest jasne, jaki punkt otrzymujemy: maksimum czy minimum. Jednak zadania są specjalnie zaprojektowane, aby nie miało to znaczenia. Sędzia dla siebie:

1. W stanie problemu nie ma segmentu. Dlatego nie jest wymagane obliczanie f(a) i f(b). Pozostaje rozważyć tylko punkty skrajne;
2. Ale jest tylko jeden taki punkt - jest to wierzchołek paraboli x 0, której współrzędne są obliczane dosłownie ustnie i bez żadnych pochodnych.

W ten sposób rozwiązanie problemu jest znacznie uproszczone i zredukowane do zaledwie dwóch kroków:

1. Zapisz równanie paraboli y = ax 2 + bx + c i znajdź jego wierzchołek ze wzoru: x 0 = −b /2a;
2. Znajdź wartość oryginalnej funkcji w tym momencie: f (x 0). Jeśli nie ma dodatkowych warunków, to będzie odpowiedź.

Na pierwszy rzut oka ten algorytm i jego uzasadnienie może wydawać się skomplikowane. Celowo nie zamieszczam „gołego” schematu rozwiązania, ponieważ bezmyślne stosowanie takich zasad jest obarczone błędami.

Rozważmy prawdziwe problemy z egzamin próbny w matematyce - tutaj ta technika występuje najczęściej. Jednocześnie upewnimy się, że w ten sposób wiele problemów związanych z B15 stanie się niemal werbalnymi.

Pod korzeniem jest funkcja kwadratowa y \u003d x 2 + 6x + 13. Wykres tej funkcji to parabola z rozgałęzieniami do góry, ponieważ współczynnik a \u003d 1\u003e 0.

Wierzchołek paraboli:

x 0 \u003d -b / (2a) \u003d -6 / (2 1) \u003d -6 / 2 \u003d -3

Ponieważ gałęzie paraboli są skierowane w górę, w punkcie x 0 \u003d -3 funkcja y \u003d x 2 + 6x + 13 przyjmuje najmniejszą wartość.

Pierwiastek rośnie monotonicznie, więc x 0 jest punktem minimalnym całej funkcji. Mamy:

Zadanie. Znajdź najmniejszą wartość funkcji:

y = log 2 (x 2 + 2x + 9)

Pod logarytmem ponownie znajduje się funkcja kwadratowa: y \u003d x 2 + 2x + 9. Wykres jest parabolą z rozgałęzieniami do góry, ponieważ a = 1 > 0.

Wierzchołek paraboli:

x 0 \u003d -b / (2a) \u003d -2 / (2 1) \u003d -2/2 \u003d -1

Tak więc w punkcie x 0 = −1, funkcja kwadratowa przyjmuje najmniejszą wartość. Ale funkcja y = log 2 x jest monotoniczna, więc:

y min = y (−1) = log 2 ((−1) 2 + 2 (−1) + 9) = ... = log 2 8 = 3

Wykładnik jest funkcją kwadratową y = 1 − 4x − x 2 . Zapiszmy to w postaci normalnej: y = −x 2 − 4x + 1.

Oczywiście wykres tej funkcji jest parabolą, rozgałęzieniami w dół (a = −1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 (−1)) = 4/(−2) = −2

Oryginalna funkcja jest wykładnicza, jest monotoniczna, więc najwyższa wartość będzie w znalezionym punkcie x 0 = −2:

Uważny czytelnik z pewnością zauważy, że nie zapisaliśmy obszaru dopuszczalnych wartości pierwiastka i logarytmu. Ale to nie było wymagane: wewnątrz znajdują się funkcje, których wartości są zawsze dodatnie.

Konsekwencje z zakresu funkcji

Czasami do rozwiązania problemu B15 nie wystarczy samo znalezienie wierzchołka paraboli. Pożądana wartość może leżeć na końcu segmentu, ale nie w punkcie ekstremalnym. Jeśli zadanie w ogóle nie określa segmentu, spójrz na zakres tolerancji oryginalna funkcja. Mianowicie:

Zwróć uwagę ponownie: zero może znajdować się pod pierwiastkiem, ale nigdy w logarytmie lub mianowniku ułamka. Zobaczmy, jak to działa na konkretnych przykładach:

Zadanie. Znajdź największą wartość funkcji:

Pod korzeniem ponownie znajduje się funkcja kwadratowa: y \u003d 3 - 2x - x 2. Jego wykres jest parabolą, ale rozgałęzia się w dół, ponieważ a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Pierwiastek kwadratowy z liczby ujemnej nie istnieje.

Wypisujemy obszar ​​dopuszczalnych wartości​​(ODZ):

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; jeden]

Teraz znajdź wierzchołek paraboli:

x 0 = −b /(2a ) = −(−2)/(2 (−1)) = 2/(−2) = −1

Punkt x 0 = -1 należy do segmentu ODZ - i to dobrze. Rozważmy teraz wartość funkcji w punkcie x 0, a także na końcach ODZ:

y(−3) = y(1) = 0

Tak więc otrzymaliśmy liczby 2 i 0. Prosimy o znalezienie największej - to jest liczba 2.

Zadanie. Znajdź najmniejszą wartość funkcji:

y = log 0,5 (6x - x 2 - 5)

Wewnątrz logarytmu jest funkcja kwadratowa y = 6x − x 2 − 5. Jest to parabola z rozgałęzieniami w dół, ale w logarytmie nie może być liczby ujemne, więc wypisujemy ODZ:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Uwaga: nierówność jest ścisła, więc końce nie należą do ODZ. W ten sposób logarytm różni się od pierwiastka, gdzie końce odcinka całkiem nam odpowiadają.

Poszukując wierzchołka paraboli:

x 0 = −b /(2a ) = −6/(2 (−1)) = −6/(−2) = 3

Wierzchołek paraboli pasuje do ODZ: x 0 = 3 ∈ (1; 5). Ale ponieważ końce odcinka nas nie interesują, rozważamy wartość funkcji tylko w punkcie x 0:

y min = y (3) = log 0,5 (6 3 - 3 2 - 5) = log 0,5 (18 - 9 - 5) = log 0,5 4 = -2

Z praktyczny punkt Najbardziej interesujące jest wykorzystanie pochodnej do znalezienia największych i najmniejszych wartości funkcji. Z czym to się wiąże? Maksymalizacja zysków, minimalizacja kosztów, wyznaczanie optymalnego obciążenia sprzętu... Innymi słowy, w wielu dziedzinach życia trzeba rozwiązać problem optymalizacji niektórych parametrów. I to jest problem ze znalezieniem największych i najmniejszych wartości funkcji.

Należy zauważyć, że największej i najmniejszej wartości funkcji szuka się zwykle na pewnym przedziale X , który jest albo całą dziedziną funkcji, albo jej częścią. Sam przedział X może być odcinkiem linii, przedziałem otwartym , nieskończony przedział .

W tym artykule porozmawiamy o wyraźnym znalezieniu największych i najmniejszych wartości. podana funkcja jedna zmienna y=f(x) .

Nawigacja po stronach.

Największa i najmniejsza wartość funkcji - definicje, ilustracje.

Zastanówmy się krótko nad głównymi definicjami.

Największa wartość funkcji , który dla każdego nierówność jest prawdziwa.

Najmniejsza wartość funkcji y=f(x) na przedziale X nazywamy taką wartością , który dla każdego nierówność jest prawdziwa.

Definicje te są intuicyjne: największa (najmniejsza) wartość funkcji to największa (najmniejsza) wartość przyjęta na rozpatrywanym przedziale z odciętą.

Punkty stacjonarne są wartościami argumentu, przy którym znika pochodna funkcji.

Dlaczego potrzebujemy punktów stacjonarnych przy znajdowaniu największych i najmniejszych wartości? Odpowiedź na to pytanie daje twierdzenie Fermata. Z tego twierdzenia wynika, że ​​jeśli funkcja różniczkowalna ma w pewnym momencie ekstremum (lokalne minimum lub lokalne maksimum), to punkt ten jest stacjonarny. Tak więc funkcja często przyjmuje swoją maksymalną (najmniejszą) wartość na przedziale X w jednym z punktów stacjonarnych z tego przedziału.

Ponadto funkcja często może przyjmować największe i najmniejsze wartości w punktach, w których nie istnieje pierwsza pochodna tej funkcji, a sama funkcja jest zdefiniowana.

Odpowiedzmy od razu na jedno z najczęstszych pytań na ten temat: „Czy zawsze można określić największą (najmniejszą) wartość funkcji”? Nie zawsze. Czasami granice przedziału X pokrywają się z granicami dziedziny funkcji lub przedział X jest nieskończony. A niektóre funkcje w nieskończoności i na granicach dziedziny definicji mogą przyjmować zarówno nieskończenie duże, jak i nieskończenie małe wartości. W takich przypadkach nie można nic powiedzieć o największej i najmniejszej wartości funkcji.

Dla jasności podajemy ilustrację graficzną. Spójrz na zdjęcia - a wiele stanie się jasne.

Na segmencie

Na pierwszym rysunku funkcja przyjmuje największą (max y ) i najmniejszą (min y ) wartość w punktach stacjonarnych wewnątrz odcinka [-6;6] .

Rozważmy przypadek pokazany na drugim rysunku. Zmień segment na . W tym przykładzie najmniejszą wartość funkcji uzyskuje się w punkcie stacjonarnym, a największą w punkcie z odciętą odpowiadającą prawej granicy przedziału.

Na rysunku nr 3 punktami brzegowymi odcinka [-3; 2] są odcięte punkty odpowiadające największej i najmniejszej wartości funkcji.

W otwartym zasięgu

Na czwartym rysunku funkcja przyjmuje największe (max y ) i najmniejsze (min y ) wartości w punktach stacjonarnych w przedziale otwartym (-6;6) .

Na przedziale nie można wyciągnąć żadnych wniosków na temat największej wartości.

W nieskończoności

W przykładzie przedstawionym na siódmym rysunku funkcja przyjmuje największą wartość (max y ) w punkcie stacjonarnym o x=1 odciętej, a najmniejszą wartość (min y ) osiągnięto na prawej granicy przedziału. Przy minus nieskończoności wartości funkcji zbliżają się asymptotycznie do y=3 .

W przedziale funkcja nie osiąga ani najmniejszej, ani największej wartości. Ponieważ x=2 zmierza w prawo, wartości funkcji mają tendencję do minus nieskończoności (linia prosta x=2 jest pionową asymptotą), a gdy odcięta dąży do plus nieskończoności, wartości funkcji zbliżają się asymptotycznie do y=3 . Graficzną ilustrację tego przykładu pokazano na rysunku 8.

Algorytm znajdowania największych i najmniejszych wartości funkcji ciągłej na odcinku.

Piszemy algorytm, który pozwala nam znaleźć największą i najmniejszą wartość funkcji na odcinku.

1. Znajdujemy dziedzinę funkcji i sprawdzamy, czy zawiera ona cały segment .
2. Znajdujemy wszystkie punkty, w których pierwsza pochodna nie istnieje i które są zawarte w segmencie (zwykle takie punkty występują w funkcjach z argumentem pod znakiem modułu i w funkcje zasilania z ułamkowym wykładnikiem wymiernym). Jeśli nie ma takich punktów, przejdź do następnego punktu.
3. Określamy wszystkie punkty stacjonarne, które wchodzą w segment. Aby to zrobić, przyrównujemy go do zera, rozwiązujemy otrzymane równanie i wybieramy odpowiednie pierwiastki. Jeśli nie ma punktów stacjonarnych lub żaden z nich nie mieści się w segmencie, przejdź do następnego kroku.
4. Obliczamy wartości funkcji w wybranych punktach stacjonarnych (jeśli występują), w punktach, w których pierwsza pochodna nie istnieje (jeśli w ogóle), a także w x=a i x=b .
5. Z uzyskanych wartości funkcji wybieramy największą i najmniejszą - będą to odpowiednio pożądana maksymalna i najmniejsza wartość funkcji.

Przeanalizujmy algorytm przy rozwiązywaniu przykładu znajdowania największych i najmniejszych wartości funkcji na segmencie.

Przykład.

Znajdź największą i najmniejszą wartość funkcji

• na segmencie;
• w przedziale [-4;-1] .

Decyzja.

Dziedziną funkcji jest cały zbiór liczb rzeczywistych, z wyjątkiem zera, czyli . Oba segmenty mieszczą się w domenie definicji.

Znajdujemy pochodną funkcji względem:

Oczywiście pochodna funkcji istnieje we wszystkich punktach odcinków i [-4;-1] .

Punkty stacjonarne wyznaczane są z równania . Jedynym prawdziwym pierwiastkiem jest x=2 . Ten punkt stacjonarny należy do pierwszego segmentu.

Dla pierwszego przypadku obliczamy wartości funkcji na końcach odcinka oraz w punkcie stacjonarnym, czyli dla x=1 , x=2 i x=4 :

Dlatego największa wartość funkcji jest osiągana przy x=1 , a najmniejsza wartość – przy x=2 .

W drugim przypadku wartości funkcji obliczamy tylko na końcach odcinka [-4;-1] (ponieważ nie zawiera on ani jednego punktu stacjonarnego):

Dana funkcja jest zdefiniowana i ciągła na pewnym przedziale . Wymagane jest znalezienie największej (najmniejszej) wartości funkcji w tym przedziale.

Podstawy teoretyczne.
Twierdzenie (drugie twierdzenie Weierstrassa):

Jeżeli funkcja jest zdefiniowana i ciągła w przedziale domkniętym, to w tym przedziale osiąga swoje wartości maksymalne i minimalne.

Funkcja może osiągnąć swoje maksymalne i minimalne wartości albo w wewnętrznych punktach przedziału, albo na jego granicach. Zilustrujmy wszystko możliwe opcje.

Wyjaśnienie:
1) Funkcja osiąga swoją wartość maksymalną na lewym brzegu przedziału w punkcie , a wartość minimalną na prawym brzegu przedziału w punkcie .
2) Funkcja osiąga wartość maksymalną w punkcie (jest to punkt maksymalny), a wartość minimalną przy prawej granicy przedziału w punkcie.
3) Funkcja osiąga swoją wartość maksymalną na lewej granicy przedziału w punkcie i wartość minimalną w punkcie (jest to punkt minimum).
4) Funkcja jest stała na przedziale, tj. osiąga swoje wartości minimalne i maksymalne w dowolnym punkcie przedziału, a wartości minimalne i maksymalne są sobie równe.
5) Funkcja osiąga wartość maksymalną w punkcie i wartość minimalną w punkcie (pomimo tego, że funkcja ma zarówno maksimum, jak i minimum na tym przedziale).
6) Funkcja osiąga w punkcie swoją wartość maksymalną (jest to punkt maksymalny), a w punkcie swoją wartość minimalną (jest to punkt minimum).
Komentarz:

„Maksymalna” i „maksymalna wartość” to różne rzeczy. Wynika to z definicji maksimum i intuicyjnego rozumienia wyrażenia „wartość maksymalna”.

Algorytm rozwiązywania problemu 2.



4) Wybierz z uzyskanych wartości największą (najmniejszą) i zapisz odpowiedź.

Przykład 4:

Określ największą i najmniejszą wartość funkcji na segmencie.
Decyzja:
1) Znajdź pochodną funkcji.

2) Znajdź punkty stacjonarne (i punkty podejrzane o ekstremum), rozwiązując równanie . Zwróć uwagę na punkty, w których nie ma dwustronnej pochodnej skończonej.

3) Oblicz wartości funkcji w punktach stacjonarnych i na granicach przedziału.

4) Wybierz z uzyskanych wartości największą (najmniejszą) i zapisz odpowiedź.

Funkcja na tym odcinku osiąga maksymalną wartość w punkcie o współrzędnych.

Funkcja na tym odcinku osiąga swoją minimalną wartość w punkcie o współrzędnych.

Poprawność obliczeń można zweryfikować patrząc na wykres badanej funkcji.


Komentarz: Funkcja osiąga wartość maksymalną w punkcie maksimum, a wartość minimalną na granicy segmentu.

Szczególny przypadek.

Załóżmy, że chcemy znaleźć maksimum i minimalna wartość niektóre funkcje na interwale. Po wykonaniu pierwszego akapitu algorytmu, tj. obliczając pochodną, ​​staje się jasne, że na przykład bierze tylko wartości ujemne na całym rozważanym segmencie. Pamiętaj, że jeśli pochodna jest ujemna, to funkcja maleje. Odkryliśmy, że funkcja maleje na całym przedziale. Sytuację tę przedstawia wykres nr 1 na początku artykułu.

Funkcja zmniejsza się na interwale, tj. nie ma punktów ekstremalnych. Z rysunku widać, że funkcja przyjmie najmniejszą wartość z prawej strony segmentu, a największą z lewej. jeśli pochodna na przedziale jest wszędzie dodatnia, to funkcja rośnie. Najmniejsza wartość znajduje się po lewej stronie segmentu, największa po prawej.

W tym artykule omówię algorytm znajdowania największej i najmniejszej wartości funkcja, punkty minimalne i maksymalne.

Z teorii na pewno będziemy potrzebować tabela pochodna oraz zasady różnicowania. To wszystko na tej tablicy:

Algorytm znajdowania największych i najmniejszych wartości.

Łatwiej mi to wyjaśnić konkretny przykład. Rozważać:

Przykład: Znajdź największą wartość funkcji y=x^5+20x^3–65x na odcinku [–4;0].

Krok 1. Bierzemy pochodną.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Krok 2 Znajdowanie punktów ekstremalnych.

punkt skrajny nazywamy takie punkty, w których funkcja osiąga swoją maksymalną lub minimalną wartość.

Aby znaleźć punkty ekstremum, należy przyrównać pochodną funkcji do zera (y "= 0)

5x^4 + 60x^2 - 65 = 0

Teraz rozwiążmy to równanie kwadratowe a znalezione korzenie są naszymi ekstremalnymi punktami.

Rozwiązuję takie równania zastępując t = x^2, następnie 5t^2 + 60t - 65 = 0.

Zmniejszmy równanie o 5, otrzymamy: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Dokonujemy odwrotnego podstawienia x^2 = t:

X_(1 i 2) = ±sqrt(1) = ±1
x_(3 i 4) = ±sqrt(-13) (wykluczamy, pod pierwiastkiem nie może być liczb ujemnych, chyba że mówimy oczywiście o liczbach zespolonych)

Razem: x_(1) = 1 i x_(2) = -1 - to są nasze punkty ekstremalne.

Krok 3 Określ największą i najmniejszą wartość.

Metoda substytucyjna.

W warunku otrzymaliśmy odcinek [b][–4;0]. Punkt x=1 nie jest zawarty w tym segmencie. Więc nie bierzemy tego pod uwagę. Ale oprócz punktu x=-1, musimy również wziąć pod uwagę lewą i prawą granicę naszego odcinka, czyli punkty -4 i 0. Aby to zrobić, podstawiamy wszystkie te trzy punkty do pierwotnej funkcji. Zauważ, że oryginalna jest ta podana w warunku (y=x^5+20x^3–65x), niektóre zaczynają zastępować pochodną...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Oznacza to, że maksymalna wartość funkcji wynosi [b]44 i jest osiągana w punktach [b]-1, co nazywamy punktem maksymalnym funkcji na odcinku [-4; 0].

Zdecydowaliśmy i otrzymaliśmy odpowiedź, jesteśmy super, można odpocząć. Ale przestań! Nie uważasz, że liczenie y(-4) jest jakoś zbyt skomplikowane? W warunkach ograniczonego czasu lepiej zastosować inną metodę, nazywam to tak:

Poprzez interwały stałości.

Przedziały te znajdują się dla pochodnej funkcji, czyli dla naszego równania dwukwadratowego.

Robię to w następujący sposób. Rysuję linię kierunkową. Ustawiłem punkty: -4, -1, 0, 1. Pomimo tego, że 1 nie jest uwzględniony w danym odcinku, należy go jeszcze odnotować, aby poprawnie wyznaczyć przedziały stałości. Weźmy pewną liczbę wielokrotnie większą od 1, powiedzmy 100, podstawiając ją w myślach do naszego dwukwadratowego równania 5(100)^4 + 60(100)^2 - 65. Nawet nie licząc czegokolwiek, staje się oczywiste, że w punkcie 100 funkcja ma znak plus. Oznacza to, że dla przedziałów od 1 do 100 ma znak plus. Przechodząc przez 1 (przechodzimy od prawej do lewej), funkcja zmieni znak na minus. Przechodząc przez punkt 0, funkcja zachowa swój znak, ponieważ jest to tylko granica odcinka, a nie pierwiastek równania. Po przejściu przez -1 funkcja ponownie zmieni znak na plus.

Z teorii wiemy, że gdzie jest pochodna funkcji (i narysowaliśmy to dla niej) zmienia znak z plusa na minus (w naszym przypadku punkt -1) funkcja osiąga jego lokalne maksimum (y(-1)=44 jak obliczono wcześniej) na tym segmencie (jest to logicznie bardzo jasne, funkcja przestała rosnąć, ponieważ osiągnęła maksimum i zaczęła spadać).

W związku z tym, gdzie pochodna funkcji zmienia znak z minusa na plus, osiągnięty lokalne minimum funkcji. Tak, tak, znaleźliśmy również lokalny punkt minimum, który wynosi 1, a y(1) jest minimalną wartością funkcji w przedziale, powiedzmy od -1 do +∞. Należy pamiętać, że jest to tylko LOKALNE MINIMUM, czyli minimum w określonym segmencie. Ponieważ rzeczywista (globalna) funkcja minimum osiągnie gdzieś tam, w -∞.

Moim zdaniem pierwsza metoda jest prostsza teoretycznie, a druga prostsza w zakresie działań arytmetycznych, ale znacznie trudniejsza teoretycznie. W końcu zdarzają się przypadki, kiedy funkcja nie zmienia znaku przy przejściu przez pierwiastek równania i rzeczywiście można się pomylić z tymi lokalnymi, globalnymi maksimami i minimami, choć i tak trzeba będzie dobrze opanować, jeśli planujesz wstąpić na politechnikę (a po co jeszcze zdać egzamin profilowy i rozwiązać to zadanie). Ale praktyka i tylko praktyka nauczy cię, jak raz na zawsze rozwiązać takie problemy. I możesz trenować na naszej stronie internetowej. Tutaj .

Jeśli masz jakieś pytania lub coś jest niejasne, koniecznie zapytaj. Chętnie odpowiem i wprowadzę zmiany, uzupełnienia do artykułu. Pamiętaj, że wspólnie tworzymy tę stronę!