Co to znaczy znaleźć najmniejszą wartość funkcji. Największe i najmniejsze wartości funkcji na segmencie

Proces znajdowania najmniejszych i największych wartości funkcji na odcinku przypomina fascynujący lot wokół obiektu (wykres funkcji) na śmigłowcu z ostrzałem z armaty dalekiego zasięgu w określonych punktach i wyborem z te punkty to bardzo szczególne punkty do strzałów kontrolnych. Punkty są wybierane w określony sposób i według określonych zasad. Na jakich zasadach? Porozmawiamy o tym dalej.

Jeśli funkcja tak = f(x) ciągły na odcinku [ a, b] , to dociera do tego odcinka najmniej oraz najwyższe wartości . Może się to zdarzyć w punkty ekstremalne lub na końcach segmentu. Dlatego, aby znaleźć najmniej oraz największe wartości funkcji , ciągła na przedziale [ a, b] , trzeba w sumie obliczyć jego wartości punkt krytyczny i na końcach segmentu, a następnie wybierz najmniejszy i największy z nich.

Załóżmy na przykład, że wymagane jest zdefiniowanie najwyższa wartość Funkcje f(x) na odcinku [ a, b] . Aby to zrobić, znajdź wszystkie jego punkty krytyczne leżące na [ a, b] .

punkt krytyczny nazywa się punktem, w którym zdefiniowana funkcja, i jej pochodna ma wartość zero lub nie istnieje. Następnie należy obliczyć wartości funkcji w punktach krytycznych. I na koniec należy porównać wartości funkcji w punktach krytycznych i na końcach odcinka ( f(a) oraz f(b) ). Największa z tych liczb będzie największa wartość funkcji na segmencie [a, b] .

Problem ze znalezieniem najmniejsze wartości funkcji .

Wspólnie poszukujemy najmniejszych i największych wartości funkcji

Przykład 1. Znajdź najmniejszą i największą wartość funkcji na segmencie [-1, 2] .

Decyzja. Znajdujemy pochodną tej funkcji. Przyrównaj pochodną do zera () i uzyskaj dwa punkty krytyczne: i . Aby znaleźć najmniejszą i największą wartość funkcji na danym odcinku, wystarczy obliczyć jej wartości na końcach odcinka oraz w punkcie, gdyż punkt nie należy do odcinka [-1, 2] . Te wartości funkcji są następujące: , , . Wynika, że najmniejsza wartość funkcji(zaznaczony na czerwono na poniższym wykresie), równy -7, osiąga prawy koniec odcinka - w punkcie , oraz największy(również czerwony na wykresie), jest równy 9, - w punkcie krytycznym .

Jeżeli funkcja jest ciągła w pewnym przedziale i przedział ten nie jest odcinkiem (ale jest na przykład przedziałem; różnica między przedziałem a odcinkiem: punkty graniczne przedziału nie są zawarte w przedziale, ale punkty brzegowe segmentu są zawarte w segmencie), wówczas wśród wartości funkcji może nie być najmniejszej i największej. Na przykład funkcja przedstawiona na poniższym rysunku jest ciągła na ]-∞, +∞[ i nie ma największej wartości.

Jednak dla dowolnego przedziału (zamkniętego, otwartego lub nieskończonego) obowiązuje następująca właściwość funkcji ciągłych.

Przykład 4. Znajdź najmniejszą i największą wartość funkcji na segmencie [-1, 3] .

Decyzja. Znajdujemy pochodną tej funkcji jako pochodną ilorazu:

.

Przyrównujemy pochodną do zera, co daje nam jeden punkt krytyczny: . Należy do przedziału [-1, 3] . Aby znaleźć najmniejszą i największą wartość funkcji na danym segmencie, znajdujemy jej wartości na końcach segmentu oraz w znalezionym punkcie krytycznym:

Porównajmy te wartości. Wniosek: równy -5/13, w punkcie i największa wartość równy 1 w punkcie .

Wspólnie poszukujemy najmniejszych i największych wartości funkcji

Są nauczyciele, którzy na temat znajdowania najmniejszych i największych wartości funkcji nie podają uczniom przykładów bardziej skomplikowanych niż te właśnie rozważane, czyli takich, w których funkcja jest wielomianem lub ułamkiem, licznikiem a mianownikiem są wielomiany. Ale nie będziemy ograniczać się do takich przykładów, ponieważ wśród nauczycieli są miłośnicy zmuszania uczniów do pełnego myślenia (tabela pochodnych). Dlatego zostanie użyty logarytm i funkcja trygonometryczna.

Przykład 6. Znajdź najmniejszą i największą wartość funkcji na segmencie .

Decyzja. Znajdujemy pochodną tej funkcji jako pochodna produktu :

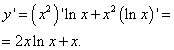
Przyrównujemy pochodną do zera, co daje jeden punkt krytyczny: . Należy do segmentu. Aby znaleźć najmniejszą i największą wartość funkcji na danym segmencie, znajdujemy jej wartości na końcach segmentu oraz w znalezionym punkcie krytycznym:

Wynik wszystkich działań: funkcja osiąga najmniejsza wartość , równy 0, w punkcie i w punkcie oraz największa wartość równy mi² , w punkcie .

Przykład 7. Znajdź najmniejszą i największą wartość funkcji na segmencie .

Decyzja. Znajdujemy pochodną tej funkcji:

Zrównaj pochodną do zera:

Jedyny punkt krytyczny należy do segmentu. Aby znaleźć najmniejszą i największą wartość funkcji na danym segmencie, znajdujemy jej wartości na końcach segmentu oraz w znalezionym punkcie krytycznym:

Wniosek: funkcja osiąga swoją minimalną wartość, równy , w punkcie i największa wartość, równy , w punkcie .

W stosowanych problemach ekstremalnych znalezienie najmniejszych (największych) wartości funkcji z reguły sprowadza się do znalezienia minimum (maksimum). Ale to nie same minima czy maksima mają większe znaczenie praktyczne, ale wartości argumentu, przy którym są osiągane. Przy rozwiązywaniu problemów aplikacyjnych pojawia się dodatkowa trudność - zestawienie funkcji opisujących rozpatrywane zjawisko lub proces.

Przykład 8 Zbiornik o pojemności 4, w kształcie równoległościanu o kwadratowej podstawie i otwarty od góry, musi być ocynowany. Jakie powinny być wymiary zbiornika, aby pokryć go jak najmniejszą ilością materiału?

Decyzja. Zostawiać x- strona podstawowa h- wysokość zbiornika, S- jego powierzchnia bez osłony, V- jego objętość. Powierzchnia zbiornika wyrażona jest wzorem tj. jest funkcją dwóch zmiennych. Wyrazić S jako funkcję jednej zmiennej wykorzystujemy fakt, że , whence . Podstawianie znalezionego wyrażenia h we wzorze na S:

Przyjrzyjmy się tej funkcji ekstremum. Jest zdefiniowana i różniczkowalna wszędzie w ]0, +∞[ , i

.

Przyrównujemy pochodną do zera () i znajdujemy punkt krytyczny. Ponadto w , pochodna nie istnieje, ale wartość ta nie jest objęta zakresem definicji i dlatego nie może być punktem ekstremum. A więc - jedyny punkt krytyczny. Sprawdźmy to pod kątem obecności ekstremum za pomocą drugiego wystarczający znak. Znajdźmy drugą pochodną. Gdy druga pochodna jest większa od zera (). Oznacza to, że gdy funkcja osiągnie minimum . Ponieważ to minimum - jedyne ekstremum tej funkcji, jest to jej najmniejsza wartość. Tak więc bok podstawy zbiornika powinien wynosić 2 m, a jego wysokość.

Przykład 9 Z akapitu A, położony na linii kolejowej, do punktu Z, w pewnej odległości od niego ja, towary muszą być transportowane. Koszt transportu jednostki wagowej na jednostkę odległości koleją wynosi , a autostradą wynosi . Do jakiego momentu? M linie kolej żelazna należy wybudować autostradę, aby transport towarów z ALE w Z był najbardziej ekonomiczny AB zakłada się, że kolej jest prosta)?

Zobaczmy, jak badać funkcję za pomocą wykresu. Okazuje się, że patrząc na wykres można dowiedzieć się wszystkiego, co nas interesuje, a mianowicie:

• zakres funkcji
• zakres funkcji
• funkcja zera
• okresy wzrostu i spadku
• wysokie i niskie punkty
• największa i najmniejsza wartość funkcji w segmencie.

Wyjaśnijmy terminologię:

Odcięta jest współrzędną poziomą punktu.
Rzędna- współrzędna pionowa.
odcięta- oś pozioma, najczęściej nazywana osią.
oś Y - Oś pionowa lub oś .

Argument jest zmienną niezależną, od której zależą wartości funkcji. Najczęściej wskazywane.
Innymi słowy sami wybieramy , podstawiamy we wzorze funkcji i otrzymujemy .

Domena funkcje - zbiór tych (i tylko tych) wartości argumentu, dla którego funkcja istnieje.
Oznaczono: lub .

Na naszym rysunku dziedziną funkcji jest segment. To na tym segmencie rysowany jest wykres funkcji. Tylko tutaj podana funkcja istnieć.

Zakres funkcji to zbiór wartości, które przyjmuje zmienna. Na naszym rysunku jest to segment - od najniższej do najwyższej wartości.

Zera funkcji- punkty, w których wartość funkcji jest równa zero, czyli . Na naszym rysunku są to punkty i .

Wartości funkcji są dodatnie gdzie . Na naszym rysunku są to interwały i .
Wartości funkcji są ujemne gdzie . Mamy ten przedział (lub przedział) od do.

Najważniejsze koncepcje - funkcje zwiększające i malejące na jakimś zestawie. Jako zestaw możesz wziąć segment, przedział, sumę przedziałów lub całą oś liczbową.

Funkcjonować wzrasta

Innymi słowy im więcej , tym bardziej , czyli wykres idzie w prawo i w górę.

Funkcjonować maleje na zbiorze jeśli dla dowolnego i przynależności do zbioru nierówność implikuje nierówność .

Dla funkcji malejącej większa wartość odpowiada niższej wartości . Wykres idzie w prawo iw dół.

Na naszym rysunku funkcja rośnie na przedziale i maleje na przedziałach i .

Zdefiniujmy, co to jest maksymalne i minimalne punkty funkcji.

Maksymalny punkt- jest to wewnętrzny punkt dziedziny definicji, taki, że wartość funkcji w nim jest większa niż we wszystkich punktach dostatecznie mu bliskich.
Innymi słowy, punkt maksymalny jest takim punktem, wartością funkcji, w której jeszcze niż w sąsiednich. To lokalne „wzgórze” na wykresie.

Na naszej figurze - maksymalny punkt.

Niski punkt- wewnętrzny punkt dziedziny definicji, taki, że wartość funkcji w nim jest mniejsza niż we wszystkich punktach wystarczająco blisko niego.
Oznacza to, że punkt minimum jest taki, że wartość funkcji w nim jest mniejsza niż w sąsiednich. Na wykresie jest to lokalna „dziura”.

Na naszej figurze - punkt minimalny.

Punkt jest granicą. Nie jest to wewnętrzny punkt dziedziny definicji i dlatego nie pasuje do definicji punktu maksymalnego. Po lewej stronie nie ma przecież sąsiadów. W ten sam sposób na naszym wykresie nie może być żadnego punktu minimalnego.

Punkty maksymalne i minimalne są zbiorczo nazywane skrajne punkty funkcji. W naszym przypadku jest to i .

Ale co jeśli potrzebujesz znaleźć na przykład funkcja minimum na kroju? W ta sprawa odpowiedź: . ponieważ funkcja minimum jest jego wartością w punkcie minimum.

Podobnie maksimum naszej funkcji to . Osiąga się to w punkcie.

Można powiedzieć, że ekstrema funkcji są równe i .

Czasami w zadaniach trzeba znaleźć największe i najmniejsze wartości funkcji na danym segmencie. Niekoniecznie pokrywają się z skrajnościami.

W naszym przypadku najmniejsza wartość funkcji na przedziale jest równy i pokrywa się z minimum funkcji. Ale jego największa wartość w tym segmencie wynosi . Osiąga się go na lewym końcu segmentu.

W każdym razie największe i najmniejsze wartości funkcji ciągłej na segmencie osiągane są albo w punktach ekstremów, albo na końcach segmentu.

Często w fizyce i matematyce wymagane jest znalezienie najmniejszej wartości funkcji. Jak to zrobić, powiemy teraz.

Jak znaleźć najmniejszą wartość funkcji: instrukcja

1. Aby obliczyć najmniejszą wartość funkcji ciągłej na danym przedziale, musisz postępować zgodnie z następującym algorytmem:
2. Znajdź pochodną funkcji.
3. Znajdź na danym odcinku punkty, w których pochodna jest równa zero, a także wszystkie punkty krytyczne. Następnie znajdź wartości funkcji w tych punktach, to znaczy rozwiąż równanie, w którym x jest równe zeru. Dowiedz się, która z wartości jest najmniejsza.
4. Dowiedz się, jaką wartość ma funkcja w punktach końcowych. Określ najmniejszą wartość funkcji w tych punktach.
5. Porównaj otrzymane dane z najmniejszą wartością. Mniejsza z otrzymanych liczb będzie najmniejszą wartością funkcji.

Zwróć uwagę, że jeśli funkcja w segmencie nie ma najmniejsze punkty, co oznacza, że ​​na tym segmencie rośnie lub maleje. Dlatego najmniejszą wartość należy obliczyć na skończonych segmentach funkcji.

We wszystkich pozostałych przypadkach wartość funkcji obliczana jest zgodnie z podanym algorytmem. Na każdym kroku algorytmu będziesz musiał rozwiązać prosty równanie liniowe z jednym korzeniem. Rozwiąż równanie za pomocą rysunku, aby uniknąć błędów.

Jak znaleźć najmniejszą wartość funkcji na półotwartym segmencie? Na półotwartym lub okres otwarty funkcji, najmniejszą wartość należy znaleźć w następujący sposób. W punktach końcowych wartości funkcji oblicz jednostronny limit funkcji. Innymi słowy, rozwiąż równanie, w którym punkty tendencji są podane przez wartości a+0 i b+0, gdzie aib są nazwami punktów krytycznych.

Teraz wiesz, jak znaleźć najmniejszą wartość funkcji. Najważniejsze jest prawidłowe, dokładne i bezbłędne wykonanie wszystkich obliczeń.

W tym artykule omówię algorytm znajdowania największej i najmniejszej wartości funkcja, punkty minimalne i maksymalne.

Z teorii na pewno będziemy potrzebować tabela pochodna oraz zasady różnicowania. To wszystko na tej tablicy:

Algorytm znajdowania największych i najmniejszych wartości.

Łatwiej mi to wyjaśnić konkretny przykład. Rozważać:

Przykład: Znajdź największą wartość funkcji y=x^5+20x^3–65x na odcinku [–4;0].

Krok 1. Bierzemy pochodną.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Krok 2 Znajdowanie punktów ekstremalnych.

punkt skrajny nazywamy takie punkty, w których funkcja osiąga swoją maksymalną lub minimalną wartość.

Aby znaleźć punkty ekstremum, należy przyrównać pochodną funkcji do zera (y "= 0)

5x^4 + 60x^2 - 65 = 0

Teraz rozwiązujemy to równanie dwukwadratowe, a znalezione pierwiastki są naszymi punktami ekstremalnymi.

Rozwiązuję takie równania zastępując t = x^2, następnie 5t^2 + 60t - 65 = 0.

Zmniejszmy równanie o 5, otrzymamy: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Dokonujemy odwrotnego podstawienia x^2 = t:

X_(1 i 2) = ±sqrt(1) = ±1
x_(3 i 4) = ±sqrt(-13) (wykluczamy, pod pierwiastkiem nie może być liczby ujemne(chyba, że ​​oczywiście mówimy o liczbach zespolonych)

Razem: x_(1) = 1 i x_(2) = -1 - to są nasze punkty ekstremalne.

Krok 3 Określ największą i najmniejszą wartość.

Metoda substytucyjna.

W warunku otrzymaliśmy odcinek [b][–4;0]. Punkt x=1 nie jest zawarty w tym segmencie. Więc nie bierzemy tego pod uwagę. Ale oprócz punktu x=-1, musimy również wziąć pod uwagę lewą i prawą granicę naszego odcinka, czyli punkty -4 i 0. Aby to zrobić, podstawiamy wszystkie te trzy punkty do pierwotnej funkcji. Zauważ, że pierwotna jest ta podana w warunku (y=x^5+20x^3–65x), niektóre zaczynają zastępować pochodną...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Oznacza to, że maksymalna wartość funkcji wynosi [b]44 i jest osiągana w punktach [b]-1, co nazywamy punktem maksymalnym funkcji na odcinku [-4; 0].

Zdecydowaliśmy i otrzymaliśmy odpowiedź, jesteśmy super, można odpocząć. Ale przestań! Nie uważasz, że liczenie y(-4) jest jakoś zbyt skomplikowane? W warunkach ograniczonego czasu lepiej zastosować inną metodę, nazywam to tak:

Poprzez interwały stałości.

Luki te znajdują się dla pochodnej funkcji, czyli dla naszego równania dwukwadratowego.

Robię to w następujący sposób. Rysuję linię kierunkową. Ustawiłem punkty: -4, -1, 0, 1. Pomimo tego, że 1 nie jest uwzględniony w danym odcinku, należy go jeszcze odnotować, aby poprawnie wyznaczyć przedziały stałości. Weźmy pewną liczbę wielokrotnie większą od 1, powiedzmy 100, podstawiając ją w myślach do naszego dwukwadratowego równania 5(100)^4 + 60(100)^2 - 65. Nawet nie licząc czegokolwiek, staje się oczywiste, że w punkcie 100 funkcja ma znak plus. Oznacza to, że dla przedziałów od 1 do 100 ma znak plus. Przechodząc przez 1 (przechodzimy od prawej do lewej), funkcja zmieni znak na minus. Przechodząc przez punkt 0, funkcja zachowa swój znak, ponieważ jest to tylko granica odcinka, a nie pierwiastek równania. Po przejściu przez -1 funkcja ponownie zmieni znak na plus.

Z teorii wiemy, że gdzie jest pochodna funkcji (i narysowaliśmy to dla niej) zmienia znak z plusa na minus (w naszym przypadku punkt -1) funkcja osiąga jego lokalne maksimum (y(-1)=44 jak obliczono wcześniej) na tym segmencie (jest to logicznie bardzo jasne, funkcja przestała rosnąć, ponieważ osiągnęła maksimum i zaczęła spadać).

W związku z tym, gdzie pochodna funkcji zmienia znak z minus na plus, osiągnięty lokalne minimum funkcji. Tak, tak, stwierdziliśmy również, że lokalny punkt minimalny to 1, a y(1) to minimalna wartość funkcje na segmencie, powiedzmy od -1 do +∞. Należy pamiętać, że jest to tylko LOKALNE MINIMUM, czyli minimum w określonym segmencie. Ponieważ rzeczywista (globalna) funkcja minimum osiągnie gdzieś tam, w -∞.

Moim zdaniem pierwsza metoda jest prostsza teoretycznie, a druga prostsza w zakresie działań arytmetycznych, ale znacznie trudniejsza teoretycznie. Przecież czasami zdarzają się przypadki, kiedy funkcja nie zmienia znaku przy przejściu przez pierwiastek równania i rzeczywiście można się pomylić z tymi lokalnymi, globalnymi maksimami i minimami, chociaż i tak trzeba będzie dobrze to opanować, jeśli planujesz wstąpić na politechnikę (a po co jeszcze zdać egzamin profilowy i rozwiązać to zadanie). Ale praktyka i tylko praktyka nauczy cię, jak raz na zawsze rozwiązać takie problemy. I możesz trenować na naszej stronie internetowej. Tutaj .

Jeśli masz jakieś pytania lub coś jest niejasne, koniecznie zapytaj. Chętnie odpowiem i wprowadzę zmiany, uzupełnienia do artykułu. Pamiętaj, że wspólnie tworzymy tę stronę!

Niech funkcja $z=f(x,y)$ będzie zdefiniowana i ciągła w pewnej ograniczonej domenie $D$. Niech dana funkcja ma skończone pochodne cząstkowe pierwszego rzędu w tym obszarze (możliwym wyjątkiem skończonej liczby punktów). Aby znaleźć największą i najmniejszą wartość funkcji dwóch zmiennych w danym obszarze zamkniętym, wymagane są trzy kroki prostego algorytmu.

Algorytm znajdowania największych i najmniejszych wartości funkcji $z=f(x,y)$ w domenie zamkniętej $D$.

1. Znajdź punkty krytyczne funkcji $z=f(x,y)$, które należą do obszaru $D$. Oblicz wartości funkcji w punktach krytycznych.
2. Zbadaj zachowanie funkcji $z=f(x,y)$ na granicy obszaru $D$, znajdując punkty o możliwych wartościach maksymalnych i minimalnych. Oblicz wartości funkcji w uzyskanych punktach.
3. Z wartości funkcji uzyskanych w poprzednich dwóch akapitach wybierz największą i najmniejszą.

Jakie są punkty krytyczne? Pokaż ukryj

Pod punkt krytyczny implikują punkty, w których obie pochodne cząstkowe pierwszego rzędu są równe zeru (tj. $\frac(\partial z)(\partial x)=0$ i $\frac(\partial z)(\partial y)=0 $) lub co najmniej jedna pochodna cząstkowa nie istnieje.

Często punkty, w których pochodne cząstkowe pierwszego rzędu są równe zeru, nazywa się punkty stacjonarne. Zatem punkty stacjonarne są podzbiorem punktów krytycznych.

Przykład 1

Znajdź maksymalne i minimalne wartości funkcji $z=x^2+2xy-y^2-4x$ w obszarze zamkniętym ograniczonym liniami $x=3$, $y=0$ i $y=x +1$.

Postępujemy zgodnie z powyższym, ale najpierw zajmiemy się rysowaniem danego obszaru, który oznaczymy literą $D$. Mamy dane równania trzech linie proste, które ograniczają ten obszar. Prosta $x=3$ przechodzi przez punkt $(3;0)$ równolegle do osi y (oś Oy). Prosta $y=0$ jest równaniem osi odciętej (oś Ox). Cóż, żeby skonstruować prostą $y=x+1$ znajdźmy dwa punkty, przez które poprowadzimy tę prostą. Możesz oczywiście podstawić kilka dowolnych wartości zamiast $x$. Na przykład zastępując $x=10$, otrzymujemy: $y=x+1=10+1=11$. Znaleźliśmy punkt $(10;11)$ leżący na linii $y=x+1$. Jednak lepiej jest znaleźć te punkty, w których prosta $y=x+1$ przecina się z liniami $x=3$ i $y=0$. Dlaczego jest lepiej? Ponieważ na jednym kamieniu ułożymy kilka ptaków: dostaniemy dwa punkty za skonstruowanie prostej $y=x+1$ i jednocześnie dowiemy się, w których punktach ta prosta przecina się z innymi liniami ograniczającymi daną powierzchnia. Prosta $y=x+1$ przecina prostą $x=3$ w punkcie $(3;4)$ oraz prostą $y=0$ - w punkcie $(-1;0)$. Aby nie zaśmiecać przebiegu rozwiązania wyjaśnieniami pomocniczymi, pytanie o uzyskanie tych dwóch punktów postawię w przypisie.

W jaki sposób uzyskano punkty $(3;4)$ i $(-1;0)$? Pokaż ukryj

Zacznijmy od punktu przecięcia prostych $y=x+1$ i $x=3$. Współrzędne żądanego punktu należą zarówno do pierwszej, jak i drugiej linii, więc aby znaleźć nieznane współrzędne, musisz rozwiązać układ równań:

$$ \left \( \begin(wyrównane) & y=x+1;\\ & x=3. \end(wyrównane) \right. $$

Rozwiązanie takiego układu jest banalne: podstawiając $x=3$ do pierwszego równania otrzymamy: $y=3+1=4$. Punkt $(3;4)$ jest żądanym punktem przecięcia prostych $y=x+1$ i $x=3$.

Teraz znajdźmy punkt przecięcia prostych $y=x+1$ i $y=0$. Ponownie tworzymy i rozwiązujemy układ równań:

$$ \left \( \begin(wyrównane) & y=x+1;\\ & y=0. \end(wyrównane) \right. $$

Podstawiając $y=0$ do pierwszego równania, otrzymujemy: $0=x+1$, $x=-1$. Punkt $(-1;0)$ jest żądanym punktem przecięcia prostych $y=x+1$ i $y=0$ (oś odciętych).

Wszystko jest gotowe do zbudowania rysunku, który będzie wyglądał tak:

Kwestia notatki wydaje się oczywista, bo z figury widać wszystko. Warto jednak pamiętać, że rysunek nie może służyć jako dowód. Rysunek jest tylko ilustracją dla jasności.

Nasz obszar został wyznaczony za pomocą równań linii, które go ograniczają. To oczywiste, że te linie definiują trójkąt, prawda? Czy nie do końca oczywiste? A może mamy inny obszar ograniczony tymi samymi liniami:

Oczywiście warunek mówi, że teren jest zamknięty, więc pokazane zdjęcie jest błędne. Ale aby uniknąć takich niejasności, lepiej jest definiować regiony przez nierówności. Interesuje nas część samolotu znajdująca się pod linią $y=x+1$? Ok, więc $y ≤ x+1$. Nasz obszar powinien znajdować się nad linią $y=0$? Świetnie, więc $y ≥ 0$. Nawiasem mówiąc, dwie ostatnie nierówności można łatwo połączyć w jedną: $0 ≤ y ≤ x+1$.

$$ \left \( \begin(aligned) & 0 ≤ y ≤ x+1;\\ & x ≤ 3. \end(aligned) \right. $$

Nierówności te definiują domenę $D$ i definiują ją jednoznacznie, bez żadnych niejasności. Ale jak to pomaga nam w pytaniu na początku przypisu? Pomoże też :) Musimy sprawdzić, czy punkt $M_1(1;1)$ należy do regionu $D$. Wstawmy $x=1$ i $y=1$ do układu nierówności definiujących ten region. Jeśli obie nierówności są spełnione, to punkt leży wewnątrz regionu. Jeżeli przynajmniej jedna z nierówności nie jest spełniona, to punkt nie należy do regionu. Więc:

$$ \left \( \begin(aligned) & 0 ≤ 1 ≤ 1+1;\\ & 1 ≤ 3. \end(aligned) \right. \;\; \left \( \begin(aligned) & 0 ≤ 1 ≤ 2;\\ & 1 ≤ 3. \end(aligned) \right.$$

Obie nierówności są prawdziwe. Punkt $M_1(1;1)$ należy do regionu $D$.

Teraz przyszła kolej na zbadanie zachowania funkcji na granicy domeny, czyli iść do. Zacznijmy od prostej $y=0$.

Linia prosta $y=0$ (oś odciętych) ogranicza obszar $D$ pod warunkiem $-1 ≤ x ≤ 3$. Zamień $y=0$ na podana funkcja$z(x,y)=x^2+2xy-y^2-4x$. Wynikowa funkcja podstawienia jednej zmiennej $x$ będzie oznaczona jako $f_1(x)$:

$$ f_1(x)=z(x,0)=x^2+2x\cdot 0-0^2-4x=x^2-4x. $$

Teraz dla funkcji $f_1(x)$ musimy znaleźć największą i najmniejszą wartość w przedziale $-1 ≤ x ≤ 3$. Znajdź pochodną tej funkcji i przyrównaj ją do zera:

$$ f_(1)^(")(x)=2x-4;\\ 2x-4=0; \; x=2. $$

Wartość $x=2$ należy do segmentu $-1 ≤ x ≤ 3$, więc do listy punktów dodajemy również $M_2(2;0)$. Dodatkowo obliczamy wartości funkcji $z$ na końcach odcinka $-1 ≤ x ≤ 3$, czyli w punktach $M_3(-1;0)$ i $M_4(3;0)$. Nawiasem mówiąc, gdyby punkt $M_2$ nie należał do rozpatrywanego odcinka, to oczywiście nie byłoby potrzeby obliczania w nim wartości funkcji $z$.

Obliczmy więc wartości funkcji $z$ w punktach $M_2$, $M_3$, $M_4$. Możesz oczywiście podstawić współrzędne tych punktów w oryginalnym wyrażeniu $z=x^2+2xy-y^2-4x$. Np. dla punktu $M_2$ otrzymujemy:

$$z_2=z(M_2)=2^2+2\cdot 2\cdot 0-0^2-4\cdot 2=-4.$$

Jednak obliczenia można nieco uprościć. W tym celu warto pamiętać, że na odcinku $M_3M_4$ mamy $z(x,y)=f_1(x)$. Opiszę to szczegółowo:

\begin(wyrównane) & z_2=z(M_2)=z(2,0)=f_1(2)=2^2-4\cdot 2=-4;\\ & z_3=z(M_3)=z(- 1,0)=f_1(-1)=(-1)^2-4\cdot (-1)=5;\\ & z_4=z(M_4)=z(3,0)=f_1(3)= 3^2-4\cdot 3=-3. \end(wyrównany)

Oczywiście zwykle nie ma potrzeby tak szczegółowych wpisów, a w przyszłości wszystkie obliczenia zaczniemy spisywać w krótszym czasie:

$$z_2=f_1(2)=2^2-4\cdot 2=-4;\; z_3=f_1(-1)=(-1)^2-4\cdot (-1)=5;\; z_4=f_1(3)=3^2-4\cdot 3=-3.$$

Przejdźmy teraz do prostej $x=3$. Linia ta ogranicza domenę $D$ pod warunkiem $0 ≤ y ≤ 4$. Podstaw $x=3$ pod podaną funkcję $z$. W wyniku takiego podstawienia otrzymujemy funkcję $f_2(y)$:

$$ f_2(y)=z(3,y)=3^2+2\cdot 3\cdot y-y^2-4\cdot 3=-y^2+6y-3. $$

Dla funkcji $f_2(y)$ musisz znaleźć największą i najmniejszą wartość w przedziale $0 ≤ y ≤ 4$. Znajdź pochodną tej funkcji i przyrównaj ją do zera:

$$ f_(2)^(")(y)=-2y+6;\\ -2y+6=0; \; y=3. $$

Wartość $y=3$ należy do segmentu $0 ≤ y ≤ 4$, więc do wcześniej znalezionych punktów dodajemy $M_5(3;3)$. Dodatkowo należy obliczyć wartość funkcji $z$ w punktach na końcach odcinka $0 ≤ y ≤ 4$, czyli w punktach $M_4(3;0)$ i $M_6(3;4)$. W punkcie $M_4(3;0)$ obliczyliśmy już wartość $z$. Obliczmy wartość funkcji $z$ w punktach $M_5$ i $M_6$. Przypomnę, że na segmencie $M_4M_6$ mamy $z(x,y)=f_2(y)$, a więc:

\begin(wyrównane) & z_5=f_2(3)=-3^2+6\cdot 3-3=6; &z_6=f_2(4)=-4^2+6\cdot 4-3=5. \end(wyrównany)

I na koniec rozważmy ostatnią granicę $D$, tj. wiersz $y=x+1$. Linia ta ogranicza region $D$ pod warunkiem $-1 ≤ x ≤ 3$. Podstawiając $y=x+1$ do funkcji $z$, otrzymamy:

$$ f_3(x)=z(x,x+1)=x^2+2x\cdot (x+1)-(x+1)^2-4x=2x^2-4x-1. $$

Po raz kolejny mamy funkcję jednej zmiennej $x$. I znowu trzeba znaleźć największe i najmniejsze wartości tej funkcji na segmencie $-1 ≤ x ≤ 3$. Znajdź pochodną funkcji $f_(3)(x)$ i przyrównaj ją do zera:

$$ f_(3)^(")(x)=4x-4;\\ 4x-4=0; \; x=1. $$

Wartość $x=1$ należy do przedziału $-1 ≤ x ≤ 3$. Jeśli $x=1$, to $y=x+1=2$. Dodajmy $M_7(1;2)$ do listy punktów i dowiedzmy się, jaka jest wartość funkcji $z$ w tym punkcie. Punkty na końcach odcinka $-1 ≤ x ≤ 3$, tj. punkty $M_3(-1;0)$ i $M_6(3;4)$ były rozważane wcześniej, znaleźliśmy już w nich wartość funkcji.

$$z_7=f_3(1)=2\cdot 1^2-4\cdot 1-1=-3.$$

Drugi etap rozwiązania został zakończony. Mamy siedem wartości:

$$z_1=-2;\;z_2=-4;\;z_3=5;\;z_4=-3;\;z_5=6;\;z_6=5;\;z_7=-3.$$

Przejdźmy do. Wybierając największe i najmniejsze wartości z tych liczb, które uzyskaliśmy w akapicie trzecim, będziemy mieli:

$$z_(min)=-4; \; z_(max)=6.$$

Problem rozwiązany, pozostaje tylko zapisać odpowiedź.

Odpowiedź: $z_(min)=-4; \; z_(maks.)=6$.

Przykład #2

Znajdź największe i najmniejsze wartości funkcji $z=x^2+y^2-12x+16y$ w obszarze $x^2+y^2 ≤ 25$.

Najpierw zbudujmy rysunek. Równanie $x^2+y^2=25$ (jest to linia graniczna danego obszaru) definiuje okrąg o środku w punkcie początkowym (czyli w punkcie $(0;0)$) i promieniu 5. Nierówność $x^2 +y^2 ≤ 25$ spełnia wszystkie punkty wewnątrz i na wspomnianym okręgu.

Będziemy działać dalej. Znajdźmy pochodne cząstkowe i znajdźmy punkty krytyczne.

$$ \frac(\częściowy z)(\częściowy x)=2x-12; \frac(\częściowy z)(\częściowy y)=2y+16. $$

Nie ma punktów, w których znalezione pochodne cząstkowe nie istnieją. Dowiedzmy się, w jakich punktach obie pochodne cząstkowe są jednocześnie równe zero, tj. znajdź punkty stacjonarne.

$$ \left \( \begin(aligned) & 2x-12=0;\\ & 2y+16=0. \end(aligned) \right. \;\; \left \( \begin(aligned) & x =6;\\ & y=-8.\end(aligned) \right.$$

Otrzymaliśmy punkt stacjonarny $(6;-8)$. Znaleziony punkt nie należy jednak do regionu $D$. Łatwo to pokazać bez uciekania się do rysowania. Sprawdźmy, czy nierówność $x^2+y^2 ≤ 25$, która definiuje naszą domenę $D$, jest aktualna. Jeśli $x=6$, $y=-8$, to $x^2+y^2=36+64=100$, czyli nierówność $x^2+y^2 ≤ 25$ nie jest spełniona. Wniosek: punkt $(6;-8)$ nie należy do regionu $D$.

Tak więc w $D$ nie ma punktów krytycznych. Przejdźmy do. Musimy zbadać zachowanie funkcji na granicy danego obszaru, tj. na okręgu $x^2+y^2=25$. Możesz oczywiście wyrazić $y$ jako $x$, a następnie zamienić otrzymane wyrażenie w naszą funkcję $z$. Z równania okręgu otrzymujemy: $y=\sqrt(25-x^2)$ lub $y=-\sqrt(25-x^2)$. Podstawiając np. $y=\sqrt(25-x^2)$ do danej funkcji, otrzymamy:

$$ z=x^2+y^2-12x+16y=x^2+25-x^2-12x+16\sqrt(25-x^2)=25-12x+16\sqrt(25-x ^2); \;\; -5≤ x ≤ 5. $$

Dalsze rozwiązanie będzie całkowicie identyczne z badaniem zachowania funkcji na granicy obszaru w poprzednim przykładzie nr 1. Jednak bardziej rozsądne wydaje mi się w tej sytuacji zastosowanie metody Lagrange'a. Interesuje nas tylko pierwsza część tej metody. Po zastosowaniu pierwszej części metody Lagrange'a uzyskamy punkty, w których i zbadamy funkcję $z$ dla wartości minimalnych i maksymalnych.

Tworzymy funkcję Lagrange'a:

$$ F=z(x,y)+\lambda\cdot(x^2+y^2-25)=x^2+y^2-12x+16y+\lambda\cdot (x^2+y^2 -25). $$

Znajdujemy pochodne cząstkowe funkcji Lagrange'a i układamy odpowiedni układ równań:

$$ F_(x)^(")=2x-12+2\lambda x; \;\; F_(y)^(")=2y+16+2\lambda y.\\ \left \( \begin (wyrównane) & 2x-12+2\lambda x=0;\\ & 2y+16+2\lambda y=0;\\ & x^2+y^2-25=0.\end(wyrównane) \ po prawej. \;\; \left \( \begin(wyrównane) & x+\lambda x=6;\\ & y+\lambda y=-8;\\ & x^2+y^2=25. \end( wyrównane)\prawo.$$

Aby rozwiązać ten system, wskażmy od razu, że $\lambda\neq -1$. Dlaczego $\lambda\neq -1$? Spróbujmy podstawić $\lambda=-1$ do pierwszego równania:

$$ x+(-1)\cdot x=6; \; x-x=6; \; 0=6. $$

Wynikowa sprzeczność $0=6$ mówi, że wartość $\lambda=-1$ jest nieprawidłowa. Dane wyjściowe: $\lambda\neq -1$. Wyraźmy $x$ i $y$ w kategoriach $\lambda$:

\begin(wyrównane) & x+\lambda x=6;\; x(1+\lambda)=6;\; x=\frac(6)(1+\lambda). \\ & y+\lambda y=-8;\; y(1+\lambda)=-8;\; y=\frac(-8)(1+\lambda). \end(wyrównany)

Uważam, że tutaj staje się oczywiste, dlaczego konkretnie określiliśmy warunek $\lambda\neq -1$. Zrobiono to, aby dopasować wyrażenie $1+\lambda$ do mianowników bez ingerencji. To znaczy, aby mieć pewność, że mianownik to $1+\lambda\neq 0$.

Wstawmy otrzymane wyrażenia na $x$ i $y$ do trzeciego równania układu, tj. w $x^2+y^2=25$:

$$ \left(\frac(6)(1+\lambda) \right)^2+\left(\frac(-8)(1+\lambda) \right)^2=25;\\ \frac( 36)((1+\lambda)^2)+\frac(64)((1+\lambda)^2)=25;\\ \frac(100)((1+\lambda)^2)=25 ; \; (1+\lambda)^2=4. $$

Z otrzymanej równości wynika, że ​​$1+\lambda=2$ lub $1+\lambda=-2$. Stąd mamy dwie wartości parametru $\lambda$, a mianowicie: $\lambda_1=1$, $\lambda_2=-3$. W związku z tym otrzymujemy dwie pary wartości $x$ i $y$:

\begin(wyrównane) & x_1=\frac(6)(1+\lambda_1)=\frac(6)(2)=3; \; y_1=\frac(-8)(1+\lambda_1)=\frac(-8)(2)=-4. \\ & x_2=\frac(6)(1+\lambda_2)=\frac(6)(-2)=-3; \; y_2=\frac(-8)(1+\lambda_2)=\frac(-8)(-2)=4. \end(wyrównany)

Tak więc otrzymaliśmy dwa punkty możliwego ekstremum warunkowego, tj. $M_1(3;-4)$ i $M_2(-3;4)$. Znajdź wartości funkcji $z$ w punktach $M_1$ i $M_2$:

\begin(wyrównane) & z_1=z(M_1)=3^2+(-4)^2-12\cdot 3+16\cdot (-4)=-75; \\ & z_2=z(M_2)=(-3)^2+4^2-12\cdot(-3)+16\cdot 4=125. \end(wyrównany)

Powinniśmy wybrać wartości największe i najmniejsze spośród tych, które uzyskaliśmy w kroku pierwszym i drugim. Ale w tym przypadku wybór jest niewielki :) Mamy:

$$z_(min)=-75; \; z_(maks.)=125. $$

Odpowiedź: $z_(min)=-75; \; z_(maks.)=125$.