Sprawdź rozwiązanie największego i najmniejszego w segmencie. Największa i najmniejsza wartość funkcji. Zadanie B15 (2014)

Zobaczmy, jak zbadać funkcję za pomocą wykresu. Okazuje się, że patrząc na wykres można dowiedzieć się wszystkiego, co nas interesuje, a mianowicie:

• zakres funkcji
• zakres funkcji
• funkcja zera
• okresy wzrostu i spadku
• wysokie i niskie punkty
• największa i najmniejsza wartość funkcji w segmencie.

Wyjaśnijmy terminologię:

Odcięta jest współrzędną poziomą punktu.
Rzędna- współrzędna pionowa.
odcięta- oś pozioma, najczęściej nazywana osią.
oś Y - Oś pionowa lub oś .

Argument jest zmienną niezależną, od której zależą wartości funkcji. Najczęściej wskazywane.
Innymi słowy sami wybieramy , podstawiamy we wzorze funkcji i otrzymujemy .

Domena funkcje - zbiór tych (i tylko tych) wartości argumentu, dla którego funkcja istnieje.
Oznaczono: lub .

Na naszym rysunku dziedziną funkcji jest segment. To na tym segmencie rysowany jest wykres funkcji. Tylko tutaj podana funkcja istnieć.

Zakres funkcji to zbiór wartości, które przyjmuje zmienna. Na naszym rysunku jest to segment - od najniższej do najwyższej wartości.

Zera funkcji- punkty, w których wartość funkcji jest równa zero, czyli . Na naszym rysunku są to punkty i .

Wartości funkcji są dodatnie gdzie . Na naszym rysunku są to interwały i .
Wartości funkcji są ujemne gdzie . Mamy ten przedział (lub przedział) od do.

Najważniejsze koncepcje - funkcje zwiększające i malejące na jakimś zestawie. Jako zestaw możesz wziąć segment, przedział, sumę przedziałów lub całą oś liczbową.

Funkcjonować wzrasta

Innymi słowy im więcej , tym bardziej , czyli wykres idzie w prawo i w górę.

Funkcjonować maleje na zbiorze jeśli dla dowolnego i przynależności do zbioru nierówność implikuje nierówność .

W przypadku funkcji malejącej większa wartość odpowiada mniejszej wartości. Wykres idzie w prawo iw dół.

Na naszym rysunku funkcja rośnie na przedziale i maleje na przedziałach i .

Zdefiniujmy, co to jest maksymalne i minimalne punkty funkcji.

Maksymalny punkt- jest to wewnętrzny punkt dziedziny definicji, taki, że wartość funkcji w nim jest większa niż we wszystkich punktach dostatecznie mu bliskich.
Innymi słowy, punkt maksymalny jest takim punktem, wartością funkcji, w której jeszcze niż w sąsiednich. To lokalne „wzgórze” na wykresie.

Na naszej figurze - maksymalny punkt.

Niski punkt- wewnętrzny punkt dziedziny definicji, taki, że wartość funkcji w nim jest mniejsza niż we wszystkich punktach wystarczająco blisko niego.
Oznacza to, że punkt minimum jest taki, że wartość funkcji w nim jest mniejsza niż w sąsiednich. Na wykresie jest to lokalna „dziura”.

Na naszej figurze - punkt minimalny.

Punktem jest granica. Nie jest to wewnętrzny punkt dziedziny definicji i dlatego nie pasuje do definicji punktu maksymalnego. Po lewej stronie nie ma przecież sąsiadów. W ten sam sposób na naszym wykresie nie może być żadnego punktu minimalnego.

Punkty maksymalne i minimalne są zbiorczo nazywane skrajne punkty funkcji. W naszym przypadku jest to i .

Ale co jeśli potrzebujesz znaleźć na przykład funkcja minimum na kroju? W ta sprawa odpowiedź: . ponieważ funkcja minimum jest jego wartością w punkcie minimum.

Podobnie maksimum naszej funkcji to . Osiąga się to w punkcie.

Można powiedzieć, że ekstrema funkcji są równe i .

Czasami w zadaniach trzeba znaleźć największe i najmniejsze wartości funkcji na danym segmencie. Niekoniecznie pokrywają się z ekstremami.

W naszym przypadku najmniejsza wartość funkcji na przedziale jest równy i pokrywa się z minimum funkcji. Ale jego największa wartość w tym segmencie wynosi . Osiąga się go na lewym końcu segmentu.

W każdym razie największe i najmniejsze wartości funkcji ciągłej na segmencie są osiągane albo w punktach ekstremów, albo na końcach segmentu.

drobna i ładna proste zadanie z kategorii tych, które służą jako koło ratunkowe dla pływającego ucznia. Na łonie natury senna kraina połowy lipca, więc czas osiąść z laptopem na plaży. Wczesnym rankiem zagrał promień teorii, by wkrótce skupić się na praktyce, która mimo deklarowanej lekkości zawiera odłamki szkła w piasku. W związku z tym polecam sumiennie rozważyć kilka przykładów z tej strony. Aby rozwiązywać praktyczne zadania, musisz umieć znajdź pochodne i zrozumieć materiał artykułu Przedziały monotoniczności i ekstrema funkcji.

Najpierw krótko o tym, co najważniejsze. W lekcji o ciągłość funkcji Podałem definicję ciągłości w punkcie i ciągłości w przedziale. W podobny sposób formułuje się przykładowe zachowanie funkcji na odcinku. Funkcja jest ciągła na segmencie, jeżeli:

1) jest ciągła na przedziale ;
2) ciągły w punkcie po prawej i w punkcie lewy.

Drugi akapit dotyczy tzw jednostronna ciągłość funkcje w punkcie. Jest kilka podejść do jego definicji, ale pozostanę przy linii rozpoczętej wcześniej:

Funkcja jest ciągła w punkcie po prawej, jeśli jest zdefiniowana w danym punkcie, a jej prawa granica pokrywa się z wartością funkcji w danym punkcie: . W punkcie jest ciągła lewy, jeśli jest zdefiniowany w danym punkcie, a jego lewa granica jest równa wartości w tym punkcie:

Wyobraź sobie, że zielone kropki to gwoździe, na których przymocowana jest magiczna gumka:

Mentalnie weź czerwoną linię w swoje ręce. Oczywiście bez względu na to, jak daleko rozciągniemy wykres w górę iw dół (wzdłuż osi), funkcja nadal pozostanie ograniczony- żywopłot powyżej, żywopłot poniżej, a nasz produkt pasie się na padoku. Zatem, funkcja ciągła na odcinku jest na nim ograniczona. W toku analizy matematycznej ten pozornie prosty fakt zostaje stwierdzony i rygorystycznie udowodniony Pierwsze twierdzenie Weierstrassa.… Wiele osób jest zirytowanych, że zdania elementarne są żmudnie uzasadniane w matematyce, ale ma to ważne znaczenie. Załóżmy, że pewien mieszkaniec średniowiecza frotte wyciągnął wykres w niebo poza granice widoczności, ten został wstawiony. Przed wynalezieniem teleskopu ograniczona funkcja w kosmosie wcale nie była oczywista! Rzeczywiście, skąd wiesz, co nas czeka za horyzontem? Wszakże kiedyś Ziemia była uważana za płaską, więc dzisiaj nawet zwykła teleportacja wymaga dowodu =)

Według drugie twierdzenie Weierstrassa, ciągły na segmenciefunkcja osiąga swoje dokładna górna krawędź i jego dokładna dolna krawędź .

Numer jest również nazywany maksymalna wartość funkcji na segmencie i oznaczone przez , a liczba - minimalna wartość funkcji na odcinku oznaczone .

W naszym przypadku:

Notatka : teoretycznie zapisy są powszechne .

Z grubsza mówiąc, najwyższa wartość znajduje się tam, gdzie najwyższy punkt wykresu, a najmniejszy - tam, gdzie najniższy punkt.

Ważny! Jak już wskazano w artykule na temat ekstrema funkcji, największa wartość funkcji oraz najmniejsza wartość funkcji – NIE TEN SAM, Co funkcja maksymalna oraz funkcja minimum. Tak więc w tym przykładzie liczba jest minimum funkcji, ale nie wartością minimalną.

A propos, co dzieje się poza segmentem? Tak, nawet powódź, w kontekście rozważanego problemu, wcale nas to nie interesuje. Zadanie polega tylko na znalezieniu dwóch liczb i to wszystko!

Ponadto rozwiązanie ma charakter czysto analityczny, dlatego nie trzeba rysować!

Algorytm leży na powierzchni i sugeruje się z powyższego rysunku:

1) Znajdź wartości funkcji w punkt krytyczny, należące do tego segmentu.

Złap jeszcze jeden gadżet: nie ma potrzeby sprawdzania wystarczającego warunku dla ekstremum, ponieważ, jak właśnie pokazano, obecność minimum lub maksimum jeszcze nie gwarantowane jaka jest minimalna lub maksymalna wartość. Funkcja demonstracyjna osiąga swoje maksimum i z woli losu ta sama liczba jest największą wartością funkcji na przedziale . Ale oczywiście taki zbieg okoliczności nie zawsze ma miejsce.

Tak więc w pierwszym kroku szybciej i łatwiej obliczyć wartości funkcji w krytycznych punktach należących do segmentu, nie przejmując się tym, czy mają ekstrema, czy nie.

2) Obliczamy wartości funkcji na końcach segmentu.

3) Wśród wartości funkcji znajdujących się w akapicie 1 i 2 wybieramy najmniejszą i największą duża liczba, zapisz odpowiedź.

Siedzimy na brzegu błękitnego morza i uderzamy po piętach w płytkiej wodzie:

Przykład 1

Znajdź największe i najmniejsze wartości funkcji na segmencie

Decyzja:
1) Oblicz wartości funkcji w krytycznych punktach należących do tego segmentu:

Obliczmy wartość funkcji w drugim punkcie krytycznym:

2) Oblicz wartości funkcji na końcach segmentu:

3) „Pogrubione” wyniki uzyskano z wykładnikami i logarytmami, co znacznie komplikuje ich porównanie. Z tego powodu uzbroimy się w kalkulator lub Excela i obliczymy przybliżone wartości, nie zapominając o tym, że:

Teraz wszystko jest jasne.

Odpowiedź:

Instancja ułamkowo-racjonalna dla niezależne rozwiązanie:

Przykład 6

Znajdź maksimum i minimalna wartość funkcje na interwale

Proces znajdowania najmniejszych i największych wartości funkcji na odcinku przypomina fascynujący lot wokół obiektu (wykres funkcji) na śmigłowcu z ostrzałem z armaty dalekiego zasięgu w określonych punktach i wyborem z te punkty to bardzo szczególne punkty do strzałów kontrolnych. Punkty są wybierane w określony sposób i według określonych zasad. Na jakich zasadach? Porozmawiamy o tym dalej.

Jeśli funkcja tak = f(x) ciągły na odcinku [ a, b] , to dociera do tego odcinka najmniej oraz najwyższe wartości . Może się to zdarzyć w punkty ekstremalne lub na końcach segmentu. Dlatego, aby znaleźć najmniej oraz największe wartości funkcji , ciągła na odcinku [ a, b] , trzeba w sumie obliczyć jego wartości punkt krytyczny i na końcach segmentu, a następnie wybierz najmniejszy i największy z nich.

Niech na przykład wymagane jest wyznaczenie maksymalnej wartości funkcji f(x) na odcinku [ a, b] . Aby to zrobić, znajdź wszystkie jego punkty krytyczne leżące na [ a, b] .

punkt krytyczny nazywa się punktem, w którym zdefiniowana funkcja, i jej pochodna ma wartość zero lub nie istnieje. Następnie należy obliczyć wartości funkcji w punktach krytycznych. I na koniec należy porównać wartości funkcji w punktach krytycznych i na końcach odcinka ( f(a) oraz f(b) ). Największa z tych liczb będzie największa wartość funkcji na segmencie [a, b] .

Problem ze znalezieniem najmniejsze wartości funkcji .

Wspólnie poszukujemy najmniejszych i największych wartości funkcji

Przykład 1. Znajdź najmniejszą i największą wartość funkcji na segmencie [-1, 2] .

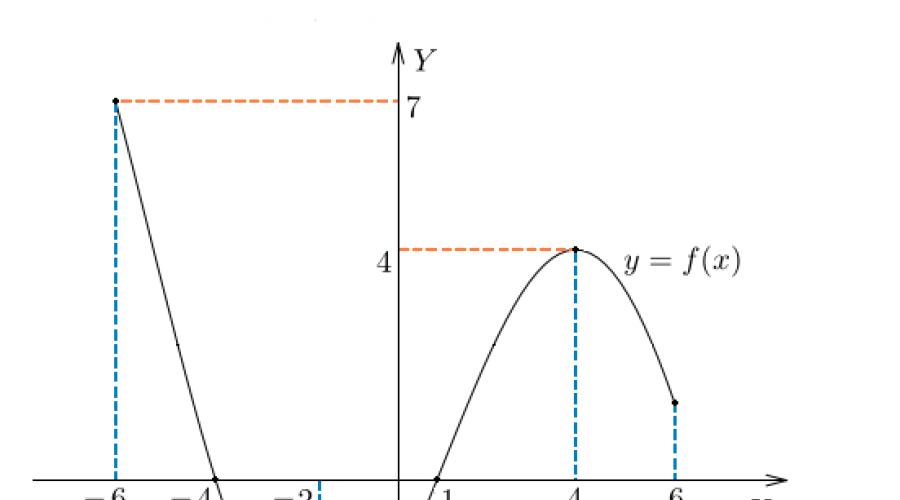
Decyzja. Znajdujemy pochodną tej funkcji. Przyrównaj pochodną do zera () i uzyskaj dwa punkty krytyczne: i . Aby znaleźć najmniejszą i największą wartość funkcji na danym odcinku, wystarczy obliczyć jej wartości na końcach odcinka oraz w punkcie, gdyż punkt nie należy do odcinka [-1, 2] . Te wartości funkcji są następujące: , , . Wynika, że najmniejsza wartość funkcji(zaznaczony na czerwono na poniższym wykresie), równy -7, osiąga prawy koniec odcinka - w punkcie , oraz największy(również czerwony na wykresie), jest równy 9, - w punkcie krytycznym .

Jeżeli funkcja jest ciągła w pewnym przedziale i przedział ten nie jest odcinkiem (ale jest na przykład przedziałem; różnica między przedziałem a odcinkiem: punkty graniczne przedziału nie są zawarte w przedziale, ale punkty brzegowe segmentu są zawarte w segmencie), wówczas wśród wartości funkcji może nie być najmniejszej i największej. Na przykład funkcja przedstawiona na poniższym rysunku jest ciągła na ]-∞, +∞[ i nie ma największej wartości.

Jednak dla dowolnego przedziału (zamkniętego, otwartego lub nieskończonego) obowiązuje następująca właściwość funkcji ciągłych.

Przykład 4. Znajdź najmniejszą i największą wartość funkcji na segmencie [-1, 3] .

Decyzja. Znajdujemy pochodną tej funkcji jako pochodną ilorazu:

.

Przyrównujemy pochodną do zera, co daje nam jeden punkt krytyczny: . Należy do przedziału [-1, 3] . Aby znaleźć najmniejszą i największą wartość funkcji na danym segmencie, znajdujemy jej wartości na końcach segmentu oraz w znalezionym punkcie krytycznym:

Porównajmy te wartości. Wniosek: równy -5/13, w punkcie i największa wartość równy 1 w punkcie .

Wspólnie poszukujemy najmniejszych i największych wartości funkcji

Są nauczyciele, którzy na temat znajdowania najmniejszych i największych wartości funkcji nie podają uczniom przykładów bardziej skomplikowanych niż te właśnie rozważane, czyli takich, w których funkcja jest wielomianem lub ułamkiem, licznikiem a mianownikiem są wielomiany. Ale nie będziemy ograniczać się do takich przykładów, ponieważ wśród nauczycieli są miłośnicy zmuszania uczniów do pełnego myślenia (tabela pochodnych). Dlatego zostanie użyty logarytm i funkcja trygonometryczna.

Przykład 6. Znajdź najmniejszą i największą wartość funkcji na segmencie .

Decyzja. Znajdujemy pochodną tej funkcji jako pochodna produktu :

Przyrównujemy pochodną do zera, co daje jeden punkt krytyczny: . Należy do segmentu. Aby znaleźć najmniejszą i największą wartość funkcji na danym segmencie, znajdujemy jej wartości na końcach segmentu oraz w znalezionym punkcie krytycznym:

Wynik wszystkich działań: funkcja osiąga swoją minimalną wartość, równy 0, w punkcie i w punkcie oraz największa wartość równy mi² , w punkcie .

Przykład 7. Znajdź najmniejszą i największą wartość funkcji na segmencie .

Decyzja. Znajdujemy pochodną tej funkcji:

Zrównaj pochodną do zera:

Jedyny punkt krytyczny należy do segmentu. Aby znaleźć najmniejszą i największą wartość funkcji na danym segmencie, znajdujemy jej wartości na końcach segmentu oraz w znalezionym punkcie krytycznym:

Wniosek: funkcja osiąga swoją minimalną wartość, równy , w punkcie i największa wartość, równy , w punkcie .

W stosowanych problemach ekstremalnych znalezienie najmniejszych (największych) wartości funkcji z reguły sprowadza się do znalezienia minimum (maksimum). Ale to nie same minima czy maksima mają większe znaczenie praktyczne, ale wartości argumentu, przy którym są osiągane. Przy rozwiązywaniu stosowanych problemów pojawia się dodatkowa trudność - zestawienie funkcji opisujących rozważane zjawisko lub proces.

Przykład 8 Zbiornik o pojemności 4, w kształcie równoległościanu o kwadratowej podstawie i otwarty od góry, musi być ocynowany. Jakie powinny być wymiary zbiornika, aby pokryć go jak najmniejszą ilością materiału?

Decyzja. Zostawiać x- strona podstawowa h- wysokość zbiornika, S- jego powierzchnia bez osłony, V- jego objętość. Powierzchnia zbiornika wyrażona jest wzorem tj. jest funkcją dwóch zmiennych. Wyrazić S jako funkcję jednej zmiennej wykorzystujemy fakt, że , whence . Podstawianie znalezionego wyrażenia h we wzorze na S:

Przyjrzyjmy się tej funkcji ekstremum. Jest zdefiniowana i różniczkowalna wszędzie w ]0, +∞[ , i

.

Przyrównujemy pochodną do zera () i znajdujemy punkt krytyczny. Ponadto w , pochodna nie istnieje, ale ta wartość nie jest objęta zakresem definicji i dlatego nie może być punktem ekstremum. A więc - jedyny punkt krytyczny. Sprawdźmy to pod kątem obecności ekstremum za pomocą drugiego wystarczający znak. Znajdźmy drugą pochodną. Gdy druga pochodna jest większa od zera (). Oznacza to, że gdy funkcja osiągnie minimum . Ponieważ to minimum - jedyne ekstremum tej funkcji, jest to jej najmniejsza wartość. Tak więc bok podstawy zbiornika powinien wynosić 2 m, a jego wysokość.

Przykład 9 Z akapitu A, położony na linii kolejowej, do punktu Z, w pewnej odległości od niego ja, towar musi być transportowany. Koszt transportu jednostki wagowej na jednostkę odległości koleją wynosi , a autostradą wynosi . Do jakiego momentu? M linie kolej żelazna należy wybudować autostradę, aby transport towarów z ALE w Z był najbardziej ekonomiczny AB zakłada się, że kolej jest prosta)?

W praktyce dość często używa się pochodnej do obliczenia największej i najmniejszej wartości funkcji. Czynność tę wykonujemy, gdy dowiadujemy się, jak minimalizować koszty, zwiększać zyski, kalkulować optymalne obciążenie do produkcji itp., czyli w przypadkach, w których konieczne jest określenie optymalna wartość dowolny parametr. Aby poprawnie rozwiązać takie problemy, trzeba dobrze rozumieć, jaka jest największa i najmniejsza wartość funkcji.

Yandex.RTB R-A-339285-1

Zwykle wartości te definiujemy w pewnym przedziale x , który z kolei może odpowiadać całemu zakresowi funkcji lub jej części. Może to być segment [ a ; b ] i przedział otwarty (a ; b) , (a ; b ] , [ a ; b) , przedział nieskończony (a ; b) , (a ; b ] , [ a ; b) lub przedział nieskończony - ∞ ; a , (- ∞ ; a ] , [ a ; + ∞ ) , ( - ∞ ; + ∞ ) .

W tym artykule wyjaśnimy, w jaki sposób obliczane są największe i najmniejsze wartości. podana funkcja z jedną zmienną y=f(x) y = f (x) .

Podstawowe definicje

Zaczynamy, jak zawsze, od sformułowania głównych definicji.

Definicja 1

Największą wartością funkcji y = f (x) na pewnym przedziale x jest wartość m a x y = f (x 0) x ∈ X , która dla dowolnej wartości x x ∈ X , x ≠ x 0 tworzy nierówność f (x ) ≤ f (x 0) .

Definicja 2

Najmniejszą wartością funkcji y = f (x) na pewnym przedziale x jest wartość m i n x ∈ X y = f (x 0) , która dla dowolnej wartości x ∈ X , x ≠ x 0 powoduje nierówność f(X f(x) ≥ f(x0) .

Te definicje są dość oczywiste. Jeszcze prościej można powiedzieć tak: największa wartość funkcji jest jej najbardziej bardzo ważne na znanym przedziale na odciętej x 0 , a najmniejsza jest najmniejszą akceptowaną wartością na tym samym przedziale na x 0 .

Definicja 3

Punkty stacjonarne to takie wartości argumentu funkcji, przy których jej pochodna wynosi 0.

Dlaczego musimy wiedzieć, jakie są punkty stacjonarne? Aby odpowiedzieć na to pytanie, musimy pamiętać o twierdzeniu Fermata. Wynika z tego, że punkt stacjonarny to punkt, w którym znajduje się ekstremum funkcji różniczkowalnej (czyli jej lokalne minimum lub maksimum). W konsekwencji funkcja przyjmie najmniejszą lub największą wartość na pewnym przedziale dokładnie w jednym z punktów stacjonarnych.

Inna funkcja może przyjąć największą lub najmniejszą wartość w tych punktach, w których sama funkcja jest określona, ​​a jej pierwsza pochodna nie istnieje.

Pierwsze pytanie, które pojawia się podczas studiowania tego tematu, brzmi: czy we wszystkich przypadkach możemy określić maksymalną lub minimalną wartość funkcji na danym przedziale? Nie, nie możemy tego zrobić, gdy granice danego przedziału będą pokrywać się z granicami dziedziny definicji lub jeśli mamy do czynienia z przedziałem nieskończonym. Zdarza się również, że funkcja w danym przedziale lub w nieskończoności przyjmie nieskończenie małą lub nieskończoną duże wartości. W takich przypadkach nie jest możliwe określenie największej i/lub najmniejszej wartości.

Te momenty staną się bardziej zrozumiałe po obrazie na wykresach:

Pierwszy rysunek pokazuje nam funkcję, która przyjmuje największe i najmniejsze wartości (m a x y i m i n y) w punktach stacjonarnych znajdujących się na przedziale [ - 6 ; 6].

Przeanalizujmy szczegółowo przypadek wskazany na drugim wykresie. Zmieńmy wartość segmentu na [1 ; 6] i otrzymujemy, że największą wartość funkcji uzyskamy w punkcie z odciętą na prawej granicy przedziału, a najmniejszą w punkcie stacjonarnym.

Na trzecim rysunku odcięte punkty reprezentują punkty brzegowe odcinka [ - 3 ; 2]. Odpowiadają one największej i najmniejszej wartości danej funkcji.

Spójrzmy teraz na czwarte zdjęcie. W nim funkcja przyjmuje m a x y (wartość największą) i m i n y (wartość najmniejszą) w punktach stacjonarnych w przedziale otwartym (-6 ; 6 ).

Jeśli weźmiemy przedział [ 1 ; 6) , to możemy powiedzieć, że najmniejsza wartość funkcji na nim zostanie osiągnięta w punkcie stacjonarnym. Nie poznamy maksymalnej wartości. Funkcja może przyjąć największą wartość przy x równą 6, jeśli x = 6 należy do przedziału. Właśnie ten przypadek pokazano na rysunku 5.

Na wykresie 6 funkcja ta uzyskuje najmniejszą wartość w prawej granicy przedziału (- 3 ; 2 ] , a co do największej wartości nie możemy wyciągnąć jednoznacznych wniosków.

Na rysunku 7 widzimy, że funkcja będzie miała m a x y w punkcie stacjonarnym, przy odciętej równej 1 . Funkcja osiąga swoją minimalną wartość na granicy przedziału po prawej stronie. Przy minus nieskończoności wartości funkcji będą asymptotycznie zbliżać się do y = 3 .

Jeśli weźmiemy przedział x ∈ 2 ; + ∞ , wtedy zobaczymy, że dana funkcja nie przyjmie ani najmniejszej, ani największej wartości. Jeśli x dąży do 2, to wartości funkcji będą miały tendencję do minus nieskończoności, ponieważ linia prosta x = 2 jest pionową asymptotą. Jeśli odcięta dąży do plus nieskończoności, wówczas wartości funkcji będą asymptotycznie zbliżać się do y = 3. Tak jest w przypadku pokazanym na rysunku 8.

W tym akapicie podamy sekwencję działań, które należy wykonać, aby znaleźć największą lub najmniejszą wartość funkcji na określonym przedziale.

1. Najpierw znajdźmy dziedzinę funkcji. Sprawdźmy, czy zawiera się w nim segment określony w warunku.
2. Teraz obliczmy punkty zawarte w tym odcinku, w których pierwsza pochodna nie istnieje. Najczęściej można je znaleźć w funkcjach, których argument jest zapisany pod znakiem modułu lub w funkcje zasilania, którego wykładnik jest liczbą ułamkową wymierną.
3. Następnie dowiadujemy się, które punkty stacjonarne wchodzą w dany odcinek. Aby to zrobić, musisz obliczyć pochodną funkcji, następnie zrównać ją z 0 i rozwiązać otrzymane równanie, a następnie wybrać odpowiednie pierwiastki. Jeżeli nie otrzymamy ani jednego punktu stacjonarnego lub nie mieszczą się one w danym odcinku, to przechodzimy do kolejnego kroku.
4. Ustalmy, jakie wartości przyjmie funkcja w danych punktach stacjonarnych (jeśli w ogóle) lub w tych punktach, w których pierwsza pochodna nie istnieje (jeśli w ogóle) lub obliczamy wartości dla x = a i x = b .
5. 5. Mamy szereg wartości funkcji, z których teraz musimy wybrać największą i najmniejszą. Będą to największe i najmniejsze wartości funkcji, którą musimy znaleźć.

Zobaczmy, jak poprawnie zastosować ten algorytm podczas rozwiązywania problemów.

Przykład 1

Stan : schorzenie: podana jest funkcja y = x 3 + 4 x 2. Określ jego największą i najmniejszą wartość na segmentach [1 ; 4 ] i [ - 4 ; - jeden ] .

Decyzja:

Zacznijmy od znalezienia dziedziny tej funkcji. W tym przypadku będzie to zbiór wszystkich liczb rzeczywistych z wyjątkiem 0 . Innymi słowy, D(y): x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . Oba segmenty określone w warunku będą znajdować się w obszarze definicji.

Teraz obliczamy pochodną funkcji zgodnie z zasadą różniczkowania ułamka:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x 3

Dowiedzieliśmy się, że pochodna funkcji będzie istniała we wszystkich punktach odcinków [1 ; 4 ] i [ - 4 ; - jeden ] .

Teraz musimy wyznaczyć punkty stacjonarne funkcji. Zróbmy to z równaniem x 3 - 8 x 3 = 0. Ma tylko jeden prawdziwy korzeń, czyli 2. Będzie to punkt stacjonarny funkcji i wpadnie do pierwszego segmentu [1 ; 4 ] .

Obliczmy wartości funkcji na końcach pierwszego odcinka i w danym punkcie, tj. dla x = 1 , x = 2 i x = 4:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Otrzymaliśmy, że największa wartość funkcji m a x y x ∈ [ 1 ; 4] = y (2) = 3 zostanie osiągnięty przy x = 1 , a najmniejsze m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – przy x = 2 .

Drugi odcinek nie zawiera żadnych punktów stacjonarnych, dlatego musimy obliczyć wartości funkcji tylko na końcach danego odcinka:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Stąd m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x [ - 4 ; - 1 ] = y ( - 4) = - 3 3 4 .

Odpowiedź: Dla segmentu [ 1 ; 4] - ma x y x [ 1 ; 4] = y (2) = 3 , m i n y x [ 1 ; 4] = y (2) = 3 , dla odcinka [ - 4 ; - 1] - ma x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x [ - 4 ; - 1 ] = y ( - 4) = - 3 3 4 .

Widzieć zdjęcie:

Przed studiami Ta metoda, radzimy powtórzyć, jak poprawnie obliczyć granicę jednostronną i granicę w nieskończoności, a także poznać podstawowe metody ich znajdowania. Aby znaleźć największą i/lub najmniejszą wartość funkcji na otwartym lub nieskończonym przedziale, wykonujemy kolejno następujące kroki.

1. Najpierw musisz sprawdzić, czy podany przedział będzie podzbiorem dziedziny danej funkcji.
2. Wyznaczmy wszystkie punkty, które są zawarte w wymaganym przedziale iw których nie istnieje pierwsza pochodna. Zwykle są one przeznaczone dla funkcji, w których argument jest zawarty w znaku modułu, oraz dla funkcji potęgowych z ułamkiem racjonalny wskaźnik. Jeśli brakuje tych punktów, możesz przejść do następnego kroku.
3. Teraz ustalamy, które punkty stacjonarne mieszczą się w danym przedziale. Najpierw przyrównujemy pochodną do 0, rozwiązujemy równanie i znajdujemy odpowiednie pierwiastki. Jeśli nie mamy ani jednego punktu stacjonarnego lub nie mieszczą się one w zadanym przedziale, to od razu przechodzimy do dalsze działanie. Są one określane przez rodzaj interwału.

• Jeśli przedział wygląda jak [ a ; b) , to musimy obliczyć wartość funkcji w punkcie x = a oraz jednostronną granicę lim x → b - 0 f (x) .
• Jeżeli przedział ma postać (a ; b ] , to musimy obliczyć wartość funkcji w punkcie x = b oraz jednostronną granicę lim x → a + 0 f (x) .
• Jeśli przedział ma postać (a ; b) , to musimy obliczyć jednostronne granice lim x → b - 0 f (x) , lim x → a + 0 f (x) .
• Jeśli przedział wygląda jak [ a ; + ∞) , to należy obliczyć wartość w punkcie x = a oraz granicę do plus nieskończoności lim x → + ∞ f (x) .
• Jeśli przedział wygląda tak (- ∞ ; b ] , obliczamy wartość w punkcie x = b i granicę w minus nieskończoność lim x → - ∞ f (x) .
• Jeśli - ∞ ; b , wtedy rozważamy jednostronną granicę lim x → b - 0 f (x) i granicę przy minus nieskończoności lim x → - ∞ f (x)
• Jeśli - ∞ ; + ∞ , wtedy rozważamy granice do minus i plus nieskończoności lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. Na koniec należy wyciągnąć wniosek na podstawie uzyskanych wartości funkcji i granic. Tutaj jest wiele opcji. Tak więc, jeśli granica jednostronna jest równa minus nieskończoności lub plus nieskończoności, to od razu staje się jasne, że nic nie można powiedzieć o najmniejszej i największej wartości funkcji. Poniżej rozważymy jeden typowy przykład. Szczegółowe opisy pomóc ci zrozumieć, co jest co. W razie potrzeby możesz wrócić do ryc. 4 - 8 w pierwszej części materiału.

Warunek: dana funkcja y = 3 e 1 x 2 + x - 6 - 4 . Oblicz jego największą i najmniejszą wartość w przedziałach - ∞ ; - 4 , - ; - 3 , ( - 3 ; 1] , ( - 3 ; 2) , [1 ; 2) , 2 ; + , [ 4 ; +∞) .

Decyzja

Przede wszystkim znajdujemy dziedzinę funkcji. Mianownik ułamka to trójmian kwadratowy, który nie powinien mieć wartości 0:

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Otrzymaliśmy zakres funkcji, do którego należą wszystkie przedziały określone w warunku.

Teraz rozróżnijmy funkcję i uzyskajmy:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

W konsekwencji pochodne funkcji istnieją na całym obszarze jej definicji.

Przejdźmy do znalezienia punktów stacjonarnych. Pochodna funkcji wynosi 0 przy x = - 1 2 . Jest to punkt stacjonarny, który znajduje się w przedziałach (-3; 1] i (-3; 2).

Obliczmy wartość funkcji w x = - 4 dla przedziału (- ∞ ; - 4 ] , a także granicę w minus nieskończoności:

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

Ponieważ 3 e 1 6 - 4 > - 1 , to m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. Nie pozwala nam to jednoznacznie określić najmniejszej wartości funkcji. Możemy tylko stwierdzić, że istnieje granica poniżej -1 , ponieważ to do tej wartości funkcja zbliża się asymptotycznie do minus nieskończoności.

Cechą drugiego przedziału jest to, że nie ma ani jednego punktu stacjonarnego, ani jednej ścisłej granicy. Dlatego nie możemy obliczyć ani największej, ani najmniejszej wartości funkcji. Definiując granicę przy minus nieskończoności i gdy argument ma tendencję do -3 po lewej stronie, otrzymujemy tylko zakres wartości:

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Oznacza to, że wartości funkcji będą znajdować się w przedziale – 1; +∞

Aby znaleźć maksymalną wartość funkcji w trzecim przedziale, wyznaczamy jej wartość w punkcie stacjonarnym x = - 1 2 jeśli x = 1 . Musimy również znać granicę jednostronną w przypadku, gdy argument ma tendencję do – 3 po prawej stronie:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Okazało się, że funkcja przyjmie największą wartość w punkcie stacjonarnym m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4. Co do najmniejszej wartości nie możemy jej wyznaczyć. wiem , to obecność dolnej granicy do -4 .

Dla przedziału (- 3 ; 2) weźmy wyniki poprzedniego obliczenia i jeszcze raz obliczmy, jaka jest granica jednostronna przy dążeniu do 2 z lewej strony:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Stąd m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 , a najmniejszej wartości nie można określić, a wartości funkcji są ograniczone od dołu liczbą - 4 .

Na podstawie tego, co zrobiliśmy w dwóch poprzednich obliczeniach, możemy stwierdzić, że na przedziale [1 ; 2) funkcja przyjmie największą wartość przy x = 1 i nie można znaleźć najmniejszej.

W przedziale (2 ; + ∞) funkcja nie osiągnie ani największej, ani najmniejszej wartości, tj. przyjmie wartości z przedziału - 1 ; +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Po obliczeniu, jaka będzie wartość funkcji przy x = 4 , dowiadujemy się, że m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , a dana funkcja w plus nieskończoności zbliży się asymptotycznie do prostej y = - 1 .

Porównajmy to, co otrzymaliśmy w każdym obliczeniu, z wykresem danej funkcji. Na rysunku asymptoty są pokazane liniami przerywanymi.

To wszystko, co chcieliśmy opowiedzieć o znalezieniu największej i najmniejszej wartości funkcji. Przedstawione przez nas sekwencje czynności pomogą Ci dokonać niezbędnych obliczeń tak szybko i prosto, jak to tylko możliwe. Pamiętaj jednak, że często warto najpierw dowiedzieć się, na jakich przedziałach funkcja będzie się zmniejszać, a na jakich będzie rosnąć, po czym można wyciągnąć dalsze wnioski. Dzięki temu można dokładniej określić największą i najmniejszą wartość funkcji oraz uzasadnić wyniki.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter