Formuły pierwiastków n-tego stopnia. Funkcja potęgowa i pierwiastki - definicja, właściwości i wzory

Lekcja wideo 2: Pierwiastki stopnia n > 1

Wykład: Pierwiastek stopnia n > 1 i jego własności

Źródło

Załóżmy, że masz równanie takie jak:

Decyzja podane równanie będzie x 1 = 2 i x 2 = (-2). Oba rozwiązania są odpowiednie jako odpowiedź, ponieważ liczby o równych modułach, podniesione do parzystej potęgi, dają ten sam wynik.

To był prosty przykład, ale co możemy zrobić, jeśli np.

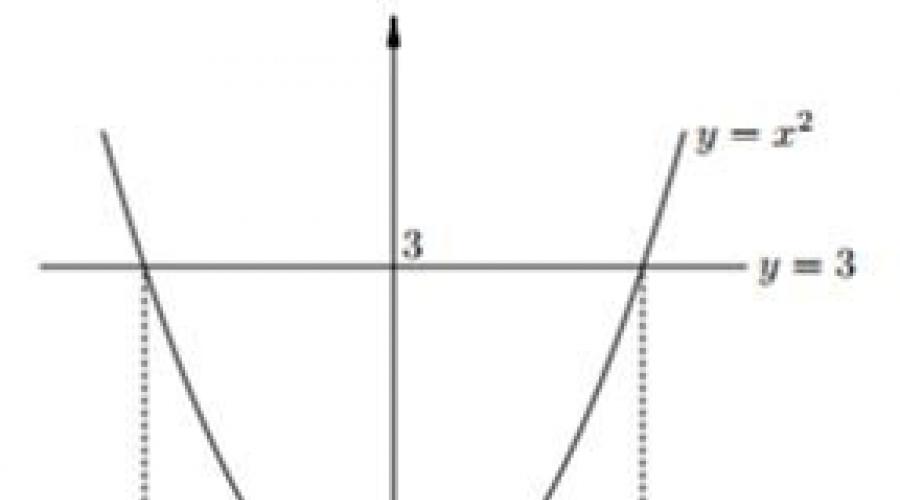
Spróbujmy narysować funkcję y=x 2 . Jego wykres to parabola:

Na wykresie musisz znaleźć punkty odpowiadające wartości y \u003d 3. Te punkty to:

Oznacza to, że tej wartości nie można nazwać liczbą całkowitą, ale można ją przedstawić jako pierwiastek kwadratowy.

Każdy korzeń to Liczba niewymierna. Liczby niewymierne obejmują pierwiastki, nieokresowe ułamki nieskończone.

Pierwiastek kwadratowy jest liczbą nieujemną „a”, której radykalne wyrażenie jest równe podanej liczbie „a” do kwadratu.

Na przykład,

Oznacza to, że w rezultacie otrzymamy tylko wartość dodatnią. Jednak jako rozwiązanie równania kwadratowego postaci

Rozwiązaniem będzie x 1 = 4, x 2 = (-4).

Właściwości pierwiastka kwadratowego

1. Bez względu na wartość x, to wyrażenie jest prawdziwe w każdym przypadku:

2. Porównanie liczb zawierających pierwiastek kwadratowy. Aby porównać te liczby, konieczne jest wpisanie zarówno jednej, jak i drugiej liczby pod znakiem pierwiastka. Ta liczba będzie większa, jeśli radykalna ekspresja jest większa.

Wpisujemy cyfrę 2 pod znakiem korzenia

Teraz umieśćmy cyfrę 4 pod znakiem korzenia. W wyniku tego otrzymujemy

I dopiero teraz można porównać dwa wynikowe wyrażenia:

3. Usunięcie mnożnika spod korzenia.

Jeśli radykalne wyrażenie można rozłożyć na dwa czynniki, z których jeden można wyjąć z podznaku korzenia, należy zastosować tę zasadę.

4. Istnieje odwrotność tej właściwości - wprowadzenie mnożnika pod pierwiastek. Oczywiście użyliśmy tej właściwości w drugiej właściwości.

Twoja prywatność jest dla nas ważna. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Przeczytaj naszą politykę prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które można wykorzystać do zidentyfikowania konkretnej osoby lub skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie, gdy się z nami skontaktujesz.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić oraz sposobu, w jaki możemy je wykorzystywać.

Jakie dane osobowe zbieramy:

• Kiedy przesyłasz wniosek na stronie, możemy zbierać różne informacje, w tym imię i nazwisko, numer telefonu, adres E-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

• Zebrane przez nas informacje osobiste pozwala nam kontaktować się z Tobą i informować Cię o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
• Od czasu do czasu możemy wykorzystywać Twoje dane osobowe, aby wysyłać Ci ważne powiadomienia i komunikaty.
• Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak audyt, analiza danych i różne studia w celu ulepszenia świadczonych przez nas usług i przedstawiania rekomendacji dotyczących naszych usług.
• Jeśli weźmiesz udział w losowaniu nagród, konkursie lub podobnym programie motywacyjnym, możemy wykorzystać podane przez Ciebie informacje do administrowania takimi programami.

Ujawnianie osobom trzecim

Nie ujawniamy informacji otrzymanych od Ciebie stronom trzecim.

Wyjątki:

• W razie potrzeby - zgodnie z prawem, nakaz sądowy, w spór, i/lub na podstawie publicznych próśb lub próśb ze strony agencje rządowe na terytorium Federacji Rosyjskiej - ujawniać swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli ustalimy, że takie ujawnienie jest konieczne lub odpowiednie dla bezpieczeństwa, egzekwowania prawa lub innych publicznych ważne okazje.
• W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane przez nas dane osobowe odpowiedniemu następcy strony trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – w celu ochrony Twoich danych osobowych przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także przed nieautoryzowanym dostępem, ujawnieniem, zmianą i zniszczeniem.

Zachowanie prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo Twoich danych osobowych, informujemy naszych pracowników o praktykach dotyczących prywatności i bezpieczeństwa oraz surowo egzekwujemy praktyki dotyczące prywatności.

Lekcja i prezentacja na temat: „Właściwości pierwiastka n-tego stopnia. Twierdzenia”

Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, opinii, sugestii! Wszystkie materiały są sprawdzane przez program antywirusowy.

Pomoce dydaktyczne i symulatory w sklepie internetowym „Integral” dla klasy 11
Interaktywny podręcznik dla klas 9-11 "Trygonometria"
Interaktywny podręcznik dla klas 10-11 „Logarytmy”

Własności pierwiastka n-tego stopnia. Twierdzenia

Chłopaki, nadal badamy korzenie n-tego stopnia liczby rzeczywistej. Jak prawie wszystkie obiekty matematyczne, pierwiastki n-tego stopnia mają pewne właściwości, dzisiaj je zbadamy.
Wszystkie rozważane przez nas właściwości są sformułowane i udowodnione tylko dla nieujemnych wartości zmiennych zawartych pod znakiem pierwiastka.
W przypadku nieparzystego wykładnika pierwiastkowego obowiązują one również dla zmiennych ujemnych.

Twierdzenie 1. N-ty pierwiastek iloczynu dwóch nieujemnych liczb jest równy iloczynowi n-tych pierwiastków tych liczb: $\sqrt[n](a*b)=\sqrt[n](a)*\ sqrt[n]( b) $ .

Udowodnijmy twierdzenie.
Dowód. Chłopaki, aby udowodnić twierdzenie, wprowadźmy nowe zmienne, oznaczamy:
$\sqrt[n](a*b)=x$.
$\sqrt[n](a)=y$.
$\sqrt[n](b)=z$.
Musimy udowodnić, że $x=y*z$.
Pamiętaj, że obowiązują również następujące tożsamości:
$a*b=x^n$.
$a=y^n$.
$b=z^n$.
W takim przypadku występuje również następująca tożsamość: $x^n=y^n*z^n=(y*z)^n$.
Stopnie dwóch liczb nieujemnych i ich wykładników są równe, to podstawy samych stopni są równe. Stąd $x=y*z$, co było wymagane do udowodnienia.

Twierdzenie 2. Jeśli $a≥0$, $b>0$ i n – Liczba naturalna, który jest większy niż 1, to obowiązuje następująca równość: $\sqrt[n](\frac(a)(b))=\frac(\sqrt[n](a))(\sqrt[n](b ))$.

Oznacza to, że n-ty pierwiastek ilorazu jest równy ilorazowi n-tego pierwiastka.

Dowód.
Aby to udowodnić, posługujemy się uproszczonym schematem w postaci tabeli:

Przykłady obliczania n-tego pierwiastka

Przykład.
Oblicz: $\sqrt(16*81*256)$.
Decyzja. Użyjmy Twierdzenia 1: $\sqrt(16*81*256)=\sqrt(16)*\sqrt(81)*\sqrt(256)=2*3*4=24$.

Przykład.
Oblicz: $\sqrt(7\frac(19)(32))$.
Decyzja. Reprezentujemy radykalne wyrażenie w formie ułamek niewłaściwy: $7\frac(19)(32)=\frac(7*32+19)(32)=\frac(243)(32)$.
Użyjmy twierdzenia 2: $\sqrt(\frac(243)(32))=\frac(\sqrt(243))(\sqrt(32))=\frac(3)(2)=1\frac(1 ) (2)$.

Przykład.
Oblicz:
a) $\sqrt(24)*\sqrt(54)$.
b) $\frac(\sqrt(256))(\sqrt(4))$.
Decyzja:
a) $\sqrt(24)*\sqrt(54)=\sqrt(24*54)=\sqrt(8*3*2*27)=\sqrt(16*81)=\sqrt(16)*\ sqrt(81)=2*3=6$.
b) $\frac(\sqrt(256))(\sqrt(4))=\sqrt(\frac(256)(4))=\sqrt(64)=24$.

Twierdzenie 3. Jeśli $a≥0$, k i n są liczbami naturalnymi większymi od 1, to równość jest prawdziwa: $(\sqrt[n](a))^k=\sqrt[n](a^k)$.

Aby zakorzenić się w naturalnej sile, wystarczy wznieść radykalną ekspresję do tej mocy.

Dowód.
Rozważmy szczególny przypadek dla $k=3$. Użyjmy Twierdzenia 1.
$(\sqrt[n](a))^k=\sqrt[n](a)*\sqrt[n](a)*\sqrt[n](a)=\sqrt[n](a*a *a)=\sqrt[n](a^3)$.
To samo można udowodnić w każdym innym przypadku. Chłopaki, udowodnijcie to sami w przypadku, gdy $k=4$ i $k=6$.

Twierdzenie 4. Jeśli $a≥0$ b n,k są liczbami naturalnymi większymi od 1, to równość jest prawdziwa: $\sqrt[n](\sqrt[k](a))=\sqrt(a)$.

Aby wydobyć korzeń z korzenia, wystarczy pomnożyć wykładniki tego korzenia.

Dowód.
Udowodnijmy jeszcze raz pokrótce za pomocą tabeli. Aby to udowodnić, posługujemy się uproszczonym schematem w postaci tabeli:

Przykład.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.

Twierdzenie 5. Jeśli indeksy pierwiastka i wyrażenie pierwiastka są pomnożone przez tę samą liczbę naturalną, to wartość pierwiastka nie zmieni się: $\sqrt(a^(kp))=\sqrt[n](a) $.

Dowód.
Zasada dowodu naszego twierdzenia jest taka sama jak w innych przykładach. Wprowadźmy nowe zmienne:
$\sqrt(a^(k*p))=x=>a^(k*p)=x^(n*p)$ (z definicji).
$\sqrt[n](a^k)=y=>y^n=a^k$ (z definicji).
Podnosimy ostatnią równość do potęgi p
$(y^n)^p=y^(n*p)=(a^k)^p=a^(k*p)$.
Dostał:
$y^(n*p)=a^(k*p)=x^(n*p)=>x=y$.
Czyli $\sqrt(a^(k*p))=\sqrt[n](a^k)$, co miało zostać udowodnione.

Przykłady:
$\sqrt(a^5)=\sqrt(a)$ (podzielone przez 5).
$\sqrt(a^(22))=\sqrt(a^(11))$ (podzielone przez 2).
$\sqrt(a^4)=\sqrt(a^(12))$ (mnożone przez 3).

Przykład.
Uruchom akcje: $\sqrt(a)*\sqrt(a)$.
Decyzja.
Wykładniki pierwiastkowe to różne liczby, więc nie możemy użyć Twierdzenia 1, ale stosując Twierdzenie 5 możemy uzyskać równe wykładniki.
$\sqrt(a)=\sqrt(a^3)$ (mnożone przez 3).
$\sqrt(a)=\sqrt(a^4)$ (mnożone przez 4).
$\sqrt(a)*\sqrt(a)=\sqrt(a^3)*\sqrt(a^4)=\sqrt(a^3*a^4)=\sqrt(a^7)$.

Zadania do samodzielnego rozwiązania

1. Oblicz: $\sqrt(32*243*1024)$.
2. Oblicz: $\sqrt(7\frac(58)(81))$.
3. Oblicz:
a) $\sqrt(81)*\sqrt(72)$.
b) $\frac(\sqrt(1215))(\sqrt(5))$.
4. Uprość:
a) $\sqrt(\sqrt(a))$.
b) $\sqrt(\sqrt(a))$.
c) $\sqrt(\sqrt(a))$.
5. Wykonaj czynności: $\sqrt(a^2)*\sqrt(a^4)$.

Przykłady:

\(\sqrt(16)=2\) ponieważ \(2^4=16\)
\(\sqrt(-\frac(1)(125))\) \(=\) \(-\frac(1)(5)\) ,ponieważ \((-\frac(1)(5) ) ^3\) \(=\) \(-\frac(1)(125)\)

Jak obliczyć pierwiastek n-tego stopnia?

Aby obliczyć \(n\)-ty pierwiastek, należy zadać sobie pytanie: jaką liczbę da \(n\)-ty stopień pod pierwiastkiem?

na przykład. Oblicz \(n\)-ty pierwiastek: a)\(\sqrt(16)\); b) \(\sqrt(-64)\); c) \(\sqrt(0.00001)\); d)\(\sqrt(8000)\); e) \(\sqrt(\frac(1)(81))\).

a) Jaka liczba do \(4\)tej potęgi da \(16\)? Oczywiście \(2\). Więc:

b) Jaką liczbę do \(3\)-tej potęgi da \(-64\)?

\(\sqrt(-64)=-4\)

c) Jaka liczba do \(5\)tej potęgi da \(0.00001\)?

\(\sqrt(0.00001)=0,1\)

d) Jaka liczba do \(3\)-tego stopnia da \(8000\)?

\(\sqrt(8000)=20\)

e) Jaką liczbę do \(4\)tej potęgi da \(\frac(1)(81)\)?

\(\sqrt(\frac(1)(81))=\frac(1)(3)\)

Sprawdziliśmy najwięcej proste przykłady z pierwiastkiem \(n\)-tym stopniu. Aby rozwiązać więcej wymagające zadania z \(n\)-tym pierwiastkiem - konieczna jest ich znajomość.

Przykład. Oblicz:

\(\sqrt 3\cdot \sqrt(-3) \cdot \sqrt(27) \cdot \sqrt(9) -\) \(=\)		W ten momentżaden z pierwiastków nie może być obliczony. Dlatego stosujemy właściwości pierwiastka \(n\)-tego stopnia i przekształcamy wyrażenie. \(\frac(\sqrt(-64))(\sqrt(2))\)\(=\)\(\sqrt(\frac(-64)(2))\) \(=\)\(\sqrt(-32)\) ponieważ \(\frac(\sqrt[n](a))(\sqrt[n](b))\)\(=\)\(\sqrt[n](\frac(a)(b))\)
\(=\sqrt(3)\cdot \sqrt(-3)\cdot \sqrt(27)\cdot \sqrt(9)-\sqrt(-32)=\)		Zmieńmy kolejność czynników w pierwszym wyrazie tak, aby pierwiastek kwadratowy i pierwiastek \(n\) stopnia były obok siebie. Ułatwi to aplikowanie właściwości. większość własności \(n\)-tego pierwiastka działa tylko z pierwiastkami tego samego stopnia. I obliczamy pierwiastek piątego stopnia.
\(=\sqrt(3) \cdot \sqrt(27) \cdot \sqrt(-3)\cdot \sqrt(9)-(-5)=\)		Zastosuj właściwość \(\sqrt[n](a)\cdot \sqrt[n](b)=\sqrt[n](a\cdot b)\) i rozwiń nawias
\(=\sqrt(81)\cdot \sqrt(-27)+5=\)		Oblicz \(\sqrt(81)\) i \(\sqrt(-27)\)
\(=9\cdot(-3)+5=-27+5=-22\)

Czy pierwiastek n-ty i pierwiastek kwadratowy są powiązane?

W każdym razie każdy rdzeń dowolnego stopnia to tylko liczba, aczkolwiek napisana w nietypowej dla ciebie formie.

Osobliwość n-tego pierwiastka

\(n\)-ty pierwiastek z nieparzystym \(n\) może być wzięty z dowolnej liczby, nawet ujemnej (patrz przykłady na początku). Ale jeśli \(n\) jest parzyste (\(\sqrt(a)\), \(\sqrt(a)\),\(\sqrt(a)\)…), to taki korzeń jest wyodrębniany tylko wtedy, gdy \(a ≥ 0\) (swoją drogą pierwiastek kwadratowy ma to samo). Wynika to z faktu, że wydobywanie korzenia jest przeciwieństwem potęgowania.

A podniesienie do równej potęgi sprawia, że ​​nawet liczba ujemna jest dodatnia. Rzeczywiście, \((-2)^6=(-2) \cdot (-2) \cdot (-2) \cdot (-2) \cdot (-2) \cdot (-2)=64\). Dlatego nie możemy uzyskać liczby ujemnej pod pierwiastkiem stopnia parzystego. Oznacza to, że nie możemy wydobyć takiego pierwiastka z liczby ujemnej.

Potęga nieparzysta nie ma takich ograniczeń — liczba ujemna podniesiona do potęgi nieparzystej pozostanie ujemna: \((-2)^5=(-2) \cdot (-2) \cdot (-2) \cdot (-2 ) \ cdot(-2)=-32\). Dlatego pod pierwiastkiem nieparzystego stopnia możesz uzyskać liczbę ujemną. Oznacza to, że możliwe jest również wyodrębnienie go z liczby ujemnej.

Źródłon-tego stopnia i jego właściwości

Co to jest korzeńnstopień? Jak wydobyć korzeń?

W ósmej klasie już zdążyłeś się zapoznać pierwiastek kwadratowy. Zdecydowany typowe przykłady z korzeniami, stosując określone właściwości korzeni. Również zdecydowano równania kwadratowe , gdzie bez wyciągania pierwiastka kwadratowego - nie ma mowy. Ale pierwiastek kwadratowy to tylko szczególny przypadek more szeroka koncepcja – źródło n stopień . Oprócz kwadratu istnieje np. pierwiastek sześcienny, pierwiastek czwartego, piątego i więcej wysokie stopnie. I dla udana praca z takimi pierwiastkami nadal fajnie byłoby zacząć od „ty” z pierwiastkami kwadratowymi.) Dlatego dla tych, którzy mają z nimi problemy, zdecydowanie zalecam powtarzanie.

Wyodrębnianie pierwiastka jest jedną z odwrotnych operacji potęgowania.) Dlaczego „jeden z”? Ponieważ wyrywając korzeń, szukamy baza według sławnych stopień i wskaźnik. I jest jeszcze inna operacja odwrotna - znajdowanie wskaźnik według sławnych stopień i podstawa. Ta operacja nazywa się znajdowaniem logarytm. Jest to bardziej złożone niż wydobywanie korzenia i jest badane w szkole średniej.)

Więc zapoznajmy się!

Po pierwsze, oznaczenie. Pierwiastek kwadratowy, jak już wiemy, jest oznaczony w ten sposób:. Ta ikona nazywa się bardzo pięknie i naukowo - rodnik. A jakie są korzenie innych stopni? To bardzo proste: nad „ogonem” radykała dodatkowo piszą wskaźnik stopnia, którego korzenia się szuka. Jeśli szukasz pierwiastka sześciennego, napisz trójkę: . Jeśli korzeń czwartego stopnia, to odpowiednio . I tak dalej.) ogólny widokźródło n-ty stopień jest oznaczony w następujący sposób:

Gdzie .

Numera , podobnie jak pierwiastki kwadratowe, nazywa się radykalna ekspresja a oto numern to dla nas nowość. I zadzwoniłem wskaźnik główny .

Jak wydobyć korzenie dowolnego stopnia? Podobnie jak kwadratowe - dowiedz się, jaka liczba do n-tej potęgi daje nam liczbęa .)

Jak na przykład wydobyć pierwiastek sześcienny z 8? Tj ? A jaki numer w kostkach da nam 8? Dwójka, oczywiście). Piszą więc:

Lub . Jaka jest liczba do czwartej potęgi liczby 81? Trzy.) Więc

A co z dziesiątym pierwiastkiem 1? Cóż, to oczywiste, że jednostka do dowolnej potęgi (w tym dziesiątej) jest równa jeden.) To znaczy:

I ogólnie mówiąc .

Z zerem ta sama historia: zero do każdej naturalnej mocy jest równe zeru. To jest, .

Jak widać, w porównaniu z pierwiastkami kwadratowymi, już trudniej jest ustalić, która liczba daje nam pierwiastek w takim czy innym stopniua . Trudniejsze ulec poprawie odpowiedz i sprawdź poprawność przez potęgowanien . Sytuacja jest znacznie ułatwiona, jeśli osobiście znasz stopień popularności liczb. Więc teraz trenujemy. :) Rozpoznajemy stopnie!)

Odpowiedzi (w nieładzie):

Tak tak! Jest więcej odpowiedzi niż zadań.) Bo na przykład 2 8 , 4 4 i 16 2 to ta sama liczba 256.

Przeszkolony? Następnie rozważymy przykłady:

Odpowiedzi (również w nieładzie): 6; 2; 3; 2; 3; 5.

Stało się? Wspaniały! Przejdźmy dalej.)

Ograniczenia roota. pierwiastek arytmetyczny nstopień.

W korzenie nth stopnie, podobnie jak kwadratowe, również mają swoje ograniczenia i żetony. W istocie nie różnią się one od tych ograniczeń dla pierwiastki kwadratowe.

Nie zostaje wybrany, prawda? Co to jest 3, co to jest -3 do czwartej potęgi będzie +81. :) I z dowolnym korzeniem parzysty stopień od liczby ujemnej będzie tą samą piosenką. A to oznacza, że nie da się wydobyć nawet pierwiastków z liczb ujemnych . To jest zakazane działanie w matematyce. Równie zabronione jak dzielenie przez zero. Dlatego wyrażenia takie jak i tym podobne - nie ma sensu.

Ale korzenie dziwne stopnie liczb ujemnych - proszę!

Na przykład, ; itp.)

A z liczb dodatnich możesz bezpiecznie wyodrębnić dowolne korzenie, dowolne stopnie:

Ogólnie rzecz biorąc, myślę, że jest to zrozumiałe.) A tak przy okazji, korzeń nie musi być dokładnie wyodrębniany. To tylko przykłady, tylko dla zrozumienia.) Zdarza się, że w procesie rozwiązywania (np. równań) pojawiają się raczej złe pierwiastki. Coś jak . Z ósemki korzeń sześcianu jest doskonale wydobyty, a tutaj siódemka znajduje się pod korzeniem. Co robić? W porządku. Wszystko jest dokładnie takie samo.- to jest liczba, która po kostce da nam 7. Tylko ta liczba jest bardzo brzydka i kudłata. Oto on:

Co więcej, ta liczba nigdy się nie kończy i nie ma kropki: liczby następują całkowicie losowo. To irracjonalne ... W takich przypadkach odpowiedź jest pozostawiona w postaci korzenia.) Ale jeśli korzeń jest wyodrębniany czysto (na przykład), to oczywiście korzeń musi zostać obliczony i zapisany:

Ponownie bierzemy nasz eksperymentalny numer 81 i wyciągamy z niego czwarty pierwiastek:

Bo trzy na czwartej będzie 81. No dobrze! Ale również minus trzy czwarty też będzie 81!

Istnieje niejednoznaczność:

A żeby go wyeliminować, podobnie jak w pierwiastkach kwadratowych, wprowadzono specjalny termin: pierwiastek arytmetycznynstopień spośród a - to tak nieujemny numer,n-ty stopień jest równy a .

A odpowiedź z plusem lub minusem nazywa się inaczej - pierwiastek algebraicznynstopień. Dla każdej parzystej potęgi pierwiastkiem algebraicznym będzie dwie przeciwne liczby. W szkole pracują tylko z pierwiastkami arytmetycznymi. Więc liczby ujemne w arytmetyce pierwiastki są po prostu odrzucane. Na przykład piszą: Sam plus oczywiście nie jest napisany: to sugerować.

Wydawałoby się, że wszystko jest proste, ale… Ale co z pierwiastkami nieparzystego stopnia z liczb ujemnych? W końcu podczas wydobywania zawsze jest liczba ujemna! Ponieważ dowolna liczba ujemna w nieparzysty stopień daje również liczbę ujemną. A pierwiastek arytmetyczny działa tylko z liczbami nieujemnymi! Dlatego to arytmetyka.)

W takich korzeniach robią to: wyjmują minus spod korzenia i umieszczają go przed korzeniem. Lubię to:

W takich przypadkach mówi się, że wyrażone w postaci arytmetycznego (tj. już nieujemnego) pierwiastka .

Ale jest jedna rzecz, która może być myląca - jest to rozwiązywanie prostych równań z potęgami. Na przykład oto równanie:

Piszemy odpowiedź: W rzeczywistości ta odpowiedź to tylko skrócona notacja dwie odpowiedzi:

Nieporozumieniem jest tutaj to, że napisałem już nieco wyżej, że w szkole brane są pod uwagę tylko nieujemne (tj. arytmetyczne) pierwiastki. A oto jedna z odpowiedzi z minusem... Jak być? Nie ma mowy! Znaki tutaj są wynik rozwiązania równania. ALE sam korzeń- wartość nadal nie jest ujemna! Sam zobacz:

Czy teraz jest to jaśniejsze? z nawiasami?)

Z dziwnym stopniem wszystko jest znacznie prostsze - zawsze się okazuje jedenźródło. Plus lub minus. Na przykład:

Więc jeśli my po prostu wyciągamy pierwiastek (parzystego stopnia) z liczby, to zawsze otrzymujemy jeden wynik nieujemny. Ponieważ jest to pierwiastek arytmetyczny. Teraz, jeśli zdecydujemy równanie w równym stopniu otrzymujemy dwa przeciwstawne korzenie, ponieważ to jest rozwiązanie równania.

Z pierwiastkami nieparzystymi (sześciennymi, piątymi itd.) nie ma problemów. Wydobywamy się i nie kąpiemy się w znakach. Plus pod korzeniem oznacza wynik ekstrakcji z plusem. Minus oznacza minus.

A teraz czas się spotkać właściwości korzenia. Niektóre będą już nam znane z pierwiastków kwadratowych, ale kilka nowych zostanie dodanych. Udać się!

Właściwości korzenia. Korzeń pracy.

Ta właściwość jest nam już znana od pierwiastka kwadratowego. W przypadku korzeni innych stopni wszystko jest podobne:

Tj, pierwiastek iloczynu jest równy iloczynowi pierwiastków każdego czynnika osobno.

Jeśli wskaźnikn nawet, to obie liczby radykalnea orazb musi oczywiście być nieujemna, w przeciwnym razie formuła nie ma znaczenia. W przypadku nieparzystego wskaźnika nie ma ograniczeń: wyciągamy minusy spod pierwiastków, a następnie pracujemy z pierwiastkami arytmetycznymi.)

Podobnie jak w przypadku pierwiastków kwadratowych, tutaj ten wzór jest równie przydatny zarówno od lewej do prawej, jak i od prawej do lewej. Nakładanie formuły od lewej do prawej pozwala wydobyć odrosty z pracy. Na przykład:

Nawiasem mówiąc, ta formuła jest ważna nie tylko dla dwóch, ale dla dowolnej liczby czynników. Na przykład:

Za pomocą tego wzoru można również wyodrębnić korzenie z dużych liczb: w tym celu liczba pod korzeniem jest rozkładana na mniejsze czynniki, a następnie korzenie są wyodrębniane oddzielnie z każdego czynnika.

Na przykład takie zadanie:

Liczba jest wystarczająco duża. Czy to się zakorzenia? gładki- również bez kalkulatora to nie jest jasne. Miło byłoby to rozłożyć na czynniki. Przez co dokładnie dzieli się liczba 3375? Wygląda na to, że przez 5: ostatnia cyfra to pięć.) Podziel:

Och, znowu podzielne przez 5! 675:5 = 135. I znowu 135 dzieli się przez pięć. Tak, kiedy to się skończy?

135:5 = 27. Z liczbą 27 wszystko jest już jasne - to trójka w sześcianie. Znaczy,

Następnie:

Zbierali korzeń kawałek po kawałku, no dobrze.)

Lub ten przykład:

Ponownie rozkładamy na czynniki według znaków podzielności. Co? Na 4, ponieważ ostatnia para liczb 40 jest podzielna przez 4. I przez 10, ponieważ ostatnia cyfra to zero. Możesz więc podzielić za jednym zamachem przez 40 naraz:

O liczbie 216 już wiemy, że to sześć sześcianów. To jest,

A 40 z kolei można rozłożyć na . Następnie

A potem w końcu otrzymujemy:

Nie wyszło czysto, aby wyodrębnić korzeń, cóż, w porządku. W każdym razie uprościliśmy wyrażenie: wiemy, że pod pierwiastkiem (przynajmniej kwadratowym, przynajmniej sześciennym - dowolnym) zwyczajowo zostawia się najwięcej mały numer to możliwe.) W tym przykładzie wykonaliśmy jedną bardzo przydatną operację, również znaną nam z pierwiastków kwadratowych. Czy rozpoznajesz? Tak! My przetrwał czynniki spod korzeni. W tym przykładzie wyjęliśmy dwójkę i szóstkę, czyli numer 12.

Jak usunąć czynnik ze znaku korzenia?

Bardzo łatwo jest usunąć czynnik (lub czynniki) poza znak główny. Rozkładamy wyrażenie pierwiastka na czynniki i wyodrębniamy to, co jest wyodrębniane). A to, co nie jest wyodrębniane, zostawiamy u podstawy. Widzieć:

Rozkładamy liczbę 9072 na czynniki. Skoro mamy pierwiastek czwartego stopnia, to przede wszystkim staramy się rozłożyć na czynniki będące czwartą potęgą liczb naturalnych - 16, 81 itd.

Spróbujmy podzielić 9072 przez 16:

Wspólny!

Ale 567 wydaje się być podzielne przez 81:

Znaczy, .

Następnie

Właściwości korzenia. Mnożenie korzeni.

Rozważ teraz odwrotne zastosowanie wzoru - od prawej do lewej:

Na pierwszy rzut oka nic nowego, ale pozory mylą.) Odwrotna aplikacja formuła znacznie poszerza nasze możliwości. Na przykład:

Hmm, więc co w tym złego? Pomnożyli wszystko. Tu naprawdę nie ma nic specjalnego. Zwykłe rozmnażanie korzeni. A oto przykład!

Oddzielnie korzenie nie są wyłącznie wyodrębniane z czynników. Ale wynik jest doskonały.)

Ponownie, wzór jest ważny dla dowolnej liczby czynników. Na przykład musisz obliczyć następujące wyrażenie:

Najważniejsza jest tutaj uwaga. Przykład zawiera różny korzenie są sześcienne i czwartego stopnia. I żaden z nich na pewno nie jest wydobyty...

A wzór na iloczyn korzeni ma zastosowanie tylko do korzeni z to samo wskaźniki. Pogrupujmy je więc w osobną grupę. korzenie kostki i osobno - czwarty stopień. A tam, widzisz, wszystko będzie rosło razem.))

I nie potrzebowałem kalkulatora.

Jak dodać mnożnik pod znakiem roota?

Następny użyteczna rzecz – wpisanie liczby pod korzeniem. Na przykład:

Czy można usunąć trójkę z korzenia? Podstawowy! Jeśli trójka zamieni się w źródło, wtedy zadziała formuła iloczynu korzeni. Więc zamieniamy te trzy w korzeń. Skoro mamy pierwiastek czwartego stopnia, to zamienimy go również na pierwiastek czwartego stopnia.) W ten sposób:

Następnie

Nawiasem mówiąc, korzeń można utworzyć z dowolnej liczby nieujemnej. I o ile chcemy (wszystko od studium przypadku zależy). Będzie to pierwiastek n-tej potęgi tej liczby:

I teraz - Uwaga!Źródło bardzo rażących błędów! Nic tu nie powiedziałem na darmo nieujemny liczby. Pierwiastek arytmetyczny działa tylko z takimi. Jeśli gdzieś w zadaniu mamy liczbę ujemną, to albo zostawiamy minus przed pierwiastkiem (jeśli jest na zewnątrz), albo usuwamy minus pod pierwiastkiem, jeśli jest w środku. Przypominam, jeśli pod korzeniem parzysty stopień okazuje się liczbą ujemną, to wyrażenie nie ma sensu.

Na przykład takie zadanie. Wpisz mnożnik pod znakiem głównym:

Jeśli teraz zakorzenimy minus po drugie, wtedy okrutnie się pomylimy:

Co tu jest nie tak? I to, że czwarty stopień, ze względu na jego równorzędność, bezpiecznie „zjadł” ten minus, w wyniku czego celowo liczba ujemna zamieniła się w dodatnią. Prawidłowe rozwiązanie wygląda tak:

W korzeniach nieparzystych stopni minus, choć nie „zjedzony”, lepiej też zostawić go na zewnątrz:

Tutaj pierwiastek nieparzystego stopnia jest sześcienny i mamy również pełne prawo umieścić minus pod pierwiastkiem. Ale w takich przykładach lepiej jest zostawić minus na zewnątrz i napisać odpowiedź wyrażoną przez pierwiastek arytmetyczny (nieujemny), ponieważ pierwiastek, chociaż ma prawo do życia, ale nie jest arytmetyka.

Tak więc wraz z wprowadzeniem liczby pod korzeń wszystko jest jasne, mam nadzieję.) Przejdźmy do następnej właściwości.

Właściwości korzenia. Korzeń ułamka. Podział korzeni.

Ta właściwość również całkowicie powtarza tę dla pierwiastków kwadratowych. Dopiero teraz rozszerzamy ją na korzenie dowolnego stopnia:

Korzeń ułamka równy pierwiastkowi od licznika podzielonego przez pierwiastek mianownika.

Jeśli n jest parzyste, to liczbaa musi być nieujemna, a liczbab - ściśle dodatnie (nie można dzielić przez zero). W przypadku nieparzystego wykładnika jedynym ograniczeniem będzie .

Ta właściwość pozwala łatwo i szybko wyodrębnić korzenie z frakcji:

Myślę, że pomysł jest jasny. Zamiast pracować z całym ułamkiem, przechodzimy do pracy osobno z licznikiem i osobno z mianownikiem.) Jeśli ułamek jest dziesiętny lub, o zgrozo, pomieszane numery, następnie najpierw przechodzimy do zwykłych ułamków:

Zobaczmy teraz, jak ta formuła działa od prawej do lewej. Tutaj również ujawniają się bardzo przydatne możliwości. Na przykład ten przykład:

Pierwiastki nie są dokładnie wyciągane z licznika i mianownika, ale z całego ułamka jest w porządku.) Możesz rozwiązać ten przykład w inny sposób - wyjmij czynnik w liczniku spod pierwiastka, a następnie zmniejsz:

Jak sobie życzysz. Odpowiedź jest zawsze taka sama – właściwa. Jeśli nie popełnisz błędów po drodze.)

Więc wymyśliliśmy mnożenie / dzielenie pierwiastków. Przechodzimy do następnego kroku i rozważamy trzecią właściwość - korzeń do stopnia oraz korzeń stopnia .

Korzeń do stopnia. Korzeń stopnia.

Jak podnieść korzeń do potęgi? Załóżmy na przykład, że mamy liczbę . Czy tę liczbę można podnieść do potęgi? Na przykład w kostce? Na pewno! Pomnóż sam korzeń trzy razy i - zgodnie ze wzorem na iloczyn korzeni:

Oto korzeń i stopień jak gdyby wzajemnie anulowane lub zrekompensowane. Rzeczywiście, jeśli podniesiemy liczbę, która po dodaniu do sześcianu da nam trójkę, podniesiemy ją do tego właśnie sześcianu, to co otrzymamy? Trzy i oczywiście zdobądź! I tak będzie dla dowolnej liczby nieujemnej. Ogólnie:

Jeśli wykładniki i pierwiastek są różne, to też nie ma problemu. Jeśli znasz właściwości stopni.)

Jeśli wykładnik jest mniejszy niż wykładnik pierwiastka, po prostu wstawiamy wykładnik pod pierwiastek:

Ogólnie będzie to:

Idea jest jasna: podnosimy radykalną ekspresję do potęgi, a następnie upraszczamy ją, usuwając czynniki spod korzeni, jeśli to możliwe. Jeślin prosto, toa musi być nieujemna. Dlaczego jest zrozumiałe, myślę.) A jeślin dziwne, to bez ograniczeńa już nie ma:

Zajmijmy się teraz korzeń stopnia . Oznacza to, że nie sam korzeń zostanie podniesiony do potęgi, ale radykalna ekspresja. Tutaj też nie ma nic skomplikowanego, ale jest znacznie więcej miejsca na błędy. Czemu? Ponieważ w grę wchodzą liczby ujemne, które mogą mylić znaki. Na razie zacznijmy od korzeni mocy nieparzystych – są one znacznie prostsze.

Powiedzmy, że mamy liczbę 2. Czy możemy to poszerzyć? Na pewno!

A teraz - z powrotem wyodrębnij korzeń sześcianu z ósemki:

Zaczęli od dwójki i wrócili do dwójki.) Nic dziwnego: podniesienie do sześcianu zostało zrekompensowane operacją odwrotną - wyciągnięciem pierwiastka sześcianu.

Inny przykład:

Tutaj też wszystko jest na dobrej drodze. Stopień i korzeń wzajemnie się kompensowały. Ogólnie dla pierwiastków nieparzystych stopni możemy napisać następującą formułę:

Ten wzór jest ważny dla dowolnej liczby rzeczywisteja . Czy pozytywne czy negatywne.

Oznacza to, że nieparzysty stopień i rdzeń tego samego stopnia zawsze kompensują się nawzajem i uzyskuje się radykalne wyrażenie. :)

Ale z parzysty stopnia, to skupienie może już nie przemijać. Sam zobacz:

Nie ma tu jeszcze nic specjalnego. Czwarty stopień i pierwiastek czwartego stopnia również się równoważyły ​​i wyszło tylko dwójka, czyli zakorzenione wyrażenie. I dla każdego nieujemny liczby będą takie same. A teraz po prostu zamieniamy dwa w tym pierwiastku na minus dwa. Więc weźmy taki korzeń:

Minus dwójki bezpiecznie „wypalił się” z powodu czwartego stopnia. A w wyniku wydobycia pierwiastka (arytmetyki!) otrzymaliśmy pozytywny numer. Było minus dwa, stało się plus dwa.) Ale gdybyśmy po prostu bezmyślnie „zmniejszyli” stopień i pierwiastek (ten sam!), dostalibyśmy

Co jest największym błędem, tak.

Dlatego dla parzysty Wzór na pierwiastek wykładnika wygląda tak:

Tutaj dodano niekochany przez wielu znak modułu, ale nie ma w tym nic strasznego: dzięki niemu formuła działa również na dowolną liczbę rzeczywistąa. A moduł po prostu odcina wady:

Dopiero w pierwiastkach n-tego stopnia pojawiło się dodatkowe rozróżnienie między stopniami parzystymi i nieparzystymi. Nawet stopnie, jak widzimy, są bardziej kapryśne, tak.)

A teraz rozważmy nową użyteczną i bardzo interesującą właściwość, już charakterystyczną dla pierwiastków n-tego stopnia: jeśli wykładnik pierwiastka i wykładnik wyrażenia pierwiastka zostaną pomnożone (podzielone) przez tę samą liczbę naturalną, wówczas wartość pierwiastka będzie nie zmieniać.

Coś przypominającego podstawową właściwość ułamka, prawda? W ułamkach możemy również pomnożyć (podzielić) licznik i mianownik przez tę samą liczbę (oprócz zera). W rzeczywistości ta właściwość korzeni jest również konsekwencją podstawowej właściwości frakcji. Kiedy się poznamy stopień z racjonalny wskaźnik wtedy wszystko stanie się jasne. Co, jak i gdzie.)

Bezpośrednie zastosowanie tej formuły pozwala nam uprościć absolutnie dowolne korzenie z dowolnego stopnia. W tym, jeśli wykładniki wyrażenia rdzenia i sam rdzeń różny. Na przykład uprośćmy następujące wyrażenie:

Działamy po prostu. Na początek wyróżniamy czwarty stopień od dziesiątego pod korzeniem i - śmiało! Jak? Oczywiście według właściwości stopni! Wyciągamy faktor spod korzenia lub pracujemy według formuły pierwiastka ze stopnia.

Ale uprośćmy, używając tylko tej właściwości. Aby to zrobić, reprezentujemy cztery pod pierwiastkiem jako:

A teraz - najciekawsze - redukujemy psychicznie wskaźnik pod korzeniem (dwa) ze wskaźnikiem korzenia (cztery)! I otrzymujemy: