Linia prosta. Równanie prostej. Równanie prostej przechodzącej przez dwa punkty Mając dane 2 punkty znajdź równanie prostej

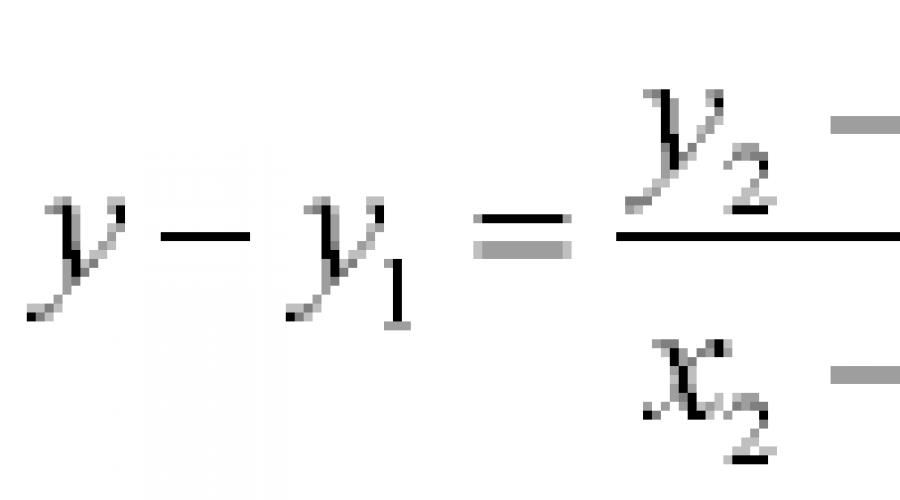
Własności linii prostej w geometrii euklidesowej.

Istnieje nieskończenie wiele linii, które można narysować przez dowolny punkt.

Przez dowolne dwa nie zbiegające się punkty jest tylko jedna prosta.

Dwie nie pokrywające się linie na płaszczyźnie albo przecinają się w jednym punkcie, albo są

równoległy (postępuje z poprzednim).

W przestrzeni trójwymiarowej istnieją trzy opcje względnego położenia dwóch linii:

• linie przecinają się;

• linie proste są równoległe;

• przecinają się proste linie.

Prosty linia- krzywa algebraiczna pierwszego rzędu: w kartezjańskim układzie współrzędnych linia prosta

jest podane na płaszczyźnie równaniem pierwszego stopnia (równanie liniowe).

Ogólne równanie prostej.

Definicja. Dowolna linia w płaszczyźnie może być określona równaniem pierwszego rzędu

Ah + Wu + C = 0,

i stały A, B nie równe zeru w tym samym czasie. To równanie pierwszego rzędu nazywa się ogólny

równanie linii prostej. W zależności od wartości stałych A, B oraz Z Możliwe są następujące przypadki szczególne:

. C = 0, A ≠ 0, B ≠ 0- linia przechodzi przez początek

. A = 0, B ≠ 0, C ≠ 0 ( przez + C = 0)- linia prosta równoległa do osi Oh

. B = 0, A 0, C ≠ 0 ( Topór + C = 0)- linia prosta równoległa do osi OU

. B = C = 0, A ≠ 0- linia pokrywa się z osią OU

. A = C = 0, B ≠ 0- linia pokrywa się z osią Oh

Równanie prostej można przedstawić w różnych postaciach w zależności od dowolnego podanego

warunki początkowe.

Równanie prostej przez punkt i wektor normalny.

Definicja. W kartezjańskim prostokątnym układzie współrzędnych wektor ze składnikami (A, B)

prostopadła do linii podanej przez równanie

Ah + Wu + C = 0.

Przykład. Znajdź równanie prostej przechodzącej przez punkt A(1, 2) prostopadle do wektora (3, -1).

Decyzja. Skomponujmy przy A \u003d 3 i B \u003d -1 równanie linii prostej: 3x - y + C \u003d 0. Aby znaleźć współczynnik C

do otrzymanego wyrażenia podstawiamy współrzędne danego punktu A. Otrzymujemy: 3 - 2 + C = 0, zatem

C = -1. Łącznie: pożądane równanie: 3x - y - 1 \u003d 0.

Równanie prostej przechodzącej przez dwa punkty.

Niech dwa punkty zostaną podane w przestrzeni M 1 (x 1 , y 1 , z 1) oraz M2 (x 2, y 2 , z 2), następnie równanie linii prostej,

przechodząc przez te punkty:

Jeśli którykolwiek z mianowników jest równy zero, odpowiadający mu licznik powinien być równy zero. Na

płaszczyzny, równanie linii prostej zapisane powyżej jest uproszczone:

jeśli x 1 x 2 oraz x = x 1, jeśli x 1 = x 2 .

Frakcja = k nazywa współczynnik nachylenia prosty.

Przykład. Znajdź równanie prostej przechodzącej przez punkty A(1, 2) i B(3, 4).

Decyzja. Stosując powyższy wzór otrzymujemy:

Równanie prostej przez punkt i nachylenie.

Jeżeli ogólne równanie prostej Ah + Wu + C = 0 wnieś do formularza:

i wyznacz , to powstałe równanie nazywa się

równanie prostej o nachyleniu k.

Równanie prostej w punkcie i wektorze kierunkowym.

Analogicznie do punktu uwzględniającego równanie prostej przechodzącej przez wektor normalny można wprowadzić zadanie

linia prosta przechodząca przez punkt i wektor kierunkowy linii prostej.

Definicja. Każdy niezerowy wektor (α 1 , α 2), którego składniki spełniają warunek

Aα1 + Bα2 = 0 nazywa wektor kierunkowy linii prostej.

Ah + Wu + C = 0.

Przykład. Znajdź równanie prostej o wektorze kierunkowym (1, -1) i przechodzącej przez punkt A (1, 2).

Decyzja. Poszukamy równania żądanej linii prostej w postaci: Topór + By + C = 0. Zgodnie z definicją,

współczynniki muszą spełniać warunki:

1 * A + (-1) * B = 0, czyli A = B.

Wtedy równanie prostej ma postać: Topór + Ay + C = 0, lub x + y + C / A = 0.

w x=1, y=2 dostajemy C/ A = -3, tj. pożądane równanie:

x + y - 3 = 0

Równanie prostej w odcinkach.

Jeśli w ogólnym równaniu linii prostej Ah + Wu + C = 0 C≠0, to dzieląc przez -C, otrzymujemy:

czy gdzie

Geometryczne znaczenie współczynników polega na tym, że współczynnik a jest współrzędną punktu przecięcia

prosty z osią Oh, a b- współrzędna punktu przecięcia prostej z osią Jednostka organizacyjna.

Przykład. Podano ogólne równanie linii prostej x - y + 1 = 0. Znajdź równanie tej prostej w odcinkach.

C \u003d 1, , a \u003d -1, b \u003d 1.

Równanie normalne prostej.

Jeśli obie strony równania Ah + Wu + C = 0 dziel przez liczbę , który jest nazywany

współczynnik normalizujący, wtedy dostajemy

xcosφ + ysinφ - p = 0 -normalne równanie prostej.

Znak ± współczynnika normalizującego należy wybrać tak, aby μ * C< 0.

R- długość prostopadłej opuszczonej od początku do linii,

a φ - kąt utworzony przez ten prostopadły z dodatnim kierunkiem osi Oh.

Przykład. Biorąc pod uwagę ogólne równanie linii prostej 12x - 5 lat - 65 = 0. Wymagany do pisania różnych typów równań

ta prosta linia.

Równanie tej prostej w odcinkach:

Równanie tej prostej ze spadkiem: (podziel przez 5)

Równanie prostej:

cos = 12/13; grzech φ= -5/13; p=5.

Należy zauważyć, że nie każdą linię prostą można przedstawić równaniem w odcinkach, na przykład linie proste,

równoległe do osi lub przechodzące przez początek.

Kąt między liniami na płaszczyźnie.

Definicja. Jeśli podane są dwie linie y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, to kąt ostry między tymi liniami

zostanie zdefiniowany jako

Dwie linie są równoległe, jeśli k 1 = k 2. Dwie linie są prostopadłe

jeśli k 1 \u003d -1 / k 2 .

Twierdzenie.

Bezpośredni Ah + Wu + C = 0 oraz A 1 x + B 1 r + C 1 \u003d 0 są równoległe, gdy współczynniki są proporcjonalne

A 1 \u003d λA, B 1 \u003d λB. Jeśli też С 1 \u003d λС, to linie się pokrywają. Współrzędne punktu przecięcia dwóch prostych

są znalezione jako rozwiązanie układu równań tych linii.

Równanie prostej przechodzącej przez dany punkt jest prostopadłe do danej prostej.

Definicja. Linia przechodząca przez punkt M 1 (x 1, y 1) i prostopadle do linii y = kx + b

reprezentowane przez równanie:

Odległość od punktu do linii.

Twierdzenie. Jeśli punkt zostanie podany M(x 0, y 0), następnie odległość do linii Ah + Wu + C = 0 zdefiniowana jako:

Dowód. Niech punkt M 1 (x 1, y 1)- podstawa pionu spadła z punktu M dla danego

bezpośredni. Następnie odległość między punktami M oraz M 1:

(1)

Współrzędne x 1 oraz 1 można znaleźć jako rozwiązanie układu równań:

Drugie równanie układu to równanie prostej przechodzącej prostopadle przez dany punkt M 0

podana linia. Jeśli przekształcimy pierwsze równanie układu do postaci:

A(x - x 0) + B(y - y 0) + Ax 0 + O 0 + C = 0,

następnie, rozwiązując, otrzymujemy:

Podstawiając te wyrażenia do równania (1), otrzymujemy:

Twierdzenie zostało udowodnione.

Niech zostaną podane dwa punkty M 1 (x 1, y 1) oraz M 2 (x 2, r 2). Piszemy równanie prostej w postaci (5), gdzie k dotychczas nieznany współczynnik:

Od punktu M 2 należy do danej prostej, to jej współrzędne spełniają równanie (5): . Wyrażając stąd i podstawiając do równania (5), otrzymujemy pożądane równanie:

Jeśli To równanie można przepisać w postaci łatwiejszej do zapamiętania:

(6)

Przykład. Napisz równanie prostej przechodzącej przez punkty M 1 (1,2) i M 2 (-2,3)

Decyzja. . Korzystając z właściwości proporcji i wykonując niezbędne przekształcenia, otrzymujemy ogólne równanie linii prostej:

Kąt między dwiema liniami

Rozważ dwie linie l 1 oraz l 2:

l 1: , , oraz

l 2: , ,

φ to kąt między nimi (). Rysunek 4 przedstawia: .

Stąd , lub

Za pomocą wzoru (7) można wyznaczyć jeden z kątów między liniami. Drugi kąt to .

Przykład. Dwie proste dane są równaniami y=2x+3 i y=-3x+2. znajdź kąt między tymi liniami.

Decyzja. Z równań widać, że k 1 \u003d 2 i k 2 \u003d-3. podstawiając te wartości do wzoru (7), znajdujemy

. Więc kąt między tymi liniami wynosi .

Warunki równoległości i prostopadłości dwóch prostych

Jeśli prosto l 1 oraz l 2 są równoległe, więc φ=0 oraz tgφ=0. ze wzoru (7) wynika, że ​​, skąd k 2 \u003d k 1. Zatem warunkiem równoległości dwóch linii jest równość ich nachylenia.

Jeśli prosto l 1 oraz l 2 prostopadle, to φ=π/2, α2 = π/2+ α1. . Zatem warunkiem, aby dwie linie proste były prostopadłe, jest to, że ich nachylenia są odwrotne pod względem wielkości i przeciwne pod względem znaku.

Odległość od punktu do linii

Twierdzenie. Jeśli podano punkt M(x 0, y 0), to odległość do linii Ax + Vy + C \u003d 0 jest zdefiniowana jako

Dowód. Niech punkt M 1 (x 1, y 1) będzie podstawą prostopadłej opuszczonej z punktu M do danej prostej. Wtedy odległość między punktami M i M 1:

Współrzędne x 1 i y 1 można znaleźć jako rozwiązanie układu równań:

Drugie równanie układu to równanie linii prostej przechodzącej przez dany punkt M 0 prostopadle do danej linii prostej.

Jeśli przekształcimy pierwsze równanie układu do postaci:

A(x - x 0) + B(y - y 0) + Ax 0 + O 0 + C = 0,

następnie, rozwiązując, otrzymujemy:

Podstawiając te wyrażenia do równania (1), otrzymujemy:

Twierdzenie zostało udowodnione.

Przykład. Określ kąt między liniami: y = -3x + 7; y = 2x + 1.

k 1 \u003d -3; k 2 = 2tgj= ; j = p/4.

Przykład. Pokaż, że proste 3x - 5y + 7 = 0 i 10x + 6y - 3 = 0 są prostopadłe.

Znajdujemy: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 k 2 \u003d -1, dlatego linie są prostopadłe.

Przykład. Podano wierzchołki trójkąta A(0;1), B(6;5)), C(12;-1). Znajdź równanie na wysokość narysowaną z wierzchołka C.

Znajdujemy równanie boku AB: ; 4x = 6 lat - 6;

2x - 3 lata + 3 = 0;

Pożądane równanie wysokości to: Ax + By + C = 0 lub y = kx + b.

k= . Wtedy y = . Ponieważ wysokość przechodzi przez punkt C, a następnie jego współrzędne spełniają to równanie: skąd b \u003d 17. Razem: .

Odpowiedź: 3x + 2 lata - 34 = 0.

Odległość od punktu do prostej jest określona przez długość prostopadłej opuszczonej z punktu do prostej.

Jeśli linia jest równoległa do płaszczyzny rzutowania (h | | P 1), a następnie w celu określenia odległości od punktu ALE prosto h konieczne jest opuszczenie z punktu prostopadłego ALE do poziomu h.

Rozważmy bardziej skomplikowany przykład, gdy linia zajmuje pozycję ogólną. Niech będzie konieczne określenie odległości od punktu M prosto a ogólne stanowisko.

Zadanie definicji odległości między liniami równoległymi rozwiązany podobnie jak poprzedni. Na jednej linii pobierany jest punkt, a od niego do innej linii narysowana jest prostopadła. Długość prostopadłej jest równa odległości między liniami równoległymi.

Krzywa drugiego rzędu jest linią określoną równaniem drugiego stopnia w odniesieniu do aktualnych współrzędnych kartezjańskich. W ogólnym przypadku Ax 2 + 2Bxy + Su 2 + 2Dx + 2Ey + F \u003d 0,

gdzie A, B, C, D, E, F to liczby rzeczywiste i przynajmniej jedna z liczb A 2 + B 2 + C 2 ≠0.

Koło

Centrum koła- jest to położenie punktów w płaszczyźnie równoodległej od punktu płaszczyzny C (a, b).

Okrąg jest określony następującym równaniem:

Gdzie x, y są współrzędnymi dowolnego punktu na okręgu, R jest promieniem okręgu.

Znak równania okręgu

1. Nie ma wyrazu z x, y

2. Współczynniki przy x 2 i y 2 są równe

Elipsa

Elipsa nazywamy położenie punktów na płaszczyźnie, suma odległości każdego z nich od dwóch danych punktów tej płaszczyzny nazywamy foci (wartość stała).

Kanoniczne równanie elipsy:

X i y należą do elipsy.

a jest główną półosią elipsy

b jest małą półosią elipsy

Elipsa ma 2 osie symetrii OX i OY. Osie symetrii elipsy są jej osiami, punktem ich przecięcia jest środek elipsy. Nazywa się oś, na której znajdują się ogniska oś ogniskowa. Punktem przecięcia elipsy z osiami jest wierzchołek elipsy.

Współczynnik kompresji (rozciągania): ε = c/a- ekscentryczność (charakteryzuje kształt elipsy), im jest mniejsza, tym elipsa jest słabiej rozciągnięta wzdłuż osi ogniskowej.

Jeżeli środki elipsy nie znajdują się w środku С(α, β)

Hiperbola

Hiperbola nazywana lokalizacją punktów na płaszczyźnie, bezwzględna wartość różnicy odległości, z których każdy od dwóch danych punktów tej płaszczyzny, zwany foci, jest wartością stałą różną od zera.

Kanoniczne równanie hiperboli

Hiperbola ma 2 osie symetrii:

a - rzeczywista półoś symetrii

b - urojona półoś symetrii

Asymptoty hiperboli:

Parabola

parabola to miejsce punktów w płaszczyźnie równoodległej od danego punktu F, zwanego ogniskiem, i danej linii, zwanej kierownicą.

Kanoniczne równanie paraboli:

Y 2 \u003d 2px, gdzie p jest odległością od ogniska do kierownicy (parametr paraboli)

Jeśli wierzchołek paraboli to C (α, β), wówczas równanie paraboli (y-β) 2 \u003d 2p (x-α)

Jeśli oś ogniskowa zostanie przyjęta jako oś y, równanie paraboli przyjmie postać: x 2 \u003d 2qy

Zastanów się, jak napisać równanie linii prostej przechodzącej przez dwa punkty, używając przykładów.

Przykład 1

Napisz równanie prostej przechodzącej przez punkty A(-3;9) i B(2;-1).

1 sposób - skomponujemy równanie linii prostej ze spadkiem.

Równanie prostej o nachyleniu ma postać . Podstawiając współrzędne punktów A i B do równania prostej (x= -3 i y=9 - w pierwszym przypadku x=2 i y= -1 - w drugim) otrzymujemy układ równań z którego znajdujemy wartości k i b:

Dodając wyraz po wyrazie pierwszego i drugiego równania, otrzymujemy: -10=5k, skąd k= -2. Podstawiając k= -2 do drugiego równania, otrzymujemy b: -1=2 (-2)+b, b=3.

Zatem y= -2x+3 jest pożądanym równaniem.

2 sposób - skomponujemy ogólne równanie linii prostej.

Ogólne równanie prostej ma postać . Podstawiając do równania współrzędne punktów A i B otrzymujemy układ:

Ponieważ liczba niewiadomych jest większa niż liczba równań, system nie jest rozwiązywalny. Ale możliwe jest wyrażenie wszystkich zmiennych za pomocą jednej. Na przykład przez b.

Mnożąc pierwsze równanie układu przez -1 i dodając wyraz po wyrazie do drugiego:

otrzymujemy: 5a-10b=0. Stąd a=2b.

Podstawmy otrzymane wyrażenie w drugim równaniu: 2·2b -b+c=0; 3b+c=0; c=-3b.
Podstaw a=2b, c= -3b do równania ax+by+c=0:

2bx+o-3b=0. Pozostaje podzielić obie części przez b:

Ogólne równanie linii prostej można łatwo sprowadzić do równania linii prostej o nachyleniu:

3 sposób - skomponujemy równanie prostej przechodzącej przez 2 punkty.

Równanie prostej przechodzącej przez dwa punkty to:

Zastąp w tym równaniu współrzędne punktów A(-3; 9) i B(2;-1)

(tj. x 1 = -3, y 1 = 9, x 2 =2, y 2 = -1):

i uprościć:

skąd 2x+y-3=0.

W kursie szkolnym najczęściej stosuje się równanie linii prostej ze współczynnikiem nachylenia. Ale najłatwiej jest wyprowadzić i użyć wzoru na równanie prostej przechodzącej przez dwa punkty.

Komentarz.

Jeżeli podstawiając współrzędne danych punktów, jeden z mianowników równania

okazuje się być równy zero, a następnie pożądane równanie uzyskuje się, przyrównując odpowiedni licznik do zera.

Przykład 2

Napisz równanie prostej przechodzącej przez dwa punkty C(5;-2) i D(7;-2).

Podstaw w równaniu prostej przechodzącej przez 2 punkty współrzędne punktów C i D.

Niech zostaną podane dwa punkty M(X 1 ,Na 1) i N(X 2,tak 2). Znajdźmy równanie prostej przechodzącej przez te punkty.

Ponieważ ta linia przechodzi przez punkt M, to zgodnie ze wzorem (1.13) jego równanie ma postać

Na – Y 1 = K(X-x 1),

Gdzie K to nieznane nachylenie.

Wartość tego współczynnika jest wyznaczana z warunku, że pożądana linia prosta przechodzi przez punkt N, co oznacza, że ​​jego współrzędne spełniają równanie (1.13)

Y 2 – Y 1 = K(X 2 – X 1),

Tutaj możesz znaleźć nachylenie tej linii:

,

Lub po konwersji

(1.14)

Formuła (1.14) definiuje Równanie prostej przechodzącej przez dwa punkty M(X 1, Y 1) i N(X 2, Y 2).

W szczególnym przypadku, gdy punkty M(A, 0), N(0, B), ALE ¹ 0, B¹ 0, leżą na osiach współrzędnych, równanie (1.14) przyjmuje prostszą postać

Równanie (1.15) nazywa Równanie prostej w odcinkach, tutaj ALE oraz B oznaczają odcinki odcięte linią prostą na osiach (rysunek 1.6).

Rysunek 1.6

Przykład 1.10. Napisz równanie prostej przechodzącej przez punkty M(1, 2) i B(3, –1).

. Zgodnie z (1.14) równanie pożądanej linii prostej ma postać

2(Y – 2) = -3(X – 1).

Przenosząc wszystkie wyrazy na lewą stronę, w końcu otrzymujemy pożądane równanie

3X + 2Y – 7 = 0.

Przykład 1.11. Napisz równanie dla prostej przechodzącej przez punkt M(2, 1) i punkt przecięcia linii X+ T- 1 = 0, X - y+ 2 = 0.

. Znajdujemy współrzędne punktu przecięcia prostych, rozwiązując te równania razem

Jeśli dodamy te równania wyraz po wyrazie, otrzymamy 2 X+ 1 = 0, skąd . Podstawiając znalezioną wartość do dowolnego równania, znajdujemy wartość rzędnej Na:

Napiszmy teraz równanie prostej przechodzącej przez punkty (2, 1) i :

lub .

Stąd lub -5( Y – 1) = X – 2.

Na koniec otrzymujemy równanie żądanej linii prostej w postaci X + 5Y – 7 = 0.

Przykład 1.12. Znajdź równanie prostej przechodzącej przez punkty M(2.1) i N(2,3).

Korzystając ze wzoru (1.14) otrzymujemy równanie

To nie ma sensu, bo drugim mianownikiem jest zero. Z warunku zadania widać, że odcięte obu punktów mają tę samą wartość. Stąd wymagana linia jest równoległa do osi OY a jego równanie to: x = 2.

Komentarz . Jeżeli podczas pisania równania prostej według wzoru (1.14) jeden z mianowników okaże się równy zero, to pożądane równanie można uzyskać, przyrównując odpowiedni licznik do zera.

Rozważmy inne sposoby ustawienia linii prostej na płaszczyźnie.

1. Niech niezerowy wektor będzie prostopadły do ​​danej prostej L i punkt M 0(X 0, Y 0) leży na tej linii (rysunek 1.7).

Rysunek 1.7

Oznaczać M(X, Y) dowolny punkt na linii L. Wektory i Prostokątny. Wykorzystując warunki ortogonalności dla tych wektorów otrzymujemy or ALE(X – X 0) + B(Y – Y 0) = 0.

Otrzymaliśmy równanie prostej przechodzącej przez punkt M 0 jest prostopadłe do wektora . Ten wektor nazywa się Wektor normalny do linii prostej L. Otrzymane równanie można przepisać jako

Oh + Wu + Z= 0, gdzie Z = –(ALEX 0 + Za pomocą 0), (1.16),

Gdzie ALE oraz W są współrzędnymi wektora normalnego.

Otrzymujemy ogólne równanie prostej w postaci parametrycznej.

2. Prostą na płaszczyźnie można zdefiniować w następujący sposób: niech niezerowy wektor będzie równoległy do ​​danej prostej L i kropka M 0(X 0, Y 0) leży na tej linii. Ponownie weź dowolny punkt M(X, y) na linii prostej (rysunek 1.8).

Rysunek 1.8

Wektory i współliniowy.

Zapiszmy warunek kolinearności tych wektorów: , gdzie T to dowolna liczba, zwana parametrem. Zapiszmy tę równość we współrzędnych:

Te równania nazywają się Równania parametryczne Prosty. Wykluczmy z tych równań parametr T:

Te równania można zapisać w postaci

. (1.18)

Otrzymane równanie nazywa się Kanoniczne równanie linii prostej. Połączenie wektorowe Kierunek wektor prosty .

Komentarz . Łatwo zauważyć, że jeśli jest wektorem normalnym do prostej L, to jego wektor kierunkowy może być wektorem , ponieważ , tj. .

Przykład 1.13. Napisz równanie prostej przechodzącej przez punkt M 0(1, 1) równolegle do linii 3 X + 2Na– 8 = 0.

Decyzja . Wektor jest wektorem normalnym do danej i pożądanej linii. Użyjmy równania prostej przechodzącej przez punkt M 0 przy danym wektorze normalnym 3( X –1) + 2(Na– 1) = 0 lub 3 X + 2 lata- 5 \u003d 0. Otrzymaliśmy równanie pożądanej linii prostej.