Nok 34 i 2 decyzja. Jak znaleźć najmniejszą wspólną wielokrotność dwóch liczb

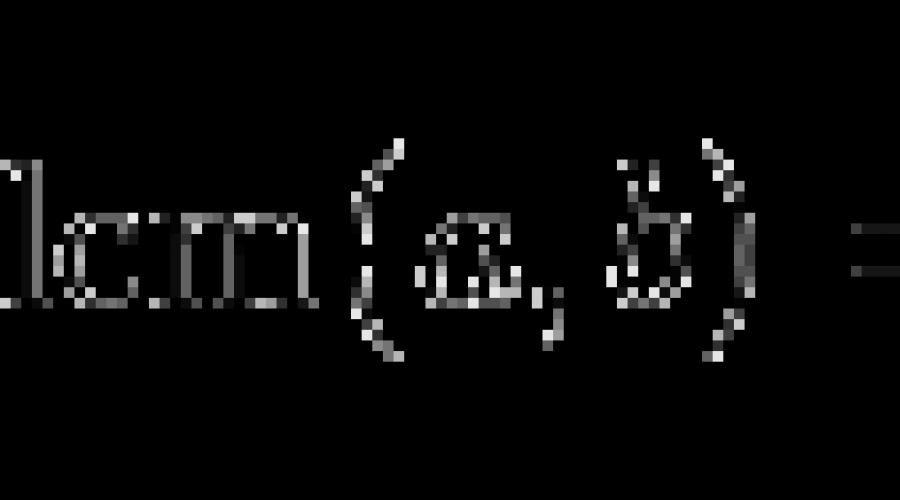
Największy wspólny dzielnik i najmniejsza wspólna wielokrotność to kluczowe pojęcia arytmetyczne, które pozwalają operować bez wysiłku zwykłe ułamki. LCM i są najczęściej używane do znalezienia wspólnego mianownika kilku ułamków.

Podstawowe koncepcje

Dzielnik liczby całkowitej X to kolejna liczba całkowita Y, przez którą X jest podzielne bez reszty. Na przykład dzielnik 4 to 2, a 36 to 4, 6, 9. Wielokrotność liczby całkowitej X to liczba Y, która jest podzielna przez X bez reszty. Na przykład 3 jest wielokrotnością 15, a 6 jest wielokrotnością 12.

Dla dowolnej pary liczb możemy znaleźć ich wspólne dzielniki i wielokrotności. Na przykład dla 6 i 9 wspólna wielokrotność wynosi 18, a wspólny dzielnik 3. Oczywiście pary mogą mieć kilka dzielników i wielokrotności, więc w obliczeniach używa się największego dzielnika NWD i najmniejszej wielokrotności LCM .

Najmniejszy dzielnik nie ma sensu, ponieważ dla dowolnej liczby jest to zawsze jeden. Największa wielokrotność jest również bez znaczenia, ponieważ ciąg wielokrotności dąży do nieskończoności.

Znajdowanie GCD

Istnieje wiele metod na znalezienie największego wspólnego dzielnika, z których najbardziej znane to:

• sekwencyjne wyliczanie dzielników, wybór wspólnych dla pary i wyszukanie największego z nich;
• rozkład liczb na niepodzielne czynniki;
• algorytm Euklidesa;
• algorytm binarny.

Dzisiaj o instytucje edukacyjne Najpopularniejszymi metodami są dekompozycja na czynniki pierwsze i algorytm Euklidesa. To drugie z kolei służy do rozwiązywania równań diofantycznych: wyszukiwanie GCD jest wymagane, aby sprawdzić równanie pod kątem możliwości rozwiązania go w liczbach całkowitych.

Znalezienie NOC

Najmniejsza wspólna wielokrotność jest również dokładnie określona przez wyliczenie lub rozłożenie na czynniki niepodzielne. Ponadto łatwo jest znaleźć LCM, jeśli ustalono już największy dzielnik. Dla liczb X i Y, LCM i NWD są powiązane następującą relacją:

LCM(X,Y) = X × Y / GCM(X,Y).

Na przykład, jeśli gcd(15,18) = 3, to LCM(15,18) = 15 × 18/3 = 90. Najbardziej oczywistym zastosowaniem LCM jest znalezienie wspólnego mianownika, który jest najmniejszą wspólną wielokrotnością podane ułamki.

Liczby względnie pierwsze

Jeśli para liczb nie ma wspólnych dzielników, wówczas taką parę nazywamy względnie pierwszą. GCM dla takich par jest zawsze równy jeden, a na podstawie połączenia dzielników i wielokrotności GCM dla względnie pierwszych jest równy ich iloczynowi. Na przykład liczby 25 i 28 są względnie pierwsze, ponieważ nie mają wspólnych dzielników, a LCM(25,28) = 700, co odpowiada ich iloczynowi. Dowolne dwie niepodzielne liczby zawsze będą względnie pierwsze.

Wspólny dzielnik i kalkulator wielokrotny

Za pomocą naszego kalkulatora możesz obliczyć GCD i LCM dla dowolnej liczby liczb do wyboru. Zadania do obliczania wspólnych dzielników i wielokrotności znajdują się w arytmetyce klas 5 i 6, jednak GCD i LCM są kluczowymi pojęciami matematyki i są używane w teorii liczb, planimetrii i algebrze komunikacyjnej.

Przykłady z życia

Wspólny mianownik ułamków

Najmniejsza wspólna wielokrotność jest używana podczas znajdowania wspólnego mianownika kilku ułamków. Niech w zadaniu arytmetycznym należy zsumować 5 ułamków:

1/8 + 1/9 + 1/12 + 1/15 + 1/18.

Aby dodać ułamki, wyrażenie musi zostać zredukowane do wspólny mianownik, co sprowadza się do problemu ze znalezieniem LCM. Aby to zrobić, wybierz w kalkulatorze 5 liczb i wprowadź wartości mianownika w odpowiednich komórkach. Program obliczy LCM (8, 9, 12, 15, 18) = 360. Teraz musisz obliczyć dodatkowe współczynniki dla każdej frakcji, które są zdefiniowane jako stosunek LCM do mianownika. Więc dodatkowe mnożniki wyglądałyby tak:

• 360/8 = 45
• 360/9 = 40
• 360/12 = 30
• 360/15 = 24
• 360/18 = 20.

Następnie mnożymy wszystkie ułamki przez odpowiedni dodatkowy czynnik i otrzymujemy:

45/360 + 40/360 + 30/360 + 24/360 + 20/360.

Bez problemu dodamy takie ułamki i otrzymamy wynik w postaci 159/360. Zmniejszamy ułamek o 3 i widzimy ostateczną odpowiedź - 53/120.

Rozwiązanie liniowych równań diofantycznych

Liniowe równania diofantyczne są wyrażeniami postaci ax + by = d. Jeśli stosunek d / gcd(a, b) jest liczbą całkowitą, to równanie można rozwiązać w liczbach całkowitych. Sprawdźmy kilka równań pod kątem możliwości rozwiązania liczb całkowitych. Najpierw sprawdź równanie 150x + 8y = 37. Używając kalkulatora, znajdujemy gcd (150,8) = 2. Podziel 37/2 = 18,5. Liczba nie jest liczbą całkowitą, dlatego równanie nie ma pierwiastków całkowitych.

Sprawdźmy równanie 1320x + 1760y = 10120. Użyj kalkulatora, aby znaleźć gcd(1320, 1760) = 440. Podziel 10120/440 = 23. W rezultacie otrzymujemy liczbę całkowitą, dlatego równanie Diophantine jest rozwiązywalne we współczynnikach całkowitych .

Wniosek

GCD i LCM odgrywają dużą rolę w teorii liczb, a same pojęcia są szeroko stosowane w większości różne obszary matematyka. Skorzystaj z naszego kalkulatora, aby obliczyć największe dzielniki i najmniejsze wielokrotności dowolnej liczby liczb.

Ale wiele liczb naturalnych jest równo podzielnych przez inne liczby naturalne.

na przykład:

Liczba 12 jest podzielna przez 1, przez 2, przez 3, przez 4, przez 6, przez 12;

Liczba 36 jest podzielna przez 1, przez 2, przez 3, przez 4, przez 6, przez 12, przez 18, przez 36.

Liczby, według których liczba jest podzielna (dla 12 jest to 1, 2, 3, 4, 6 i 12) są nazywane dzielniki liczb. Dzielnik liczby naturalnej a jest liczbą naturalną dzielącą podaną liczbę a bez śladu. Liczba naturalna, która ma więcej niż dwa czynniki, nazywa się złożony .

Zauważ, że liczby 12 i 36 mają wspólne dzielniki. Są to liczby: 1, 2, 3, 4, 6, 12. Największym dzielnikiem tych liczb jest 12. Wspólny dzielnik tych dwóch liczb a oraz b to liczba, przez którą obie podane liczby są podzielne bez reszty a oraz b.

wspólna wielokrotność kilka liczb nazywamy liczbą podzielną przez każdą z tych liczb. na przykład, liczby 9, 18 i 45 mają wspólną wielokrotność 180. Ale 90 i 360 są również ich wspólnymi wielokrotnościami. Wśród wszystkich jwspólnych wielokrotności zawsze jest najmniejsza, in ta sprawa to 90. Ten numer nazywa się najmniejwspólna wielokrotność (LCM).

LCM jest zawsze liczbą naturalną, która musi być większa niż największa z liczb, dla których jest zdefiniowana.

Najmniejsza wspólna wielokrotność (LCM). Nieruchomości.

Przemienność:

Stowarzyszenie:

W szczególności, jeśli i są liczbami względnie pierwszymi , to:

Najmniejsza wspólna wielokrotność dwóch liczb całkowitych m oraz n jest dzielnikiem wszystkich innych wspólnych wielokrotności m oraz n. Ponadto zbiór wspólnych wielokrotności m, n pokrywa się ze zbiorem wielokrotności dla LCM( m, n).

Asymptotyka dla może być wyrażona w postaci pewnych funkcji teorii liczb.

Więc, Funkcja Czebyszewa. Jak również:

Wynika to z definicji i własności funkcji Landaua g(n).

Co wynika z prawa rozkładu liczb pierwszych.

Znalezienie najmniejszej wspólnej wielokrotności (LCM).

NOC( a, b) można obliczyć na kilka sposobów:

1. Jeśli znany jest największy wspólny dzielnik, możesz wykorzystać jego związek z LCM:

2. Niech będzie znany rozkład kanoniczny obu liczb na czynniki pierwsze:

gdzie p 1 ,...,p k- różny liczby pierwsze, a d 1 ,...,dk oraz e 1 ,...,ek są nieujemnymi liczbami całkowitymi (mogą wynosić zero, jeśli odpowiadająca im liczba pierwsza nie znajduje się w rozkładzie).

Następnie LCM ( a,b) oblicza się według wzoru:

Innymi słowy, rozwinięcie LCM zawiera wszystkie czynniki pierwsze, które są zawarte w co najmniej jednym z rozwinięć liczb a, b i brany jest pod uwagę największy z dwóch wykładników tego czynnika.

Przykład:

Obliczenie najmniejszej wspólnej wielokrotności kilku liczb można sprowadzić do kilku kolejnych obliczeń LCM dwóch liczb:

Reguła. Aby znaleźć LCM szeregu liczb, potrzebujesz:

- rozłożyć liczby na czynniki pierwsze;

- przenieść największą ekspansję na czynniki pożądanego produktu (iloczyn czynników duża liczba z podanych), a następnie dodaj czynniki z rozkładu innych liczb, które nie występują w pierwszej liczbie lub są w niej mniejszą liczbę razy;

- otrzymany iloczyn czynników pierwszych będzie LCM podanych liczb.

Dowolne dwa lub więcej liczby naturalne mają własny NOC. Jeżeli liczby nie są wielokrotnościami siebie lub nie mają tych samych współczynników w rozwinięciu, to ich LCM jest równy iloczynowi tych liczb.

Czynniki pierwsze liczby 28 (2, 2, 7) zostały uzupełnione o czynnik 3 (liczba 21), otrzymany iloczyn (84) będzie najmniejsza liczba, która jest podzielna przez 21 i 28 .

Czynniki pierwsze największej liczby 30 zostały uzupełnione o czynnik 5 liczby 25, wynikowy iloczyn 150 jest większy od największej liczby 30 i jest podzielny przez wszystkie podane liczby bez reszty. Jest to najmniejszy możliwy iloczyn (150, 250, 300...), którego wszystkie podane liczby są wielokrotnościami.

Liczby 2,3,11,37 są pierwsze, więc ich LCM jest równy iloczynowi danych liczb.

reguła. Aby obliczyć LCM liczb pierwszych, musisz pomnożyć wszystkie te liczby.

Inna opcja:

Aby znaleźć najmniejszą wspólną wielokrotność (LCM) kilku liczb, potrzebujesz:

1) reprezentują każdą liczbę jako iloczyn jej czynników pierwszych, na przykład:

504 \u003d 2 2 2 3 3 7,

2) zapisz potęgi wszystkich czynników pierwszych:

504 \u003d 2 2 2 3 3 7 \u003d 2 3 3 2 7 1,

3) wypisz wszystkie dzielniki pierwsze (mnożniki) każdej z tych liczb;

4) wybrać największy stopień każdego z nich, znaleziony we wszystkich rozwinięciach tych liczb;

5) pomnóż te uprawnienia.

Przykład. Znajdź LCM liczb: 168, 180 i 3024.

Decyzja. 168 \u003d 2 2 2 3 7 \u003d 2 3 3 1 7 1,

180 \u003d 2 2 3 3 5 \u003d 2 2 3 2 5 1,

3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1 .

Wypisujemy największe potęgi wszystkich dzielników pierwszych i mnożymy je:

LCM = 2 4 3 3 5 1 7 1 = 15120.

Wielokrotność liczby to liczba podzielna przez daną liczbę bez reszty. Najmniejsza wspólna wielokrotność (LCM) grupy liczb to najmniejsza liczba podzielna równomiernie przez każdą liczbę w grupie. Aby znaleźć najmniejszą wspólną wielokrotność, musisz znaleźć czynniki pierwsze podanych liczb. Ponadto LCM można obliczyć przy użyciu wielu innych metod, które mają zastosowanie do grup składających się z dwóch lub więcej liczb.

Kroki

Seria wielokrotności

Spójrz na te liczby. Opisaną tutaj metodę najlepiej zastosować, gdy podano dwie liczby, z których każda jest mniejsza niż 10. Jeśli podano duże liczby, użyj innej metody.

• Na przykład znajdź najmniejszą wspólną wielokrotność liczb 5 i 8. Są to małe liczby, więc można użyć tej metody.

1. Wielokrotność liczby to liczba podzielna przez daną liczbę bez reszty. W tabliczce mnożenia można znaleźć wiele liczb.

   • Na przykład liczby będące wielokrotnościami 5 to: 5, 10, 15, 20, 25, 30, 35, 40.

2. Zapisz serię liczb, które są wielokrotnościami pierwszej liczby. Zrób to pod wielokrotnościami pierwszej liczby, aby porównać dwa rzędy liczb.

   • Na przykład liczby będące wielokrotnościami 8 to: 8, 16, 24, 32, 40, 48, 56 i 64.

3. Znajdź najmniejszą liczbę, która pojawia się w obu seriach wielokrotności. Być może będziesz musiał napisać długą serię wielokrotności, aby znaleźć Łączna. Najmniejsza liczba występująca w obu seriach wielokrotności to najmniejsza wspólna wielokrotność.

   • Na przykład najmniejsza liczba występująca w szeregu wielokrotności 5 i 8 to 40. Dlatego 40 jest najmniejszą wspólną wielokrotnością 5 i 8.

   Rozkład na czynniki pierwsze

   1. Spójrz na te liczby. Opisanej tutaj metody najlepiej używać, gdy podano dwie liczby, które są większe niż 10. Jeśli podano mniejsze liczby, użyj innej metody.

      • Na przykład znajdź najmniejszą wspólną wielokrotność liczb 20 i 84. Każda z liczb jest większa od 10, więc można użyć tej metody.

   2. Faktoryzuj pierwszą liczbę. Oznacza to, że musisz znaleźć takie liczby pierwsze, po pomnożeniu otrzymasz daną liczbę. Po znalezieniu czynników pierwszych zapisz je jako równość.

      • Na przykład, 2 × 10 = 20 (\displaystyle (\mathbf (2) )\razy 10=20) oraz 2 × 5 = 10 (\displaystyle (\mathbf (2))\times (\mathbf (5))=10). Czynnikami pierwszymi liczby 20 są więc liczby 2, 2 i 5. Zapisz je jako wyrażenie: .

   3. Podziel drugą liczbę na czynniki pierwsze. Zrób to w taki sam sposób, jak rozłożyłeś pierwszą liczbę na czynniki, to znaczy znajdź takie liczby pierwsze, które po pomnożeniu otrzymają tę liczbę.

      • Na przykład, 2 × 42 = 84 (\displaystyle (\mathbf (2))\razy 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7))\razy 6=42) oraz 3 × 2 = 6 (\displaystyle (\mathbf (3))\times (\mathbf (2))=6). Czynnikami pierwszymi liczby 84 są więc liczby 2, 7, 3 i 2. Zapisz je jako wyrażenie: .

   4. Zapisz czynniki wspólne dla obu liczb. Napisz takie czynniki jak operacja mnożenia. Zapisując każdy czynnik, wykreśl go w obu wyrażeniach (wyrażeniach opisujących rozkład liczb na czynniki pierwsze).

      • Na przykład wspólny dzielnik dla obu liczb to 2, więc napisz 2 × (\displaystyle 2\razy) i skreślić 2 w obu wyrażeniach.
      • Wspólny czynnik dla obu liczb to kolejny czynnik 2, więc napisz 2 × 2 (\displaystyle 2\razy 2) i skreśl drugie 2 w obu wyrażeniach.

   5. Dodaj pozostałe czynniki do operacji mnożenia. Są to czynniki, które nie są przekreślone w obu wyrażeniach, czyli czynniki, które nie są wspólne dla obu liczb.

      • Na przykład w wyrażeniu 20 = 2 × 2 × 5 (\displaystyle 20=2\razy 2\razy 5) obie dwójki (2) są przekreślone, ponieważ są to czynniki wspólne. Współczynnik 5 nie jest przekreślony, więc zapisz operację mnożenia w następujący sposób: 2 × 2 × 5 (\displaystyle 2\razy 2\razy 5)
      • W wyrażeniu 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\razy 7\razy 3\razy 2) obie dwójki (2) są również przekreślone. Czynniki 7 i 3 nie są przekreślone, więc zapisz operację mnożenia w następujący sposób: 2 × 2 × 5 × 7 × 3 (\displaystyle 2\razy 2\razy 5\razy 7\razy 3).

   6. Oblicz najmniejszą wspólną wielokrotność. Aby to zrobić, pomnóż liczby w operacji mnożenia pisanego.

      • Na przykład, 2 × 2 × 5 × 7 × 3 = 420 (\displaystyle 2\times 2\times 5\times 7\times 3=420). Tak więc najmniejsza wspólna wielokrotność 20 i 84 wynosi 420.

   Znalezienie wspólnych dzielników

   1. Narysuj siatkę tak, jak podczas gry w kółko i krzyżyk. Taka siatka składa się z dwóch równoległych linii, które przecinają się (pod kątem prostym) z dwoma innymi równoległymi liniami. Spowoduje to powstanie trzech wierszy i trzech kolumn (siatka wygląda bardzo podobnie do znaku #). Wpisz pierwszą liczbę w pierwszym wierszu i drugiej kolumnie. Wpisz drugą liczbę w pierwszym wierszu i trzeciej kolumnie.

      • Na przykład znajdź najmniejszą wspólną wielokrotność liczby 18 i 30. Wpisz 18 w pierwszym wierszu i drugiej kolumnie, a 30 w pierwszym wierszu i trzeciej kolumnie.

   2. Znajdź dzielnik wspólny dla obu liczb. Zapisz to w pierwszym wierszu i pierwszej kolumnie. Lepiej poszukać dzielników pierwszych, ale nie jest to warunek konieczny.

      • Na przykład 18 i 30 to liczby parzyste, więc ich wspólnym dzielnikiem jest 2. Wpisz więc 2 w pierwszym wierszu i pierwszej kolumnie.

   3. Podziel każdą liczbę przez pierwszy dzielnik. Napisz każdy iloraz pod odpowiednią liczbą. Iloraz jest wynikiem dzielenia dwóch liczb.

      • Na przykład, 18 ÷ 2 = 9 (\displaystyle 18\div 2=9), więc napisz 9 poniżej 18.
      • 30 ÷ 2 = 15 (\displaystyle 30\div 2=15), więc napisz 15 pod 30.

   4. Znajdź dzielnik wspólny dla obu ilorazów. Jeśli nie ma takiego dzielnika, pomiń kolejne dwa kroki. W przeciwnym razie zapisz dzielnik w drugim wierszu i pierwszej kolumnie.

      • Na przykład 9 i 15 są podzielne przez 3, więc wpisz 3 w drugim wierszu i pierwszej kolumnie.

   5. Podziel każdy iloraz przez drugi dzielnik. Zapisz każdy wynik dzielenia pod odpowiednim ilorazem.

      • Na przykład, 9 ÷ 3 = 3 (\displaystyle 9\div 3=3), więc napisz 3 pod 9.
      • 15 ÷ 3 = 5 (\displaystyle 15\div 3=5), więc napisz 5 pod 15.

   6. W razie potrzeby uzupełnij siatkę o dodatkowe komórki. Powtarzaj powyższe kroki, aż iloraz będzie miał wspólny dzielnik.

   7. Zakreśl liczby w pierwszej kolumnie i ostatnim wierszu siatki. Następnie zapisz podświetlone liczby jako operację mnożenia.

      • Na przykład liczby 2 i 3 znajdują się w pierwszej kolumnie, a liczby 3 i 5 w ostatnim wierszu, więc zapisz operację mnożenia w ten sposób: 2 × 3 × 3 × 5 (\displaystyle 2\razy 3\razy 3\razy 5).

   8. Znajdź wynik mnożenia liczb. Spowoduje to obliczenie najmniejszej wspólnej wielokrotności dwóch podanych liczb.

      • Na przykład, 2 × 3 × 3 × 5 = 90 (\displaystyle 2\razy 3\razy 3\razy 5=90). Tak więc najmniejsza wspólna wielokrotność 18 i 30 wynosi 90.

   Algorytm Euklidesa

   1. Zapamiętaj terminologię związaną z operacją dzielenia. Dywidenda to liczba, która jest dzielona. Dzielnik to liczba, przez którą należy podzielić. Iloraz jest wynikiem dzielenia dwóch liczb. Reszta to liczba pozostała po podzieleniu dwóch liczb.

      • Na przykład w wyrażeniu 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) reszta. 3:
        15 jest podzielne
        6 jest dzielnikiem
        2 jest prywatne
        3 to reszta.

Poniższy materiał to logiczna kontynuacja teorie z artykułu LCM - Least Common Multiple, definicja, przykłady, związek między LCM a GCM. Tutaj porozmawiamy znalezienie najmniejszej wspólnej wielokrotności (LCM), oraz Specjalna uwaga Przyjrzyjmy się przykładom. Najpierw pokażmy, w jaki sposób LCM dwóch liczb jest obliczany w kategoriach NWD tych liczb. Następnie rozważ znalezienie najmniejszej wspólnej wielokrotności przez rozłożenie liczb na czynniki pierwsze. Następnie skupimy się na znalezieniu LCM trzech i jeszcze liczb, a także zwróć uwagę na obliczanie LCM liczb ujemnych.

Nawigacja po stronach.

Obliczanie najmniejszej wspólnej wielokrotności (LCM) przez gcd

Jednym ze sposobów znalezienia najmniejszej wspólnej wielokrotności jest związek między LCM a GCD. Istniejąca zależność między LCM a NWD pozwala obliczyć najmniejszą wspólną wielokrotność dwóch dodatnich liczb całkowitych przez znany największy wspólny dzielnik. Odpowiednia formuła ma postać LCM(a, b)=a b: NCM(a, b) . Rozważ przykłady znalezienia LCM zgodnie z powyższym wzorem.

Przykład.

Znajdź najmniejszą wspólną wielokrotność dwóch liczb 126 i 70 .

Decyzja.

W tym przykładzie a=126 , b=70 . Wykorzystajmy zależność między LCM a NWD wyrażoną wzorem LCM(a, b)=a b: NCM(a, b). Oznacza to, że najpierw musimy znaleźć największy wspólny dzielnik liczb 70 i 126, po czym możemy obliczyć LCM tych liczb zgodnie z zapisanym wzorem.

Znajdź gcd(126, 70) używając algorytmu Euclida: 126=70 1+56 , 70=56 1+14 , 56=14 4 , stąd gcd(126, 70)=14 .

Teraz znajdujemy wymaganą najmniejszą wspólną wielokrotność: LCM(126, 70)=126 70: GCM(126, 70)= 126 70:14=630.

Odpowiedź:

LCM(126,70)=630.

Przykład.

Co to jest LCM(68, 34)?

Decyzja.

Jak 68 jest podzielne przez 34 , a następnie gcd(68, 34)=34 . Teraz obliczamy najmniejszą wspólną wielokrotność: LKM(68, 34)=68 34: LKM(68, 34)= 68 34:34=68.

Odpowiedź:

LCM(68,34)=68.

Zauważ, że poprzedni przykład pasuje do następującej zasady znajdowania LCM dla dodatnich liczb całkowitych aib : jeśli liczba a jest podzielna przez b , najmniejszą wspólną wielokrotnością tych liczb jest a .

Znalezienie LCM przez rozłożenie liczb na czynniki pierwsze

Innym sposobem znalezienia najmniejszej wspólnej wielokrotności jest rozłożenie liczb na czynniki pierwsze. Jeśli zrobimy iloczyn wszystkich czynników pierwszych tych liczb, po czym wykluczymy z tego iloczynu wszystkie wspólne czynniki pierwsze, które występują w rozwinięciach tych liczb, to otrzymany iloczyn będzie równy najmniejszej wspólnej wielokrotności tych liczb.

Ogłoszona zasada znajdowania LCM wynika z równości LCM(a, b)=a b: NCM(a, b). Rzeczywiście, iloczyn liczb a i b jest równy iloczynowi wszystkich czynników zaangażowanych w rozwinięcia liczb a i b. Z kolei gcd(a, b) jest równe iloczynowi wszystkich czynników pierwszych, które są jednocześnie obecne w rozwinięciach liczb a i b (co jest opisane w rozdziale dotyczącym znajdowania gcd za pomocą rozkładu liczb na czynniki pierwsze ).

Weźmy przykład. Wiedzmy, że 75=3 5 5 i 210=2 3 5 7 . Skomponuj iloczyn wszystkich czynników tych rozszerzeń: 2 3 3 5 5 5 7 . Teraz wykluczamy z tego iloczynu wszystkie czynniki, które występują zarówno w rozwinięciu liczby 75, jak iw rozwinięciu liczby 210 (takie czynniki to 3 i 5), wtedy iloczyn przyjmie postać 2 3 5 5 7 . Wartość tego iloczynu jest równa najmniejszej wspólnej wielokrotności liczb 75 i 210, czyli LCM(75, 210)= 2 3 5 5 7=1 050.

Przykład.

Po rozłożeniu liczb 441 i 700 na czynniki pierwsze, znajdź najmniejszą wspólną wielokrotność tych liczb.

Decyzja.

Rozłóżmy liczby 441 i 700 na czynniki pierwsze:

Otrzymujemy 441=3 3 7 7 i 700=2 2 5 5 7 .

Teraz zróbmy iloczyn wszystkich czynników związanych z rozwinięciami tych liczb: 2 2 3 3 5 5 7 7 7 . Wykluczmy z tego iloczynu wszystkie czynniki, które występują jednocześnie w obu rozwinięciach (jest tylko jeden taki czynnik - jest to liczba 7): 2 2 3 3 5 5 7 7 . Zatem, LCM(441, 700)=2 2 3 3 5 5 7 7=44 100.

Odpowiedź:

LCM(441,700)=44100.

Nieco inaczej można sformułować zasadę znajdowania LCM za pomocą rozkładu liczb na czynniki pierwsze. Jeżeli dodamy brakujące czynniki z rozwinięcia liczby b do czynników z rozwinięcia liczby a, to wartość otrzymanego iloczynu będzie równa najmniejszej wspólnej wielokrotności liczb a i b.

Na przykład weźmy te same liczby 75 i 210, ich rozwinięcia na czynniki pierwsze są następujące: 75=3 5 5 i 210=2 3 5 7 . Do czynników 3, 5 i 5 z rozkładu liczby 75 dodajemy brakujące czynniki 2 i 7 z rozkładu liczby 210, otrzymujemy iloczyn 2 3 5 5 7 , którego wartość to LCM(75 , 210).

Przykład.

Znajdź najmniejszą wspólną wielokrotność 84 i 648.

Decyzja.

Najpierw otrzymujemy rozkład liczb 84 i 648 na czynniki pierwsze. Wyglądają jak 84=2 2 3 7 i 648=2 2 2 3 3 3 3 . Do czynników 2 , 2 , 3 i 7 z rozkładu liczby 84 dodajemy brakujące czynniki 2 , 3 , 3 i 3 z rozkładu liczby 648 , otrzymujemy iloczyn 2 2 2 3 3 3 3 7 , co jest równe 4 536 . Zatem pożądana najmniejsza wspólna wielokrotność liczb 84 i 648 wynosi 4536.

Odpowiedź:

LCM(84,648)=4 536.

Znalezienie LCM trzech lub więcej liczb

Najmniejszą wspólną wielokrotność trzech lub więcej liczb można znaleźć, kolejno znajdując LCM dwóch liczb. Przypomnij sobie odpowiednie twierdzenie, które pozwala znaleźć LCM trzech lub więcej liczb.

Twierdzenie.

Niech zostaną podane liczby całkowite dodatnie a 1 , a 2 , …, a k, najmniej wspólna wielokrotność m k tych liczb zostanie znaleziona w obliczeniu sekwencyjnym m 2 = LCM (a 1 , a 2) , m 3 = LCM (m 2 , a 3) , … , m k =LCM(m k−1 , a k) .

Rozważ zastosowanie tego twierdzenia na przykładzie znajdowania najmniejszej wspólnej wielokrotności czterech liczb.

Przykład.

Znajdź LCM czterech liczb 140 , 9 , 54 i 250 .

Decyzja.

W tym przykładzie 1 =140 , 2 =9 , 3 =54 , 4 =250 .

Najpierw znajdujemy m 2 \u003d LCM (a 1, a 2) \u003d LCM (140, 9). Aby to zrobić, używając algorytmu Euklidesa, określamy gcd(140,9) , mamy 140=9 15+5 , 9=5 1+4 , 5=4 1+1 , 4=1 4 , zatem gcd( 140, 9)=1 , skąd LKM(140, 9)=140 9: LKM(140, 9)= 140 9:1=1 260 . Czyli m 2 =1 260 .

Teraz znajdujemy m 3 \u003d LCM (m 2, a 3) \u003d LCM (1 260, 54). Obliczmy to za pomocą gcd(1 260, 54) , które jest również określone przez algorytm Euclid: 1 260=54 23+18 , 54=18 3 . Wtedy gcd(1 260, 54)=18 , skąd LCM(1 260, 54)= 1 260 54:gcd (1 260, 54)= 1 260 54:18=3 780 . To znaczy m 3 \u003d 3 780.

Pozostawiony do znalezienia m 4 \u003d LCM (m 3, a 4) \u003d LCM (3 780, 250). Aby to zrobić, znajdujemy GCD(3 780, 250) za pomocą algorytmu Euclid: 3 780=250 15+30 , 250=30 8+10 , 30=10 3 . Dlatego gcd(3 780, 250)=10 , skąd gcd(3 780, 250)= 3 780 250: gcd (3 780, 250)= 3780 250:10=94 500 . Oznacza to, że m 4 \u003d 94 500.

Tak więc najmniejsza wspólna wielokrotność pierwotnych czterech liczb to 94500.

Odpowiedź:

LCM (140, 9, 54, 250) = 94 500.

W wielu przypadkach najmniejszą wspólną wielokrotność trzech lub więcej liczb można wygodnie znaleźć za pomocą faktoryzacji liczb pierwszych. W takim przypadku należy przestrzegać następującej zasady. Najmniejsza wspólna wielokrotność kilku liczb jest równa iloczynowi, który składa się w następujący sposób: brakujące czynniki z rozwinięcia drugiej liczby są dodawane do wszystkich czynników z rozwinięcia pierwszej liczby, brakujące czynniki z rozwinięcia liczby pierwszej trzecia liczba jest dodawana do uzyskanych współczynników i tak dalej.

Rozważ przykład znajdowania najmniejszej wspólnej wielokrotności przy użyciu rozkładu liczb na czynniki pierwsze.

Przykład.

Znajdź najmniejszą wspólną wielokrotność pięciu liczb 84 , 6 , 48 , 7 , 143 .

Decyzja.

Najpierw otrzymujemy rozwinięcia tych liczb na czynniki pierwsze: 84=2 2 3 7 , 6=2 3 , 48=2 2 2 2 3 , 7 czynników pierwszych) i 143=11 13 .

Aby znaleźć LCM tych liczb, do czynników pierwszej liczby 84 (są to 2 , 2 , 3 i 7 ) należy dodać brakujące czynniki z rozwinięcia drugiej liczby 6 . Rozszerzenie liczby 6 nie zawiera brakujących czynników, ponieważ zarówno 2, jak i 3 są już obecne w rozwinięciu pierwszej liczby 84 . Oprócz czynników 2 , 2 , 3 i 7 dodajemy brakujące czynniki 2 i 2 z rozwinięcia trzeciej liczby 48 , otrzymujemy zestaw czynników 2 , 2 , 2 , 2 , 3 i 7 . Nie ma potrzeby dodawania czynników do tego zestawu w następnym kroku, ponieważ 7 jest już w nim zawarte. Na koniec do czynników 2 , 2 , 2 , 2 , 3 i 7 dodajemy brakujące czynniki 11 i 13 z rozwinięcia liczby 143 . Otrzymujemy iloczyn 2 2 2 2 3 7 11 13 , który jest równy 48 048 .

Największy wspólny dzielnik

Definicja 2

Jeśli liczba naturalna a jest podzielna przez liczbę naturalną $b$, to $b$ nazywamy dzielnikiem $a$, a liczbę $a$ wielokrotnością $b$.

Niech $a$ i $b$ będą liczbami naturalnymi. Liczba $c$ nazywana jest wspólnym dzielnikiem zarówno dla $a$, jak i $b$.

Zbiór wspólnych dzielników liczb $a$ i $b$ jest skończony, ponieważ żaden z tych dzielników nie może być większy niż $a$. Oznacza to, że wśród tych dzielników występuje największy, który nazywamy największym wspólnym dzielnikiem liczb $a$ i $b$, a do jego oznaczenia używa się notacji:

$gcd \ (a;b) \ ​​​​lub \ D \ (a;b)$

Aby znaleźć największy wspólny dzielnik dwóch liczb:

1. Znajdź iloczyn liczb znalezionych w kroku 2. Otrzymana liczba będzie pożądanym największym wspólnym dzielnikiem.

Przykład 1

Znajdź gcd liczb 121$ i 132.$

$242=2\cdot 11\cdot 11$

$132=2\cdot 2\cdot 3\cdot 11$

Wybierz liczby, które są zawarte w rozszerzeniu tych liczb

$242=2\cdot 11\cdot 11$

$132=2\cdot 2\cdot 3\cdot 11$

Znajdź iloczyn liczb znalezionych w kroku 2. Otrzymana liczba będzie pożądanym największym wspólnym dzielnikiem.

$gcd=2\cdot 11=22$

Przykład 2

Znajdź GCD jednomianów 63$ i 81$.

Znajdziemy zgodnie z przedstawionym algorytmem. Dla tego:

Rozłóżmy liczby na czynniki pierwsze

63 $ = 3 \ cpunkt 3 \ cpunkt 7 $

81 $=3\cdot 3\cdot 3\cdot 3$

Wybieramy liczby, które są zawarte w rozwinięciu tych liczb

63 $ = 3 \ cpunkt 3 \ cpunkt 7 $

81 $=3\cdot 3\cdot 3\cdot 3$

Znajdźmy iloczyn liczb znalezionych w kroku 2. Otrzymana liczba będzie pożądanym największym wspólnym dzielnikiem.

$gcd=3\cdot 3=9$

Możesz znaleźć NWD dwóch liczb w inny sposób, używając zestawu dzielników liczb.

Przykład 3

Znajdź gcd liczb 48$ i 60$.

Decyzja:

Znajdź zbiór dzielników $48$: $\left\((\rm 1,2,3.4.6,8,12,16,24,48)\right\)$

Teraz znajdźmy zbiór dzielników $60$:$\ \left\((\rm 1,2,3,4,5,6,10,12,15,20,30,60)\right\)$

Znajdźmy przecięcie tych zbiorów: $\left\((\rm 1,2,3,4,6,12)\right\)$ - ten zbiór określi zbiór wspólnych dzielników liczb $48$ i $60 $. Największy element w dany zestaw będzie liczba $12$. Zatem największym wspólnym dzielnikiem 48$ i 60$ jest 12$.

Definicja NOC

Definicja 3

wspólna wielokrotność liczb naturalnych$a$ i $b$ to liczba naturalna będąca wielokrotnością zarówno $a$, jak i $b$.

Wspólne wielokrotności liczb to liczby, które są podzielne przez oryginał bez reszty.Na przykład dla liczb 25$ i 50$ wspólnymi wielokrotnościami będą liczby 50,100,150,200$ itd.

Najmniejsza wspólna wielokrotność będzie nazywana najmniejszą wspólną wielokrotnością i oznaczana przez LCM$(a;b)$ lub K$(a;b).$

Aby znaleźć LCM dwóch liczb, potrzebujesz:

1. Rozłóż liczby na czynniki pierwsze
2. Wypisz czynniki, które są częścią pierwszej liczby i dodaj do nich czynniki, które są częścią drugiej i nie przechodź do pierwszej

Przykład 4

Znajdź LCM liczb 99 $ i 77 $.

Znajdziemy zgodnie z przedstawionym algorytmem. Dla tego

Rozłóż liczby na czynniki pierwsze

99 $ = 3 \ cpunkt 3 \ cpunkt 11 $

Zapisz czynniki zawarte w pierwszym

dodaj do nich czynniki, które są częścią drugiego i nie przechodź do pierwszego

Znajdź iloczyn liczb znalezionych w kroku 2. Otrzymana liczba będzie najmniejszą wspólną wielokrotnością

$LCC=3\cdot 3\cdot 11\cdot 7=693$

Tworzenie list dzielników liczb jest często bardzo czasochłonne. Istnieje sposób na znalezienie GCD zwany algorytmem Euklidesa.

Stwierdzenia, na których oparty jest algorytm Euklidesa:

Jeśli $a$ i $b$ są liczbami naturalnymi, a $a\vdots b$, to $D(a;b)=b$

Jeśli $a$ i $b$ są liczbami naturalnymi takimi, że $b

Używając $D(a;b)= D(a-b;b)$, możemy sukcesywnie zmniejszać rozważane liczby, aż dojdziemy do pary liczb takiej, że jedna z nich jest podzielna przez drugą. Wtedy mniejsza z tych liczb będzie pożądanym największym wspólnym dzielnikiem dla liczb $a$ i $b$.

Właściwości GCD i LCM

1. Dowolna wspólna wielokrotność $a$ i $b$ jest podzielna przez K$(a;b)$
2. Jeśli $a\vdots b$ , to K$(a;b)=a$

Jeśli K$(a;b)=k$ i $m$-liczba naturalna, to K$(am;bm)=km$

Jeśli $d$ jest wspólnym dzielnikiem dla $a$ i $b$, to K($\frac(a)(d);\frac(b)(d)$)=$\ \frac(k)(d ) $

Jeśli $a\vdots c$ i $b\vdots c$ , to $\frac(ab)(c)$ jest wspólną wielokrotnością $a$ i $b$

Dla dowolnych liczb naturalnych $a$ i $b$ równość

$D(a;b)\cdot K(a;b)=ab$

Każdy wspólny dzielnik $a$ i $b$ jest dzielnikiem $D(a;b)$