Znajdowanie pierwiastków trójmianu kwadratowego

Cele: wprowadzić pojęcie trójmianu kwadratowego i jego korzenie; uformować umiejętność znajdowania pierwiastków trójmianu kwadratowego.

Podczas zajęć

I. Moment organizacyjny.

II. praca ustna.

Która z liczb: -2; -jeden; jeden; 2 - czy pierwiastki równań?

a) 8 X+ 16 = 0; w) X 2 + 3X – 4 = 0;

b) 5 X 2 – 5 = 0; G) X 3 – 3X – 2 = 0.

III. Wyjaśnienie nowego materiału.

Wyjaśnienie nowego materiału należy przeprowadzić według następującego schematu:

1) Wprowadź pojęcie pierwiastka wielomianowego.

2) Przedstaw pojęcie trójmianu kwadratowego i jego pierwiastki.

3) Przeanalizuj pytanie o możliwą liczbę pierwiastków trójmianu kwadratowego.

Kwestią wyodrębnienia kwadratu dwumianu z trójmianu kwadratowego lepiej zająć się w następnej lekcji.

Na każdym etapie wyjaśniania nowego materiału należy zaproponować studentom ustne zadanie sprawdzające przyswojenie głównych punktów teorii.

Zadanie 1. Która z liczb: -1; jeden; ; 0 - są pierwiastkami wielomianu X 4 + 2X 2 – 3?

Zadanie 2. Które z poniższych wielomianów są trójmianami kwadratowymi?

1) 2X 2 + 5X – 1; 6) X 2 – X – ;

2) 2X – ; 7) 3 – 4X + X 2 ;

3) 4X 2 + 2X + X 3 ; 8) X + 4X 2 ;

4) 3X 2 – ; 9) + 3X – 6;

5) 5X 2 – 3X; 10) 7X 2 .

Który z trójmianów kwadratowych ma pierwiastek 0?

Zadanie 3. Czy trójmian kwadratowy może mieć trzy pierwiastki? Czemu? Ile pierwiastków ma trójmian kwadratowy X 2 + X – 5?

IV. Kształtowanie umiejętności i zdolności.

Ćwiczenia:

1. № 55, № 56, № 58.

2. Nr 59 (a, c, e), nr 60 (a, c).

W tym zadaniu nie musisz szukać pierwiastków trójmianów kwadratowych. Wystarczy znaleźć ich wyróżnik i odpowiedzieć na postawione pytanie.

a) 5 X 2 – 8X + 3 = 0;

D 1 = 16 – 15 = 1;

D 10, więc ten trójmian kwadratowy ma dwa pierwiastki.

b) 9 X 2 + 6X + 1 = 0;

D 1 = 9 – 9 = 0;

D 1 = 0, więc trójmian kwadratowy ma jeden pierwiastek.

w 7 X 2 + 6X – 2 = 0;

7X 2 – 6X + 2 = 0;

D 1 = 9 – 14 = –5;

Jeśli jest czas, możesz zrobić numer 63.

Decyzja

Zostawiać topór 2 + bx + c jest danym trójmianem kwadratowym. O ile a+ b +
+c= 0, to jeden z pierwiastków tego trójmianu jest równy 1. Zgodnie z twierdzeniem Vieta, drugi pierwiastek jest równy . Zgodnie z warunkiem z = 4a, więc drugim pierwiastkiem tego trójmianu kwadratowego jest
.

Odpowiedzi: 1 i 4.

V. Wyniki lekcji.

pytania

Co to jest pierwiastek wielomianowy?

Jaki wielomian nazywamy trójmianem kwadratowym?

Jak znaleźć pierwiastki trójmianu kwadratowego?

Jaki jest wyróżnik trójmianu kwadratowego?

Ile pierwiastków może mieć trójmian kwadratowy? Od czego to zależy?

Zadanie domowe: nr 57, nr 59 (b, d, f), nr 60 (b, d), nr 62.

Nauczyciel najwyższej kategorii: Minaichenko N.S., gimnazjum nr 24, Sewastopol

Lekcja w 8 klasie: „Trójmian kwadratowy i jego korzenie”

Rodzaj lekcji : lekcja nowej wiedzy.

Cel lekcji:

organizować zajęcia uczniów w celu utrwalenia i rozwijania wiedzy na temat rozkładu trójmianu kwadratowego na czynniki liniowe, redukcji ułamków;

rozwijać umiejętności stosowania znajomości wszystkich metod faktoryzacji: nawiasów, stosowania skróconych wzorów mnożenia i metody grupowania w celu przygotowania się do udana dostawa egzamin z algebry;

stworzyć warunki do rozwoju zainteresowanie poznawcze do tematu, formacji logiczne myślenie i samokontroli podczas korzystania z faktoryzacji.

Ekwipunek: rzutnik multimedialny, ekran, prezentacja: „Korzenie trójmianu kwadratowego”, krzyżówka, test, handout.

Podstawowe koncepcje . Rozkład trójmian kwadratowy dla mnożników.

Samodzielna aktywność studentów. Zastosowanie twierdzenia o faktoryzacji dla trójmianu kwadratowego w rozwiązywaniu problemów.

Plan lekcji

Rozwiązywanie problemów.

Odpowiedzi na pytania uczniów

IV. Podstawowy sprawdzian opanowania wiedzy. Odbicie

Wiadomość od nauczyciela.

Wiadomość dla ucznia

V. Praca domowa

pisanie na tablicy

Komentarz metodologiczny:

Ten temat jest fundamentalny w sekcji „Przekształcenia tożsamości wyrażenia algebraiczne”. Dlatego ważne jest, aby uczniowie automatycznie mogli nie tylko zobaczyć wzory na faktoryzację w przykładach, ale także zastosować je w innych zadaniach: takich jak rozwiązywanie równań, przekształcanie wyrażeń, udowadnianie tożsamości.

Ten temat koncentruje się na rozkładaniu trójmianu kwadratowego na czynniki:

topór+ bx + c = a(x – x)(x – x),

gdzie x i x - korzenie równanie kwadratowe topór + bx + c = 0.

Pozwala to poszerzyć pole widzenia ucznia, nauczyć go myślenia w nietypowa sytuacja podczas korzystania z badanego materiału, tj. korzystając ze wzoru na faktoryzację trójmianu kwadratowego:

umiejętność redukcji ułamków algebraicznych;

umiejętność upraszczania wyrażeń algebraicznych;

umiejętność rozwiązywania równań;

umiejętność udowodnienia tożsamości.

Główna treść lekcji:

a) 3x + 5x - 2;

b) –x + 16x – 15;

c) x - 12x + 24;

d) -5x + 6x - 1.

№2. Zmniejsz ułamek:

№3. Uprość wyrażenie:

№4. Rozwiąż równanie:

b)

Podczas zajęć:

I. Etap aktualizacji wiedzy.

Motywacja działalności edukacyjnej.

a) z historii:

b) krzyżówka:

Rozgrzewka-trening umysłu - krzyżówka:

Poziomo:

1) Korzeń drugiego stopnia nazywa się .... (kwadrat)

2) Zmienne wartości, przy których równanie staje się prawdziwą równością (pierwsze)

3) Równość zawierająca niewiadomą nazywa się ... (równanie)

4) indyjski naukowieckto przedstawił? główna zasada rozwiązywanie równań kwadratowych (Brahmagupta)

5) Współczynniki równania kwadratowego to ... (liczby)

6) Starożytny grecki naukowiec, który wynalazł geometryczną metodę rozwiązywania równań (Euklid)

7) Twierdzenie łączące współczynniki i pierwiastki równania kwadratowego (Vieta)

8) „rozróżnianie”, definiowanie pierwiastków równania kwadratowego to ... (dyskryminacja)

Do tego:

Jeśli D>0, ile pierwiastków? (dwa)

Jeśli D=0, ile pierwiastków? (jeden)

Jeśli D<0, сколько корней? (нет действительных корней)

Poziomo i pionowo temat lekcji: „Trójmian kwadratowy”

b) motywacja:

Temat ten jest fundamentalny w rozdziale „Przekształcenia tożsamościowe wyrażeń algebraicznych”. Dlatego ważne jest, abyś automatycznie mógł nie tylko zobaczyć wzory na faktoryzację w przykładach, ale także zastosować je w innych zadaniach: takich jak zmniejszanie ułamków, rozwiązywanie równań, przekształcanie wyrażeń, udowadnianie tożsamości.

Dzisiaj skupimy się na faktoryzacji trójmianu kwadratowego:

II. Nauka nowego materiału.

Temat: Trójmian kwadratowy i jego pierwiastki.

Ogólna teoria wielomianów w wielu zmiennych wykracza daleko poza ramy kursu szkolnego. Dlatego ograniczamy się do badania wielomianów jednej zmiennej rzeczywistej i to nawet w najprostszych przypadkach. Rozważ wielomiany jednej zmiennej zredukowane do postaci standardowej.

Korzeń wielomianu jest wartością zmiennej, przy której wartość wielomianu jest równa zero. Oznacza to, że aby znaleźć pierwiastki wielomianu, konieczne jest zrównanie go z zero, tj. Rozwiązać równanie.

Pierwiastek wielomianu pierwszego stopnia
łatwe do znalezienia
. Badanie:
.

Pierwiastki trójmianu kwadratowego można znaleźć, rozwiązując równanie:
.

Zgodnie ze wzorem pierwiastków równania kwadratowego znajdujemy:

;

Twierdzenie (na faktoryzacji trójmianu kwadratowego ):

Jeśli oraz - pierwiastki trójmianu kwadratowego
, gdzie ≠ 0,

następnie .

Dowód:

Wykonujemy następujące przekształcenia trójmianu kwadratowego:

=
=
=

=
=
=

=
=

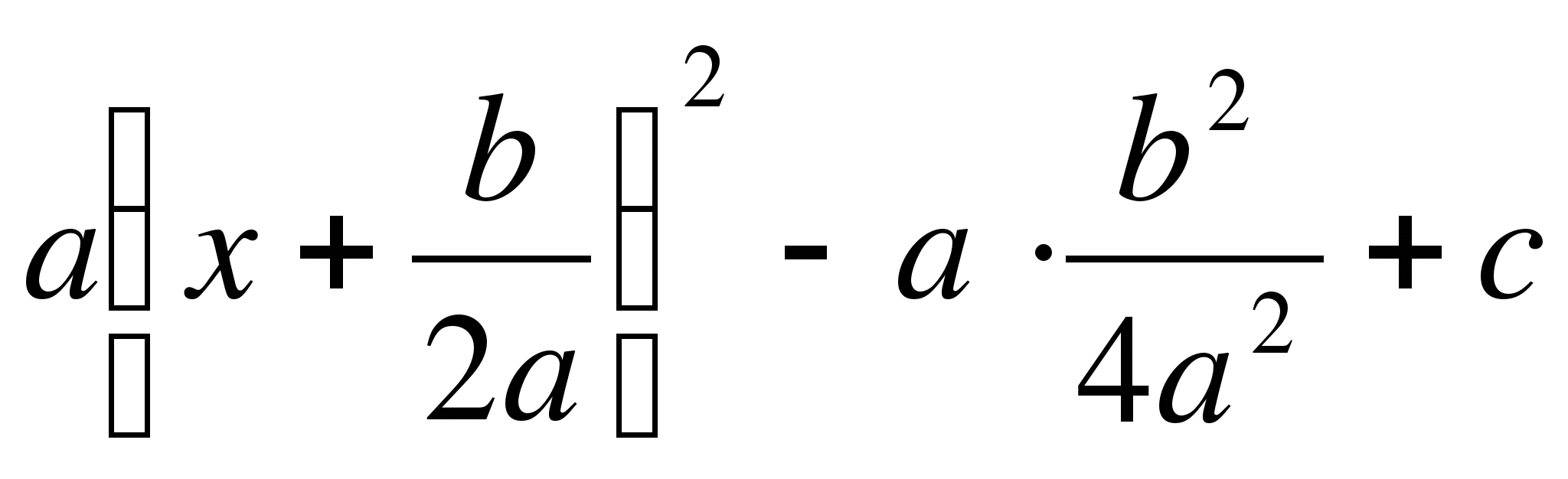Ponieważ wyróżnik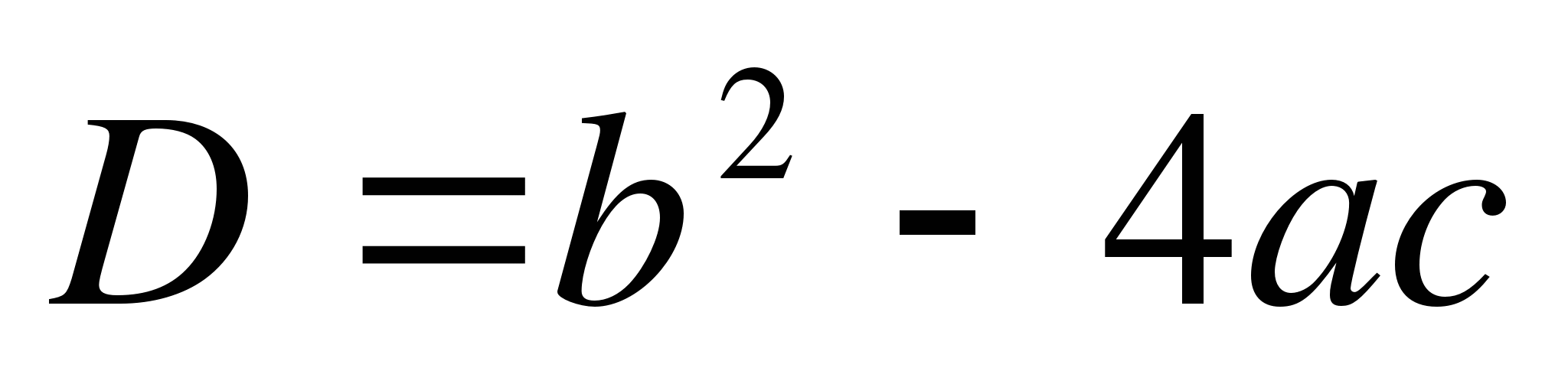
, otrzymujemy:

=
=

Stosujemy wzór różnicy kwadratów w nawiasach i otrzymujemy:

=
=
,

jak
;
. Twierdzenie zostało udowodnione.

Otrzymana formuła nazywa się formułąfaktoryzacja trójmianu kwadratowego.

III. Kształtowanie umiejętności i zdolności.

№1. Rozkład na czynniki kwadratowe trójmianu:

a) 3x + 5x - 2;

Decyzja:

Odpowiedź: 3x+5x–2=3(x+2)(x-)=(x+2)(3x-1)

Na biurku:

b) –5x + 6x – 1;

Do tego:

c) x - 12x + 24;

d) –x + 16x – 15.

№2. Zmniejsz ułamek:

a)

№4. Rozwiąż równanie:

b)

IV. Podstawowy sprawdzian opanowania wiedzy.

a) Test.

Opcja 1.

1. Znajdź pierwiastki trójmianu kwadratowego:2x 2 -9x-5

Odpowiedź:

2. Który wielomian należy zastąpić wielomianem, aby równość była prawdziwa:

b) Wzajemna weryfikacja według opcji (odpowiedzi i parametry oceny są zilustrowane).

c) Refleksja.

V. Praca domowa.

Możesz znaleźć pierwiastek z trójmianu kwadratowego poprzez dyskryminator. Ponadto dla wielomianu zredukowanego drugiego stopnia ważne jest twierdzenie Vieta, oparte na stosunku współczynników.

Instrukcja

• Równania kwadratowe to dość szeroki temat w szkolnej algebrze. Lewa strona takiego równania jest wielomianem drugiego stopnia postaci A x² + B x + C, tj. wyrażenie trzech jednomianów o różnym stopniu nieznanego x. Aby znaleźć pierwiastek z trójmianu kwadratowego, musisz obliczyć wartość x, dla której to wyrażenie jest równe zero.
• Aby rozwiązać równanie kwadratowe, musisz znaleźć dyskryminator. Jego wzór jest konsekwencją podświetlenia pełnego kwadratu wielomianu i jest pewnym stosunkiem jego współczynników: D = B² - 4 A C.
• Wyróżnik może przybierać różne wartości, w tym być negatywnym. A jeśli młodsi uczniowie mogą z ulgą powiedzieć, że takie równanie nie ma pierwiastków, to już licealiści potrafią je wyznaczyć na podstawie teorii liczb zespolonych. Tak więc mogą być trzy opcje: Wyróżnik jest liczbą dodatnią. Wtedy pierwiastki równania to: x1 = (-B + √D)/2 A; x2 = (-B - √D) / 2 A;
  Dyskryminator zszedł do zera. Teoretycznie w tym przypadku równanie ma również dwa pierwiastki, ale praktycznie są one takie same: x1 \u003d x2 \u003d -B / 2 A;
  Dyskryminator jest mniejszy od zera. Do obliczeń wprowadzana jest pewna wartość i² = -1, która pozwala na zapisanie rozwiązania złożonego: x1 = (-B + i √|D|)/2 A; x2 \u003d (-B - i √ | D |) / 2 A.
• Metoda dyskryminacyjna jest ważna dla dowolnego równania kwadratowego, jednak zdarzają się sytuacje, w których wskazane jest zastosowanie szybszej metody, zwłaszcza dla małych współczynników całkowitych. Metoda ta nazywana jest twierdzeniem Vieta i polega na parze relacji między współczynnikami w trójmianu zredukowanym: x² + P x + Q
  x1 + x2 = -P;
  x1 x2 = Q. Pozostaje tylko zebrać korzenie.
• Należy zauważyć, że równanie można sprowadzić do podobnej postaci. Aby to zrobić, musisz podzielić wszystkie wyrazy trójmianu przez współczynnik w najwyższym stopniu A: A x² + B x + C | A
  x² + B/A x + C/A
  x1 + x2 = -B/A;
  x1 x2 = C/A.

Kalkulator online.
Wybór kwadratu dwumianu i faktoryzacja trójmianu kwadratowego.

Ten program do matematyki wyodrębnia kwadrat z dwumianu z trójmianu kwadratowego, tj. dokonuje przekształcenia formy:
\(ax^2+bx+c \rightarrow a(x+p)^2+q \) and faktoryzuje trójmian kwadratowy: \(ax^2+bx+c \rightarrow a(x+n)(x+m) \)

Tych. problemy sprowadzają się do znalezienia liczb \(p, q \) i \(n, m \)

Program nie tylko daje odpowiedź na problem, ale także wyświetla proces rozwiązania.

Ten program może być przydatny dla uczniów szkół średnich w ramach przygotowań do testów i egzaminów, podczas sprawdzania wiedzy przed egzaminem Unified State Exam, dla rodziców do kontrolowania rozwiązywania wielu problemów z matematyki i algebry. A może za drogo zatrudnisz korepetytora lub kupisz nowe podręczniki? A może po prostu chcesz jak najszybciej odrobić pracę domową z matematyki lub algebry? W tym przypadku możesz również skorzystać z naszych programów ze szczegółowym rozwiązaniem.

W ten sposób możesz prowadzić własne szkolenie i/lub szkolenie swoich młodszych braci lub sióstr, jednocześnie podnosząc poziom edukacji w zakresie zadań do rozwiązania.

Jeśli nie znasz zasad wpisywania trójmianu kwadratowego, zalecamy zapoznanie się z nimi.

Zasady wprowadzania wielomianu kwadratowego

Każda litera łacińska może działać jako zmienna.
Na przykład: \(x, y, z, a, b, c, o, p, q \) itp.

Liczby można wprowadzać jako liczby całkowite lub ułamki.
Co więcej, liczby ułamkowe można wprowadzać nie tylko w postaci ułamka dziesiętnego, ale także w postaci ułamka zwykłego.

Zasady wprowadzania ułamków dziesiętnych.
W ułamkach dziesiętnych część ułamkową od liczby całkowitej można oddzielić kropką lub przecinkiem.
Na przykład możesz wprowadzić liczby dziesiętne w następujący sposób: 2,5x - 3,5x^2

Zasady wprowadzania zwykłych ułamków.
Tylko liczba całkowita może pełnić funkcję licznika, mianownika i części całkowitej ułamka.

Mianownik nie może być ujemny.

Przy wprowadzaniu ułamka liczbowego licznik jest oddzielony od mianownika znakiem dzielenia: /
Część całkowita jest oddzielona od ułamka znakiem ampersandu: &
Wejście: 3&1/3 - 5&6/5x +1/7x^2
Wynik: \(3\frac(1)(3) - 5\frac(6)(5) x + \frac(1)(7)x^2 \)

Podczas wprowadzania wyrażenia możesz użyć nawiasów. W tym przypadku podczas rozwiązywania wprowadzone wyrażenie jest najpierw uproszczone.
Na przykład: 1/2(x-1)(x+1)-(5x-10&1/2)

Szczegółowy przykład rozwiązania

Wybór kwadratu dwumianu.$$ ax^2+bx+c \rightarrow a(x+p)^2+q $$ $$2x^2+2x-4 = $$ $$2x^2 +2 \cdot 2 \cdot\left( \frac(1)(2) \right)\cdot x+2 \cdot \left(\frac(1)(2) \right)^2-\frac(9)(2) = $$ $$2\left (x^2 + 2 \cdot\left(\frac(1)(2) \right)\cdot x + \left(\frac(1)(2) \right)^2 \right)-\frac(9 )(2) = $$ $$2\left(x+\frac(1)(2) \right)^2-\frac(9)(2) $$ Odpowiedź:$$2x^2+2x-4 = 2\left(x+\frac(1)(2) \right)^2-\frac(9)(2) $$ Faktoryzacja.$$ ax^2+bx+c \rightarrow a(x+n)(x+m) $$ $$2x^2+2x-4 = $$
$$ 2\lewo(x^2+x-2 \prawo) = $$
$$ 2 \left(x^2+2x-1x-1 \cdot 2 \right) = $$ $$ 2 \left(x \left(x +2 \right) -1 \left(x +2 \right ) \right) = $$ $$ 2 \left(x -1 \right) \left(x +2 \right) $$ Odpowiedź:$$2x^2+2x-4 = 2 \left(x -1 \right) \left(x +2 \right) $$

Zdecydować

Stwierdzono, że niektóre skrypty potrzebne do rozwiązania tego zadania nie zostały załadowane, a program może nie działać.
Możesz mieć włączony AdBlock.
W takim przypadku wyłącz go i odśwież stronę.

Masz wyłączoną obsługę JavaScript w swojej przeglądarce.
Aby rozwiązanie się pojawiło, musi być włączony JavaScript.
Oto instrukcje, jak włączyć JavaScript w przeglądarce.

Ponieważ Jest wiele osób, które chcą rozwiązać problem, Twoja prośba jest w kolejce.
Po kilku sekundach rozwiązanie pojawi się poniżej.
Poczekaj proszę sek...

Jeśli ty zauważyłem błąd w rozwiązaniu, możesz o tym napisać w Formularzu Informacji Zwrotnej .
Nie zapomnij wskaż, które zadanie Ty decydujesz co? wpisz w polach.

Nasze gry, puzzle, emulatory:

Trochę teorii.

Wyodrębnianie dwumianu kwadratowego z trójmianu kwadratowego

Jeśli kwadrat trójmianu ax 2 + bx + c jest reprezentowany jako a (x + p) 2 + q, gdzie p i q są liczbami rzeczywistymi, to mówią, że z trójmian kwadratowy, kwadrat dwumianu jest podświetlony.

Wydzielmy kwadrat dwumianu z trójmianu 2x 2 +12x+14.

\(2x^2+12x+14 = 2(x^2+6x+7) \)

Aby to zrobić, reprezentujemy 6x jako iloczyn 2 * 3 * x, a następnie dodajemy i odejmujemy 3 2 . Otrzymujemy:
$$ 2(x^2+2 \cdot 3 \cdot x + 3^2-3^2+7) = 2((x+3)^2-3^2+7) = $$ $$ = 2 ((x+3)^2-2) = 2(x+3)^2-4 $$

To. my wybrał kwadrat dwumianu z trójmianu kwadratowego i pokazał, że:
$ 2x^2+12x+14 = 2(x+3)^2-4 $$

Faktoryzacja trójmianu kwadratowego

Jeśli kwadrat trójmianu ax 2 +bx+c jest reprezentowany jako a(x+n)(x+m), gdzie n i m są liczbami rzeczywistymi, to operacja jest wykonywana faktoryzacja trójmianu kwadratowego.

Użyjmy przykładu, aby pokazać, jak odbywa się ta transformacja.

Rozliczmy trójmian kwadratowy 2x 2 + 4x-6.

Wyjmijmy współczynnik a z nawiasów, tj. 2:
\(2x^2+4x-6 = 2(x^2+2x-3) \)

Przekształćmy wyrażenie w nawiasach.
Aby to zrobić, reprezentujemy 2x jako różnicę 3x-1x, a -3 jako -1*3. Otrzymujemy:
$$ = 2(x^2+3 \cdot x -1 \cdot x -1 \cdot 3) = 2(x(x+3)-1 \cdot (x+3)) = $$
$$ = 2(x-1)(x+3) $$

To. my faktoryzować trójmian kwadratowy i pokazał, że:
$ 2x^2+4x-6 = 2(x-1)(x+3) $$

Zauważ, że faktoryzacja trójmianu kwadratowego jest możliwa tylko wtedy, gdy równanie kwadratowe odpowiadające temu trójmianowi ma pierwiastki.
Tych. w naszym przypadku rozłożenie na czynniki trójmianu 2x 2 +4x-6 jest możliwe, jeśli równanie kwadratowe 2x 2 +4x-6 =0 ma pierwiastki. W procesie faktoryzacji odkryliśmy, że równanie 2x 2 +4x-6 =0 ma dwa pierwiastki 1 i -3, ponieważ przy tych wartościach równanie 2(x-1)(x+3)=0 zamienia się w prawdziwą równość.

Książki (podręczniki) Streszczenia z Jednolitego Egzaminu Państwowego i testów OGE online Gry, zagadki Wykresy funkcji Słownik ortografii języka rosyjskiego Słownik slangu młodzieżowego Katalog szkół rosyjskich Katalog szkół średnich w Rosji Katalog uniwersytetów rosyjskich Lista zadań

Rozszerzanie wielomianów w celu uzyskania produktu czasami wydaje się mylące. Ale nie jest to takie trudne, jeśli rozumiesz proces krok po kroku. Artykuł szczegółowo opisuje faktoryzację trójmianu kwadratowego.

Wielu nie rozumie, jak rozkładać trójmian kwadratowy na czynniki i dlaczego tak się dzieje. Na pierwszy rzut oka może się wydawać, że jest to bezużyteczne ćwiczenie. Ale w matematyce nic się tak nie robi. Przekształcenie jest konieczne, aby uprościć wyrażenie i wygodę obliczeń.

Wielomian o postaci - ax² + bx + c, nazywa się trójmianem kwadratowym. Termin „a” musi być ujemny lub dodatni. W praktyce to wyrażenie nazywa się równaniem kwadratowym. Dlatego czasami mówią inaczej: jak rozwinąć równanie kwadratowe.

Ciekawe! Wielomian kwadratowy nazywamy ze względu na swój największy stopień - kwadrat. Oraz trójmian - ze względu na 3 wyrazy składowe.

Niektóre inne rodzaje wielomianów:

• dwumian liniowy (6x+8);
• sześcienny czworokąt (x³+4x²-2x+9).

Faktoryzacja trójmianu kwadratowego

Najpierw wyrażenie jest równe zero, następnie musisz znaleźć wartości pierwiastków x1 i x2. Może nie być korzeni, może być jeden lub dwa korzenie. O obecności korzeni decyduje wyróżnik. Jego wzór musi być znany na pamięć: D=b²-4ac.

Jeśli wynik D jest ujemny, nie ma pierwiastków. Jeśli jest dodatni, istnieją dwa pierwiastki. Jeśli wynik to zero, pierwiastek to jeden. Korzenie są również obliczane według wzoru.

Jeśli wynik obliczenia dyskryminatora wynosi zero, można zastosować dowolną formułę. W praktyce formuła jest po prostu skrócona: -b/2a.

Wzory dla różnych wartości dyskryminatora są różne.

Jeśli D jest dodatnie:

Jeśli D wynosi zero:

Kalkulatory online

W Internecie dostępny jest kalkulator online. Może być używany do faktoryzacji. Niektóre zasoby umożliwiają zapoznanie się z rozwiązaniem krok po kroku. Takie usługi pomagają lepiej zrozumieć temat, ale musisz spróbować dobrze zrozumieć.

Przydatne wideo: Rozkładanie trójmianu kwadratowego na czynniki

Przykłady

Sugerujemy przyjrzenie się prostym przykładom rozkładania równania kwadratowego na czynniki.

Przykład 1

Tutaj wyraźnie widać, że wynikiem będzie dwa x, ponieważ D jest dodatnie. Muszą być podstawione w formule. Jeśli pierwiastki są ujemne, znak we wzorze jest odwrócony.

Znamy wzór na rozkład trójmianu kwadratowego: a(x-x1)(x-x2). Wartości umieszczamy w nawiasach: (x+3)(x+2/3). W wykładniku nie ma liczby przed terminem. Oznacza to, że jest jednostka, jest ona obniżona.

Przykład 2

Ten przykład wyraźnie pokazuje, jak rozwiązać równanie, które ma jeden pierwiastek.

Podstaw wynikową wartość:

Przykład 3

Biorąc pod uwagę: 5x²+3x+7

Najpierw obliczamy dyskryminator, tak jak w poprzednich przypadkach.

D=9-4*5*7=9-140= -131.

Wyróżnik jest ujemny, co oznacza, że ​​nie ma korzeni.

Po otrzymaniu wyniku warto otworzyć nawiasy i sprawdzić wynik. Powinien pojawić się oryginalny trójmian.

Alternatywne rozwiązanie

Niektórzy ludzie nigdy nie byli w stanie zaprzyjaźnić się z dyskryminacją. Istnieje inny sposób na faktoryzację trójmianu kwadratowego. Dla wygody metodę przedstawiono na przykładzie.

Biorąc pod uwagę: x²+3x-10

Wiemy, że powinniśmy skończyć z 2 nawiasami: (_)(_). Gdy wyrażenie wygląda tak: x² + bx + c, umieszczamy x na początku każdego nawiasu: (x_) (x_). Pozostałe dwie liczby to iloczyn dający „c”, czyli w tym przypadku -10. Aby dowiedzieć się, jakie są te liczby, możesz użyć tylko metody wyboru. Podstawione liczby muszą być zgodne z pozostałym terminem.

Na przykład pomnożenie następujących liczb daje -10:

• -1, 10;
• -10, 1;
• -5, 2;
• -2, 5.

1. (x-1)(x+10) = x2+10x-x-10 = x2+9x-10. Nie.
2. (x-10)(x+1) = x2+x-10x-10 = x2-9x-10. Nie.
3. (x-5)(x+2) = x2+2x-5x-10 = x2-3x-10. Nie.
4. (x-2)(x+5) = x2+5x-2x-10 = x2+3x-10. Pasuje.

Zatem przekształcenie wyrażenia x2+3x-10 wygląda tak: (x-2)(x+5).

Ważny! Należy uważać, aby nie pomylić znaków.

Rozkład złożonego trójmianu

Jeśli „a” jest większe niż jeden, zaczynają się trudności. Ale nie wszystko jest takie trudne, jak się wydaje.

Aby dokonać faktoryzacji, trzeba najpierw sprawdzić, czy da się coś rozłożyć na czynniki.

Na przykład, biorąc pod uwagę wyrażenie: 3x²+9x-30. Tutaj cyfra 3 jest wyjęta z nawiasów:

3(x²+3x-10). Rezultatem jest znany już trójmian. Odpowiedź wygląda tak: 3(x-2)(x+5)

Jak rozłożyć, jeśli wyraz do kwadratu jest ujemny? W tym przypadku liczba -1 jest wyjęta z nawiasu. Na przykład: -x²-10x-8. Wyrażenie będzie wtedy wyglądać tak:

Schemat niewiele różni się od poprzedniego. Jest tylko kilka nowych rzeczy. Powiedzmy, że dane wyrażenie: 2x²+7x+3. Odpowiedź jest również zapisana w 2 nawiasach, które należy wypełnić (_) (_). X jest zapisane w drugim nawiasie, a to, co zostało w pierwszym. Wygląda to tak: (2x_)(x_). W przeciwnym razie poprzedni schemat jest powtarzany.

Cyfra 3 daje liczby:

• -1, -3;
• -3, -1;
• 3, 1;
• 1, 3.

Równania rozwiązujemy, podstawiając podane liczby. Ostatnia opcja pasuje. Zatem przekształcenie wyrażenia 2x²+7x+3 wygląda tak: (2x+1)(x+3).

Inne przypadki

Przekształcenie wyrażenia nie zawsze jest możliwe. W drugiej metodzie rozwiązanie równania nie jest wymagane. Ale możliwość zamiany terminów na produkt jest sprawdzana tylko przez dyskryminator.

Warto poćwiczyć rozwiązywanie równań kwadratowych, aby nie było trudności przy korzystaniu z formuł.

Przydatne wideo: faktoryzacja trójmianu

Wniosek

Możesz go używać w dowolny sposób. Ale lepiej pracować zarówno na automatyzmie. Ponadto ci, którzy zamierzają połączyć swoje życie z matematyką, muszą nauczyć się dobrze rozwiązywać równania kwadratowe i rozkładać wielomiany na czynniki. Wszystkie poniższe zagadnienia matematyczne są na tym zbudowane.