Istotne miejsce zajmują problemy z budową odcinków wielościanów, ponieważ kurs szkolny geometria do liceum oraz na egzaminach na różnych poziomach. Rozwiązanie tego typu problemów przyczynia się do przyswajania aksjomatów stereometrii, systematyzacji wiedzy i umiejętności, rozwoju reprezentacji przestrzennej i umiejętności konstruktywnych. Znane są trudności, jakie pojawiają się w rozwiązywaniu problemów związanych z budową odcinków.

Od wczesnego dzieciństwa mamy do czynienia z sekcjami. Kroimy chleb, kiełbasę i inne produkty, kroimy kij lub ołówek nożem. Sieczną płaszczyzną we wszystkich tych przypadkach jest płaszczyzna noża. Sekcje (sekcje sztuk) są różne.

Przekrój wielościanu wypukłego jest wielokątem wypukłym, którego wierzchołki w ogólnym przypadku są punktami przecięcia płaszczyzny tnącej z krawędziami wielokąta, a boki są liniami przecięcia płaszczyzny tnącej z twarze.

Aby skonstruować linię przecięcia dwóch płaszczyzn wystarczy znaleźć dwie punkty wspólne te płaszczyzny i narysuj przez nie linię prostą. Opiera się to na następujących stwierdzeniach:

1. jeżeli dwa punkty prostej należą do płaszczyzny, to cała prosta należy do tej płaszczyzny;

2. jeżeli dwie różne płaszczyzny mają wspólny punkt, to przecinają się one wzdłuż linii prostej przechodzącej przez ten punkt.

Jak już powiedziałem, konstrukcję odcinków wielościanów można przeprowadzić na podstawie aksjomatów stereometrii i twierdzeń o równoległości prostych i płaszczyzn. Jednocześnie istnieją pewne metody konstruowania płaskich odcinków wielościanów. Najskuteczniejsze są następujące trzy metody:

metoda śledzenia

Metoda projektowania wewnętrznego

Metoda kombinowana.

W badaniu geometrii, a w szczególności w tych sekcjach, w których brane są pod uwagę obrazy figur geometrycznych, obrazy figur geometrycznych pomagają w korzystaniu z prezentacji komputerowych. Z pomocą komputera wiele lekcji geometrii staje się bardziej wizualnych i dynamicznych. Aksjomaty, twierdzenia, dowody, problemy konstrukcyjne, problemy konstrukcyjne przekrojów mogą towarzyszyć kolejnym konstrukcjom na ekranie monitora. Rysunki wygenerowane komputerowo można zapisywać i wklejać do innych dokumentów.

Chcę pokazać kilka slajdów na temat: „Budowa przekrojów w bryłach geometrycznych”

Aby skonstruować punkt przecięcia linii i płaszczyzny, znajdź linię w płaszczyźnie, która przecina daną linię. Wtedy pożądanym punktem jest punkt przecięcia znalezionej linii z daną. Zobaczmy to na następnych slajdach.

Zadanie 1.

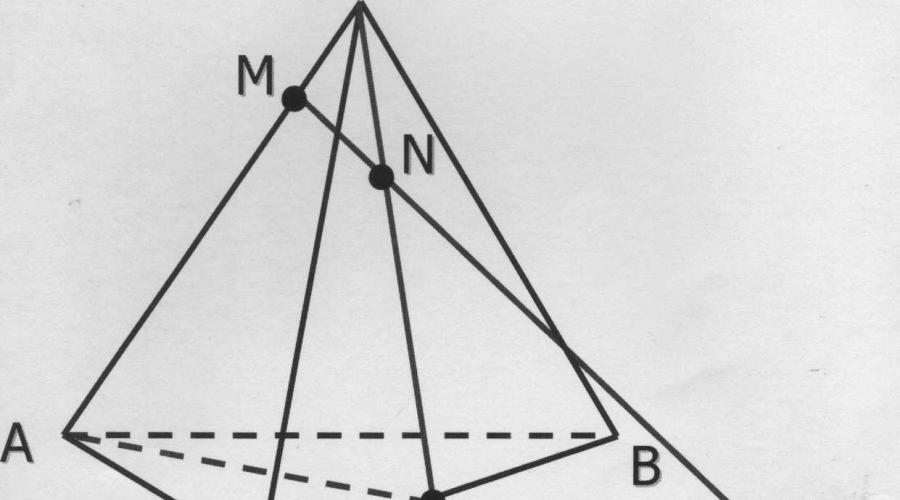
Na krawędziach czworościanu DABC zaznaczono dwa punkty M i N; M GAD, Nb DC. Wybierz punkt przecięcia linii MN z płaszczyzną podstawy.

Rozwiązanie: aby znaleźć punkt przecięcia prostej MN z płaszczyzną

bazę będziemy kontynuować AC i segment MN. Zaznaczmy punkt przecięcia tych prostych przez X. Punkt X należy do prostej MN i ściany AC, a AC leży w płaszczyźnie podstawy, co oznacza, że ​​punkt X leży również w płaszczyźnie podstawy . Dlatego punkt X jest punktem przecięcia prostej MN z płaszczyzną podstawy.

Rozważmy drugi problem. Skomplikujmy to trochę.

Zadanie 2.

Biorąc pod uwagę czworościan DABC punktów M i N, gdzie M € DA, N C (DBC). Znajdź punkt przecięcia prostej MN z płaszczyzną ABC .

Rozwiązanie: Punkt przecięcia prostej MN z płaszczyzną ABC musi leżeć na płaszczyźnie zawierającej prostą MN iw płaszczyźnie podstawy. Kontynuujemy odcinek DN do punktu przecięcia z krawędzią DC. Zaznaczamy punkt przecięcia przez E. Kontynuujemy prostą AE i MN do punktu ich przecięcia. Uwaga X. Punkt X należy do MN, więc leży na płaszczyźnie zawierającej prostą MN, a X należy do AE, a AE leży na płaszczyźnie ABC. Więc X również leży w płaszczyźnie ABC. Stąd X jest punktem przecięcia prostej MN i płaszczyzny ABC.

Skomplikujmy zadanie. Rozważ przekrój figur geometrycznych przez płaszczyzny przechodzące przez trzy podane punkty.

Zadanie 3

Na krawędziach AC, AD i DB czworościanu DABC zaznaczono punkty M, N i P. Skonstruuj przekrój czworościanu przez płaszczyznę MNP.

Rozwiązanie: skonstruuj linię prostą, wzdłuż której płaszczyzna MNP. Przecina płaszczyznę ABC. Punkt M jest wspólnym punktem tych płaszczyzn. Aby zbudować kolejny wspólny punkt, kontynuujemy odcinek AB i NP. Zaznaczamy punkt przecięcia przez X, który będzie drugim wspólnym punktem płaszczyzny MNP i ABC. Więc te płaszczyzny przecinają się wzdłuż linii prostej MX. MX przecina krawędź BC w pewnym punkcie E. Ponieważ E leży na MX, a MX jest linią należącą do płaszczyzny MNP, wynika z tego, że PE należy do MNP. Wymaganą sekcją jest czworoboczny MNPE.

Zadanie 4

Konstruujemy odcinek prostego graniastosłupa ABCA1B1C1 przez płaszczyznę przechodzącą przez punkty P , Q,R, gdzie R należy do ( AA 1C 1C), R należy W 1C1,

Q należy do AB

Decyzja: Wszystkie trzy punkty P,Q,R leżą w różnych ścianach, więc nie możemy jeszcze skonstruować linii przecięcia siecznej płaszczyzny z żadną ścianą pryzmatu. Znajdźmy punkt skrzyżowania PR z ABC. Znajdźmy rzuty punktów P i R na płaszczyznę bazową PP1 prostopadłą do BC i RR1 prostopadłą do AC. Linia P1R1 przecina prostą PR w punkcie X. X jest punktem przecięcia prostej PR z płaszczyzną ABC. Leży w żądanej płaszczyźnie K iw płaszczyźnie podstawy, podobnie jak punkt Q. XQ jest prostą przecinającą K z płaszczyzną podstawy. XQ przecina AC w ​​punkcie K. Dlatego KQ jest odcinkiem przecięcia płaszczyzny X ze ścianą ABC. K i R leżą w płaszczyźnie X iw płaszczyźnie ściany AA1C1C. Narysuj linię KR i zaznacz punkt przecięcia z A1Q E. KE jest linią przecięcia płaszczyzny X z tą ścianą. Znajdź linię przecięcia płaszczyzny X z płaszczyzną ścian BB1A1A. KE przecina A1A w punkcie Y. Linia QY jest linią przecięcia siecznej płaszczyzny z płaszczyzną AA1B1B. FPEKQ - pożądana sekcja.

Metoda przekrojów wielościanów w stereometrii znajduje zastosowanie w problemach konstrukcyjnych. Opiera się na umiejętności zbudowania odcinka wielościanu i określenia rodzaju przekroju.

Materiał ten charakteryzuje się następującymi cechami:

1. Metodę sekcji stosuje się tylko w przypadku wielościanów, ponieważ różne złożone (nachylone) typy sekcji ciał rewolucji nie są uwzględnione w programie nauczania szkoły średniej.
2. Zadania wykorzystują głównie najprostsze wielościany.
3. Zadania prezentowane są w większości bez danych liczbowych w celu stworzenia możliwości ich wielokrotnego wykorzystania.

Aby rozwiązać problem budowy odcinka wielościanu, uczeń musi wiedzieć:

• co to znaczy skonstruować odcinek wielościanu przez samolot;
• jak wielościan i płaszczyzna mogą być umieszczone względem siebie;
• jak samolot jest ustawiony;
• gdy problem budowy odcinka wielościanu przez samolot zostanie uznany za rozwiązany.

Ponieważ płaszczyzna jest zdefiniowana:

• trzy kropki;
• linia prosta i kropka;
• dwie równoległe linie;
• dwie przecinające się linie

budowa płaszczyzny przekroju odbywa się w zależności od przeznaczenia tej płaszczyzny. Dlatego wszystkie metody konstruowania odcinków wielościanów można podzielić na metody.

Istnieć trzy główne metody konstruowanie przekrojów wielościanów:

1. metoda śledzenia.
2. Metoda przekrojów pomocniczych.
3. Metoda kombinowana.

Pierwsze dwie metody to odmiany metoda aksjomatyczna budowa przekrojów.

Możemy również wyróżnić następujące metody konstruowania przekrojów wielościanów:

• budowa odcinka wielościanu przez przelatujący samolot dany punkt równolegle do danej płaszczyzny;
• budowa odcinka przechodzącego przez daną linię równolegle do innej danej linii;
• budowa odcinka przechodzącego przez dany punkt równolegle do dwóch podanych ukośnych linii;
• budowa odcinka wielościanu przez płaszczyznę przechodzącą przez daną linię prostopadłą do danej płaszczyzny;
• konstrukcja odcinka wielościanu przez płaszczyznę przechodzącą przez dany punkt prostopadle do danej linii prostej.

Federalna lista podręczników do geometrii dla klas 10-11 obejmuje podręczniki autorów:

• Atanasyan L.S., Butuzova V.F., Kadomtseva S.B. i inne (Geometria, 10-11);
• Pogorelova A.V. (Geometria, 7-11);
• Aleksandrova A.D., Vernera A.L., Ryzhik V.I. (Geometria, 10-11);
• Smirnowa I.M. (Geometria, 10-11);
• Sharygina I.F. (Geometria, 10-11).

Rozważmy bardziej szczegółowo podręczniki L.S., Atanasyan i Pogorelov A.V.

W podręczniku L.S. Atanasyan na temat „Budowa odcinków wielościanów” przeznaczono dwie godziny. W klasie 10, w temacie „Równoległość linii i płaszczyzn”, po przestudiowaniu czworościanu i równoległościanu, przeznaczono godzinę na przedstawienie akapitu „Problemy z konstruowaniem przekrojów”. Rozważane są sekcje czworościanu i równoległościanu. A temat „Równoległość linii i płaszczyzn” kończy się rozwiązywaniem zadań przez jedną lub dwie godziny (w podręczniku jest osiem zadań do konstruowania sekcji).

W podręczniku Pogorelov A.V. na skonstruowanie sekcji w rozdziale „Wielościany” przeznaczono około trzech godzin: jedna - na przestudiowanie tematu „Obraz pryzmatu i konstruowanie jego przekrojów”, druga - na przestudiowanie tematu „Budowa piramidy i jej przekrojów płaskich” oraz po trzecie - do rozwiązywania problemów. Na liście zadań podanej po temacie znajduje się tylko około dziesięciu zadań na sekcję.

Oferujemy system lekcji na temat „Budowa odcinków wielościanów” do podręcznika Pogorelova A.V.

Proponuje się ułożenie materiału w takiej kolejności, w jakiej można go wykorzystać do nauczania uczniów. Z prezentacji tematu „Wielościany” proponuje się wykluczyć następujące akapity: „Budowa odcinków pryzmatu” i „Budowa odcinków piramidy” w celu usystematyzowania dany materiał na końcu tego tematu „Wielościany”. Można go sklasyfikować według tematu zadań z przybliżonym przestrzeganiem zasady „od prostych do złożonych” bardzo warunkowo w następujący sposób:

1. Definicja przekroju wielościanów.
2. Konstrukcja odcinków graniastosłupa, równoległościanu, ostrosłupa metodą śladową. (Z reguły w szkolnym toku stereometrii zadania służą do konstruowania przekrojów wielościanów, które rozwiązywane są głównymi metodami. Pozostałe metody, ze względu na ich większą wysoki poziom złożoności, nauczyciel może pozostawić do rozważenia na zajęciach fakultatywnych lub do samodzielnej nauki. W zadaniach budowlanych główne metody wymagają skonstruowania płaszczyzny przekroju przechodzącej przez trzy punkty).
3. Znalezienie obszaru przekrojów w wielościanach (bez korzystania z twierdzenia o obszarze rzutu ortogonalnego wielokąta).
4. Znajdowanie obszaru przekrojów w wielościanach (za pomocą twierdzenia o obszarze rzutu ortogonalnego wielokąta).

ZADANIA STEREOMETRYCZNE DOTYCZĄCE BUDOWY PRZEKROJÓW WIELOŚCIANÓW I SPOSÓB ICH WYKORZYSTANIA NA LEKCJACH W KLASACH 10-11.

(system lekcji i zajęć fakultatywnych na temat „Budowa przekrojów wielościanów”)

LEKCJA 1.

Temat lekcji: „Budowa przekrojów wielościanów”.

Cel lekcji: zapoznanie się z metodami konstruowania przekrojów wielościanów.

Etapy lekcji:

1. Aktualizacja podstawowej wiedzy.
2. Sformułowanie problemu.
3. Nauka nowego materiału:

A) Definicja sekcji.

B) Metody konstruowania przekrojów:

a) metodę śladów;

b) sposób odcinków pomocniczych;

c) metoda łączona.

1. Mocowanie materiału.

Przykłady konstruowania przekrojów metodą trace.

1. Podsumowując lekcję.

Podczas zajęć.

1. Aktualizacja podstawowej wiedzy.

Zapamiętajmy:
- przecięcie linii prostej z płaszczyzną;
- przecięcie płaszczyzn;
- właściwości płaszczyzn równoległych.

2. Sformułowanie problemu.

Pytania do klasy:
- Co to znaczy skonstruować odcinek wielościanu samolotem?
- Jak można ustawić wielościan i płaszczyznę względem siebie?
- Jak definiuje się samolot?
- Kiedy problem budowy odcinka wielościanu przez samolot uważa się za rozwiązany?

3. Nauka nowego materiału.

A) Zadanie polega więc na zbudowaniu skrzyżowania dwóch figur: wielościanu i płaszczyzny (ryc. 1). Mogą to być: pusta figura (a), punkt (b), odcinek (c), wielokąt (d). Jeśli przecięcie wielościanu i płaszczyzny jest wielokątem, to ten wielokąt nazywa się przekrój wielościanu przez samolot.

Rozważymy tylko przypadek, w którym samolot przecina wielościan wzdłuż swojego wnętrza. W tym przypadku przecięcie tej płaszczyzny z każdą ścianą wielościanu będzie pewnym odcinkiem. Tak więc problem uważa się za rozwiązany, jeśli zostaną znalezione wszystkie segmenty, wzdłuż których płaszczyzna przecina ściany wielościanu.

Zbadaj sekcje sześcianu (rys. 2) i odpowiedz na następujące pytania:

Jakie wielokąty uzyskuje się w przekroju sześcianu przez samolot? (Istotna jest liczba boków wielokąta);

[Sugerowane odpowiedzi: trójkąt, czworokąt, pięciokąt, sześciokąt.]

Czy płaski przekrój sześcianu może wytworzyć siedmiokąt? A ośmiokąt itd.? Czemu?

Przyjrzyjmy się pryzmatowi i jego możliwym przekrojom po płaszczyźnie (na modelu). Jakie wielokąty są otrzymywane?

Jaki może być wniosek? Jaka jest największa liczba boków wielokąta uzyskana przez przecięcie wielościanu płaszczyzną?

[ Największa liczba boki wieloboku uzyskane w przekroju wielościanu przez płaszczyznę są równe liczbie ścian wielościanu.]

b) metoda śledzenia polega na konstruowaniu śladów siecznej płaszczyzny na płaszczyźnie każdej ściany wielościanu. Budowa odcinka wielościanu metodą śladową zwykle rozpoczyna się od budowy tzw. śladu głównego siecznej płaszczyzny, czyli tzw. ślad płaszczyzny cięcia na płaszczyźnie podstawy wielościanu.

b) Metoda sekcji pomocniczej konstrukcja przekrojów wielościanów jest wystarczająco uniwersalna. W przypadkach, gdy pożądany ślad (lub ślady) płaszczyzny cięcia znajduje się poza rysunkiem, ta metoda ma nawet pewne zalety. Jednocześnie należy mieć na uwadze, że konstrukcje wykonywane tą metodą często okazują się „zatłoczone”. Niemniej jednak w niektórych przypadkach sposób prowadzenia odcinków pomocniczych okazuje się najbardziej racjonalny.

Metoda śladów i metoda przekrojów pomocniczych to odmiany metoda aksjomatyczna konstruowanie odcinków wielościanów za pomocą samolotu.

c) esencja metoda łączona konstrukcja przekrojów wielościanów polega na zastosowaniu twierdzeń o równoległości prostych i płaszczyzn w przestrzeni w połączeniu z metodą aksjomatyczną.

Spójrzmy teraz na przykład rozwiązywania problemów metoda śledzenia.

4. Mocowanie materiału.

Zadanie 1.

Skonstruuj przekrój graniastosłupa ABCDA 1 B 1 C 1 D 1 przez płaszczyznę przechodzącą przez punkty P, Q, R (punkty zaznaczono na rysunku (rys. 3)).

Decyzja.

Ryż. 3

1. Skonstruujmy ślad siecznej płaszczyzny na płaszczyźnie dolnej podstawy pryzmatu. Rozważ ścianę AA 1 B 1 B. Na tej ścianie leżą punkty przecięcia P i Q. Narysuj linię PQ.
2. Kontynuujemy linię PQ, która należy do odcinka, do przecięcia z linią AB. Znajdźmy punkt S 1 należący do śladu.
3. Podobnie punkt S 2 otrzymujemy przez przecięcie linii QR i BC.
4. Linia prosta S 1 S 2 jest śladem siecznej płaszczyzny na płaszczyźnie dolnej podstawy pryzmatu.
5. Prosta S 1 S 2 przecina bok AD w punkcie U, bok CD w punkcie T. Połączmy punkty P i U, ponieważ leżą w tej samej płaszczyźnie ściany AA 1 D 1 D. uzyskać TU i RT.
6. Wymaganą sekcją jest PQRTU.

Skonstruuj przekrój równoległościanu ABCDA 1 B 1 C 1 D 1 przez płaszczyznę przechodzącą przez punkty M, N, P (punkty są wskazane na rysunku (rys. 4)).

Decyzja.

1. Punkty N i P leżą w płaszczyźnie przekroju iw płaszczyźnie dolnej podstawy równoległościanu. Skonstruujmy linię przechodzącą przez te punkty. Linia ta jest śladem siecznej płaszczyzny na płaszczyźnie podstawy równoległościanu.
2. Kontynuujmy linię, na której leży bok AB równoległościanu. Linie AB i NP przecinają się w pewnym punkcie S. Ten punkt należy do płaszczyzny przekroju.
3. Ponieważ punkt M również należy do płaszczyzny przekroju i przecina prostą AA 1 w pewnym punkcie X.
4. Punkty X i N leżą w tej samej płaszczyźnie ściany AA 1 D 1 D, połącz je i uzyskaj linię XN.
5. Ponieważ płaszczyzny ścian równoległościanu są równoległe, możliwe jest poprowadzenie linii przez punkt M na powierzchni A 1 B 1 C 1 D 1 równolegle do linii NP. Ta linia przetnie bok B 1 C 1 w punkcie Y.
6. Podobnie rysujemy linię YZ, równoległą do linii XN. Łączymy Z z P i otrzymujemy pożądaną sekcję - MYZPNX.

Zadanie 3 (do samodzielnego rozwiązania).

Skonstruuj przekrój czworościanu DACB przez płaszczyznę przechodzącą przez punkty M, N, P (punkty te zaznaczono na rysunku (rys. 5)).

5. Podsumowanie lekcji.

Odpowiedz na pytanie: Czy zacieniowane figury są przekrojami przedstawionej wielościanu przy płaszczyźnie PQR? I wykonaj prawidłową konstrukcję (ryc. 6).

Opcja 1.

Opcja 2.

Temat lekcji: ZNAJDOWANIE OBSZARU PRZEKROJU.

Cel lekcji: zapoznanie się ze sposobami wyznaczania pola przekroju wielościanu.

Etapy lekcji:

1. Aktualizacja podstawowej wiedzy.

Przypomnij sobie twierdzenie o obszarze rzutu ortogonalnego wielokąta.

2. Rozwiązywanie problemów ze znalezieniem pola przekroju:

Bez użycia twierdzenia o prostokątnym rzutowaniu wielokąta;

Korzystanie z twierdzenia o prostokątnym rzucie wielokąta.

3. Podsumowanie lekcji.

Podczas zajęć.

1. Aktualizacja podstawowej wiedzy.

Zapamiętajmy twierdzenie o obszarze rzutu ortogonalnego wielokąta: obszar rzutu ortogonalnego wielokąta na płaszczyznę jest równy iloczynowi jego pola i cosinusowi kąta między płaszczyzną wielokąta a płaszczyzną rzutu.

2. Rozwiązywanie problemów.

ABCD jest poprawne trójkątna piramida ze stroną bazową AB równą a i wysokość DH równa h. Skonstruuj przekrój piramidy przez płaszczyznę przechodzącą przez punkty D, C i M, gdzie M jest środkiem boku AB i znajdź jego powierzchnię (rys. 7).

Przekrój piramidy to trójkąt MCD. Znajdźmy jego obszar.

S = 1/2 DH CM = 1/2 =

Znajdź pole przekroju sześcianu ABCDA 1 B 1 C 1 D 1 z krawędzią a płaszczyzna przechodząca przez wierzchołek D oraz punkty E i F odpowiednio na krawędziach A 1 D 1 i C 1 D 1, jeżeli A 1 E = k D 1 E i C 1 F = k D 1 F.

Budowa sekcji:

1. Ponieważ punkty E i F należą do płaszczyzny przekroju i płaszczyzny ściany A 1 B 1 C 1 D 1, a obie płaszczyzny przecinają się w linii prostej, linia EF będzie śladem siecznej płaszczyzny do płaszczyzna lica A 1 B 1 C 1 D 1 (rys. 8 ).
2. Podobnie otrzymuje się linie proste ED i FD.
3. Wymaganą sekcją jest EDF.

Zadanie 3 (do samodzielnego rozwiązania).

Skonstruuj przekrój sześcianu ABCDA 1 B 1 C 1 D 1 o boku a płaszczyzna przechodząca przez punkty B, M i N, gdzie b jest środkiem krawędzi AA 1, a N jest środkiem krawędzi CC 1.

Sekcja jest tworzona metodą śledzenia.

Obszar przekroju znajduje się za pomocą twierdzenia o obszarze rzutu ortogonalnego wielokąta. Odpowiedź: S = 1/2 2.

KONSTRUKCJA PRZEKROJÓW I PRZEKROJÓW NA RYSUNKACH

Rysunek części powstaje przez kolejne dodawanie niezbędnych rzutów, nacięć i przekrojów. Początkowo widok niestandardowy jest tworzony z modelem określonym przez użytkownika, a orientacja modelu jest ustawiona tak, aby najlepiej pasowała do widoku głównego. Ponadto dla tego i kolejnych typów tworzone są niezbędne cięcia i sekcje.

Widok główny (widok z przodu) dobierany jest w taki sposób, aby dawał jak najpełniejszy obraz kształtów i wymiarów części.

Przekroje na rysunkach

W zależności od położenia płaszczyzny cięcia istnieją następujące typy nacięcia:

A) pozioma, jeżeli płaszczyzna cięcia jest równoległa do płaszczyzny rzutu poziomego;

B) pionowa, jeżeli płaszczyzna cięcia jest prostopadła do płaszczyzny rzutu poziomego;

C) nachylona - płaszczyzna cięcia jest nachylona do płaszczyzn rzutowania.

Sekcje pionowe dzielą się na:

· czołowa - płaszczyzna cięcia jest równoległa do płaszczyzny rzutu czołowego;

· profil — płaszczyzna cięcia jest równoległa do płaszczyzny rzutowania profilu.
W zależności od liczby płaszczyzn tnących cięcia są:

· prosty - z jedną płaszczyzną cięcia (ryc. 107);

· złożony - z dwiema lub więcej płaszczyznami cięcia (ryc. 108)
Norma przewiduje następujące rodzaje cięć złożonych:

· schodkowy, gdy sieczne płaszczyzny są równoległe (ryc. 108 a) i linie przerywane - sieczne płaszczyzny przecinają się (ryc. 108 b)

Rys.107 Proste cięcie

a) b)

Rys.108 Cięcia złożone

Oznaczenie nacięć

W przypadku, gdy w przekroju prostym sieczna płaszczyzna pokrywa się z płaszczyzną symetrii obiektu, przekrój nie jest wskazany (ryc. 107). We wszystkich innych przypadkach sekcje są oznaczone wielkimi literami alfabetu rosyjskiego, zaczynając od litery A, na przykład A-A.

Położenie płaszczyzny cięcia na rysunku wskazuje linia przekroju - pogrubiona linia otwarta. Przy złożonym cięciu pociągnięcia są również wykonywane na przegięciach linii przekroju. Strzałki wskazujące kierunek patrzenia powinny być umieszczone na początkowych i końcowych uderzeniach, strzałki powinny znajdować się w odległości 2-3 mm od zewnętrznych końców uderzeń. Na zewnątrz każdej strzałki wskazującej kierunek patrzenia zastosowano tę samą wielką literę.

Ten sam przycisk służy do oznaczania nacięć i przekrojów w systemie KOMPAS Linia przekroju znajdująca się na stronie Legenda (rys.109).

Rys.109 Przycisk linii przekroju

Łączenie połowy widoku z połówkową sekcją

Jeśli widok i przekrój są figurami symetrycznymi (ryc. 110), wówczas można połączyć połowę widoku i połowę przekroju, oddzielając je cienką linią przerywaną, która jest osią symetrii. Część przekroju jest zwykle umieszczana na prawo od osi symetrii oddzielającej część widoku od części przekroju lub poniżej osi symetrii. Ukryte linie warstwic na połączonych częściach widoku i przekroju zwykle nie są pokazywane. Jeżeli linia osiowa oddzielająca widok i przekrój pokrywa się z rzutem dowolnej linii, na przykład krawędzią figury fasetowej, to widok i przekrój są oddzielone ciągłą linią falistą narysowaną na lewo od osi symetrii , jeśli krawędź leży wewnętrzna powierzchnia lub w prawo, jeśli krawędź jest zewnętrzna.

Ryż. 110 Łączenie części widoku i przekroju

Cięcia budowlane

Przestudiujemy budowę przekrojów w systemie KOMPAS na przykładzie budowy rysunku pryzmatu, którego zadanie pokazano na ryc. 111.

Sekwencja rysowania jest następująca:

1. Na podstawie podanych wymiarów zbudujemy model bryłowy pryzmatu (rys. 109 b). Zapiszmy model w pamięci komputera w pliku o nazwie „Pryzmat”.

Rys.112 Panel linii

3. Aby zbudować sekcję profilu (ryc. 113) Narysuj linię sekcja A-A w głównym widoku za pomocą przycisku Linia cięcia.

Rys.113 Budowa przekroju profilu

Kierunek patrzenia i tekst oznaczenia można wybrać na panelu sterowania poleceniem u dołu ekranu (Rys. 114). Budowa linii przekroju jest zakończona poprzez naciśnięcie przycisku Utwórz obiekt.

Rys.114 Panel sterowania polecenia do konstruowania cięć i przekrojów

4. W panelu Widoki skojarzone (Rys. 115) wybierz przycisk Linia cięcia, a następnie określ linię cięcia z pułapką, która pojawi się na ekranie. Jeśli wszystko zostało wykonane poprawnie (linia cięcia musi być narysowana w aktywnym widoku), to linia cięcia zmieni kolor na czerwony. Po określeniu linii cięcia A-A na ekranie pojawi się fantom obrazu w postaci ogólnego prostokąta.

Rys.115 Panel widoków skojarzonych

Za pomocą przełącznika Cięcie/przekrój na pasku właściwości wybierany jest typ obrazu – Cięcie (Rys. 116) oraz skala wyświetlanego cięcia.

Rys.116 Panel sterowania polecenia do konstruowania cięć i przekrojów

Przekrój profilu zostanie zbudowany automatycznie w połączeniu rzutu i ze standardowym zapisem. W razie potrzeby połączenie projekcji można wyłączyć przełącznikiem Połączenie projekcyjne (Rys. 116). Aby ustawić parametry kreskowania, które będą używane w tworzonej sekcji (sekcji), użyj elementów sterujących na karcie Kreskowanie.

Rys.117 Budowanie poziomego sekcja B-B i sekcje B-B

Jeżeli wybrana płaszczyzna cięcia podczas konstruowania przekroju pokrywa się z płaszczyzną symetrii części, to zgodnie z normą taka sekcja nie jest wskazana. Ale jeśli po prostu usuniesz oznaczenie sekcji, to ze względu na to, że widok i sekcja w pamięci komputera są ze sobą połączone, cała sekcja zostanie usunięta. Dlatego, aby usunąć oznaczenie, musisz najpierw zniszczyć połączenie między widokiem a przekrojem. Aby to zrobić, klikając lewym przyciskiem myszy, zaznacza się sekcję, a następnie klikając prawym przyciskiem myszy, wywoływane jest menu kontekstowe, z którego wybierany jest element widoku Destroy (ryc. 97). Symbol przekroju można teraz usunąć.

5. Aby skonstruować przekrój poziomy, narysujmy linię przekroju B-B przez dolną płaszczyznę otworu w widoku z przodu. Widok z przodu musi najpierw zostać zaktualizowany dwoma kliknięciami lewego przycisku myszy. Następnie budowany jest odcinek poziomy (ryc. 117).

6. Podczas konstruowania sekcji czołowej część widoku i część przekroju są kompatybilne, ponieważ są to figury symetryczne. Zewnętrzna krawędź pryzmatu rzutowana jest na linię oddzielającą widok i cięcie, więc delimitujemy widok i przekrój ciągłej cienkiej falistej linii narysowanej na prawo od osi symetrii, ponieważ zewnętrzne żebro. Przycisk służy do rysowania falistej linii. Krzywa Beziera znajdująca się na panelu Geometria narysowana stylem Linia obcinania (Rys. 118). Kolejno określ punkty, przez które powinna przechodzić krzywa Beziera. Aby zakończyć wykonywanie polecenia, kliknij przycisk Utwórz obiekt.

Rys.118 Wybór stylu linii dla przerwy

Sekcje

Przekrój jest obrazem przedmiotu, który uzyskuje się poprzez mentalne rozcięcie przedmiotu za pomocą płaszczyzny. Sekcja pokazuje tylko to, co znajduje się w płaszczyźnie cięcia.

Położenie płaszczyzny cięcia, za pomocą której tworzony jest przekrój, jest oznaczone na rysunku linią przekroju, podobnie jak w przypadku przekrojów.

Przekroje, w zależności od ich położenia na rysunkach, dzielą się na rozszerzone i nałożone. Usunięte sekcje najczęściej znajdują się na wolnym polu rysunku i są obrysowane linią główną. Nałożone sekcje są umieszczane bezpośrednio na obrazie obiektu i obrysowywane cienkimi liniami (ryc. 119).

Rys.119 Budowa sekcji

Rozważ sekwencję konstruowania rysunku pryzmatu z rozszerzonym ukośnym sekcja B-B(ryc. 117).

1. Uaktywnij widok z przodu, klikając dwukrotnie lewym przyciskiem myszy na widoku i narysuj linię przekroju za pomocą przycisku przecinanie liny . Zaznaczmy tekst napisu В-В.

2. Za pomocą przycisku Linia cięcia znajdującego się na panelu Widoki skojarzone (Rys. 115), który pojawia się jako pułapka, wskaż sieczną linię samoloty B-B. Za pomocą przełącznika Cięcie/przekrój na pasku właściwości wybierz typ obrazu - Przekrój (Rys. 116), skala wyświetlanego przekroju jest wybierana z okna Skala.

Konstruowany przekrój znajduje się w relacji rzutowania, co ogranicza jego ruch na rysunku, ale relację rzutowania można wyłączyć za pomocą przycisku połączenie projekcji.

Na gotowym rysunku narysuj linie środkowe, jeśli to konieczne, zapisz wymiary.

Cała historia geometrii i niektórych innych działów matematyki jest ściśle związana z rozwojem teorii konstrukcji geometrycznych. Najważniejsze aksjomaty geometrii, sformułowane przez Euklidesa około 300 rpne, wyraźnie pokazują rolę konstrukcji geometrycznych w tworzeniu geometrii.

W szkolnej geometrii są specjalne tematy, na które nie możesz się doczekać, przewidując spotkanie z niesamowicie piękny materiał. Do takich tematów należą „Wielościany i budowa ich odcinków.” Tutaj nie tylko otwierają się cudowny świat bryły geometryczne o wyjątkowych właściwościach, ale też ciekawe hipotezy naukowe. A potem lekcja geometrii staje się rodzajem studiowania nieoczekiwanych aspektów zwykłego przedmiotu szkolnego.

Na tegorocznych lekcjach geometrii omówiliśmy temat „Budowa przekrojów wielościanów”. W ramach programu przestudiowaliśmy jedną metodę konstruowania przekrojów, ale zainteresowałem się, jakie metody jeszcze istnieją.

Cel mojej pracy: Poznaj wszystkie metody konstruowania przekrojów wielościanów.

Żadne z ciał geometrycznych nie posiada takiej doskonałości i piękna jak wielościany. „Jest wyzywająco mało wielościanów”, napisał kiedyś L. Carroll, „ale ten oddział, który jest bardzo skromny, zdołał dotrzeć do głębi różnych nauk”.

Obecnie teoria konstrukcji geometrycznych to rozległy i głęboko rozwinięty obszar matematyki związany z rozwiązywaniem różnych fundamentalnych pytań, które trafiają do innych działów matematyki.

1. Historia geometrii wykreślnej

Już w starożytności człowiek rysował i malował obrazy przedmiotów, drzew, zwierząt i ludzi na skałach, kamieniach, ścianach i przedmiotach gospodarstwa domowego. Robił to dla zaspokojenia swoich potrzeb, także estetycznych. Jednocześnie głównym wymogiem dla takich obrazów było to, aby obraz wywoływał poprawną wizualną reprezentację kształtu przedstawianego obiektu.

Wraz ze wzrostem praktycznych i aplikacje techniczne obrazy (w budowie budynków i innych budowli cywilnych i wojskowych itp.) Zaczęli stawiać takie wymagania, aby obraz mógł być wykorzystany do oceny właściwości geometrycznych, rozmiarów i względnych pozycji poszczególne elementy pewien temat. Takie wymagania może ocenić wiele starożytnych zabytków, które przetrwały do ​​dziś. Jednak ścisłe, geometryczne, ugruntowane zasady i metody przedstawiania postaci przestrzennych (z uwzględnieniem perspektywy) zaczęły być systematycznie rozwijane przez artystów, architektów i rzeźbiarzy dopiero w okresie renesansu: Leonardo da Vinci, Dürer, Rafael, Michał Anioł, Tycjan itp.

Geometria opisowa jako nauka powstała w koniec XVIII wieku przez wielkiego francuskiego geometra i inżyniera Gasparda Monge (1746 - 1818). W 1637 r. francuski geometr i filozof Rene Descartes (1596 - 1650) stworzył metodę współrzędnych i położył podwaliny pod geometrię analityczną, a jego rodak, inżynier i matematyk Girard Desag (1593 - 1662) wykorzystał tę metodę współrzędnych do zbudowania rzutów perspektywicznych i uzasadnił teorię rzutów aksonometrycznych.

W XVII wieku w Rosji z powodzeniem opracowano rysunki techniczne, wykonane w formie planów i profili w skali. Tutaj przede wszystkim powinniśmy wymienić rysunki wybitnego rosyjskiego mechanika i wynalazcy I.P. Kulibin (1735 - 1818). W jego projekcie drewnianego mostu łukowego po raz pierwszy zastosowano rzuty ortogonalne (1773). (Rzut prostopadły płaszczyzny na leżącą w niej prostą lub przestrzeni na płaszczyznę to: szczególny przypadek rzut równoległy, w którym kierunek rzutowania jest prostopadły do ​​rzutowanej linii lub płaszczyzny).

Wielki wkład w rozwój rzutów ortogonalnych wniósł francuski inżynier A. Frezier (1682–1773), który jako pierwszy rozważył rzut obiektu na dwie płaszczyzny – poziomą i czołową.

Największą zasługą G. Monge było uogólnienie wszystkich prac naukowych jego poprzedników, całej teorii metod przedstawiania figur przestrzennych i stworzenie zunifikowanej nauki matematycznej o rzucie ortogonalnym - geometrii wykreślnej.

Narodziny tego nowa nauka prawie zbiegł się z założeniem w Petersburgu pierwszego wyższego transportu Rosji instytucja edukacyjna- Instytut Korpusu Inżynierów Kolejnictwa (2 grudnia 1809)

Absolwenci tego instytutu, jego profesorowie i naukowcy wnieśli znaczący wkład w rozwój geometrycznych metod reprezentacji, w teorię i praktykę geometrii wykreślnej.

1. Definicje wielościanów

W stereometrii badane są figury w przestrzeni, zwane ciała . Wizualnie należy wyobrazić sobie (geometryczne) ciało jako część przestrzeni zajmowanej przez ciało fizyczne i ograniczona powierzchnia.

Wielościan - jest to ciało, którego powierzchnia składa się z kilku płaskich wielokątów. Wielościan nazywa się wypukły , jeśli znajduje się po jednej stronie płaszczyzny każdego wielokąta płaskiego na jego powierzchni. Wspólna część takiej płaszczyzny i powierzchnia wielościanu wypukłego nazywa się krawędź . Ściany wielościanu wypukłego są płaskimi wielokątami wypukłymi. Boki twarzy nazywane sąkrawędzie wielościanu, a wierzchołki wierzchołki wielościanu.

Przekrój wielościan nazywany jest samolotem figura geometryczna, czyli zbiór wszystkich punktów w przestrzeni, które jednocześnie należą do danego wielościanu i płaszczyzny; samolot nazywa się sieczną płaszczyzną.

Powierzchnia wielościanu składa się z krawędzi, segmentów i ścian płaskich wielokątów. Ponieważ linia i płaszczyzna przecinają się w punkcie, a dwie płaszczyzny przecinają się wzdłuż linii prostej, przekrój wielościanu przez płaszczyznę jestpłaski wielokąt; wierzchołki tego wielokąta to punkty przecięcia płaszczyzny tnącej z krawędziami wielościanu, a boki to odcinki, wzdłuż których płaszczyzna tnąca przecina swoje powierzchnie. Oznacza to, że aby skonstruować żądany odcinek danego wielościanu przez płaszczyznę α, wystarczy skonstruować punkty jego przecięcia z krawędziami wielościanu. Następnie kolejno połącz te punkty z segmentami, podkreślając ciągłymi liniami widoczne i przerywane niewidoczne boki powstałego wielokąta przekroju.

III. Metody konstruowania przekrojów wielościanów

Metoda przekrojów wielościanów w stereometrii znajduje zastosowanie w problemach konstrukcyjnych. Opiera się na umiejętności zbudowania odcinka wielościanu i określenia rodzaju przekroju.

Materiał ten charakteryzuje się następującymi cechami:

• Metodę sekcji stosuje się tylko w przypadku wielościanów, ponieważ różne złożone (nachylone) typy sekcji ciał rewolucji nie są uwzględnione w programie nauczania szkoły średniej.
• Zadania wykorzystują głównie najprostsze wielościany.
• Zadania prezentowane są w większości bez danych liczbowych w celu stworzenia możliwości ich wielokrotnego wykorzystania.

Aby rozwiązać problem budowy odcinka wielościanu, uczeń musi wiedzieć:

• Co to znaczy skonstruować odcinek wielościanu przez samolot;
• Jak wielościan i płaszczyzna mogą być umieszczone względem siebie;
• Jak ustawiony jest samolot;
• Kiedy problem budowy odcinka wielościanu przez samolot zostanie uznany za rozwiązany.

Ponieważ płaszczyzna jest zdefiniowana:

• trzy punkty;
• Prosta i kropkowana;
• dwie równoległe linie;
• dwie przecinające się linie,

Budowa płaszczyzny przekroju odbywa się w zależności od przeznaczenia tej płaszczyzny. Dlatego wszystkie metody konstruowania odcinków wielościanów można podzielić na metody.

3.1 Konstrukcja przekrojów wielościanów w oparciu o układ aksjomatów stereometrii

Zadanie 1 . Skonstruuj przekrój ostrosłupa RABC wzdłuż płaszczyzny α = (MKH), gdzie M, K i H są odpowiednio wewnętrznymi punktami żeber PC, RV i AB (ryc. 1, a).

Decyzja .

pierwszy krok . Punkty M i K leżą w każdej z dwóch płaszczyzn α i PBC. Zatem, zgodnie z aksjomatem przecięcia dwóch płaszczyzn, płaszczyzna α przecina płaszczyznę RVS wzdłuż prostej MK. W konsekwencji segment MK jest jednym z boków pożądanej sekcji (ryc. 1, b).

Drugi krok . Podobnie segment KN jest drugą stroną pożądanej sekcji (ryc. 1, c).

3 krok . Punkty M i H nie leżą jednocześnie na żadnej ze ścian ostrosłupa RABC, dlatego odcinek MH nie jest bokiem przekroju tego ostrosłupa. Linie proste KH i RA leżą w płaszczyźnie ściany ABP i przecinają się. Skonstruujmy punkt T= KN ∩AR (rys. 1d).

Ponieważ prosta KN leży w płaszczyźnie α, punkt T również leży na płaszczyźnie α. Teraz widzimy, że płaszczyzny α i APC mają wspólne punkty M i T. Dlatego zgodnie z aksjomatem przecięcia dwóch płaszczyzn płaszczyzna α i APC przecinają się wzdłuż prostej MT, która z kolei przecina krawędź AC w ​​punkcie R (ryc. 1, e).

4 krok . Teraz, tak jak w kroku 1, ustalamy, że płaszczyzna α przecina ściany ACP i ABC odpowiednio wzdłuż segmentów MR i HR. Dlatego pożądaną sekcją jest czworoboczny MKHR (ryc. 1, f).

Ryż. 2

Zadanie 2. Skonstruuj przekrój ostrosłupa MABCD przez płaszczyznę α = (PRC), gdzie K, H i P są odpowiednio wewnętrznymi punktami krawędzi MA, MB i MD (rys. 2, a).

Decyzja. Pierwsze dwa kroki są takie same jak kroki 1 i 2 poprzedniego problemu. W rezultacie otrzymujemy boki KR i KH (ryc. 2, b) pożądanej sekcji. Zbudujmy pozostałe wierzchołki i boki wielokąta - przekroje.

3 krok . Kontynuujmy odcinek KR, aż przetnie się z prostą AD w punkcie F (ryc. 2, c). Ponieważ prosta KP leży w siecznej płaszczyźnie α, punkt F= KP ∩ AD = KP ∩ (ABC) jest wspólny dla płaszczyzn α i ABC.

4 krok . Kontynuujmy odcinek KH, aż przetnie się z prostą AB w punkcie L (ryc. 2, d). Ponieważ prosta KN leży w siecznej płaszczyźnie α, to punkt L = KN ∩ AB = KN ∩ (ABC) jest wspólny dla płaszczyzn α i ABC.

Zatem , punkty F i L są wspólne dla płaszczyzn α i ABC. Oznacza to, że płaszczyzna α przecina płaszczyznę ABC podstawy ostrosłupa wzdłuż linii prostej FL.

5 krok . Narysujmy prostą FL. Linia ta przecina odpowiednio krawędzie BC i DC w punktach R i T (rys. 2e), które służą jako wierzchołki wymaganego przekroju. Oznacza to, że płaszczyzna α przecina lico podstawy ABCD wzdłuż odcinka RT - boku żądanego przekroju.

6 krok . Teraz rysujemy segmenty RH i PT (ryc. 2, f), wzdłuż których płaszczyzna α przecina ściany BMC i MCD tej piramidy. Otrzymujemy pięciokąt PKHRT - pożądaną część piramidy MABCD (ryc. 2, f).

Rozważmy bardziej złożony problem.

Zadanie 3 . Skonstruuj przekrój ostrosłupa pięciokątnego PABCDE przez płaszczyznę α = (KQR), gdzie K, Q są odpowiednio wewnętrznymi punktami krawędzi PA i PC, a punkt R leży wewnątrz ściany DPE (rys. 3, a) .

Decyzja . Proste (QK i AC leżą w tej samej płaszczyźnie ASR (zgodnie z aksjomatem prostej i płaszczyzny) i przecinają się w pewnym punkcie T1, (rys. 3b), natomiast T1 є α, ponieważ QК є α.

Linia prosta PR przecina DE w pewnym punkcie F (ryc. 3, c), który jest punktem przecięcia płaszczyzny AR i boku DE podstawy piramidy. Wtedy proste KR i AF leżą w tej samej płaszczyźnie AR i przecinają się w pewnym punkcie T2 (rys. 3, d), natomiast T2 є α jako punkt prostej KR є α (zgodnie z aksjomatem prostej i samolot).

Dostał: linia T1 T2 leży w siecznej płaszczyźnie α i w płaszczyźnie podstawy ostrosłupa (zgodnie z aksjomatem prostej i płaszczyzny), natomiast prosta przecina odpowiednio boki DE i AE podstawy ABCDE ostrosłupa , w punktach M i N (ryc. 3, e), które są punktami płaszczyzn przecięcia α z krawędziami DE i AE ostrosłupa i służą jako wierzchołki pożądanego przekroju.

Dalej , linia MR leży w płaszczyźnie czoła DPE i w płaszczyźnie siecznej α (zgodnie z aksjomatem prostej i płaszczyzny), jednocześnie przecinając krawędź PD w pewnym punkcie H - kolejny wierzchołek pożądanego przekroju (ryc. 3, f).

Dalej, skonstruujmy punkt Т3 - Т1Т2 ∩ AB (rys. 3, g), który podobnie jak punkt prostej Т1Т2 є α leży na płaszczyźnie a (zgodnie z aksjomatem prostej i płaszczyzny). Teraz płaszczyzna ściany RAB zawiera dwa punkty T3 i K siecznej płaszczyzny α, co oznacza, że ​​prosta T3K jest linią przecięcia tych płaszczyzn. Linia prosta Т3К przecina krawędź РВ w punkcie L (ryc. 3, h), która służy jako kolejny wierzchołek wymaganej sekcji.

Ryż. 3

Tak więc „łańcuch” sekwencji konstruowania pożądanej sekcji jest następujący:

jeden . Т1 = QK AC;

2. F = PR DE;

3. Т2 = KR AF;

4 . M = T1T2 ∩ DE;

5 . N = T1T2 ∩ AE;

6. H = MR 5 PD;

7. T3 = T1T2 ∩ AB;

osiem . L = T3K ∩ PB.

Sześciokąt MNKLQH - żądany przekrój.

Przekrój piramidy na ryc. 1 i przekrój kostki na ryc. 2 zbudowane są na podstawie tylko aksjomatów stereometrii.

Jednocześnie można zbudować odcinek wielościanu o równoległych ścianach (pryzmat, równoległościan, sześcian) wykorzystując właściwości płaszczyzn równoległych.

3.2 Metoda śladowa w konstruowaniu płaskich przekrojów wielościanów

Linia, wzdłuż której płaszczyzna cięcia α przecina płaszczyznę podstawy wielościanu, nazywana jest śladem płaszczyzny α w płaszczyźnie tej podstawy.

Z definicji śladu otrzymujemy: w każdym z jego punktów przecinają się proste, z których jedna leży w płaszczyźnie siecznej, druga w płaszczyźnie podstawy. To właśnie ta właściwość śladu jest wykorzystywana do budowy płaskich odcinków wielościanów metodą śladową. Ponadto w płaszczyźnie cięcia wygodnie jest stosować takie proste linie, które przecinają krawędzie wielościanu.

Najpierw definiujemy płaszczyznę cięcia przez jej ślad w płaszczyźnie podstawy graniastosłupa (piramidy) i punktu należącego do powierzchni graniastosłupa (piramidy).

Zadanie 1 . Skonstruuj przekrój graniastosłupa ABCBEA1B1C1D1E1 przez płaszczyznę α, którą daje ślad lw płaszczyźnie ABC podstawy pryzmatu i punktu M należącego do krawędzi DD1.

Decyzja. Analiza . Załóżmy, że pożądanym przekrojem jest pięciokąt MNPQR (rys. 4). Aby skonstruować ten pięciokąt płaski, wystarczy skonstruować jego wierzchołki N, P, Q, R (podany jest punkt M) - punkty przecięcia siecznej płaszczyzny α z krawędziami CC1, BB1, AA1, EE1 danego graniastosłupa , odpowiednio.

E1 D1

Aby skonstruować punkt N =α ∩ CC1, wystarczy skonstruować linię przecięcia siecznej płaszczyzny α z płaszczyzną ściany CDD1C1. W tym celu z kolei wystarczy skonstruować w płaszczyźnie tej ściany jeszcze jeden punkt należący do siecznej płaszczyzny α. Jak zbudować taki punkt?

Ponieważ prosta l leży w płaszczyźnie podstawy pryzmatu, może przecinać płaszczyznę ściany CDD1C1 tylko w punkcie należącym do prostej CD = (CDD1) ∩ (ABC), tj. punkt X = l ∩ CD = l ∩ (CDD1) należy do siecznej płaszczyzny α. Tak więc, aby skonstruować punkt N = α ∩ CC1, wystarczy skonstruować punkt X = l ∩ CD.

Podobnie, aby skonstruować punkty P= α ∩ BB1, Q = α ∩ AA1 i R = α ∩ EE1, wystarczy skonstruować punkty Y = l ∩ BC, Z = 1 ∩ AB i T = 1 ∩ AE, odpowiednio.

Budynek . Budujemy (ryc. 5):

1. X = l ∩ CD (ryc. 5b);

2. N = МХ ∩ СС1 (ryc. 5, c);

3. Y = l BC (ryc. 5d);

4. P = NY ∩ BB1 (ryc. 5e);

5. Z = 1 ∩ AB (ryc. 5, f);

6. Q= PZ ∩ AA1 (ryc. 5, g);

7. T= l ∩ AE (ryc. 5, h);

8. R= QT ∩ EE1 (rys. 5i).

Pożądaną sekcją jest pięciokąt MNPQR (ryc. 5, j).

Dowód. Ponieważ prosta l jest śladem siecznej płaszczyzny α, to punkty X = l CD, Y = l ∩ BC, Z = 1 ∩ AB i T= l ∩ AE należą do tej płaszczyzny.

Dlatego mamy:

М Є α, X Є α => МХ є α, wtedy МХ ∩ СС1 = N є α, stąd N = α ∩ СС1;

N Є α, Y Є α => NY Є α, następnie NY ∩ BB1= P Є α, stąd P = α ∩ BB1;

Р Є α, Z Є α => РZ Є α, to PZ ∩ AA1 = Q Є α, stąd Q = α ∩ AA1;

Q Є α, T Є α => QТ Є α, następnie QТ ∩ EE1 =R Є α, stąd R = α ∩ EE1.

Dlatego MNPQR jest wymaganą sekcją.

Nauka. Ślad l siecznej płaszczyzny α nie przecina podstawy pryzmatu, a punkt M siecznej płaszczyzny należy do krawędzi bocznej DD1 pryzmatu. Dlatego płaszczyzna cięcia α nie jest równoległa do krawędzi bocznych. Dlatego zawsze istnieją punkty N, P, Q i R przecięcia tej płaszczyzny z bocznymi krawędziami pryzmatu (lub przedłużeniami tych krawędzi). A ponieważ dodatkowo punkt M nie należy do śladu l, wyznaczona przez nie płaszczyzna α jest jednoznaczna. Oznacza to, że problem ma (zawsze) unikalne rozwiązanie.

3.3 Metoda projektowania wewnętrznego w konstruowaniu płaskich odcinków wielościanów

W niektórych podręcznikach metoda konstruowania przekrojów wielościanów, którą teraz rozważymy, nazywana jest metodą projektowania wewnętrznego lub metodą korespondencji lub metodą przekrojów ukośnych.

Zadanie 1 . Skonstruuj przekrój ostrosłupa PABCDE przez płaszczyznę α = (MFR), jeśli punkty M, F i R są odpowiednio wewnętrznymi punktami krawędzi PA, PC i PE. (rys. 6)

Decyzja . Płaszczyznę podstawy piramidy oznaczamy przez β. Aby skonstruować żądany przekrój, konstruujemy punkty przecięcia siecznej płaszczyzny α z krawędziami ostrosłupa.

Skonstruujmy punkt przecięcia siecznej płaszczyzny z krawędzią РD danej piramidy.

Płaszczyzny APD i CPE przecinają płaszczyznę β wzdłuż, odpowiednio, linii AD i CE, które przecinają się w pewnym punkcie K. Prosta PK = (APD) ∩ (CPE) przecina prostą FR є α w pewnym punkcie K1: K1 = PK ∩ FR, z tym K1 є α. Wtedy: M є α, K1 є α => prosta MK є a. Zatem punkt Q = MK1 ∩ PD jest punktem przecięcia krawędzi PD i siecznej płaszczyzny: Q = α ∩ PD. Punkt Q jest wierzchołkiem żądanej sekcji. Podobnie konstruujemy punkt przecięcia płaszczyzny α i krawędzi РВ. Płaszczyzny BPE i APD przecinają płaszczyznę β odpowiednio wzdłuż prostych BE i AD, które przecinają się w punkcie H. Prosta PH = (BPE) ∩ (APD) przecina prostą MQ w punkcie H1 Następnie prosta RN1 przecina się krawędź PB w punkcie N = α ∩ PB - wierzchołek przekroju.

Zatem , sekwencja kroków do konstruowania żądanej sekcji jest następująca:

jeden . K = AD ∩ WE; 2. K1 = RK ∩ RF;

3 . Q = MK1 ∩ PD; 4. H = BE AD;

5 . H1 = PH ∩ MQ; 6. N = RН1 ∩ РВ.

Wymaganą sekcją jest pięciokąt MNFQR.

3.4 Metoda łączona w konstruowaniu płaskich odcinków wielościanów

Istota połączonej metody konstruowania odcinków wielościanów jest następująca. Na niektórych etapach konstruowania przekroju stosuje się metodę śladów lub metodę projektowania wewnętrznego, a na innych etapach konstruowania tego samego przekroju stosuje się badane twierdzenia dotyczące równoległości, prostopadłości linii i płaszczyzn.

Aby zilustrować zastosowanie tej metody, rozważmy następujący problem.

Zadanie 1.

Skonstruuj przekrój równoległościanu ABCDА1В1С1D1 przez płaszczyznę α określoną przez punkty P, Q i R, jeśli punkt P leży na przekątnej A1C1, punkt Q na krawędzi BB1 i punkt R na krawędzi DD1. (rys. 7)

Decyzja

Rozwiążemy ten problem za pomocą metody śladu i twierdzeń o równoległości dla prostych i płaszczyzn.

Najpierw konstruujemy ślad siecznej płaszczyzny α = (PQR) na płaszczyźnie ABC W tym celu konstruujemy punkty T1 = PQ ∩ P1B (gdzie PP1 ║AA1,P1є AC) i T2 = RQ ∩ BD . Po zbudowaniu śladu T1T2 zauważamy, że punkt P leży na płaszczyźnie A1B1C1, która jest równoległa do płaszczyzny ABC. Oznacza to, że płaszczyzna α przecina płaszczyznę A1B1C1 wzdłuż linii prostej przechodzącej przez punkt P i równoległej do prostej T1T2. Narysuj tę linię i oznacz przez M i E punkty jej przecięcia odpowiednio z krawędziami A1B1 i A1D1 Otrzymujemy: M = α ∩ A1B1, E = α ∩ A1D1. Wtedy segmenty ER i QM są bokami wymaganej sekcji.

Ponadto, ponieważ płaszczyzna BCC1 jest równoległa do płaszczyzny ściany ADD1A1, to płaszczyzna α przecina ścianę BCC1B1 wzdłuż linii QF (F= α ∩ CC1) równoległej do linii ER. Dlatego wymaganym przekrojem jest pięciokąt ERFQM. (Punkt F można uzyskać, wykonując RF║ MQ)

Rozwiążmy ten problem za pomocą metody projektowania wewnętrznego i twierdzeń o równoległości prostych i płaszczyzn.(rys. 8)

Ryż. osiem

Niech H=AC ∩ BD. Rysując prostą HH1 równolegle do krawędzi BB1 (H1 є RQ), konstruujemy punkt F: F=РН1 ∩ CC1 Punkt F jest punktem przecięcia płaszczyzny α z krawędzią CC1, ponieważ РН1 є α . Następnie segmenty RF i QF, wzdłuż których płaszczyzna α przecina odpowiednio powierzchnie CC1D1D i BCC1B1 tego równoległościanu, są bokami jego wymaganego przekroju.

Ponieważ płaszczyzna ABB1 jest równoległa do płaszczyzny CDD1, przecięcie płaszczyzny α i powierzchni ABB1A1 stanowi odcinek QM (M Є A1B1), równoległy do ​​odcinka FR; segment QM - strona przekroju. Ponadto punkt E = MP ∩ A1D1 jest punktem przecięcia płaszczyzny α i krawędzi A1D1, ponieważ MP є α. Dlatego punkt E jest kolejnym wierzchołkiem pożądanej sekcji. Dlatego wymaganym przekrojem jest pięciokąt ERFQM. (Punkt E można skonstruować rysując prostą RE ║ FQ. Wtedy M = PE ∩ A1B1).

IV. Wniosek

Dzięki tej pracy podsumowałem i usystematyzowałem wiedzę zdobytą na tegorocznym kursie geometrii, zapoznałem się z zasadami kreatywna praca zdobył nową wiedzę i zastosował ją w praktyce.

Chciałabym częściej wykorzystywać zdobytą wiedzę w praktyce.

Niestety nie rozważyłem wszystkich metod konstruowania przekrojów wielościanów. Istnieje wiele innych specjalnych przypadków:

• budowa odcinka wielościanu przez płaszczyznę przechodzącą przez dany punkt równoległy do ​​danej płaszczyzny;
• budowa odcinka przechodzącego przez daną linię równolegle do innej danej linii;
• budowa odcinka przechodzącego przez dany punkt równolegle do dwóch podanych ukośnych linii;
• budowa odcinka wielościanu przez płaszczyznę przechodzącą przez daną linię prostopadłą do danej płaszczyzny;
• budowa odcinka wielościanu przez płaszczyznę przechodzącą przez dany punkt prostopadły do ​​danej linii itp.

W przyszłości planuję poszerzyć badania i uzupełnić swoją pracę o analizę powyższych konkretnych przypadków.

Uważam, że moja praca jest istotna, ponieważ może być wykorzystana przez uczniów gimnazjów i liceów do: samokształcenie do Jednolitego Egzaminu Państwowego z matematyki, za dogłębne przestudiowanie materiału o fakultatywnych i samokształcenie młodych nauczycieli. Absolwenci szkół średnich muszą nie tylko opanować materiał programy szkolne, ale też umieć kreatywnie go zastosować, znaleźć rozwiązanie każdego problemu.

V. Literatura

1. Potoskuev E.V., Zvavich L.I. Geometria. Klasa 10: Podręcznik dla instytucje edukacyjne z pogłębioną i specjalistyczną nauką matematyki. - M.: Drop, 2008.
2. Potoskuev E.V., Zvavich L.I. Geometria. Klasa 10: Zeszyt zadań dla placówek oświatowych z pogłębioną i profilową nauką matematyki. - M.: Drop, 2008.
3. Potoskuev E.V. Obraz figur przestrzennych na płaszczyźnie. Budowa przekrojów wielościanów. Instruktaż dla studentów Wydziału Fizyki i Matematyki Uniwersytetu Pedagogicznego. - Togliatti: TSU, 2004.
4. Czasopismo naukowo-praktyczne dla uczniów szkół ponadgimnazjalnych „Matematyka dla uczniów”, 2009, nr 2/nr 3,1-64.
5. Geometria w tablicach - Podręcznik dla uczniów szkół średnich - Nelin E.P.
6. Geometria, stopnie 7-11, Materiały odniesienia, Bezrukova G.K., Litvinenko V.N., 2008.
7. Matematyka, Poradnik, Dla uczniów szkół średnich i studentów, Ryvkin A.A., Ryvkin A.Z., 2003.
8. Algebra i geometria w tabelach i diagramach, Roganin A.N., Dergachev V.A., 2006.

Zadania do konstruowania odcinków sześcianu przez płaszczyznę są z reguły prostsze niż na przykład zadania dotyczące odcinków piramidy.

Możemy narysować linię przez dwa punkty, jeśli leżą na tej samej płaszczyźnie. Podczas konstruowania przekrojów sześcianu możliwa jest jeszcze jedna opcja konstruowania śladu płaszczyzny cięcia. Skoro trzecia płaszczyzna przecina dwie równoległe płaszczyzny wzdłuż równoległych linii prostych, to jeśli w jednej ze ścian została już zbudowana linia prosta, a na drugiej jest punkt, przez który przechodzi przekrój, to możemy poprowadzić linię prostą ten punkt równoległy do ​​danego.

Zastanów się konkretne przykłady jak skonstruować sekcje sześcianu przez samolot.

1) Skonstruuj przekrój sześcianu przez płaszczyznę przechodzącą przez punkty A, C i M.

Problemy tego typu są najprostszym ze wszystkich problemów konstruowania przekrojów sześcianu. Ponieważ punkty A i C leżą na tej samej płaszczyźnie (ABC), możemy narysować przez nie linię. Jego ślad to odcinek AC. Jest niewidoczny, więc AC przedstawiamy kreską. Podobnie łączymy punkty M i C, które leżą na tej samej płaszczyźnie (CDD1) oraz punkty A i M, które leżą na tej samej płaszczyźnie (ADD1). Trójkąt ACM to wymagana sekcja.

2) Skonstruuj przekrój sześcianu przez płaszczyznę przechodzącą przez punkty M, N, P.

Tutaj tylko punkty M i N leżą na tej samej płaszczyźnie (ADD1), więc rysujemy przez nie linię prostą i otrzymujemy ślad MN (niewidoczny). Ponieważ leżą przeciwległe ściany sześcianu płaszczyzny równoległe, wówczas płaszczyzna cięcia przecina równoległe płaszczyzny (ADD1) i (BCC1) wzdłuż równoległych linii. Zbudowaliśmy już jedną z równoległych linii - to jest MN.

Przez punkt P rysujemy linię równoległą do MN. Przecina krawędź BB1 w punkcie S. PS to ślad siecznej płaszczyzny w lico (BCC1).

Narysujemy linię prostą przez punkty M i S, które leżą na tej samej płaszczyźnie (ABB1). Mam ślad MS (widoczny).

Płaszczyzny (ABB1) i (CDD1) są równoległe. W płaszczyźnie (ABB1) jest już prosta MS, więc przez punkt N na płaszczyźnie (CDD1) rysujemy prostą równoległą do MS. Linia ta przecina krawędź D1C1 w punkcie L. Jej ślad to NL (niewidoczny). Punkty P i L leżą na tej samej płaszczyźnie (A1B1C1), więc rysujemy przez nie prostą.

Wymaganą sekcją jest pięciokąt MNLPS.

3) Skonstruuj przekrój sześcianu przez płaszczyznę przechodzącą przez punkty M, N, P.

Punkty M i N leżą na tej samej płaszczyźnie (BCC1), więc można przez nie poprowadzić linię prostą. Otrzymujemy ślad MN (widoczny). Płaszczyzna (BCC1) jest równoległa do płaszczyzny (ADD1), więc przez leżący w niej punkt P (ADD1) rysujemy linię równoległą do MN. Przecina krawędź AD w punkcie E. Otrzymaliśmy ślad PE (niewidoczny).

Nie ma już punktów leżących na tej samej płaszczyźnie ani linii i punktu na równoległych płaszczyznach. Dlatego jedna z istniejących już linii musi być kontynuowana w celu uzyskania dodatkowego punktu.

Jeśli będziemy kontynuować prostą MN, to ponieważ leży ona w płaszczyźnie (BCC1), musimy poszukać punktu przecięcia MN z jedną z prostych tej płaszczyzny. Istnieją już punkty przecięcia z CC1 i B1C1 - są to M i N. Pozostały linie BC i BB1. Kontynuujemy BC i MN do przecięcia w punkcie K. Punkt K leży na prostej BC, co oznacza, że ​​należy do płaszczyzny (ABC), więc możemy przez niego narysować prostą i punkt E leżący na tej płaszczyźnie . Przecina krawędź CD w punkcie H. EH jest jej śladem (niewidocznym). Ponieważ H i N leżą w tej samej płaszczyźnie (CDD1), można przez nie poprowadzić linię prostą. Otrzymujemy ślad HN (niewidoczny).

Płaszczyzny (ABC) i (A1B1C1) są równoległe. Jedna z nich zawiera prostą EH, druga zawiera punkt M. Możemy narysować prostą przez M równolegle do EH. Otrzymujemy ślad MF (widoczny). Narysujemy linię prostą przez punkty M i F.

Sześciokąt MNHEPF to wymagana sekcja.

Gdybyśmy kontynuowali prostą MN do przecięcia z inną prostą w płaszczyźnie (BCC1), z BB1, to otrzymalibyśmy punkt G należący do płaszczyzny (ABB1). Oznacza to, że poprzez G i P można narysować linię, której ślad to PF. Dalej rysujemy linie proste przez punkty leżące w równoległych płaszczyznach i otrzymujemy ten sam wynik.

Praca z linią prostą PE daje ten sam przekrój MNHEPF.

4) Skonstruuj przekrój sześcianu przez płaszczyznę przechodzącą przez punkt M, N, P.

Tutaj możemy narysować linię prostą przez punkty M i N leżące na tej samej płaszczyźnie (A1B1C1). Jej ślad to MN (widoczny). Nie ma już punktów leżących na tej samej lub równoległych płaszczyznach.

Kontynuujemy linię MN. Leży w płaszczyźnie (A1B1C1), więc może przecinać się tylko z jedną z linii na tej płaszczyźnie. Istnieją już punkty przecięcia z A1D1 i C1D1 - N i M. Dwie kolejne linie tej płaszczyzny to A1B1 i B1C1. Punktem przecięcia A1B1 i MN jest S. Ponieważ leży na prostej A1B1, należy do płaszczyzny (ABB1), co oznacza, że ​​można przez nią poprowadzić prostą i punkt P, który leży na tej samej płaszczyźnie. Linia PS przecina krawędź AA1 w punkcie E. PE jest jej śladem (widocznym). Poprzez punkty N i E, leżące w tej samej płaszczyźnie (ADD1), można narysować linię prostą, której ślad jest NE (niewidoczny). Na płaszczyźnie (ADD1) znajduje się prosta NE, aw płaszczyźnie równoległej do niej (BCC1) punkt P. Przez punkt P możemy narysować prostą PL równoległą do NE. Przecina krawędź CC1 w punkcie L. PL jest śladem tej prostej (widoczny). Punkty M i L leżą na tej samej płaszczyźnie (CDD1), co oznacza, że ​​można przez nie poprowadzić linię prostą. Jej ślad to ML (niewidoczny). Wymaganą sekcją jest pięciokąt MLPEN.

Można było kontynuować prostą NM w obu kierunkach i szukać jej punktów przecięcia nie tylko z prostą A1B1, ale także z prostą B1C1, która również leży w płaszczyźnie (A1B1C1). W tym przypadku od razu rysujemy dwie proste przez punkt P: jedną w płaszczyźnie (ABB1) przez punkty P i S, a drugą w płaszczyźnie (BCC1) przez punkty P i R. pozostaje połączyć punkty leżące na tej samej płaszczyźnie: M c L, E - z N.