Jak znaleźć całkowitą powierzchnię wzoru piramidy. Znajdź pole powierzchni regularnej trójkątnej piramidy

Przygotowując się do egzaminu z matematyki, studenci muszą usystematyzować swoją wiedzę z algebry i geometrii. Chciałbym połączyć wszystkie znane informacje, na przykład jak obliczyć powierzchnię piramidy. Co więcej, począwszy od podstawy i ścian bocznych po całą powierzchnię. Jeśli sytuacja jest jasna w przypadku ścian bocznych, ponieważ są to trójkąty, podstawa jest zawsze inna.

Co zrobić, gdy znajduje się obszar podstawy piramidy?

Może to być absolutnie dowolna figura: od dowolnego trójkąta do n-kąta. A ta podstawa, oprócz różnicy w liczbie kątów, może być liczbą zwykłą lub nieprawidłową. W zadaniach USE interesujących dzieci w wieku szkolnym u podstawy znajdują się tylko zadania z prawidłowymi liczbami. Dlatego porozmawiamy tylko o nich.

trójkąt prostokątny

To jest równoboczne. Taki, w którym wszystkie boki są równe i oznaczone literą „a”. W takim przypadku obszar podstawy piramidy oblicza się według wzoru:

S = (a 2 * √3) / 4.

Kwadrat

Wzór na obliczenie jego powierzchni jest najprostszy, tutaj „a” to znowu bok:

Arbitralny regularny n-gon

Bok wielokąta ma to samo oznaczenie. Jako liczbę rogów stosuje się łacińską literę n.

S = (n * a 2) / (4 * tg (180º/n)).

Jak postępować przy obliczaniu powierzchni bocznej i całkowitej?

Ponieważ podstawą jest poprawna figura, wtedy wszystkie ściany piramidy są równe. Co więcej, każdy z nich jest trójkątem równoramiennym, ponieważ krawędzie boczne są równe. Następnie w celu obliczenia obszar boczny piramidy, będziesz potrzebować wzoru składającego się z sumy identycznych jednomianów. Liczba terminów zależy od liczby boków podstawy.

Kwadrat Trójkąt równoramienny oblicza się według wzoru, w którym połowę iloczynu podstawy mnoży się przez wysokość. Ta wysokość w piramidzie nazywa się apotem. Jego oznaczenie to „A”. Ogólna formuła bo powierzchnia boczna wygląda tak:

S \u003d ½ P * A, gdzie P jest obwodem podstawy piramidy.

Zdarzają się sytuacje, w których boki podstawy nie są znane, ale podane są krawędzie boczne (c) i kąt płaski na jej wierzchołku (α). Następnie należy użyć takiego wzoru do obliczenia bocznej powierzchni piramidy:

S = n/2 * w 2 sin α .

Zadanie 1

Stan : schorzenie. Znaleźć Powierzchnia całkowita ostrosłup, jeśli jego podstawa ma bok 4 cm, a apotem ma wartość √3 cm.

Decyzja. Musisz zacząć od obliczenia obwodu bazy. Ponieważ jest to trójkąt regularny, to P \u003d 3 * 4 \u003d 12 cm Ponieważ apotem jest znany, możesz natychmiast obliczyć pole całej powierzchni bocznej: ½ * 12 * √3 = 6 3 cm2.

W przypadku trójkąta u podstawy uzyskana zostanie następująca wartość pola: (4 2 * √3) / 4 \u003d 4√3 cm 2.

Aby określić cały obszar, musisz dodać dwie wynikowe wartości: 6√3 + 4√3 = 10√3 cm2.

Odpowiedź. 10√3 cm2.

Zadanie nr 2

Stan : schorzenie. Istnieje regularna czworokątna piramida. Długość boku podstawy 7 mm, krawędź boczna 16 mm. Musisz znać jego powierzchnię.

Decyzja. Ponieważ wielościan jest czworokątny i regularny, jego podstawa jest kwadratem. Po poznaniu obszarów podstawy i ścian bocznych możliwe będzie obliczenie obszaru piramidy. Wzór na kwadrat podano powyżej. A na bocznych ścianach znane są wszystkie boki trójkąta. Dlatego możesz użyć wzoru Herona do obliczenia ich powierzchni.

Pierwsze obliczenia są proste i prowadzą do tej liczby: 49 mm 2. Dla drugiej wartości musisz obliczyć półobwód: (7 + 16 * 2): 2 = 19,5 mm. Teraz możesz obliczyć powierzchnię trójkąta równoramiennego: √ (19,5 * (19,5-7) * (19,5-16) 2) = √2985,9375 = 54,644 mm 2. Są tylko cztery takie trójkąty, więc obliczając ostateczną liczbę, musisz ją pomnożyć przez 4.

Okazuje się: 49 + 4 * 54,644 \u003d 267,576 mm 2.

Odpowiedź. Pożądana wartość to 267,576 mm 2.

Zadanie nr 3

Stan : schorzenie. W przypadku zwykłej piramidy czworokątnej musisz obliczyć powierzchnię. W nim bok kwadratu ma 6 cm, a wysokość 4 cm.

Decyzja. Najprostszym sposobem jest użycie wzoru z iloczynem obwodu i apotem. Pierwsza wartość jest łatwa do znalezienia. Drugi jest trochę trudniejszy.

Musimy pamiętać twierdzenie Pitagorasa i rozważyć, że jest ono utworzone przez wysokość piramidy i apotem, który jest przeciwprostokątną. Druga noga jest równa połowie boku kwadratu, ponieważ wysokość wielościanu przypada na jego środek.

Pożądany apotem (przeciwprostokątna trójkąta prostokątnego) to √(3 2 + 4 2) = 5 (cm).

Teraz możesz obliczyć żądaną wartość: ½ * (4 * 6) * 5 + 6 2 \u003d 96 (cm 2).

Odpowiedź. 96 cm2.

Zadanie #4

Stan : schorzenie. Dana prawa strona jego podstawy mają 22 mm, boczne żebra - 61 mm. Jaka jest powierzchnia bocznej powierzchni tego wielościanu?

Decyzja. Rozumowanie w nim jest takie samo, jak opisane w zadaniu nr 2. Tylko tam podano piramidę z kwadratem u podstawy, a teraz jest to sześciokąt.

Przede wszystkim obszar podstawy oblicza się przy użyciu powyższego wzoru: (6 * 22 2) / (4 * tg (180º / 6)) \u003d 726 / (tg30º) \u003d 726√3 cm 2.

Teraz musisz znaleźć półobwód trójkąta równoramiennego, który jest boczną ścianą. (22 + 61 * 2): 2 = 72 cm Pozostaje obliczyć powierzchnię każdego takiego trójkąta za pomocą wzoru Czapla, a następnie pomnożyć go przez sześć i dodać do tego, który okazał się dla baza.

Obliczenia z wykorzystaniem wzoru Czapla: √ (72 * (72-22) * (72-61) 2) \u003d √ 435600 \u003d 660 cm 2. Obliczenia, które dadzą powierzchnię boczną: 660 * 6 \u003d 3960 cm 2. Pozostaje je dodać, aby dowiedzieć się o całej powierzchni: 5217,47≈5217 cm 2.

Odpowiedź. Podstawa - 726√3 cm2, powierzchnia boczna - 3960 cm2, cała powierzchnia - 5217 cm2.

Piramida- jedna z odmian wielościanu utworzonego z wielokątów i trójkątów leżących u podstawy i będących jego ścianami.

Co więcej, na szczycie piramidy (tj. w jednym punkcie) wszystkie twarze są połączone.

Aby obliczyć powierzchnię piramidy, warto ustalić, że jej boczna powierzchnia składa się z kilku trójkątów. I możemy łatwo znaleźć ich obszary za pomocą

różne formuły. W zależności od tego, jakie dane trójkątów znamy, szukamy ich powierzchni.

Podajemy kilka formuł, za pomocą których można znaleźć obszar trójkątów:

1. S = (a*h)/2 . W ta sprawa znamy wysokość trójkąta h , który jest obniżony na bok a .
2. S = a*b*sinβ . Tutaj boki trójkąta a , b , a kąt między nimi wynosi β .
3. S = (r*(a + b + c))/2 . Tutaj boki trójkąta a, b, c . Promień okręgu wpisanego w trójkąt wynosi r .
4. S = (a*b*c)/4*R . Promień okręgu opisanego wokół trójkąta wynosi R .
5. S = (a*b)/2 = r² + 2*r*R . Ta formuła należy używać tylko wtedy, gdy trójkąt jest trójkątem prostokątnym.
6. S = (a²*√3)/4 . Stosujemy tę formułę do trójkąta równobocznego.

Dopiero po obliczeniu pól wszystkich trójkątów, które są ścianami naszej piramidy, możemy obliczyć pole powierzchni bocznej. Aby to zrobić, użyjemy powyższych formuł.

Aby obliczyć powierzchnię bocznej powierzchni piramidy, nie pojawiają się żadne trudności: musisz znaleźć sumę pól wszystkich trójkątów. Wyraźmy to wzorem:

Sp = Si

Tutaj Si to pole pierwszego trójkąta, a S P to powierzchnia bocznej powierzchni piramidy.

Spójrzmy na przykład. Biorąc pod uwagę regularną piramidę, jej boczne powierzchnie tworzą kilka równobocznych trójkątów,

« Geometria jest najpotężniejszym narzędziem doskonalenia naszych zdolności umysłowych.».

Galileo Galilei.

a kwadrat jest podstawą piramidy. Co więcej, krawędź piramidy ma długość 17 cm, znajdźmy obszar bocznej powierzchni tej piramidy.

Rozumujemy w ten sposób: wiemy, że ściany piramidy są trójkątami, są równoboczne. Wiemy też, jaka jest długość krawędzi tej piramidy. Wynika z tego, że wszystkie trójkąty mają równe boki, ich długość wynosi 17 cm.

Aby obliczyć powierzchnię każdego z tych trójkątów, możesz użyć następującego wzoru:

S = (17²*√3)/4 = (289*1.732)/4 = 125,137 cm²

Ponieważ wiemy, że kwadrat leży u podstawy piramidy, okazuje się, że mamy cztery trójkąty równoboczne. Oznacza to, że pole powierzchni bocznej piramidy można łatwo obliczyć za pomocą następującego wzoru: 125,137 cm² * 4 = 500,548 cm²

Nasza odpowiedź jest następująca: 500,548 cm² - to powierzchnia bocznej powierzchni tej piramidy.

Powierzchnia piramidy. W tym artykule rozważymy z Tobą problemy ze zwykłymi piramidami. Przypomnę, że zwykła piramida to piramida, której podstawą jest wielokąt foremny, wierzchołek piramidy jest rzutowany na środek tego wielokąta.

Boczna ściana takiej piramidy to trójkąt równoramienny.Wysokość tego trójkąta, narysowanego od wierzchołka regularnej piramidy, nazywa się apotemem, SF jest apotemem:

W przedstawionych poniżej rodzajach problemów wymagane jest znalezienie pola powierzchni całej piramidy lub pola jej powierzchni bocznej. Na blogu pojawiło się już kilka problemów ze zwykłymi piramidami, gdzie pojawiło się pytanie o znalezienie elementów (wysokość, krawędź podstawy, krawędź boczna), .

W UŻYWAJ zadań, z reguły brane są pod uwagę regularne piramidy trójkątne, czworokątne i sześciokątne. Nie widziałem problemów z regularnymi piramidami pięciokątnymi i siedmiokątnymi.

Wzór na powierzchnię całej powierzchni jest prosty - musisz znaleźć sumę powierzchni podstawy piramidy i powierzchni jej bocznej powierzchni:

Rozważ zadania:

Boki podstawy regularnej czworokątnej piramidy to 72, boczne krawędzie to 164. Znajdź pole powierzchni tej piramidy.

Powierzchnia piramidy jest równa sumie powierzchni powierzchni bocznej i podstawy:

*Powierzchnia boczna składa się z czterech trójkątów o równej powierzchni. Podstawą piramidy jest kwadrat.

Powierzchnię boku piramidy można obliczyć za pomocą:

Zatem powierzchnia piramidy to:

Odpowiedź: 28224

Boki podstawy regularnej sześciokątnej piramidy mają 22, boczne krawędzie 61. Znajdź obszar bocznej powierzchni tej piramidy.

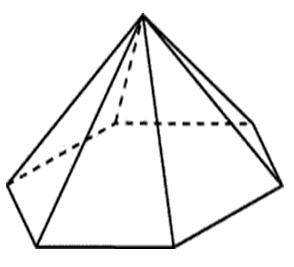
Podstawą foremnej sześciokątnej piramidy jest foremny sześciokąt.

Boczna powierzchnia tej piramidy składa się z sześciu obszarów równych trójkątów o bokach 61,61 i 22:

Znajdź obszar trójkąta za pomocą wzoru Herona:

Zatem powierzchnia boczna to:

Odpowiedź: 3240

*W przedstawionych powyżej problemach obszar powierzchni bocznej można znaleźć za pomocą innego wzoru na trójkąt, ale w tym celu należy obliczyć apotem.

27155. Znajdź pole powierzchni regularnej czworokątnej piramidy o boku podstawy 6 i wysokości 4.

Aby znaleźć pole powierzchni piramidy, musimy znać pole podstawy i pole powierzchni bocznej:

Powierzchnia podstawy wynosi 36, ponieważ jest to kwadrat o boku 6.

Powierzchnia boczna składa się z czterech ścian, które są trójkąty równe. Aby znaleźć obszar takiego trójkąta, musisz znać jego podstawę i wysokość (apotema):

* Powierzchnia trójkąta jest równa połowie iloczynu podstawy i wysokości narysowanej do tej podstawy.

Baza jest znana, jest równa sześciu. Znajdźmy wysokość. Rozważać trójkąt prostokątny(podświetlony na żółto):

Jedna noga jest równa 4, ponieważ jest to wysokość piramidy, druga jest równa 3, ponieważ jest równa połowie krawędzi podstawy. Przeciwprostokątną możemy znaleźć za pomocą twierdzenia Pitagorasa:

Tak więc powierzchnia bocznej powierzchni piramidy to:

Zatem powierzchnia całej piramidy to:

Odpowiedź: 96

27069. Boki podstawy regularnej czworokątnej piramidy to 10, boczne krawędzie to 13. Znajdź pole powierzchni tej piramidy.

27070. Boki podstawy regularnej sześciokątnej piramidy to 10, boczne krawędzie to 13. Znajdź pole powierzchni bocznej tej piramidy.

Istnieją również wzory na powierzchnię boczną regularnej piramidy. W regularnej piramidzie podstawa jest rzutem prostopadłym powierzchni bocznej, a więc:

P- obwód podstawy, ja- apotem piramidy

*Ta formuła jest oparta na wzorze na pole trójkąta.

Jeśli chcesz dowiedzieć się więcej o tym, jak te formuły są wyprowadzane, nie przegap tego, śledź publikację artykułów.To wszystko. Powodzenia!

Z poważaniem Aleksander Krutitskikh.

PS: Byłbym wdzięczny, gdybyś opowiedział o stronie w sieciach społecznościowych.

Cylinder jest geometrycznym ciałem ograniczonym przez dwa płaszczyzny równoległe i cylindryczna powierzchnia. W artykule porozmawiamy o tym, jak znaleźć powierzchnię cylindra i korzystając ze wzoru, rozwiążemy na przykład kilka problemów.

Cylinder ma trzy powierzchnie: górną, dolną i boczną.

Górna i dolna część cylindra są okręgami i można je łatwo zdefiniować.

Wiadomo, że powierzchnia koła jest równa πr 2 . Zatem wzór na pole dwóch okręgów (góra i dół walca) będzie wyglądał tak: πr 2 + πr 2 = 2πr 2 .

Trzecia, boczna powierzchnia cylindra, to zakrzywiona ściana cylindra. Aby lepiej przedstawić tę powierzchnię, spróbujmy ją przekształcić, aby uzyskać rozpoznawalny kształt. Wyobraź sobie, że cylinder jest zwykły cyna, który nie ma górnej i dolnej pokrywy. Zróbmy pionowe nacięcie na bocznej ściance od góry do dołu słoika (krok 1 na rysunku) i spróbuj maksymalnie otworzyć (wyprostować) powstałą figurę (krok 2).

Po pełnym ujawnieniu powstałego słoika zobaczymy znajomą figurę (krok 3), jest to prostokąt. Powierzchnia prostokąta jest łatwa do obliczenia. Ale wcześniej wróćmy na chwilę do oryginalnego cylindra. Wierzchołek pierwotnego cylindra jest kołem, a wiemy, że obwód koła oblicza się ze wzoru: L = 2πr. Jest zaznaczony na rysunku kolorem czerwonym.

Kiedy ściana boczna walec jest w pełni rozciągnięty, widzimy, że obwód staje się długością powstałego prostokąta. Bokami tego prostokąta będą obwód (L = 2πr) i wysokość walca (h). Powierzchnia prostokąta jest równa iloczynowi jego boków - S = długość x szerokość = L x h = 2πr x h = 2πrh. W rezultacie otrzymaliśmy wzór na obliczenie pola powierzchni bocznej cylindra.

Wzór na pole powierzchni bocznej walca
Strona S = 2prh

Pełna powierzchnia cylindra

Wreszcie, jeśli zsumujemy obszar wszystkich trzy powierzchnie, otrzymujemy formułę powierzchni pełna powierzchnia cylinder. Pole powierzchni cylindra jest równe powierzchni górnej części cylindra + powierzchni podstawy cylindra + powierzchni bocznej powierzchni cylindra lub S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Czasami wyrażenie to jest zapisane identyczną formułą 2πr (r + h).

Wzór na całkowitą powierzchnię cylindra
S = 2πr 2 + 2πrh = 2πr(r + h)
r to promień walca, h to wysokość walca

Przykłady obliczania pola powierzchni walca

Aby zrozumieć powyższe wzory, spróbujmy obliczyć powierzchnię cylindra na przykładach.

1. Promień podstawy cylindra wynosi 2, wysokość 3. Określ pole powierzchni bocznej cylindra.

Całkowitą powierzchnię oblicza się według wzoru: strona S. = 2prh

Strona S = 2 * 3,14 * 2 * 3

Strona S = 6,28 * 6

Strona S = 37,68

Powierzchnia boczna cylindra wynosi 37,68.

2. Jak znaleźć pole powierzchni walca, jeśli wysokość wynosi 4, a promień 6?

Całkowitą powierzchnię oblicza się ze wzoru: S = 2πr 2 + 2πrh

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Powierzchnia bocznej powierzchni dowolnej piramidy jest równa sumie powierzchni jej bocznych ścian. Sensowne jest podanie specjalnej formuły wyrażania tego obszaru w przypadku regularnej piramidy. Dajmy więc regularną piramidę, u podstawy której leży regularny n-gon o boku równym a. Niech h będzie wysokością ściany bocznej, zwanej również apotema piramidy. Powierzchnia jednej ściany bocznej wynosi 1/2ah, a cała powierzchnia boczna piramidy ma powierzchnię równą n/2ha.Ponieważ na jest obwodem podstawy piramidy, znalezioną formułę możemy zapisać w następujący sposób :

Powierzchnia boczna piramidy foremnej jest równy iloczynowi jej apotemu przez połowę obwodu podstawy.

Dotyczący całkowita powierzchnia, a następnie po prostu dodaj obszar podstawy z boku.

Wpisana i ograniczona kula i kula. Należy zauważyć, że środek kuli wpisanej w piramidę leży na przecięciu dwusiecznych płaszczyzn wewnętrznych kątów dwuściennych piramidy. Środek kuli opisanej w pobliżu piramidy leży na przecięciu płaszczyzn przechodzących przez środki krawędzi piramidy i prostopadłych do nich.

Skrócona piramida. Jeśli piramida jest przecięta płaszczyzną równoległą do jej podstawy, wówczas nazywa się część zamkniętą między płaszczyzną cięcia a podstawą ścięta piramida. Rysunek przedstawia piramidę, odrzucając jej część leżącą nad płaszczyzną cięcia, otrzymujemy ściętą piramidę. Oczywiste jest, że mała piramida, która ma zostać odrzucona, jest jednorodna z dużą piramidą, której środek znajduje się na wierzchołku. współczynnik podobieństwa jest równy stosunkowi wysokości: k=h 2 /h 1 , lub krawędzie boczne lub inne odpowiednie wymiary liniowe obie piramidy. Wiemy, że obszary podobnych figur są powiązane jako kwadraty o wymiarach liniowych; więc obszary podstaw obu piramid (tj. oszczędzaj podstawy ściętej piramidy) są powiązane jako

Tutaj S 1 to obszar dolnej podstawy, a S 2 to obszar górnej podstawy ściętej piramidy. W tej samej relacji są powierzchnie boczne piramidy. Podobna zasada dotyczy tomów.

Tomy podobnych ciał są powiązane jak sześciany o ich liniowych wymiarach; na przykład, objętości piramid są powiązane jako iloczyny ich wysokości przez powierzchnię podstaw, z której bezpośrednio wynika nasza reguła. Ma absolutnie ogólny charakter i wynika wprost z faktu, że objętość ma zawsze wymiar trzeciej potęgi długości. Korzystając z tej reguły, wyprowadzamy wzór wyrażający objętość ściętego ostrosłupa pod względem wysokości i powierzchni podstaw.

Niech zostanie podany ostrosłup ścięty o wysokości h i polach bazowych S 1 i S 2 . Jeśli wyobrazimy sobie, że trwa do kompletna piramida, to współczynnik podobieństwa pełnej piramidy i małej piramidy jest łatwy do znalezienia jako pierwiastek stosunku S 2 /S 1. Wysokość ściętego ostrosłupa jest wyrażona jako h = h 1 - h 2 = h 1 (1 - k). Teraz mamy dla objętości ściętej piramidy (V 1 i V 2 oznaczają objętości pełnej i małej piramidy)

skrócona formuła objętości piramidy

Wyprowadzamy wzór na pole powierzchni S powierzchni bocznej ostrosłupa ściętego foremnego przez obwody podstaw P 1 i P 2 oraz długość apotemu a. Argumentujemy dokładnie tak samo, jak przy wyprowadzaniu wzoru na objętość. Uzupełniamy piramidę górną częścią, mamy P 2 \u003d kP 1, S 2 \u003d k 2 S 1, gdzie k jest współczynnikiem podobieństwa, P 1 i P 2 są obwodami podstaw, a S 1 i S 2 to odpowiednio konie powierzchni bocznych całej powstałej piramidy i jej wierzchołka. Dla powierzchni bocznej znajdujemy (a 1 i a 2 - apotemy piramid, a \u003d a 1 - a 2 \u003d a 1 (1-k))

wzór na powierzchnię boczną regularnej ściętej piramidy