Klasyczny problem prezentacji wielokątów foremnych. Prezentacja regularnych wielokątów na lekcję geometrii (klasa 9) na dany temat. Aktualizacja podstawowej wiedzy

Aby skorzystać z podglądu prezentacji, załóż konto (konto) Google i zaloguj się: https://accounts.google.com

Podpisy slajdów:

WIELOKĄTY REGULARNE (klasa geometrii 9) Volodina n.l.

Cele lekcji: 1. Powtórz pojęcie wielokąta, wzór na sumę kątów wielokąta wypukłego. 2. Przedstaw wielokąty foremne, naucz budować wielokąty foremne. 3. Kształtowanie umiejętności rozwiązywania problemów na ten temat.

PYTANIA USTNE: 1. Jaka jest suma kątów wielokąta wypukłego? (n - 2) ∙ 180 ⁰ 2. Jak znaleźć jeden róg sześciokąta, jeśli wszystkie rogi są równe? (6 - 2) ∙ 180 ⁰ / 6 = 120⁰ 3. Jak znaleźć kąt n-kąta, jeśli wszystkie kąty są równe? (n - 2) ∙ 180 ⁰ / n

Jaka jest suma kątów trójkąta? 180⁰

Suma kątów wielokąta 1. Jaka jest suma kątów czworoboku wypukłego? 360 ⁰ 2. Jaka jest suma kątów sześciokąta wypukłego? 720⁰

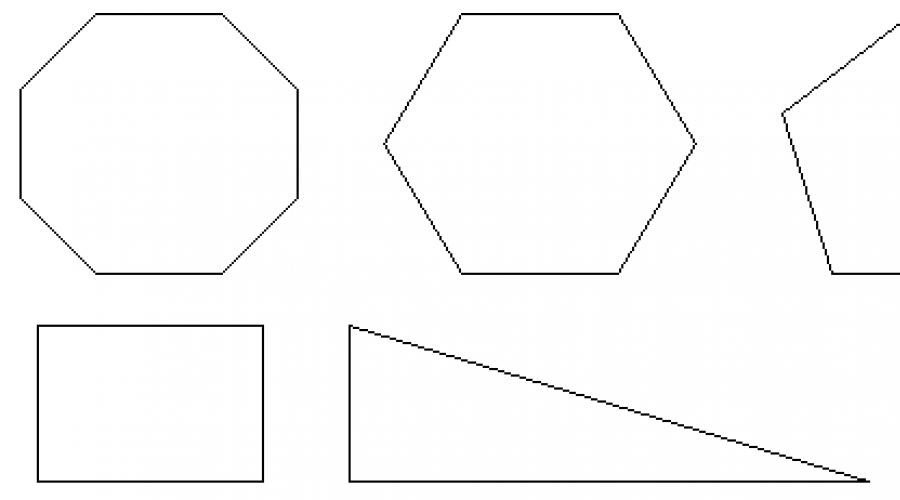
Podziel wielokąty na dwie grupy

REGULARNE WIELOKONY Dowolne wielokąty

DEFINICJA: Wielokąt wypukły nazywany jest regularnym, jeśli wszystkie boki są równe i wszystkie kąty są równe.

Trójkąt prawy Trójkąt równoboczny Wszystkie boki są równe. Wszystkie kąty to 60.⁰

Regularny czworokąt Kwadrat Wszystkie boki są równe. Wszystkie kąty to 90.⁰

Pięciokąt foremny Wszystkie boki są równe Wszystkie kąty mają 108⁰

Sześciokąt foremny Wszystkie boki są równe Wszystkie kąty to 120⁰

PYTANIA KOŃCOWE: 1. Jaki wielokąt nazywamy poprawnym? 2. Czy istnieje zwykły 10-gon? 20-gonów? 3.Jak zbudować wielokąt foremny?

Na temat: opracowania metodologiczne, prezentacje i notatki

Niestandardowa lekcja geometrii w klasie 9. Gra „Matematyk - biznesmen” na temat „Regularne wielokąty. Obwód i pole koła...

Opracowanie lekcji geometrii Grade 9 "Wzory do obliczania pola wielokąta foremnego, jego boku i promienia okręgu wpisanego"

Opracowanie lekcji-studium nowego materiału z geometrii w klasie 9 „Wzory do obliczania pola wielokąta foremnego, jego boku i promienia okręgu wpisanego” Podsumowanie lekcji na temat geometrii...

Wielokąty regularne. Porządek i chaos.

Streszczenie lekcji geometrii w klasie 9 na temat: "Wielokąty regularne. Porządek i chaos". Jeden temat to temat, drugi to meta-temat ....

Prezentacja „Obszar wielokąta foremnego”

Prezentacja geometrii lekcji w klasie 9 zawiera niezbędne definicje i wzory do obliczania powierzchni wielokątów regularnych ....

Aby skorzystać z podglądu prezentacji, załóż konto (konto) Google i zaloguj się: https://accounts.google.com

Podpisy slajdów:

Wielościan to ciało, którego powierzchnia składa się ze skończonej liczby płaskich wielokątów.

Wielościany regularne

Ile jest regularnych wielościanów? - Jak są definiowane, jakie mają właściwości? -Gdzie się spotykają, czy mają praktyczne zastosowanie?

Wielościan wypukły nazywany jest regularnym, jeśli wszystkie jego ściany są równymi wielokątami foremnymi, a na każdym z jego wierzchołków zbiega się taka sama liczba krawędzi.

"hedra" - twarz "tetra" - cztery heksy "- sześć "octa" - osiem "dodeca" - dwanaście "icos" - dwadzieścia Nazwy tych wielościanów pochodzą ze starożytnej Grecji i wskazują liczbę twarzy.

Nazwa wielościanu foremnego Typ ściany Liczba wierzchołków krawędzi ścian zbieżnych w jednym wierzchołku Czworościan Trójkąt regularny 4 6 4 3 Oktaedr Trójkąt regularny 6 12 8 4 Dwudziestościan Trójkąt regularny 12 30 20 5 Sześcian (sześcian) Kwadrat 8 12 6 3 Dwunastościan Pięciokąt foremny 20 30 12 3 Dane dotyczące wielościanu foremnego

Pytanie (problem): Ile jest wielościanów regularnych? Jak ustawić ich liczbę?

α n = (180 °(n -2)) : n Każdy wierzchołek wielościanu ma co najmniej trzy płaskie kąty, a ich suma musi być mniejsza niż 360 ° . Kształt ścian Liczba ścian w jednym wierzchołku Suma kątów płaskich w wierzchołku wielościanu Wniosek o istnieniu wielościanu α = 3 α = 4 α = 5 α = 6 α = 3 α = 4 α = 3 α = 4 α = 3

L. Carroll

Wielcy matematycy starożytności Archimedes Euklides Pitagoras

Starożytny grecki naukowiec Platon szczegółowo opisał właściwości wielościanów regularnych. Dlatego wielościany regularne nazywane są bryłami platońskimi.

czworościan - kostka ognia - ośmiościan ziemi - dwudziestościan powietrza - dwunastościan wody - wszechświat

Wielościany w naukach o kosmosie i Ziemi

Johannes Kepler (1571-1630) Niemiecki astronom i matematyk. Jeden z twórców współczesnej astronomii – odkrył prawa ruchu planet (prawa Keplera)

Przestrzeń Pucharu Keplera

„Ecosahedron – dwunastościan budowy Ziemi”

Wielościany w sztuce i architekturze

Albrecht Dürer (1471-1528) „Melancholia”

Salvador Dali „Ostatnia Wieczerza”

Nowoczesne konstrukcje architektoniczne w formie wielościanów

Latarnia aleksandryjska

Ceglany wielościan autorstwa szwajcarskiego architekta

Nowoczesny budynek w Anglii

Wielościany w przyrodzie

Piryt (piryt siarkawy) Monokryształ ałunu potasowego Kryształy rudy miedzi czerwonej KRYSZTAŁY NATURALNE

Sól kuchenna składa się z kryształów w formie sześcianu, mineralny sylwin posiada również sieć krystaliczną w formie sześcianu. Cząsteczki wody mają kształt czworościanu. Kupryt mineralny tworzy kryształy w postaci ośmiościanów. Kryształy pirytu mają kształt dwunastościanu

Diament Diament, chlorek sodu, fluoryt, oliwin i inne substancje krystalizują w postaci oktaedru.

Historycznie pierwszą formą cięcia, która pojawiła się w XIV wieku był ośmiościan. Diamond Shah Diamond waga 88,7 karata

Zadanie Królowa Anglii poleciła przeciąć krawędzie diamentu złotą nicią. Ale cięcie nie zostało wykonane, ponieważ jubiler nie był w stanie obliczyć maksymalnej długości złotej nici, a samego diamentu nie pokazano mu. Jubiler otrzymał następujące dane: ilość wierzchołków B=54, ilość ścian G=48, długość największej krawędzi L=4mm. Znajdź maksymalną długość złotej nici.

Wielościan foremny Liczba ścian Wierzchołki Krawędzie Czworościan 4 4 6 Sześcian 6 8 12 Oktaedr 8 6 12 Dwunastościan 12 20 30 Dwudziestościan 20 12 30 Praca badawcza „Wzór Eulera”

Twierdzenie Eulera. Dla dowolnego wielościanu wypukłego В + Г - 2 = Р gdzie В to liczba wierzchołków, Г to liczba ścian, Р to liczba krawędzi tego wielościanu.

FIZYMINUTĘ!

Zadanie Znajdź kąt między dwiema krawędziami ośmiościanu foremnego, które mają wspólny wierzchołek, ale nie należą do tej samej ściany.

Zadanie Znajdź wysokość czworościanu foremnego o krawędzi 12 cm.

Kryształ ma kształt ośmiościanu, składający się z dwóch regularnych piramid o wspólnej podstawie, krawędź podstawy piramidy wynosi 6 cm Wysokość ośmiościanu wynosi 8 cm Znajdź powierzchnię boczną kryształ

Powierzchnia czworościanu dwudziestościan dwunastościan dwunastościan ośmiościan ośmiościan

Praca domowa: mnogogranniki.ru Korzystając z osiągnięć, wykonaj modele 1. wielościanu foremnego o boku 15 cm, 1. wielościanu półregularnego

Dziękujemy za Twoją pracę!

slajd 3

Wielokąty regularne

slajd 4

„Trzy cechy: rozległa wiedza, nawyk myślenia i szlachetność uczuć - są niezbędne, aby osoba była wykształcona w pełnym tego słowa znaczeniu.” N.G. Chernyshevsky

zjeżdżalnia 5

zjeżdżalnia 6

Klasztor Simonov

Slajd 7

Czy wiesz?

Jakie kształty geometryczne już badaliśmy? Jakie są ich elementy? Jaki kształt nazywa się wielokątem? Jaka jest najmniejsza liczba boków wielokąta? Co to jest wielokąt wypukły? Pokaż na rysunku wielokąty wypukłe i niewypukłe. Wyjaśnij, jakie kąty nazywamy narożnikami wielokąta wypukłego, narożnikami zewnętrznymi. Jaki jest wzór na obliczenie sumy kątów wielokąta wypukłego? Jaki jest obwód wielokąta?

Slajd 8

Pytania krzyżówkowe: Boki, kąty i wierzchołki wielokąta? Jak nazywa się wielokąt o równych bokach i kątach? 3. Jak nazywa się figura, którą można podzielić na skończoną liczbę trójkątów? 4. Część koła? 5.Granica wielokąta? 6. Element koła? 7. Element wieloboku? 8. Granica koła? 9.Wielokąt o najmniejszej liczbie boków? 10. Kąt, którego wierzchołek znajduje się w środku okręgu? 11. Inny rodzaj kąta koła? 12. Suma długości boków wielokąta? 13. Wielokąt znajdujący się w jednej półpłaszczyźnie w stosunku do linii prostej zawierającej dowolny z jego boków?

Slajd 9

Slajd 10

slajd 11

Jaki jest każdy z rogów regularnego a) dziesięciokąta; b) n-gon.

zjeżdżalnia 12

Kąt regularnego n-gon

slajd 13

Slajd 14

Praktyczna praca. 1. Siedmiogłowa wieża Białego Miasta była na planie regularnym sześciokątem, którego wszystkie boki mają 14 m. Narysuj plan tej wieży. 2. Zmierz kąt AOB. Jaka część jego wartości jest wartością całkowitego kąta O? Jak obliczyć wartość tego kąta, znając liczbę boków wielokąta? 3. Zmierz kąt CAK - zewnętrzny narożnik wielokąta. Oblicz sumę kąta zewnętrznego CAK i kąta wewnętrznego CAB. Dlaczego te kąty zawsze sumują się do 180°? Jaka jest suma zewnętrznych kątów sześciokąta foremnego, obliczonych po jednym na każdym wierzchołku?

zjeżdżalnia 15

zjeżdżalnia 16

Średnica podstawy wieży Dulo wynosi 16m. Narysuj plan podstawy szesnastobocznej wieży, używając kąta, pod którym bok wieloboku jest widoczny ze środka okręgu. Oblicz kąty wewnętrzne i zewnętrzne tego 16-kąta. Jaka jest suma kątów zewnętrznych szesnastokąta foremnego, wziętych jeden w każdym wierzchołku?Jaka jest suma kątów zewnętrznych n-kąta foremnego, wziętych jeden w każdym wierzchołku? nr 1082, 1083.

Lekcja na temat „Regularne wielokąty”

Cele Lekcji:

edukacyjny: zapoznanie studentów z pojęciem i typami wielokątów foremnych, wraz z niektórymi ich własnościami, nauczenie posługiwania się wzorem do obliczania kąta wielokąta foremnego

- opracowanie:

- edukacyjny:

Przebieg lekcji:

1. Moment organizacyjny

Motto lekcji:

Do wiedzy prowadzą trzy ścieżki:

Chiński filozof i mędrzec Konfucjusz.

2. Motywacja lekcji.

Drodzy Chłopaki!

Mam nadzieję, że ta lekcja będzie interesująca, z wielką korzyścią dla wszystkich. Bardzo zależy mi na tym, aby ci, którym królowa wszystkich nauk wciąż pozostawała obojętna, wyszli z naszej lekcji z głębokim przekonaniem, że geometria to interesujący i potrzebny temat.

Francuski pisarz z XIX wieku, Anatole France, powiedział kiedyś: „Nauka może być tylko zabawą… Aby przetrawić wiedzę, musisz ją przyswoić z apetytem”.

Postępujmy zgodnie z radą pisarza w dzisiejszej lekcji: bądź aktywny, uważny, z wielką chęcią przyswajaj wiedzę, która przyda ci się w późniejszym życiu.

3. Aktualizacja podstawowej wiedzy.

Sonda przednia:

Jakie są ich elementy?

Widoki wieloboków

4. Nauka nowego materiału.

Wśród wielu różnych kształtów geometrycznych na płaszczyźnie wyróżnia się duża rodzina POLYGONS.

Nazwy kształtów geometrycznych mają bardzo konkretne znaczenie. Przyjrzyj się uważnie słowu „wielokąt” i powiedz, z jakich części się składa. Słowo „wielokąt” wskazuje, że wszystkie postacie z tej rodziny mają „wiele narożników”.

Zastąp w słowie „wielokąt” zamiast części „wiele” konkretną liczbę, na przykład 5. Otrzymasz PENTAGON. Lub 6. Następnie - SZEŚCIOKĄT. Zwróć uwagę, ile kątów, tyle boków, aby te liczby można było nazwać wielostronnymi.

Rysunek przedstawia kształty geometryczne. Nazwij te figury za pomocą rysunku.

Definicja.Wielokąt foremny to wielokąt wypukły, w którym wszystkie kąty są równe i wszystkie boki są równe.

Znasz już niektóre wielokąty foremne - trójkąt równoboczny (trójkąt regularny), kwadrat (czworokąt regularny).

Zapoznajmy się z niektórymi właściwościami, które posiadają wszystkie wielokąty foremne.

Suma kątów wielokąta
n - liczba boków
n-2 - liczba trójkątów
Suma kątów jednego trójkąta wynosi 180º, pomnóż przez liczbę trójkątów n-2, otrzymujemy S= (n-2)*180.

S=(n-2)*180
Wzór na obliczenie kąta x wielokąta foremnego .
Wyprowadzamy wzór do obliczania kąt x regularnego n-kąta.
W wielokącie foremnym wszystkie kąty są równe, dzielimy sumę kątów przez liczbę kątów, otrzymujemy wzór:
x=(n-2)*180/n

5. Konsolidacja nowego materiału.

Zdecyduj #179, 181, 183 (1), 184.

Nie odwracając głowy, rozejrzyj się wokół ściany klasy zgodnie z ruchem wskazówek zegara, tablicę wokół obwodu w kierunku przeciwnym do ruchu wskazówek zegara, trójkąt przedstawiony na stojaku zgodnie z ruchem wskazówek zegara i jego równy trójkąt w kierunku przeciwnym do ruchu wskazówek zegara. Odwróć głowę w lewo i spójrz na linię horyzontu, a teraz na czubek nosa. Zamknij oczy, policz do 5, otwórz oczy i...

Przykładamy ręce do oczu,
Postawmy mocne nogi.
Skręcając w prawo
Wyglądajmy majestatycznie.
I na lewo też
Spójrz spod dłoni.
I - w prawo! I dalej
Nad lewym ramieniem!
a teraz będziemy kontynuować pracę.

7. Samodzielna praca studentów.

Rozwiąż #183(2).

8. Wyniki lekcji. Odbicie. D / s.

Co najbardziej pamiętasz z lekcji?

Co zaskoczyło?

Co Ci się najbardziej podobało?

Jak chciałbyś zobaczyć następną lekcję?

D / s. Naucz się pozycji 6. Rozwiąż nr 180, 182 185.

Zadanie twórcze:

Internet :

Wyświetl zawartość prezentacji
„regularne wielokąty”

• - edukacyjny: zapoznanie studentów z pojęciem i rodzajami wielokątów foremnych, z niektórymi ich własnościami; naucz korzystać ze wzoru do obliczania kąta wielokąta foremnego
• - opracowanie: rozwijanie aktywności poznawczej, wyobraźni przestrzennej, umiejętność wyboru właściwego rozwiązania, zwięzłego wyrażania myśli, analizowania i wyciągania wniosków.
• - edukacyjny: rozwijanie zainteresowania tematem, umiejętności pracy w zespole, kultury komunikacji.

Motto lekcji:

Do wiedzy prowadzą trzy ścieżki:

Droga refleksji jest drogą najszlachetniejszą;

Sposób naśladowania jest najłatwiejszy;

Ścieżka doświadczenia jest najbardziej gorzką ścieżką.

Chiński filozof i mędrzec

Konfucjusz.

• Jakie kształty geometryczne już badaliśmy?
• Jakie są ich elementy?
• Jaki kształt nazywa się wielokątem?
• Widoki wieloboków
• Jaki jest obwód wielokąta?
• Jaka jest suma kątów wewnętrznych wielokąta?

Nieprawidłowo Prawidłowo wielokąty

• Wielokąt wypukły nazywany jest regularnym, jeśli wszystkie jego kąty są równe i wszystkie boki są równe.

Właściwości wielokątów foremnych

Suma kątów

wielokąt

n - liczba boków n-2 - liczba trójkątów Suma kątów jednego trójkąta wynosi 180º, 180º mnożymy przez liczbę trójkątów (n-2), otrzymujemy S= (n-2)*180.

Wzór na obliczenie kąta prostego P - kwadrat

po prawej P- w kwadracie wszystkie kąty są równe, sumę kątów dzielimy przez liczbę kątów, otrzymujemy wzór:

a n =(n-2)*180/n

Test Wybierz liczby prawidłowych stwierdzeń.

• Wielokąt wypukły jest regularny, jeśli wszystkie jego boki są równe.
• Każdy wielokąt foremny jest wypukły.
• Każdy czworobok o równych bokach jest prawidłowy.
• Trójkąt jest regularny, jeśli wszystkie jego kąty są równe.
• Każdy trójkąt równoboczny jest prawidłowy.
• Każdy wielokąt wypukły jest regularny.
• Każdy czworobok o równych kątach jest regularny.

Niezależna praca

a P =(n-2)*180/n

a 3 =(3-2)*180/3= 180/3= 60

Zadanie domowe

nr 1079 (ustnie), nr 1081 (b, e), nr 1083 (b)

Zadanie twórcze:

* Historyczne informacje o regularnych wielokątach. Możliwe zapytania do wyszukiwarki internetowej Internet :

• Wielokąty w szkole Pitagorasa. Konstrukcja wielokątów, Euklides. Wielokąty regularne, Klaudiusz Ptolemeusz.
• Wielokąty w szkole Pitagorasa.
• Konstrukcja wielokątów, Euklides.
• Wielokąty regularne, Klaudiusz Ptolemeusz.

slajd 1

slajd 2

Definicja wielokąta foremnego. Wielokąt foremny to wielokąt wypukły, w którym wszystkie boki i wszystkie (wewnętrzne) kąty są równe.

slajd 3

slajd 4

Okrąg otoczony wielokątem foremnym. Twierdzenie: wokół dowolnego wielokąta foremnego można opisać okrąg, a ponadto tylko jeden. Mówi się, że okrąg jest opisany wokół wielokąta, jeśli wszystkie jego wierzchołki leżą na tym okręgu.

zjeżdżalnia 5

Okrąg wpisany w wielokąt foremny. Mówi się, że okrąg jest wpisany w wielokąt, jeśli wszystkie boki wielokąta dotykają okręgu. Twierdzenie: W dowolny wielokąt foremny można wpisać okrąg, a ponadto tylko jeden.

zjeżdżalnia 6

Niech А1 А 2 …А n będzie wielokątem foremnym, О będzie środkiem okręgu opisanego. Dowodząc Twierdzenia 1, odkryliśmy, że ∆ OA1A2 = ∆OA2A3= ∆OAnA1 , więc wysokości tych trójkątów narysowanych z wierzchołka O są również równe. Dlatego okrąg o środku O i promieniu OH przechodzi przez punkty H1, H2, Hn i dotyka boków wielokąta w tych punktach, tj. okrąg jest wpisany w dany wielokąt. Biorąc pod uwagę: ABCD…An jest wielokątem foremnym. Udowodnij, że każdy wielokąt foremny może być wpisany w okrąg, a ponadto tylko jeden.

Slajd 7

Udowodnijmy, że istnieje tylko jeden wpisany okrąg. Załóżmy, że istnieje inny wpisany okrąg o środku O i promieniu OA. Wtedy jego środek znajduje się w równej odległości od boków wielokąta, tj. punkt O1 leży na każdej z dwusiecznych kąta wielokąta, a zatem pokrywa się z punktem O przecięcia tych dwusiecznych.

Slajd 8

A D B C O Dane: ABCD…An jest wielokątem foremnym. Udowodnij, że można narysować okrąg wokół dowolnego wielokąta foremnego, a ponadto tylko jednego. Dowód: Narysujmy dwusieczne BO i CO równych kątów ABC i BCD. Będą się przecinać, ponieważ narożniki wielokąta są wypukłe i każdy ma mniej niż 180⁰. Niech punktem ich przecięcia będzie O. Następnie, po narysowaniu odcinków OA i OD, otrzymamy ΔBOA, ΔBOC i ΔCOD. ΔBOA \u003d ΔBOC zgodnie z pierwszym kryterium równości trójkątów (BO - ogólnie, AB \u003d BC, kąt 2 \u003d kąt 3). Podobnie, ΔVOC=ΔCOD. 1 2 3 4 angle2 = kąt 3 jako połówki równych kątów, wtedy ΔBOC jest równoramienny. Ten trójkąt jest równy ΔBOA i ΔCOD => są one również równoramienne, więc OA=OB=OC=OD, tj. punkty A, B, C i D są w równej odległości od punktu O i leżą na okręgu (O; OB). Podobnie inne wierzchołki wielokąta leżą na tym samym okręgu.

Slajd 9

Udowodnijmy teraz, że istnieje tylko jeden ograniczony okrąg. Rozważ dowolne trzy wierzchołki wielokąta, na przykład A, B, C. tylko jeden okrąg przechodzi przez te punkty, wtedy tylko jeden okrąg może być opisany w pobliżu wielokąta ABC...An. o A B C D

zjeżdżalnia 10

Konsekwencje. Wniosek #1 Okrąg wpisany w wielokąt foremny dotyka boków wielokąta w ich punktach środkowych. Wniosek nr 2 Środek okręgu opisanego w pobliżu wielokąta foremnego pokrywa się ze środkiem okręgu wpisanego w ten sam wielokąt.

slajd 11

Wzór do obliczania powierzchni wielokąta foremnego. Niech S będzie polem regularnego n-kąta, a1 jego bokiem, P obwodem, a r i R odpowiednio promieniami okręgów wpisanego i opisanego. Udowodnijmy, że

zjeżdżalnia 12

Aby to zrobić, połącz środek danego wielokąta z jego wierzchołkami. Następnie wielokąt zostanie podzielony na n równych trójkątów, których powierzchnia jest równa Dlatego,

slajd 13

Wzór do obliczania boku wielokąta foremnego. Wyprowadźmy formuły: Aby wyprowadzić te formuły, użyjemy figury. W trójkącie prostokątnym А1Н1О O А1 А2 А3 Аn H2 H1 Hn H3 Zatem

slajd 14

Zakładając we wzorze n = 3, 4 i 6 otrzymujemy wyrażenia dla boków trójkąta foremnego, kwadratu i sześciokąta foremnego:

zjeżdżalnia 15

Zadanie nr 1 Dane: okrąg (O; R) Skonstruuj n-kąt foremny. okrąg jest podzielony na n równych łuków. Aby to zrobić, narysuj promienie OA1, OA2, ..., OAn tego okręgu tak, aby kąt A1OA2 = kąt A2OA3 = ... = kąt An-1OAn = kąt AnOA1 = 360 ° / n (na rysunku n = 8). Jeśli teraz narysujemy odcinki A1A2, A2A3, ..., An-1An, AnA1, to otrzymamy n-kąt A1A2 ... An. Trójkąty А1ОА2, А2ОА3,…, АnОА1 są sobie równe, dlatego А1А2= А2А3=…= Аn-1Аn= АnА1. Wynika z tego, że A1A2…An jest zwykłym n-kątem. Budowa wielokątów foremnych.

zjeżdżalnia 16

Zadanie nr 2 Dane: A1, A2...An - n-kąt foremny Skonstruuj rozwiązanie 2n-kąt foremny. Opiszmy okrąg wokół niego. Aby to zrobić, konstruujemy dwusieczne kątów A1 i A2 i oznaczamy literą O punkt ich przecięcia. Następnie narysuj okrąg o środku O o promieniu OA1. Podziel łuki A1A2, A2A3..., An A1 na pół Każdy z punktów podziału B1, B2,..., Bn zostanie połączony odcinkami z końcami odpowiedniego łuku. Aby skonstruować punkty B1, B2, ..., Bn, możesz użyć dwusiecznych prostopadłych do boków danego n-kąta. Na rysunku w ten sposób skonstruowany jest regularny dwunastokąt A1 B1 A2 B2 ... A6 B6.