Znaczenie pochodnej. Pochodna funkcji. Geometryczne znaczenie pochodnej

10.10.2019

Przeczytaj także

Ciekawe fakty z historii wojskowości

Slangowe słowa i wyrażenia

Jak odgadnąć fusy z kawy?

Ocena najbardziej pijących krajów na świecie: gdzie jest Rosja?

Posyp solą pod stołem na weselu

Co to jest pochodna?
Definicja i znaczenie pochodnej funkcji

Wielu będzie zaskoczonych nieoczekiwanym umiejscowieniem tego artykułu w moim autorskim kursie dotyczącym pochodnej funkcji jednej zmiennej i jej zastosowań. Przecież jak to było ze szkoły: standardowy podręcznik przede wszystkim podaje definicję pochodnej, jej geometryczne, mechaniczne znaczenie. Następnie uczniowie z definicji znajdują pochodne funkcji i tak naprawdę dopiero wtedy doskonali się technikę różniczkowania za pomocą tabele pochodne.

Ale z mojego punktu widzenia bardziej pragmatyczne jest następujące podejście: przede wszystkim wskazane jest DOBRZE ZROZUMIEĆ ograniczenie funkcji, a szczególnie nieskończenie małe. Fakt jest taki definicja pochodnej oparta jest na pojęciu granicy, co jest słabo brane pod uwagę w kurs szkolny. Dlatego znaczna część młodych konsumentów wiedzy o granitach słabo wnika w samą istotę pochodnej. Tak więc, jeśli jesteś słabo zorientowany w rachunek różniczkowy lub mądry mózg dla długie lata pomyślnie pozbyłeś się tego bagażu, zacznij od ograniczenia funkcji. Jednocześnie opanuj/zapamiętaj swoją decyzję.

Ten sam praktyczny sens podpowiada, że najpierw się opłaca naucz się znajdować pochodne, łącznie z pochodne funkcji złożonych. Teoria to teoria, ale, jak mówią, zawsze chcesz różnicować. W związku z tym lepiej jest wypracować wymienione podstawowe lekcje i być może stać się mistrz różnicowania nawet nie zdając sobie sprawy z istoty swoich działań.

Po przeczytaniu artykułu polecam rozpocząć materiały na tej stronie. Najprostsze problemy z pochodną, gdzie w szczególności rozważany jest problem stycznej do wykresu funkcji. Ale może się to opóźnić. Faktem jest, że wiele zastosowań pochodnej nie wymaga jej zrozumienia i nic dziwnego, że lekcja teoretyczna pojawiła się dość późno - kiedy musiałem wyjaśnić znajdowanie interwałów wzrostu/spadku i ekstremów Funkcje. Co więcej, był w temacie przez dość długi czas ” Funkcje i wykresy”, dopóki nie zdecydowałem się umieścić go wcześniej.

Dlatego, drogie czajniczki, nie spieszcie się z wchłonięciem esencji pochodnej, jak głodne zwierzęta, ponieważ nasycenie będzie bez smaku i niepełne.

Pojęcie zwiększania, zmniejszania, maksimum, minimum funkcji

Wiele przewodniki po studiach doprowadzić do pojęcia pochodnej z pomocą kilku praktycznych problemów, a ja też wymyśliłem ciekawy przykład. Wyobraź sobie, że musimy udać się do miasta, do którego można dotrzeć na różne sposoby. Natychmiast odrzucamy zakrzywione kręte ścieżki i rozważymy tylko linie proste. Jednak kierunki w linii prostej są również inne: do miasta można dojechać płaską autostradą. Lub na pagórkowatej autostradzie - w górę iw dół, w górę iw dół. Kolejna droga prowadzi tylko pod górę, a inna cały czas schodzi w dół. Poszukiwacze mocnych wrażeń wybiorą trasę przez wąwóz ze stromym klifem i stromym podejściem.

Ale bez względu na preferencje, dobrze jest znać obszar, a przynajmniej go zlokalizować. Mapa topograficzna. A jeśli nie ma takich informacji? W końcu możesz wybrać np. płaską ścieżkę, ale w efekcie natkniesz się na stok narciarski z zabawnymi Finami. Nie fakt, że nawigator, a nawet obraz satelitarny poda wiarygodne dane. Dlatego fajnie byłoby sformalizować odciążenie ścieżki za pomocą matematyki.

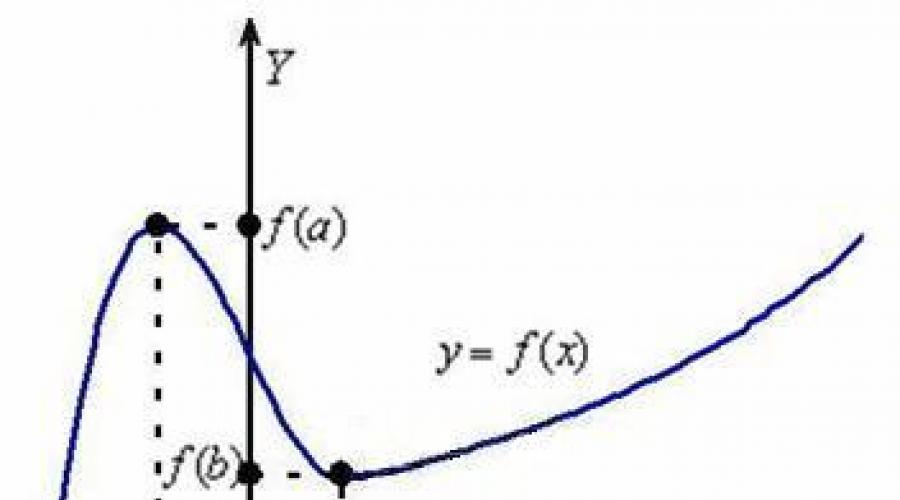
Rozważ jakąś drogę (widok z boku):

Na wszelki wypadek przypomnę elementarny fakt: podróż ma miejsce od lewej do prawej. Dla uproszczenia zakładamy, że funkcja ciągły w rozważanym obszarze.

Jakie są cechy tego wykresu?

W przerwach funkcjonować wzrasta, czyli każda z jego kolejnych wartości jeszcze Poprzedni. Z grubsza harmonogram idzie w dół w górę(wspinamy się na wzgórze). A w przedziale funkcja maleje- każda następna wartość mniejszy poprzedni, a nasz harmonogram idzie z góry na dół(schodząc ze stoku).

Zwracamy również uwagę na punkty specjalne. W punkcie, do którego docieramy maksymalny, tj istnieć taki odcinek ścieżki, na którym wartość będzie największa (najwyższa). W tym samym momencie minimum, oraz istnieć takie jego sąsiedztwo, w którym wartość jest najmniejsza (najniższa).

Podczas lekcji zostanie rozważona bardziej rygorystyczna terminologia i definicje. o ekstremach funkcji podczas gdy my uczymy się jeszcze jednego ważna cecha: pomiędzy funkcja rośnie, ale rośnie z inna prędkość . A pierwszą rzeczą, która rzuca się w oczy, jest to, że wykres szybuje w górę na interwale o wiele bardziej fajnie niż na interwale. Czy można zmierzyć stromość drogi za pomocą narzędzi matematycznych?

Szybkość zmiany funkcji

Pomysł jest taki: weź jakąś wartość (czytaj „delta x”), który nazwiemy przyrost argumentów i zacznijmy „przymierzać” w różnych punktach naszej ścieżki:

1) Spójrzmy na skrajny lewy punkt: omijając odległość, wspinamy się po zboczu na wysokość (zielona linia). Wartość nazywa się przyrost funkcji, i w ta sprawa ten przyrost jest dodatni (różnica wartości wzdłuż osi jest większa od zera). Ustalmy stosunek , który będzie miarą stromości naszej drogi. Oczywiście jest to bardzo konkretna liczba, a ponieważ oba przyrosty są dodatnie, to .

Uwaga! Oznaczenia są JEDEN symbol, to znaczy nie można „oderwać” „delty” od „x” i rozpatrywać te litery osobno. Oczywiście komentarz dotyczy również symbolu przyrostu funkcji.

Przyjrzyjmy się bardziej znaczącej naturze otrzymanej frakcji. Załóżmy, że początkowo jesteśmy na wysokości 20 metrów (w lewym czarnym punkcie). Po pokonaniu dystansu metrów (lewa czerwona linia) znajdziemy się na wysokości 60 metrów. Wtedy przyrost funkcji będzie metrów (zielona linia) oraz: . Zatem, na każdym metrze ten odcinek drogi wzrost wzrasta przeciętny o 4 metry…zapomniałeś swojego sprzętu wspinaczkowego? =) Innymi słowy, skonstruowany wskaźnik charakteryzuje ŚREDNĄ STOPIEŃ ZMIAN (w tym przypadku wzrostu) funkcji.

Notatka : Wartości liczbowe omawianego przykładu odpowiadają proporcjom rysunku tylko w przybliżeniu.

2) Teraz przejdźmy na tę samą odległość od skrajnej prawej czarnej kropki. Tutaj wzrost jest łagodniejszy, więc przyrost (karmazynowa linia) jest stosunkowo niewielki, a stosunek w porównaniu do poprzedniego przypadku będzie dość skromny. Obiektywnie mówiąc, metrów i tempo wzrostu funkcji jest . Oznacza to, że tutaj na każdy metr drogi jest przeciętny pół metra w górę.

3) Mała przygoda na zboczu góry. Spójrzmy na górę czarna kropka znajduje się na osi Y. Załóżmy, że jest to znak 50 metrów. Ponownie pokonujemy dystans, w wyniku czego znajdujemy się niżej – na poziomie 30 metrów. Odkąd powstał ruch z góry na dół(w kierunku „przeciwnym” do osi), następnie finał przyrost funkcji (wysokość) będzie ujemny: metrów (brązowa linia na rysunku). A w tym przypadku mówimy o szybkość zaniku funkcje: czyli z każdym metrem ścieżki tego odcinka wysokość maleje przeciętny o 2 metry. Zadbaj o ubrania w piątym punkcie.

Zadajmy teraz pytanie: jaka jest najlepsza wartość „standardu pomiarowego” do zastosowania? Oczywiste jest, że 10 metrów to bardzo trudne zadanie. Z łatwością zmieści się na nich kilkanaście wybojów. Dlaczego są wyboje, poniżej może być głęboki wąwóz, a po kilku metrach jego druga strona z dalszym stromym podejściem. Tak więc przy dziesięciometrowym nie uzyskamy zrozumiałej charakterystyki takich odcinków ścieżki przez przełożenie.

Z powyższej dyskusji wynika następujący wniosek: Jak mniejsza wartość , tym dokładniej opiszemy rzeźbę drogi. Ponadto prawdziwe są następujące fakty:

– Dla każdego punkty podnoszenia możesz wybrać wartość (choć bardzo małą), która mieści się w granicach jednego lub drugiego wzrostu. A to oznacza, że odpowiedni przyrost wysokości będzie gwarantowany jako dodatni, a nierówność będzie prawidłowo wskazywać wzrost funkcji w każdym punkcie tych przedziałów.

- Podobnie, dla każdego punkt nachylenia, istnieje wartość, która będzie pasować całkowicie do tego nachylenia. Dlatego odpowiedni wzrost wysokości jest jednoznacznie ujemny, a nierówność poprawnie pokaże spadek funkcji w każdym punkcie danego przedziału.

– Szczególnie interesujący jest przypadek, gdy tempo zmian funkcji wynosi zero: . Po pierwsze, przyrost wysokości zerowej () jest oznaką równej ścieżki. Po drugie, są inne ciekawe sytuacje, których przykłady widać na rysunku. Wyobraź sobie, że los zaprowadził nas na sam szczyt wzgórza z szybującymi orłami lub na dno wąwozu z rechotającymi żabami. Jeśli zrobisz mały krok w dowolnym kierunku, to zmiana wysokości będzie znikoma i możemy powiedzieć, że tempo zmian funkcji wynosi w rzeczywistości zero. Ten sam wzór obserwuje się w punktach.

W ten sposób zbliżyliśmy się do niesamowitej okazji, aby idealnie dokładnie scharakteryzować tempo zmian funkcji. W końcu analiza matematyczna pozwala nam skierować przyrost argumentu do zera: to znaczy sprawić, by nieskończenie mały.

W rezultacie pojawia się kolejne logiczne pytanie: czy można znaleźć drogę i jej rozkład? inna funkcja, który powiedziałby nam o wszystkich płaskich, podjazdach, zjazdach, szczytach, nizinach, a także o tempie wzrostu/spadku w każdym punkcie ścieżki?

Co to jest pochodna? Definicja pochodnej.
Geometryczne znaczenie pochodnej i różniczki

Przeczytaj uważnie i nie za szybko - materiał jest prosty i dostępny dla każdego! Jeśli w niektórych miejscach coś wydaje się nie do końca jasne, zawsze możesz wrócić do artykułu później. Powiem więcej, warto kilkakrotnie przestudiować teorię, aby jakościowo zrozumieć wszystkie punkty (rada jest szczególnie istotna dla studentów „technicznych”, którzy mają wyższa matematyka odgrywa znaczącą rolę w procesie edukacyjnym).

Oczywiście w samej definicji pochodnej w punkcie zastąpimy ją:

Do czego doszliśmy? I doszliśmy do wniosku, że dla funkcji zgodnie z prawem jest wyrównany inna funkcja, który jest nazywany funkcja pochodna(lub po prostu pochodna).

Pochodna charakteryzuje tempo zmian Funkcje . Jak? Myśl idzie jak czerwona nić od samego początku artykułu. Zastanów się nad pewnym punktem domeny Funkcje . Niech funkcja będzie różniczkowalna w danym punkcie. Następnie:

1) Jeżeli , to funkcja wzrasta w punkcie . I oczywiście jest interwał(nawet jeśli bardzo mały) zawierający punkt, w którym funkcja rośnie, a jej wykres przebiega „od dołu do góry”.

2) Jeżeli , to funkcja maleje w punkcie . I jest przedział zawierający punkt, w którym funkcja maleje (wykres idzie „od góry do dołu”).

3) Jeśli , to nieskończenie blisko w pobliżu punktu funkcja utrzymuje stałą prędkość. Dzieje się tak, jak zauważono, dla funkcji stałej i w krytycznych punktach funkcji, w szczególności w punktach minimalnych i maksymalnych.

Trochę semantyki. Co w szerokim znaczeniu Co oznacza czasownik „rozróżniać”? Zróżnicować oznacza wyróżnić cechę. Różniczkując funkcję „wybieramy” tempo jej zmiany w postaci pochodnej funkcji . A nawiasem mówiąc, co oznacza słowo „pochodna”? Funkcjonować stało się z funkcji.

Terminy bardzo skutecznie interpretują mechaniczne znaczenie pochodnej :
Rozważmy prawo zmiany współrzędnych ciała, które zależy od czasu, oraz funkcję prędkości ruchu danego ciała. Funkcja charakteryzuje szybkość zmian współrzędnej ciała, dlatego jest pierwszą pochodną funkcji po czasie: . Gdyby pojęcie „ruchu ciała” nie istniało w przyrodzie, to by nie istniało pochodna pojęcie „prędkości”.

Przyspieszenie ciała to tempo zmian prędkości, a więc: . Gdyby pierwotne pojęcia „ruchu ciała” i „prędkości ruchu ciała” nie istniały w przyrodzie, to nie byłoby pochodna pojęcie przyspieszenia ciała.

Decydując różne zadania geometrii, mechanice, fizyce i innych dziedzinach wiedzy, konieczne stało się zastosowanie tego samego procesu analitycznego z danej funkcji y=f(x) pobierz nową funkcję o nazwie funkcja pochodna(lub po prostu pochodna) tej funkcji f(x) i są symbolizowane

Proces, w którym dana funkcja f(x) zdobądź nową funkcję f"(x), nazywa różnicowanie i składa się z następujących trzech kroków: 1) podajemy argument x przyrost  x i określić odpowiedni przyrost funkcji  y = f(x+ x)-f(x); 2) nawiązać relację

3) liczenie x stały i  x0, znajdujemy
, który jest oznaczony przez f"(x), jakby podkreślając, że wynikowa funkcja zależy tylko od wartości x, przy którym przechodzimy do granicy. Definicja: Pochodna y „=f” (x) dana funkcja y=f(x) biorąc pod uwagę x nazywamy granicą stosunku przyrostu funkcji do przyrostu argumentu, pod warunkiem, że przyrost argumentu dąży do zera, jeśli oczywiście taki limit istnieje, tj. skończone. Zatem,
, lub

Zauważ, że jeśli dla jakiejś wartości x, na przykład kiedy x=a, relacja
w  x0 nie dąży do skończonej granicy, to w tym przypadku mówimy, że funkcja f(x) w x=a(lub w punkcie x=a) nie ma pochodnej lub nie jest różniczkowalna w punkcie x=a.

2. Geometryczne znaczenie pochodnej.

Rozważ wykres funkcji y \u003d f (x), różniczkowalnej w pobliżu punktu x 0

f(x)

Rozważmy dowolną linię prostą przechodzącą przez punkt wykresu funkcji - punkt A (x 0, f (x 0)) i przecinającą wykres w pewnym punkcie B (x; f (x)). Taką linię prostą (AB) nazywamy sieczną. Od ∆ABC: AC = ∆x; BC \u003d ∆y; tgβ=∆y/∆x .

Od AC || Ox, to ALO = BAC = β (jako odpowiednik równolegle). Ale ALO jest kątem nachylenia siecznej AB do dodatniego kierunku osi Ox. Stąd tgβ = k - nachylenie bezpośredni AB.

Teraz zmniejszymy ∆x, czyli ∆x→ 0. W tym przypadku punkt B zbliży się do punktu A zgodnie z wykresem, a sieczna AB będzie się obracać. Ograniczeniem pozycji siecznej AB przy ∆x → 0 będzie linia prosta (a), zwana styczną do wykresu funkcji y \u003d f (x) w punkcie A.

Jeśli przejdziemy do granicy jako ∆х → 0 w równości tgβ =∆y/∆x, to otrzymamy
lub tg \u003d f "(x 0), ponieważ
-kąt nachylenia stycznej do dodatniego kierunku osi Ox
, z definicji pochodnej. Ale tg \u003d k jest nachyleniem stycznej, co oznacza, że k \u003d tg \u003d f ”(x 0).

Zatem geometryczne znaczenie pochodnej jest następujące:

Pochodna funkcji w punkcie x 0 równa nachyleniu stycznej do wykresu funkcji narysowanej w punkcie odciętym x 0 .

3. Fizyczne znaczenie pochodnej.

Rozważ ruch punktu wzdłuż linii prostej. Niech zostanie podana współrzędna punktu w dowolnym momencie x(t). Wiadomo (z przebiegu fizyki), że średnia prędkość w czasie jest równa stosunkowi przebytej w tym okresie drogi do czasu, czyli

Vav = ∆x/∆t. Przejdźmy do granicy w ostatniej równości jako ∆t → 0.

lim Vav (t) = (t 0) - prędkość chwilowa w czasie t 0, ∆t → 0.

oraz lim = ∆x/∆t = x "(t 0) (z definicji pochodnej).

Zatem (t) = x"(t).

Fizyczne znaczenie pochodnej jest następujące: pochodna funkcjitak = f(x) w punkciex 0 to tempo zmian funkcjif(x) w punkciex 0

Pochodna jest używana w fizyce, aby znaleźć prędkość ze znanej funkcji współrzędnych z czasu, przyspieszenie ze znanej funkcji prędkości z czasu.

 (t) \u003d x „(t) - prędkość,

a(f) = "(t) - przyspieszenie lub

Znając prawo ruchu punktu materialnego po okręgu, można wyznaczyć prędkość kątową i przyspieszenie kątowe podczas ruchu obrotowego:

φ = φ(t) - zmiana kąta w czasie,

ω \u003d φ „(t) - prędkość kątowa,

ε = φ"(t) - przyspieszenie kątowe lub ε = φ"(t).

Jeśli znane jest prawo rozkładu masy niejednorodnego pręta, to można znaleźć gęstość liniową niejednorodnego pręta:

m \u003d m (x) - masa,

x  , l - długość pręta,

p \u003d m ”(x) - gęstość liniowa.

Za pomocą pochodnej rozwiązywane są problemy z teorii sprężystości i drgań harmonicznych. Tak, zgodnie z prawem Hooke'a

F = -kx, x – współrzędna zmienna, k – współczynnik sprężystości sprężyny. Kładąc ω 2 \u003d k / m, otrzymujemy równanie różniczkowe wahadła sprężynowego x „(t) + ω 2 x (t) \u003d 0,

gdzie ω = √k/√m to częstotliwość drgań (l/c), k to sztywność sprężyny (H/m).

Równanie postaci y "+ ω 2 y \u003d 0 nazywa się równaniem oscylacji harmonicznych (mechanicznych, elektrycznych, elektromagnetycznych). Rozwiązaniem takich równań jest funkcja

y = Asin(ωt + φ 0) lub y = Acos(ωt + φ 0), gdzie

A - amplituda drgań, ω - częstotliwość cykliczna,

φ 0 - faza początkowa.

(\large\bf Pochodna funkcji)

Rozważ funkcję y=f(x), podany na przedziale (a,b). Zostawiać x- dowolny stały przedział punktowy (a,b), a x- dowolna liczba, taka, że wartość x+Δx również należy do przedziału (a,b). Ten numer x nazywa się przyrostem argumentów.

Definicja. Przyrost funkcji y=f(x) w punkcie x, odpowiadający przyrostowi argumentu x, zadzwońmy pod numer

Δy = f(x+Δx) - f(x).

Wierzymy, że Δx ≠ 0. Rozważ w danym punkcie stałym x stosunek przyrostu funkcji w tym punkcie do odpowiedniego przyrostu argumentu x

Relacja ta będzie nazywana relacją różnicy. Ponieważ wartość x uważamy za stały, relacja różnicy jest funkcją argumentu x. Ta funkcja jest zdefiniowana dla wszystkich wartości argumentów x, należące do jakiegoś wystarczająco małego sąsiedztwa punktu ∆x=0, z wyjątkiem punktu ∆x=0. Mamy więc prawo do rozważenia kwestii istnienia granicy określonej funkcji dla ∆x → 0.

Definicja. Funkcja pochodna y=f(x) w danym punkcie stałym x nazywa się limitem ∆x → 0 relacja różniczkowa, czyli

Pod warunkiem, że ten limit istnieje.

Przeznaczenie. y (x) lub f′(x).

Geometryczne znaczenie pochodnej: Pochodna funkcji f(x) w tym momencie x równy tangensowi kąta między osią Wół oraz styczną do wykresu tej funkcji w odpowiednim punkcie:

f′(x 0) = \tgα.

Mechaniczne znaczenie pochodnej: Pochodna toru po czasie jest równa prędkości prostoliniowego ruchu punktu:

Równanie stycznej prostej y=f(x) w punkcie M0 (x0,y0) przybiera formę

y-y 0 = f (x 0) (x-x 0).

Normalna do krzywej w pewnym punkcie jest prostopadłą do stycznej w tym samym punkcie. Jeśli f′(x0)≠ 0, to równanie normalnej do prostej y=f(x) w punkcie M0 (x0,y0) jest napisane tak:

Pojęcie różniczkowalności funkcji

Niech funkcja y=f(x) zdefiniowany w pewnym przedziale (a,b), x- pewna stała wartość argumentu z tego przedziału, x- dowolny przyrost argumentu taki, że wartość argumentu x+Δx ∈ (a, b).

Definicja. Funkcjonować y=f(x) nazywa się różniczkowalnym w danym punkcie x jeśli przyrost y ta funkcja w punkcie x, odpowiadający przyrostowi argumentu x, można przedstawić jako

Δy = A Δx +αΔx,

gdzie A jest jakaś liczba niezależna od x, a α - funkcja argumentu x, który jest nieskończenie mały w ∆x → 0.

Ponieważ iloczyn dwóch nieskończenie małych funkcji αΔx jest nieskończenie małym rzędem wyższym niż x(własność 3 funkcji nieskończenie małych), możemy napisać:

∆y = A ∆x +o(∆x).

Twierdzenie. W celu funkcji y=f(x) była różniczkowalna w danym punkcie x, konieczne i wystarczające jest, aby w tym momencie miała skończoną pochodną. W której A=f′(x), tj

Δy = f′(x) Δx +o(Δx).

Operacja znajdowania pochodnej jest zwykle nazywana różniczkowaniem.

Twierdzenie. Jeśli funkcja y=f(x) x, to w tym momencie jest ciągła.

Komentarz. Z ciągłości funkcji y=f(x) w tym momencie x, ogólnie rzecz biorąc, nie wynika z tego, że funkcja jest różniczkowalna f(x) w tym momencie. Na przykład funkcja y=|x|- ciągły w punkcie x=0, ale nie ma pochodnej.

Pojęcie różniczki funkcji

Definicja. różnica funkcji y=f(x) nazywana jest iloczynem pochodnej tej funkcji i przyrostu zmiennej niezależnej x:

dy = y′ ∆x, df(x) = f′(x) ∆x.

Dla funkcji y=x dostajemy dy=dx=x'Δx = 1 Δx= Δx, tj dx=Δx- różniczka zmiennej niezależnej jest równa przyrostowi tej zmiennej.

W ten sposób możemy pisać

dy = y′dx, df(x) = f′(x)dx

Mechanizm różnicowy dy i przyrost y Funkcje y=f(x) w tym momencie x, oba odpowiadają temu samemu przyrostowi argumentu x na ogół nie są sobie równe.

Geometryczne znaczenie różniczki: różniczka funkcji jest równa przyrostowi rzędnej stycznej do wykresu danej funkcji, gdy argument jest zwiększany x.

Zasady różnicowania

Twierdzenie. Jeśli każda z funkcji u(x) oraz v(x) różniczkowalna w danym punkcie x, to suma, różnica, iloczyn i iloraz tych funkcji (iloraz pod warunkiem, że v(x)≠ 0) są również różniczkowalne w tym momencie i obowiązują następujące formuły:

Rozważ złożoną funkcję y=f(φ(x))≡ F(x), gdzie y=f(u), u=φ(x). W tym przypadku ty nazywa pośredni argument, x - zmienna niezależna.

Twierdzenie. Jeśli y=f(u) oraz u=φ(x) są różniczkowalnymi funkcjami ich argumentów, to pochodna złożona funkcja y=f(φ(x)) istnieje i jest równy iloczynowi tej funkcji względem argumentu pośredniego i pochodnej argumentu pośredniego względem zmiennej niezależnej, tj.

Komentarz. Dla funkcji złożonej, która jest superpozycją trzech funkcji y=F(f(φ(x))), reguła różniczkowania ma postać

y′ x = y′ u u′ v v′ x,

gdzie funkcje v=φ(x), u=f(v) oraz y=F(u) są różniczkowalnymi funkcjami ich argumentów.

Twierdzenie. Niech funkcja y=f(x) jest rosnąca (lub malejąca) i ciągła w pewnym sąsiedztwie punktu x0. Niech dodatkowo ta funkcja będzie różniczkowalna we wskazanym punkcie x0 i jego pochodna w tym momencie f′(x0) ≠ 0. Następnie w sąsiedztwie odpowiedniego punktu y0=f(x0) odwrotność y=f(x) funkcjonować x=f -1 (y), a określony funkcja odwrotna różniczkowalna w odpowiednim punkcie y0=f(x0) i dla jego pochodnej w tym momencie tak formuła jest poprawna

Tabela pochodna

Niezmienniczość postaci pierwszej różniczki

Rozważ różnicę funkcji złożonej. Jeśli y=f(x), x=φ(t) są funkcjami różniczkowymi ich argumentów, to pochodna funkcji y=f(φ(t)) wyraża się wzorem

y′ t = y′ x x′ t.

A-prioryte dy=nie dt, wtedy dostajemy

dy = y′ t dt = y′ x x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y′ x dx.

Tak więc udowodniliśmy

Własność niezmienności postaci pierwszej różniczki funkcji: jak w przypadku, gdy argument x jest zmienną niezależną, a w przypadku, gdy argument x sama jest różniczkowalną funkcją nowej zmiennej, różniczką dy Funkcje y=f(x) jest równa pochodnej tej funkcji pomnożonej przez różniczkę argumentu dx.

Zastosowanie różniczki w obliczeniach przybliżonych

Pokazaliśmy, że różnica dy Funkcje y=f(x), ogólnie rzecz biorąc, nie jest równy przyrostowi y tę funkcję. Niemniej jednak aż do nieskończenie małej funkcji wyższego rzędu małości niż x, przybliżona równość

y ≈ dy.

Stosunek nazywa się błędem względnym równości tej równości. Jak ∆y-dy=o(∆x), następnie względny błąd tej równości staje się arbitralnie mały, ponieważ |Δх|.

Jeśli się uwzględni Δy=f(x+δx)-f(x), dy=f′(x)Δx, dostajemy f(x+δx)-f(x) ≈ f′(x)Δx lub

f(x+δx) ≈ f(x) + f′(x)Δx.

Ta przybliżona równość pozwala z błędem o(Δx) wymień funkcję f(x) w małej dzielnicy punktu x(tj. dla małych wartości x) funkcja liniowa argument x stojąc po prawej stronie.

Pochodne wyższych rzędów

Definicja. Druga pochodna (lub pochodna drugiego rzędu) funkcji y=f(x) nazywa się pochodną swojej pierwszej pochodnej.

Notacja drugiej pochodnej funkcji y=f(x):

Mechaniczne znaczenie drugiej pochodnej. Jeśli funkcja y=f(x) opisuje prawo ruchu punkt materialny w linii prostej, to druga pochodna f”(x) jest równe przyspieszeniu poruszającego się punktu w czasie x.

Podobnie definiuje się trzecią i czwartą pochodną.

Definicja. n-ta pochodna (lub pochodna n rzędu) funkcje y=f(x) nazwany pochodną tego n-1-ta pochodna:

y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.

Oznaczenia: y”′, y IV, y V itp.

W zadaniu B9 podany jest wykres funkcji lub pochodnej, z którego należy wyznaczyć jedną z następujących wielkości:

Wartość pochodnej w pewnym punkcie x 0,
Punkty wysokie lub niskie (punkty ekstremalne),
Przedziały funkcji narastających i malejących (przedziały monotoniczności).

Funkcje i pochodne przedstawione w tym zadaniu są zawsze ciągłe, co znacznie upraszcza rozwiązanie. Pomimo tego, że zadanie należy do sekcji Analiza matematyczna, jest to w mocy nawet najsłabszych uczniów, ponieważ nie jest tu wymagana głęboka wiedza teoretyczna.

Aby znaleźć wartość pochodnej, ekstrema i przedziały monotoniczności, istnieją proste i uniwersalne algorytmy - wszystkie zostaną omówione poniżej.

Uważnie przeczytaj stan problemu B9, aby nie popełniać głupich błędów: czasami pojawiają się dość obszerne teksty, ale ważne warunki, które wpływają na przebieg rozwiązania, jest ich niewiele.

Obliczanie wartości pochodnej. Metoda dwupunktowa

Jeżeli do zadania zadany zostanie wykres funkcji f(x), stycznej do tego wykresu w pewnym punkcie x 0 , i wymagane jest znalezienie wartości pochodnej w tym punkcie, to stosuje się następujący algorytm:

Znajdź dwa „odpowiednie” punkty na wykresie stycznej: ich współrzędne muszą być liczbami całkowitymi. Oznaczmy te punkty jako A (x 1 ; y 1) i B (x 2 ; y 2). Poprawnie wypisz współrzędne - to jest kluczowy moment rozwiązania, a każdy błąd tutaj prowadzi do błędnej odpowiedzi.
Znając współrzędne łatwo obliczyć przyrost argumentu Δx = x 2 − x 1 oraz przyrost funkcji Δy = y 2 − y 1 .
Na koniec znajdujemy wartość pochodnej D = Δy/Δx. Innymi słowy, musisz podzielić przyrost funkcji przez przyrost argumentu - i to będzie odpowiedź.

Znowu zauważamy: punkty A i B należy szukać właśnie na stycznej, a nie na wykresie funkcji f(x), jak to często bywa. Styczna będzie koniecznie zawierać co najmniej dwa takie punkty, w przeciwnym razie problem zostanie sformułowany niepoprawnie.

Rozważ punkty A (-3; 2) i B (-1; 6) i znajdź przyrosty:
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Znajdźmy wartość pochodnej: D = Δy/Δx = 4/2 = 2.

Zadanie. Rysunek przedstawia wykres funkcji y \u003d f (x) i styczną do niej w punkcie z odciętą x 0. Znajdź wartość pochodnej funkcji f(x) w punkcie x 0 .

Rozważ punkty A (0; 3) i B (3; 0), znajdź przyrosty:
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

Teraz znajdujemy wartość pochodnej: D = Δy/Δx = -3/3 = -1.

Zadanie. Rysunek przedstawia wykres funkcji y \u003d f (x) i styczną do niej w punkcie z odciętą x 0. Znajdź wartość pochodnej funkcji f(x) w punkcie x 0 .

Rozważ punkty A (0; 2) i B (5; 2) i znajdź przyrosty:
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.

Pozostaje znaleźć wartość pochodnej: D = Δy/Δx = 0/5 = 0.

Z ostatniego przykładu możemy sformułować regułę: jeśli styczna jest równoległa do osi OX, to pochodna funkcji w miejscu styku jest równa zero. W takim przypadku nie musisz nawet niczego obliczać - wystarczy spojrzeć na wykres.

Obliczanie najwyższych i najniższych punktów

Czasami zamiast wykresu funkcji w zadaniu B9 podaje się wykres pochodnej i wymagane jest znalezienie maksymalnego lub minimalnego punktu funkcji. W tym scenariuszu metoda dwupunktowa jest bezużyteczna, ale istnieje inny, jeszcze prostszy algorytm. Najpierw zdefiniujmy terminologię:

Punkt x 0 nazywamy punktem maksymalnym funkcji f(x), jeśli w pewnym sąsiedztwie tego punktu zachodzi nierówność: f(x 0) ≥ f(x).
Punkt x 0 nazywamy punktem minimum funkcji f(x), jeśli w pewnym sąsiedztwie tego punktu zachodzi nierówność: f(x 0) ≤ f(x).

Aby znaleźć maksymalne i minimalne punkty na wykresie pochodnej, wystarczy wykonać następujące czynności:

Przerysuj wykres pochodnej, usuwając wszystkie niepotrzebne informacje. Jak pokazuje praktyka, dodatkowe dane tylko przeszkadzają w podjęciu decyzji. Dlatego zaznaczamy oś współrzędnych zera pochodnej - i tyle.
Znajdź znaki pochodnej na odstępach między zerami. Jeżeli dla jakiegoś punktu x 0 wiadomo, że f'(x 0) ≠ 0, to możliwe są tylko dwie opcje: f'(x 0) ≥ 0 lub f'(x 0) ≤ 0. Znak pochodnej łatwe do ustalenia na podstawie oryginalnego rysunku: jeśli wykres pochodnej leży powyżej osi OX, to f'(x) ≥ 0. I odwrotnie, jeśli wykres pochodnej leży poniżej osi OX, to f'(x) ≤ 0.
Ponownie sprawdzamy zera i znaki pochodnej. Tam, gdzie znak zmienia się z minus na plus, jest punkt minimum. I odwrotnie, jeśli znak pochodnej zmienia się z plusa na minus, jest to punkt maksymalny. Liczenie odbywa się zawsze od lewej do prawej.

Ten schemat działa tylko dla funkcji ciągłych - nie ma innych w problemie B9.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na przedziale [−5; 5]. Znajdź minimalny punkt funkcji f(x) na tym odcinku.

Pozbądźmy się informacje dodatkowe— zostaw tylko granice [−5; 5] oraz zera pochodnej x = -3 i x = 2,5. Zwróć także uwagę na znaki:

Oczywiście w punkcie x = -3 znak pochodnej zmienia się z minus na plus. To jest minimum.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na odcinku [−3; 7]. Znajdź maksymalny punkt funkcji f(x) na tym odcinku.

Przerysujmy wykres, pozostawiając tylko granice [−3; 7] oraz zera pochodnej x = -1,7 i x = 5. Zanotuj znaki pochodnej na wykresie wynikowym. Mamy:

Oczywiście w punkcie x = 5 znak pochodnej zmienia się z plus na minus - to jest punkt maksymalny.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na odcinku [−6; 4]. Znajdź liczbę maksymalnych punktów funkcji f(x) należących do przedziału [−4; 3].

Z warunków zadania wynika, że wystarczy wziąć pod uwagę tylko część grafu ograniczoną odcinkiem [−4; 3]. Dlatego budujemy nowy graf, na którym zaznaczamy tylko granice [−4; 3] i zera pochodnej w nim zawartej. Mianowicie punkty x = -3,5 i x = 2. Otrzymujemy:

Na tym wykresie jest tylko jeden punkt maksymalny x = 2. To na nim znak pochodnej zmienia się z plusa na minus.

Mała uwaga na temat punktów o współrzędnych niecałkowitych. Na przykład w ostatnim zadaniu uwzględniono punkt x = -3,5, ale z takim samym sukcesem możemy przyjąć x = -3,4. Jeśli problem jest sformułowany poprawnie, takie zmiany nie powinny wpływać na odpowiedź, ponieważ punkty „bez stałego miejsca zamieszkania” nie są bezpośrednio zaangażowane w rozwiązanie problemu. Oczywiście przy liczbach całkowitych taka sztuczka nie zadziała.

Znajdowanie przedziałów wzrostu i spadku funkcji

W takim zadaniu, podobnie jak punkty maksimum i minimum, proponuje się znaleźć obszary, w których sama funkcja rośnie lub maleje z wykresu pochodnej. Najpierw zdefiniujmy, czym są rosnąco i malejąco:

Funkcję f(x) nazywamy rosnącą na odcinku, jeśli dla dowolnych dwóch punktów x 1 i x 2 z tego odcinka twierdzenie jest prawdziwe: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Innymi słowy, im większa wartość argumentu, tym większa wartość funkcji.
Funkcję f(x) nazywamy malejącą na odcinku, jeśli dla dowolnych dwóch punktów x 1 i x 2 z tego odcinka twierdzenie jest prawdziwe: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Tych. większa wartość argument odpowiada mniejszej wartości funkcji.

Formułujemy wystarczające warunki do zwiększania i zmniejszania:

Aby funkcja ciągła f(x) rosła na odcinku wystarczy, że jej pochodna wewnątrz odcinka będzie dodatnia, tj. f'(x) ≥ 0.
Aby funkcja ciągła f(x) zmniejszała się na odcinku wystarczy, że jej pochodna wewnątrz odcinka będzie ujemna, tj. f'(x) ≤ 0.

Przyjmujemy te twierdzenia bez dowodu. W ten sposób otrzymujemy schemat znajdowania przedziałów wzrostu i spadku, który pod wieloma względami jest podobny do algorytmu obliczania punktów ekstremów:

Usuń wszystkie zbędne informacje. Na oryginalnym wykresie pochodnej interesują nas przede wszystkim zera funkcji, więc zostawiamy tylko je.
Zaznacz znaki pochodnej w odstępach między zerami. Gdy f'(x) ≥ 0, funkcja rośnie, a gdy f'(x) ≤ 0, maleje. Jeżeli problem ma ograniczenia na zmienną x, dodatkowo zaznaczamy je na nowym wykresie.
Teraz, gdy znamy zachowanie funkcji i ograniczenia, pozostaje obliczyć wymaganą wartość w zadaniu.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na odcinku [−3; 7,5]. Znajdź przedziały malejącej funkcji f(x). W swojej odpowiedzi wpisz sumę liczb całkowitych zawartych w tych przedziałach.

Jak zwykle przerysowujemy wykres i zaznaczamy granice [−3; 7,5] oraz zera pochodnej x = -1,5 i x = 5,3. Następnie zaznaczamy znaki pochodnej. Mamy:

Ponieważ pochodna jest ujemna na przedziale (−1,5), jest to przedział funkcji malejącej. Pozostaje zsumować wszystkie liczby całkowite znajdujące się w tym przedziale:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na odcinku [−10; 4]. Znajdź przedziały rosnącej funkcji f(x). W swojej odpowiedzi wpisz długość największego z nich.

Pozbądźmy się zbędnych informacji. Zostawiamy tylko granice [−10; 4] oraz zerami pochodnej, które tym razem okazały się być czterema: x = -8, x = -6, x = -3 i x = 2. Zanotuj znaki pochodnej i uzyskaj następujący obrazek:

Interesują nas przedziały funkcji narastania, tj. gdzie f'(x) ≥ 0. Na wykresie są dwa takie przedziały: (−8; −6) i (−3; 2). Obliczmy ich długości:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Ponieważ wymagane jest znalezienie długości największego z przedziałów, w odpowiedzi wpisujemy wartość l 2 = 5.

Pochodna funkcji jednej zmiennej.

Wstęp.

prawdziwy rozwój metodologiczny przeznaczony dla studentów Wydziału Inżynierii Przemysłowej i Lądowej. Są one zestawiane w odniesieniu do programu kursu matematyki w rozdziale „Rachunek różniczkowy funkcji jednej zmiennej”.

Zmiany stanowią jeden przewodnik metodologiczny, który zawiera: krótkie informacje teoretyczne; „typowe” zadania i ćwiczenia ze szczegółowymi rozwiązaniami i objaśnieniami tych rozwiązań; opcje sterowania.

Dodatkowe ćwiczenia na końcu każdego akapitu. Taka struktura opracowań sprawia, że nadają się one do samodzielnego opanowania sekcji przy minimalnej pomocy nauczyciela.

§jeden. Definicja pochodnej.

Znaczenie mechaniczne i geometryczne

pochodna.

Pojęcie pochodnej jest jednym z najważniejszych pojęć w analizie matematycznej, powstało już w XVII wieku. Powstanie pojęcia pochodnej historycznie wiąże się z dwoma problemami: problemem prędkości ruchu zmiennego oraz problemem stycznej do krzywej.

Zadania te, mimo różnej treści, prowadzą do tej samej operacji matematycznej, którą należy wykonać na funkcji, która otrzymała w matematyce specjalną nazwę. Nazywa się to operacją różniczkowania funkcji. Wynik operacji różniczkowania nazywamy pochodną.

Zatem pochodna funkcji y=f(x) w punkcie x0 jest granicą (jeśli istnieje) stosunku przyrostu funkcji do przyrostu argumentu
w
.

Pochodna jest zwykle oznaczana w następujący sposób:
.

Więc z definicji

Symbole są również używane do oznaczenia pochodnej
.

Mechaniczne znaczenie pochodnej.

Jeżeli s=s(t) jest prawem ruchu prostoliniowego punktu materialnego, to
to prędkość tego punktu w czasie t.

Geometryczne znaczenie pochodnej.

Jeśli funkcja y=f(x) ma pochodną w punkcie , to nachylenie stycznej do wykresu funkcji w punkcie
równa się
.

Przykład.

Znajdź pochodną funkcji
w punkcie =2:

1) Dajmy punkt =2 przyrost
. Zauważ, że.

2) Znajdź przyrost funkcji w punkcie =2:

3) Skomponuj stosunek przyrostu funkcji do przyrostu argumentu:

Znajdźmy granicę relacji przy
:

Zatem,
.

§ 2. Pochodne niektórych

najprostsze funkcje.

Student musi nauczyć się obliczać pochodne poszczególnych funkcji: y=x,y= i ogólnie y= .

Znajdź pochodną funkcji y=x.

tych. (x)′=1.

Znajdźmy pochodną funkcji

Pochodna

Zostawiać
następnie

Łatwo zauważyć wzór w wyrażeniach na pochodne funkcji potęgowej
przy n=1,2,3.

Stąd,

. (1)

Ten wzór jest ważny dla każdego rzeczywistego n.

W szczególności, korzystając ze wzoru (1), mamy:

;

Przykład.

Znajdź pochodną funkcji

Ta funkcja jest szczególnym przypadkiem funkcji postaci

w
.

Korzystając ze wzoru (1), mamy

Pochodne funkcji y=sin x i y=cos x.

Niech y=sinx.

Podziel przez ∆x, otrzymamy

Przechodząc do granicy jako ∆x→0, mamy

Niech y=cosx .

Przechodząc do granicy jako ∆x→0, otrzymujemy

;
. (2)

§3. Podstawowe zasady różnicowania.

Rozważ zasady różnicowania.

Twierdzenie1 . Jeżeli funkcje u=u(x) i v=v(x) są różniczkowalne w danym punkcie x, to ich suma jest również różniczkowalna w tym punkcie, a pochodna sumy jest równa sumie wyrazów pochodnych: (u+v)"=u"+v".(3 )

Dowód: rozważ funkcję y=f(x)=u(x)+v(x).

Przyrost ∆x argumentu x odpowiada przyrostom ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) funkcji u i v. Wtedy funkcja y zostanie zwiększona

∆y=f(x+∆x)-f(x)=

=--=∆u+∆v.

Stąd,

A więc (u+v)”=u”+v”.

Twierdzenie2. Jeżeli funkcje u=u(x) i v=v(x) są różniczkowalne w danym punkcie x, to ich iloczyn również jest różniczkowalny w tym samym punkcie. W tym przypadku pochodną iloczynu wyznacza się wzorem : (uv) "=u" v + uv ". (4)

Dowód: Niech y=uv, gdzie u i v są różnymi funkcjami x. Niech x będzie zwiększane o ∆x; wtedy u będzie zwiększane o ∆u, v będzie zwiększane o ∆v, a y będzie zwiększane o ∆y.

Mamy y+∆y=(u+∆u)(v+∆v), lub

y+∆y=uv+u∆v+v∆u+∆u∆v.

Zatem ∆y=u∆v+v∆u+∆u∆v.

Stąd

Przechodząc do granicy jako ∆x→0 i biorąc pod uwagę, że u i v nie zależą od ∆x, mamy

Twierdzenie 3. Pochodna ilorazu dwóch funkcji jest równa ułamkowi, którego mianownik jest równy kwadratowi dzielnika, a licznik jest różnicą między iloczynem pochodnej dzielnika przez dzielnik a iloczynem dywidenda przez pochodną dzielnika, tj.

Jeśli
następnie
(5)