Metoda współrzędnych do znajdowania kąta między liniami. Metoda współrzędnych w przestrzeni: wzory i komentarze prowadzącego
Przeczytaj także
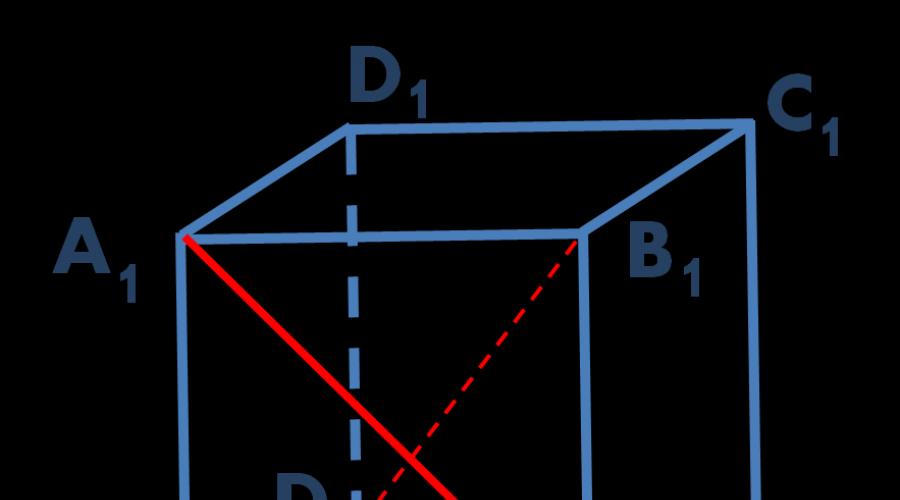
W niniejszym artykule na przykładzie rozwiązania problemu C2 z Unified State Examination przeanalizowano sposób znajdowania współrzędnych za pomocą metody. Przypomnij sobie, że linie są skośne, jeśli nie leżą na tej samej płaszczyźnie. W szczególności, jeśli jedna linia leży w płaszczyźnie, a druga linia przecina tę płaszczyznę w punkcie, który nie leży na pierwszej linii, to takie linie są skośne (patrz rysunek).
Za znalezienie odległości między przecinającymi się liniami niezbędny:
- Narysuj płaszczyznę przez jedną z linii skosu, która jest równoległa do drugiej linii skosu.
- Upuść prostopadłą z dowolnego punktu drugiej linii prostej do wynikowej płaszczyzny. Długość tej prostopadłej będzie pożądaną odległością między liniami.
Przeanalizujmy ten algorytm bardziej szczegółowo na przykładzie rozwiązania problemu C2 z egzaminu Unified State Examination z matematyki.
Odległość między liniami w przestrzeni
Zadanie. w jednej kostce ABCDA 1 B 1 C 1 D 1 znajdź odległość między liniami BA 1 i DB 1 .
Ryż. 1. Rysowanie do zadania
Decyzja. Przez środek przekątnej sześcianu DB 1 (kropka O) narysuj linię równoległą do linii A 1 B. Punkty przecięcia danej linii z krawędziami pne oraz A 1 D 1 oznacza odpowiednio N oraz M. Prosty MN leży w samolocie MNB 1 i równolegle do linii A 1 B, który nie leży w tej płaszczyźnie. Oznacza to, że bezpośredni A 1 B równolegle do płaszczyzny MNB 1 na podstawie równoległości linii prostej i płaszczyzny (rys. 2).
Ryż. 2. Żądana odległość między krzyżującymi się liniami jest równa odległości od dowolnego punktu wybranej linii do przedstawionej płaszczyzny
Szukamy teraz odległości od jakiegoś punktu na linii prostej A 1 B do samolotu MNB jeden . Ta odległość z definicji będzie pożądaną odległością między liniami skosu.
Aby znaleźć tę odległość, używamy metody współrzędnych. Wprowadzamy prostokątny kartezjański układ współrzędnych, tak aby jego początek pokrywał się z punktem B, czyli osią X był skierowany wzdłuż krawędzi BA, oś Y- wzdłuż żebra pne, oś Z- wzdłuż żebra nocleg ze śniadaniem 1 (rys. 3).
Ryż. 3. Wybieramy prostokątny układ współrzędnych kartezjańskich, jak pokazano na rysunku
Znajdujemy równanie płaszczyzny MNB 1 w tym układzie współrzędnych. Aby to zrobić, najpierw określamy współrzędne punktów M, N oraz B 1: 
Otrzymane współrzędne podstawiamy do ogólnego równania prostej i otrzymujemy następujący układ równań:
Z drugiego równania układu otrzymujemy z trzeciego, a następnie z pierwszego, otrzymane wartości podstawiamy do ogólnego równania prostej:
Zauważ, że inaczej samolot MNB Przejdę przez źródło. Dzielimy obie strony tego równania przez i otrzymujemy:
Odległość od punktu do płaszczyzny określa wzór.
Korzystanie z metody współrzędnych podczas obliczania kąta
między samolotami
Bardzo metoda ogólna znalezienie kątamiędzy płaszczyznami - metoda współrzędnych (czasami - z udziałem wektorów). Może być używany, gdy wszystkie inne zostały wypróbowane. Są jednak sytuacje, w których zastosowanie metody współrzędnych ma sens natychmiast, a mianowicie, gdy układ współrzędnych jest w naturalny sposób powiązany z wielościanem określonym w opisie problemu, tj. wyraźnie widoczne są trzy parami prostopadłe linie, na których można ustawić osie współrzędnych. Takie wielościany są prostopadłościan i regularna czworokątna piramida. W pierwszym przypadku układ współrzędnych może być wyznaczony przez krawędzie wychodzące z jednego wierzchołka (rys. 1), w drugim - przez wysokość i przekątne podstawy (rys. 2)
Zastosowanie metody współrzędnych jest następujące.
W przestrzeni wprowadzony zostaje prostokątny układ współrzędnych. Pożądane jest wprowadzenie go w "naturalny" sposób - "dołączenie" go do trzech parami prostopadłych linii, które mają wspólny punkt.
Dla każdej z płaszczyzn, między którymi szukany jest kąt, sporządzane jest równanie. Najłatwiejszym sposobem napisania takiego równania jest znajomość współrzędnych trzech punktów na płaszczyźnie, które nie leżą na jednej prostej.
Równanie płaszczyzny w ogólny widok ma formę Topór + By + Cz + D = 0.
Współczynniki A, B, C w tym równaniu to współrzędne wektora normalnego płaszczyzny (wektor prostopadły do płaszczyzny). Następnie wyznaczamy długości i iloczyn skalarny wektorów normalnych do płaszczyzn, między którymi szukamy kąta. Jeśli współrzędne tych wektorów(A 1, B 1; C 1) i (A 2; B 2; C 2 ), następnie żądany kątobliczone według wzoru
Komentarz. Należy pamiętać, że kąt między wektorami (w przeciwieństwie do kąta między płaszczyznami) może być rozwarty i aby uniknąć ewentualnej niepewności, moduł znajduje się w liczniku po prawej stronie wzoru.
Rozwiąż następujący problem za pomocą metody współrzędnych.
Zadanie 1. Dany jest sześcian ABCDA 1 B 1 C 1 D 1 . Punkt K jest środkiem krawędzi AD, punkt L jest środkiem krawędzi CD. Jaki jest kąt między płaszczyznami A 1 KL i A 1 AD?
Decyzja . Niech początek układu współrzędnych będzie w punkcie ALE, a osie współrzędnych idą wzdłuż promieni AD, AB, AA 1 (rys. 3). Bierzemy krawędź sześcianu równą 2 (wygodnie jest podzielić na pół). Następnie współrzędne punktów A1, K, L to: A 1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).
Ryż. 3
Piszemy równanie samolotu 1 tys ogólnie. Następnie podstawiamy do niego współrzędne wybranych punktów tej płaszczyzny. Otrzymujemy układ trzech równań z czterema niewiadomymi:
Wyrażamy współczynniki A, B, C do D i dojdź do równania
Dzieląc obie części na D (dlaczego D= 0?), a następnie mnożąc przez -2, otrzymujemy równanie płaszczyzny A 1 KL: 2x - 2 y + z - 2 = 0. Wtedy wektor normalny do tej płaszczyzny ma współrzędne (2: -2; 1). Równanie płaszczyzny 1 AD to: y=0, i współrzędne wektora normalnego do niego, na przykład (0; 2: 0) . Zgodnie z powyższym wzorem na cosinus kąta między płaszczyznami otrzymujemy:
W zadaniu C2 z matematyki najczęściej musisz rozwiązać problem, w którym musisz określić:
- Odległość między dwoma punktami
- Odległość od punktu do linii
- Odległość od punktu do płaszczyzny
- Odległość między przecinającymi się liniami
- Kąt między dwiema liniami
- Kąt między linią a płaszczyzną
- Kąt między płaszczyznami
Przejdźmy teraz do algorytmów.
1. Aby określić odległość między dwoma punktami A i B, korzystamy z jednej z dwóch metod:
- Uwzględniamy AB w jakimś trójkącie i określamy jego długość jako bok trójkąta
- Zgodnie ze wzorem
Co więcej, metoda współrzędnych, moim zdaniem, jest najprostsza, wystarczy dokładnie określić współrzędne każdego punktu.
2. Aby określić odległość od punktu do prostej, oblicz
- jako długość odcinka prostopadłego, jeśli można ten odcinek zaliczyć do jakiegoś trójkąta jako jedną z wysokości
3. Odległość od punktu do płaszczyzny wynosi
- długość prostopadłej spadła z tego punktu do płaszczyzny. Aby to zrobić, ostrożnie zbuduj sekcję prostopadłą do płaszczyzny i przechodzącą przez nią dany punkt. Pożądana odległość będzie równa wysokości powstałego nowego wielościanu.
- Korzystanie z metody współrzędnych
Równanie znajdujemy zastępując współrzędne trzech punktów należących do tej płaszczyzny
- Korzystanie z metody wektorowej
- Stosując metodę objętościową, jeśli istnieje ostrosłup ABCM, to odległość od punktu M do płaszczyzny zawierającej trójkąt ABC jest obliczana ze wzoru
- Metodą problemów referencyjnych, które można obejrzeć
4.1. Metoda obliczeniowa krok po kroku:
- skonstruuj wspólny prostopadły dwóch przecinających się linii i znajdź jego długość;
- skonstruować płaszczyznę zawierającą jedną z linii i równoległą do drugiej. Wtedy pożądana odległość będzie równa odległości od punktu do prostej zbudowanej w płaszczyźnie;
- uwzględnij podane linie w płaszczyzny równoległe przechodząc przez podane przecinające się linie, znajdź odległość między tymi płaszczyznami
- skonstruuj płaszczyznę prostopadłą do jednej z tych linii i skonstruuj rzut prostopadły drugiej linii
4.2. Metoda współrzędnych wektora
- Znajdź współrzędne końców odcinka, który jest wspólnym prostopadłym dwóch przecinających się linii
- Znajdowanie odległości między dwoma punktami
Sprowadzamy problem do wyznaczenia długości wektora należącego do prostopadłej, która jest prostopadłą wspólną dwóch przecinających się linii
6. Kąt między linią a płaszczyzną określony przez włączenie go do trójkąt prostokątny jako jeden z ostre rogi, lub metodą koordynatora wektorów
Sposób określania kąta między płaszczyznami zostanie rozważony w następnej lekcji. Te algorytmy rozwiązywania C2 przyczyniają się do pełnego zrozumienia metody rozwiązania problemu. „Aby pomóc magazynowi studenckiemu dla uczniów i ich rodziców”. Czytaj więcej: http://education-club.ru/#ixzz2IXf5GOJU
7. Kąt między płaszczyznami(metoda geometryczna)
- 1. Znajdź linię, wzdłuż której przecinają się samoloty.
- 2. Wybierz punkt na tej linii i narysuj do niego dwie prostopadłe, leżące w tych płaszczyznach. Lub narysuj płaszczyznę prostopadłą do linii przecięcia płaszczyzn.
- 3. Znajdź funkcję trygonometryczną kąta utworzonego przez prostopadłe do linii przecięcia płaszczyzn. Z reguły robimy to za pomocą trójkąta, który zawiera pożądany kąt.
- 4. W odpowiedzi zapisz wartość kąta lub funkcja trygonometryczna kąt.
Kąt między płaszczyznami. metoda współrzędnych. Zadanie C2
Dwie przecinające się płaszczyzny tworzą dwie pary równych kątów dwuściennych: 
Wartość kąta dwuściennego mierzy się wartością odpowiedniego kąta liniowego.
Aby skonstruować kąt liniowy o kącie dwuściennym, musisz wziąć dowolny punkt na linii przecięcia płaszczyzn iw każdej płaszczyźnie narysować promień do tego punktu prostopadle do linii przecięcia płaszczyzn. Kąt utworzony przez te promienie to kąt liniowy kąta dwuściennego:
Wartość kąta między płaszczyznami jest wartością niecałego roku kąta dwuściennego.
Niech nasze samoloty będą dane równaniami:
Cosinus kąta między płaszczyznami znajduje się za pomocą następującego wzoru:
W odpowiedzi piszemy , ponieważ wartość kąta między płaszczyznami jest wartością mniejszego kąta dwuściennego.
Po prawej pryzmat czworokątny 
o boku podstawy 12 i wysokości 21, punkt M jest przyjmowany na krawędzi tak, że . Punkt K jest brane na krawędzi tak, że . Znajdź kąt między płaszczyzną a płaszczyzną.
Zróbmy rysunek. Ponieważ użyjemy metody współrzędnych, od razu wprowadzimy układ współrzędnych: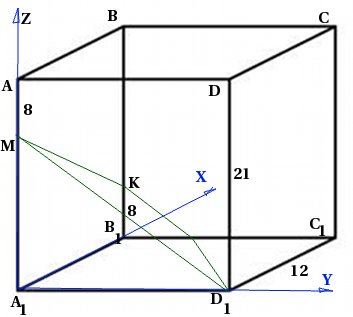 
Teraz stajemy przed zadaniem napisania równań płaszczyzny i płaszczyzny.
Opisałem szczegółowy algorytm znajdowania równania płaszczyzny za pomocą trzech punktów.
Po znalezieniu współczynników w równaniach płaszczyzny i płaszczyzny podstawiamy je do wzoru na znalezienie cosinusa kąta między płaszczyznami i znajdujemy kąt.
Proponuję obejrzeć szczegółowe rozwiązanie wideo tego problemu:
Kolejne zadanie od Inny Vladimirovna Feldman
Lekcje wideo „Koordynacyjna metoda rozwiązywania problemów c-2”
Lekcja 2 http://youtu.be/dKQWG8OZRGo
lekcja 3 http://youtu.be/ddgr0PnbFno
lekcja 4 http://youtu.be/n6yx2pQC0Lo
lekcja 5 http://youtu.be/JkWbxAw1YLI
lekcja 6 http://youtu.be/gybIqCMKBiI
lekcja 7 http://youtu.be/_LpARpYxp5g
lekcja 8 http://youtu.be/XJhyZQoofD8
Metoda współrzędnych jest bardzo wydajna i uniwersalny sposób znajdowanie dowolnych kątów lub odległości między obiektami stereometrycznymi w przestrzeni. Jeśli twój nauczyciel matematyki ma wysokie kwalifikacje, powinien o tym wiedzieć. W przeciwnym razie radziłbym, aby część „C” zmieniła korepetytora. Moje przygotowanie do egzaminu z matematyki C1-C6 zazwyczaj obejmuje analizę podstawowych algorytmów i wzorów opisanych poniżej.
Kąt między liniami a i b
Kąt między liniami w przestrzeni to kąt między wszelkimi przecinającymi się liniami do nich równoległymi. Ten róg równy kątowi między wektorami kierunkowymi tych linii (lub uzupełnia je o 180 stopni).
Jakiego algorytmu używa nauczyciel matematyki, aby znaleźć kąt?
1) Wybierz dowolne wektory 
i posiadanie kierunków linii a i b (równoległych do nich).
2) Określamy współrzędne wektorów oraz przez odpowiednie współrzędne ich początków i końców (współrzędne początku należy odjąć od współrzędnych końca wektora).
3) Znalezione współrzędne podstawiamy do wzoru:
. Aby znaleźć sam kąt, musisz znaleźć cosinus łuku wyniku.
Normalny do samolotu
Normalna do płaszczyzny to dowolny wektor prostopadły do tej płaszczyzny.
Jak znaleźć normalne? Aby znaleźć współrzędne normalnej, wystarczy znać współrzędne dowolnych trzech punktów M, N i K leżących na danej płaszczyźnie. Korzystając z tych współrzędnych, znajdujemy współrzędne wektorów i wymagamy spełnienia warunków i. Przyrównując iloczyn skalarny wektorów do zera, składamy układ równań z trzema zmiennymi, z których możemy znaleźć współrzędne normalnej.
Notatka nauczyciela matematyki : Nie jest konieczne całkowite rozwiązywanie systemu, ponieważ wystarczy wybrać przynajmniej jeden normalny. Aby to zrobić, możesz podstawić dowolną liczbę (na przykład jeden) zamiast dowolnej z jej nieznanych współrzędnych i rozwiązać układ dwóch równań z pozostałymi dwiema niewiadomymi. Jeśli nie ma rozwiązań, oznacza to, że w rodzinie normalnych nie ma takiej, która posiada jednostkę dla wybranej zmiennej. Następnie zastąp je inną zmienną (inną współrzędną) i rozwiąż nowy system. Jeśli znowu spudłujesz, to twoja normalna będzie miała jednostkę na ostatniej współrzędnej i okaże się, że jest równoległa do jakiejś płaszczyzny współrzędnych (w tym przypadku łatwo ją znaleźć bez systemu).
Powiedzmy, że dana jest prosta i płaszczyzna ze współrzędnymi wektora kierunku i normalnej
Kąt pomiędzy linią prostą a płaszczyzną obliczany jest według wzoru:
Niech i będą dowolnymi dwiema normalnymi do danych płaszczyzn. 
Wtedy cosinus kąta między płaszczyznami jest równy modułowi cosinusa kąta między normalnymi:
Równanie płaszczyzny w przestrzeni
Punkty spełniające równość tworzą płaszczyznę z normalną . Współczynnik odpowiada za wielkość odchylenia (przesunięcie równoległe) między dwiema płaszczyznami o tej samej zadanej normalnej. Aby napisać równanie płaszczyzny, musisz najpierw znaleźć jej normalną (jak opisano powyżej), a następnie podstawić współrzędne dowolnego punktu na płaszczyźnie wraz ze współrzędnymi znalezionej normalnej do równania i znaleźć współczynnik .
Średnia MOU Szkoła ogólnokształcąca №13
Metoda współrzędnych
2008
Plan:
Wstęp
Istota metody współrzędnych
Systemy metod współrzędnych
Podstawowe wzory metody współrzędnych
Zadania o różnych poziomach złożoności na temat „Metoda współrzędnych”
Wniosek
Bibliografia
Wstęp
W geometrii zastosuj różne metody rozwiązywanie problemów to metoda syntetyczna (czysto geometryczna), metoda przekształceń, metoda wektorowa, metoda współrzędnych i inne. Zajmują różne stanowiska w szkole. Główną metodę uważa się za syntetyczną, a spośród pozostałych metoda współrzędnych zajmuje najwyższą pozycję, ponieważ jest ściśle związana z algebrą. Elegancję metody syntetycznej osiąga się za pomocą intuicji, domysłów, dodatkowych konstrukcji. Metoda współrzędnych tego nie wymaga: rozwiązywanie problemów jest w dużej mierze zalgorytmizowane, co w większości przypadków upraszcza wyszukiwanie i rozwiązywanie samego problemu.
Metoda współrzędnych- sposób na określenie położenia punktu lub ciała za pomocą liczb lub innych symboli.
System współrzędnych- zbiór definicji implementujący metodę współrzędnych, tj. sposób na zdefiniowanie położenia punktu lub ciała za pomocą liczb lub innych symboli.
Nadając badaniom geometrycznym charakter algebraiczny, metoda współrzędnych najbardziej przenosi się na geometrię ważna cecha algebra - jednolitość sposobów rozwiązywania problemów. Jeśli w geometrii arytmetycznej i elementarnej z reguły trzeba szukać specjalnego sposobu rozwiązania każdego problemu, to w algebrze i geometrii analitycznej rozwiązania są przeprowadzane według planu wspólnego dla wszystkich problemów, łatwo dopasowującego się do każdego problemu . Główną wartością metody współrzędnych jest przejście na geometrię metod rozwiązywania problemów związanych z algebrą, a co za tym idzie posiadanie dużej ogólności. Kolejną zaletą metody współrzędnych jest to, że jej zastosowanie eliminuje potrzebę odwoływania się do wizualnej reprezentacji złożonych obrazów przestrzennych.
Cele badania metody współrzędnych
Można wyróżnić następujące cele badania metody współrzędnych na szkolnym kursie geometrii:
daj uczniom skuteczna metoda rozwiązywanie problemów i dowodzenie szeregu twierdzeń;
pokazać na podstawie tej metody ścisły związek między algebrą a geometrią;
promowanie rozwoju komputerowej i graficznej kultury studentów.
Istota metody współrzędnych
Istota metody współrzędnych jako metody rozwiązywania zadań polega na tym, że wyznaczając figury równaniami i wyrażając różne zależności geometryczne we współrzędnych, możemy rozwiązać problem geometryczny za pomocą algebry. I odwrotnie, używając współrzędnych, można geometrycznie interpretować relacje i fakty algebraiczne i analityczne, a tym samym stosować geometrię do rozwiązywania problemów algebraicznych.
Metoda współrzędnych jest metodą ogólną.
W związku kurs szkolny geometrii, można powiedzieć, że w niektórych przypadkach metoda współrzędnych umożliwia budowanie dowodów i rozwiązywanie wielu problemów bardziej racjonalnie, piękniej niż metodami czysto geometrycznymi. Metoda współrzędnych wiąże się jednak z jedną złożonością geometryczną. Ten sam problem otrzymuje inną reprezentację analityczną w zależności od tego czy innego wyboru układu współrzędnych. I tylko wystarczające doświadczenie pozwala wybrać najbardziej odpowiedni układ współrzędnych.
Układy współrzędnych:
1. Prostokątny (kartezjański) układ współrzędnych (René Kartezjusza (1596-1650))
Urodzony w Turynie w zamożnej rodzinie szlacheckiej. Kilka dni później jego matka zmarła na gruźlicę, pielęgniarka wyszła i uratowała mu życie. W wieku 8 lat Rene został objęty pełną opieką jednej z najlepszych kolegiów jezuickich. Kartezjusz od dzieciństwa uwielbiał rozwiązywać problemy i wszystko czas wolny poświęcony nauce matematyki. Kartezjusz studiował filozofię, matematykę, fizykę, astronomię i filologię. Kartezjusz jako pierwszy pokazał, jak matematykę można zastosować do reprezentacji wizualnej i Analiza matematyczna dla szerokiej gamy zjawisk przyrodniczych i społecznych.
Po raz pierwszy pojawił się w jego pracy:
zmienne
surowe prawa geometrii przetłumaczone na język algebraiczny
proponowano zobrazować związki między zjawiskami naturalnymi liniami krzywymi i zapisać je za pomocą wyrażeń algebraicznych
Łacińskie litery stałych i zmienne, a także notacja stopni
3.
Biegunowy układ współrzędnych
. Współrzędne biegunowe punktu definiuje się w następujący sposób: promień numeryczny OX jest określony na płaszczyźnie. Początek wiązki, punkt O, nazywamy biegunem, a oś OX nazywamy osią biegunową. Aby określić położenie punktu M w układzie współrzędnych biegunowych, należy wskazać odległość od bieguna do tego punktu oraz kierunek, w którym się on znajduje. Odległość od punktu do bieguna nazywana jest promieniem biegunowym punktu i jest oznaczona literą 
(wymawiane „ro”).
Kierunek wyznacza kąt obrotu od belki OX do belki OM
Metoda współrzędnych
formuły
Długość wektora według jego współrzędnych 
Wzór na znalezienie współrzędnych punktu środkowego odcinka 
Odległość między dwoma punktami 
Równanie okręgu,(koło w środku 
,promień r)
Równanie prostej 
, biorąc pod uwagę to 
(równanie prostej w prostokątnym układzie współrzędnych jest równaniem pierwszego stopnia)
Każda linia jest podana przez równanie. W której liczby a,b,c są wyznaczane dla każdej prostej jednoznacznie aż do proporcjonalności (jeśli pomnożymy je przez tę samą liczbę) 
, to wynikowe równanie 
zdefiniuje tę samą linię).
Odległość od punktu 
prosto m ,równa się 
Odległość od punktu 
do samolotu 
, równa się 
Wyprowadzanie formuł .
Upuść z punktu prostopadle AB do płaszczyzny , podane przez równanie .Zostawiać 
- punkt przecięcia tej prostopadłej z płaszczyzną . Następnie 
- odległość od punktu do samolotu .Ponieważ wektor jest prostopadły do płaszczyzny , jest współliniowy z wektorem 
.To znaczy, że 
,jeśli 
, lub 
,jeśli 
, tj 
.Przepiszmy tę równość we współrzędnych: .Ale punkt 
, Dlatego 
oraz =
.
(Twierdzenie Stuarta)
Dany trójkąt ABC i na jego podstawie punkt D leżący między punktami B i C, to równość jest prawdziwa:
Dowód:
Wybierzmy układ współrzędnych, jak pokazano na rysunku.
W wybranym układzie współrzędnych wierzchołki trójkąta ABC będzie miał następujące współrzędne:
Topór 1 ;y 1 ), B(x 2 ;0), C(0;0) i kropka D(x 3 ;0) .
Obliczamy wszystkie wielkości zawarte w równości:
Zamień wszystkie te wartości na lewa strona równość:
co było do okazania
Zadanie 1. Znajdź odległość od punktu A(-1,3,0) do płaszczyzny , podane przez równanie x -3y -2z +5=0.
Decyzja. Zgodnie ze wzorem 
otrzymujemy:
.
Odpowiedź: .
Zadanie 2. Wektory
oraz 
są wzajemnie prostopadłe, a wektor 
tworzy z każdym z nich kąt 60˚. Wiedząc co 
, oblicz iloczyn skalarny 
Decyzja. Zgodnie z właściwością iloczynu skalarnego rozszerzamy nawiasy:
=
Z definicji iloczynu skalarnego otrzymujemy: 
(jak oraz prostopadły);
Podstawiając te wartości do wyrażenia =, znajdź iloczyn skalarny: =0 – 50+9 12 -120=-62
Odpowiedź: =0 – 50+9 12 -120=-62
Zadanie 3.Dan kwadrat ABCD
z imprezą a
. Określ odległość między punktem środkowym segmentu JESTEM
, gdzie M
- środek Słońce
i punkt N
od strony płyta CD
dzieląc to tak, że CN:ND=3:1
.
Decyzja:
Wybierzmy układ współrzędnych, jak pokazano na rysunku.
Następnie punkty M oraz N , w zależności od warunku będzie miał współrzędne:
odpowiednio.
Jak mi - środek JESTEM , wtedy jego współrzędne będą następujące:
Znaczy, mi
.
Znajdź odległość między punktami mi oraz N :
Odpowiedź: EN = 
Zadanie 4 Mając sześcian ABCDA1B1C1D1 o krawędziach o długości 1. Punkt E jest brany na jego bocznej krawędzi AA 1 tak, że
.Punkt F jest brany na krawędzi BC tak, że 
Płaszczyzna przebiega przez środek sześcianu i punkty E i F . Znajdź odległość od wierzchołka B do płaszczyzny .
Decyzja. 
Wprowadzamy układ współrzędnych wyśrodkowany na wierzchołku B. Wtedy 
Znajdźmy równanie samolotu . Niech to równanie będzie . Zauważ, że nie przechodzi przez źródło, więc 
a równanie można podzielić przez D; otrzymujemy następujące równanie: 
lub topór + przez + cz +1=0
Aby wyznaczyć nieznane współczynniki a, b i c, podstawiamy do równania ax + przez + cz +1=0 współrzędne trzech punktów E, F i O, które spełniają to równanie (ponieważ punkty te leżą na płaszczyźnie ). Otrzymujemy układ równań: 
Przekształcamy układ mnożąc pierwsze równanie przez 3, drugie przez 4, trzecie przez -6 i dodając pierwsze równanie do trzeciego, otrzymujemy 
,b=-4, 
.Więc równanie płaszczyzny ma postać:
5x + 8y - 9z - 2 = 0. Teraz znajdujemy odległość od punktu В1(0,0,1) do płaszczyzny 
.
Odpowiedź: .
Zadanie 5.baza trójkątna piramida SABC to trójkąt równoboczny ABC, którego bok jest równy 4. Wiadomo również, że AS = BS =
i CS = 3. Znajdź obszar kuli opisanej przez tę piramidę.