Suma logarytmów o tej samej podstawie. Podstawowa tożsamość logarytmiczna. Podstawienie granic całkowych
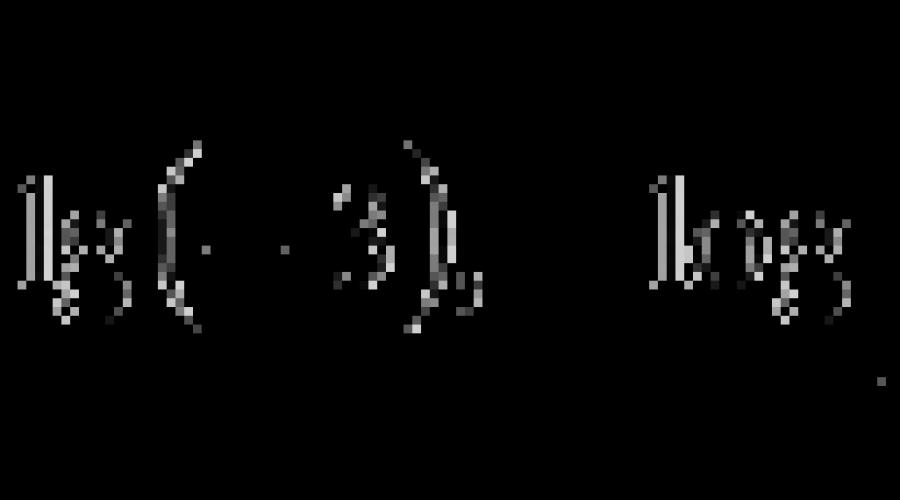
Celem tego artykułu jest logarytm. Tutaj podamy definicję logarytmu, pokażemy akceptowaną notację, podamy przykłady logarytmów oraz porozmawiamy o logarytmach naturalnych i dziesiętnych. Następnie spójrzmy na główny tożsamość logarytmiczna.
Nawigacja strony.
Definicja logarytmu
Pojęcie logarytmu pojawia się podczas rozwiązywania problemu w pewnym sensie odwrotnie, gdy trzeba znaleźć wykładnik według znana wartość stopień i znana podstawa.
Ale dość wstępów, czas odpowiedzieć na pytanie „co to jest logarytm”? Podajmy odpowiednią definicję.
Definicja.
Logarytm b na podstawie a, gdzie a>0, a≠1 i b>0 to wykładnik, do którego należy podnieść liczbę a, aby w rezultacie otrzymać b.
Na tym etapie zauważamy, że wypowiadane słowo „logarytm” powinno natychmiast rodzić dwa pytania uzupełniające: „jaka liczba” i „na jakiej podstawie”. Innymi słowy, po prostu nie ma logarytmu, a jedynie logarytm liczby o jakiejś podstawie.
Wejdźmy od razu zapis logarytmiczny: logarytm liczby b o podstawie a jest zwykle oznaczany jako log a b. Logarytm liczby b do podstawy e i logarytm do podstawy 10 mają swoje specjalne oznaczenia odpowiednio lnb i logb, to znaczy piszą nie log e b, ale lnb, a nie log 10 b, ale lgb.
Teraz możemy dać: .
I zapisy  nie ma sensu, ponieważ w pierwszym z nich pod znakiem logarytmu znajduje się liczba ujemna, w drugim liczba ujemna w podstawie, a w trzecim liczba ujemna pod znakiem logarytmu i jednostka w baza.
nie ma sensu, ponieważ w pierwszym z nich pod znakiem logarytmu znajduje się liczba ujemna, w drugim liczba ujemna w podstawie, a w trzecim liczba ujemna pod znakiem logarytmu i jednostka w baza.
Teraz porozmawiajmy o zasady czytania logarytmów. Zapis log a b odczytuje się jako „logarytm b o podstawie a”. Na przykład log 2 3 to logarytm z trzech do podstawy 2 i logarytm z dwóch i dwóch trzecich przy podstawie 2 Pierwiastek kwadratowy z pięciu. Nazywa się logarytm o podstawie e naturalny logarytm, a zapis lnb brzmi „logarytm naturalny b”. Na przykład ln7 jest logarytmem naturalnym liczby siedem i będziemy go czytać jako logarytm naturalny liczby pi. Logarytm o podstawie 10 ma również specjalną nazwę - logarytm dziesiętny, a lgb odczytuje się jako „logarytm dziesiętny z b”. Na przykład lg1 to logarytm dziesiętny z jednego, a lg2,75 to logarytm dziesiętny z dwóch przecinek siedem pięć setnych.
Warto osobno zająć się warunkami a>0, a≠1 i b>0, przy których podana jest definicja logarytmu. Wyjaśnijmy, skąd wzięły się te ograniczenia. Pomoże nam w tym równość postaci zwanej , która bezpośrednio wynika z podanej powyżej definicji logarytmu.
Zacznijmy od a≠1. Ponieważ jeden do dowolnej potęgi jest równy jeden, równość może być prawdziwa tylko wtedy, gdy b=1, ale log 1 1 może być dowolną liczbą rzeczywistą. Aby uniknąć tej dwuznaczności, przyjmuje się a≠1.
Uzasadnijmy celowość warunku a>0. Przy a=0, z definicji logarytmu, mielibyśmy równość, co jest możliwe tylko przy b=0. Ale wtedy log 0 0 może być dowolną niezerową liczbą rzeczywistą, ponieważ zero do dowolnej niezerowej potęgi wynosi zero. Warunek a≠0 pozwala uniknąć tej dwuznaczności. A kiedy A<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и ирracjonalny wskaźnik zdefiniowane tylko dla zasad nieujemnych. Zatem warunek a>0 jest akceptowany.
Wreszcie warunek b>0 wynika z nierówności a>0, ponieważ , a wartość potęgi o podstawie dodatniej a jest zawsze dodatnia.
Na zakończenie tego punktu powiedzmy, że podana definicja logarytmu pozwala od razu wskazać wartość logarytmu, gdy liczba pod znakiem logarytmu jest pewną potęgą podstawy. Rzeczywiście, definicja logarytmu pozwala nam stwierdzić, że jeśli b=a p, to logarytm liczby b o podstawie a jest równy p. Oznacza to, że log równości a a p = p jest prawdziwy. Na przykład wiemy, że 2 3 = 8, a następnie log 2 8 = 3. Porozmawiamy o tym więcej w artykule.
Logarytmy, jak każdą liczbę, można dodawać, odejmować i przekształcać na różne sposoby. Ale ponieważ logarytmy nie są dokładnie zwykłe liczby, istnieją tu zasady, które są tzw główne właściwości.
Zdecydowanie musisz znać te zasady - bez nich nie da się rozwiązać ani jednego poważnego problemu logarytmicznego. W dodatku jest ich bardzo mało – wszystkiego można się nauczyć w jeden dzień. Więc zacznijmy.
Dodawanie i odejmowanie logarytmów
Rozważmy dwa logarytmy o tych samych podstawach: log A X i zaloguj się A y. Następnie można je dodawać i odejmować oraz:
- dziennik A X+ log A y=log A (X · y);
- dziennik A X− log A y=log A (X : y).
Zatem suma logarytmów jest równa logarytmowi iloczynu, a różnica jest równa logarytmowi ilorazu. Notatka: kluczowy moment Tutaj - identyczne podstawy. Jeśli przyczyny są inne, zasady te nie działają!
Te formuły pomogą ci obliczyć wyrażenie logarytmiczne, nawet jeśli nie uwzględnisz jego poszczególnych części (patrz lekcja „Co to jest logarytm”). Spójrz na przykłady i zobacz:
Dziennik 6 4 + dziennik 6 9.
Ponieważ logarytmy mają tę samą podstawę, stosujemy wzór na sumę:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Zadanie. Znajdź wartość wyrażenia: log 2 48 − log 2 3.
Podstawy są takie same, używamy wzoru na różnicę:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Zadanie. Znajdź wartość wyrażenia: log 3 135 − log 3 5.
Ponownie podstawy są takie same, więc mamy:
log 3 135 - log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Jak widać, oryginalne wyrażenia składają się ze „złych” logarytmów, których nie oblicza się osobno. Ale po przekształceniach otrzymuje się liczby całkowicie normalne. Wiele z nich opiera się na tym fakcie papiery testowe. Tak, wyrażenia przypominające test są oferowane z całą powagą (czasami praktycznie bez zmian) w ramach ujednoliconego egzaminu państwowego.
Wyodrębnianie wykładnika z logarytmu
Teraz skomplikujmy trochę zadanie. A co jeśli podstawą lub argumentem logarytmu jest potęga? Następnie wykładnik tego stopnia można odjąć od znaku logarytmu według następujących zasad:
Łatwo to zauważyć ostatnia zasada podąża za pierwszymi dwoma. Ale i tak lepiej o tym pamiętać - w niektórych przypadkach znacznie zmniejszy to ilość obliczeń.
Oczywiście wszystkie te zasady mają sens, jeśli przestrzega się ODZ logarytmu: A > 0, A ≠ 1, X> 0. I jeszcze jedno: naucz się stosować wszystkie formuły nie tylko od lewej do prawej, ale także odwrotnie, tj. Liczby przed znakiem logarytmu można wprowadzić do samego logarytmu. To jest to, czego najczęściej potrzeba.
Zadanie. Znajdź wartość wyrażenia: log 7 49 6 .
Pozbądźmy się stopnia w argumencie, korzystając z pierwszej formuły:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Zadanie. Znajdź znaczenie wyrażenia:
[Podpis do zdjęcia]
Zauważ, że w mianowniku znajduje się logarytm, którego podstawą i argumentem są dokładne potęgi: 16 = 2 4 ; 49 = 7 2. Mamy:
 [Podpis do zdjęcia]
[Podpis do zdjęcia] Myślę, że ostatni przykład wymaga pewnego wyjaśnienia. Gdzie się podziały logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawiliśmy podstawę i argument stojącego tam logarytmu w postaci potęg i wyciągnęliśmy wykładniki - otrzymaliśmy ułamek „trzypiętrowy”.
Teraz spójrzmy na ułamek główny. Licznik i mianownik zawierają tę samą liczbę: log 2 7. Ponieważ log 2 7 ≠ 0, możemy ułamek skrócić - w mianowniku pozostanie 2/4. Zgodnie z zasadami arytmetyki czwórkę można przenieść do licznika, co też uczyniono. W rezultacie otrzymaliśmy odpowiedź: 2.
Przejście na nowy fundament
Mówiąc o zasadach dodawania i odejmowania logarytmów, szczególnie podkreśliłem, że działają one tylko na tych samych podstawach. A co jeśli przyczyny są inne? A co jeśli nie są to dokładne potęgi tej samej liczby?
Na ratunek przychodzą formuły przejścia na nowy fundament. Sformułujmy je w formie twierdzenia:
Niech zostanie podany logarytm A X. Następnie dla dowolnej liczby C takie, że C> 0 i C≠ 1, prawdziwa jest równość:
[Podpis do zdjęcia]
W szczególności, jeśli umieścimy C = X, otrzymujemy:
[Podpis do zdjęcia]
Z drugiego wzoru wynika, że podstawę i argument logarytmu można zamienić, ale w tym przypadku całe wyrażenie zostaje „odwrócone”, tj. logarytm pojawia się w mianowniku.
Formuły te rzadko występują w zwykłych wyrażeniach liczbowych. Można ocenić, jak wygodne są one tylko przy rozwiązywaniu równań logarytmicznych i nierówności.
Istnieją jednak problemy, których w ogóle nie można rozwiązać, chyba że przeprowadzka do nowego fundamentu. Przyjrzyjmy się kilku z nich:
Zadanie. Znajdź wartość wyrażenia: log 5 16 log 2 25.
Należy zauważyć, że argumenty obu logarytmów zawierają dokładne potęgi. Wyjmijmy wskaźniki: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
Teraz „odwróćmy” drugi logarytm:
[Podpis do zdjęcia]Ponieważ iloczyn nie zmienia się przy przestawianiu czynników, spokojnie pomnożyliśmy cztery przez dwa, a potem zajęliśmy się logarytmami.
Zadanie. Znajdź wartość wyrażenia: log 9 100 lg 3.
Podstawą i argumentem pierwszego logarytmu są potęgi dokładne. Zapiszmy to i pozbądźmy się wskaźników:
[Podpis do zdjęcia]Teraz pozbądźmy się logarytmu dziesiętnego, przechodząc do nowej podstawy:
[Podpis do zdjęcia]Podstawowa tożsamość logarytmiczna
Często w procesie rozwiązywania konieczne jest przedstawienie liczby jako logarytm o danej podstawie. W takim przypadku pomocne będą nam następujące formuły:
W pierwszym przypadku liczba N staje się wyznacznikiem stopnia stojącego w argumentacji. Numer N może być absolutnie dowolna, ponieważ jest to tylko wartość logarytmiczna.
Druga formuła jest właściwie sparafrazowaną definicją. Tak to się nazywa: podstawowa tożsamość logarytmiczna.
W rzeczywistości, co się stanie, jeśli numer B podnieść do takiej potęgi, że liczba B do tej potęgi daje liczbę A? Zgadza się: otrzymujesz ten sam numer A. Przeczytaj uważnie ten akapit jeszcze raz – wiele osób utknie na nim.
Podobnie jak wzory na przejście do nowej bazy, podstawowa tożsamość logarytmiczna jest czasami jedynym możliwym rozwiązaniem.
Zadanie. Znajdź znaczenie wyrażenia:
[Podpis do zdjęcia]
Zauważ, że log 25 64 = log 5 8 - po prostu wzięliśmy kwadrat z podstawy i argumentu logarytmu. Uwzględniając zasady mnożenia potęg o tej samej podstawie otrzymujemy:
[Podpis do zdjęcia]Jeśli ktoś nie wie, to było prawdziwe zadanie z Egzaminu Państwowego Unified :)
Jednostka logarytmiczna i zero logarytmiczne
Podsumowując, podam dwie tożsamości, które trudno nazwać właściwościami - są one raczej konsekwencjami definicji logarytmu. Ciągle pojawiają się w problemach i, co zaskakujące, stwarzają problemy nawet dla „zaawansowanych” uczniów.
- dziennik A A= 1 jest jednostką logarytmiczną. Zapamiętaj raz na zawsze: logarytm do dowolnej podstawy A od tej podstawy jest równa jeden.
- dziennik A 1 = 0 to zero logarytmiczne. Baza A może być dowolna, ale jeśli argument zawiera jeden, logarytm jest równy zeru! Ponieważ A 0 = 1 jest bezpośrednią konsekwencją definicji.
To wszystkie właściwości. Pamiętaj, aby przećwiczyć ich wdrażanie! Pobierz ściągawkę znajdującą się na początku lekcji, wydrukuj ją i rozwiąż zadania.
Jak wiadomo, przy mnożeniu wyrażeń przez potęgi ich wykładniki zawsze się sumują (a b *a c = a b+c). Ten prawo matematyczne został wyprowadzony przez Archimedesa, a później, w VIII wieku, matematyk Virasen stworzył tabelę wykładników całkowitych. To oni posłużyli do dalszego odkrycia logarytmów. Przykłady wykorzystania tej funkcji można znaleźć niemal wszędzie tam, gdzie konieczne jest uproszczenie uciążliwego mnożenia poprzez proste dodawanie. Jeśli poświęcisz 10 minut na przeczytanie tego artykułu, wyjaśnimy Ci, czym są logarytmy i jak z nimi pracować. Prostym i przystępnym językiem.
Definicja w matematyce
Logarytm jest wyrażeniem w następującej postaci: log a b=c, to znaczy logarytm dowolnej liczby nieujemnej (czyli dowolnej liczby dodatniej) „b” do jej podstawy „a” jest uważany za potęgę „c” ”, do którego należy podnieść podstawę „a”, aby ostatecznie uzyskać wartość „b”. Przeanalizujmy logarytm na przykładach, powiedzmy, że istnieje wyrażenie log 2 8. Jak znaleźć odpowiedź? To bardzo proste, trzeba znaleźć taką potęgę, aby od 2 do wymaganej potęgi otrzymać 8. Po wykonaniu kilku obliczeń w głowie otrzymamy liczbę 3! I to prawda, ponieważ 2 do potęgi 3 daje odpowiedź 8.
Rodzaje logarytmów
Dla wielu uczniów i studentów ten temat wydaje się skomplikowany i niezrozumiały, ale w rzeczywistości logarytmy nie są takie straszne, najważniejsze jest zrozumienie ich ogólnego znaczenia i zapamiętanie ich właściwości i niektórych zasad. Są trzy poszczególne gatunki wyrażenia logarytmiczne:
- Logarytm naturalny ln a, gdzie podstawą jest liczba Eulera (e = 2,7).
- Dziesiętne a, gdzie podstawa wynosi 10.
- Logarytm dowolnej liczby b o podstawie a>1.
Każdy z nich jest zdecydowany w standardowy sposób, co obejmuje uproszczenie, redukcję i późniejszą redukcję do jednego logarytmu za pomocą twierdzeń logarytmicznych. Za zdobycie prawidłowe wartości logarytmy, przy ich rozwiązywaniu należy pamiętać o ich właściwościach i kolejności działań.
Zasady i pewne ograniczenia
W matematyce istnieje kilka reguł-ograniczeń, które są akceptowane jako aksjomat, to znaczy nie podlegają dyskusji i są prawdą. Na przykład nie da się podzielić liczb przez zero, nie da się też z nich wydobyć pierwiastka parzystego liczby ujemne. Logarytmy również mają swoje własne zasady, zgodnie z którymi można łatwo nauczyć się pracy nawet z długimi i pojemnymi wyrażeniami logarytmicznymi:
- Podstawa „a” musi być zawsze większa od zera, a nie równa 1, w przeciwnym razie wyrażenie straci sens, ponieważ „1” i „0” w dowolnym stopniu są zawsze równe swoim wartościom;
- jeśli a > 0, to a b > 0, to okazuje się, że „c” również musi być większe od zera.
Jak rozwiązywać logarytmy?
Na przykład podano zadanie znalezienia odpowiedzi na równanie 10 x = 100. Jest to bardzo proste, trzeba wybrać potęgę, podnosząc liczbę dziesięć do uzyskania 100. To oczywiście jest 10 2 = 100.
Przedstawmy teraz to wyrażenie w formie logarytmicznej. Otrzymujemy log 10 100 = 2. Przy rozwiązywaniu logarytmów wszystkie działania praktycznie zbiegają się, aby znaleźć potęgę, do której należy wprowadzić podstawę logarytmu, aby otrzymać daną liczbę.
Aby dokładnie określić wartość nieznanego stopnia, musisz nauczyć się pracować z tabelą stopni. To wygląda tak:

Jak widać, niektóre wykładniki można odgadnąć intuicyjnie, jeśli masz techniczny umysł i wiedzę o tabliczce mnożenia. Jednak dla duże wartości będziesz potrzebować tabeli stopni. Mogą z niego korzystać nawet ci, którzy nie mają zielonego pojęcia o skomplikowanych zagadnieniach matematycznych. W lewej kolumnie znajdują się liczby (podstawa a), górny rząd liczb to wartość potęgi c, do której podnoszona jest liczba a. Na przecięciu komórki zawierają wartości liczbowe będące odpowiedzią (a c =b). Weźmy na przykład pierwszą komórkę z liczbą 10 i podnieś ją do kwadratu, otrzymamy wartość 100, która jest wskazana na przecięciu naszych dwóch komórek. Wszystko jest tak proste i łatwe, że nawet najbardziej prawdziwy humanista zrozumie!
Równania i nierówności
Okazuje się, że w pewnych warunkach wykładnikiem jest logarytm. Dlatego dowolne matematyczne wyrażenia liczbowe można zapisać jako równość logarytmiczną. Na przykład 3 4 = 81 można zapisać jako logarytm o podstawie 3 z 81 równy cztery (log 3 81 = 4). Dla potęg ujemnych zasady są takie same: 2 -5 = 1/32 zapisujemy jako logarytm, otrzymujemy log 2 (1/32) = -5. Jednym z najbardziej fascynujących działów matematyki jest temat „logarytmów”. Przyjrzymy się przykładom i rozwiązaniom równań poniżej, zaraz po przestudiowaniu ich właściwości. Przyjrzyjmy się teraz, jak wyglądają nierówności i jak odróżnić je od równań.

Biorąc pod uwagę wyrażenie w postaci: log 2 (x-1) > 3 - tak nierówność logarytmiczna, ponieważ nieznana wartość „x” znajduje się pod znakiem logarytmu. A także w wyrażeniu porównywane są dwie wielkości: logarytm żądanej liczby do podstawy dwa jest większy niż liczba trzy.
Najważniejsza różnica między równaniami logarytmicznymi a nierównością polega na tym, że równania z logarytmami (przykład - logarytm 2 x = √9) implikują w odpowiedzi jedną lub więcej określonych wartości liczbowych, natomiast przy rozwiązywaniu nierówności definiuje się je jako obszar dopuszczalne wartości i punkty przerwania tej funkcji. W rezultacie odpowiedź nie jest prostym zbiorem pojedynczych liczb, jak w przypadku odpowiedzi na równanie, ale ciągłą serią lub zbiorem liczb.

Podstawowe twierdzenia o logarytmach
Podczas rozwiązywania prymitywnych zadań znajdowania wartości logarytmu jego właściwości mogą nie być znane. Jeśli jednak chodzi o równania czy nierówności logarytmiczne, to przede wszystkim należy jasno zrozumieć i zastosować w praktyce wszystkie podstawowe właściwości logarytmów. Przyjrzymy się przykładom równań później; najpierw przyjrzyjmy się każdej właściwości bardziej szczegółowo.
- Główna tożsamość wygląda następująco: a logaB =B. Ma zastosowanie tylko wtedy, gdy a jest większe niż 0, a nie równe jedności, a B jest większe niż zero.
- Logarytm iloczynu można przedstawić za pomocą następującego wzoru: log d (s 1 * s 2) = log d s 1 + log d s 2. W tym przypadku warunkiem obowiązkowym jest: d, s 1 i s 2 > 0; a≠1. Możesz przedstawić dowód tej formuły logarytmicznej wraz z przykładami i rozwiązaniem. Zapiszmy a s 1 = f 1 i zalogujmy a s 2 = f 2, następnie a f1 = s 1, a f2 = s 2. Otrzymujemy, że s 1 * s 2 = a f1 *a f2 = a f1+f2 (własności stopnie ), a następnie z definicji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log as 2, co należało udowodnić.
- Logarytm ilorazu wygląda następująco: log a (s 1/ s 2) = log a s 1 - log a s 2.
- Twierdzenie w formie wzoru przyjmuje się następny widok: log a q b n = n/q log a b.
Wzór ten nazywany jest „właściwością stopnia logarytmu”. Przypomina to właściwości zwykłych stopni i nie jest w tym nic dziwnego, gdyż cała matematyka opiera się na naturalnych postulatach. Spójrzmy na dowód.
Niech log a b = t, okaże się, że a t = b. Jeśli podniesiemy obie części do potęgi m: a tn = b n ;
ale ponieważ a tn = (a q) nt/q = b n, zatem log a q b n = (n*t)/t, to log a q b n = n/q log a b. Twierdzenie zostało udowodnione.
Przykłady problemów i nierówności
Najczęstszym typem problemów logarytmicznych są przykłady równań i nierówności. Można je znaleźć w prawie wszystkich podręcznikach problemowych, a także są wymaganą częścią egzaminów z matematyki. O przyjęcie na uniwersytet lub zaliczenie Egzaminy wstępne na matematyce trzeba wiedzieć, jak poprawnie rozwiązywać takie problemy.

Niestety nie ma jednego planu ani schematu rozwiązywania i wyznaczania nieznanej wartości logarytmu, ale do każdej nierówności matematycznej lub równania logarytmicznego można zastosować pewne zasady. Przede wszystkim powinieneś dowiedzieć się, czy wyrażenie można uprościć, czy też do niego doprowadzić Ogólny wygląd. Uprość długie wyrażenia logarytmiczne możliwe, jeśli prawidłowo wykorzystasz ich właściwości. Poznajmy je szybko.
Rozwiązując równania logarytmiczne, musimy określić, jaki rodzaj logarytmu mamy: przykładowe wyrażenie może zawierać logarytm naturalny lub dziesiętny.
Oto przykłady ln100, ln1026. Ich rozwiązanie sprowadza się do tego, że muszą wyznaczyć potęgę, do której podstawa 10 będzie równa odpowiednio 100 i 1026. Aby rozwiązać logarytmy naturalne, należy zastosować tożsamości logarytmiczne lub ich właściwości. Spójrzmy na przykłady rozwiązywania problemów logarytmicznych różnego typu.

Jak korzystać ze wzorów logarytmicznych: z przykładami i rozwiązaniami
Przyjrzyjmy się więc przykładom użycia podstawowych twierdzeń o logarytmach.
- Właściwość logarytmu iloczynu można wykorzystać w zadaniach, w których konieczne jest rozwinięcie bardzo ważne liczby b na prostsze czynniki. Na przykład log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odpowiedź brzmi 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - jak widać, korzystając z czwartej własności potęgi logarytmu, udało nam się rozwiązać pozornie złożone i nierozwiązywalne wyrażenie. Wystarczy rozłożyć podstawę, a następnie wyjąć wartości wykładników ze znaku logarytmu.

Zadania z jednolitego egzaminu państwowego
Często spotyka się logarytmy egzaminy wstępne, zwłaszcza wiele problemów logarytmicznych na egzaminie Unified State Exam ( Egzamin państwowy dla wszystkich absolwentów). Zazwyczaj zadania te występują nie tylko w części A (najłatwiejsza część testowa egzaminu), ale także w części C (zadania najbardziej złożone i obszerne). Egzamin wymaga dokładności i doskonała wiedza tematy „Logarity naturalne”.
Przykłady i rozwiązania problemów pochodzą z oficjalnych źródeł Opcje ujednoliconego egzaminu stanowego. Zobaczmy, jak rozwiązuje się takie zadania.
Biorąc pod uwagę log 2 (2x-1) = 4. Rozwiązanie:
przepiszmy wyrażenie, nieco je upraszczając log 2 (2x-1) = 2 2, z definicji logarytmu otrzymujemy, że 2x-1 = 2 4, zatem 2x = 17; x = 8,5.
- Najlepiej jest sprowadzić wszystkie logarytmy do tej samej podstawy, aby rozwiązanie nie było kłopotliwe i mylące.
- Wszystkie wyrażenia pod znakiem logarytmu są oznaczone jako dodatnie, dlatego też, gdy wykładnik wyrażenia znajdującego się pod znakiem logarytmu i jako jego podstawa zostanie wyjęty jako mnożnik, wyrażenie pozostające pod logarytmem musi być dodatnie.
W miarę rozwoju społeczeństwa i coraz bardziej złożonej produkcji rozwijała się także matematyka. Przejście od prostego do złożonego. Ze zwykłej księgowości metodą dodawania i odejmowania, z ich wielokrotnym powtarzaniem, doszliśmy do pojęcia mnożenia i dzielenia. Ograniczenie powtarzającej się operacji mnożenia stało się koncepcją potęgowania. Pierwsze tablice zależności liczb od podstawy i liczby potęgowań zostały opracowane już w VIII wieku przez indyjskiego matematyka Varasenę. Z nich można policzyć czas wystąpienia logarytmów.
Szkic historyczny
Odrodzenie Europy w XVI wieku pobudziło także rozwój mechaniki. T wymagało dużej ilości obliczeń związane z mnożeniem i dzieleniem liczby wielocyfrowe. Starożytne stoły były bardzo przydatne. Umożliwiły zastąpienie skomplikowanych operacji prostszymi - dodawaniem i odejmowaniem. Dużym krokiem naprzód była praca matematyka Michaela Stiefela, opublikowana w 1544 roku, w której zrealizował ideę wielu matematyków. Umożliwiło to wykorzystanie tablic nie tylko dla potęg w postaci liczb pierwszych, ale także dla dowolnych liczb wymiernych.
W 1614 roku po raz pierwszy przedstawił Szkot Jan Napier, rozwijając te idee nowy semestr„logarytm liczby”. Opracowano nowe złożone tabele do obliczania logarytmów sinusów i cosinusów, a także stycznych. To znacznie ograniczyło pracę astronomów.
Zaczęły pojawiać się nowe tablice, z których naukowcy z powodzeniem korzystali przez trzy stulecia. Dużo czasu minęło wcześniej nowa operacja w algebrze uzyskał on swoją gotową formę. Podano definicję logarytmu i zbadano jego właściwości.
Dopiero w XX wieku, wraz z pojawieniem się kalkulatora i komputera, ludzkość porzuciła starożytne tablice, które z powodzeniem działały przez cały XIII wiek.
 Dzisiaj nazywamy logarytm b opierając a na liczbie x, która jest potęgą a dającą b. Zapisuje się to jako wzór: x = log a(b).
Dzisiaj nazywamy logarytm b opierając a na liczbie x, która jest potęgą a dającą b. Zapisuje się to jako wzór: x = log a(b).
Na przykład log 3(9) będzie równy 2. Jest to oczywiste, jeśli postępujesz zgodnie z definicją. Jeśli podniesiemy 3 do potęgi 2, otrzymamy 9.
Tak więc sformułowana definicja stawia tylko jedno ograniczenie: liczby a i b muszą być rzeczywiste.
Rodzaje logarytmów
Klasyczna definicja nazywa się logarytmem rzeczywistym i jest w rzeczywistości rozwiązaniem równania a x = b. Opcja a = 1 jest na granicy i nie jest interesująca. Uwaga: 1 do dowolnej potęgi równa się 1.
Rzeczywista wartość logarytmu zdefiniowane tylko wtedy, gdy podstawa i argument są większe niż 0, a podstawa nie może być równa 1.
Szczególne miejsce w dziedzinie matematyki zagraj w logarytmy, które będą nazywane w zależności od wielkości ich podstawy:

Zasady i ograniczenia
Podstawową właściwością logarytmów jest zasada: logarytm iloczynu jest równy sumie logarytmicznej. log abp = log a(b) + log a(p).
Wariantem tego stwierdzenia będzie: log c(b/p) = log c(b) - log c(p), iloraz funkcji jest równy różnicy funkcji.
Z dwóch poprzednich reguł łatwo zauważyć, że: log a(b p) = p * log a(b).
Inne właściwości obejmują:

Komentarz. Nie ma potrzeby popełniać typowego błędu - logarytm sumy nie jest równy sumie logarytmów.
 Przez wiele stuleci operacja znajdowania logarytmu była zadaniem dość czasochłonnym. Używali matematycy dobrze znana formuła logarytmiczna teoria rozwinięcia wielomianu:
Przez wiele stuleci operacja znajdowania logarytmu była zadaniem dość czasochłonnym. Używali matematycy dobrze znana formuła logarytmiczna teoria rozwinięcia wielomianu:
ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n), gdzie n - Liczba naturalna większa niż 1, co określa dokładność obliczeń.
Logarytmy o innych podstawach obliczono, korzystając z twierdzenia o przejściu z jednej podstawy do drugiej i własności logarytmu iloczynu.
Ponieważ metoda ta jest bardzo pracochłonna i przy rozwiązywaniu problemów praktycznych trudne do wdrożenia, wykorzystaliśmy gotowe tablice logarytmów, co znacznie przyspieszyło całą pracę.
W niektórych przypadkach wykorzystano specjalnie zaprojektowane wykresy logarytmiczne, co dawało mniejszą dokładność, ale znacznie przyspieszało poszukiwania Pożądana wartość. Krzywa funkcji y = log a(x), zbudowana w kilku punktach, pozwala za pomocą zwykłej linijki znaleźć wartość funkcji w dowolnym innym punkcie. Inżynierowie długi czas Do tych celów używano tzw. papieru milimetrowego.
W XVII wieku pojawiły się pierwsze pomocnicze warunki obliczeniowe analogowe, które 19 wiek uzyskał wykończony wygląd. Najbardziej udane urządzenie nazwano suwakiem logarytmicznym. Pomimo prostoty urządzenia, jego wygląd znacznie przyspieszał proces wszelkich obliczeń inżynierskich, a to jest trudne do przecenienia. Obecnie niewiele osób zna to urządzenie.
Pojawienie się kalkulatorów i komputerów sprawiło, że korzystanie z jakichkolwiek innych urządzeń stało się bezcelowe.
Równania i nierówności
Aby rozwiązać różne równania i nierówności za pomocą logarytmów, stosuje się następujące wzory:
- Przejście z jednej podstawy do drugiej: log a(b) = log c(b) / log c(a);
- w konsekwencji Poprzednia wersja: log a(b) = 1 / log b(a).
Aby rozwiązać nierówności, warto wiedzieć:
- Wartość logarytmu będzie dodatnia tylko wtedy, gdy podstawa i argument będą większe lub mniejsze od jedności; jeżeli zostanie naruszony przynajmniej jeden warunek, wartość logarytmu będzie ujemna.
- Jeżeli funkcję logarytmu zastosujemy do prawej i lewej strony nierówności, a podstawa logarytmu jest większa niż jeden, to znak nierówności zostaje zachowany; inaczej to się zmienia.
Przykładowe problemy
Rozważmy kilka opcji użycia logarytmów i ich właściwości. Przykłady rozwiązywania równań:

Rozważ możliwość umieszczenia logarytmu w potędze:
- Zadanie 3. Oblicz 25^log 5(3). Rozwiązanie: w warunkach problemu wpis jest podobny do następującego (5^2)^log5(3) lub 5^(2 * log 5(3)). Zapiszmy to inaczej: 5^log 5(3*2), czyli kwadrat liczby jako argumentu funkcji, można zapisać jako kwadrat samej funkcji (5^log 5(3))^2. Korzystając z właściwości logarytmów, to wyrażenie jest równe 3^2. Odpowiedź: w wyniku obliczeń otrzymujemy 9.
Praktyczne użycie
Będąc narzędziem czysto matematycznym, wydaje się to dalekie od ideału prawdziwe życieże logarytm nagle zyskał ogromne znaczenie w opisie obiektów prawdziwy świat. Trudno znaleźć naukę, w której nie jest ona wykorzystywana. Dotyczy to w pełni nie tylko naturalnego, ale także obszary humanitarne wiedza.
Zależności logarytmiczne
Oto kilka przykładów zależności numerycznych:

Mechanika i fizyka
Historycznie rzecz biorąc, mechanika i fizyka zawsze rozwijały się przy użyciu metody matematyczne badań, a jednocześnie stanowił zachętę do rozwoju matematyki, w tym logarytmów. Teoria większości praw fizyki jest napisana w języku matematyki. Podajmy tylko dwa przykłady opisu praw fizycznych za pomocą logarytmu.
Problem obliczenia tak złożonej wielkości, jak prędkość rakiety, można rozwiązać za pomocą wzoru Ciołkowskiego, który położył podwaliny pod teorię eksploracji kosmosu:
V = I * ln (M1/M2), gdzie
- V to prędkość końcowa samolotu.
- I – impuls właściwy silnika.
- M 1 – masa początkowa rakiety.
- M 2 – masa końcowa.
Inny ważny przykład - jest to stosowane we wzorze innego wielkiego naukowca Maxa Plancka, który służy do oceny stanu równowagi w termodynamice.
S = k * ln (Ω), gdzie
- S – właściwość termodynamiczna.
- k – stała Boltzmanna.
- Ω jest wagą statystyczną różnych stanów.
Chemia
Mniej oczywiste jest stosowanie w chemii wzorów zawierających iloraz logarytmów. Podajmy tylko dwa przykłady:
- Równanie Nernsta, stan potencjału redoks ośrodka w zależności od aktywności substancji i stałej równowagi.
- Obliczenia takich stałych jak wskaźnik autolizy i kwasowość roztworu również nie da się wykonać bez naszej funkcji.
Psychologia i biologia
 I wcale nie jest jasne, co ma z tym wspólnego psychologia. Okazuje się, że siłę doznania dobrze opisuje ta funkcja jako odwrotny stosunek natężenia bodźca do niższa wartość intensywność.
I wcale nie jest jasne, co ma z tym wspólnego psychologia. Okazuje się, że siłę doznania dobrze opisuje ta funkcja jako odwrotny stosunek natężenia bodźca do niższa wartość intensywność.
Po powyższe przykłady Nic już dziwnego, że temat logarytmów jest szeroko stosowany w biologii. O formach biologicznych odpowiadających spiralom logarytmicznym można napisać całe tomy.
Inne obszary
Wydaje się, że istnienie świata nie jest możliwe bez związku z tą funkcją i rządzi ona wszelkimi prawami. Zwłaszcza, gdy prawa natury są powiązane postęp geometryczny. Warto zajrzeć na stronę MatProfi, a takich przykładów jest wiele w następujących obszarach działalności:

Lista może nie mieć końca. Po opanowaniu podstawowych zasad tej funkcji możesz zanurzyć się w świat nieskończonej mądrości.
Mamy więc potęgę dwójki. Jeśli weźmiesz liczbę z dolnej linii, możesz łatwo znaleźć potęgę, do której będziesz musiał podnieść dwa, aby otrzymać tę liczbę. Na przykład, aby uzyskać 16, musisz podnieść dwa do potęgi czwartej. Aby otrzymać 64, musisz podnieść dwa do potęgi szóstej. Można to zobaczyć z tabeli.
A teraz - właściwie definicja logarytmu:
Podstawą logarytmu x jest potęga, do której należy podnieść a, aby otrzymać x.
Oznaczenie: log a x = b, gdzie a to podstawa, x to argument, b to faktyczna wartość logarytmu.
Na przykład 2 3 = 8 ⇒ log 2 8 = 3 (logarytm o podstawie 2 z 8 to trzy, ponieważ 2 3 = 8). Z tym samym logiem sukcesu 2 64 = 6, ponieważ 2 6 = 64.
Operację znajdowania logarytmu liczby o podanej podstawie nazywa się logarytmizacją. Dodajmy więc nową linię do naszej tabeli:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
Niestety, nie wszystkie logarytmy można obliczyć tak łatwo. Na przykład spróbuj znaleźć log 2 5 . Cyfry 5 nie ma w tabeli, ale logika podpowiada, że logarytm będzie leżał gdzieś na segmencie. Ponieważ 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Liczby takie nazywane są niewymiernymi: liczby po przecinku można zapisywać w nieskończoność i nigdy się nie powtarzają. Jeśli logarytm okaże się irracjonalny, lepiej go tak zostawić: log 2 5, log 3 8, log 5 100.
Ważne jest, aby zrozumieć, że logarytm jest wyrażeniem zawierającym dwie zmienne (podstawę i argument). Na początku wiele osób myli, gdzie jest podstawa, a gdzie argument. Aby uniknąć irytujących nieporozumień, wystarczy spojrzeć na zdjęcie:
Przed nami nic więcej niż definicja logarytmu. Pamiętać: logarytm jest potęgą, w który należy wbudować bazę, aby uzyskać argument. Jest to podstawa podniesiona do potęgi - na zdjęciu jest ona zaznaczona na czerwono. Okazuje się, że podstawa jest zawsze na dole! Tę cudowną zasadę powtarzam moim uczniom już na pierwszej lekcji – i nie pojawia się żadne zamieszanie.
Mamy już definicję – pozostaje tylko nauczyć się liczyć logarytmy, czyli: pozbądź się znaku „log”. Na początek zauważmy, że z definicji wynikają dwa ważne fakty:
- Argument i podstawa muszą być zawsze większe od zera. Wynika to z definicji stopnia przez wykładnik wymierny, do którego sprowadza się definicja logarytmu.
- Podstawa musi być różna od jednej, ponieważ jeden w jakimkolwiek stopniu nadal pozostaje jednym. Z tego powodu pytanie „do jakiej potęgi trzeba podnieść jedną, aby otrzymać dwie” jest pozbawione sensu. Nie ma takiego stopnia!
Takie ograniczenia nazywane są zakres akceptowalnych wartości(ODZ). Okazuje się, że ODZ logarytmu wygląda następująco: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Należy pamiętać, że nie ma ograniczeń co do liczby b (wartości logarytmu). Na przykład logarytm może być ujemny: log 2 · 0,5 = −1, ponieważ 0,5 = 2-1.
Jednak teraz tylko się zastanawiamy wyrażenia numeryczne, gdzie nie jest wymagana znajomość CVD logarytmu. Wszystkie ograniczenia zostały już uwzględnione przez autorów problemów. Ale kiedy odejdą równania logarytmiczne i nierówności, wymogi DHS staną się obowiązkowe. Przecież podstawa i argumentacja mogą zawierać bardzo mocne konstrukcje, które niekoniecznie odpowiadają powyższym ograniczeniom.
Teraz rozważmy ogólny schemat obliczanie logarytmów. Składa się z trzech kroków:
- Przedstaw podstawę a i argument x jako potęgę z minimum możliwa przyczyna, większy niż jeden. Po drodze lepiej pozbyć się ułamków dziesiętnych;
- Rozwiąż równanie dla zmiennej b: x = a b ;
- Wynikowa liczba b będzie odpowiedzią.
To wszystko! Jeśli logarytm okaże się niewymierny, będzie to widoczne już w pierwszym kroku. Wymóg, aby podstawa była większa niż jedność, jest bardzo ważny: zmniejsza to prawdopodobieństwo błędu i znacznie upraszcza obliczenia. Tak samo z miejsca dziesiętne: jeśli natychmiast zamienisz je na zwykłe, błędów będzie znacznie mniej.
Zobaczmy, jak działa ten schemat na konkretnych przykładach:
Zadanie. Oblicz logarytm: log 5 25
- Wyobraźmy sobie podstawę i argument jako potęgę piątki: 5 = 5 1 ; 25 = 5 2 ;
- Otrzymaliśmy odpowiedź: 2.
Utwórzmy i rozwiążmy równanie:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;
Zadanie. Oblicz logarytm:
Zadanie. Oblicz logarytm: log 4 64
- Wyobraźmy sobie podstawę i argument jako potęgę dwójki: 4 = 2 2 ; 64 = 2 6 ;
- Utwórzmy i rozwiążmy równanie:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Otrzymaliśmy odpowiedź: 3.
Zadanie. Oblicz logarytm: log 16 1
- Wyobraźmy sobie podstawę i argument jako potęgę dwójki: 16 = 2 4 ; 1 = 2 0 ;
- Utwórzmy i rozwiążmy równanie:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Otrzymaliśmy odpowiedź: 0.
Zadanie. Oblicz logarytm: log 7 14
- Wyobraźmy sobie podstawę i argument jako potęgę siódemki: 7 = 7 1 ; 14 nie można przedstawić w postaci potęgi siódemki, ponieważ 7 1< 14 < 7 2 ;
- Z poprzedniego akapitu wynika, że logarytm się nie liczy;
- Odpowiedź brzmi bez zmian: log 7 14.
Mała uwaga do ostatniego przykładu. Jak możesz mieć pewność, że liczba nie jest dokładną potęgą innej liczby? To bardzo proste – wystarczy podzielić to na czynniki pierwsze. Jeśli rozwinięcie ma co najmniej dwa różne czynniki, liczba nie jest dokładną potęgą.
Zadanie. Dowiedz się, czy liczby są dokładnymi potęgami: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 - dokładny stopień, ponieważ jest tylko jeden mnożnik;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nie jest dokładną potęgą, ponieważ istnieją dwa czynniki: 3 i 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - dokładny stopień;
35 = 7 · 5 – znowu nie jest to dokładna potęga;
14 = 7 · 2 – znowu nie jest to dokładny stopień;
Zauważmy też, że my sami liczby pierwsze są zawsze dokładnymi stopniami siebie.
Logarytm dziesiętny
Niektóre logarytmy są tak powszechne, że mają specjalną nazwę i symbol.
Logarytm dziesiętny x to logarytm o podstawie 10, tj. Potęga, do której należy podnieść liczbę 10, aby otrzymać liczbę x. Oznaczenie: lg x.
Na przykład log 10 = 1; lg100 = 2; lg 1000 = 3 - itd.
Od teraz, gdy w podręczniku pojawi się sformułowanie typu „Znajdź lg 0,01”, wiedz: to nie jest literówka. To jest logarytm dziesiętny. Jeśli jednak nie znasz tego zapisu, zawsze możesz go przepisać:
log x = log 10 x
Wszystko, co jest prawdziwe w przypadku logarytmów zwykłych, jest również prawdziwe w przypadku logarytmów dziesiętnych.
Naturalny logarytm
Istnieje inny logarytm, który ma swoje własne oznaczenie. W pewnym sensie jest to nawet ważniejsze niż liczba dziesiętna. To jest o o logarytmie naturalnym.
Logarytm naturalny x jest logarytmem o podstawie e, tj. potęga, do której należy podnieść liczbę e, aby otrzymać liczbę x. Oznaczenie: ln x .
Wielu zapyta: jaka jest liczba e? To liczba niewymierna Dokładna wartość niemożliwe do odnalezienia i nagrania. Podam tylko pierwsze liczby:
e = 2,718281828459...
Nie będziemy szczegółowo omawiać, czym jest ta liczba i dlaczego jest potrzebna. Pamiętaj tylko, że e jest podstawą logarytmu naturalnego:
ln x = log e x
Zatem ln e = 1; ln mi 2 = 2; ln mi 16 = 16 - itd. Z drugiej strony ln 2 jest liczbą niewymierną. Ogólnie rzecz biorąc, logarytm naturalny dowolnego Liczba wymierna irracjonalny. Z wyjątkiem oczywiście jednego: ln 1 = 0.
W przypadku logarytmów naturalnych obowiązują wszystkie zasady obowiązujące dla logarytmów zwykłych.