Jaka jest formuła cosinus alfa. Formuły podwójnego kąta i dodawanie argumentów. Wykres funkcji cotangens, y = ctg x
Wyśrodkowany w punkcie A .
α to kąt wyrażony w radianach.
Styczna ( tgα) jest funkcją trygonometryczną zależną od kąta α między przeciwprostokątną a nogą trójkąt prostokątny, równy stosunkowi długość przeciwległej nogi |BC| do długości sąsiedniej nogi |AB| .
Cotangens ( ctgα) jest funkcją trygonometryczną zależną od kąta α między przeciwprostokątną a odnogą trójkąta prostokątnego, równą stosunkowi długości sąsiedniego ramienia |AB| do długości przeciwległej nogi |BC| .
Tangens
Gdzie n- cały.
W literaturze zachodniej tangens oznaczany jest następująco:
.
;
;
.
Wykres funkcji stycznej, y = tg x
Cotangens
Gdzie n- cały.
W literaturze zachodniej cotangens oznacza się następująco:
.
Przyjęto również następującą notację:
;
;
.
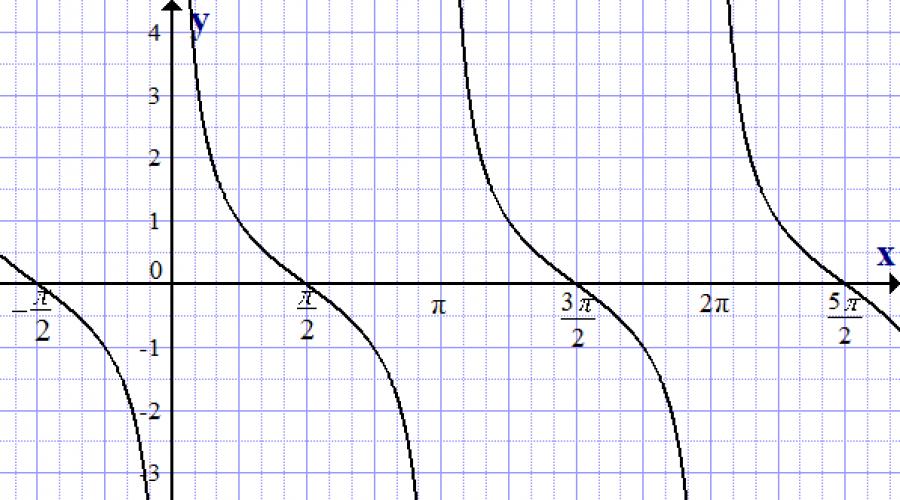
Wykres funkcji cotangens, y = ctg x

Własności tangensa i cotangensa
Okresowość
Funkcje y= tg x i y= ctg x są okresowe z okresem π.
Parytet
Funkcje tangens i cotangens są nieparzyste.
Domeny definicji i wartości, rosnąco, malejąco
Funkcje tangens i cotangens są ciągłe w swojej dziedzinie definicji (patrz dowód ciągłości). Główne właściwości stycznej i cotangensa przedstawiono w tabeli ( n- liczba całkowita).
| y= tg x | y= ctg x | |
| Zakres i ciągłość | ||
| Zakres wartości | -∞ < y < +∞ | -∞ < y < +∞ |
| Rosnąco | - | |
| Malejąco | - | |
| Ekstrema | - | - |
| Zera, y= 0 | ||
| Punkty przecięcia z osią y, x = 0 | y= 0 | - |
Formuły
Wyrażenia w postaci sinusa i cosinusa
;
;
;
;
;
Wzory na tangens i cotangens sumy i różnicy
Reszta formuł jest łatwa do zdobycia, na przykład
Iloczyn stycznych
Wzór na sumę i różnicę stycznych
Ta tabela pokazuje wartości tangensów i cotangensów dla niektórych wartości argumentu. 
Wyrażenia w postaci liczb zespolonych
Wyrażenia w kategoriach funkcji hiperbolicznych
;
;
Pochodne
; .
.
Pochodna n-tego rzędu względem zmiennej x funkcji :
.
Wyprowadzenie wzorów na styczną > > > ; dla cotangensa > > >
Całki
Rozszerzenia w serie
Aby uzyskać rozwinięcie tangensa w potęgach x, musisz wziąć kilka wyrazów rozwinięcia w seria mocy dla funkcji grzech x oraz bo x i podziel te wielomiany na siebie , . Daje to następujące formuły.
Na .
w .
gdzie B n- Liczby Bernoulliego. Są one wyznaczane albo z relacji rekurencyjności:
;
;
gdzie .
Lub według formuły Laplace'a: 
Funkcje odwrotne
Funkcje odwrotne do tangensa i cotangensa to odpowiednio arcus tangens i arccotangens.
Arcus tangens, arctg
, gdzie n- cały.
Arc tangens, arcctg
, gdzie n- cały.
Bibliografia:
W. Bronstein, K.A. Semendyaev, Podręcznik matematyki dla inżynierów i studentów wyższych uczelni, Lan, 2009.
G. Korn, Podręcznik matematyki dla naukowcy i inżynierowie, 2012.
- 2. Zakres wartości: [-1;1]
- 3. Nieparzysta funkcja.
- 7. Przedziały, w których funkcja jest dodatnia: (2*pi*n; pi+2*pi*n)
- 8. Przedziały, w których funkcja jest ujemna: (-pi + 2*pi*n; 2*pi*n)
- 9. Zwiększanie interwałów: [-pi/2 +2*pi*n; pi/2 +2*pi*n]
- 10. Przedziały malejące:
- 11. Niskie punkty: -pi/2 +2*pi*n
- 12. Minimalna funkcja: -1
- 13. Punkty szczytowe: pi/2 +2*pi*n
- 14. Maksymalna funkcja: 1
Właściwości cosinusa
.jpg)
- 1. Dziedzina definicji: cała oś liczbowa
- 2. Zakres wartości: [-1;1]
- 3. Nawet funkcja.
- 4. Najmniejszy dodatni okres: 2*pi
- 5. Współrzędne punktów przecięcia wykresu funkcji z osią Wół: (pi/2 + pi * n; 0)
- 6. Współrzędne punktów przecięcia wykresu funkcji z osią Oy: (0;1)
- 7. Przedziały, w których funkcja jest dodatnia: (-pi/2 +2*pi*n; pi/2 +2*pi*n)
- 8. Przedziały, w których funkcja jest ujemna: (pi/2 +2*pi*n; 3*pi/2 +2*pi*n)
- 9. Zwiększanie interwałów: [-pi + 2*pi*n; 2*pi*n]
- 10. Przedziały malejące:
- 11. Niskie punkty: pi+2*pi*n
- 12. Minimalna funkcja: -1
- 13. Punkty szczytowe: 2*pi*n
- 14. Maksymalna funkcja: 1
Właściwości styczne
.jpg)
- 1. Dziedzina definicji: (-pi/2 +pi*n; pi/2 +pi*n)
- 3. Nieparzysta funkcja.
- 5. Współrzędne punktów przecięcia wykresu funkcji z osią Wół: (pi * n; 0)
- 6. Współrzędne punktów przecięcia wykresu funkcji z osią Oy: (0; 0)
- 9. Funkcja wzrasta na interwałach (-pi/2 + pi*n; pi/2 + pi*n)
Właściwości cotangensa
.jpg)
- 1. Dziedzina definicji: (pi*n; pi +pi*n)
- 2. Zakres wartości: cała oś liczbowa
- 3. Nieparzysta funkcja.
- 4. Najmniejszy dodatni okres: pi
- 5. Współrzędne punktów przecięcia wykresu funkcji z osią Wół: (pi/2 + pi * n; 0)
- 6. Współrzędne punktów przecięcia wykresu funkcji z osią Oy: no
- 7. Przedziały, w których funkcja jest dodatnia: (pi*n; pi/2 + pi*n)
- 8. Przedziały, w których funkcja jest ujemna: (-pi/2 + pi*n; pi*n)
- 9. Funkcja maleje na interwałach (pi*n; pi + pi*n)
- 10. Nie ma punktów maksymalnych i minimalnych.
Poniższy rysunek przedstawia kilka okręgów jednostkowych, w których znaki sinusa, cosinusa, tangensa i cotangensa są wskazane w różnych ćwiartkach współrzędnych.
Początkowo sinus i cosinus powstały ze względu na konieczność obliczania wielkości w trójkątach prostokątnych. Zauważono, że jeśli wartość miary stopnia kątów w trójkącie prostokątnym nie ulega zmianie, to proporcje, niezależnie od tego, jak bardzo zmieniają się te boki, zawsze pozostają takie same.
W ten sposób wprowadzono pojęcia sinusa i cosinusa. Sinus kąta ostrego w trójkącie prostokątnym jest stosunkiem nogi przeciwnej do przeciwprostokątnej, a cosinus jest stosunkiem nogi sąsiedniej do przeciwprostokątnej.
Twierdzenia o cosinusach i sinusach
Ale cosinusy i sinusy mogą być używane nie tylko w trójkątach prostokątnych. Aby znaleźć wartość kąta rozwartego lub ostrego, czyli boku dowolnego trójkąta, wystarczy zastosować twierdzenie cosinus i sinus.
Twierdzenie o cosinusach jest dość proste: „Kwadrat boku trójkąta jest równy sumie kwadratów pozostałych dwóch boków minus dwukrotność iloczynu tych boków przez cosinus kąta między nimi”.
Istnieją dwie interpretacje twierdzenia sinus: mała i rozszerzona. Według małego: „W trójkącie kąty są proporcjonalne do przeciwnych boków”. Twierdzenie to jest często rozszerzane ze względu na właściwość koła opisanego wokół trójkąta: „W trójkącie kąty są proporcjonalne do przeciwnych boków, a ich stosunek jest równy średnicy koła opisanego”.
Pochodne
Pochodna to narzędzie matematyczne, które pokazuje, jak szybko zmienia się funkcja w odniesieniu do zmiany jej argumentu. Pochodne są używane w geometrii oraz w wielu dyscyplinach technicznych.
Rozwiązując problemy, musisz wiedzieć wartości tabeli pochodne funkcje trygonometryczne: sinus i cosinus. Pochodną sinusa jest cosinus, a pochodną cosinusa jest sinus, ale ze znakiem minus.
Zastosowanie w matematyce
Szczególnie często sinusy i cosinusy są używane w rozwiązywaniu trójkątów prostokątnych i problemów z nimi związanych.
Wygoda sinusów i cosinusów znajduje również odzwierciedlenie w technologii. Kąty i boki były łatwe do oceny przy użyciu twierdzeń cosinusów i sinusów, dzieląc złożone kształty i obiekty na „proste” trójkąty. Inżynierowie i często zajmujący się obliczeniami współczynników kształtu i miar stopnia, spędzili dużo czasu i wysiłku na obliczaniu cosinusów i sinusów kątów nietabelowych.
Wtedy na ratunek przyszły tablice Bradis, zawierające tysiące wartości sinusów, cosinusów, tangensów i cotangensów różne kąty. W czasach sowieckich niektórzy nauczyciele zmuszali swoich podopiecznych do zapamiętywania stron tablic Bradisa.
Radiany — wielkość kątowałuki wzdłużne równy promieniowi lub 57.295779513 stopni.
Stopień (w geometrii) - 1/360 okręgu lub 1/90 kąta prostego.
π = 3,141592653589793238462… (przybliżona wartość pi).
Tabela cosinusów dla kątów: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Kąt x (w stopniach) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kąt x (w radianach) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3xπ/4 | 5xπ/6 | π | 7xπ/6 | 5xπ/4 | 4xπ/3 | 3xπ/2 | 5xπ/3 | 7xπ/4 | 11xπ/6 | 2xπ |
| bo x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Ważne notatki!
1. Jeśli zamiast formuł widzisz abrakadabra, wyczyść pamięć podręczną. Jak to zrobić w przeglądarce jest napisane tutaj:
2. Zanim zaczniesz czytać artykuł, najbardziej zwróć uwagę na naszego nawigatora przydatny zasób dla
Sinus, cosinus, tangens, cotangens
Pojęcia sinus (), cosinus (), tangens (), cotangens () są nierozerwalnie związane z pojęciem kąta. Aby dobrze zrozumieć te na pierwszy rzut oka skomplikowane koncepcje (które wywołują u wielu uczniów stan przerażenia) i upewnić się, że „diabeł nie jest taki straszny, jak go malują”, zacznijmy od początku i zrozum pojęcie kąta.
Pojęcie kąta: radian, stopień
Spójrzmy na zdjęcie. Wektor „obrócił się” względem punktu o określoną wartość. Tak więc miarą tego obrotu w stosunku do pozycji początkowej będzie zastrzyk.
Co jeszcze musisz wiedzieć o pojęciu kąta? Oczywiście jednostki kąta!
Kąt, zarówno w geometrii, jak i trygonometrii, można mierzyć w stopniach i radianach.
Nazywa się kąt (jeden stopień) centralny róg w okręgu, opartym na łuku kołowym równym części okręgu. Tak więc cały okrąg składa się z „kawałków” łuków kołowych lub kąt opisany przez okrąg jest równy.

Oznacza to, że powyższy rysunek pokazuje równy kąt, to znaczy ten kąt jest oparty na łuku kołowym o rozmiarze obwodu.
Kąt w radianach nazywany jest kątem środkowym okręgu, opartym na łuku kołowym, którego długość jest równa promieniowi okręgu. Cóż, zrozumiałeś? Jeśli nie, spójrzmy na zdjęcie.

Tak więc rysunek pokazuje kąt równy radianowi, to znaczy kąt ten opiera się na łuku kołowym, którego długość jest równa promieniowi okręgu (długość jest równa długości lub promieniowi równa długościłuki). Zatem długość łuku oblicza się według wzoru:
Gdzie jest kąt środkowy w radianach.
Wiedząc o tym, czy możesz odpowiedzieć, ile radianów zawiera kąt opisany przez okrąg? Tak, w tym celu musisz zapamiętać wzór na obwód koła. Tutaj jest:
Cóż, teraz skorelujmy te dwie formuły i uzyskajmy, że kąt opisany przez okrąg jest równy. To znaczy, skorelując wartość w stopniach i radianach, otrzymujemy to. Odpowiednio . Jak widać, w przeciwieństwie do „stopni”, słowo „radiany” jest pomijane, ponieważ jednostka miary jest zwykle jasna z kontekstu.
Ile jest radianów? Zgadza się!
Rozumiem? Następnie przewiń do przodu:
Jakieś trudności? Potem spójrz odpowiedzi:
Trójkąt prostokątny: sinus, cosinus, tangens, cotangens kąta
Tak więc, z koncepcją kąta. Ale jaki jest sinus, cosinus, tangens, cotangens kąta? Rozwiążmy to. W tym pomoże nam trójkąt prostokątny.

Jak nazywają się boki trójkąta prostokątnego? Zgadza się, przeciwprostokątna i nogi: przeciwprostokątna to strona leżąca naprzeciwko kąta prostego (w naszym przykładzie jest to bok); nogi to dwie pozostałe strony i (te przylegające do prosty kąt), ponadto, jeśli weźmiemy pod uwagę nogi względem kąta, to noga jest nogą sąsiednią, a noga przeciwną. A teraz odpowiedzmy na pytanie: jaki jest sinus, cosinus, tangens i cotangens kąta?
Sinus kąta jest stosunkiem przeciwnej (dalekiej) nogi do przeciwprostokątnej.
w naszym trójkącie.
Cosinus kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
w naszym trójkącie.
Styczna kąta- jest to stosunek przeciwnej (dalekiej) nogi do sąsiedniej (bliskiej).
w naszym trójkącie.
Cotangens kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (daleko).
w naszym trójkącie.
Te definicje są konieczne Zapamiętaj! Aby łatwiej było zapamiętać, którą nogę podzielić przez co, musisz to jasno zrozumieć w tangens oraz cotangens tylko nogi siedzą, a przeciwprostokątna pojawia się tylko w Zatoka oraz cosinus. A potem możesz wymyślić łańcuch skojarzeń. Na przykład ten:
cosinus→dotyk→dotyk→sąsiadujący;
Cotangens→dotyk→dotyk→sąsiadujący.
Przede wszystkim należy pamiętać, że sinus, cosinus, tangens i cotangens jako stosunki boków trójkąta nie zależą od długości tych boków (pod jednym kątem). Nie wierz? Następnie upewnij się, patrząc na zdjęcie:

Rozważmy na przykład cosinus kąta. Z definicji z trójkąta: , ale możemy obliczyć cosinus kąta z trójkąta: . Widzisz, długości boków są różne, ale wartość cosinusa jednego kąta jest taka sama. Zatem wartości sinusa, cosinusa, tangensa i cotangensa zależą wyłącznie od wielkości kąta.
Jeśli rozumiesz definicje, śmiało je napraw!
Dla trójkąta pokazanego na poniższym rysunku znajdujemy.

Cóż, dostałeś to? Następnie spróbuj sam: oblicz to samo dla rogu.
Koło jednostkowe (trygonometryczne)
Rozumiejąc pojęcia stopni i radianów, rozważyliśmy okrąg o promieniu równym. Taki krąg nazywa się pojedynczy. Jest bardzo przydatny w badaniach trygonometrii. Dlatego zajmiemy się tym bardziej szczegółowo.

Jak widać, okrąg ten zbudowany jest w kartezjańskim układzie współrzędnych. Promień okręgu jest równy jeden, natomiast środek okręgu leży w początku, początkowe położenie wektora promienia jest ustalone wzdłuż dodatniego kierunku osi (w naszym przykładzie jest to promień).
Każdy punkt okręgu odpowiada dwóm liczbom: współrzędnej wzdłuż osi i współrzędnej wzdłuż osi. Jakie są te liczby współrzędnych? A ogólnie, co mają wspólnego z omawianym tematem? Aby to zrobić, pamiętaj o rozważanym trójkącie prostokątnym. Na powyższym rysunku widać dwa całe prawe trójkąty. Rozważ trójkąt. Jest prostokątny, ponieważ jest prostopadły do osi.
Co jest równe z trójkąta? Zgadza się. Ponadto wiemy, że jest to promień okręgu jednostkowego, a więc . Podstaw tę wartość do naszego wzoru cosinusa. Oto, co się dzieje:
A co jest równe z trójkąta? Ależ oczywiście, ! Podstaw wartość promienia do tego wzoru i uzyskaj:
Czy możesz powiedzieć, jakie współrzędne ma punkt, należący do kręgu? Cóż, nie ma mowy? A jeśli zdajesz sobie z tego sprawę i to tylko liczby? Jakiej współrzędnej to odpowiada? Oczywiście współrzędne! Jakiej współrzędnej to odpowiada? Zgadza się, koordynuj! Tak więc punkt.

A co wtedy są równe i? Zgadza się, użyjmy odpowiednich definicji tangensa i cotangensa i zdobądźmy to.
Co jeśli kąt jest większy? Tutaj na przykład jak na tym obrazku:

Co się zmieniło w tym przykładzie? Rozwiążmy to. Aby to zrobić, ponownie zwracamy się do trójkąta prostokątnego. Rozważmy trójkąt prostokątny: kąt (jako sąsiadujący z kątem). Jaka jest wartość sinusa, cosinusa, tangensa i cotangensa kąta? Zgadza się, przestrzegamy odpowiednich definicji funkcji trygonometrycznych:
Jak widać, wartość sinusa kąta nadal odpowiada współrzędnej; wartość cosinusa kąta - współrzędna; oraz wartości tangensa i cotangensa do odpowiednich stosunków. Zatem te relacje mają zastosowanie do dowolnych obrotów wektora promienia.
Wspomniano już, że początkowe położenie wektora promienia leży wzdłuż dodatniego kierunku osi. Do tej pory obróciliśmy ten wektor w kierunku przeciwnym do ruchu wskazówek zegara, ale co się stanie, jeśli obrócimy go zgodnie z ruchem wskazówek zegara? Nic nadzwyczajnego, dostaniesz też kąt o określonej wielkości, ale tylko to będzie ujemne. Tak więc, obracając wektor promienia w kierunku przeciwnym do ruchu wskazówek zegara, otrzymujemy dodatnie kąty, a przy obrocie w prawo - negatywny.
Wiemy więc, że cały obrót wektora promienia wokół okręgu to lub. Czy można obrócić wektor promienia o lub o? Oczywiście, że możesz! Dlatego w pierwszym przypadku wektor promienia wykona jeden pełny obrót i zatrzyma się w pozycji lub.
W drugim przypadku wektor promienia wykona trzy pełne obroty i zatrzyma się w pozycji lub.
Zatem z powyższych przykładów możemy wywnioskować, że kąty różniące się o lub (gdzie jest dowolną liczbą całkowitą) odpowiadają temu samemu położeniu wektora promienia.
Poniższy rysunek przedstawia kąt. Ten sam obraz odpowiada narożnikowi i tak dalej. Ta lista może być kontynuowana w nieskończoność. Wszystkie te kąty można zapisać za pomocą ogólnego wzoru lub (gdzie jest dowolną liczbą całkowitą)

Teraz, znając definicje podstawowych funkcji trygonometrycznych i korzystając z okręgu jednostkowego, spróbuj odpowiedzieć, jakie wartości są równe:
Oto krąg jednostek, który może ci pomóc:

Jakieś trudności? Więc zastanówmy się. Wiemy więc, że:
Stąd określamy współrzędne punktów odpowiadających pewnym miarom kąta. Cóż, zacznijmy w kolejności: róg w odpowiada punktowi o współrzędnych, a zatem:
Nie istnieje;
Ponadto, przestrzegając tej samej logiki, dowiadujemy się, że rogi odpowiadają odpowiednio punktom o współrzędnych. Wiedząc o tym łatwo wyznaczyć wartości funkcji trygonometrycznych w odpowiednich punktach. Najpierw spróbuj sam, a potem sprawdź odpowiedzi.
Odpowiedzi:
W ten sposób możemy wykonać następującą tabelę:

Nie trzeba pamiętać wszystkich tych wartości. Wystarczy pamiętać o zgodności współrzędnych punktów na okręgu jednostkowym z wartościami funkcji trygonometrycznych:
Ale wartości funkcji trygonometrycznych kątów w i podane w poniższej tabeli: trzeba pamiętać:

Nie bój się, teraz pokażemy jeden z przykładów dość proste zapamiętywanie odpowiednich wartości:
Aby skorzystać z tej metody, należy pamiętać wartości sinusa dla wszystkich trzech miar kąta () oraz wartość tangensa kąta w. Znając te wartości dość łatwo jest odtworzyć całą tabelę - wartości cosinusów są przenoszone zgodnie ze strzałkami, czyli:
Wiedząc o tym, możesz przywrócić wartości. Licznik „ ” będzie zgodny, a mianownik „ ” będzie zgodny. Wartości cotangens są przenoszone zgodnie ze strzałkami pokazanymi na rysunku. Jeśli to zrozumiesz i zapamiętasz schemat ze strzałkami, wystarczy zapamiętać całą wartość z tabeli.
Współrzędne punktu na okręgu
Czy można znaleźć punkt (jego współrzędne) na okręgu, znając współrzędne środka okręgu, jego promień i kąt obrotu?
Oczywiście, że możesz! Wydobądźmy ogólna formuła znaleźć współrzędne punktu.
Tutaj np. mamy taki krąg:

Dano nam, że punkt jest środkiem koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrót punktu o stopnie.
Jak widać na rysunku, współrzędna punktu odpowiada długości odcinka. Długość segmentu odpowiada współrzędnej środka koła, czyli jest równa. Długość segmentu można wyrazić za pomocą definicji cosinusa:
Wtedy mamy to dla punktu współrzędnej.
Zgodnie z tą samą logiką znajdujemy wartość współrzędnej y punktu. Zatem,
tak w ogólny widok współrzędne punktów wyznaczają wzory:
Współrzędne środka okręgu,
promień okręgu,
Kąt obrotu wektora promienia.
Jak widać, dla rozpatrywanego okręgu jednostkowego wzory te są znacznie zmniejszone, ponieważ współrzędne środka wynoszą zero, a promień jest równy jeden:
Cóż, wypróbujmy te formuły dla smaku, ćwicząc znajdowanie punktów na kole?
1. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez włączenie punktu.
2. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez obrót punktu.
3. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym przez włączenie punktu.
4. Punkt - środek koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrócenie wektora promienia początkowego o.
5. Punkt - środek koła. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego przez obrócenie wektora promienia początkowego o.
Masz problem ze znalezieniem współrzędnych punktu na okręgu?
Rozwiąż te pięć przykładów (lub dobrze zrozum rozwiązanie), a dowiesz się, jak je znaleźć!
PODSUMOWANIE I PODSTAWOWA FORMUŁA
Sinus kąta to stosunek przeciwnej (dalekiej) nogi do przeciwprostokątnej.
Cosinus kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
Tangens kąta to stosunek przeciwnej (dalekiej) nogi do sąsiedniej (bliskiej).
Cotangens kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (daleko).
Cóż, temat się skończył. Jeśli czytasz te linijki, to jesteś bardzo fajny.
Ponieważ tylko 5% ludzi jest w stanie opanować coś samodzielnie. A jeśli doczytałeś do końca, to jesteś w 5%!
Teraz najważniejsza rzecz.
Rozgryzłeś teorię na ten temat. I powtarzam, to jest… po prostu super! Już jesteś lepszy niż większość twoich rówieśników.
Problem w tym, że to może nie wystarczyć...
Po co?
Do udana dostawa Jednolity egzamin państwowy, o przyjęcie do instytutu z budżetu i, CO NAJWAŻNIEJSZE, dożywotnio.
Do niczego Cię nie przekonam, powiem tylko jedno...
Osoby, które otrzymały Dobra edukacja zarabiają znacznie więcej niż ci, którzy jej nie otrzymali. To są statystyki.
Ale to nie jest najważniejsze.
Najważniejsze, że są BARDZIEJ SZCZĘŚLIWI (są takie badania). Być może dlatego, że wiele się przed nimi otwiera. więcej możliwości a życie staje się jaśniejsze? Nie wiem...
Ale pomyśl sam...
Co trzeba zrobić, aby być lepszym od innych na egzaminie i być ostatecznie… szczęśliwszym?
WYPEŁNIJ SWOJĄ RĘKĘ, ROZWIĄZUJĄC PROBLEMY W TYM TEMACIE.
Na egzaminie nie zostaniesz zapytany o teorię.
Będziesz potrzebować rozwiązywać problemy na czas.
A jeśli ich nie rozwiązałeś (DUŻO!), na pewno popełnisz gdzieś głupi błąd lub po prostu nie zdążysz na czas.
To jak w sporcie – trzeba wiele razy powtórzyć, żeby na pewno wygrać.
Znajdź kolekcję w dowolnym miejscu koniecznie z rozwiązaniami szczegółowa analiza i zdecyduj, zdecyduj, zdecyduj!
Możesz skorzystać z naszych zadań (niekoniecznie) i na pewno je polecamy.
Aby uzyskać pomoc w naszych zadaniach, musisz pomóc przedłużyć żywotność podręcznika YouClever, który właśnie czytasz.
Jak? Istnieją dwie opcje:
- Odblokuj dostęp do wszystkich ukrytych zadań w tym artykule -
- Odblokuj dostęp do wszystkich ukrytych zadań we wszystkich 99 artykułach samouczka — Kup podręcznik - 499 rubli
Tak, mamy w podręczniku 99 takich artykułów i dostęp do wszystkich zadań i wszystkich ukrytych w nich tekstów można od razu otworzyć.
Dostęp do wszystkich ukrytych zadań jest zapewniony przez cały okres użytkowania witryny.
Podsumowując...
Jeśli nie lubisz naszych zadań, znajdź inne. Tylko nie poprzestawaj na teorii.
„Zrozumiałem” i „Wiem, jak rozwiązać” to zupełnie inne umiejętności. Potrzebujesz obu.
Znajdź problemy i rozwiąż!
Trygonometria jako nauka wywodzi się ze starożytnego Wschodu. Pierwszy relacje trygonometryczne zostały wyhodowane przez astronomów, aby stworzyć dokładny kalendarz i orientację gwiazd. Obliczenia te dotyczyły trygonometrii sferycznej, podczas gdy in kurs szkolny zbadaj stosunek boków i kąt płaskiego trójkąta.
Trygonometria to dział matematyki zajmujący się właściwościami funkcji trygonometrycznych oraz relacjami między bokami i kątami trójkątów.
W okresie rozkwitu kultury i nauki w I tysiącleciu n.e. wiedza rozprzestrzeniała się od starożytny wschód do Grecji. Ale główne odkrycia trygonometrii to zasługa ludzi z arabskiego kalifatu. W szczególności turkmeński naukowiec al-Marazvi wprowadził takie funkcje, jak tangens i cotangens, skompilował pierwsze tabele wartości dla sinusów, tangensów i cotangensów. Pojęcie sinusa i cosinusa zostało wprowadzone przez indyjskich naukowców. Wiele uwagi poświęca się trygonometrii w dziełach tak wielkich postaci starożytności jak Euklides, Archimedes i Eratostenes.
Podstawowe wielkości trygonometrii
Podstawowe funkcje trygonometryczne argument liczbowy są sinus, cosinus, tangens i cotangens. Każdy z nich ma własny wykres: sinus, cosinus, tangens i cotangens.
Wzory do obliczania wartości tych wielkości oparte są na twierdzeniu Pitagorasa. Jest lepiej znany uczniom w sformułowaniu: „Pitagorejskie spodnie, równe we wszystkich kierunkach”, ponieważ dowód podano na przykładzie równoramiennego trójkąta prostokątnego.
Sinus, cosinus i inne zależności ustalają związek między ostre rogi i boki dowolnego trójkąta prostokątnego. Podajemy wzory do obliczania tych wielkości dla kąta A i śledzimy zależność funkcji trygonometrycznych:

Jak widać, tg i ctg są funkcje odwrotne. Jeśli reprezentujemy nogę a jako iloczyn sin A i przeciwprostokątnej c, a nogę b jako cos A * c, to otrzymujemy następujące wzory na tangens i cotangens:

koło trygonometryczne
Graficznie stosunek wymienionych wielkości można przedstawić w następujący sposób:

koło, w ta sprawa, reprezentuje wszystkie możliwe wartości kąta α — od 0° do 360°. Jak widać na rysunku, każda funkcja przyjmuje wartość ujemną lub dodatnią w zależności od kąta. Na przykład sin α będzie ze znakiem „+”, jeśli α należy do ćwiartek koła I i II, czyli znajduje się w zakresie od 0 ° do 180 °. Przy α od 180° do 360° (ćwiartka III i IV), sin α może mieć tylko wartość ujemną.
Spróbujmy zbudować tabele trygonometryczne dla określonych kątów i poznaj znaczenie wielkości.

Wartości α równe 30°, 45°, 60°, 90°, 180° itd. nazywane są przypadkami specjalnymi. Wartości funkcji trygonometrycznych dla nich są obliczane i prezentowane w postaci specjalnych tabel.

Te kąty nie zostały wybrane przypadkowo. Oznaczenie π w tabelach dotyczy radianów. Rad to kąt, pod którym długość łuku koła odpowiada jego promieniowi. Wartość ta została wprowadzona w celu ustalenia uniwersalnej zależności, przy obliczaniu w radianach rzeczywista długość promienia w cm nie ma znaczenia.

Kąty w tabelach funkcji trygonometrycznych odpowiadają wartościom w radianach:

Nietrudno więc zgadnąć, że 2π to pełne koło lub 360°.
Własności funkcji trygonometrycznych: sinus i cosinus
W celu rozważenia i porównania podstawowych właściwości sinusa i cosinusa, tangensa i cotangensa konieczne jest narysowanie ich funkcji. Można to zrobić w postaci krzywej znajdującej się w dwuwymiarowym układzie współrzędnych.
Rozważać tabela porównawcza właściwości dla fali sinusoidalnej i cosinusoidalnej:

| sinusoida | cosinus fala |
|---|---|
| y = grzech x | y = cos x |
| ODZ [-1; jeden] | ODZ [-1; jeden] |
| sin x = 0, dla x = πk, gdzie k ϵ Z | cos x = 0, dla x = π/2 + πk, gdzie k ϵ Z |
| sin x = 1, dla x = π/2 + 2πk, gdzie k ϵ Z | cos x = 1, dla x = 2πk, gdzie k ϵ Z |
| sin x = - 1, przy x = 3π/2 + 2πk, gdzie k ϵ Z | cos x = - 1, dla x = π + 2πk, gdzie k ϵ Z |
| sin (-x) = - sin x, czyli funkcja nieparzysta | cos (-x) = cos x, czyli funkcja jest parzysta |
| funkcja jest okresowa, najmniejszy okres to 2π | |
| sin x › 0, gdzie x należy do ćwiartek I i II lub od 0° do 180° (2πk, π + 2πk) | cos x › 0, gdzie x należy do ćwiartek I i IV lub od 270° do 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, gdzie x należy do ćwiartek III i IV lub od 180° do 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, gdzie x należy do ćwiartek II i III lub od 90° do 270° (π/2 + 2πk, 3π/2 + 2πk) |
| wzrasta na przedziale [- π/2 + 2πk, π/2 + 2πk] | przyrosty na przedziale [-π + 2πk, 2πk] |
| spadki na przedziałach [ π/2 + 2πk, 3π/2 + 2πk] | spadki w interwałach |
| pochodna (sin x)' = cos x | pochodna (cos x)’ = - sin x |
Ustalenie, czy funkcja jest parzysta, czy nie, jest bardzo proste. Wystarczy wyobrazić sobie okrąg trygonometryczny ze znakami wielkości trygonometrycznych i mentalnie „zwinąć” wykres względem osi OX. Jeśli znaki są takie same, funkcja jest parzysta, w przeciwnym razie jest nieparzysta.

Wprowadzenie radianów i wyliczenie głównych właściwości fali sinusoidalnej i cosinusoidalnej pozwala na sprowadzenie następującego wzoru:

Bardzo łatwo jest zweryfikować poprawność formuły. Na przykład dla x = π/2 sinus jest równy 1, podobnie jak cosinus x = 0. Weryfikację można przeprowadzić patrząc na tabele lub śledząc krzywe funkcji dla danych wartości.
Właściwości tangensa i kotangtoidu
Wykresy funkcji tangensa i cotangensa znacznie różnią się od przebiegu sinusoidalnego i cosinusoidalnego. Wartości tg i ctg są względem siebie odwrotne.


- Y = tgx.
- Styczna dąży do wartości y przy x = π/2 + πk, ale nigdy ich nie osiąga.
- Najmniejszy dodatni okres stycznej to π.
- Tg (- x) \u003d - tg x, tj. funkcja jest nieparzysta.
- Tg x = 0, dla x = πk.
- Funkcja rośnie.
- Tg x › 0, dla x (πk, π/2 + πk).
- Tg x ‹ 0, dla x ϵ (— π/2 + πk, πk).
- Pochodna (tg x)' = 1/cos 2 x .
Rozważać obraz graficzny kotangentoidy poniżej.

Główne właściwości kotangentoidu:
- Y = ctgx.
- W przeciwieństwie do funkcji sinus i cosinus, w stycznej Y może przyjmować wartości zbioru wszystkich liczb rzeczywistych.
- Cotangentoid dąży do wartości y przy x = πk, ale nigdy ich nie osiąga.
- Najmniejszy dodatni okres cotangentoidu to π.
- Ctg (- x) \u003d - ctg x, tj. funkcja jest nieparzysta.
- Ctg x = 0, dla x = π/2 + πk.
- Funkcja maleje.
- Ctg x › 0, dla x (πk, π/2 + πk).
- Ctg x ‹ 0, dla x (π/2 + πk, πk).
- Pochodna (ctg x)' = - 1/sin 2 x Fix