Przykłady rozwiązywania nierówności logarytmicznych o zwiększonej złożoności. Wszystko o nierównościach logarytmicznych. Analiza przykładów

Czy uważasz, że do egzaminu Unified State Exam jest jeszcze trochę czasu i będziesz miał czas na przygotowanie się? Być może tak jest. Ale w każdym razie im wcześniej uczeń rozpocznie przygotowania, tym skuteczniej zdaje egzaminy. Dziś postanowiliśmy poświęcić artykuł nierównościom logarytmicznym. To jedno z zadań, co oznacza możliwość zdobycia dodatkowego zaliczenia.

Czy wiesz już, czym jest logarytm? Naprawdę mamy taką nadzieję. Ale nawet jeśli nie znasz odpowiedzi na to pytanie, nie stanowi to problemu. Zrozumienie, czym jest logarytm, jest bardzo proste.

Dlaczego 4? Musisz podnieść liczbę 3 do tej potęgi, aby otrzymać 81. Kiedy zrozumiesz zasadę, możesz przystąpić do bardziej złożonych obliczeń.

Kilka lat temu przeżyłeś nierówności. I od tego czasu stale spotykasz je w matematyce. Jeśli masz problemy z rozwiązaniem nierówności, sprawdź odpowiednią sekcję.
Skoro już zapoznaliśmy się z pojęciami indywidualnie, przejdźmy do ich ogólnego rozważenia.

Najprostsza nierówność logarytmiczna.

Najprostsze nierówności logarytmiczne nie ograniczają się do tego przykładu; są jeszcze trzy, tylko z różnymi znakami. Dlaczego jest to konieczne? Aby lepiej zrozumieć, jak rozwiązywać nierówności za pomocą logarytmów. Podajmy teraz bardziej odpowiedni przykład, wciąż całkiem prosty; złożone nierówności logarytmiczne zostawmy na później.

Jak to rozwiązać? Wszystko zaczyna się od ODZ. Warto dowiedzieć się o tym więcej, jeśli chcesz zawsze łatwo rozwiązać każdą nierówność.

Co to jest ODZ? ODZ dla nierówności logarytmicznych

Skrót oznacza obszar dopuszczalne wartości. To sformułowanie często pojawia się w zadaniach do egzaminu Unified State Exam. ODZ przyda Ci się nie tylko w przypadku nierówności logarytmicznych.

Spójrz jeszcze raz na powyższy przykład. Na jego podstawie rozważymy ODZ, abyście zrozumieli zasadę, a rozwiązywanie nierówności logarytmicznych nie rodziło pytań. Z definicji logarytmu wynika, że ​​2x+4 musi być większe od zera. W naszym przypadku oznacza to co następuje.

Liczba ta z definicji musi być dodatnia. Rozwiąż nierówność przedstawioną powyżej. Można to nawet zrobić ustnie; tutaj jest jasne, że X nie może być mniejsze niż 2. Rozwiązaniem nierówności będzie określenie zakresu dopuszczalnych wartości.
Przejdźmy teraz do rozwiązania najprostszej nierówności logarytmicznej.

Odrzucamy same logarytmy z obu stron nierówności. Z czym nas to pozostawia? Prosta nierówność.

Nie jest to trudne do rozwiązania. X musi być większe niż -0,5. Teraz łączymy dwie uzyskane wartości w system. Zatem,

Będzie to zakres dopuszczalnych wartości rozważanej nierówności logarytmicznej.

Po co nam w ogóle ODZ? Jest to okazja do wyeliminowania błędnych i niemożliwych odpowiedzi. Jeśli odpowiedź nie mieści się w dopuszczalnych wartościach, to odpowiedź po prostu nie ma sensu. Warto o tym długo pamiętać, gdyż na egzaminie Unified State Exam często pojawia się konieczność poszukiwania ODZ i dotyczy to nie tylko nierówności logarytmicznych.

Algorytm rozwiązywania nierówności logarytmicznej

Rozwiązanie składa się z kilku etapów. Najpierw musisz znaleźć zakres akceptowalnych wartości. W ODZ będą dwie wartości, omówiliśmy to powyżej. Następnie musisz rozwiązać samą nierówność. Metody rozwiązania są następujące:

• metoda zamiany mnożnika;
• rozkład;
• metoda racjonalizacji.

W zależności od sytuacji warto skorzystać z jednej z powyższych metod. Przejdźmy bezpośrednio do rozwiązania. Przedstawmy najpopularniejszą metodę, która jest odpowiednia do rozwiązywania zadań Unified State Examination w prawie wszystkich przypadkach. Następnie przyjrzymy się metodzie rozkładu. Może to pomóc, jeśli natkniesz się na szczególnie trudną nierówność. A więc algorytm rozwiązywania nierówności logarytmicznej.

Przykłady rozwiązań :

Nie bez powodu wzięliśmy właśnie tę nierówność! Zwróć uwagę na podstawę. Pamiętaj: jeśli jest większa niż jeden, znak pozostaje ten sam przy znajdowaniu zakresu dopuszczalnych wartości; w przeciwnym razie należy zmienić znak nierówności.

W rezultacie otrzymujemy nierówność:

Teraz przedstawiamy lewa strona do postaci równania równego zero. Zamiast znaku „mniej niż” stawiamy „równa się” i rozwiązujemy równanie. W ten sposób znajdziemy ODZ. Mamy nadzieję, że dzięki rozwiązaniu tego problemu proste równanie nie będziesz mieć żadnych problemów. Odpowiedzi to -4 i -2. To nie wszystko. Należy wyświetlić te punkty na wykresie, umieszczając „+” i „-”. Co należy w tym celu zrobić? Zastąp liczby z przedziałów do wyrażenia. Tam, gdzie wartości są dodatnie, stawiamy tam „+”.

Odpowiedź: x nie może być większe niż -4 i mniejsze niż -2.

Znaleźliśmy zakres dopuszczalnych wartości tylko dla lewej strony, teraz musimy znaleźć zakres dopuszczalnych wartości dla prawej strony. To jest o wiele łatwiejsze. Odpowiedź: -2. Przecinamy oba powstałe obszary.

Dopiero teraz zaczynamy zajmować się samą nierównością.

Uprośćmy to tak bardzo, jak to możliwe, aby ułatwić rozwiązanie.

W rozwiązaniu ponownie stosujemy metodę przedziałową. Pomińmy obliczenia; z poprzedniego przykładu wszystko jest już jasne. Odpowiedź.

Ale ta metoda jest odpowiednia, jeśli nierówność logarytmiczna ma te same podstawy.

Rozwiązywanie równań logarytmicznych i nierówności za pomocą Z różnych powodów zakłada początkową redukcję do jednej podstawy. Następnie zastosuj metodę opisaną powyżej. Ale jest coś więcej trudny przypadek. Rozważmy jeden z najbardziej gatunki złożone nierówności logarytmiczne.

Nierówności logarytmiczne o zmiennej podstawie

Jak rozwiązać nierówności o takich cechach? Tak, i takie osoby można znaleźć w Unified State Examination. Rozwiązanie nierówności w następujący sposób również przyniesie korzyści Twojemu proces edukacyjny. Rozumiemy problem szczegółowo. Odrzućmy teorię i przejdźmy od razu do praktyki. Aby rozwiązać nierówności logarytmiczne, wystarczy raz zapoznać się z przykładem.

Aby rozwiązać nierówność logarytmiczną przedstawionej postaci, należy sprowadzić prawą stronę do logarytmu o tej samej podstawie. Zasada przypomina przejścia równoważne. W rezultacie nierówność będzie wyglądać następująco.

Właściwie pozostaje tylko stworzyć system nierówności bez logarytmów. Stosując metodę racjonalizacji, przechodzimy do równoważnego układu nierówności. Sama regułę zrozumiesz, gdy zastąpisz odpowiednie wartości i prześledzisz ich zmiany. Układ będzie miał następujące nierówności.

Stosując metodę racjonalizacji przy rozwiązywaniu nierówności należy pamiętać o następujących kwestiach: od podstawy należy odjąć jedną, x z definicji logarytmu odejmuje się od obu stron nierówności (prawa od lewej), mnoży się dwa wyrażenia i ustawić pod oryginalnym znakiem w stosunku do zera.

Dalsze rozwiązanie odbywa się metodą interwałową, tutaj wszystko jest proste. Ważne jest, abyś zrozumiał różnice w metodach rozwiązywania, wtedy wszystko zacznie się łatwo układać.

Nierówności logarytmiczne mają wiele niuansów. Najprostsze z nich są dość łatwe do rozwiązania. Jak rozwiązać każdy z nich bez problemów? Otrzymałeś już wszystkie odpowiedzi w tym artykule. Teraz przed tobą długa praktyka. Ciągle ćwicz rozwiązywanie różne zadania na egzaminie i będziesz mógł uzyskać jak najlepszy wynik. Powodzenia w trudnym zadaniu!

Spośród całej gamy nierówności logarytmicznych osobno bada się nierówności o zmiennej podstawie. Rozwiązuje się je za pomocą specjalnej formuły, której z jakiegoś powodu rzadko uczy się w szkole:

log k (x) fa (x) ∨ log k (x) g (x) ⇒ (f (x) - g (x)) (k (x) - 1) ∨ 0

Zamiast checkboxa „∨” można wstawić dowolny znak nierówności: mniej więcej. Najważniejsze jest to, że w obu nierównościach znaki są takie same.

W ten sposób pozbędziemy się logarytmów i sprowadzimy problem do postaci racjonalna nierówność. To drugie jest znacznie łatwiejsze do rozwiązania, ale po odrzuceniu logarytmów mogą pojawić się dodatkowe pierwiastki. Aby je odciąć, wystarczy znaleźć zakres dopuszczalnych wartości. Jeśli zapomniałeś ODZ logarytmu, zdecydowanie zalecam powtórzenie tego - zobacz „Co to jest logarytm”.

Wszystko, co dotyczy zakresu dopuszczalnych wartości, należy zapisać i rozwiązać osobno:

f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.

Te cztery nierówności tworzą system i muszą być spełnione jednocześnie. Gdy zostanie znaleziony zakres dopuszczalnych wartości, pozostaje tylko przeciąć go rozwiązaniem nierówności racjonalnej - i odpowiedź jest gotowa.

Zadanie. Rozwiąż nierówność:

Najpierw zapiszmy ODZ logarytmu:

Dwie pierwsze nierówności są spełnione automatycznie, ale ostatnią trzeba będzie zapisać. Ponieważ kwadrat liczby wynosi zero wtedy i tylko wtedy, gdy sama liczba wynosi zero, mamy:

x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.

Okazuje się, że ODZ logarytmu to wszystkie liczby z wyjątkiem zera: x ∈ (−∞ 0)∪(0; +∞). Teraz rozwiązujemy główną nierówność:

Dokonujemy przejścia od nierówności logarytmicznej do nierówności racjonalnej. Oryginalna nierówność ma znak „mniej niż”, co oznacza, że ​​wynikająca z niej nierówność również musi mieć znak „mniej niż”. Mamy:

(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 - x 2) x 2< 0;
(3 - x) · (3 + x) · x 2< 0.

Zera tego wyrażenia to: x = 3; x = −3; x = 0. Ponadto x = 0 jest pierwiastkiem drugiej krotności, co oznacza, że ​​przy przejściu przez nią znak funkcji się nie zmienia. Mamy:

Otrzymujemy x ∈ (−∞ −3)∪(3; +∞). Ten zestaw jest całkowicie zawarta w ODZ logarytmu, co oznacza, że ​​to jest odpowiedź.

Przeliczanie nierówności logarytmicznych

Często pierwotna nierówność różni się od powyższej. Można to łatwo skorygować, stosując standardowe zasady pracy z logarytmami - patrz „Podstawowe właściwości logarytmów”. Mianowicie:

1. Dowolną liczbę można przedstawić jako logarytm o danej podstawie;
2. Sumę i różnicę logarytmów o tej samej podstawie można zastąpić jednym logarytmem.

Osobno chciałbym przypomnieć o zakresie dopuszczalnych wartości. Ponieważ w pierwotnej nierówności może być kilka logarytmów, konieczne jest znalezienie VA każdego z nich. Zatem, ogólny schemat rozwiązania nierówności logarytmicznych są następujące:

1. Znajdź VA każdego logarytmu uwzględnionego w nierówności;
2. Zmniejsz nierówność do standardowej, korzystając ze wzorów na dodawanie i odejmowanie logarytmów;
3. Rozwiąż powstałą nierówność zgodnie ze schematem podanym powyżej.

Zadanie. Rozwiąż nierówność:

Znajdźmy dziedzinę definicji (DO) pierwszego logarytmu:

Rozwiązujemy metodą przedziałową. Znajdowanie zer licznika:

3x - 2 = 0;
x = 2/3.

Następnie - zera mianownika:

x - 1 = 0;
x = 1.

Na strzałce współrzędnych zaznaczamy zera i znaki:

Otrzymujemy x ∈ (−∞ 2/3)∪(1; +∞). Drugi logarytm będzie miał tę samą wartość VA. Jeśli nie wierzysz, możesz to sprawdzić. Teraz przekształcamy drugi logarytm tak, aby podstawa wynosiła dwa:

Jak widać, trójki u podstawy i przed logarytmem zostały zmniejszone. Mamy dwa logarytmy o tej samej podstawie. Dodajmy je:

log 2 (x - 1) 2< 2;
log 2 (x - 1) 2< log 2 2 2 .

Otrzymaliśmy standardową nierówność logarytmiczną. Pozbywamy się logarytmów za pomocą wzoru. Ponieważ pierwotna nierówność zawiera znak „mniej niż”, wynikowa racjonalna ekspresja musi być również mniejsza od zera. Mamy:

(f (x) - g (x)) (k (x) - 1)< 0;
((x - 1) 2 - 2 2)(2 - 1)< 0;
x 2 - 2x + 1 - 4< 0;
x 2 - 2x - 3< 0;
(x - 3)(x + 1)< 0;
x ∈ (−1; 3).

Dostaliśmy dwa zestawy:

1. ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
2. Odpowiedź kandydata: x ∈ (−1; 3).

Pozostaje przeciąć te zbiory - otrzymujemy prawdziwą odpowiedź:

Nas interesuje przecięcie zbiorów, dlatego wybieramy przedziały, które są zacienione na obu strzałkach. Otrzymujemy x ∈ (−1; 2/3)∪(1; 3) - wszystkie punkty są przebite.

Definicja logarytmu Najłatwiej zapisać to matematycznie:

Definicję logarytmu można zapisać w inny sposób:

Zwróć uwagę na ograniczenia nałożone na podstawę logarytmu ( A) i do wyrażenia sublogarytmicznego ( X). W przyszłości warunki te staną się ważnymi ograniczeniami dla OD, które należy wziąć pod uwagę przy rozwiązywaniu dowolnego równania z logarytmami. Zatem teraz, oprócz standardowych warunków prowadzących do ograniczeń ODZ (dodatnia wyrażenia pod pierwiastkiem potęg parzystych, nierówny mianownik do zera itp.), należy również wziąć pod uwagę następujące warunki:

• Wyrażenie sublogarytmiczne może być tylko dodatnie.
• Podstawa logarytmu może być tylko dodatnia i nie równa jedności.

Należy pamiętać, że ani podstawa logarytmu, ani wyrażenie sublogarytmiczne nie mogą być równe zero. Należy również pamiętać, że sama wartość logarytmu może przyjmować wszystkie możliwe wartości, tj. Logarytm może być dodatni, ujemny lub zerowy. Logarytmy mają wiele różne właściwości, które wynikają z własności potęg i definicji logarytmu. Wymieńmy je. Zatem właściwości logarytmów:

Logarytm iloczynu:

Logarytm ułamka:

Odejmując stopień ze znaku logarytmu:

Zwróć szczególną uwagę na te z ostatnich wymienionych właściwości, w których znak modułu pojawia się po przyjęciu stopnia. Nie zapominaj, że umieszczając potęgę parzystą poza znakiem logarytmu, pod logarytmem lub u podstawy, musisz pozostawić znak modułu.

Inny korzystne cechy logarytmy:

Ta ostatnia właściwość jest bardzo często wykorzystywana w złożonych równaniach logarytmicznych i nierównościach. Należy o nim pamiętać tak samo jak o wszystkich innych, choć często się o nim zapomina.

Najprostsze równania logarytmiczne wyglądają następująco:

A ich rozwiązanie podaje wzór wynikający bezpośrednio z definicji logarytmu:

Inne najprostsze równania logarytmiczne to takie, które wykorzystując przekształcenia algebraiczne oraz powyższe wzory i własności logarytmów można sprowadzić do postaci:

Rozwiązanie takich równań z uwzględnieniem ODZ jest następujące:

Jacyś inni równania logarytmiczne ze zmienną u podstawy można sprowadzić do postaci:

W takich równaniach logarytmicznych forma ogólna rozwiązanie również wynika bezpośrednio z definicji logarytmu. Tylko w tym przypadku istnieją dodatkowe ograniczenia dla DZ, które należy wziąć pod uwagę. W rezultacie, aby rozwiązać równanie logarytmiczne ze zmienną w podstawie, należy rozwiązać następujący układ:

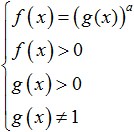
Przy rozwiązywaniu bardziej złożonych równań logarytmicznych, których nie można sprowadzić do jednego z równań przedstawionych powyżej, jest on również aktywnie wykorzystywany metoda zastępowania zmiennych. Jak zwykle, korzystając z tej metody, należy pamiętać, że po wprowadzeniu podstawienia równanie powinno się uprościć i nie zawierać już starej niewiadomej. Należy także pamiętać o wykonaniu odwrotnego podstawienia zmiennych.

Czasami przy rozwiązywaniu równań logarytmicznych trzeba również użyć metoda graficzna . Ta metoda polega na skonstruowaniu wykresów funkcji znajdujących się po lewej i prawej stronie równania możliwie najdokładniej na jednej płaszczyźnie współrzędnych, a następnie odnalezieniu z rysunku współrzędnych punktów ich przecięcia. Otrzymane w ten sposób pierwiastki należy sprawdzić poprzez podstawienie do pierwotnego równania.

Często jest to również przydatne przy rozwiązywaniu równań logarytmicznych metoda grupowania. Korzystając z tej metody, należy przede wszystkim pamiętać, że: aby iloczyn kilku czynników był równy zero, konieczne jest, aby przynajmniej jeden z nich był równy zero, a reszta istniała. Kiedy czynnikami są logarytmy lub nawiasy z logarytmami, a nie tylko nawiasy ze zmiennymi, jak w równania racjonalne, może wystąpić wiele błędów. Ponieważ logarytmy mają wiele ograniczeń w regionie, w którym istnieją.

Decydując układy równań logarytmicznych najczęściej trzeba zastosować albo metodę podstawienia, albo metodę zastępowania zmiennych. Jeżeli istnieje taka możliwość, to przy rozwiązywaniu układów równań logarytmicznych należy dążyć do tego, aby każde z równań układu indywidualnie doprowadzić do postaci, w której możliwe będzie dokonanie przejścia od równania logarytmicznego do równania racjonalny.

Najprostsze nierówności logarytmiczne rozwiązuje się w przybliżeniu w taki sam sposób, jak podobne równania. Po pierwsze, korzystając z przekształceń algebraicznych i własności logarytmów, musimy spróbować doprowadzić je do postaci, w której logarytmy po lewej i prawej stronie nierówności będą miały tę samą podstawę, tj. uzyskaj nierówność postaci:

Następnie należy przejść do nierówności wymiernej, biorąc pod uwagę, że przejście to należy wykonać w następujący sposób: jeśli podstawa logarytmu jest większa niż jeden, to znaku nierówności nie trzeba zmieniać, a jeśli podstawa logarytmu jest mniejsza niż jeden, to należy zmienić znak nierówności na przeciwny (oznacza to zmianę „mniej” na „więcej” i odwrotnie). W takim przypadku nie ma potrzeby zmiany znaków minus na plusy, omijając wcześniej poznane zasady. Zapiszmy matematycznie, co otrzymamy w wyniku wykonania takiego przejścia. Jeśli podstawa jest większa od jedności, otrzymujemy:

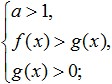
Jeżeli podstawa logarytmu jest mniejsza niż jeden, zmieniamy znak nierówności i otrzymujemy następujący układ:

Jak widzimy, przy rozwiązywaniu nierówności logarytmicznych tradycyjnie brany jest pod uwagę także ODZ (jest to trzeci warunek w powyższych układach). Co więcej, w tym przypadku można nie wymagać dodatniości obu wyrażeń sublogarytmicznych, lecz wymagać jedynie dodatniości mniejszego z nich.

Decydując nierówności logarytmiczne ze zmienną u podstawy logarytm, należy niezależnie rozważyć obie opcje (gdy podstawa jest mniejsza niż jeden i większa niż jeden) i połączyć rozwiązania tych przypadków w zbiór. Jednocześnie nie można zapominać o DL, czyli tzw. o tym, że zarówno podstawa, jak i wszystkie wyrażenia sublogarytmiczne muszą być dodatnie. Zatem rozwiązując nierówność postaci:

Otrzymujemy następujący zestaw układów:

Bardziej złożone nierówności logarytmiczne można również rozwiązać za pomocą zmiany zmiennych. Niektóre inne nierówności logarytmiczne (a także równania logarytmiczne) wymagają do rozwiązania procedury obliczania logarytmu obu stron nierówności lub równania. ta sama podstawa. Tak więc, przeprowadzając taką procedurę z nierównościami logarytmicznymi, istnieje subtelność. Należy pamiętać, że przy logarytmach o podstawie większej niż jeden znak nierówności się nie zmienia, ale jeśli podstawa jest mniejsza niż jeden, znak nierówności zostaje odwrócony.

Jeżeli nierówności logarytmicznej nie da się sprowadzić do wymiernej lub rozwiązać metodą podstawienia, to w tym przypadku należy zastosować uogólniona metoda przedziałowa, czyli następująco:

• Zdefiniuj DL;
• Przekształć nierówność tak, aby po prawej stronie było zero (po lewej stronie, jeśli to możliwe, sprowadź do wspólny mianownik, rozkład na czynniki itp.);
• Znajdź wszystkie pierwiastki licznika i mianownika i nanieś je na oś liczb, a jeśli nierówność nie jest ścisła, zamaluj pierwiastki licznika, ale w każdym razie pozostaw pierwiastki mianownika jako kropkowane;
• Znajdź znak całego wyrażenia na każdym z przedziałów, podstawiając liczbę z danego przedziału do przekształconej nierówności. W takim przypadku nie ma już możliwości zmiany znaków podczas przechodzenia przez punkty na osi. Konieczne jest określenie znaku wyrażenia w każdym przedziale poprzez podstawienie wartości z przedziału do tego wyrażenia i tak dalej dla każdego przedziału. Nie ma innego wyjścia (o to właśnie chodzi, ogólnie mówiąc, różnica między uogólnioną metodą przedziałową a zwykłą);
• Znajdź przecięcie ODZ i przedziałów spełniających nierówność, ale nie trać poszczególnych punktów spełniających nierówność (pierwiastki licznika w nierównościach nieścisłych) i nie zapomnij wykluczyć z odpowiedzi wszystkich pierwiastków mianownik we wszystkich nierównościach.

• Z powrotem
• Do przodu

Jak skutecznie przygotować się do tomografii komputerowej z fizyki i matematyki?

Aby skutecznie przygotować się do egzaminu TK z fizyki i matematyki, należy spełnić trzy najważniejsze warunki:

1. Zapoznaj się ze wszystkimi tematami i wykonaj wszystkie testy i zadania podane w materiałach edukacyjnych na tej stronie. Aby to zrobić, nie potrzebujesz niczego, a mianowicie: poświęcaj trzy do czterech godzin dziennie na przygotowanie się do CT z fizyki i matematyki, studiowanie teorii i rozwiązywanie problemów. Faktem jest, że TK to egzamin, na którym nie wystarczy znać fizykę czy matematykę, trzeba też umieć je rozwiązać szybko i bezbłędnie duża liczba zadania dla różne tematy I o różnej złożoności. Tego ostatniego można się nauczyć jedynie rozwiązując tysiące problemów.
2. Naucz się wszystkich wzorów i praw fizyki oraz wzorów i metod matematyki. W rzeczywistości jest to również bardzo proste do zrobienia, niezbędne formuły w fizyce jest ich tylko około 200, a w matematyce jeszcze trochę mniej. Każdy z tych przedmiotów ma kilkanaście standardowych metod rozwiązywania problemów Poziom podstawowy trudności, których można się również nauczyć, a tym samym rozwiązać je całkowicie automatycznie i bez trudności odpowiedni moment większość DH. Potem będziesz musiał myśleć tylko o najtrudniejszych zadaniach.
3. Weź udział we wszystkich trzech etapach próbnych testów z fizyki i matematyki. Każdy RT można odwiedzić dwukrotnie, aby zdecydować się na obie opcje. Ponownie na CT oprócz umiejętności szybkiego i sprawnego rozwiązywania problemów oraz znajomości wzorów i metod trzeba także umieć odpowiednio zaplanować czas, rozłożyć siły i co najważniejsze poprawnie wypełnić formularz odpowiedzi, bez myląc liczbę odpowiedzi i problemów lub własne nazwisko. Ponadto podczas RT ważne jest, aby przyzwyczaić się do stylu zadawania pytań w problemach, który może wydawać się bardzo nietypowy dla nieprzygotowanej osoby w DT.

Pomyślne, sumienne i odpowiedzialne wdrożenie tych trzech punktów pozwoli Ci pojawić się na CT doskonały wynik, maksimum tego, na co Cię stać.

Znalazłeś błąd?

Jeśli uważasz, że znalazłeś błąd w materiały edukacyjne, to proszę napisać o tym mailem. Możesz także zgłosić błąd do sieć społeczna(). W piśmie podaj temat (fizyka lub matematyka), nazwę lub numer tematu lub testu, numer zadania lub miejsce w tekście (stronie), w którym Twoim zdaniem znajduje się błąd. Opisz również, na czym polega podejrzewany błąd. Twój list nie pozostanie niezauważony, błąd zostanie poprawiony lub zostaniesz wyjaśniony, dlaczego nie jest to błąd.

Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.

Jakie dane osobowe zbieramy:

• Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres E-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

• Zebrane przez nas informacje osobiste pozwala nam kontaktować się z Tobą i informować Cię o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
• Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
• Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak audyt, analiza danych i różne badania w celu ulepszania świadczonych przez nas usług i przekazywania Państwu rekomendacji dotyczących naszych usług.
• Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.

Ujawnianie informacji osobom trzecim

Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.

Wyjątki:

• Jeżeli zajdzie taka potrzeba, zgodnie z prawem, postępowanie sądowe, V test i/lub na podstawie publicznych żądań lub żądań od agencje rządowe na terytorium Federacji Rosyjskiej – ujawnij swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub właściwe ze względów bezpieczeństwa, egzekwowania prawa lub innych celów związanych ze zdrowiem publicznym. ważne sprawy.
• W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.

Szanowanie Twojej prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.

Nierówności logarytmiczne

Na poprzednich lekcjach zapoznaliśmy się z równaniami logarytmicznymi i teraz wiemy, czym są i jak je rozwiązać. Dzisiejsza lekcja poświęcona będzie badaniu nierówności logarytmicznych. Czym są te nierówności i jaka jest różnica między rozwiązaniem równania logarytmicznego a nierównością?

Nierówności logarytmiczne- są to nierówności, które mają zmienną pod znakiem logarytmu lub u jego podstawy.

Można też powiedzieć, że nierówność logarytmiczna to nierówność, w której jej nieznana wartość, jak w równaniu logarytmicznym, pojawi się pod znakiem logarytmu.

Najprostsze nierówności logarytmiczne mają postać:

gdzie f(x) i g(x) to pewne wyrażenia zależne od x.

Spójrzmy na to na przykładzie: f(x)=1+2x+x2, g(x)=3x−1.

Rozwiązywanie nierówności logarytmicznych

Przed rozwiązaniem nierówności logarytmicznych warto zauważyć, że po rozwiązaniu są one podobne nierówności wykładnicze, a mianowicie:

Po pierwsze, przechodząc od logarytmów do wyrażeń pod znakiem logarytmu, musimy także porównać podstawę logarytmu z jednością;

Po drugie, rozwiązując nierówność logarytmiczną za pomocą zmiany zmiennych, musimy rozwiązywać nierówności ze względu na zmianę, aż otrzymamy najprostszą nierówność.

Ale ty i ja rozważaliśmy podobne aspekty rozwiązywania nierówności logarytmicznych. Zwróćmy teraz uwagę na dość istotną różnicę. Ty i ja to wiemy funkcja logarytmiczna ma ograniczony obszar definicjedlatego przechodząc od logarytmów do wyrażeń pod znakiem logarytmu, należy wziąć pod uwagę zakres dopuszczalnych wartości (APV).

Oznacza to, że należy to wziąć pod uwagę przy podejmowaniu decyzji równanie logarytmiczne Ty i ja możemy najpierw znaleźć pierwiastki równania, a następnie sprawdzić to rozwiązanie. Ale rozwiązanie nierówności logarytmicznej nie będzie działać w ten sposób, ponieważ przy przejściu od logarytmów do wyrażeń pod znakiem logarytmu konieczne będzie zapisanie ODZ nierówności.

Ponadto warto pamiętać, że teoria nierówności składa się z liczb rzeczywistych, które są dodatnie i liczby ujemne, a także cyfrę 0.

Na przykład, gdy liczba „a” jest dodatnia, należy zastosować następującą notację: a >0. W tym przypadku zarówno suma, jak i iloczyn tych liczb również będą dodatnie.

Główną zasadą rozwiązywania nierówności jest zastąpienie jej prostszą nierównością, ale najważniejsze jest to, aby była ona równoważna podanej. Ponadto uzyskaliśmy również nierówność i ponownie zastąpiliśmy ją inną, która ma prostszą formę itp.

Rozwiązując nierówności ze zmienną, musisz znaleźć wszystkie jej rozwiązania. Jeżeli dwie nierówności mają tę samą zmienną x, to nierówności takie są równoważne, pod warunkiem, że ich rozwiązania są zbieżne.

Wykonując zadania dotyczące rozwiązywania nierówności logarytmicznych należy pamiętać, że gdy a > 1 to funkcja logarytmiczna rośnie, a gdy 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.

Metody rozwiązywania nierówności logarytmicznych

Przyjrzyjmy się teraz niektórym metodom stosowanym przy rozwiązywaniu nierówności logarytmicznych. Dla lepszego zrozumienia i przyswojenia postaramy się je zrozumieć na konkretnych przykładach.

Wszyscy wiemy, że najprostsza nierówność logarytmiczna ma postać:

W tej nierówności V – jest jednym z następujących znaków nierówności:<,>, ≤ lub ≥.

Gdy podstawa danego logarytmu jest większa od jedności (a>1), dokonując przejścia od logarytmów do wyrażeń pod znakiem logarytmu, to w tej wersji znak nierówności zostaje zachowany i nierówność będzie miała postać:

co jest równoważne temu systemowi:

W przypadku, gdy podstawa logarytmu jest większa od zera i mniejsza od jedności (0

Jest to równoważne temu systemowi:

Przyjrzyjmy się kolejnym przykładom rozwiązywania najprostszych nierówności logarytmicznych pokazanych na poniższym obrazku:

Rozwiązywanie przykładów

Ćwiczenia. Spróbujmy rozwiązać tę nierówność:

Rozwiązywanie zakresu wartości dopuszczalnych.

Spróbujmy teraz pomnożyć jego prawą stronę przez:

Zobaczmy, co możemy wymyślić:

Przejdźmy teraz do konwersji wyrażeń sublogarytmicznych. Ponieważ podstawa logarytmu wynosi 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный:

3x - 8 > 16;
3x > 24;
x > 8.

I z tego wynika, że ​​uzyskany przez nas przedział w całości należy do ODZ i jest rozwiązaniem takiej nierówności.

Oto odpowiedź jaką otrzymaliśmy:

Co jest potrzebne do rozwiązania nierówności logarytmicznych?

Spróbujmy teraz przeanalizować, czego potrzebujemy, aby skutecznie rozwiązać nierówności logarytmiczne?

Najpierw skup całą swoją uwagę i staraj się nie popełnić błędów podczas wykonywania przekształceń podanych w tej nierówności. Należy również pamiętać, że przy rozwiązywaniu takich nierówności należy unikać rozszerzania i kurczenia ODZ nierówności, co może prowadzić do utraty lub nabycia obcych rozwiązań.

Po drugie, rozwiązując nierówności logarytmiczne, trzeba nauczyć się myśleć logicznie i rozumieć różnicę między pojęciami takimi jak system nierówności i zbiór nierówności, aby móc łatwo wybierać rozwiązania nierówności, kierując się jej DL.

Po trzecie, aby skutecznie rozwiązać takie nierówności, każdy z Was musi doskonale znać wszystkie właściwości funkcje elementarne i jasno rozumiem ich znaczenie. Takie funkcje obejmują nie tylko logarytmiczne, ale także wymierne, potęgowe, trygonometryczne itp., Jednym słowem wszystkie te, które studiowałeś przez cały czas szkolenie algebra.

Jak widać, po przestudiowaniu tematu nierówności logarytmicznych, nie ma nic trudnego w rozwiązaniu tych nierówności, pod warunkiem, że będziesz ostrożny i wytrwały w osiąganiu swoich celów. Aby uniknąć problemów w rozwiązywaniu nierówności, należy jak najwięcej ćwiczyć przy rozwiązywaniu różnych zadań, a jednocześnie pamiętać o podstawowych metodach rozwiązywania takich nierówności i ich układach. Jeśli nie uda Ci się rozwiązać nierówności logarytmicznej, powinieneś dokładnie przeanalizować swoje błędy, aby nie wracać do nich ponownie w przyszłości.

Praca domowa

Aby lepiej zrozumieć temat i utrwalić omawiany materiał, rozwiąż następujące nierówności: