1 lekcja na temat

Wykonywane:

Telegina L.B.

Cel lekcji:

1. powtórz cały badany materiał według funkcji.
2. wprowadzić definicję odwrotnej proporcjonalności i nauczyć, jak budować jej wykres.
3. rozwijać logiczne myślenie.
4. pielęgnuj uwagę, dokładność, dokładność.

Plan lekcji:

1. Powtórzenie.
2. Wyjaśnienie nowego materiału.
3. Fizkultminutka.
4. Konsolidacja.

Wyposażenie: plakaty.

Podczas zajęć:

1. Lekcja zaczyna się od powtórek. Uczniowie proszeni są o rozwiązanie krzyżówki (która jest przygotowana wcześniej na duży arkusz papier).

Pytania krzyżówkowe:

1. Zależność między zmiennymi, w której każdej wartości zmiennej niezależnej odpowiada pojedyncza wartość zmiennej zależnej. [Funkcjonować].

2. Zmienna niezależna. [Argument].

3. Zbiór punktów płaszczyzny współrzędnych odciętej, które są równe wartościom argumentu, a rzędne - wartościom funkcji. [Harmonogram].

4. Funkcja dana wzorem y=kx+b. [Liniowy].

5. Jaka jest liczba nazywana współczynnikiem? k we wzorze y=kx+b? [Kątowy].

6. Co służy jako wykres funkcji liniowej? [Prosty].

7. Jeśli k≠0, to wykres y=kx+b przecina tę oś, a jeśli k=0, to jest do niej równoległy. Jaka jest litera tej osi? [X].

8. Słowo w nazwie funkcji y=kx? [Proporcjonalność].

9. Funkcja dana wzorem y=x 2. [Kwadratowy].

10. Tytuł wykresu funkcja kwadratowa. [Parabola].

11. Litera alfabetu łacińskiego, która często oznacza funkcję. [Yy].

12. Jeden ze sposobów ustawienia funkcji. [Formuła].

Nauczyciel : Jakie są główne sposoby definiowania funkcji, które znamy?

(Jeden uczeń otrzymuje przy tablicy zadanie: wypełnić tabelę wartości funkcji 12/x zgodnie z podanymi wartościami jej argumentu, a następnie zbudować odpowiadające im punkty na płaszczyźnie współrzędnych).

Reszta odpowiada na pytania nauczyciela: (które są wstępnie nagrane na tablicy)

1. Jak nazywają się następujące funkcje podane wzorami: y=kx, y=kx+b, y=x 2 , y=x 3 ?

2. Określ zakres następujących funkcji: y=x 2 +8, y=1/x-7, y=4x-1/5, y=2x, y=7-5x, y=2/x, y=x 3, y=-10/x.

Następnie uczniowie pracują na stole, odpowiadając na pytania postawione przez nauczyciela:

1. Który rysunek z tabeli przedstawia wykresy:

a) funkcja liniowa;

b) bezpośrednia proporcjonalność;

c) funkcja kwadratowa;

d) funkcje postaci y=kx 3 ?

2. Jaki jest znak współczynnika k we wzorach postaci y=kx+b, które odpowiadają wykresom na rysunkach 1, 2, 4, 5 tabeli?

3. Znajdź grafikę w tabeli funkcje liniowe, którego współczynniki nachylenia wynoszą:

a) są równe;

b) są równe w wartości bezwzględnej i przeciwne w znaku.

(Następnie cała klasa sprawdza, czy uczeń wezwany na tablicę poprawnie wypełnił tabelę i umieścił punkty na płaszczyźnie współrzędnych).

2. Wyjaśnienie zaczyna się od motywacji.

Nauczyciel: Jak wiadomo, każda funkcja opisuje pewne procesy zachodzące w otaczającym nas świecie.

Rozważmy na przykład prostokąt z bokami x i y oraz powierzchnia 12cm 2 . Wiadomo, że x*y=12, ale co się stanie, jeśli zaczniesz zmieniać jeden z boków prostokąta, powiedzmy, że bok jest długi x?

Długość boku y można znaleźć ze wzoru y=12/x. Jeśli x wzrośnie 2 razy, to będzie miał y=12/2x, czyli strona tak zmniejszy się 2 razy. Jeśli wartość x zwiększ o 3, 4, 5 ... razy, a następnie wartość tak zmniejszy się o tę samą kwotę. Wręcz przeciwnie, jeśli x zmniejszyć kilka razy tak wzrośnie o tę samą kwotę. (Praca na stole).

Dlatego funkcję postaci y=12/x nazywamy odwrotna proporcjonalność. W ogólny widok zapisujemy ją jako y=k/x, gdzie k jest stałą, a k≠0.

To temat dzisiejszej lekcji, zapisany w zeszytach. Podaję ścisłą definicję. Dla funkcji y=12/x, która jest szczególną postacią odwrotnej proporcjonalności, zapisaliśmy już szereg wartości argumentu i funkcji w tabeli i przedstawimy odpowiadające im punkty na płaszczyźnie współrzędnych. Jak wygląda wykres tej funkcji? Trudno jest ocenić cały wykres po skonstruowanych punktach, ponieważ punkty można połączyć w dowolny sposób. Spróbujmy wspólnie wyciągnąć wnioski dotyczące wykresu funkcji wynikającego z rozpatrzenia tabeli i formuły.

Pytania do klasy:

1. Jaki jest zakres funkcji y=12/x?
2. Czy wartości y są dodatnie czy ujemne, jeśli?

a) x

b) x>0?

3. Jak zmienia się wartość zmiennej tak ze zmianą wartości x?

Więc,

1. punkt (0,0) nie należy do wykresu, tj. nie przecina ani osi OX, ani OY;
2. wykres jest w ćwiartkach współrzędnych Ι i ΙΙΙ;
3. płynnie zbliża się do osi współrzędnych zarówno w ćwiartce współrzędnych Ι, jak iw i zbliża się do osi tak blisko, jak jest to pożądane.

Mając te informacje, możemy już połączyć kropki na rysunku (nauczyciel robi to sam na tablicy) i zobaczyć wykres funkcji y=12/x w całości. Powstała krzywa nazywana jest hiperbolą, co po grecku oznacza „przechodzenie przez coś”. Ta krzywa została odkryta przez matematyków starożytnej szkoły greckiej około IV wieku p.n.e. Termin hiperbola został wprowadzony przez Apoloniusza z miasta Pergamon (Azja Mniejsza), żyjącego w -ΙΙ w. PNE.

Teraz obok wykresu funkcji y=12/x narysujemy wykres funkcji y=-12/x. (Uczniowie wykonują to zadanie w zeszytach, a jeden uczeń przy tablicy).

Porównując oba wykresy, uczniowie zauważają, że drugi zajmuje 2 i 4 ćwiartki współrzędnych. Dodatkowo, jeżeli wykres funkcji y=12/x jest wyświetlany symetrycznie względem osi OS, to otrzymamy wykres funkcji y=-12/x.

Pytanie: Jak położenie wykresu hiperboli y=k/x zależy od znaku i wartości współczynnika k?

Uczniowie upewniają się, że jeśli k>0, to wykres znajduje się w Ι oraz ΙΙΙ współrzędne ćwiartki, a jeśli k

1. Wychowanie fizyczne prowadzi nauczyciel.

1. Utrwalenie badanych ma miejsce podczas wykonywania nr 180, 185 z podręcznika.

1. Lekcja jest podsumowana, oceny, praca domowa: poz. 8 nr 179, 184.

2 lekcje na ten temat

„Funkcja odwrotnej proporcjonalności i jej wykres”.

Wykonywane:

Telegina L.B.

Cel lekcji:

1. utrwalić umiejętność kreślenia wykresu funkcji odwrotnej proporcjonalności;
2. rozwijać zainteresowanie tematem, logiczne myślenie;
3. pielęgnuj niezależność, uwagę.

Plan lekcji:

1. Kontrola wykonania zadanie domowe.
2. praca ustna.
3. Rozwiązywanie problemów.
4. Fizkultminutka.
5. Wielopoziomowa niezależna praca.
6. Podsumowanie, ocena, praca domowa.

Wyposażenie: karty.

Podczas zajęć:

1. Nauczyciel ogłasza temat lekcji, cele i plan lekcji.

Następnie dwóch uczniów uzupełnia numery 179, 184 przypisane do domu na tablicy.

1. Reszta uczniów pracuje frontalnie, odpowiadając na pytania nauczyciela.

Pytania:

• Zdefiniuj funkcję odwrotnej proporcjonalności.
• Jaki jest wykres odwrotnej funkcji proporcjonalnej.
• Jak położenie wykresu hiperboli y=k/x zależy od wartości współczynnika k?

Zadania:

1. Wśród funkcji podanych przez formuły nazwij funkcje odwrotnej proporcjonalności:

a) y=x2 +5, b) y=1/x, c) y= 4x-1, d) y=2x, e) y=7-5x, f) y=-11/x, g) y=x 3, h) y=15/x-2.

2. W przypadku funkcji odwrotnej proporcjonalności nazwij współczynnik i wskaż, w których ćwiartkach leży wykres.

3. Znajdź dziedzinę definicji funkcji odwrotnej proporcjonalności.

(Następnie uczniowie sprawdzają nawzajem swoją pracę domową ołówkiem według rozwiązań numerów sprawdzanych przez nauczyciela na tablicy i wystawiają ocenę).

Praca frontalna nad podręcznikiem nr 190, 191, 192, 193 (ustna).

1. Wykonanie w zeszytach i na tablicy z podręcznika nr 186 (b), 187 (b), 182.

4. Sesję wychowania fizycznego prowadzi nauczyciel.

5. Niezależna praca podane w trzy opcje o różnej złożoności(rozprowadzane na kartach).

c. (lekki).

Wykreśl odwrotną funkcję proporcjonalności y=-6/x korzystając z tabeli:

Korzystając z wykresu, znajdź:

a) wartość y, jeśli x = - 1,5; 2;

b) wartość x, przy której y \u003d - 1; 4.

c. (średni poziom trudności)

Wykreśl odwrotną funkcję proporcjonalności y=16/x, wypełniając najpierw tabelę.

Korzystając z wykresu, znajdź przy jakich wartościach x y >0.

ΙΙΙ cala (podwyższona trudność)

Wykreśl odwrotną funkcję proporcjonalności y=10/x-2, wypełniając najpierw tabelę.

Znajdź dziedzinę danej funkcji.

(Uczniowie przekazują do weryfikacji arkusze ze skonstruowanymi wykresami).

6. Podsumowanie lekcji, oceny, praca domowa: nr 186 (a), 187 (a).

Powtórzmy teorię o funkcjach. Funkcja to reguła, zgodnie z którą każdemu elementowi jednego zbioru (argumentu) przypisuje się jakieś ( jedyny!) element innego zestawu (zbiór wartości funkcji). To znaczy, jeśli istnieje funkcja \(y = f(x)\), co oznacza, że ​​każdy dozwolona wartość zmienny \(x\)(co nazywa się „argumentem”) odpowiada jednej wartości zmiennej \(y\)(zwane „funkcją”).

Funkcja opisująca odwrotną zależność

Jest to funkcja formy \(y = \frac(k)(x)\) gdzie \(k \ne 0.\)

Inaczej nazywa się to odwrotną proporcjonalnością: wzrost argumentu powoduje proporcjonalny spadek funkcji.
Zdefiniujmy dziedzinę definicji. Czemu może być \(x\)? Innymi słowy, czemu nie może być równa?

Jedyna liczba, przez którą nie możesz podzielić, to 0, więc \(x \ne 0.\):

\(D(y) = (- \infty ;0) \cup (0; + \infty)\)

czyli to samo:

\(D(y) = R\ukośnik odwrotny \( 0\) .\)

Taki zapis oznacza, że ​​\(x\) może być dowolną liczbą z wyjątkiem 0: znak „R” oznacza zbiór liczb rzeczywistych, czyli wszystkie możliwe liczby; znak „\" oznacza wyłączenie czegoś z tego zestawu (analogicznie do znaku „minus”), a liczba 0 w nawiasach klamrowych oznacza po prostu liczbę 0; okazuje się, że wykluczamy 0 ze wszystkich możliwych liczb.

Okazuje się, że zbiór wartości funkcji jest dokładnie taki sam: w końcu, jeśli \(k \ne 0.\) , to bez względu na to, przez co go podzielimy, 0 nie zadziała:

\(E(y) = (- \infty ;0) \cup (0; + \infty)\)

lub \(E(y) = R\ukośnik odwrotny \( 0\) .\)

Możliwe są również pewne odmiany formuły. \(y = \frac(k)(x)\). Na przykład, \(y = \frac(k)((x + a))\)- jest również funkcją opisującą zależność odwrotną. Zakres i zakres tej funkcji są następujące:

\(D(y) = (- \infty ; - a) \cup (- a; + \infty)\)

\(E(y) = (- \infty ;0) \cup (0; + \infty).\)

Rozważać przykład, sprowadzimy wyrażenie do postaci relacji odwrotnej:

\(y = \frac((x + 2))((x - 3)).\)

\(y = \frac((x + 2))((x - 3)) = \frac((x - 3 + 3 + 2))((x - 3)) = \frac(((x - 3 ) + 5))((x - 3)).\)

Sztucznie wprowadziliśmy do licznika wartość 3, a teraz dzielimy licznik przez mianownik wyraz po wyrazie, otrzymujemy:

\(y = \frac(((x - 3) + 5))((x - 3)) = \frac((x - 3))((x - 3)) + \frac(5)((x - 3)) = 1 + \frac(5)((x - 3)).\)

Otrzymaliśmy zależność odwrotną plus liczba 1.

Odwrotny wykres

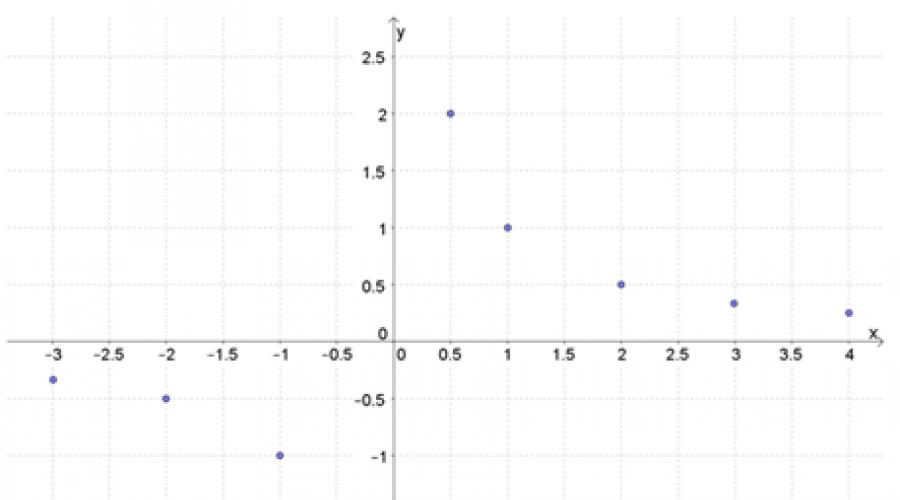
Zacznijmy od prostego przypadku \(y = \frac(1)(x).\)

Zróbmy tabelę wartości:

Narysuj punkty na płaszczyźnie współrzędnych:

Połącz kropki, wykres będzie wyglądał tak:

Ten wykres nazywa się "hiperbola". Podobnie jak parabola, hiperbola ma dwie gałęzie, tyle że nie są one ze sobą połączone. Każdy z nich dąży końcami do zbliżenia się do osi Wół oraz Oy ale nigdy do nich nie dociera.

Zwróćmy uwagę na niektóre cechy funkcji:

1. Jeśli funkcja ma minus przed ułamkiem, to wykres jest odwracany, to znaczy jest wyświetlany symetrycznie wokół osi Wół.
2. Im większa liczba w mianowniku, tym dalej wykres „odbiega” od początku.

Odwrotna zależność w życiu

Gdzie w praktyce spotykamy się z taką funkcją? Jest wiele przykładów. Najczęstszym jest ruch: im większa prędkość, z jaką się poruszamy, tym mniej czasu potrzebujemy na pokonanie tej samej odległości. Zapamiętajmy formułę prędkości:

\(v = \frac(S)(t),\)

gdzie v - prędkość, t - czas podróży, S - odległość (droga).

Stąd możemy wyrazić czas: \(t = \frac(S)(v).\)

Dzisiaj przyjrzymy się, jakie wielkości nazywamy odwrotnie proporcjonalnymi, jak wygląda wykres odwrotnej proporcjonalności i jak to wszystko może Ci się przydać nie tylko na lekcjach matematyki, ale także poza murami szkoły.

Takie różne proporcje

Proporcjonalność wymień dwie wielkości, które są od siebie zależne.

Zależność może być bezpośrednia i odwrotna. Dlatego związek między wielkościami opisuje proporcjonalność bezpośrednią i odwrotną.

Proporcjonalność bezpośrednia- jest to taki związek między dwiema wielkościami, w którym wzrost lub spadek jednej z nich prowadzi do wzrostu lub spadku drugiej. Tych. ich nastawienie się nie zmienia.

Na przykład im więcej wysiłku włożysz w przygotowanie do egzaminów, tym wyższe będą Twoje oceny. Albo im więcej rzeczy zabierzesz ze sobą na wędrówkę, tym trudniej będzie nosić plecak. Tych. ilość wysiłku włożonego w przygotowanie do egzaminów jest wprost proporcjonalna do otrzymanych ocen. A ilość rzeczy spakowanych w plecaku jest wprost proporcjonalna do jego wagi.

Odwrotna proporcjonalność- Ten zależność funkcjonalna, przy której kilkukrotny spadek lub wzrost wartości niezależnej (nazywa się to argumentem) powoduje proporcjonalny (tj. o tę samą kwotę) wzrost lub spadek wartości zależnej (nazywa się to funkcją).

Zilustrować prosty przykład. Chcesz kupić jabłka na targu. Jabłka na ladzie i ilość pieniędzy w twoim portfelu są ze sobą odwrotnie proporcjonalne. Tych. im więcej kupisz jabłek, tym mniej pieniędzy Ci zostanie.

Funkcja i jej wykres

Odwrotną funkcję proporcjonalności można opisać jako y = k/x. W której x≠ 0 i k≠ 0.

Ta funkcja ma następujące właściwości:

1. Jego domeną definicji jest zbiór wszystkich liczb rzeczywistych z wyjątkiem x = 0. D(tak): (-∞; 0) U (0; +∞).
2. Zakres obejmuje wszystkie liczby rzeczywiste z wyjątkiem tak= 0. E(y): (-∞; 0) U (0; +∞) .
3. Nie ma wartości maksymalnych ani minimalnych.
4. Jest dziwny, a jego wykres jest symetryczny względem pochodzenia.
5. Nieokresowe.
6. Jego wykres nie przecina osi współrzędnych.
7. Nie ma zer.
8. Jeśli k> 0 (czyli argument rośnie), funkcja zmniejsza się proporcjonalnie na każdym ze swoich przedziałów. Jeśli k< 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
9. Wraz ze wzrostem argumentu ( k> 0) wartości ujemne funkcji znajdują się w przedziale (-∞; 0), a wartości dodatnie w przedziale (0; +∞). Kiedy argument maleje ( k< 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

Wykres funkcji odwrotnej proporcjonalności nazywa się hiperbolą. Przedstawione w następujący sposób:

Odwrotne problemy proporcjonalne

Aby było to jaśniejsze, spójrzmy na kilka zadań. Nie są one zbyt skomplikowane, a ich rozwiązanie pomoże Ci zobrazować, czym jest odwrotna proporcja i jak ta wiedza może być przydatna w Twoim codziennym życiu.

Zadanie numer 1. Samochód porusza się z prędkością 60 km/h. Dotarcie do celu zajęło mu 6 godzin. Ile czasu zajmie mu pokonanie tego samego dystansu, jeśli porusza się z podwójną prędkością?

Możemy zacząć od wypisania wzoru opisującego zależność czasu, odległości i prędkości: t = S/V. Zgadzam się, to bardzo przypomina nam funkcję odwrotnej proporcjonalności. A wskazuje, że czas, jaki samochód spędza na drodze, i prędkość, z jaką się porusza, są odwrotnie proporcjonalne.

Aby to zweryfikować, znajdźmy V 2, które według warunków jest 2 razy wyższe: V 2 \u003d 60 * 2 \u003d 120 km / h. Następnie obliczamy odległość ze wzoru S = V * t = 60 * 6 = 360 km. Teraz nie jest trudno znaleźć czas t 2, który jest od nas wymagany w zależności od stanu problemu: t 2 = 360/120 = 3 godziny.

Jak widać, czas podróży i prędkość są rzeczywiście odwrotnie proporcjonalne: przy prędkości 2 razy większej niż pierwotna samochód spędzi na drodze 2 razy mniej czasu.

Rozwiązanie tego problemu można również zapisać proporcjonalnie. Dlaczego tworzymy taki diagram:

↓ 60 km/h – 6 h

↓120 km/h – x h

Strzałki wskazują odwrotną zależność. Sugerują również, że podczas sporządzania proporcji należy odwrócić prawą stronę rekordu: 60/120 \u003d x / 6. Gdzie otrzymujemy x \u003d 60 * 6/120 \u003d 3 godziny.

Zadanie nr 2. Warsztat zatrudnia 6 pracowników, którzy radzą sobie z zadanym nakładem pracy w ciągu 4 godzin. Jeśli liczba pracowników zmniejszy się o połowę, ile czasu zajmie pozostałym pracownikom wykonanie tej samej pracy?

Warunki zadania zapisujemy w formularzu schemat wizualny:

↓ 6 pracowników - 4 godziny

↓ 3 pracowników - x h

Zapiszmy to jako proporcję: 6/3 = x/4. I otrzymujemy x \u003d 6 * 4/3 \u003d 8 godzin. Jeśli jest 2 razy mniej pracowników, reszta poświęci 2 razy więcej czasu na wykonanie całej pracy.

Zadanie nr 3. Do basenu prowadzą dwie rury. Przez jedną rurę woda wchodzi z prędkością 2 l / s i wypełnia basen w 45 minut. Inną rurą basen zostanie napełniony w 75 minut. Jak szybko woda dostaje się do basenu przez tę rurę?

Na początek sprowadzimy wszystkie podane nam wielkości zgodnie ze stanem problemu do tych samych jednostek miary. Aby to zrobić, wyrażamy szybkość napełniania basenu w litrach na minutę: 2 l / s \u003d 2 * 60 \u003d 120 l / min.

Ponieważ wynika to z tego, że basen jest napełniany wolniej przez drugą rurę, oznacza to, że prędkość dopływu wody jest mniejsza. Na twarzy odwrotnej proporcji. Wyraźmy nieznaną nam prędkość w postaci x i sporządźmy następujący schemat:

↓ 120 l/min - 45 min

↓ x l/min – 75 min

A potem zrobimy proporcję: 120 / x \u003d 75/45, skąd x \u003d 120 * 45/75 \u003d 72 l / min.

W zadaniu szybkość napełniania basenu wyrażona jest w litrach na sekundę, sprowadźmy naszą odpowiedź do tej samej postaci: 72/60 = 1,2 l/s.

Zadanie nr 4. Wizytówki drukowane są w małej prywatnej drukarni. Pracownik drukarni pracuje z prędkością 42 wizytówek na godzinę i pracuje w pełnym wymiarze godzin - 8 godzin. Gdyby pracował szybciej i drukował 48 wizytówek na godzinę, o ile wcześniej mógłby wrócić do domu?

Idziemy w sprawdzony sposób i sporządzamy schemat zgodnie ze stanem problemu, oznaczając żądaną wartość jako x:

↓ 42 wizytówki/h – 8 h

↓ 48 wizytówek/h – xh

Przed nami relacja odwrotnie proporcjonalna: ile razy więcej wizytówek pracownik drukarni drukuje na godzinę, tyle samo czasu zajmie mu wykonanie tej samej pracy. Wiedząc o tym, możemy ustawić proporcje:

42/48 \u003d x / 8, x \u003d 42 * 8/48 \u003d 7 godzin.

Tak więc, po wykonaniu pracy w 7 godzin, pracownik drukarni mógł wrócić do domu godzinę wcześniej.

Wniosek

Wydaje nam się, że te problemy z odwrotną proporcjonalnością są naprawdę proste. Mamy nadzieję, że teraz i Ty tak uważasz. A co najważniejsze ta wiedza o plecach zależność proporcjonalna wartości naprawdę mogą Ci się przydać więcej niż raz.

Nie tylko na lekcjach matematyki i egzaminach. Ale nawet wtedy, gdy wybierasz się w podróż, na zakupy, decydujesz się zarobić w wakacje itp.

Powiedz nam w komentarzach, jakie przykłady odwrotnej i bezpośredniej proporcjonalności zauważysz wokół siebie. Niech to będzie gra. Zobaczysz, jakie to ekscytujące. Nie zapomnij udostępnić tego artykułu portale społecznościowe aby twoi przyjaciele i koledzy z klasy również mogli grać.

stronie, przy pełnym lub częściowym skopiowaniu materiału, wymagany jest link do źródła.

Pierwszy poziom

Odwrotna zależność. Pierwszy poziom.

Teraz porozmawiamy o odwrotnej zależności, czyli o odwrotnej proporcjonalności, jako funkcji. Czy pamiętasz, że funkcja to pewien rodzaj zależności? Jeśli jeszcze nie czytałeś tego tematu, zdecydowanie zalecam, abyś rzucił wszystko i przeczytał go, ponieważ nie możesz studiować żadnej konkretnej funkcji bez zrozumienia, co to jest - funkcja.

Bardzo przydatne jest również opanowanie dwóch kolejnych przed rozpoczęciem tego tematu proste funkcje: oraz . Tam skonsolidujesz pojęcie funkcji i nauczysz się pracować ze współczynnikami i wykresami.

Czy pamiętasz, czym jest funkcja?
Powtarzamy: funkcja to reguła, zgodnie z którą każdy element jednego zbioru (argumentu) jest powiązany z jakimś ( jedyny!) element innego zestawu (zbiór wartości funkcji). Oznacza to, że jeśli masz funkcję, oznacza to, że dla każdej prawidłowej wartości zmiennej (zwanej „argumentem”) istnieje jedna wartość zmiennej (zwana „funkcją”). Co oznacza „dopuszczalne”? Jeśli nie możesz odpowiedzieć na to pytanie, wróć ponownie do tematu „”! Chodzi o koncepcję "domena": dla niektórych funkcji, nie wszystkie argumenty są równie przydatne, można je podstawić w zależności. Na przykład dla funkcji ujemne wartości argumentów są nieprawidłowe.

Funkcja opisująca odwrotną zależność

Jest to funkcja formy gdzie.

Inaczej nazywa się to odwrotną proporcjonalnością: wzrost argumentu powoduje proporcjonalny spadek funkcji.
Zdefiniujmy zakres. Co może być równe? Innymi słowy, czemu nie może być równa?

Jedyną liczbą, której nie można podzielić przez, jest zatem:

lub, co jest tym samym,

(taki zapis oznacza, że ​​może to być dowolna liczba, z wyjątkiem: znak „” oznacza zbiór liczb rzeczywistych, czyli wszystkie możliwe liczby; znak „” oznacza wykluczenie czegoś z tego zbioru (analog znaku minus ), a liczba w nawiasach okrągłych oznacza tylko liczbę; okazuje się, że wykluczamy ze wszystkich możliwych liczb).

Okazuje się, że zbiór wartości funkcji jest dokładnie taki sam: w końcu jeśli, to bez względu na to, na co go podzielimy, to nie zadziała:

Możliwe są również pewne odmiany formuły. Na przykład jest to również funkcja opisująca zależność odwrotną.
Sam określ zakres i zakres tej funkcji. Powinno się okazać:

Spójrzmy na tę funkcję: . Czy to odwrotna zależność?

Na pierwszy rzut oka trudno powiedzieć: przecież wraz ze wzrostem rośnie zarówno mianownik ułamka, jak i licznik, więc nie jest jasne, czy funkcja będzie się zmniejszać, a jeśli tak, to czy proporcjonalnie? Aby to zrozumieć, musimy przekształcić wyrażenie tak, aby w liczniku nie było zmiennej:

Rzeczywiście uzyskaliśmy zależność odwrotną, ale z zastrzeżeniem: .

Oto kolejny przykład: .

Tutaj sprawa jest bardziej skomplikowana: w końcu licznik i mianownik z pewnością nie są teraz redukowane. Ale nadal możemy spróbować:

Czy rozumiesz, co zrobiłem? W liczniku dodałem i odjąłem tę samą liczbę (), więc wydawało mi się, że nic nie zmieniam, ale teraz licznik ma część równą mianownikowi. Teraz podzielę wyraz po wyrazie, czyli podzielę ten ułamek na sumę dwóch ułamków:

(i to prawda, jeśli przyniesiesz to, co mam) wspólny mianownik, nasz początkowy ułamek okaże się tylko raz):

Wow! Okazuje się ponownie odwrotna zależność, dopiero teraz dodawana jest do niego liczba.
Ta metoda będzie dla nas bardzo przydatna później podczas kreślenia wykresów.

A teraz niezależnie sprowadź wyrażenia do postaci relacji odwrotnej:

Odpowiedzi:

2. Tutaj musisz pamiętać jak trójmian kwadratowy jest faktoryzowany (jest to szczegółowo opisane w temacie „”). Przypomnę, że w tym celu musisz znaleźć korzenie odpowiedniego równanie kwadratowe: . Znajdę je werbalnie korzystając z twierdzenia Viety: , . Jak to jest zrobione? Możesz się tego dowiedzieć, czytając temat.
Otrzymujemy więc: , a więc:

3. Czy próbowałeś już sam go rozwiązać? Jaki jest haczyk? Zapewne w tym, że w liczniku mamy, aw mianowniku - po prostu. To nie problem. Będziemy musieli zmniejszyć o, więc licznik należy wyjąć z nawiasów (aby wyszedł w nawiasach bez współczynnika):

Odwrotny wykres

Jak zwykle zacznijmy od najprostszego przypadku: .
Zróbmy stół:

Narysuj punkty na płaszczyźnie współrzędnych:

Teraz muszą być płynnie połączone, ale jak? Widać, że punkty w prawej i lewej części tworzą pozornie niepowiązane ze sobą zakrzywione linie. Tak jest. Wykres będzie wyglądał tak:

Ten wykres nazywa się "hiperbola"(w tej nazwie jest coś podobnego do „paraboli”, prawda?). Podobnie jak parabola, hiperbola ma dwie gałęzie, tyle że nie są one ze sobą połączone. Każdy z nich ma tendencję do zbliżania się końcami do osi, ale nigdy do nich nie dociera. Jeśli spojrzysz na tę samą hiperbolę z daleka, otrzymasz następujący obraz:

To zrozumiałe: ponieważ wykres nie może przecinać osi. Ale także, więc wykres nigdy nie dotknie osi.

Cóż, teraz zobaczmy, na co wpływają współczynniki. Rozważ te funkcje:
:

Wow, co za piękno!
Wszystkie wykresy są zbudowane różne kolory aby łatwiej je odróżnić.

Na co więc przede wszystkim zwracamy uwagę? Na przykład, jeśli funkcja ma minus przed ułamkiem, to wykres jest odwracany, to znaczy jest wyświetlany symetrycznie wokół osi.

Po drugie: im większa liczba w mianowniku, tym dalej wykres „odbiega” od początku.

Ale co, jeśli funkcja wygląda na bardziej skomplikowaną, na przykład ?

W takim przypadku hiperbola będzie dokładnie taka sama jak zwykła, tylko trochę się przesunie. Zastanówmy się, gdzie?

Co nie może być teraz równe? Prawidłowo . Oznacza to, że wykres nigdy nie osiągnie linii prostej. Co nie może być równe? Teraz. Oznacza to, że teraz wykres będzie dążył do linii prostej, ale nigdy jej nie przekroczy. Więc teraz są hetero i pełnią tę samą rolę, którą pełnią osie współrzędnych dla funkcji. Takie linie nazywają się asymptoty(linie, do których wykres zmierza, ale których nie osiąga):

Więcej o tym, jak takie wykresy są zbudowane, dowiemy się w temacie.

A teraz spróbuj rozwiązać kilka przykładów, aby skonsolidować:

1. Rysunek przedstawia wykres funkcji. Określać.

2. Rysunek przedstawia wykres funkcji. Określać

3. Rysunek przedstawia wykres funkcji. Określać.

4. Rysunek przedstawia wykres funkcji. Określać.

5. Rysunek przedstawia wykresy funkcji i.

Wybierz odpowiedni stosunek:

Odpowiedzi:

Odwrotna relacja w życiu

Gdzie w praktyce spotykamy się z taką funkcją? Jest wiele przykładów. Najczęstszym jest ruch: im większa prędkość, z jaką się poruszamy, tym mniej czasu potrzebujemy na pokonanie tej samej odległości. Przypomnijmy sobie wzór na prędkość: , gdzie to prędkość, to czas podróży, to odległość (droga).

Stąd możemy wyrazić czas:

Przykład:

Człowiek idzie do pracy Średnia prędkość km/h i dociera za godzinę. Ile minut spędzi na tej samej drodze, jeśli będzie jechał z prędkością km/h?

Decyzja:

Ogólnie rzecz biorąc, rozwiązałeś już takie problemy w piątej i szóstej klasie. Czy zrobiłeś proporcje?

Oznacza to, że pojęcie odwrotnej proporcjonalności jest ci już dokładnie znane. Tak właśnie zapamiętali. A teraz to samo, tylko w dorosły sposób: poprzez funkcję.

Funkcja (czyli zależność) czasu w minutach od prędkości:

Wiadomo, że wtedy:

Trzeba znaleźć:

Teraz wymyśl kilka przykładów z życia, w których występuje odwrotna proporcjonalność.
Wynaleziony? Dobra robota, jeśli tak. Powodzenia!

ODWRÓCONA ZALEŻNOŚĆ. KRÓTKO O GŁÓWNYM

1. Definicja

Funkcja opisująca odwrotną zależność jest funkcją formy gdzie.

Inaczej funkcja ta nazywana jest odwrotną proporcjonalnością, ponieważ wzrost argumentu powoduje proporcjonalny spadek funkcji.

lub, co jest tym samym,

Wykres odwrotnej zależności jest hiperbolą.

2. Współczynniki, i.

Odpowiedzialny za „nachylenie” i kierunek wykresu: im większy ten współczynnik, tym dalej od początku znajduje się hiperbola, a zatem „skręca” mniej ostro (patrz rysunek). Znak współczynnika wpływa na kwartały, w których znajduje się wykres:

• jeśli, to gałęzie hiperboli znajdują się w ćwiartkach;
• jeśli, to w i.

x=a jest pionowa asymptota, to znaczy pion, do którego zmierza wykres.

Liczba odpowiada za przesunięcie wykresu funkcji w górę o kwotę if , oraz przesunięcie w dół if .

Stąd jest asymptota pozioma.