Tabela proporcjonalności bezpośredniej i odwrotnej. Posty oznaczone „bezpośrednia proporcjonalność”

Przykład

Współczynnik proporcjonalności

Nazywa się stały stosunek proporcjonalnych wielkości współczynnik proporcjonalności. Współczynnik proporcjonalności pokazuje, ile jednostek jednej wielkości przypada na jednostkę innej.

Proporcjonalność bezpośrednia

Proporcjonalność bezpośrednia- zależność funkcjonalna, w której pewna wielkość zależy od innej wielkości w taki sposób, że ich stosunek pozostaje stały. Innymi słowy, te zmienne się zmieniają proporcjonalnie, w równych częściach, to znaczy, jeśli argument zmienił się dwukrotnie w dowolnym kierunku, to funkcja zmienia się również dwukrotnie w tym samym kierunku.

Matematycznie bezpośrednia proporcjonalność jest zapisana jako formuła:

f(x) = ax,a = const

Odwrotna proporcjonalność

Odwrotna proporcja- jest to zależność funkcjonalna, w której wzrost wartości niezależnej (argumentu) powoduje proporcjonalny spadek wartości zależnej (funkcji).

Matematycznie odwrotna proporcjonalność jest zapisana jako formuła:

Właściwości funkcji:

Źródła

Fundacja Wikimedia. 2010 .

Rodzaje zależności

Rozważ ładowanie baterii. Jako pierwszą wartość weźmy czas potrzebny do naładowania. Druga wartość to czas, w którym będzie działać po naładowaniu. Im dłużej bateria jest ładowana, tym dłużej będzie działać. Proces będzie kontynuowany do pełnego naładowania baterii.

Zależność żywotności baterii od czasu jej ładowania

Uwaga 1

Ta zależność nazywa się prosty:

Wraz ze wzrostem jednej wartości rośnie również druga. Gdy jedna wartość maleje, druga wartość również maleje.

Rozważmy inny przykład.

Im więcej książek czyta student, tym więcej mniej błędów zrobi w dyktando. Albo im wyżej wspinasz się po górach, tym niższe będzie ciśnienie atmosferyczne.

Uwaga 2

Ta zależność nazywa się odwrócić:

Gdy jedna wartość wzrasta, druga maleje. Gdy jedna wartość spada, druga wzrasta.

Tak więc w przypadku bezpośrednia zależność obie wielkości zmieniają się w ten sam sposób (zarówno wzrastają, jak i maleją), a w przypadku odwrotna zależność - przeciwnie (jeden wzrasta, a drugi maleje lub odwrotnie).

Określanie zależności między wielkościami

Przykład 1

Czas potrzebny na odwiedzenie znajomego to 20 $ minut. Wraz ze wzrostem prędkości (pierwszej wartości) o 2$ razy, przekonamy się, jak zmieni się czas (druga wartość), który spędzimy na drodze do przyjaciela.

Oczywiście czas zmniejszy się o 2$ razy.

Uwaga 3

Ta zależność nazywa się proporcjonalny:

Ile razy zmieni się jedna wartość, ile razy zmieni się druga.

Przykład 2

Za 2 dolary bochenka chleba w sklepie trzeba zapłacić 80 rubli. Jeśli musisz kupić bochenki chleba za 4 $ (ilość chleba wzrasta 2 $ razy), o ile więcej będziesz musiał zapłacić?

Oczywiście koszt również wzrośnie o 2$ razy. Mamy przykład zależności proporcjonalnej.

W obu przykładach uwzględniono zależności proporcjonalne. Ale w przykładzie z bochenkami chleba wartości zmieniają się w jednym kierunku, dlatego zależność jest prosty. A w przykładzie z wycieczką do przyjaciela związek między szybkością a czasem jest odwrócić. Tak więc istnieje wprost proporcjonalna zależność oraz zależność odwrotnie proporcjonalna.

Proporcjonalność bezpośrednia

Weź pod uwagę proporcjonalne ilości 2$: ilość bochenków chleba i ich koszt. Niech bochenki chleba 2$ kosztują 80$ rubli. Przy wzroście liczby rolek o 4$ razy (8$ rolek), ich łączny koszt wyniesie 320$ rubli.

Stosunek liczby rolek: $\frac(8)(2)=4$.

Stosunek kosztów rzutu: $\frac(320)(80)=4$.

Jak widać, te wskaźniki są sobie równe:

$\frac(8)(2)=\frac(320)(80)$.

Definicja 1

Równość dwóch relacji nazywa się proporcja.

Przy relacji wprost proporcjonalnej stosunek uzyskuje się, gdy zmiana pierwszej i drugiej wartości jest taka sama:

$\frac(A_2)(A_1)=\frac(B_2)(B_1)$.

Definicja 2

Te dwie wielkości są nazywane wprost proporcjonalne jeżeli przy zmianie (zwiększeniu lub zmniejszeniu) jednej z nich, druga wartość zmienia się (odpowiednio rośnie lub maleje) o tę samą wartość.

Przykład 3

Samochód przejechał 180$ km w 2$ godziny. Znajdź czas potrzebny mu na pokonanie 2$-krotności dystansu z tą samą prędkością.

Decyzja.

Czas jest wprost proporcjonalny do odległości:

$t=\frac(S)(v)$.

Ile razy zwiększy się odległość stała prędkość, czas wydłuży się o tę samą kwotę:

$\frac(2S)(v)=2t$;

$\frac(3S)(v)=3t$.

Samochód przejechał 180$ km - w czasie 2$ godziny

Auto przejeżdża 180$ \cdot 2=360$ km - w czasie $x$ godzin

Im większą odległość przejedzie samochód, tym więcej czasu zajmie. Dlatego związek między wielkościami jest wprost proporcjonalny.

Zróbmy proporcję:

$\frac(180)(360)=\frac(2)(x)$;

$x=\frac(360 \cdot 2)(180)$;

Odpowiedź: Samochód będzie potrzebował 4 $ godzin.

Odwrotna proporcjonalność

Definicja 3

Decyzja.

Czas jest odwrotnie proporcjonalny do prędkości:

$t=\frac(S)(v)$.

Ile razy prędkość wzrasta, przy tej samej ścieżce, czas zmniejsza się o tę samą wartość:

$\frac(S)(2v)=\frac(t)(2)$;

$\frac(S)(3v)=\frac(t)(3)$.

Zapiszmy stan problemu w formie tabeli:

Auto przejechało $60$km - w czasie $6$godzin

Samochód pokonuje 120$ km - w czasie $x$ godzin

Im szybszy samochód, tym mniej czasu zajmie. Dlatego związek między wielkościami jest odwrotnie proporcjonalny.

Zróbmy proporcję.

Ponieważ proporcjonalność jest odwrotna, drugi stosunek obracamy proporcjonalnie:

$\frac(60)(120)=\frac(x)(6)$;

$x=\frac(60 \cdot 6)(120)$;

Odpowiedź: Samochód będzie potrzebował 3 $ godzin.

Pojęcie bezpośredniej proporcjonalności

Wyobraź sobie, że myślisz o zakupie ulubionego cukierka (lub czegokolwiek, co naprawdę lubisz). Słodycze w sklepie mają swoją cenę. Załóżmy 300 rubli za kilogram. Im więcej cukierków kupisz, tym więcej pieniędzy płacić. Oznacza to, że jeśli chcesz 2 kilogramy - zapłać 600 rubli, a jeśli chcesz 3 kilogramy - daj 900 rubli. Wszystko wydaje się jasne, prawda?

Jeśli tak, to teraz jest dla ciebie jasne, czym jest bezpośrednia proporcjonalność - jest to koncepcja opisująca stosunek dwóch wielkości, które są od siebie zależne. A stosunek tych wielkości pozostaje niezmienny i stały: o ile części jedna z nich wzrasta lub maleje, o tę samą liczbę części druga proporcjonalnie wzrasta lub maleje.

Proporcjonalność bezpośrednią można opisać wzorem: f(x) = a*x, a w tym wzorze a jest wartością stałą (a = const). W naszym przykładzie z cukierkami cena jest stałą, stałą. Nie zwiększa się ani nie zmniejsza, bez względu na to, ile słodyczy zdecydujesz się kupić. Zmienna niezależna (argument) x to ile kilogramów słodyczy zamierzasz kupić. A zmienna zależna f(x) (funkcja) określa, ile pieniędzy ostatecznie płacisz za swój zakup. Możemy więc podstawić liczby we wzorze i otrzymać: 600 r. = 300 r. * 2 kg.

Wniosek pośredni jest taki: jeśli argument rośnie, funkcja również rośnie, jeśli argument maleje, funkcja również maleje

Funkcja i jej właściwości

Bezpośrednia funkcja proporcjonalna jest szczególny przypadek funkcja liniowa. Jeśli funkcja liniowa to y = k*x + b, to dla bezpośredniej proporcjonalności wygląda to tak: y = k*x, gdzie k nazywamy współczynnikiem proporcjonalności i jest to zawsze liczba niezerowa. Obliczenie k jest proste - znajdujemy je jako iloraz funkcji i argumentu: k = y/x.

Aby było to jaśniejsze, weźmy inny przykład. Wyobraź sobie, że samochód porusza się z punktu A do punktu B. Jego prędkość wynosi 60 km/h. Jeśli założymy, że prędkość ruchu pozostaje stała, to można ją przyjąć jako stałą. A następnie zapisujemy warunki w postaci: S \u003d 60 * t, a ta formuła jest podobna do funkcji bezpośredniej proporcjonalności y \u003d k * x. Narysujmy dalej równolegle: jeśli k \u003d y / x, to prędkość samochodu można obliczyć, znając odległość między A i B oraz czas spędzony na drodze: V \u003d S / t.

A teraz, od zastosowanego zastosowania wiedzy o bezpośredniej proporcjonalności, wróćmy do jej funkcji. Do właściwości których należą:

jego domeną definicji jest zbiór wszystkich liczb rzeczywistych (a także jego podzbiór);

funkcja jest nieparzysta;

zmiana zmiennych jest wprost proporcjonalna do całej długości osi liczbowej.

Proporcjonalność bezpośrednia i jej wykres

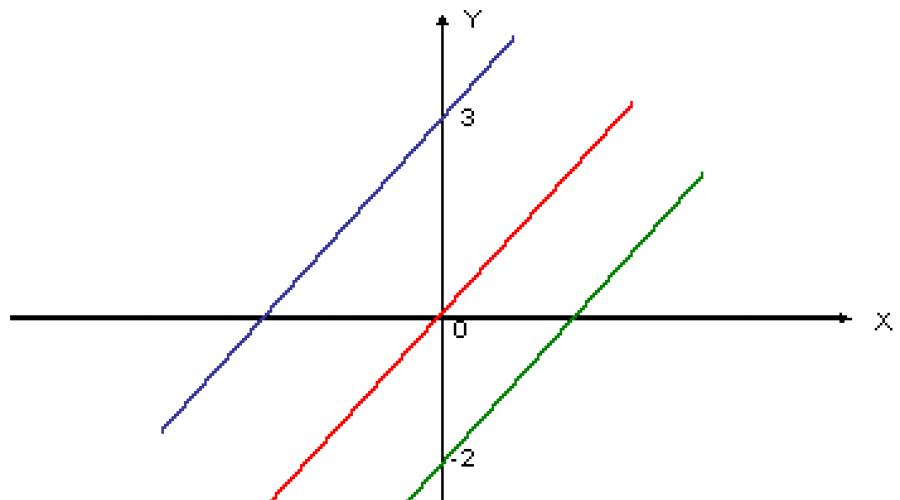
Wykres funkcji proporcjonalnej wprost to linia prosta, która przecina punkt początkowy. Aby go zbudować wystarczy zaznaczyć jeszcze tylko jeden punkt. I połącz to i pochodzenie linii.

W przypadku wykresu jest to nachylenie. Jeśli nachylenie jest mniejsze od zera (k< 0), то угол между графиком функции прямой пропорциональности и осью абсцисс тупой, а функция убывающая. Если угловой коэффициент больше нуля (k >0), wykres i formularz na osi x ostry róg, a funkcja rośnie.

I jeszcze jedna właściwość wykresu funkcji proporcjonalności bezpośredniej jest bezpośrednio związana z nachyleniem k. Załóżmy, że mamy dwie nieidentyczne funkcje i odpowiednio dwa wykresy. Tak więc, jeśli współczynniki k tych funkcji są równe, ich wykresy są równoległe do osi współrzędnych. A jeśli współczynniki k nie są sobie równe, wykresy przecinają się.

Przykłady zadań

Zdecydujmy się na parę bezpośrednie problemy z proporcjonalnością

Zacznijmy od prostych.

Zadanie 1: Wyobraź sobie, że 5 kur złożyło 5 jaj w ciągu 5 dni. A jeśli jest 20 kur, to ile jaj zniosą w ciągu 20 dni?

Rozwiązanie: Oznacz niewiadomą jako x. I będziemy rozumować w następujący sposób: ile razy było więcej kurczaków? Podziel 20 przez 5 i dowiedz się, że 4 razy. A ile razy więcej jaj złoży 20 kur w ciągu tych samych 5 dni? Również 4 razy więcej. Tak więc znajdujemy nasze tak: 5 * 4 * 4 \u003d 80 jaj złoży 20 kur w ciągu 20 dni.

Teraz przykład jest trochę bardziej skomplikowany, przeformułujmy problem z „Ogólnej arytmetyki” Newtona. Zadanie 2: Pisarz może napisać 14 stron nowej książki w 8 dni. Gdyby miał asystentów, ile osób zajęłoby napisanie 420 stron w 12 dni?

Rozwiązanie: Uważamy, że liczba osób (pisarz + asystenci) rośnie wraz ze wzrostem ilości pracy, jeśli trzeba ją wykonać w tym samym czasie. Ale ile razy? Dzieląc 420 przez 14, dowiadujemy się, że wzrasta ona 30 razy. Ale ponieważ, zgodnie z warunkami zadania, więcej czasu na pracę, liczba asystentów nie wzrasta 30 razy, ale w ten sposób: x \u003d 1 (pisarz) * 30 (razy): 12/8 (dni). Przekształćmy się i dowiedzmy się, że x = 20 osób napisze 420 stron w 12 dni.

Rozwiążmy inny problem podobny do tych, które mieliśmy w przykładach.

Zadanie 3: W tę samą podróż wyruszają dwa samochody. Jeden poruszał się z prędkością 70 km/h i ten sam dystans pokonał w 2 godziny, a drugi w 7 godzin. Znajdź prędkość drugiego samochodu.

Rozwiązanie: Jak pamiętasz, droga jest wyznaczana przez prędkość i czas - S = V *t. Ponieważ oba samochody jechały tą samą drogą, możemy zrównać te dwa wyrażenia: 70*2 = V*7. Gdzie stwierdzimy, że prędkość drugiego samochodu to V = 70*2/7 = 20 km/h.

I jeszcze kilka przykładów zadań z funkcjami bezpośredniej proporcjonalności. Czasami w problemach wymagane jest znalezienie współczynnika k.

Zadanie 4: Biorąc pod uwagę funkcje y \u003d - x / 16 i y \u003d 5x / 2, określ ich współczynniki proporcjonalności.

Rozwiązanie: Jak pamiętasz, k = y/x. Stąd dla pierwszej funkcji współczynnik wynosi -1/16, a dla drugiej k = 5/2.

Możesz również natknąć się na zadanie takie jak Zadanie 5: Zapisz wzór na bezpośrednią proporcjonalność. Jego wykres i wykres funkcji y \u003d -5x + 3 znajdują się równolegle.

Rozwiązanie: Funkcja podana nam w warunku jest liniowa. Wiemy, że bezpośrednia proporcjonalność jest szczególnym przypadkiem funkcji liniowej. Wiemy też, że jeśli współczynniki funkcji k są równe, to ich wykresy są równoległe. Oznacza to, że wystarczy obliczyć współczynnik znanej funkcji i ustawić bezpośrednią proporcjonalność za pomocą znanej nam formuły: y \u003d k * x. Współczynnik k \u003d -5, bezpośrednia proporcjonalność: y \u003d -5 * x.

Wniosek

Teraz nauczyłeś się (lub pamiętasz, jeśli już omówiłeś ten temat wcześniej), co się nazywa bezpośrednia proporcjonalność i rozważyłem to przykłady. Rozmawialiśmy również o funkcji proporcjonalności bezpośredniej i jej wykresie, rozwiązaliśmy na przykład kilka problemów.

Jeśli ten artykuł był przydatny i pomógł zrozumieć temat, powiedz nam o tym w komentarzach. Abyśmy wiedzieli, czy możemy Ci pomóc.

blog.site, z pełnym lub częściowym skopiowaniem materiału, wymagany jest link do źródła.

Przykład

Współczynnik proporcjonalności

Nazywa się stały stosunek proporcjonalnych wielkości współczynnik proporcjonalności. Współczynnik proporcjonalności pokazuje, ile jednostek jednej wielkości przypada na jednostkę innej.

Proporcjonalność bezpośrednia

Proporcjonalność bezpośrednia- zależność funkcjonalna, w której pewna wielkość zależy od innej wielkości w taki sposób, że ich stosunek pozostaje stały. Innymi słowy, te zmienne się zmieniają proporcjonalnie, w równych częściach, to znaczy, jeśli argument zmienił się dwukrotnie w dowolnym kierunku, to funkcja zmienia się również dwukrotnie w tym samym kierunku.

Matematycznie bezpośrednia proporcjonalność jest zapisana jako formuła:

f(x) = ax,a = const

Odwrotna proporcjonalność

Odwrotna proporcja- jest to zależność funkcjonalna, w której wzrost wartości niezależnej (argumentu) powoduje proporcjonalny spadek wartości zależnej (funkcji).

Matematycznie odwrotna proporcjonalność jest zapisana jako formuła:

Właściwości funkcji:

Źródła

Fundacja Wikimedia. 2010 .

Zobacz, co „Bezpośrednia proporcjonalność” znajduje się w innych słownikach:

bezpośrednia proporcjonalność- - [A.S. Goldberg. Angielsko-rosyjski słownik energetyczny. 2006] Tematy energia ogólnie EN stosunek bezpośredni … Podręcznik tłumacza technicznego

bezpośrednia proporcjonalność- tiesioginis proporcingumas statusas T sritis fizika atitikmenys: angl. bezpośrednia proporcjonalność vok. direkte Proportionalitat, f rus. bezpośrednia proporcjonalność, f pranc. proporcjonalnalité directe, f … Fizikos terminų žodynas

- (od łac. proporcjonalny proporcjonalny, proporcjonalny). Proporcjonalność. Słownictwo obcojęzyczne słowa zawarte w języku rosyjskim. Chudinov A.N., 1910. PROPORCJONALNOŚĆ otlat. proporcjonalny, proporcjonalny. Proporcjonalność. Wyjaśnienie dotyczące 25000… … Słownik wyrazów obcych języka rosyjskiego

PROPORCJONALNOŚĆ, proporcjonalność, pl. nie, kobieta (książka). 1. rozproszenie rzeczownik proporcjonalne. Proporcjonalność części. Proporcjonalność ciała. 2. Taki związek między ilościami, gdy są one proporcjonalne (patrz proporcjonalny ... Słownik Uszakow

Dwie wzajemnie zależne wielkości nazywane są proporcjonalnymi, jeśli stosunek ich wartości pozostaje niezmieniony. Spis treści 1 Przykład 2 Współczynnik proporcjonalności ... Wikipedia

PROPORCJONALNOŚĆ i żony. 1. patrz proporcjonalna. 2. W matematyce: taki związek między wielkościami, gdy wzrost jednej z nich pociąga za sobą zmianę drugiej o tę samą wielkość. Bezpośrednie p. (przy cięciu ze wzrostem o jedną wartość ... ... Słownik wyjaśniający Ożegowa

ORAZ; dobrze. 1. do proporcjonalnego (1 cyfra); proporcjonalność. P. części. P. budowa ciała. P. reprezentacja w parlamencie. 2. Matematyka. Zależność między proporcjonalnie zmieniającymi się wielkościami. Współczynnik proporcjonalności. Bezpośrednie p. (w którym z ... ... słownik encyklopedyczny

Proporcjonalność to relacja między dwiema wielkościami, w której zmiana jednej z nich pociąga za sobą zmianę drugiej o tę samą wartość.

Proporcjonalność jest prosta i odwrotna. W tej lekcji przyjrzymy się każdemu z nich.

Proporcjonalność bezpośrednia

Załóżmy, że samochód porusza się z prędkością 50 km/h. Pamiętamy, że prędkość to odległość przebyta w jednostce czasu (1 godzina, 1 minuta lub 1 sekunda). W naszym przykładzie samochód porusza się z prędkością 50 km/h, czyli w ciągu godziny przejedzie dystans równy pięćdziesięciu kilometrom.

Wykreślmy odległość przebytą przez samochód w ciągu 1 godziny.

Niech samochód jedzie przez kolejną godzinę z tą samą prędkością pięćdziesięciu kilometrów na godzinę. Potem okazuje się, że auto przejedzie 100 km

Jak widać na przykładzie, podwojenie czasu spowodowało zwiększenie przebytej odległości o tę samą wartość, czyli dwukrotnie.

Mówi się, że wielkości takie jak czas i odległość są wprost proporcjonalne. Zależność między tymi wielkościami nazywa się bezpośrednia proporcjonalność.

Proporcjonalność bezpośrednia to stosunek między dwiema wielkościami, w którym wzrost jednej z nich pociąga za sobą wzrost drugiej o tę samą wielkość.

i odwrotnie, jeśli jedna wartość zmniejszy się określoną liczbę razy, to druga zmniejszy się o tę samą wartość.

Załóżmy, że pierwotnie planowano przejechać autem 100 km w 2 godziny, ale po przejechaniu 50 km kierowca postanowił zrobić sobie przerwę. Wtedy okazuje się, że zmniejszając odległość o połowę, czas zmniejszy się o tę samą wartość. Innymi słowy, zmniejszenie przebytej odległości prowadzi do skrócenia czasu o ten sam czynnik.

Interesującą cechą wielkości wprost proporcjonalnych jest to, że ich stosunek jest zawsze stały. Oznacza to, że przy zmianie wartości wielkości wprost proporcjonalnych ich stosunek pozostaje niezmieniony.

W rozważanym przykładzie odległość początkowo wynosiła 50 km, a czas jednej godziny. Stosunek odległości do czasu to liczba 50.

Ale zwiększyliśmy czas ruchu 2 razy, co równa się dwóm godzinom. W efekcie przebyty dystans zwiększył się o tę samą wartość, czyli osiągnął wartość 100 km. Stosunek stu kilometrów do dwóch godzin to znowu liczba 50

Numer 50 nazywa się bezpośredni współczynnik proporcjonalności. Pokazuje, jaka jest odległość na godzinę ruchu. W ta sprawa współczynnik odgrywa rolę prędkości ruchu, ponieważ prędkość jest stosunkiem przebytej odległości do czasu.

Proporcje mogą być wykonane z ilości wprost proporcjonalnych. Na przykład proporcje i uzupełnij proporcję:

Pięćdziesiąt kilometrów odnosi się do jednej godziny, a sto kilometrów do dwóch godzin.

Przykład 2. Koszt i ilość zakupionego towaru są wprost proporcjonalne. Jeśli 1 kg słodyczy kosztuje 30 rubli, to 2 kg tych samych słodyczy kosztuje 60 rubli, 3 kg - 90 rubli. Wraz ze wzrostem kosztu zakupionego towaru jego ilość wzrasta o tę samą kwotę.

Ponieważ wartość towaru i jego ilość są wprost proporcjonalne, ich stosunek jest zawsze stały.

Zapiszmy stosunek trzydziestu rubli do jednego kilograma

Teraz zapiszmy, jaki jest stosunek sześćdziesięciu rubli do dwóch kilogramów. Ten stosunek będzie ponownie równy trzydziestu:

Tutaj bezpośredni współczynnik proporcjonalności to liczba 30. Ten współczynnik pokazuje, ile rubli za kilogram słodyczy. W tym przykładzie współczynnik pełni rolę ceny jednego kilograma towaru, ponieważ cena jest stosunkiem kosztu towaru do jego ilości.

Odwrotna proporcjonalność

Rozważać następny przykład. Odległość między dwoma miastami wynosi 80 km. Motocyklista wyjechał z pierwszego miasta iz prędkością 20 km/h dotarł do drugiego miasta w 4 godziny.

Jeśli prędkość motocyklisty wynosiła 20 km/h, oznacza to, że co godzinę pokonywał dystans równy dwudziestu kilometrom. Przedstawmy na rysunku odległość przebytą przez motocyklistę i czas jego ruchu:

W drodze powrotnej motocyklista jechał z prędkością 40 km/h, a na tej samej trasie spędził 2 godziny.

Łatwo zauważyć, że gdy zmienia się prędkość, czas ruchu zmienia się o tyle samo. I to się zmieniło Odwrotna strona- to znaczy prędkość wzrosła, a czas, przeciwnie, spadł.

Wielkości takie jak prędkość i czas nazywane są odwrotnie proporcjonalnymi. Zależność między tymi wielkościami nazywa się odwrotna proporcjonalność.

Odwrotna proporcjonalność to relacja między dwiema wielkościami, w której wzrost jednej z nich pociąga za sobą zmniejszenie drugiej o tę samą wielkość.

i odwrotnie, jeśli jedna wartość zmniejszy się określoną liczbę razy, druga wzrośnie o tę samą wartość.

Przykładowo, gdyby w drodze powrotnej motocyklista miał prędkość 10 km/h, to te same 80 km przebyłby w 8 godzin:

Jak widać na przykładzie, spadek prędkości spowodował wydłużenie czasu podróży o ten sam czynnik.

Osobliwością odwrotnie proporcjonalnych ilości jest to, że ich iloczyn jest zawsze stały. Oznacza to, że przy zmianie wartości odwrotnie proporcjonalnych ilości ich produkt pozostaje niezmieniony.

W rozważanym przykładzie odległość między miastami wynosiła 80 km. Przy zmianie prędkości i czasu motocyklisty dystans ten zawsze pozostawał bez zmian.

Motocyklista mógłby pokonać ten dystans z prędkością 20 km/hw 4 godziny, 40 km/hw 2 godziny i 10 km/hw 8 godzin. We wszystkich przypadkach iloczyn prędkości i czasu wynosił 80 km

Podobała Ci się lekcja?
Dołączć do naszego Nowa grupa Vkontakte i zacznij otrzymywać powiadomienia o nowych lekcjach