Formule korijena n-tog stepena. Funkcija snage i korijeni - definicija, svojstva i formule

Video lekcija 2: Svojstva korijena stepena n > 1

Predavanje: Koren stepena n > 1 i njegova svojstva

Root

Pretpostavimo da imate jednačinu poput:

Odluka zadata jednačinaće biti x 1 = 2 i x 2 = (-2). Oba rješenja su prikladna kao odgovor, jer brojevi sa jednakim modulima, kada se podignu na paran stepen, daju isti rezultat.

Ovo je bio jednostavan primjer, međutim, šta možemo učiniti ako npr.

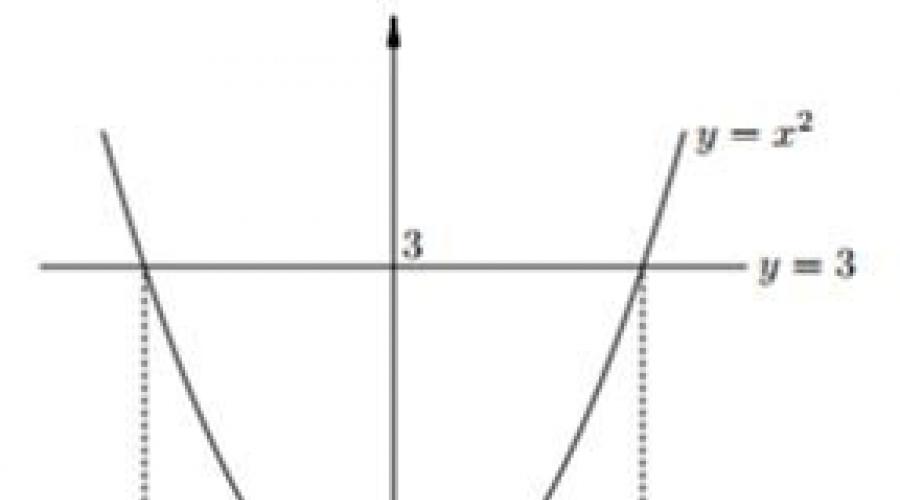
Pokušajmo grafički prikazati funkciju y=x 2 . Njegov graf je parabola:

Na grafikonu morate pronaći točke koje odgovaraju vrijednosti y = 3. Ove točke su:

To znači da se ova vrijednost ne može nazvati cijelim brojem, već se može predstaviti kao kvadratni korijen.

Bilo koji korijen je iracionalan broj. Iracionalni brojevi uključuju korijene, neperiodične beskonačne razlomke.

Kvadratni korijen je nenegativan broj "a", čiji je radikalni izraz jednak datom broju "a" na kvadrat.

Na primjer,

Odnosno, kao rezultat, dobit ćemo samo pozitivnu vrijednost. Međutim, kao rješenje kvadratne jednadžbe oblika

Rješenje će biti x 1 = 4, x 2 = (-4).

Svojstva kvadratnog korijena

1. Bez obzira na vrijednost x, ovaj izraz je u svakom slučaju istinit:

2. Poređenje brojeva koji sadrže kvadratni korijen. Za upoređivanje ovih brojeva potrebno je upisati i jedan i drugi broj pod znakom korijena. Taj će broj biti veći čiji je radikalni izraz veći.

Upisujemo broj 2 pod znakom korijena

Sada stavimo broj 4 ispod znaka korijena. Kao rezultat ovoga, dobijamo

I tek sada se dva rezultujuća izraza mogu uporediti:

3. Uklanjanje množitelja ispod korijena.

Ako se radikalni izraz može rastaviti na dva faktora, od kojih se jedan može izvaditi iz podznaka korijena, onda se ovo pravilo mora koristiti.

4. Postoji svojstvo inverzno ovome - uvođenje množitelja ispod korijena. Očigledno smo koristili ovo svojstvo u drugom posjedu.

Vaša privatnost nam je važna. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Molimo pročitajte našu politiku privatnosti i javite nam ako imate pitanja.

Prikupljanje i korištenje ličnih podataka

Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.

Koje lične podatke prikupljamo:

• Kada podnesete prijavu na stranici, možemo prikupljati različite informacije, uključujući vaše ime, broj telefona, adresu Email itd.

Kako koristimo vaše lične podatke:

• Prikupljeno od nas lična informacija nam omogućava da vas kontaktiramo i informiramo o jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše lične podatke kako bismo vam poslali važna obavještenja i komunikacije.
• Također možemo koristiti lične podatke za interne svrhe kao što su revizija, analiza podataka i razne studije da poboljšamo usluge koje pružamo i da vam damo preporuke u vezi sa našim uslugama.
• Ako učestvujete u nagradnoj igri, natjecanju ili sličnom poticaju, možemo koristiti informacije koje nam date za upravljanje takvim programima.

Otkrivanje trećim licima

Podatke koje dobijemo od vas ne otkrivamo trećim licima.

Izuzeci:

• Po potrebi - u skladu sa zakonom, sudski nalog, in parnica, i/ili na osnovu javnih zahtjeva ili zahtjeva od vladine agencije na teritoriji Ruske Federacije - otkrijte svoje lične podatke. Također možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno za sigurnost, provođenje zakona ili druge javne važnim prilikama.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo relevantnom nasljedniku treće strane.

Zaštita ličnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše lične podatke od gubitka, krađe i zloupotrebe, kao i od neovlašćenog pristupa, otkrivanja, izmjene i uništenja.

Održavanje vaše privatnosti na nivou kompanije

Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima komuniciramo o privatnosti i sigurnosnoj praksi i striktno provodimo praksu privatnosti.

Lekcija i prezentacija na temu: "Svojstva korijena n-tog stepena. Teoreme"

Dodatni materijali
Dragi korisnici, ne zaboravite ostaviti svoje komentare, povratne informacije, sugestije! Svi materijali su provjereni antivirusnim programom.

Nastavna sredstva i simulatori u internet prodavnici "Integral" za 11. razred
Interaktivni priručnik za 9-11 razred "Trigonometrija"
Interaktivni priručnik za 10-11 razred "Logaritmi"

Svojstva korijena n-tog stepena. Teoreme

Ljudi, nastavljamo proučavati korijene n-og stepena realnog broja. Kao i gotovo svi matematički objekti, korijeni n-tog stepena imaju neka svojstva, danas ćemo ih proučavati.
Sva svojstva koja razmatramo formulirana su i dokazana samo za nenegativne vrijednosti varijabli sadržanih pod predznakom korijena.
U slučaju neparnog korijenskog eksponenta, vrijede i za negativne varijable.

Teorema 1. N-ti korijen proizvoda dva nenegativna broja jednak je proizvodu n-tog korijena ovih brojeva: $\sqrt[n](a*b)=\sqrt[n](a)*\ sqrt[n]( b) $ .

Dokažimo teoremu.
Dokaz. Ljudi, da bismo dokazali teoremu, uvedemo nove varijable, označimo:
$\sqrt[n](a*b)=x$.
$\sqrt[n](a)=y$.
$\sqrt[n](b)=z$.
Moramo dokazati da je $x=y*z$.
Imajte na umu da vrijede i sljedeći identiteti:
$a*b=x^n$.
$a=y^n$.
$b=z^n$.
Tada vrijedi i sljedeći identitet: $x^n=y^n*z^n=(y*z)^n$.
Stepeni dva nenegativna broja i njihovi eksponenti su jednaki, tada su baze samih stepeni jednake. Otuda $x=y*z$, što je trebalo dokazati.

Teorema 2. Ako je $a≥0$, $b>0$ i n - prirodni broj, što je veće od 1, tada vrijedi sljedeća jednakost: $\sqrt[n](\frac(a)(b))=\frac(\sqrt[n](a))(\sqrt[n](b) ))$.

To jest, n-ti korijen količnika jednak je količniku n-tog korijena.

Dokaz.
Da bismo to dokazali, koristimo pojednostavljenu shemu u obliku tabele:

Primjeri izračunavanja n-tog korijena

Primjer.
Izračunajte: $\sqrt(16*81*256)$.
Odluka. Koristimo teoremu 1: $\sqrt(16*81*256)=\sqrt(16)*\sqrt(81)*\sqrt(256)=2*3*4=24$.

Primjer.
Izračunajte: $\sqrt(7\frac(19)(32))$.
Odluka. Radikalni izraz predstavljamo u obliku nepravilan razlomak: $7\frac(19)(32)=\frac(7*32+19)(32)=\frac(243)(32)$.
Koristimo teoremu 2: $\sqrt(\frac(243)(32))=\frac(\sqrt(243))(\sqrt(32))=\frac(3)(2)=1\frac(1 ) (2)$.

Primjer.
Izračunati:
a) $\sqrt(24)*\sqrt(54)$.
b) $\frac(\sqrt(256))(\sqrt(4))$.
Odluka:
a) $\sqrt(24)*\sqrt(54)=\sqrt(24*54)=\sqrt(8*3*2*27)=\sqrt(16*81)=\sqrt(16)*\ sqrt(81)=2*3=6$.
b) $\frac(\sqrt(256))(\sqrt(4))=\sqrt(\frac(256)(4))=\sqrt(64)=24$.

Teorema 3. Ako su $a≥0$, k i n prirodni brojevi veći od 1, tada je tačna jednakost: $(\sqrt[n](a))^k=\sqrt[n](a^k)$.

Da bi se korijen uzdigao do prirodne moći, dovoljno je podići radikalni izraz do ove moći.

Dokaz.
hajde da razmotrimo poseban slučaj za $k=3$. Koristimo teoremu 1.
$(\sqrt[n](a))^k=\sqrt[n](a)*\sqrt[n](a)*\sqrt[n](a)=\sqrt[n](a*a *a)=\sqrt[n](a^3)$.
Isto se može dokazati za bilo koji drugi slučaj. Ljudi, dokažite to sami za slučaj kada je $k=4$ i $k=6$.

Teorema 4. Ako su $a≥0$ b n,k prirodni brojevi veći od 1, tada vrijedi sljedeća jednakost: $\sqrt[n](\sqrt[k](a))=\sqrt(a)$.

Da biste izvukli korijen iz korijena, dovoljno je pomnožiti eksponente korijena.

Dokaz.
Dokažimo još jednom ukratko koristeći tabelu. Da bismo to dokazali, koristimo pojednostavljenu shemu u obliku tabele:

Primjer.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.

Teorema 5. Ako se indeksi korijena i korijenskog izraza pomnože sa istim prirodnim brojem, tada se vrijednost korijena neće promijeniti: $\sqrt(a^(kp))=\sqrt[n](a) $.

Dokaz.
Princip dokaza naše teoreme je isti kao iu drugim primjerima. Hajde da predstavimo nove varijable:
$\sqrt(a^(k*p))=x=>a^(k*p)=x^(n*p)$ (po definiciji).
$\sqrt[n](a^k)=y=>y^n=a^k$ (po definiciji).
Posljednju jednakost dižemo na stepen p
$(y^n)^p=y^(n*p)=(a^k)^p=a^(k*p)$.
dobio:
$y^(n*p)=a^(k*p)=x^(n*p)=>x=y$.
To jest, $\sqrt(a^(k*p))=\sqrt[n](a^k)$, što je trebalo dokazati.

primjeri:
$\sqrt(a^5)=\sqrt(a)$ (podeljeno sa 5).
$\sqrt(a^(22))=\sqrt(a^(11))$ (podeljeno sa 2).
$\sqrt(a^4)=\sqrt(a^(12))$ (množeno sa 3).

Primjer.
Pokrenite akcije: $\sqrt(a)*\sqrt(a)$.
Odluka.
Korijenski eksponenti su različiti brojevi, tako da ne možemo koristiti teoremu 1, ali primjenom teoreme 5 možemo dobiti jednake eksponente.
$\sqrt(a)=\sqrt(a^3)$ (množeno sa 3).
$\sqrt(a)=\sqrt(a^4)$ (množeno sa 4).
$\sqrt(a)*\sqrt(a)=\sqrt(a^3)*\sqrt(a^4)=\sqrt(a^3*a^4)=\sqrt(a^7)$.

Zadaci za samostalno rješavanje

1. Izračunajte: $\sqrt(32*243*1024)$.
2. Izračunajte: $\sqrt(7\frac(58)(81))$.
3. Izračunajte:
a) $\sqrt(81)*\sqrt(72)$.
b) $\frac(\sqrt(1215))(\sqrt(5))$.
4. Pojednostavite:
a) $\sqrt(\sqrt(a))$.
b) $\sqrt(\sqrt(a))$.
c) $\sqrt(\sqrt(a))$.
5. Izvršite radnje: $\sqrt(a^2)*\sqrt(a^4)$.

primjeri:

\(\sqrt(16)=2\) jer \(2^4=16\)
\(\sqrt(-\frac(1)(125))\) \(=\) \(-\frac(1)(5)\) , jer \((-\frac(1)(5) ) ^3\) \(=\) \(-\frac(1)(125)\)

Kako izračunati korijen n-tog stepena?

Da biste izračunali \(n\)-ti korijen, morate sebi postaviti pitanje: koji će broj na \(n\)-tom stepenu dati ispod korijena?

na primjer. Izračunajte \(n\)-ti korijen: a)\(\sqrt(16)\); b) \(\sqrt(-64)\); c) \(\sqrt(0,00001)\); d)\(\sqrt(8000)\); e) \(\sqrt(\frac(1)(81))\).

a) Koji će broj na \(4\) stepen dati \(16\)? Očigledno, \(2\). dakle:

b) Koji broj na \(3\)-ti stepen daje \(-64\)?

\(\sqrt(-64)=-4\)

c) Koji će broj na \(5\) stepen dati \(0,00001\)?

\(\sqrt(0,00001)=0,1\)

d) Koji broj na \(3\)-tom stepenu daje \(8000\)?

\(\sqrt(8000)=20\)

e) Koji će broj na \(4\) stepen dati \(\frac(1)(81)\)?

\(\sqrt(\frac(1)(81))=\frac(1)(3)\)

Najviše smo pregledali jednostavni primjeri sa korijenom \(n\)-og stepena. Da riješim više izazovni zadaci sa \(n\)-tim korijenima - bitno ih je poznavati.

Primjer. Izračunati:

\(\sqrt 3\cdot \sqrt(-3) \cdot \sqrt(27) \cdot \sqrt(9) -\) \(=\)		AT ovog trenutka nijedan od korijena se ne može izračunati. Stoga primjenjujemo svojstva korijena \(n\)-tog stepena i transformiramo izraz. \(\frac(\sqrt(-64))(\sqrt(2))\)\(=\)\(\sqrt(\frac(-64)(2))\) \(=\)\(\sqrt(-32)\) jer \(\frac(\sqrt[n](a))(\sqrt[n](b))\)\(=\)\(\sqrt[n](\frac(a)(b))\)
\(=\sqrt(3)\cdot \sqrt(-3)\cdot \sqrt(27)\cdot \sqrt(9)-\sqrt(-32)=\)		Preuredimo faktore u prvom članu tako da kvadratni korijen i korijen \(n\)-tog stepena budu jedan pored drugog. Ovo će olakšati primjenu svojstava. većina svojstava \(n\)-tih korijena radi samo sa korijenima istog stepena. I izračunavamo korijen 5. stepena.
\(=\sqrt(3) \cdot \sqrt(27) \cdot \sqrt(-3)\cdot \sqrt(9)-(-5)=\)		Primijenite svojstvo \(\sqrt[n](a)\cdot \sqrt[n](b)=\sqrt[n](a\cdot b)\) i proširite zagradu
\(=\sqrt(81)\cdot \sqrt(-27)+5=\)		Izračunajte \(\sqrt(81)\) i \(\sqrt(-27)\)
\(=9\cdot(-3)+5=-27+5=-22\)

Jesu li n-ti korijen i kvadratni korijen povezani?

U svakom slučaju, bilo koji korijen bilo kojeg stepena je samo broj, iako napisan u neobičnom obliku za vas.

Singularnost n-tog korijena

\(n\)-ti korijen sa neparnim \(n\) može se uzeti iz bilo kojeg broja, čak i negativnih (pogledajte primjere na početku). Ali ako je \(n\) paran (\(\sqrt(a)\), \(\sqrt(a)\),\(\sqrt(a)\)...), tada se takav korijen izdvaja samo ako \( a ≥ 0\) (usput, kvadratni korijen ima isto). To je zbog činjenice da je vađenje korijena suprotno eksponencijaciji.

A podizanje na paran stepen čini čak i negativan broj pozitivnim. Zaista, \((-2)^6=(-2) \cdot (-2) \cdot (-2) \cdot (-2) \cdot (-2) \cdot (-2)=64\). Stoga ne možemo dobiti negativan broj ispod korijena parnog stepena. To znači da ne možemo izdvojiti takav korijen iz negativnog broja.

Neparni stepen nema takvih ograničenja - negativan broj podignut na neparan stepen ostat će negativan: \((-2)^5=(-2) \cdot (-2) \cdot (-2) \cdot (-2 ) \ cdot(-2)=-32\). Stoga, ispod korijena neparnog stepena, možete dobiti negativan broj. To znači da ga je također moguće izdvojiti iz negativnog broja.

Rootn-. stepen i njegova svojstva

Šta je korijennth stepen? Kako izvaditi korijen?

U osmom razredu već ste uspjeli da se upoznate kvadratni korijen. Odlučeno tipični primjeri s korijenima, primjenjujući određena svojstva korijena. Takođe odlučeno kvadratne jednačine , gdje bez vađenja kvadratnog korijena - nikako. Ali kvadratni korijen je samo poseban slučaj više širok koncept – root n th stepen . Osim kvadrata, tu je, na primjer, kubni korijen, korijen četvrtog, petog i više visoki stepeni. I za uspješan rad s takvim korijenima, ipak bi bilo lijepo početi s "ti" s kvadratnim korijenima.) Stoga, za one koji imaju problema s njima, toplo preporučujem da ponove.

Izdvajanje korijena je jedna od inverznih operacija eksponencijacije.) Zašto "jedna od"? Jer, vađenje korijena, tražimo baza prema poznatim stepen i indikator. A postoji još jedna inverzna operacija - pronalaženje indikator prema poznatim stepen i osnova. Ova operacija se zove pronalaženje logaritam. To je složenije od vađenja korijena i proučava se u srednjoj školi.)

Pa hajde da se upoznamo!

Prvo, notacija. Kvadratni korijen, kao što već znamo, označava se ovako:. Ova ikona se zove veoma lepo i naučno - radikalan. A koji su korijeni drugih diploma? Vrlo je jednostavno: iznad "repa" radikala dodatno ispisuju indikator stepena čiji se korijen traži. Ako tražite kubni korijen, onda napišite trojku: . Ako je korijen četvrtog stepena, onda, respektivno, . I tako dalje.) opšti pogled root n-ti stepen je označeno ovako:

Gdje .

Broja , kao u kvadratnim korijenima, se zove radikalan izraz a evo i brojan ovo je novo za nas. I zvao korijenski indikator .

Kako izvući korijene bilo kojeg stepena? Baš kao i kvadratni - shvatite koji nam broj na n-ti stepen daje broja .)

Kako, na primjer, izvući kubni korijen od 8? I.e ? I koji broj cubed će nam dati 8? Dvojka, naravno.) Tako pišu:

Ili . Koji je broj na četvrti stepen od 81? tri.) Dakle,

Šta je sa desetim korijenom od 1? Pa, nije pametno da je jedinica na bilo koju potenciju (uključujući deseti) jednaka jedinici.) To jest:

I uopšteno govoreći.

Sa nulom, ista priča: nula na bilo koju prirodnu snagu jednaka je nuli. To je, .

Kao što vidite, u poređenju s kvadratnim korijenima, već je teže odgonetnuti koji nam broj daje korijenski broj na ovaj ili onaj stepena . Teže pokupiti odgovorite i provjerite točnost po stepenovanjun . Situacija je znatno olakšana ako lično znate stepen popularnih brojeva. Dakle, sada treniramo. :) Priznajemo diplome!)

Odgovori (u neredu):

Da da! Više je odgovora nego zadataka.) Jer, na primjer, 2 8 , 4 4 i 16 2 su svi isti broj 256.

Obučeni? Zatim razmatramo primjere:

Odgovori (takođe u neredu): 6; 2; 3; 2; 3; 5.

Desilo se? Fabulous! Idemo dalje.)

Root ograničenja. aritmetički korijen nth stepen.

AT korijeni n-tog stepeni, kao i u kvadratima, takođe imaju svoja ograničenja i svoje čipove. U suštini, oni se ne razlikuju od onih ograničenja za kvadratni korijeni.

Ne bira se, zar ne? Koliko je 3, koliko je -3 na četvrti stepen biće +81. :) I sa bilo kojim root-om čak stepen od negativnog broja će biti ista pjesma. A ovo znači to nemoguće je izdvojiti parne korijene iz negativnih brojeva . Ovo je zabranjena radnja u matematici. Zabranjeno kao dijeljenje sa nulom. Stoga, izrazi kao što su , i slično - nema smisla.

Ali koreni odd stepeni negativnih brojeva - molim!

Na primjer, ; , itd.)

A iz pozitivnih brojeva možete sigurno izdvojiti bilo koje korijene, bilo koje stupnjeve:

Generalno, to je razumljivo, mislim.) I, usput, root ne mora biti tačno izvučen. Ovo su samo primjeri, čisto za razumijevanje.) Dešava se da u procesu rješavanja (na primjer, jednačina) iskrsnu prilično loši korijeni. Nešto kao . Iz osmice se kockasti korijen izvlači savršeno, a ovdje je sedam ispod korijena. šta da radim? Uredu je. Sve je potpuno isto.- ovo je broj koji će nam, kada se kocka, dati 7. Samo je broj jako ružan i čupav. Evo ga:

Štaviše, ovaj broj nikada ne prestaje i nema tačku: brojevi slijede potpuno nasumično. To je iracionalno... U takvim slučajevima, odgovor se ostavlja u obliku korijena.) Ali ako se korijen ekstrahira čisto (na primjer,), tada se, naravno, korijen mora izračunati i zapisati:

Opet uzimamo naš eksperimentalni broj 81 i iz njega izdvajamo četvrti korijen:

Jer tri u četvrtom će biti 81. Pa dobro! Ali takođe minus tričetvrti će takođe imati 81!

Postoji nejasnoća:

A da bi se to eliminisalo, baš kao i kod kvadratnih korijena, uveden je poseban termin: aritmetički korijennstepena iz među a - to je tako nenegativan broj,n-th stepen koji je jednak a .

A odgovor sa plusom ili minusom naziva se drugačije - algebarski korijennth stepen. Za bilo koji parni stepen, algebarski korijen će biti dva suprotna broja. U školi rade samo sa aritmetičkim korijenima. Dakle negativni brojevi u aritmetičkim korijenima se jednostavno odbacuju. Na primjer, pišu: Sam plus, naravno, nije napisan: it implicirati.

Sve je, čini se, jednostavno, ali ... Ali šta je s korijenima neparnog stepena iz negativnih brojeva? Na kraju krajeva, uvijek postoji negativan broj prilikom izdvajanja! Budući da bilo koji negativan broj u neparan stepen takođe daje negativan broj. A aritmetički korijen radi samo sa nenegativnim brojevima! Zato je to aritmetika.)

U takvim korijenima rade ovo: vade minus ispod korijena i stavljaju ga ispred korijena. Volim ovo:

U takvim slučajevima se kaže da izraženo u terminima aritmetičkog (tj. već nenegativnog) korijena .

Ali postoji jedna stvar koja može biti zbunjujuća - ovo je rješenje jednostavnih jednačina sa potencijama. Na primjer, evo jednadžbe:

Pišemo odgovor: U stvari, ovaj odgovor je samo skraćena oznaka dva odgovora:

Ovdje je nesporazum što sam već malo više napisao da se u školi smatraju samo nenegativni (tj. aritmetički) korijeni. A evo jednog od odgovora sa minusom... Kako biti? Nema šanse! Znakovi su ovdje rezultat rješavanja jednačine. ALI sam koren- vrijednost i dalje nije negativna! Uvjerite se sami:

Pa, je li sada jasnije? sa zagradama?)

Sa neparnim stepenom, sve je mnogo jednostavnije - uvijek se ispostavi jedan root. Plus ili minus. Na primjer:

Pa ako mi jednostavno izvučemo korijen (parnog stepena) iz broja, onda uvijek dobijemo jedan nenegativan rezultat. Zato što je to aritmetički korijen. Sada, ako odlučimo jednačina sa parnim stepenom, dobijamo dva suprotna korena, pošto je ovo rješenje jednačine.

Sa korijenima neparnih stupnjeva (kubni, peti stepen, itd.) nema problema. Izvlačimo se i ne kupamo se znakovima. Plus ispod korijena znači rezultat ekstrakcije sa plusom. Minus znači minus.

A sada je vrijeme da se upoznamo svojstva korijena. Neki će nam već biti poznati iz kvadratnog korijena, ali će se dodati nekoliko novih. Idi!

Svojstva korijena. Koren rada.

Ovo svojstvo nam je već poznato iz kvadratnog korijena. Za korijene drugih stupnjeva sve je slično:

tj. korijen proizvoda jednak je proizvodu korijena svakog faktora posebno.

Ako indikatorn paran, zatim oba radikalna brojaa ib mora, naravno, biti nenegativna, inače formula nema značenje. U slučaju neparnog indikatora, nema ograničenja: minuse uzimamo naprijed ispod korijena, a zatim radimo s aritmetičkim korijenima.)

Kao i kod kvadratnih korijena, ovdje je ova formula podjednako korisna i s lijeva na desno i s desna na lijevo. Primjena formule s lijeva na desno omogućava vam da izvučete korijenje od posla. Na primjer:

Ova formula, inače, vrijedi ne samo za dva, već za bilo koji broj faktora. Na primjer:

Također, koristeći ovu formulu, možete izdvojiti korijene iz velikih brojeva: za to se broj ispod korijena razlaže na manje faktore, a zatim se korijeni izdvajaju zasebno iz svakog faktora.

Na primjer, takav zadatak:

Broj je dovoljno velik. Da li se ukorijeni? glatko- takođe bez kalkulatora nije jasno. Bilo bi lijepo to izdvojiti. Sa čime je tačno djeljiv broj 3375? Sa 5, čini se: zadnja cifra je pet.) Podijelite:

Oh, opet deljivo sa 5! 675:5 = 135. I 135 je opet podijeljeno sa pet. Da, kada će se završiti?

135:5 = 27. Sa brojem 27 sve je već jasno - ovo je trojka u kocki. znači,

onda:

Uzeli su korijen dio po dio, pa, dobro.)

Ili ovaj primjer:

Opet, činimo faktore prema znakovima djeljivosti. Šta? Na 4, jer posljednji par brojeva 40 je djeljiv sa 4. I sa 10, jer zadnja cifra je nula. Dakle, možete podijeliti jednim potezom za 40 odjednom:

O broju 216 već znamo da je ovo šest kub. To je,

A 40, zauzvrat, može se razložiti kao . Onda

I onda konačno dobijamo:

Nije išlo čisto da izvadim korijen, pa, u redu je. U svakom slučaju, pojednostavili smo izraz: znamo da je ispod korijena (barem kvadratnog, barem kubnog - bilo kojeg) uobičajeno ostaviti najviše mali broj moguće.) U ovom primjeru smo uradili jednu vrlo korisnu operaciju, koja nam je također već poznata iz kvadratnog korijena. Da li prepoznajete? Da! Mi izdržao faktori ispod korijena. U ovom primjeru smo izvadili dvojku i šesticu, tj. broj 12.

Kako izvaditi faktor iz predznaka korijena?

Vrlo je lako izvaditi faktor (ili faktore) izvan korijenskog znaka. Razlažemo korijenski izraz na faktore i izdvajamo ono što je ekstrahovano.) A ono što nije izvučeno ostavljamo u korijenu. vidi:

Razlažemo broj 9072 na faktore. Pošto imamo koren četvrtog stepena, prvo pokušavamo da dekomponujemo na faktore koji su četvrti stepen prirodnih brojeva - 16, 81 itd.

Pokušajmo podijeliti 9072 sa 16:

Shared!

Ali čini se da je 567 djeljivo sa 81:

Znači,.

Onda

Svojstva korijena. Množenje korijena.

Razmotrite sada obrnutu primjenu formule - s desna na lijevo:

Na prvi pogled ništa novo, ali izgled vara.) Reverse Application formula uvelike proširuje naše mogućnosti. Na primjer:

Hmm, pa šta nije u redu s tim? Sve su umnožili. Ovdje zaista nema ništa posebno. Uobičajeno množenje korijena. A evo primjera!

Zasebno, korijeni nisu samo izvučeni iz faktora. Ali rezultat je odličan.)

Opet, formula vrijedi za bilo koji broj faktora. Na primjer, trebate izračunati sljedeći izraz:

Glavna stvar ovdje je pažnja. Primjer sadrži razne korijeni su kubni i četvrtog stepena. I nijedan od njih nije definitivno izvađen...

A formula za proizvod korijena primjenjiva je samo na korijenje sa isto indikatori. Pa hajde da ih grupišemo u posebnu grupu. kubni korijeni i posebno - četvrti stepen. A tamo će, vidite, sve srasti.))

I nije mi trebao kalkulator.

Kako dodati množitelj ispod korijenskog znaka?

Sljedeći korisna stvar – unos broja ispod korijena. Na primjer:

Da li je moguće ukloniti trojku unutar korijena? Osnovno! Ako se trojka pretvori u root, tada će formula za proizvod korijena funkcionirati. Dakle, pretvaramo tri u korijen. Pošto imamo koren četvrtog stepena, onda ćemo i njega pretvoriti u koren četvrtog stepena.) Ovako:

Onda

Usput, korijen se može napraviti od bilo kojeg nenegativnog broja. I to u mjeri u kojoj želimo (sve od studija slučaja zavisi). Ovo će biti korijen n-tog stepena ovog broja:

I sada - Pažnja! Izvor veoma grubih grešaka! Nisam ništa rekao ovdje uzalud nenegativan brojevi. Aritmetički korijen radi samo s takvima. Ako negdje u zadatku imamo negativan broj, onda ili ostavimo minus ispred korijena (ako je izvan), ili se riješimo minusa ispod korijena, ako je unutra. Podsjećam te ako je pod korijenom čak stepen ispada kao negativan broj izraz nema smisla.

Na primjer, takav zadatak. Unesite množitelj ispod predznaka korijena:

Ako sada root oduzeti dva, onda ćemo se surovo prevariti:

Šta nije u redu? I činjenica da je četvrti stepen, zbog svog pariteta, sigurno "pojeo" ovaj minus, zbog čega se namjerno negativan broj pretvorio u pozitivan. Ispravno rješenje izgleda ovako:

U korijenima neparnih stupnjeva, minus, iako nije "pojeden", također je bolje ostaviti ga vani:

Ovdje je korijen neparnog stepena kubičan, a mi imamo pravo da i minus zabijemo ispod korijena. Ali poželjno je u takvim primjerima i minus ostaviti izvan i napisati odgovor izražen kroz aritmetički (nenegativni) korijen, budući da korijen, iako ima pravo na život, ali nije aritmetika.

Dakle, sa uvođenjem broja ispod korena, takođe je sve jasno, nadam se.) Pređimo na sledeće svojstvo.

Svojstva korijena. Korijen razlomka. Podjela korijena.

Ovo svojstvo također u potpunosti ponavlja ono za kvadratne korijene. Tek sada to proširujemo na korijene bilo kojeg stepena:

Korijen razlomka jednaka korijenu od brojnika podijeljenog korijenom nazivnika.

Ako je n paran, onda je broja mora biti nenegativna, a brojb - strogo pozitivno (ne možete dijeliti sa nulom). U slučaju neparnog eksponenta, jedino ograničenje će biti .

Ovo svojstvo vam omogućava da lako i brzo izvučete korijenje iz frakcija:

Ideja je jasna, mislim. Umjesto da radimo s cijelim razlomkom, prelazimo na rad odvojeno s brojicom i odvojeno s nazivnikom.) Ako je razlomak decimalni ili, oh užas, mješoviti broj, onda prvo prelazimo na obične razlomke:

Sada da vidimo kako ova formula funkcionira s desna na lijevo. I ovdje se otkrivaju vrlo korisne mogućnosti. Na primjer, ovaj primjer:

Korijeni nisu baš izvučeni iz brojila i nazivnika, ali iz cijelog razlomka je u redu.) Ovaj primjer možete riješiti na drugačiji način - izvadite faktor u brojniku ispod korijena, a zatim smanjite:

Kako želiš. Odgovor je uvijek isti – tačan. Ako usput ne griješiš.)

Dakle, shvatili smo množenje / dijeljenje korijena. Idemo na sljedeći korak i razmatramo treće svojstvo - korijen do stepena i korijen stepena .

Koren do stepena. Koren stepena.

Kako podići korijen na moć? Na primjer, recimo da imamo broj. Može li se ovaj broj podići na stepen? U kocki, na primjer? Svakako! Pomnožite korijen sam po sebi tri puta, i - prema formuli za umnožak korijena:

Ovdje je korijen i stepen kao da međusobno poništene ili nadoknađene. Zaista, ako podignemo broj koji će nam, kada je narezan na kocku, dati trojku, podignemo ga upravo na ovu kocku, šta ćemo onda dobiti? Tri i dobiti, naravno! I tako će biti za bilo koji nenegativan broj. Uglavnom:

Ako su eksponenti i korijen različiti, onda također nema problema. Ako znate svojstva stupnjeva.)

Ako je eksponent manji od eksponenta korijena, onda jednostavno guramo eksponent ispod korijena:

Općenito će biti:

Ideja je jasna: radikalni izraz podižemo na potenciju, a zatim ga pojednostavljujemo vadeći faktore ispod korijena, ako je moguće. Ako an onda pravoa mora biti nenegativna. Zašto je razumljivo, mislim.) I akon čudno, onda nema ograničenja naa već otišao:

Pozabavimo se sada korijen stepena . Odnosno, neće sam korijen biti podignut na stepen, već radikalan izraz. Ni tu nema ništa komplikovano, ali ima mnogo više prostora za greške. Zašto? Jer negativni brojevi dolaze u igru, što može zbuniti znakove. Za sada, počnimo s korijenima neparnih moći - oni su mnogo jednostavniji.

Recimo da imamo broj 2. Možemo li ga kockati? Svakako!

A sada - natrag izvucite kockasti korijen iz osmice:

Počeli su s dvojkom, a vratili se na dvojku.) Nije ni čudo: podizanje na kocku je kompenzirano inverznom operacijom - izvlačenjem kubnog korijena.

Drugi primjer:

I ovdje je sve na pravom putu. Stepen i korijen jedan drugog su kompenzirali. Općenito, za korijene neparnih stupnjeva možemo napisati sljedeću formulu:

Ova formula vrijedi za bilo koji realan broja . Bilo pozitivno ili negativno.

To jest, neparni stepen i korijen istog stepena uvijek se međusobno kompenzuju i dobije se radikalan izraz. :)

Ali sa čak stepen, ovaj fokus možda više neće proći. Uvjerite se sami:

Nema tu još ništa posebno. Četvrti stepen i koren četvrtog stepena su takođe uravnotežili jedan drugog i ispalo je samo dvojka, tj. ukorijenjeni izraz. I za bilo koga nenegativan brojevi će biti isti. A sada samo zamjenjujemo dva u ovom korijenu sa minus dva. Pa hajde da uzmemo korijen ovako:

Minus dvojke sigurno je "izgorio" zbog četvrtog stepena. I kao rezultat vađenja korijena (aritmetike!) dobili smo pozitivno broj. Bilo je minus dva, postalo je plus dva.) Ali kada bismo samo nepromišljeno „smanjili“ stepen i koren (isto!), dobili bismo

Što je najveća greška, da.

Stoga, za čak Formula za korijen eksponenta izgleda ovako:

Ovdje je dodan znak modula, kojeg mnogi ne vole, ali u njemu nema ničeg strašnog: zahvaljujući njemu formula radi i za bilo koji realan broja. A modul jednostavno uklanja nedostatke:

Tek u korijenima n-tog stepena pojavila se dodatna razlika između parnih i neparnih stupnjeva. Čak su i stepeni, kao što vidimo, hirovitiji, da.)

A sada razmotrite novo korisno i vrlo zanimljivo svojstvo, već karakteristično za korijene n-tog stepena: ako se korijenski eksponent i eksponent korijenskog izraza pomnože (podijele) istim prirodnim brojem, tada će vrijednost korijena ne mijenjati.

Nešto što podsjeća na osnovnu osobinu razlomka, zar ne? U razlomcima također možemo pomnožiti (podijeliti) brojilac i imenilac istim brojem (osim nule). Zapravo, ovo svojstvo korijena je također posljedica osnovne osobine razlomka. Kad se upoznamo stepen sa racionalni indikator onda će sve postati jasno. Šta, kako i gde.)

Direktna primjena ove formule omogućava nam da pojednostavimo apsolutno sve korijene iz bilo kojeg stepena. Uključujući, ako su eksponenti korijenskog izraza i sam korijen razne. Na primjer, pojednostavimo sljedeći izraz:

Ponašamo se jednostavno. Za početak izdvajamo četvrti stepen od desetog ispod korena i - samo napred! Kako? Po svojstvima stepeni, naravno! Faktor vadimo ispod korijena ili radimo prema formuli korijena iz stepena.

Ali hajde da pojednostavimo, koristeći samo ovo svojstvo. Da bismo to učinili, četiri ispod korijena predstavljamo kao:

A sada - najzanimljivije - mentalno smanjujemo indikator ispod korena (dva) sa indikatorom korena (četiri)! I dobijamo: