Jak ręcznie znaleźć pierwiastek kwadratowy z liczby. Wyodrębnianie pierwiastków: metody, przykłady, rozwiązania

Jeśli masz pod ręką kalkulator, wyciągnięcie pierwiastka sześciennego dowolnej liczby nie będzie stanowić żadnego problemu. Jeśli jednak nie masz kalkulatora lub po prostu chcesz zaimponować innym, znajdź pierwiastek sześcienny ręcznie. Większość ludzi uzna opisany tutaj proces za dość skomplikowany, ale w praktyce korzenie sześcienne stanie się to znacznie łatwiejsze. Zanim zaczniesz czytać ten artykuł, pamiętaj o podstawowych operacjach matematycznych i obliczeniach na liczbach sześciennych.

Kroki

Część 1

Zapisz zadanie. Ręczne pobieranie korzeni sześciennych jest podobne do dzielenia długich, ale z pewnymi niuansami. Najpierw zapisz zadanie w określonej formie.

• Zapisz liczbę, z której chcesz wyliczyć pierwiastek sześcienny. Podziel liczbę na grupy składające się z trzech cyfr, zaczynając od kropki dziesiętnej. Na przykład musisz wziąć pierwiastek sześcienny z 10. Zapisz tę liczbę w ten sposób: 10 000 000 Dodatkowe zera mają na celu zwiększenie dokładności wyniku.
• Narysuj znak pierwiastka obok i nad liczbą. Pomyśl o tym jak o poziomych i pionowych liniach, które rysujesz podczas dzielenia. Jedyną różnicą jest kształt obu znaków.
• Umieść kropkę dziesiętną nad linią poziomą. Zrób to bezpośrednio nad przecinkiem oryginalnej liczby.

1. Zapamiętaj wyniki liczb całkowitych sześciennych. Zostaną one wykorzystane w obliczeniach.

   • 1 3 = 1 ∗ 1 ∗ 1 = 1 (\ Displaystyle 1 ^ (3) = 1 * 1 * 1 = 1)
   • 2 3 = 2 ∗ 2 ∗ 2 = 8 (\ Displaystyle 2 ^ (3) = 2 * 2 * 2 = 8)
   • 3 3 = 3 ∗ 3 ∗ 3 = 27 (\ Displaystyle 3 ^ (3) = 3*3*3 = 27)
   • 4 3 = 4 ∗ 4 ∗ 4 = 64 (\ Displaystyle 4 ^ (3) = 4*4*4 = 64)
   • 5 3 = 5 ∗ 5 ∗ 5 = 125 (\ Displaystyle 5 ^ (3) = 5 * 5 * 5 = 125)
   • 6 3 = 6 ∗ 6 ∗ 6 = 216 (\ Displaystyle 6 ^ (3) = 6 * 6 * 6 = 216)
   • 7 3 = 7 ∗ 7 ∗ 7 = 343 (\ Displaystyle 7 ^ (3) = 7 * 7 * 7 = 343)
   • 8 3 = 8 ∗ 8 ∗ 8 = 512 (\ Displaystyle 8 ^ (3) = 8 * 8 * 8 = 512)
   • 9 3 = 9 ∗ 9 ∗ 9 = 729 (\ Displaystyle 9 ^ (3) = 9 * 9 * 9 = 729)
   • 10 3 = 10 ∗ 10 ∗ 10 = 1000 (\ Displaystyle 10 ^ (3) = 10 * 10 * 10 = 1000)

2. Znajdź pierwszą cyfrę odpowiedzi. Wybierz sześcian liczby całkowitej, która jest najbliższa, ale mniejsza niż pierwsza grupa trzech cyfr.

   • W naszym przykładzie pierwszą grupą trzech cyfr jest liczba 10. Znajdź największy sześcian, który jest mniejszy niż 10. Ten sześcian to 8, a pierwiastek sześcienny z 8 to 2.
   • Nad poziomą linią nad liczbą 10 wpisz cyfrę 2. Następnie zapisz wartość operacji 2 3 (\ displaystyle 2 ^ (3))= 8 poniżej 10. Narysuj linię i odejmij 8 od 10 (jak w przypadku zwykłego długiego dzielenia). Wynik to 2 (jest to pierwsza reszta).
   • W ten sposób znalazłeś pierwszą cyfrę odpowiedzi. Pomyśl czy ten wynik dość dokładne. W większości przypadków będzie to bardzo przybliżona odpowiedź. Pokrój wynik w kostkę, aby dowiedzieć się, jak blisko jest pierwotnej liczby. W naszym przykładzie: 2 3 (\ displaystyle 2 ^ (3))= 8, co nie jest zbyt bliskie 10, dlatego obliczenia należy kontynuować.

3. Znajdź następną cyfrę odpowiedzi. Dodaj drugą grupę trzech cyfr do pierwszej reszty i narysuj pionową linię na lewo od wynikowej liczby. Korzystając z otrzymanej liczby, znajdziesz drugą cyfrę odpowiedzi. W naszym przykładzie musimy dodać drugą grupę trzech cyfr (000) do pierwszej reszty (2), aby otrzymać liczbę 2000.

   • Na lewo od pionowej linii napiszesz trzy liczby, których suma jest równa pewnemu pierwszemu czynnikowi. Pozostaw puste miejsca na te liczby i umieść między nimi znaki plus.

4. Znajdź pierwszy wyraz (z trzech). W pierwszym pustym miejscu wpisz wynik pomnożenia liczby 300 przez kwadrat pierwszej cyfry odpowiedzi (jest on zapisany nad znakiem pierwiastka). W naszym przykładzie pierwszą cyfrą odpowiedzi jest 2, więc 300*(2^2) = 300*4 = 1200. Wpisz 1200 w pierwsze puste miejsce. Pierwszy wyraz to liczba 1200 (plus dwie kolejne liczby do znalezienia).

   Znajdź drugą cyfrę odpowiedzi. Dowiedz się, przez jaką liczbę należy pomnożyć 1200, aby wynik był bliski, ale nie większy niż 2000. Ta liczba może wynosić tylko 1, ponieważ 2 * 1200 = 2400, czyli więcej niż 2000. Wpisz 1 (druga cyfra liczby odpowiedź) po 2 i kropce dziesiętnej nad znakiem pierwiastka.

   Znajdź drugi i trzeci wyraz (z trzech). Mnożnik składa się z trzech liczb (wyrazów), z których pierwszą już znalazłeś (1200). Teraz musimy znaleźć pozostałe dwa wyrazy.

   • Pomnóż 3 przez 10 i przez każdą cyfrę odpowiedzi (są zapisane nad znakiem pierwiastka). W naszym przykładzie: 3*10*2*1 = 60. Dodaj ten wynik do 1200 i otrzymaj 1260.
   • Na koniec podnieś ostatnią cyfrę swojej odpowiedzi do kwadratu. W naszym przykładzie ostatnią cyfrą odpowiedzi jest 1, więc 1^2 = 1. Zatem pierwszy współczynnik jest równy sumie następujących liczb: 1200 + 60 + 1 = 1261. Zapisz tę liczbę po lewej stronie pionowy pasek.

5. Pomnóż i odejmij. Pomnóż ostatnią cyfrę odpowiedzi (w naszym przykładzie jest to 1) przez znaleziony współczynnik (1261): 1*1261 = 1261. Zapisz tę liczbę pod 2000 i odejmij od 2000. Otrzymasz 739 (jest to druga reszta ).

6. Zastanów się, czy odpowiedź, którą otrzymasz, jest wystarczająco dokładna. Rób to za każdym razem, gdy wykonasz kolejne odejmowanie. Po pierwszym odjęciu odpowiedź brzmiała 2, co nie jest dokładnym wynikiem. Po drugim odjęciu odpowiedź brzmi 2,1.

   • Aby sprawdzić poprawność swojej odpowiedzi, połóż ją w kostce: 2,1*2,1*2,1 = 9,261.
   • Jeśli uważasz, że odpowiedź jest wystarczająco dokładna, nie musisz kontynuować obliczeń; w przeciwnym razie wykonaj kolejne odejmowanie.

7. Znajdź drugi czynnik. Aby przećwiczyć obliczenia i uzyskać dokładniejszy wynik, powtórz powyższe kroki.

   • Do drugiej reszty (739) dodaj trzecią grupę trzech cyfr (000). Otrzymasz numer 739000.
   • Pomnóż 300 przez kwadrat liczby zapisanej nad znakiem pierwiastka (21): 300 ∗ 21 2 (\ displaystyle 300 * 21 ^ (2)) = 132300.
   • Znajdź trzecią cyfrę odpowiedzi. Dowiedz się, przez jaką liczbę należy pomnożyć 132300, aby wynik był bliski, ale nie większy niż 739000. Ta liczba to 5: 5 * 132200 = 661500. Wpisz 5 (trzecia cyfra odpowiedzi) po 1 nad liczbą znak korzenia.
   • Pomnóż 3 przez 10 przez 21 i przez ostatnią cyfrę odpowiedzi (są zapisane nad znakiem pierwiastka). W naszym przykładzie: 3 ∗ 21 ∗ 5 ∗ 10 = 3150 (\ Displaystyle 3 * 21 * 5 * 10 = 3150).
   • Na koniec podnieś ostatnią cyfrę swojej odpowiedzi do kwadratu. W naszym przykładzie ostatnia cyfra odpowiedzi to 5, a więc 5 2 = 25. (\ Displaystyle 5 ^ (2) = 25.)
   • Zatem drugi mnożnik wynosi: 132300 + 3150 + 25 = 135475.

8. Pomnóż ostatnią cyfrę odpowiedzi przez drugi współczynnik. Po znalezieniu drugiego czynnika i trzeciej cyfry odpowiedzi wykonaj następujące czynności:

   • Pomnóż ostatnią cyfrę odpowiedzi przez znaleziony współczynnik: 135475*5 = 677375.
   • Odejmij: 739000-677375 = 61625.
   • Zastanów się, czy odpowiedź, którą otrzymasz, jest wystarczająco dokładna. Aby to zrobić, pokrój go w kostkę: 2 , 15 ∗ 2 , 15 ∗ 2 , 15 = 9 , 94 (\ Displaystyle 2,15 * 2,15 * 2,15 = 9,94).

9. Zapisz swoją odpowiedź. Wynik zapisany nad znakiem pierwiastka jest odpowiedzią z dokładnością do dwóch miejsc po przecinku. W naszym przykładzie pierwiastek sześcienny z 10 wynosi 2,15. Sprawdź swoją odpowiedź, łącząc ją w kostkę: 2,15^3 = 9,94, czyli w przybliżeniu 10. Jeśli potrzebujesz większej precyzji, kontynuuj obliczenia (jak opisano powyżej).

   Część 2

   Wyodrębnianie pierwiastka sześciennego metodą estymacji

   1. Użyj kostek liczbowych, aby określić górę i dolne limity. Jeśli chcesz obliczyć pierwiastek sześcienny niemal dowolnej liczby, znajdź kostki (niektórych liczb) znajdujące się najbliżej podanej liczby.

      • Na przykład musisz wziąć pierwiastek sześcienny z 600. Ponieważ 8 3 = 512 (\ displaystyle 8 ^ (3) = 512) I 9 3 = 729 (\ displaystyle 9 ^ (3) = 729), wówczas wartość pierwiastka sześciennego z 600 mieści się w przedziale od 8 do 9. Dlatego użyj liczb 512 i 729 jako górnej i dolnej granicy odpowiedzi.

   2. Oszacuj drugą liczbę. Pierwszą liczbę znalazłeś dzięki znajomości sześcianów liczb całkowitych. Teraz zamień liczbę całkowitą na dziesiętny, dodając do niego (po przecinku) określoną liczbę od 0 do 9. Konieczne jest znalezienie ułamka dziesiętnego, którego sześcian będzie bliski, ale mniejszy niż liczba pierwotna.

      • W naszym przykładzie liczba 600 znajduje się pomiędzy liczbami 512 i 729. Na przykład dodaj liczbę 5 do pierwszej znalezionej liczby (8). Otrzymana liczba to 8,5.
   3. • W naszym przykładzie: 8, 5 ∗ 8, 5 ∗ 8, 5 = 614, 1. (\ Displaystyle 8,5 * 8,5 * 8,5 = 614,1.)

   4. Porównaj sześcian otrzymanej liczby z liczbą pierwotną. Jeśli sześcian otrzymanej liczby jest większy od liczby pierwotnej, spróbuj oszacować mniejszą liczbę. Jeżeli sześcian otrzymanej liczby jest znacznie mniejszy od liczby pierwotnej, obliczaj większe liczby, aż sześcian jednej z nich przekroczy liczbę pierwotną.

      • W naszym przykładzie: 8 , 5 3 (\ Displaystyle 8,5 ^ (3))> 600. Zatem oceń mniejszą liczbę na 8,4. Pokrój tę liczbę w kostkę i porównaj z liczbą pierwotną: 8 , 4 ∗ 8 , 4 ∗ 8 , 4 = 592 , 7 (\ Displaystyle 8,4 * 8,4 * 8,4 = 592,7). Wynik ten jest mniejszy niż liczba pierwotna. Zatem pierwiastek sześcienny z 600 wynosi pomiędzy 8,4 a 8,5.

   5. Wskaźnik Następny numer aby poprawić dokładność odpowiedzi. Do każdej ostatniej oszacowanej liczby dodawaj liczbę od 0 do 9, aż uzyskasz dokładną odpowiedź. W każdej rundzie ewaluacyjnej musisz znaleźć górną i dolną granicę, pomiędzy którymi mieści się pierwotna liczba.

      • W naszym przykładzie: 8 , 4 3 = 592 , 7 (\ displaystyle 8,4 ^ (3) = 592,7) I 8 , 5 3 = 614 , 1 (\ Displaystyle 8,5 ^ (3) = 614,1). Pierwotna liczba 600 jest bliżej 592 niż 614. Dlatego ostatniej oszacowanej liczbie przypisz liczbę bliższą 0 niż 9. Na przykład taka liczba to 4. Zatem sześcian liczbę 8,44.

   6. W razie potrzeby oszacuj inną liczbę. Porównaj sześcian otrzymanej liczby z liczbą pierwotną. Jeśli sześcian otrzymanej liczby jest większy od liczby pierwotnej, spróbuj oszacować mniejszą liczbę. Krótko mówiąc, musisz znaleźć dwie liczby, których kostki są nieco większe i nieco mniejsze niż pierwotna liczba.

      • W naszym przykładzie 8, 44 ∗ 8, 44 ∗ 8, 44 = 601, 2 (\ Displaystyle 8,44 * 8,44 * 8,44 = 601,2). Jest to nieco więcej niż pierwotna liczba, więc oszacuj inną (mniejszą) liczbę, na przykład 8,43: 8, 43 ∗ 8, 43 ∗ 8, 43 = 599, 07 (\ Displaystyle 8,43 * 8,43 * 8,43 = 599,07). Zatem pierwiastek sześcienny z 600 mieści się pomiędzy 8,43 a 8,44.

   7. Postępuj zgodnie z opisanym procesem, aż uzyskasz odpowiedź, z której będziesz zadowolony. Oszacuj kolejną liczbę, porównaj ją z oryginałem, a następnie, jeśli to konieczne, oszacuj kolejną liczbę i tak dalej. Należy pamiętać, że każda dodatkowa cyfra po przecinku zwiększa dokładność odpowiedzi.

      • W naszym przykładzie sześcian 8,43 jest o mniej niż 1 mniejszy od pierwotnej liczby. Jeśli potrzebujesz większej precyzji, sześcian 8,434 i uzyskaj: 8, 434 3 = 599, 93 (\ displaystyle 8434 ^ (3) = 599,93), czyli wynik jest o mniej niż 0,1 mniejszy od pierwotnej liczby.

Rozwiązaliśmy już dużą liczbę bez kalkulatora. W tym artykule przyjrzymy się, jak wyodrębnić pierwiastek sześcienny (pierwiastek trzeciego stopnia). Zastrzegam, że mówimy o liczbach naturalnych. Jak myślisz, ile czasu zajmuje słowne obliczenie pierwiastków, takich jak:

Całkiem sporo, a jeśli ćwiczysz dwa lub trzy razy przez 20 minut, możesz wydobyć taki korzeń doustnie w 5 sekund.

* Należy zauważyć, że mówimy o liczbach pod pierwiastkiem, które są wynikiem sześcianu liczb naturalnych od 0 do 100.

Wiemy to:

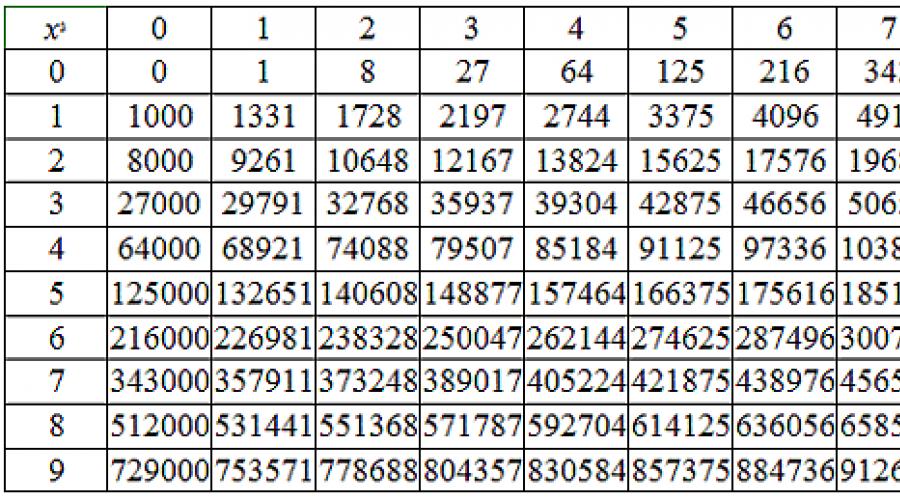
Zatem liczba a, którą znajdziemy, to Liczba naturalna od 0 do 100. Spójrz na tabelę kostek tych liczb (wyniki podniesienia do trzeciej potęgi):

W tej tabeli możesz łatwo wyodrębnić pierwiastek sześcienny dowolnej liczby. Co chcesz wiedzieć?

1. Są to kostki liczb będących wielokrotnościami dziesięciu:

Powiedziałabym nawet, że to „piękne” liczby, łatwo je zapamiętać. Łatwo się tego nauczyć.

2. Jest to właściwość liczb w momencie ich tworzenia.

Jego istota polega na tym, że gdy pewna liczba zostanie podniesiona do trzeciej potęgi, wynik będzie miał osobliwość. Który?

Na przykład ułóżmy kostkę 1, 11, 21, 31, 41 itd. Możesz spojrzeć na tabelę.

1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …

Oznacza to, że jeśli będziemy sześcianować liczbę z jednostką na końcu, wynikiem zawsze będzie liczba z jednostką na końcu.

Kiedy kostkujesz liczbę z dwójką na końcu, wynikiem zawsze będzie liczba z ósemką na końcu.

Pokażmy zgodność w tabeli dla wszystkich liczb:

Znajomość dwóch przedstawionych punktów jest wystarczająca.

Spójrzmy na przykłady:

Weź pierwiastek sześcienny z 21952.

Liczba ta mieści się w przedziale od 8000 do 27000. Oznacza to, że wynik pierwiastka mieści się w przedziale od 20 do 30. Liczba 29952 kończy się na 2. Ta opcja jest możliwa tylko wtedy, gdy liczba z ósemką na końcu jest pokrojone w kostkę. Zatem wynik pierwiastka wynosi 28.

Znajdź pierwiastek sześcienny z 54852.

Liczba ta mieści się w przedziale od 27000 do 64000. Oznacza to, że wynik pierwiastka mieści się w przedziale od 30 do 40. Liczba 54852 kończy się na 2. Ta opcja jest możliwa tylko wtedy, gdy liczba z ósemką na końcu jest pokrojone w kostkę. Zatem wynik pierwiastka wynosi 38.

Weź pierwiastek sześcienny z 571787.

Liczba ta mieści się w przedziale od 512000 do 729000. Oznacza to, że wynik pierwiastka mieści się w przedziale od 80 do 90. Liczba 571787 kończy się na 7. Ta opcja jest możliwa tylko wtedy, gdy liczba z trójką na końcu jest pokrojone w kostkę. Zatem wynik pierwiastka wynosi 83.

Weź pierwiastek sześcienny z 614125.

Liczba ta mieści się w przedziale od 512000 do 729000. Oznacza to, że wynik pierwiastka mieści się w przedziale od 80 do 90. Liczba 614125 kończy się na 5. Ta opcja jest możliwa tylko wtedy, gdy liczba z piątką na końcu jest pokrojone w kostkę. Zatem wynik pierwiastka wynosi 85.

Myślę, że teraz możesz łatwo wyodrębnić pierwiastek sześcienny z liczby 681472.

Oczywiście ekstrakcja takich korzeni drogą doustną wymaga trochę praktyki. Ale przywracając dwie wskazane tabletki na papierze, w każdym razie możesz łatwo wyodrębnić taki korzeń w ciągu minuty.

Po znalezieniu wyniku koniecznie go sprawdź (podnieś go do trzeciej potęgi). *Nikt nie anulował mnożenia po kolumnie 😉

Faktycznie Problemy z egzaminem jednolitym z takimi „paskudnymi” korzeniami, nie. Na przykład musisz wyodrębnić pierwiastek sześcienny z 1728. Myślę, że nie stanowi to już dla ciebie problemu.

Jeśli znasz jakieś ciekawe metody obliczeń bez kalkulatora, prześlij je, w odpowiednim czasie je opublikuję.To wszystko. Powodzenia!

Z poważaniem, Aleksander Krutitskikh.

P.S: Byłbym wdzięczny, gdybyś powiedział mi o tej stronie w sieciach społecznościowych.

Przed pojawieniem się kalkulatorów uczniowie i nauczyciele obliczali pierwiastki kwadratowe ręcznie. Istnieje kilka sposobów obliczeń pierwiastek kwadratowy numery ręcznie. Niektóre z nich oferują jedynie przybliżone rozwiązanie, inne dają dokładną odpowiedź.

Kroki

Faktoryzacja pierwsza

Rozłóż liczbę pierwiastkową na czynniki będące liczbami kwadratowymi. W zależności od liczby radykalnej otrzymasz odpowiedź przybliżoną lub dokładną. Liczby kwadratowe to liczby, z których można wyciągnąć cały pierwiastek kwadratowy. Czynniki to liczby, które po pomnożeniu dają liczbę pierwotną. Na przykład współczynniki liczby 8 to 2 i 4, ponieważ 2 x 4 = 8, liczby 25, 36, 49 są liczbami kwadratowymi, ponieważ √25 = 5, √36 = 6, √49 = 7. Czynniki kwadratowe są czynnikami, które są liczbami kwadratowymi. Najpierw spróbuj rozłożyć liczbę pierwiastkową na czynniki kwadratowe.

• Na przykład oblicz pierwiastek kwadratowy z 400 (ręcznie). Najpierw spróbuj rozłożyć 400 na czynniki kwadratowe. 400 to wielokrotność 100, czyli podzielna przez 25 - jest to liczba kwadratowa. Dzielenie 400 przez 25 daje 16. Liczba 16 jest również liczbą kwadratową. Zatem 400 można rozłożyć na współczynniki kwadratowe 25 i 16, czyli 25 x 16 = 400.
• Można to zapisać w następujący sposób: √400 = √(25 x 16).

1. Pierwiastek kwadratowy iloczynu niektórych wyrazów jest równy iloczynowi pierwiastków kwadratowych każdego wyrazu, czyli √(a x b) = √a x √b. Użyj tej reguły, aby obliczyć pierwiastek kwadratowy z każdego współczynnika kwadratowego i pomnożyć wyniki, aby znaleźć odpowiedź.

   • W naszym przykładzie weź pierwiastek z 25 i 16.
     • √(25 x 16)
     • √25 x √16
     • 5x4 = 20

2. Jeśli liczba rodnikowa nie rozkłada się na dwa współczynnik kwadratowy(a tak się dzieje w większości przypadków), nie będziesz w stanie znaleźć dokładnej odpowiedzi w postaci liczby całkowitej. Ale możesz uprościć problem, rozkładając liczbę pierwiastkową na współczynnik kwadratowy i zwykły czynnik (liczbę, z której nie można wyciągnąć całego pierwiastka kwadratowego). Następnie weźmiesz pierwiastek kwadratowy ze współczynnika kwadratowego i wyciągniesz pierwiastek ze wspólnego czynnika.

   • Na przykład oblicz pierwiastek kwadratowy z liczby 147. Liczby 147 nie można rozłożyć na dwa czynniki kwadratowe, ale można ją rozłożyć na następujące czynniki: 49 i 3. Rozwiąż problem w następujący sposób:
     • = √(49 x 3)
     • = √49 x √3
     • = 7√3

3. Jeśli to konieczne, oszacuj wartość pierwiastka. Teraz możesz oszacować wartość pierwiastka (znaleźć wartość przybliżoną), porównując ją z wartościami pierwiastków liczb kwadratowych, które są najbliżej (po obu stronach osi liczbowej) liczby pierwiastkowej. Wartość pierwiastkową otrzymasz w postaci ułamka dziesiętnego, który należy pomnożyć przez liczbę znajdującą się za znakiem pierwiastka.

   • Wróćmy do naszego przykładu. Pierwiastkiem jest liczba 3. Najbliższe jej liczby kwadratowe to liczby 1 (√1 = 1) i 4 (√4 = 2). Zatem wartość √3 mieści się pomiędzy 1 a 2. Ponieważ wartość √3 jest prawdopodobnie bliższa 2 niż 1, nasze oszacowanie wynosi: √3 = 1,7. Mnożymy tę wartość przez liczbę przy znaku pierwiastka: 7 x 1,7 = 11,9. Jeśli wykonasz obliczenia na kalkulatorze, otrzymasz 12,13, co jest dość bliskie naszej odpowiedzi.
     • Ta metoda działa również w przypadku dużych liczb. Rozważmy na przykład √35. Pierwiastkiem jest liczba 35. Najbliższe jej liczby kwadratowe to liczby 25 (√25 = 5) i 36 (√36 = 6). Zatem wartość √35 mieści się pomiędzy 5 a 6. Ponieważ wartość √35 jest znacznie bliższa 6 niż 5 (ponieważ 35 to tylko 1 mniej niż 36), możemy powiedzieć, że √35 jest nieco mniejsze niż 6 Sprawdź na kalkulatorze, co daje nam odpowiedź 5,92 – mieliśmy rację.

4. Innym sposobem jest rozłożenie liczby pierwiastkowej na czynniki pierwsze. Czynniki pierwsze to liczby, które dzielą się tylko przez 1 i samą siebie. Zapisz czynniki pierwsze w szeregu i znajdź pary identycznych czynników. Takie czynniki można wyjąć ze znaku głównego.

   • Na przykład oblicz pierwiastek kwadratowy z 45. Rozłóż liczbę pierwiastkową na czynniki pierwsze: 45 = 9 x 5 i 9 = 3 x 3. Zatem √45 = √(3 x 3 x 5). Jako pierwiastek można wyjąć 3: √45 = 3√5. Teraz możemy oszacować √5.
   • Spójrzmy na inny przykład: √88.
     • = √(2 x 44)
     • = √ (2 x 4 x 11)
     • = √ (2 x 2 x 2 x 11). Otrzymałeś trzy mnożniki liczby 2; weź kilka z nich i przesuń je poza znak korzenia.
     • = 2√(2 x 11) = 2√2 x √11. Teraz możesz ocenić √2 i √11 i znaleźć przybliżoną odpowiedź.

   Ręczne obliczanie pierwiastka kwadratowego

   Używanie długiego dzielenia

   1. Ta metoda obejmuje proces podobny do dzielenia długich i zapewnia dokładną odpowiedź. Najpierw narysuj pionową linię dzielącą arkusz na dwie połowy, a następnie w prawo i nieco poniżej górnej krawędzi arkusza narysuj poziomą linię do linii pionowej. Teraz podziel liczbę pierwiastkową na pary liczb, zaczynając od części ułamkowej po przecinku. Tak więc liczba 79520789182.47897 jest zapisana jako „7 95 20 78 91 82, 47 89 70”.

      • Na przykład obliczmy pierwiastek kwadratowy z liczby 780,14. Narysuj dwie linie (jak pokazano na rysunku) i wpisz podaną liczbę w postaci „7 80, 14” w lewym górnym rogu. To normalne, że pierwsza cyfra od lewej jest cyfrą niesparowaną. Odpowiedź (pierwiastek tej liczby) napiszesz w prawym górnym rogu.

   2. Dla pierwszej pary liczb (lub pojedynczej liczby) od lewej strony znajdź największą liczbę całkowitą n, której kwadrat jest mniejszy lub równy danej parze liczb (lub pojedynczej liczbie). Innymi słowy, znajdź liczbę kwadratową najbliższą pierwszej parze liczb (lub pojedynczej liczbie) od lewej, ale mniejszą od niej, i spierwiastkuj tę liczbę liczba kwadratowa; otrzymasz liczbę n. Wpisz n, które znalazłeś, w prawym górnym rogu i wpisz kwadrat n w prawym dolnym rogu.

      • W naszym przypadku pierwszą liczbą po lewej będzie 7. Następnie 4< 7, то есть 2 2 < 7 и n = 2. Напишите 2 сверху справа - это первая цифра в искомом квадратном корне. Напишите 2×2=4 справа снизу; вам понадобится это число для последующих вычислений.

   3. Odejmij kwadrat liczby n, którą właśnie znalazłeś, od pierwszej pary liczb (lub pojedynczej liczby) po lewej stronie. Wynik obliczeń zapisz pod odejmowaniem (kwadratem liczby n).

      • W naszym przykładzie odejmij 4 od 7 i uzyskaj 3.

   4. Zapisz drugą parę liczb i zapisz ją obok wartości uzyskanej w poprzednim kroku. Następnie podwoj liczbę w prawym górnym rogu i zapisz wynik w prawym dolnym rogu z dodatkiem „_×_=".

      • W naszym przykładzie druga para liczb to „80”. Wpisz „80” po 3. Następnie dwukrotność liczby w prawym górnym rogu daje 4. Wpisz „4_×_=" w prawym dolnym rogu.

   5. Wypełnij puste pola po prawej stronie.

      • W naszym przypadku, jeśli zamiast myślników wstawimy liczbę 8, to 48 x 8 = 384, czyli więcej niż 380. Zatem 8 to za duża liczba, ale wystarczy 7. Zamiast myślników wpisz 7 i uzyskaj: 47 x 7 = 329. Wpisz 7 w prawym górnym rogu - jest to druga cyfra żądanego pierwiastka kwadratowego z liczby 780,14.

   6. Odejmij wynikową liczbę od bieżącej liczby po lewej stronie. Wynik z poprzedniego kroku zapisz pod aktualną liczbą po lewej stronie, znajdź różnicę i zapisz ją pod odjemnikiem.

      • W naszym przykładzie odejmij 329 od 380, co równa się 51.

   7. Powtórz krok 4. Jeżeli przenoszona para liczb jest częścią ułamkową pierwotnej liczby, należy umieścić separator (przecinek) pomiędzy liczbą całkowitą a częścią ułamkową w wymaganym pierwiastku kwadratowym w prawym górnym rogu. Po lewej stronie obniż następną parę liczb. Podwój liczbę w prawym górnym rogu i zapisz wynik w prawym dolnym rogu z dodatkiem „_×_=".

      • W naszym przykładzie następną parą liczb do usunięcia będzie część ułamkowa liczby 780,14, dlatego umieść separator części całkowitej i ułamkowej w żądanym pierwiastku kwadratowym w prawym górnym rogu. Zapisz liczbę 14 i wpisz ją w lewym dolnym rogu. Podwójna liczba w prawym górnym rogu (27) to 54, więc wpisz „54_×_=" w prawym dolnym rogu.

   8. Powtórz kroki 5 i 6. Znajdź taki największa liczba w miejsce myślników po prawej stronie (zamiast myślników należy podstawić tę samą liczbę), tak aby wynik mnożenia był mniejszy lub równy aktualnej liczbie po lewej stronie.

      • W naszym przykładzie 549 x 9 = 4941, czyli mniej niż bieżąca liczba po lewej stronie (5114). Wpisz 9 w prawym górnym rogu i odejmij wynik mnożenia od bieżącej liczby po lewej stronie: 5114 - 4941 = 173.

   9. Jeśli chcesz znaleźć więcej miejsc po przecinku dla pierwiastka kwadratowego, wpisz kilka zer na lewo od bieżącej liczby i powtórz kroki 4, 5 i 6. Powtarzaj kroki, aż uzyskasz dokładność odpowiedzi (liczbę miejsc po przecinku) potrzebować.

   Zrozumienie procesu

   Do asymilacji Ta metoda pomyśl o liczbie, której pierwiastek kwadratowy chcesz znaleźć, jako o polu kwadratu S. W tym przypadku będziesz szukać długości boku L takiego kwadratu. Obliczamy wartość L w taki sposób, że L² = S.

   Podaj literę do każdej cyfry w odpowiedzi. Oznaczmy przez A pierwszą cyfrę wartości L (pożądany pierwiastek kwadratowy). B będzie drugą cyfrą, C trzecią i tak dalej.

   Określ literę dla każdej pary pierwszych cyfr. Oznaczmy przez S a pierwszą parę cyfr wartości S, przez S b drugą parę cyfr i tak dalej.

   Zrozum związek między tą metodą a długim dzieleniem. Podobnie jak przy dzieleniu, gdzie za każdym razem interesuje nas tylko kolejna cyfra liczby, którą dzielimy, tak przy obliczaniu pierwiastka kwadratowego pracujemy kolejno przez parę cyfr (aby otrzymać kolejną cyfrę wartości pierwiastka kwadratowego) .

   1. Rozważmy pierwszą parę cyfr Sa liczby S (w naszym przykładzie Sa = 7) i znajdź jej pierwiastek kwadratowy. W tym przypadku pierwszą cyfrą A żądanej wartości pierwiastka kwadratowego będzie cyfra, której kwadrat jest mniejszy lub równy S a (to znaczy szukamy takiego A, że nierówność A² ≤ Sa< (A+1)²). В нашем примере, S1 = 7, и 2² ≤ 7 < 3²; таким образом A = 2.

      • Powiedzmy, że musimy podzielić 88962 przez 7; tutaj pierwszy krok będzie podobny: rozważamy pierwszą cyfrę liczby podzielnej 88962 (8) i wybieramy największą liczbę, która pomnożona przez 7 daje wartość mniejszą lub równą 8. Oznacza to, że szukamy liczba d, dla której prawdziwa jest nierówność: 7 × d ≤ 8< 7×(d+1). В этом случае d будет равно 1.

   2. W myślach wyobraź sobie kwadrat, którego powierzchnię musisz obliczyć. Szukasz L, czyli długości boku kwadratu, którego pole wynosi S. A, B, C to liczby w liczbie L. Można to zapisać inaczej: 10A + B = L (dla numer dwucyfrowy) lub 100A + 10V + C = L (dla liczba trzycyfrowa) i tak dalej.

      • Pozwalać (10A+B)² = L² = S = 100A² + 2×10A×B + B². Pamiętaj, że 10A+B to liczba, w której cyfra B oznacza jednostki, a cyfra A oznacza dziesiątki. Na przykład, jeśli A=1 i B=2, wówczas 10A+B równa się liczbie 12. (10A+B)² to pole całego kwadratu, 100A²- powierzchnia dużego placu wewnętrznego, B²- powierzchnia małego wewnętrznego placu, 10A×B- powierzchnia każdego z dwóch prostokątów. Dodając pola opisanych figur, znajdziesz pole pierwotnego kwadratu.

Czas to uporządkować metody ekstrakcji korzeni. Opierają się na właściwościach pierwiastków, w szczególności na równości, co jest prawdą dla każdego Liczba ujemna B.

Poniżej przyjrzymy się głównym metodom wydobywania korzeni jeden po drugim.

Zacznijmy od najprostszego przypadku - wyciągania pierwiastków z liczb naturalnych za pomocą tabeli kwadratów, tabeli kostek itp.

Jeśli tabele kwadratów, sześcianów itp. Jeśli nie masz go pod ręką, logiczne jest zastosowanie metody wyodrębniania pierwiastka, która polega na rozłożeniu liczby pierwiastkowej na czynniki pierwsze.

Warto szczególnie wspomnieć, co jest możliwe dla pierwiastków o wykładnikach nieparzystych.

Na koniec rozważmy metodę, która pozwala nam sekwencyjnie znajdować cyfry wartości pierwiastkowej.

Zacznijmy.

Korzystanie z tabeli kwadratów, tabeli kostek itp.

W najprostszych przypadkach tabele kwadratów, kostek itp. pozwalają na wyodrębnienie pierwiastków. Co to za tabele?

Tabela kwadratów liczb całkowitych od 0 do 99 włącznie (pokazana poniżej) składa się z dwóch stref. Pierwsza strefa tabeli zlokalizowana jest na szarym tle; wybierając konkretny wiersz i konkretną kolumnę, można ułożyć liczbę od 0 do 99. Na przykład wybierzmy wiersz składający się z 8 dziesiątek i kolumnę zawierającą 3 jednostki, w ten sposób ustaliliśmy liczbę 83. Druga strefa zajmuje resztę stołu. Każda komórka znajduje się na przecięciu określonego wiersza i określonej kolumny i zawiera kwadrat odpowiedniej liczby od 0 do 99. Na przecięciu wybranego przez nas rzędu 8 dziesiątek i kolumny 3 jedności znajduje się komórka z liczbą 6889, która jest kwadratem liczby 83.

Tablice kostek, tablice czwartych potęg liczb od 0 do 99 itd. są podobne do tablicy kwadratów, tyle że zawierają kostki, czwarte potęgi itp. w drugiej strefie. odpowiednie liczby.

Tablice kwadratów, sześcianów, czwartych potęg itp. pozwalają wyodrębnić pierwiastki kwadratowe, pierwiastki sześcienne, pierwiastki czwarte itp. odpowiednio na podstawie liczb w tych tabelach. Wyjaśnijmy zasadę ich stosowania podczas wydobywania korzeni.

Powiedzmy, że musimy wyodrębnić n-ty pierwiastek z liczby a, podczas gdy liczba a jest zawarta w tabeli n-tych potęg. Korzystając z tej tabeli, znajdujemy liczbę b taką, że a=b n. Następnie dlatego liczba b będzie pożądanym pierwiastkiem n-tego stopnia.

Jako przykład pokażmy, jak użyć tabeli kostek do wyodrębnienia pierwiastka sześciennego z 19 683. W tabeli kostek znajdujemy liczbę 19 683, z niej dowiadujemy się, że ta liczba jest sześcianem liczby 27, dlatego też .

Jest oczywiste, że tablice n-tych potęg są bardzo wygodne do wyodrębniania pierwiastków. Często jednak nie są one pod ręką, a ich skompilowanie zajmuje trochę czasu. Ponadto często konieczne jest wyodrębnienie pierwiastków z liczb, które nie są zawarte w odpowiednich tabelach. W takich przypadkach należy zastosować inne metody ekstrakcji korzeni.

Rozkładanie liczby pierwiastkowej na czynniki pierwsze

Wystarczająco w wygodny sposób, który umożliwia wyodrębnienie pierwiastka z liczby naturalnej (o ile oczywiście pierwiastek zostanie wyodrębniony), to rozkład liczby pierwiastkowej na czynniki pierwsze. Jego chodzi o to: potem dość łatwo jest przedstawić to jako potęgę za pomocą niezbędny wskaźnik, co pozwala uzyskać wartość pierwiastka. Wyjaśnijmy tę kwestię.

Weźmy n-ty pierwiastek liczby naturalnej a i jego wartość będzie równa b. W tym przypadku prawdziwa jest równość a=bn. Liczbę b, jak każdą liczbę naturalną, można przedstawić jako iloczyn wszystkich jej czynników pierwszych p 1 , p 2 , …, p m w postaci p 1 ·p 2 ·…·p m , oraz w tym przypadku liczby pierwiastkowej a jest reprezentowane jako (p 1 ·p 2 ·…·p m) n . Ponieważ rozkład liczby na czynniki pierwsze jest jednoznaczny, rozkład pierwiastka liczby a na czynniki pierwsze będzie miał postać (p 1 ·p 2 ·…·p m) n, co pozwala obliczyć wartość pierwiastka Jak.

Należy zauważyć, że jeśli rozkładu liczby a na czynniki pierwsze nie można przedstawić w postaci (p 1 ·p 2 ·…·p m) n, to n-ty pierwiastek takiej liczby a nie jest wyodrębniony całkowicie.

Rozwiążmy to, rozwiązując przykłady.

Przykład.

Weź pierwiastek kwadratowy ze 144.

Rozwiązanie.

Jeśli spojrzysz na tabelę kwadratów podaną w poprzednim akapicie, wyraźnie zobaczysz, że 144 = 12 2, z czego jasno wynika, że ​​pierwiastek kwadratowy z 144 jest równy 12.

Jednak w świetle tego punktu interesuje nas sposób wyodrębnienia pierwiastka poprzez rozkład pierwiastka liczby 144 na czynniki pierwsze. Przyjrzyjmy się temu rozwiązaniu.

Rozłóżmy się 144 do czynników pierwszych:

Oznacza to, że 144=2,2,2,2,3,3. Na podstawie powstałego rozkładu można przeprowadzić następujące przekształcenia: 144=2·2·2·2·3·3=(2,2) 2,3 2 =(2,2,3) 2 =12 2. Stąd, .

Korzystając z właściwości stopnia i właściwości pierwiastków, rozwiązanie można sformułować nieco inaczej: .

Odpowiedź:

Aby skonsolidować materiał, rozważ rozwiązania dwóch kolejnych przykładów.

Przykład.

Oblicz wartość pierwiastka.

Rozwiązanie.

Rozkład na czynniki pierwsze rodnika 243 ma postać 243=3 5 . Zatem, .

Odpowiedź:

Przykład.

Czy wartość pierwiastkowa jest liczbą całkowitą?

Rozwiązanie.

Aby odpowiedzieć na to pytanie, rozłóżmy liczbę pierwiastkową na czynniki pierwsze i zobaczmy, czy można ją przedstawić w postaci sześcianu liczby całkowitej.

Mamy 285 768=2 3 ·3 6 ·7 2. Wynikowe rozwinięcie nie jest przedstawiane jako sześcian liczby całkowitej, ponieważ stopień podstawowy czynnik 7 nie jest wielokrotnością trzech. Dlatego nie można całkowicie wyodrębnić pierwiastka sześciennego z 285 768.

Odpowiedź:

NIE.

Wyodrębnianie pierwiastków z liczb ułamkowych

Czas dowiedzieć się, jak wyodrębnić korzeń liczba ułamkowa. Niech rodnik ułamkowy zostanie zapisany jako p/q. Zgodnie z właściwością pierwiastka ilorazu prawdziwa jest następująca równość. Z tej równości wynika zasada wyodrębniania pierwiastka ułamka: Pierwiastek ułamka jest równy ilorazowi pierwiastka licznika podzielonego przez pierwiastek mianownika.

Spójrzmy na przykład wyodrębnienia pierwiastka z ułamka.

Przykład.

Z czego wynika pierwiastek kwadratowy ułamek wspólny 25/169 .

Rozwiązanie.

Korzystając z tabeli kwadratów, stwierdzamy, że pierwiastek kwadratowy licznika ułamka pierwotnego jest równy 5, a pierwiastek kwadratowy mianownika jest równy 13. Następnie . Na tym kończy się ekstrakcja pierwiastka frakcji wspólnej 25/169.

Odpowiedź:

Pierwiastek ułamka dziesiętnego lub liczby mieszanej wyodrębnia się po zastąpieniu liczb pierwiastkowych ułamkami zwykłymi.

Przykład.

Weź pierwiastek sześcienny ułamka dziesiętnego 474,552.

Rozwiązanie.

Wyobraźmy sobie pierwotny ułamek dziesiętny jako ułamek zwykły: 474,552=474552/1000. Następnie . Pozostaje wyodrębnić pierwiastki sześcienne znajdujące się w liczniku i mianowniku powstałego ułamka. Ponieważ 474 552=2·2·2·3·3·3·13·13·13=(2 3 13) 3 =78 3 i 1 000 = 10 3, wtedy I . Pozostaje tylko dokończyć obliczenia .

Odpowiedź:

.

Biorąc pierwiastek z liczby ujemnej

Warto zastanowić się nad wyodrębnianiem pierwiastków z liczb ujemnych. Badając pierwiastki, powiedzieliśmy, że jeśli wykładnik pierwiastkowy jest liczbą nieparzystą, wówczas pod znakiem pierwiastka może znajdować się liczba ujemna. Nadaliśmy tym wpisom następujące znaczenie: dla liczby ujemnej −a i nieparzystego wykładnika pierwiastka 2 n−1, . Ta równość daje zasada wyodrębniania pierwiastków nieparzystych z liczb ujemnych: aby wyodrębnić pierwiastek z liczby ujemnej, musisz wziąć pierwiastek z przeciwnej liczby dodatniej i umieścić znak minus przed wynikiem.

Spójrzmy na przykładowe rozwiązanie.

Przykład.

Znajdź wartość pierwiastka.

Rozwiązanie.

Przekształćmy oryginalne wyrażenie tak, aby pod pierwiastkiem znajdowała się liczba dodatnia: . Teraz pomieszane numery zastąp go ułamkiem zwykłym: . Stosujemy regułę wyodrębniania pierwiastka ułamka zwykłego: . Pozostaje obliczyć pierwiastki w liczniku i mianowniku powstałego ułamka: .

Oto krótkie podsumowanie rozwiązania: .

Odpowiedź:

.

Bitowe określenie wartości pierwiastkowej

W ogólnym przypadku pod pierwiastkiem znajduje się liczba, której przy użyciu technik omówionych powyżej nie można przedstawić jako n-tą potęgę dowolnej liczby. Ale w tym przypadku trzeba znać znaczenie danego pierwiastka, przynajmniej do pewnego znaku. W takim przypadku, aby wyodrębnić pierwiastek, możesz użyć algorytmu, który pozwala sekwencyjnie uzyskać wystarczającą liczbę wartości cyfr żądanej liczby.

Pierwszym krokiem tego algorytmu jest sprawdzenie, jaki jest najbardziej znaczący bit wartości pierwiastkowej. W tym celu liczby 0, 10, 100, ... są kolejno podnoszone do potęgi n, aż do momentu, gdy liczba przekroczy liczbę pierwiastkową. Następnie liczba, którą podnieśliśmy do potęgi n na poprzednim etapie, wskaże odpowiednią najbardziej znaczącą cyfrę.

Rozważmy na przykład ten krok algorytmu podczas wyodrębniania pierwiastka kwadratowego z pięciu. Weź liczby 0, 10, 100, ... i podnieś je do kwadratu, aż otrzymamy liczbę większą niż 5. Mamy 0 2 = 0<5 , 10 2 =100>5, co oznacza, że ​​najbardziej znaczącą cyfrą będzie cyfra jedności. Wartość tego bitu, jak i niższych, zostanie odnaleziona w kolejnych krokach algorytmu ekstrakcji pierwiastka.

Wszystkie kolejne kroki algorytmu mają na celu sekwencyjne doprecyzowanie wartości pierwiastka poprzez znalezienie wartości kolejnych bitów pożądanej wartości pierwiastka, zaczynając od najwyższej i przechodząc do najniższych. Przykładowo wartość pierwiastka w pierwszym kroku okazuje się wynosić 2, w drugim – 2,2, w trzecim – 2,23 i tak dalej 2,236067977…. Opiszmy, jak znaleźć wartości cyfr.

Cyfry można znaleźć, przeszukując ich możliwe wartości 0, 1, 2, ..., 9. W tym przypadku n-te potęgi odpowiednich liczb są obliczane równolegle i porównywane z liczbą pierwiastkową. Jeżeli na pewnym etapie wartość stopnia przekracza liczbę pierwiastkową, wówczas uznaje się, że wartość cyfry odpowiadająca poprzedniej wartości została znaleziona i jeżeli tak się nie dzieje, następuje przejście do kolejnego kroku algorytmu ekstrakcji pierwiastka; wówczas wartość tej cyfry wynosi 9.

Wyjaśnijmy te punkty na tym samym przykładzie wyodrębnienia pierwiastka kwadratowego z pięciu.

Najpierw znajdujemy wartość cyfry jedności. Będziemy przechodzić przez wartości 0, 1, 2, ..., 9, obliczając odpowiednio 0 2, 1 2, ..., 9 2, aż otrzymamy wartość większą niż pierwiastek 5. Wszystkie te obliczenia wygodnie jest przedstawić w formie tabeli:

Zatem wartość cyfry jedności wynosi 2 (ponieważ 2 2<5 , а 2 3 >5). Przejdźmy do znalezienia wartości miejsca dziesiątego. W tym przypadku podniesiemy liczby 2,0, 2,1, 2,2, ..., 2,9 do kwadratu, porównując uzyskane wartości z rodnikiem 5:

Od 2.2 2<5 , а 2,3 2 >5, wówczas wartość miejsca dziesiątego wynosi 2. Możesz przystąpić do znajdowania wartości miejsca setnego:

W ten sposób znaleziono kolejną wartość pierwiastka z pięciu, która wynosi 2,23. Możesz więc nadal znajdować wartości: 2,236, 2,2360, 2,23606, 2,236067, … .

Aby utrwalić materiał, przeanalizujemy ekstrakcję pierwiastka z dokładnością do setnych, stosując rozważany algorytm.

Najpierw określamy najbardziej znaczącą cyfrę. Aby to zrobić, dzielimy liczby 0, 10, 100 itd. dopóki nie otrzymamy liczby większej niż 2 151 186. Mamy 0 3 = 0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151.186, więc najbardziej znaczącą cyfrą jest cyfra dziesiątek.

Ustalmy jego wartość.

Od 10 3<2 151,186 , а 20 3 >2 151,186, wówczas wartość miejsca dziesiątek wynosi 1. Przejdźmy do jednostek.

Zatem wartość cyfry jedności wynosi 2. Przejdźmy do dziesiątek.

Ponieważ nawet 12,9 3 jest mniejsze niż pierwiastek 2 151,186, wówczas wartość miejsca dziesiątego wynosi 9. Pozostaje wykonać ostatni krok algorytmu, który da nam wartość pierwiastka z wymaganą dokładnością.

Na tym etapie wartość pierwiastka ustala się z dokładnością do setnych: .

Podsumowując ten artykuł, chciałbym powiedzieć, że istnieje wiele innych sposobów ekstrakcji korzeni. Ale w przypadku większości zadań wystarczą te, które przestudiowaliśmy powyżej.

Bibliografia.

• Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: podręcznik dla klasy 8. instytucje edukacyjne.
• Kołmogorow A.N., Abramov A.M., Dudnitsyn Yu.P. i inne. Algebra i początki analizy: Podręcznik dla klas 10 - 11 szkół ogólnokształcących.
• Gusiew V.A., Mordkovich A.G. Matematyka (podręcznik dla rozpoczynających naukę w technikach).

Instrukcje

Aby podnieść liczbę do potęgi 1/3, wprowadź liczbę, a następnie kliknij przycisk potęgowania i wprowadź przybliżoną wartość 1/3 - 0,333. Dokładność ta jest wystarczająca do większości obliczeń. Jednak dokładność obliczeń można bardzo łatwo zwiększyć - wystarczy dodać tyle trójek, ile zmieści się na wskaźniku kalkulatora (na przykład 0,33333333333333333). Następnie kliknij przycisk „=".

Aby obliczyć trzeci pierwiastek za pomocą komputera, uruchom program kalkulatora systemu Windows. Procedura obliczania trzeciego pierwiastka jest całkowicie podobna do opisanej powyżej. Jedyna różnica polega na konstrukcji przycisku potęgowania. Na wirtualnej klawiaturze kalkulatora jest to oznaczone jako „x^y”.

Trzeci pierwiastek można również obliczyć w programie MS Excel. Aby to zrobić, wpisz „=” w dowolnej komórce i wybierz ikonę „wstaw” (fx). W wyświetlonym oknie wybierz funkcję „STOPIEŃ” i kliknij przycisk „OK”. W wyświetlonym oknie wprowadź wartość liczby, dla której chcesz obliczyć trzeci pierwiastek. W polu „Stopień” wpisz liczbę „1/3”. Dokładnie w tej formie wpisz liczbę 1/3 - jak zwykłą. Następnie kliknij przycisk „OK”. Pierwiastek sześcienny podanej liczby pojawi się w komórce tabeli, w której została utworzona.

Jeśli trzeba stale obliczać trzeci pierwiastek, należy nieco ulepszyć metodę opisaną powyżej. Dla liczby, z której chcesz wyodrębnić pierwiastek, podaj nie samą liczbę, ale komórkę tabeli. Następnie wystarczy za każdym razem wpisać do tej komórki oryginalną liczbę - jej pierwiastek sześcienny pojawi się w komórce ze wzorem.

Wideo na ten temat

notatka

Wniosek. W artykule zbadano różne metody obliczania wartości pierwiastka sześciennego. Okazało się, że wartości pierwiastka sześciennego można znaleźć metodą iteracyjną, pierwiastek można też przybliżyć, podnieść liczbę do potęgi 1/3, poszukać wartości trzeciego pierwiastka za pomocą Microsoft Office Ecxel, ustawianie formuł w komórkach.

Pomocna rada

Korzenie drugiego i trzeciego stopnia są używane szczególnie często i dlatego mają specjalne nazwy. Pierwiastek kwadratowy: W tym przypadku wykładnik jest zwykle pomijany, a określenie „pierwiastek” bez określenia wykładnika najczęściej oznacza pierwiastek kwadratowy. Praktyczne obliczanie pierwiastków Algorytm znajdowania pierwiastka n-tego stopnia. Pierwiastki kwadratowe i sześcienne są zwykle podawane we wszystkich kalkulatorach.

Źródła:

• trzeci korzeń
• Jak wyciągnąć pierwiastek kwadratowy do potęgi N w programie Excel

Operacja znalezienia korzenia trzeci stopni nazywa się to zwykle ekstrakcją pierwiastka „sześciennego” i polega na znalezieniu liczby rzeczywistej, której sześcian da wartość równą liczbie pierwiastkowej. Operacja wyodrębniania dowolnego pierwiastka arytmetycznego stopni n jest równoważne operacji podniesienia do potęgi 1/n. Istnieje kilka metod praktycznego obliczania pierwiastków sześciennych.