Zbir logaritama sa istom bazom. Osnovni logaritamski identitet. Zamjena granica integracije

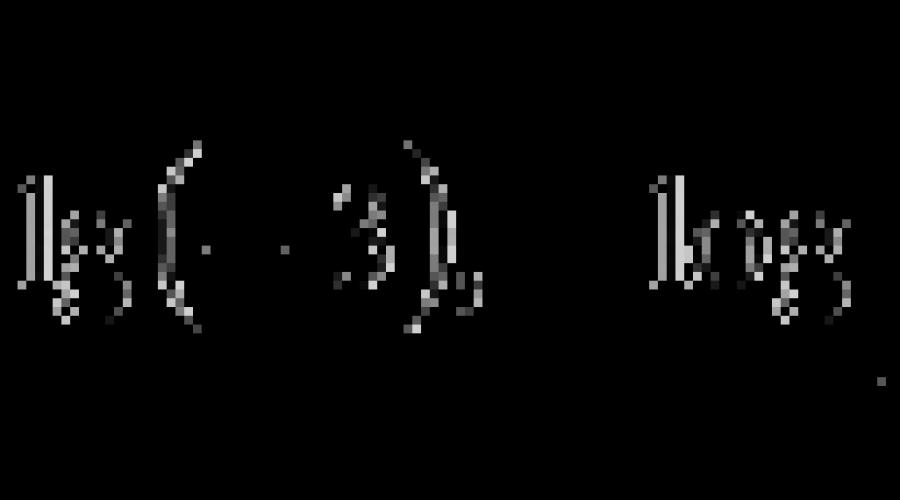
Fokus ovog članka je logaritam. Ovdje ćemo dati definiciju logaritma, pokazati prihvaćenu notaciju, dati primjere logaritama i govoriti o prirodnim i decimalnim logaritmima. Nakon toga, pogledajmo glavno logaritamski identitet.

Navigacija po stranici.

Definicija logaritma

Koncept logaritma nastaje kada se rješava problem u u određenom smislu inverzno, kada trebate pronaći eksponent poznata vrijednost stepen i poznata osnova.

Ali dosta predgovora, vrijeme je da odgovorimo na pitanje „šta je logaritam“? Dajemo odgovarajuću definiciju.

Definicija.

Logaritam od b prema bazi a, gdje je a>0, a≠1 i b>0 eksponent na koji trebate podići broj a da dobijete b kao rezultat.

U ovoj fazi, napominjemo da izgovorena riječ „logaritam” treba odmah pokrenuti dva dodatna pitanja: „koji broj” i „na osnovu čega”. Drugim riječima, jednostavno ne postoji logaritam, već samo logaritam broja prema nekoj bazi.

Uđimo odmah logaritamski zapis: logaritam broja b prema bazi a obično se označava kao log a b. Logaritam broja b na osnovu e i logaritam na osnovu 10 imaju svoje posebne oznake lnb i logb, odnosno ne pišu log e b, već lnb, i ne log 10 b, već lgb.

Sada možemo dati: .
I zapisi nema smisla, jer u prvom od njih je negativan broj pod znakom logaritma, u drugom je negativan broj u osnovi, a u trećem je negativan broj ispod predznaka logaritma i jedinica u baza.

Hajde sada da pričamo o tome pravila za čitanje logaritama. Log a b se čita kao "logaritam od b prema bazi a". Na primjer, log 2 3 je logaritam od tri do baze 2, a logaritam je dvije tačke dvije trećine na osnovu 2 Kvadratni korijen od pet. Poziva se logaritam bazi e prirodni logaritam, a oznaka lnb glasi "prirodni logaritam od b". Na primjer, ln7 je prirodni logaritam od sedam, a mi ćemo ga čitati kao prirodni logaritam broja pi. Logaritam sa bazom 10 takođe ima poseban naziv - decimalni logaritam, a lgb se čita kao "decimalni logaritam od b". Na primjer, lg1 je decimalni logaritam od jedan, a lg2.75 je decimalni logaritam dvije zareze sedam pet stotinki.

Vrijedi se posebno zadržati na uslovima a>0, a≠1 i b>0, pod kojima je data definicija logaritma. Hajde da objasnimo odakle dolaze ova ograničenja. Jednakost oblika zvanog , koja direktno slijedi iz gore navedene definicije logaritma, pomoći će nam u tome.

Počnimo sa a≠1. Pošto je jedan na bilo koji stepen jednak jedan, jednakost može biti tačna samo kada je b=1, ali log 1 1 može biti bilo koji realan broj. Da bi se izbjegla ova dvosmislenost, pretpostavlja se a≠1.

Hajde da opravdamo svrsishodnost uslova a>0. Sa a=0, po definiciji logaritma, imali bismo jednakost, što je moguće samo sa b=0. Ali onda log 0 0 može biti bilo koji realni broj različit od nule, budući da je nula prema bilo kojoj stepenu različitoj od nule nula. Uslov a≠0 nam omogućava da izbjegnemo ovu dvosmislenost. I kada a<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и ирracionalni indikator definirano samo za ne-negativne baze. Stoga je uslov a>0 prihvaćen.

Konačno, uvjet b>0 slijedi iz nejednakosti a>0, budući da je , a vrijednost snage s pozitivnom bazom a uvijek je pozitivna.

Da zaključimo ovu poentu, recimo da navedena definicija logaritma omogućava da odmah naznačite vrijednost logaritma kada je broj ispod znaka logaritma određena snaga baze. Zaista, definicija logaritma nam omogućava da kažemo da ako je b=a p, onda je logaritam broja b na bazi a jednak p. To jest, log jednakosti a a p =p je tačan. Na primjer, znamo da je 2 3 =8, a zatim log 2 8=3. O tome ćemo više govoriti u članku.

Logaritmi, kao i svi brojevi, mogu se sabirati, oduzimati i transformirati na sve načine. Ali pošto logaritmi nisu baš obični brojevi, ovdje postoje pravila koja se zovu glavna svojstva.

Svakako morate znati ova pravila - bez njih se ne može riješiti nijedan ozbiljan logaritamski problem. Osim toga, vrlo ih je malo - sve možete naučiti u jednom danu. Pa počnimo.

Sabiranje i oduzimanje logaritama

Razmotrimo dva logaritma sa istim osnovama: log a x i log a y. Tada se mogu sabirati i oduzimati i:

1. log a x+ log a y=log a (x · y);
2. log a x− log a y=log a (x : y).

Dakle, zbir logaritama je jednak logaritmu proizvoda, a razlika je jednaka logaritmu količnika. Bilješka: ključni trenutak ovdje - identične osnove. Ako su razlozi drugačiji, ova pravila ne funkcionišu!

Ove formule će vam pomoći da izračunate logaritamski izraz čak i kada se njegovi pojedinačni dijelovi ne uzimaju u obzir (pogledajte lekciju “Šta je logaritam”). Pogledajte primjere i pogledajte:

Dnevnik 6 4 + log 6 9.

Pošto logaritmi imaju iste baze, koristimo formulu sume:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadatak. Pronađite vrijednost izraza: log 2 48 − log 2 3.

Osnove su iste, koristimo formulu razlike:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadatak. Pronađite vrijednost izraza: log 3 135 − log 3 5.

Opet su baze iste, tako da imamo:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kao što vidite, originalni izrazi su sastavljeni od „loših“ logaritama, koji se ne računaju zasebno. Ali nakon transformacija dobijaju se sasvim normalni brojevi. Mnogi su izgrađeni na ovoj činjenici test papiri. Da, izrazi poput testa se nude u potpunosti (ponekad i bez ikakvih promjena) na Jedinstvenom državnom ispitu.

Izdvajanje eksponenta iz logaritma

Sada da malo zakomplikujemo zadatak. Šta ako je osnova ili argument logaritma potencija? Tada se eksponent ovog stepena može izvaditi iz predznaka logaritma prema sljedećim pravilima:

Lako je to primijetiti poslednje pravilo prati prva dva. Ali ipak je bolje zapamtiti to - u nekim slučajevima to će značajno smanjiti količinu izračuna.

Naravno, sva ova pravila imaju smisla ako se poštuje ODZ logaritma: a > 0, a ≠ 1, x> 0. I još nešto: naučite primjenjivati ​​sve formule ne samo s lijeva na desno, već i obrnuto, tj. Možete unijeti brojeve prije znaka logaritma u sam logaritam. To je ono što se najčešće traži.

Zadatak. Pronađite vrijednost izraza: log 7 49 6 .

Oslobodimo se stepena u argumentu koristeći prvu formulu:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadatak. Pronađite značenje izraza:

[Natpis za sliku]

Imajte na umu da nazivnik sadrži logaritam, čija su osnova i argument tačni potenci: 16 = 2 4 ; 49 = 7 2. Imamo:

Mislim da posljednji primjer zahtijeva pojašnjenje. Gdje su nestali logaritmi? Do poslednjeg trenutka radimo samo sa imeniocem. Osnovu i argument logaritma koji tu stoji predstavili smo u obliku stepena i iznijeli eksponente - dobili smo razlomak od tri sprata.

Pogledajmo sada glavni razlomak. Brojilac i imenilac sadrže isti broj: log 2 7. Pošto je log 2 7 ≠ 0, možemo smanjiti razlomak - 2/4 će ostati u nazivniku. Prema pravilima aritmetike, četvorka se može prenijeti u brojilac, što je i učinjeno. Rezultat je bio odgovor: 2.

Prelazak na novu osnovu

Govoreći o pravilima za sabiranje i oduzimanje logaritama, posebno sam naglasio da oni rade samo sa istim osnovama. Šta ako su razlozi drugačiji? Šta ako nisu tačne snage istog broja?

Formule za prelazak na novu podlogu dolaze u pomoć. Formulirajmo ih u obliku teoreme:

Neka je dat log logaritam a x. Zatim za bilo koji broj c takav da c> 0 i c≠ 1, jednakost je tačna:

[Natpis za sliku]

Konkretno, ako stavimo c = x, dobijamo:

[Natpis za sliku]

Iz druge formule proizilazi da se baza i argument logaritma mogu zamijeniti, ali se u ovom slučaju cijeli izraz „obrće“, tj. logaritam se pojavljuje u nazivniku.

Ove formule se rijetko nalaze u običnim numeričkim izrazima. Koliko su zgodne moguće je procijeniti samo pri rješavanju logaritamskih jednačina i nejednačina.

Međutim, postoje problemi koji se nikako ne mogu riješiti osim preseljenjem u novu osnovu. Pogledajmo par ovih:

Zadatak. Pronađite vrijednost izraza: log 5 16 log 2 25.

Imajte na umu da argumenti oba logaritma sadrže tačne potencije. Izvadimo indikatore: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Sada "obrnimo" drugi logaritam:

Kako se proizvod ne mijenja pri preraspodjelu faktora, mirno smo pomnožili četiri i dva, a zatim se pozabavili logaritmima.

Zadatak. Pronađite vrijednost izraza: log 9 100 lg 3.

Osnova i argument prvog logaritma su tačni potenci. Zapišimo ovo i riješimo se indikatora:

Sada se riješimo decimalnog logaritma pomicanjem na novu bazu:

Osnovni logaritamski identitet

Često je u procesu rješavanja potrebno predstaviti broj kao logaritam na datu bazu. U ovom slučaju pomoći će nam sljedeće formule:

U prvom slučaju broj n postaje indikator stepena statusa u argumentu. Broj n može biti apsolutno bilo šta, jer je to samo logaritamska vrijednost.

Druga formula je zapravo parafrazirana definicija. To se zove: osnovni logaritamski identitet.

U stvari, šta će se dogoditi ako broj b podići na takav stepen da broj b ovoj potenciji daje broj a? Tako je: dobijate isti broj a. Pažljivo pročitajte ovaj odlomak ponovo - mnogi ljudi zaglave u njemu.

Kao i formule za prelazak na novu bazu, osnovni logaritamski identitet je ponekad jedino moguće rješenje.

Zadatak. Pronađite značenje izraza:

[Natpis za sliku]

Imajte na umu da je log 25 64 = log 5 8 - jednostavno uzet kvadrat iz baze i argumenta logaritma. Uzimajući u obzir pravila za množenje potencija sa istom osnovom, dobijamo:

Ako neko ne zna, ovo je bio pravi zadatak sa Jedinstvenog državnog ispita :)

Logaritamska jedinica i logaritamska nula

U zaključku ću dati dva identiteta koja se teško mogu nazvati svojstvima – radije su to posljedice definicije logaritma. Stalno se pojavljuju u problemima i, iznenađujuće, stvaraju probleme čak i „naprednim“ učenicima.

1. log a a= 1 je logaritamska jedinica. Zapamtite jednom za svagda: logaritam na bilo koju bazu a iz same ove baze jednak je jedan.
2. log a 1 = 0 je logaritamska nula. Baza a može biti bilo šta, ali ako argument sadrži jedan, logaritam je jednak nuli! Jer a 0 = 1 je direktna posljedica definicije.

To je sva imovina. Obavezno vježbajte u njihovoj primjeni! Preuzmite cheat sheet na početku lekcije, odštampajte ga i riješite probleme.

Kao što znate, kada se množe izrazi sa stepenom, njihovi eksponenti se uvijek sabiraju (a b *a c = a b+c). Ovo matematički zakon je izveo Arhimed, a kasnije, u 8. veku, matematičar Virasen je napravio tabelu celobrojnih eksponenata. Upravo su oni poslužili za dalje otkrivanje logaritama. Primjeri korištenja ove funkcije mogu se naći gotovo svugdje gdje trebate pojednostaviti glomazno množenje jednostavnim sabiranjem. Ako odvojite 10 minuta čitajući ovaj članak, objasnit ćemo vam što su logaritmi i kako s njima raditi. Jednostavnim i pristupačnim jezikom.

Definicija u matematici

Logaritam je izraz sljedećeg oblika: log a b=c, to jest, logaritam bilo kojeg nenegativnog broja (tj. bilo kojeg pozitivnog) “b” na njegovu bazu “a” smatra se stepenom “c ” na koju se baza “a” mora podići da bi se na kraju dobila vrijednost “b”. Analizirajmo logaritam na primjerima, recimo da postoji izraz log 2 8. Kako pronaći odgovor? Vrlo je jednostavno, potrebno je pronaći takvu snagu da od 2 do tražene snage dobijete 8. Nakon nekih proračuna u glavi, dobijamo broj 3! I to je tačno, jer 2 na stepen od 3 daje odgovor kao 8.

Vrste logaritama

Za mnoge učenike i studente ova se tema čini komplikovanom i nerazumljivom, ali zapravo logaritmi nisu toliko strašni, najvažnije je razumjeti njihovo općenito značenje i zapamtiti njihova svojstva i neka pravila. Ima ih tri pojedinačne vrste logaritamski izrazi:

1. Prirodni logaritam ln a, gdje je baza Ojlerov broj (e = 2,7).
2. Decimala a, gdje je osnova 10.
3. Logaritam bilo kojeg broja b na osnovu a>1.

Svako od njih je odlučeno na standardan način, što uključuje pojednostavljenje, redukciju i naknadno svođenje na jedan logaritam korištenjem logaritamskih teorema. Za dobijanje ispravne vrijednosti logaritma, trebali biste zapamtiti njihova svojstva i redoslijed radnji kada ih rješavate.

Pravila i neka ograničenja

U matematici postoji nekoliko pravila-ograničenja koja su prihvaćena kao aksiom, odnosno nisu predmet rasprave i predstavljaju istinu. Na primjer, nemoguće je podijeliti brojeve sa nulom, a također je nemoguće izvući paran korijen negativni brojevi. Logaritmi također imaju svoja pravila, slijedeći koja možete lako naučiti raditi čak i sa dugim i prostranim logaritamskim izrazima:

• Osnova “a” uvijek mora biti veća od nule, a ne jednaka 1, inače će izraz izgubiti svoje značenje, jer su “1” i “0” u bilo kojem stepenu uvijek jednaki njihovim vrijednostima;
• ako je a > 0, onda a b > 0, ispada da “c” takođe mora biti veće od nule.

Kako riješiti logaritme?

Na primjer, daje se zadatak pronaći odgovor na jednadžbu 10 x = 100. Ovo je vrlo lako, potrebno je odabrati stepen podizanjem broja deset na koji dobijamo 100. Ovo je, naravno, 10 2 = 100.

Sada predstavimo ovaj izraz u logaritamskom obliku. Dobijamo log 10 100 = 2. Prilikom rješavanja logaritma, sve radnje se praktično konvergiraju da bi se pronašla potencija na koju je potrebno unijeti bazu logaritma da bi se dobio dati broj.

Da biste precizno odredili vrijednost nepoznatog stepena, morate naučiti kako raditi s tablicom stupnjeva. izgleda ovako:

Kao što vidite, neki eksponenti se mogu pogoditi intuitivno ako imate tehnički um i poznavanje tablice množenja. Međutim za velike vrijednosti trebaće vam tabela stepeni. Mogu ga koristiti čak i oni koji ne znaju ništa o složenim matematičkim temama. Lijeva kolona sadrži brojeve (osnova a), gornji red brojeva je vrijednost stepena c na koji je broj a podignut. Na raskrsnici ćelije sadrže brojčane vrijednosti koje su odgovor (a c =b). Uzmimo, na primjer, prvu ćeliju sa brojem 10 i kvadriramo je, dobićemo vrijednost 100, koja je naznačena na sjecištu naše dvije ćelije. Sve je tako jednostavno i lako da će i najistinskiji humanista razumjeti!

Jednačine i nejednačine

Ispada da je pod određenim uslovima eksponent logaritam. Stoga se bilo koji matematički numerički izrazi može zapisati kao logaritamska jednakost. Na primjer, 3 4 =81 se može napisati kao logaritam 81 na bazi 3 jednak četiri (log 3 81 = 4). Za negativne potencije pravila su ista: 2 -5 = 1/32 zapišemo to kao logaritam, dobijemo log 2 (1/32) = -5. Jedna od najfascinantnijih sekcija matematike je tema "logaritma". U nastavku ćemo pogledati primjere i rješenja jednadžbi, odmah nakon proučavanja njihovih svojstava. Pogledajmo sada kako izgledaju nejednakosti i kako ih razlikovati od jednačina.

Dat je izraz sljedećeg oblika: log 2 (x-1) > 3 - jeste logaritamska nejednakost, pošto je nepoznata vrijednost "x" pod znakom logaritma. I u izrazu se upoređuju dvije veličine: logaritam željenog broja prema bazi dva je veći od broja tri.

Najvažnija razlika između logaritamskih jednačina i nejednačina je u tome što jednadžbe sa logaritmima (primjer - logaritam 2 x = √9) podrazumijevaju jednu ili više specifičnih brojčanih vrijednosti u odgovoru, dok se pri rješavanju nejednačina definiraju kao regija prihvatljive vrijednosti, i tačke prekida ove funkcije. Kao posljedica toga, odgovor nije jednostavan skup pojedinačnih brojeva, kao u odgovoru na jednadžbu, već kontinuirani niz ili skup brojeva.

Osnovne teoreme o logaritmima

Prilikom rješavanja primitivnih zadataka pronalaženja vrijednosti logaritma, njegova svojstva možda neće biti poznata. Međutim, kada su u pitanju logaritamske jednačine ili nejednačine, prije svega, potrebno je jasno razumjeti i primijeniti u praksi sva osnovna svojstva logaritama. Kasnije ćemo pogledati primjere jednadžbi; hajde da prvo pogledamo svako svojstvo detaljnije.

1. Glavni identitet izgleda ovako: a logaB =B. Primjenjuje se samo kada je a veće od 0, nije jednako jedan, a B je veće od nule.
2. Logaritam proizvoda se može predstaviti sljedećom formulom: log d (s 1 * s 2) = log d s 1 + log d s 2. U ovom slučaju, obavezan uslov je: d, s 1 i s 2 > 0; a≠1. Možete dati dokaz za ovu logaritamsku formulu, sa primjerima i rješenjem. Neka log a s 1 = f 1 i log a s 2 = f 2, tada a f1 = s 1, a f2 = s 2. Dobijamo da je s 1 * s 2 = a f1 *a f2 = a f1+f2 (osobine stepeni ), a zatim po definiciji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, što je trebalo dokazati.
3. Logaritam količnika izgleda ovako: log a (s 1/s 2) = log a s 1 - log a s 2.
4. Teorema u obliku formule preuzima se sljedeći pogled: log a q b n = n/q log a b.

Ova formula se naziva “svojstvo stepena logaritma”. Podsjeća na svojstva običnih stupnjeva, i nije iznenađujuće, jer se sva matematika zasniva na prirodnim postulatima. Pogledajmo dokaz.

Neka log a b = t, ispada da je a t = b. Ako oba dijela podignemo na stepen m: a tn = b n ;

ali pošto je a tn = (a q) nt/q = b n, dakle log a q b n = (n*t)/t, onda log a q b n = n/q log a b. Teorema je dokazana.

Primjeri problema i nejednakosti

Najčešći tipovi zadataka o logaritmima su primjeri jednačina i nejednačina. Nalaze se u gotovo svim knjigama zadataka, a također su obavezan dio ispita iz matematike. Za upis na fakultet ili polaganje prijemni ispiti u matematici morate znati kako pravilno rješavati takve probleme.

Nažalost, ne postoji jedinstveni plan ili shema za rješavanje i određivanje nepoznate vrijednosti logaritma, ali se određena pravila mogu primijeniti na svaku matematičku nejednačinu ili logaritamsku jednačinu. Prije svega, trebali biste saznati da li se izraz može pojednostaviti ili do njega dovesti opšti izgled. Pojednostavite duge logaritamski izrazi moguće ako pravilno koristite njihova svojstva. Hajde da ih brzo upoznamo.

Prilikom rješavanja logaritamskih jednadžbi moramo odrediti koji tip logaritma imamo: primjer izraza može sadržavati prirodni logaritam ili decimalni.

Evo primjera ln100, ln1026. Njihovo rješenje se svodi na činjenicu da treba odrediti snagu kojoj će baza 10 biti jednaka 100 i 1026, respektivno. Da biste riješili prirodne logaritme, morate primijeniti logaritamske identitete ili njihova svojstva. Pogledajmo primjere rješavanja logaritamskih problema različitih tipova.

Kako koristiti logaritamske formule: s primjerima i rješenjima

Dakle, pogledajmo primjere korištenja osnovnih teorema o logaritmima.

1. Svojstvo logaritma proizvoda može se koristiti u zadacima gdje je potrebno proširiti veliki značaj brojeve b u jednostavnije činioce. Na primjer, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odgovor je 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kao što vidite, koristeći četvrto svojstvo stepena logaritma, uspjeli smo riješiti naizgled složen i nerješiv izraz. Vi samo trebate faktorisati bazu, a zatim izvući vrijednosti eksponenta iz predznaka logaritma.

Zadaci sa Jedinstvenog državnog ispita

Logaritmi se često nalaze u prijemni ispiti, posebno puno logaritamskih problema na Jedinstvenom državnom ispitu ( Državni ispit za sve maturante). Obično su ovi zadaci prisutni ne samo u dijelu A (najlakši dio ispita), već i u dijelu C (najsloženiji i najobimniji zadaci). Ispit zahtijeva tačan i savršeno znanje teme "Prirodni logaritmi".

Primjeri i rješenja problema preuzeti su od zvaničnika Opcije objedinjenog državnog ispita. Pogledajmo kako se takvi zadaci rješavaju.

Dat log 2 (2x-1) = 4. Rješenje:
prepišimo izraz, pojednostavljujući ga malo log 2 (2x-1) = 2 2, po definiciji logaritma dobijamo da je 2x-1 = 2 4, dakle 2x = 17; x = 8,5.

• Najbolje je sve logaritme svesti na istu bazu kako rješenje ne bi bilo glomazno i ​​zbunjujuće.
• Svi izrazi pod predznakom logaritma su označeni kao pozitivni, stoga, kada se eksponent izraza koji je pod predznakom logaritma i kao njegova baza izvadi kao množitelj, izraz koji ostaje pod logaritmom mora biti pozitivan.

Kako se društvo razvijalo i proizvodnja postajala složenija, razvijala se i matematika. Kretanje od jednostavnog ka složenom. Od običnog računovodstva metodom sabiranja i oduzimanja, uz njihovo višestruko ponavljanje, došli smo do pojma množenja i dijeljenja. Smanjenje ponovljene operacije množenja postalo je koncept eksponencijalnosti. Prve tabele zavisnosti brojeva od baze i broja eksponencijalnosti sastavio je još u 8. veku indijski matematičar Varasena. Od njih možete računati vrijeme pojavljivanja logaritama.

Istorijska skica

Preporod Evrope u 16. veku takođe je podstakao razvoj mehanike. T zahtevala veliku količinu proračuna vezano za množenje i dijeljenje višecifrenih brojeva. Drevni stolovi bili su od velike pomoći. Omogućili su zamjenu složenih operacija jednostavnijim - zbrajanjem i oduzimanjem. Veliki iskorak bio je rad matematičara Michaela Stiefela, objavljen 1544. godine, u kojem je realizovao ideju mnogih matematičara. To je omogućilo korištenje tablica ne samo za stepene u obliku prostih brojeva, već i za proizvoljne racionalne.

Godine 1614, Škot Džon Napier, razvijajući ove ideje, prvi je predstavio novi termin"logaritam broja." Sastavljene su nove kompleksne tablice za izračunavanje logaritama sinusa i kosinusa, kao i tangenta. To je znatno smanjilo rad astronoma.

Počele su da se pojavljuju nove tablice koje su naučnici uspješno koristili tri stoljeća. Mnogo je vremena prošlo ranije nova operacija u algebri je dobio svoj potpuni oblik. Data je definicija logaritma i proučavana su njegova svojstva.

Tek u 20. veku, sa pojavom kalkulatora i kompjutera, čovečanstvo je napustilo drevne tablice koje su uspešno radile tokom 13. veka.

Danas logaritam od b na bazi a nazivamo brojem x koji je snaga a da bi se stvorilo b. Ovo je zapisano kao formula: x = log a(b).

Na primjer, log 3(9) bi bio jednak 2. Ovo je očigledno ako slijedite definiciju. Ako podignemo 3 na stepen 2, dobićemo 9.

Dakle, formulirana definicija postavlja samo jedno ograničenje: brojevi a i b moraju biti realni.

Vrste logaritama

Klasična definicija se zove realni logaritam i zapravo je rješenje jednadžbe a x = b. Opcija a = 1 je granična i nije od interesa. Pažnja: 1 na bilo koji stepen je jednako 1.

Realna vrijednost logaritma definiran samo kada su baza i argument veći od 0, a baza ne smije biti jednaka 1.

Posebno mjesto u oblasti matematike igrajte logaritme, koji će se imenovati ovisno o veličini njihove baze:

Pravila i ograničenja

Osnovno svojstvo logaritama je pravilo: logaritam proizvoda jednak je logaritamskom zbroju. log abp = log a(b) + log a(p).

Kao varijanta ove izjave biće: log c(b/p) = log c(b) - log c(p), kvocijentna funkcija je jednaka razlici funkcija.

Iz prethodna dva pravila lako je vidjeti da je: log a(b p) = p * log a(b).

Ostala svojstva uključuju:

Komentar. Nema potrebe praviti uobičajenu grešku - logaritam zbira nije jednak zbiru logaritama.

Tokom mnogih stoljeća, operacija pronalaženja logaritma bila je prilično dugotrajan zadatak. Koristili su matematičari dobro poznata formula logaritamska teorija polinomske ekspanzije:

ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n), gdje je n - prirodni broj veći od 1, što određuje tačnost proračuna.

Logaritmi s drugim bazama izračunati su korištenjem teoreme o prijelazu s jedne baze na drugu i svojstva logaritma proizvoda.

Budući da je ova metoda vrlo radno intenzivna i prilikom rješavanja praktičnih problema teška za implementaciju, koristili smo unaprijed sastavljene tabele logaritama, što je značajno ubrzalo sav rad.

U nekim slučajevima korišteni su posebno dizajnirani logaritamski grafovi koji su davali manju preciznost, ali znatno ubrzavali pretragu željenu vrijednost. Kriva funkcije y = log a(x), konstruisana preko nekoliko tačaka, omogućava vam da koristite regularni lenjir da pronađete vrednost funkcije u bilo kojoj drugoj tački. Inženjeri dugo vrijeme U te svrhe korišten je tzv.

U 17. veku pojavili su se prvi pomoćni analogni računarski uslovi, koji 19. vek dobio gotov izgled. Najuspješniji uređaj zvao se klizač. Unatoč jednostavnosti uređaja, njegov izgled značajno je ubrzao proces svih inženjerskih proračuna, a to je teško precijeniti. Trenutno je malo ljudi upoznato s ovim uređajem.

Pojava kalkulatora i kompjutera učinila je besmislenom upotrebu bilo kojih drugih uređaja.

Jednačine i nejednačine

Za rješavanje različitih jednadžbi i nejednačina pomoću logaritama koriste se sljedeće formule:

• Kretanje s jedne baze na drugu: log a(b) = log c(b) / log c(a);
• Shodno tome prethodna verzija: log a(b) = 1 / log b(a).

Za rješavanje nejednakosti korisno je znati:

• Vrijednost logaritma će biti pozitivna samo ako su baza i argument veći ili manji od jedan; ako je barem jedan uvjet prekršen, vrijednost logaritma će biti negativna.
• Ako je funkcija logaritma primijenjena na desnu i lijevu stranu nejednakosti, a baza logaritma je veća od jedan, onda je znak nejednakosti sačuvan; inače se menja.

Problemi sa uzorcima

Razmotrimo nekoliko opcija za korištenje logaritama i njihovih svojstava. Primjeri sa rješavanjem jednadžbi:

Razmotrimo opciju stavljanja logaritma u stepen:

• Zadatak 3. Izračunajte 25^log 5(3). Rešenje: u uslovima problema, unos je sličan sledećem (5^2)^log5(3) ili 5^(2 * log 5(3)). Zapišimo to drugačije: 5^log 5(3*2), ili kvadrat broja kao argument funkcije može se napisati kao kvadrat same funkcije (5^log 5(3))^2. Koristeći svojstva logaritma, ovaj izraz je jednak 3^2. Odgovor: kao rezultat izračuna dobijamo 9.

Praktična upotreba

Budući da je čisto matematički alat, izgleda daleko od toga pravi zivot da je logaritam odjednom dobio veliku važnost za opisivanje objekata stvarnom svijetu. Teško je naći nauku u kojoj se ne koristi. Ovo se u potpunosti odnosi ne samo na prirodne, već i na prirodne humanitarne oblasti znanje.

Logaritamske zavisnosti

Evo nekoliko primjera numeričkih ovisnosti:

Mehanika i fizika

Istorijski gledano, mehanika i fizika su se uvijek razvijale korištenjem matematičke metode istraživanja i istovremeno je poslužio kao poticaj za razvoj matematike, uključujući i logaritme. Teorija većine zakona fizike napisana je jezikom matematike. Navedimo samo dva primjera opisivanja fizičkih zakona pomoću logaritma.

Problem izračunavanja tako složene veličine kao što je brzina rakete može se riješiti korištenjem formule Tsiolkovsky, koja je postavila temelje za teoriju istraživanja svemira:

V = I * ln (M1/M2), gdje je

• V je konačna brzina aviona.
• I – specifični impuls motora.
• M 1 – početna masa rakete.
• M 2 – konačna masa.

Drugi važan primjer - ovo se koristi u formuli drugog velikog naučnika Maxa Plancka, koja služi za procjenu stanja ravnoteže u termodinamici.

S = k * ln (Ω), gdje je

• S – termodinamičko svojstvo.
• k – Boltzmannova konstanta.
• Ω je statistička težina različitih stanja.

hemija

Manje očigledna je upotreba formula u hemiji koje sadrže omjer logaritama. Navedimo samo dva primjera:

• Nernstova jednadžba, stanje redoks potencijala medija u odnosu na aktivnost supstanci i konstantu ravnoteže.
• Proračun takvih konstanti kao što su indeks autolize i kiselost otopine također se ne može obaviti bez naše funkcije.

Psihologija i biologija

I uopće nije jasno kakve veze psihologija ima s tim. Pokazalo se da je snaga osjeta dobro opisana ovom funkcijom kao inverzni omjer intenziteta stimulusa prema niža vrijednost intenzitet.

Poslije gore navedenim primjerima Više nije iznenađujuće što se tema logaritma široko koristi u biologiji. O biološkim oblicima koji odgovaraju logaritamskim spiralama mogli bi se napisati čitavi tomovi.

Ostala područja

Čini se da je postojanje svijeta nemoguće bez veze s ovom funkcijom, a ona vlada svim zakonima. Pogotovo kada su u vezi sa zakonima prirode geometrijska progresija. Vrijedi se obratiti na web stranicu MatProfi, a takvih primjera ima mnogo u sljedećim područjima djelovanja:

Lista može biti beskonačna. Nakon što ste savladali osnovne principe ove funkcije, možete uroniti u svijet beskonačne mudrosti.

Dakle, imamo moći dvojke. Ako uzmete broj iz donje linije, lako ćete pronaći stepen na koji ćete morati podići dva da biste dobili ovaj broj. Na primjer, da biste dobili 16, trebate podići dva na četvrti stepen. A da biste dobili 64, trebate podići dva na šesti stepen. To se vidi iz tabele.

A sada - zapravo, definicija logaritma:

Osnova logaritma od x je stepen na koji se a mora podići da bi se dobilo x.

Oznaka: log a x = b, gdje je a baza, x je argument, b je ono čemu je logaritam zapravo jednak.

Na primjer, 2 3 = 8 ⇒ log 2 8 = 3 (osnovni 2 logaritam od 8 je tri jer je 2 3 = 8). Sa istim uspjehom log 2 64 = 6, budući da je 2 6 = 64.

Operacija pronalaženja logaritma broja na datu bazu naziva se logaritmizacija. Dakle, dodajmo novi red u našu tabelu:

Nažalost, nisu svi logaritmi izračunati tako lako. Na primjer, pokušajte pronaći dnevnik 2 5 . Broj 5 nije u tabeli, ali logika nalaže da će logaritam ležati negdje na segmentu. Jer 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Takvi brojevi se nazivaju iracionalni: brojevi iza decimalnog zareza mogu se pisati beskonačno i nikada se ne ponavljaju. Ako se ispostavi da je logaritam iracionalan, bolje je ostaviti ga tako: log 2 5, log 3 8, log 5 100.

Važno je shvatiti da je logaritam izraz sa dvije varijable (osnovom i argumentom). U početku, mnogi ljudi brkaju gdje je osnova, a gdje argument. Da biste izbjegli dosadne nesporazume, samo pogledajte sliku:

Pred nama nije ništa drugo do definicija logaritma. Zapamtite: logaritam je stepen, u koji se baza mora ugraditi da bi se dobio argument. To je baza koja je podignuta na snagu - na slici je istaknuta crvenom bojom. Ispostavilo se da je baza uvijek na dnu! Svojim učenicima govorim ovo divno pravilo već na prvoj lekciji - i ne nastaje zabuna.

Shvatili smo definiciju - preostaje samo da naučimo kako računati logaritme, tj. oslobodite se znaka "log". Za početak, napominjemo da iz definicije proizlaze dvije važne činjenice:

1. Argument i baza uvijek moraju biti veći od nule. Ovo proizilazi iz definicije stepena racionalnim eksponentom, na koji se svodi definicija logaritma.
2. Baza mora biti različita od jedinice, jer jedan u bilo kom stepenu i dalje ostaje jedan. Zbog toga je besmisleno pitanje „na koju snagu se mora podići da bi se dobilo dva“. Ne postoji takva diploma!

Takva ograničenja se nazivaju raspon prihvatljivih vrijednosti(ODZ). Ispada da ODZ logaritma izgleda ovako: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Imajte na umu da nema ograničenja za broj b (vrijednost logaritma). Na primjer, logaritam može biti negativan: log 2 0,5 = −1, jer 0,5 = 2 −1.

Međutim, sada samo razmatramo numeričke izraze, pri čemu nije potrebno znati CVD logaritma. Autori problema su već uzeli u obzir sva ograničenja. Ali kad odu logaritamske jednačine i nejednakosti, zahtjevi DHS-a će postati obavezni. Uostalom, osnova i argument mogu sadržavati vrlo jake konstrukcije koje nužno ne odgovaraju gornjim ograničenjima.

Sada razmotrimo opšta šema izračunavanje logaritama. Sastoji se od tri koraka:

1. Predstavite bazu a i argument x kao stepen sa minimumom mogući razlog, veće od jedan. Usput je bolje da se riješite decimala;
2. Riješite jednačinu za varijablu b: x = a b ;
3. Rezultirajući broj b će biti odgovor.

To je sve! Ako se pokaže da je logaritam iracionalan, to će biti vidljivo već u prvom koraku. Zahtjev da baza bude veća od jedan je vrlo važan: to smanjuje vjerovatnoću greške i uvelike pojednostavljuje proračune. Isto sa decimale: ako ih odmah pretvorite u obične, bit će mnogo manje grešaka.

Pogledajmo kako ova shema funkcionira na konkretnim primjerima:

Zadatak. Izračunajte logaritam: log 5 25

1. Zamislimo bazu i argument kao stepen petice: 5 = 5 1 ; 25 = 5 2 ;

Kreirajmo i riješimo jednačinu:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;

2. Dobili smo odgovor: 2.

Zadatak. Izračunaj logaritam:

Zadatak. Izračunajte logaritam: log 4 64

1. Zamislimo bazu i argument kao stepen dvojke: 4 = 2 2 ; 64 = 2 6 ;
2. Kreirajmo i riješimo jednačinu:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ;
3. Dobili smo odgovor: 3.

Zadatak. Izračunajte logaritam: log 16 1

1. Zamislimo bazu i argument kao stepen dvojke: 16 = 2 4 ; 1 = 2 0 ;
2. Kreirajmo i riješimo jednačinu:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ;
3. Dobili smo odgovor: 0.

Zadatak. Izračunajte logaritam: log 7 14

1. Zamislimo bazu i argument kao stepen od sedam: 7 = 7 1 ; 14 se ne može predstaviti kao stepen sedam, jer 7 1< 14 < 7 2 ;
2. Iz prethodnog stava proizilazi da se logaritam ne računa;
3. Odgovor je bez promjene: dnevnik 7 14.

Mala napomena o posljednjem primjeru. Kako možete biti sigurni da broj nije tačan stepen drugog broja? Vrlo je jednostavno - samo ga razdvojite na primarni faktori. Ako ekspanzija ima najmanje dva različita faktora, broj nije točna snaga.

Zadatak. Saznajte da li su brojevi tačni potenci: 8; 48; 81; 35; 14 .

8 = 2 · 2 · 2 = 2 3 - tačan stepen, jer postoji samo jedan množitelj;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - nije tačna snaga, jer postoje dva faktora: 3 i 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - tačan stepen;
35 = 7 · 5 - opet nije tačna snaga;
14 = 7 · 2 - opet nije tačan stepen;

Napomenimo i mi sami primarni brojevi su uvek tačni stepeni za sebe.

Decimalni logaritam

Neki logaritmi su toliko uobičajeni da imaju poseban naziv i simbol.

Decimalni logaritam od x je logaritam na osnovu 10, tj. Potencija na koju se broj 10 mora podići da bi se dobio broj x. Oznaka: lg x.

Na primjer, log 10 = 1; LG 100 = 2; lg 1000 = 3 - itd.

Od sada, kada se u udžbeniku pojavi fraza poput „Pronađi lg 0,01“, znajte da ovo nije greška u kucanju. Ovo je decimalni logaritam. Međutim, ako niste upoznati s ovom notacijom, uvijek je možete prepisati:
log x = log 10 x

Sve što vrijedi za obične logaritme vrijedi i za decimalne logaritme.

Prirodni logaritam

Postoji još jedan logaritam koji ima svoju oznaku. Na neki način, to je čak i važnije od decimalnog. Radi se o o prirodnom logaritmu.

Prirodni logaritam od x je logaritam bazi e, tj. stepen na koji se broj e mora podići da bi se dobio broj x. Oznaka: ln x .

Mnogi će se zapitati: koji je broj e? Ovo je iracionalan broj tačna vrijednost nemoguće pronaći i snimiti. Navest ću samo prve brojke:
e = 2,718281828459...

Nećemo ulaziti u detalje koji je to broj i zašto je potreban. Samo zapamtite da je e baza prirodnog logaritma:
ln x = log e x

Dakle, ln e = 1; ln e 2 = 2; ln e 16 = 16 - itd. S druge strane, ln 2 je iracionalan broj. Općenito, prirodni logaritam bilo kojeg racionalni broj iracionalno. Osim, naravno, jednog: ln 1 = 0.

Za prirodne logaritme vrijede sva pravila koja vrijede za obične logaritme.