Provjerite rješenje najvećeg i najmanjeg na segmentu. Najveća i najmanja vrijednost funkcije. Zadatak B15 (2014)

Pogledajmo kako istražiti funkciju koristeći graf. Ispada da gledajući grafikon možete saznati sve što nas zanima, naime:

• opseg funkcije
• opseg funkcija
• nule funkcije
• periodi porasta i smanjenja
• visoke i niske tačke
• najveća i najmanja vrijednost funkcije na segmentu.

Hajde da pojasnimo terminologiju:

Abscisa je horizontalna koordinata tačke.
Ordinate- vertikalna koordinata.
apscisa- horizontalna osa, koja se najčešće naziva osa.
Y-osa - vertikalna osa, ili osa .

Argument je nezavisna varijabla o kojoj ovise vrijednosti funkcije. Najčešće indicirano.
Drugim riječima, mi sami biramo , zamjenjujemo u formulu funkcije i dobivamo .

Domain funkcije - skup onih (i samo onih) vrijednosti argumenta za koje funkcija postoji.
Označeno: ili .

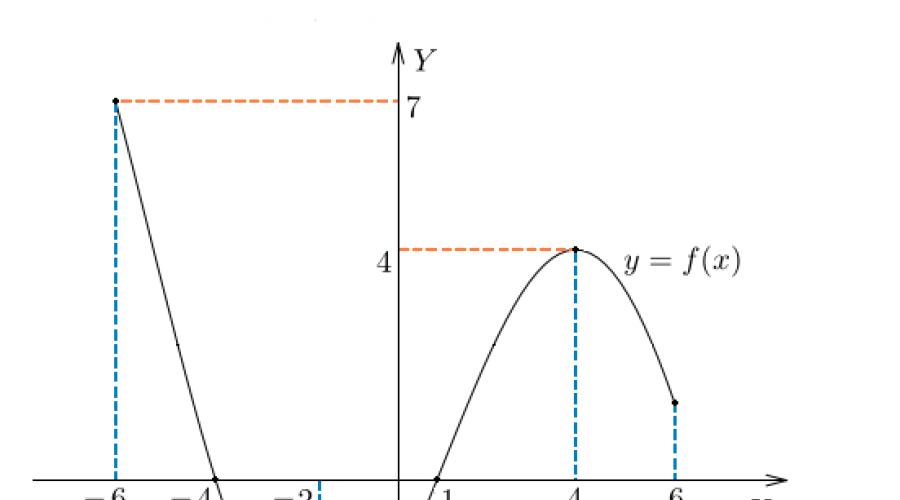
Na našoj slici, domen funkcije je segment. Na ovom segmentu je nacrtan graf funkcije. Samo ovdje datu funkciju postoje.

Raspon funkcija je skup vrijednosti koje varijabla uzima. Na našoj slici, ovo je segment - od najniže do najveće vrijednosti.

Funkcija nule- tačke u kojima je vrijednost funkcije jednaka nuli, tj. Na našoj slici, to su točke i .

Vrijednosti funkcije su pozitivne gdje . Na našoj slici, to su intervali i .
Vrijednosti funkcije su negativne gdje . Imamo ovaj interval (ili interval) od do.

Najvažniji koncepti - rastuća i opadajuća funkcija na nekom setu. Kao skup, možete uzeti segment, interval, uniju intervala ili cijelu brojevnu pravu.

Funkcija povećava

Drugim riječima, što više, to više, odnosno graf ide udesno i gore.

Funkcija opadajući na skupu ako za bilo koji i pripada skupu nejednakost implicira nejednakost .

Za opadajuću funkciju, veća vrijednost odgovara manjoj vrijednosti. Grafikon ide desno i dolje.

Na našoj slici, funkcija raste na intervalu i opada na intervalima i .

Hajde da definišemo šta je maksimalne i minimalne tačke funkcije.

Maksimalni poen- ovo je unutrašnja tačka domene definicije, takva da je vrijednost funkcije u njoj veća nego u svim tačkama koje su joj dovoljno blizu.
Drugim riječima, maksimalna tačka je takva tačka, vrijednost funkcije u kojoj više nego u susednim. Ovo je lokalno "brdo" na grafikonu.

Na našoj slici - maksimalna tačka.

Niska tačka- unutrašnja tačka domene definicije, takva da je vrednost funkcije u njoj manja nego u svim tačkama koje su joj dovoljno blizu.
Odnosno, minimalna tačka je takva da je vrijednost funkcije u njoj manja nego u susjednim. Na grafikonu je ovo lokalna „rupa“.

Na našoj slici - minimalna tačka.

Tačka je granica. To nije unutrašnja tačka domene definicije i stoga se ne uklapa u definiciju maksimalne tačke. Na kraju krajeva, ona nema komšije sa leve strane. Na isti način, ne može postojati minimalna tačka na našem grafikonu.

Maksimalni i minimalni bodovi se zajednički nazivaju ekstremne tačke funkcije. U našem slučaju, ovo je i .

Ali šta ako trebate pronaći npr. funkcija minimum na rezu? AT ovaj slučaj odgovor: . jer funkcija minimum je njegova vrijednost na minimalnoj tački.

Slično, maksimum naše funkcije je . Doseže se na tački .

Možemo reći da su ekstremi funkcije jednaki i .

Ponekad u zadacima morate pronaći najveća i najmanja vrijednost funkcije na datom segmentu. Ne poklapaju se nužno sa ekstremima.

U našem slučaju najmanja vrijednost funkcije na intervalu je jednak i poklapa se sa minimumom funkcije. Ali njegova najveća vrijednost na ovom segmentu je jednaka . Dostiže se na lijevom kraju segmenta.

U svakom slučaju, najveća i najmanja vrijednost kontinuirane funkcije na segmentu se postižu ili u tačkama ekstrema ili na krajevima segmenta.

sitna i lepa jednostavan zadatak iz kategorije onih koji služe kao spas za plutajućeg studenta. U prirodi, uspavanom carstvu sredine jula, pa je vrijeme da se smjestite uz laptop na plaži. Rano ujutru zasvirao je sunčev snop teorije da bi se ubrzo fokusirao na praksu, koja, uprkos svojoj deklarisanoj lakoći, sadrži krhotine stakla u pijesku. U tom smislu, preporučujem da savjesno razmotrite nekoliko primjera ove stranice. Da biste riješili praktične zadatke, morate biti sposobni pronađite derivate i razumjeti materijal članka Intervali monotonosti i ekstremi funkcije.

Prvo, ukratko o glavnoj stvari. U lekciji o kontinuitet funkcije Dao sam definiciju kontinuiteta u tački i kontinuiteta u intervalu. Primer ponašanja funkcije na segmentu je formulisan na sličan način. Funkcija je kontinuirana na segmentu ako:

1) kontinuirano je na intervalu;
2) kontinuirano u tački desno i u tački lijevo.

Drugi paragraf se bavi tzv jednostrani kontinuitet funkcioniše u jednom trenutku. Postoji nekoliko pristupa njegovoj definiciji, ali ja ću se držati linije započete ranije:

Funkcija je kontinuirana u jednoj tački desno, ako je definirana u datoj tački i njena desna granica se poklapa s vrijednošću funkcije u datoj tački: . Kontinuirano je u tački lijevo, ako je definiran u datoj tački i njegova lijeva granica je jednaka vrijednosti u toj tački:

Zamislite da su zelene tačke nokti na kojima je pričvršćena čarobna gumica:

Mentalno uzmite crvenu liniju u svoje ruke. Očigledno, bez obzira koliko daleko rastežemo graf gore i dolje (duž ose), funkcija će i dalje ostati ograničeno- živa ograda gore, živa ograda ispod, a naš proizvod pase u ogradi. dakle, funkcija kontinuirana na segmentu je ograničena na njega. U toku matematičke analize ova naizgled jednostavna činjenica se iznosi i rigorozno dokazuje Weierstrassova prva teorema.… Mnoge ljude nervira što se elementarne tvrdnje zamorno potkrepljuju u matematici, ali to ima važno značenje. Pretpostavimo da je određeni stanovnik frotirnog srednjeg vijeka povukao graf u nebo izvan granica vidljivosti, ovo je umetnuto. Prije pronalaska teleskopa, ograničena funkcija u svemiru uopće nije bila očigledna! Zaista, kako znaš šta nas čeka iza horizonta? Uostalom, nekada se Zemlja smatrala ravnom, pa je danas i obična teleportacija zahtijeva dokaz =)

Prema druga Weierstrassova teorema, kontinuirano na segmentufunkcija dostiže svoje tačna gornja ivica i njegov tačna donja ivica .

Broj se također poziva maksimalna vrijednost funkcije na segmentu i označen sa , a broj - minimalna vrijednost funkcije na segmentu označeno .

u našem slučaju:

Bilješka : u teoriji, zapisi su uobičajeni .

grubo govoreći, najveća vrijednost nalazi se tamo gdje je najviša tačka grafa, a najmanja - gdje je najniža tačka.

Bitan! Kao što je već istaknuto u članku o ekstremi funkcije, najveća vrijednost funkcije i najmanja vrijednost funkcije – NIJE ISTO, šta funkcija maksimalno i funkcija minimum. Dakle, u ovom primjeru, broj je minimum funkcije, ali ne i minimalna vrijednost.

Usput, šta se dešava izvan segmenta? Da, čak i poplava, u kontekstu problema koji se razmatra, to nas uopšte ne zanima. Zadatak uključuje samo pronalaženje dva broja i to je to!

Štaviše, rješenje je čisto analitičko, dakle, nema potrebe za crtanjem!

Algoritam leži na površini i sugeriše se iz gornje slike:

1) Pronađite vrijednosti funkcije u kritične tačke, koji pripadaju ovom segmentu.

Uhvatite još jednu dobrotu: nema potrebe provjeravati dovoljan uslov za ekstrem, jer, kao što je upravo prikazano, prisustvo minimuma ili maksimuma još nije zagarantovano koja je minimalna ili maksimalna vrijednost. Demonstracijska funkcija dostiže svoj maksimum i, voljom sudbine, isti broj je najveća vrijednost funkcije na intervalu . Ali, naravno, takva koincidencija se ne dešava uvek.

Dakle, u prvom koraku brže je i lakše izračunati vrijednosti funkcije u kritičnim tačkama koje pripadaju segmentu, ne obazirući se na to da li imaju ekstreme ili ne.

2) Izračunavamo vrijednosti funkcije na krajevima segmenta.

3) Među vrijednostima funkcije koje se nalaze u 1. i 2. paragrafu, odabiremo najmanju i najviše veliki broj, zapišite odgovor.

Sjedimo na obali sinjeg mora i udaramo petama u plitku vodu:

Primjer 1

Pronađite najveću i najmanju vrijednost funkcije na segmentu

Odluka:
1) Izračunajte vrijednosti funkcije u kritičnim tačkama koje pripadaju ovom segmentu:

Izračunajmo vrijednost funkcije u drugoj kritičnoj tački:

2) Izračunajte vrijednosti funkcije na krajevima segmenta:

3) "Podebljani" rezultati su dobijeni sa eksponencijalima i logaritmima, što značajno otežava njihovo poređenje. Iz tog razloga ćemo se naoružati kalkulatorom ili Excelom i izračunati približne vrijednosti, ne zaboravljajući da:

Sada je sve jasno.

Odgovori:

Razlomno-racionalna instanca za nezavisno rešenje:

Primjer 6

Pronađite maksimum i minimalna vrijednost funkcije na segmentu

Proces pronalaženja najmanjih i najvećih vrijednosti funkcije na segmentu podsjeća na fascinantan let oko objekta (grafikon funkcije) na helikopteru s pucanjem iz dalekometnog topa u određenim točkama i biranjem između ove tačke su veoma posebne tačke za kontrolne udarce. Bodovi se biraju na određeni način i prema određenim pravilima. Po kojim pravilima? O tome ćemo dalje.

Ako je funkcija y = f(x) kontinuirano na segmentu [ a, b] , zatim dopire do ovog segmenta najmanje i najviše vrijednosti . Ovo se može dogoditi ili u ekstremne tačke ili na krajevima segmenta. Stoga, pronaći najmanje i najveće vrijednosti funkcije , kontinuirano na segmentu [ a, b] , potrebno je izračunati njegove vrijednosti u svemu kritične tačke i na krajevima segmenta, a zatim odaberite najmanji i najveći od njih.

Neka je, na primjer, potrebno odrediti maksimalnu vrijednost funkcije f(x) na segmentu [ a, b] . Da biste to učinili, pronađite sve njegove kritične točke koje leže na [ a, b] .

kritična tačka naziva se tačka u kojoj definirana funkcija, i ona derivat je ili nula ili ne postoji. Zatim biste trebali izračunati vrijednosti funkcije u kritičnim točkama. I, na kraju, treba uporediti vrijednosti funkcije u kritičnim točkama i na krajevima segmenta ( f(a) i f(b) ). Najveći od ovih brojeva će biti najveća vrijednost funkcije na segmentu [a, b] .

Problem nalaženja najmanje vrijednosti funkcije .

Zajedno tražimo najmanju i najveću vrijednost funkcije

Primjer 1. Pronađite najmanju i najveću vrijednost funkcije na segmentu [-1, 2] .

Odluka. Nalazimo derivaciju ove funkcije. Izjednačite derivaciju sa nulom () i dobijete dvije kritične točke: i . Da biste pronašli najmanju i najveću vrijednost funkcije na datom segmentu, dovoljno je izračunati njene vrijednosti na krajevima segmenta i u tački, jer tačka ne pripada segmentu [-1, 2] . Ove vrijednosti funkcije su sljedeće: , , . Iz toga slijedi najmanja vrijednost funkcije(označeno crvenom bojom na donjem grafikonu), jednako -7, dostiže se na desnom kraju segmenta - u tački , i najveći(takođe crvena na grafikonu), jednaka je 9, - u kritičnoj tački.

Ako je funkcija kontinuirana u određenom intervalu i ovaj interval nije segment (ali je, na primjer, interval; razlika između intervala i segmenta: granične točke intervala nisu uključene u interval, već granične točke segmenta su uključene u segment), tada među vrijednostima funkcije možda neće biti najmanja i najveća. Tako, na primjer, funkcija prikazana na donjoj slici je kontinuirana na ]-∞, +∞[ i nema najveću vrijednost.

Međutim, za bilo koji interval (zatvoren, otvoren ili beskonačan) vrijedi sljedeće svojstvo kontinuiranih funkcija.

Primjer 4. Pronađite najmanju i najveću vrijednost funkcije na segmentu [-1, 3] .

Odluka. Izvod ove funkcije nalazimo kao derivaciju kvocijenta:

.

Derivat izjednačavamo sa nulom, što nam daje jednu kritičnu tačku: . Pripada intervalu [-1, 3] . Da bismo pronašli najmanju i najveću vrijednost funkcije na datom segmentu, nalazimo njene vrijednosti na krajevima segmenta i na pronađenoj kritičnoj tački:

Hajde da uporedimo ove vrednosti. Zaključak: jednako -5/13, u tački i najveća vrijednost jednako 1 u tački .

Nastavljamo zajedno tražiti najmanju i najveću vrijednost funkcije

Ima nastavnika koji na temu pronalaženja najmanjih i najvećih vrijednosti funkcije učenicima ne daju primjere složenije od upravo razmatranih, odnosno onih u kojima je funkcija polinom ili razlomak, brojilac a imenilac su polinomi. Ali nećemo se ograničavati na takve primjere, jer među nastavnicima postoje ljubitelji da učenici razmišljaju u potpunosti (tabela izvedenica). Stoga će se koristiti logaritam i trigonometrijska funkcija.

Primjer 6. Pronađite najmanju i najveću vrijednost funkcije na segmentu .

Odluka. Izvod ove funkcije nalazimo kao derivat proizvoda :

Derivat izjednačavamo sa nulom, što daje jednu kritičnu tačku: . Pripada segmentu. Da bismo pronašli najmanju i najveću vrijednost funkcije na datom segmentu, nalazimo njene vrijednosti na krajevima segmenta i na pronađenoj kritičnoj tački:

Rezultat svih akcija: funkcija dostigne svoju minimalnu vrijednost, jednako 0, u tački i u tački i najveća vrijednost jednak e² , u tački .

Primjer 7. Pronađite najmanju i najveću vrijednost funkcije na segmentu .

Odluka. Nalazimo derivaciju ove funkcije:

Izjednačite derivaciju sa nulom:

Jedina kritična tačka pripada segmentu. Da bismo pronašli najmanju i najveću vrijednost funkcije na datom segmentu, nalazimo njene vrijednosti na krajevima segmenta i na pronađenoj kritičnoj tački:

zaključak: funkcija dostigne svoju minimalnu vrijednost, jednako , u točki i najveća vrijednost, jednako , u točki .

U primijenjenim ekstremnim problemima, pronalaženje najmanjih (najvećih) vrijednosti funkcije, po pravilu, svodi se na pronalaženje minimuma (maksimuma). Ali od većeg praktičnog interesa nisu sami minimumi ili maksimumi, već vrijednosti argumenta na kojem se postižu. Prilikom rješavanja primijenjenih problema javlja se dodatna poteškoća - kompilacija funkcija koje opisuju fenomen ili proces koji se razmatra.

Primjer 8 Rezervoar kapaciteta 4, koji ima oblik paralelepipeda sa kvadratnom bazom i otvoren na vrhu, mora biti kalajisan. Koje bi trebalo da budu dimenzije rezervoara da bi se prekrio sa najmanjom količinom materijala?

Odluka. Neka bude x- osnovna strana h- visina rezervoara, S- njegovu površinu bez pokrova, V- njen volumen. Površina rezervoara se izražava formulom, tj. je funkcija dvije varijable. Da izrazim S kao funkciju jedne varijable, koristimo činjenicu da , odakle . Zamjena pronađenog izraza h u formulu za S:

Hajde da ispitamo ovu funkciju za ekstrem. Definiran je i diferencibilan svuda u ]0, +∞[ i

.

Izjednačavamo derivaciju sa nulom () i nalazimo kritičnu tačku. Osim toga, na , derivacija ne postoji, ali ova vrijednost nije uključena u domenu definicije i stoga ne može biti tačka ekstrema. Dakle, - jedina kritična tačka. Provjerimo prisustvo ekstremuma pomoću drugog dovoljan znak. Nađimo drugi izvod. Kada je drugi izvod veći od nule (). To znači da kada funkcija dostigne minimum . Jer ovo minimum - jedini ekstrem ove funkcije, to je njena najmanja vrijednost. Dakle, strana osnove rezervoara treba da bude jednaka 2 m, a njegova visina.

Primjer 9 Iz paragrafa A, nalazi se na željezničkoj pruzi, do tač With, na udaljenosti od njega l, roba se mora transportovati. Cijena transporta jedinice težine po jedinici udaljenosti željeznicom je jednaka , a autoputem je jednaka . Do koje tačke M linije željeznica treba izgraditi autoput tako da se prevoz robe iz ALI in With bio najekonomičniji AB pretpostavlja se da je pruga prava)?

U praksi je prilično uobičajeno koristiti derivaciju za izračunavanje najveće i najmanje vrijednosti funkcije. Ovu radnju izvodimo kada shvatimo kako da minimiziramo troškove, povećamo profit, izračunamo optimalno opterećenje za proizvodnju i sl. odnosno u slučajevima kada je to potrebno utvrditi optimalna vrijednost bilo koji parametar. Da bi se takvi problemi ispravno riješili, mora se dobro razumjeti koja je najveća i najmanja vrijednost funkcije.

Yandex.RTB R-A-339285-1

Obično ove vrijednosti definiramo unutar nekog intervala x, što zauzvrat može odgovarati cijelom opsegu funkcije ili njenom dijelu. To može biti ili segment [ a ; b ] , i otvoreni interval (a ; b) , (a ; b ] , [ a ; b) , beskonačni interval (a ; b) , (a ; b ] , [ a ; b) ili beskonačan interval - ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .

U ovom članku ćemo objasniti kako se najveće i najmanje vrijednosti eksplicitno izračunavaju. datu funkciju sa jednom varijablom y=f(x) y = f (x) .

Osnovne definicije

Počinjemo, kao i uvijek, sa formulacijom glavnih definicija.

Definicija 1

Najveća vrijednost funkcije y = f (x) na nekom intervalu x je vrijednost m a x y = f (x 0) x ∈ X , što za bilo koju vrijednost x x ∈ X , x ≠ x 0 čini nejednakost f (x ) ≤ f (x 0) .

Definicija 2

Najmanja vrijednost funkcije y = f (x) na nekom intervalu x je vrijednost m i n x ∈ X y = f (x 0) , što za bilo koju vrijednost x ∈ X , x ≠ x 0 čini nejednakost f(X f (x) ≥ f(x0) .

Ove definicije su prilično očigledne. Još lakše, možete reći ovo: najveća vrijednost funkcije je njena najveća veliki značaj na poznatom intervalu na apscisi x 0 , a najmanja je najmanja prihvaćena vrijednost na istom intervalu na x 0 .

Definicija 3

Stacionarne tačke su takve vrednosti argumenta funkcije u kojima njena derivacija postaje 0.

Zašto moramo znati šta su stacionarne tačke? Da bismo odgovorili na ovo pitanje, moramo se sjetiti Fermatove teoreme. Iz toga slijedi da je stacionarna tačka tačka u kojoj se nalazi ekstrem diferencijabilne funkcije (tj. njen lokalni minimum ili maksimum). Posljedično, funkcija će uzeti najmanju ili najveću vrijednost na određenom intervalu tačno u jednoj od stacionarnih tačaka.

Druga funkcija može poprimiti najveću ili najmanju vrijednost u onim točkama u kojima je sama funkcija određena, a njen prvi izvod ne postoji.

Prvo pitanje koje se nameće prilikom proučavanja ove teme je: možemo li u svim slučajevima odrediti maksimalnu ili minimalnu vrijednost funkcije na datom intervalu? Ne, to ne možemo učiniti kada će se granice datog intervala poklapati sa granicama domene definicije, ili ako imamo posla sa beskonačnim intervalom. Takođe se dešava da će funkcija u datom intervalu ili u beskonačnosti biti beskonačno mala ili beskonačna velike vrednosti. U tim slučajevima nije moguće odrediti najveću i/ili najmanju vrijednost.

Ovi trenuci će postati razumljiviji nakon slike na grafikonima:

Prva slika nam prikazuje funkciju koja poprima najveću i najmanju vrijednost (m a x y i m i n y) u stacionarnim tačkama koje se nalaze na intervalu [ - 6 ; 6].

Hajde da detaljno ispitamo slučaj prikazan u drugom grafikonu. Promijenimo vrijednost segmenta u [ 1 ; 6] i dobijamo da će se najveća vrijednost funkcije postići u tački sa apscisom na desnoj granici intervala, a najmanja - u stacionarnoj tački.

Na trećoj slici, apscise tačaka predstavljaju granične tačke segmenta [ - 3 ; 2]. Oni odgovaraju najvećoj i najmanjoj vrijednosti date funkcije.

Pogledajmo sada četvrtu sliku. U njemu funkcija uzima m a x y (najveća vrijednost) i m i n y (najmanja vrijednost) u stacionarnim tačkama u otvorenom intervalu (- 6 ; 6).

Ako uzmemo interval [ 1 ; 6) , tada možemo reći da će najmanja vrijednost funkcije na njemu biti dostignuta u stacionarnoj tački. Nećemo znati maksimalnu vrijednost. Funkcija bi mogla uzeti najveću vrijednost na x jednaku 6 ako je x = 6 pripadalo intervalu. Upravo je ovaj slučaj prikazan na slici 5.

Na grafikonu 6, ova funkcija dobija najmanju vrijednost u desnoj granici intervala (- 3 ; 2 ] , a ne možemo izvući definitivne zaključke o najvećoj vrijednosti.

Na slici 7 vidimo da će funkcija imati m a x y u stacionarnoj tački, a apscisa je jednaka 1. Funkcija dostiže svoju minimalnu vrijednost na granici intervala na desnoj strani. Na minus beskonačnosti, vrijednosti funkcije će se asimptotski približiti y = 3.

Ako uzmemo interval x ∈ 2 ; + ∞ , tada ćemo vidjeti da data funkcija na njoj neće poprimiti ni najmanju ni najveću vrijednost. Ako x teži 2, tada će vrijednosti funkcije težiti minus beskonačnosti, jer je prava linija x = 2 vertikalna asimptota. Ako apscisa teži plus beskonačnosti, tada će se vrijednosti funkcije asimptotski približiti y = 3. Ovo je slučaj prikazan na slici 8.

U ovom paragrafu ćemo dati niz radnji koje se moraju izvršiti da bi se pronašla najveća ili najmanja vrijednost funkcije u određenom intervalu.

1. Prvo, pronađimo domenu funkcije. Provjerimo da li je segment naveden u uvjetu uključen u njega.
2. Sada izračunajmo tačke sadržane u ovom segmentu u kojima prvi izvod ne postoji. Najčešće se mogu naći u funkcijama čiji je argument napisan pod znakom modula ili u funkcije snage, čiji je eksponent razlomački racionalan broj.
3. Zatim saznajemo koje stacionarne tačke spadaju u dati segment. Da biste to učinili, morate izračunati derivaciju funkcije, zatim je izjednačiti sa 0 i riješiti rezultirajuću jednadžbu, a zatim odabrati odgovarajuće korijene. Ako ne dobijemo ni jednu stacionarnu tačku ili one ne spadaju u dati segment, onda prelazimo na sljedeći korak.
4. Odredimo koje će vrijednosti funkcija zauzeti u datim stacionarnim točkama (ako ih ima), ili u onim tačkama gdje prvi izvod ne postoji (ako postoji), ili izračunamo vrijednosti za x = a i x = b .
5. 5. Imamo niz vrijednosti funkcije, od kojih sada trebamo izabrati najveću i najmanju. Ovo će biti najveća i najmanja vrijednost funkcije koju trebamo pronaći.

Pogledajmo kako pravilno primijeniti ovaj algoritam prilikom rješavanja problema.

Primjer 1

Stanje: data je funkcija y = x 3 + 4 x 2. Odrediti njegovu najveću i najmanju vrijednost na segmentima [ 1 ; 4 ] i [ - 4 ; - jedan] .

Odluka:

Počnimo s pronalaženjem domene ove funkcije. U ovom slučaju, to će biti skup svih realnih brojeva osim 0. Drugim riječima, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . Oba segmenta navedena u uvjetu bit će unutar područja definicije.

Sada izračunavamo derivaciju funkcije prema pravilu diferencijacije razlomka:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x 3

Naučili smo da će izvod funkcije postojati u svim tačkama segmenata [1; 4 ] i [ - 4 ; - jedan] .

Sada moramo odrediti stacionarne tačke funkcije. Uradimo to sa jednačinom x 3 - 8 x 3 = 0. Ima samo jedan pravi korijen, a to je 2. To će biti stacionarna tačka funkcije i pasti u prvi segment [ 1 ; 4 ] .

Izračunajmo vrijednosti funkcije na krajevima prvog segmenta i u datoj tački, tj. za x = 1 , x = 2 i x = 4:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Dobili smo da je najveća vrijednost funkcije m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 će se postići pri x = 1 , a najmanji m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – pri x = 2 .

Drugi segment ne uključuje nikakve stacionarne tačke, tako da moramo izračunati vrijednosti funkcije samo na krajevima datog segmenta:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Dakle, m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

odgovor: Za segment [ 1 ; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , za segment [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

pogledajte sliku:

Prije studiranja ovu metodu, savjetujemo vam da ponovite kako pravilno izračunati jednostranu granicu i granicu u beskonačnosti, kao i da naučite osnovne metode za njihovo pronalaženje. Da bismo pronašli najveću i/ili najmanju vrijednost funkcije na otvorenom ili beskonačnom intervalu, izvodimo sljedeće korake u nizu.

1. Prvo morate provjeriti da li će dati interval biti podskup domene date funkcije.
2. Odredimo sve tačke koje se nalaze u traženom intervalu i u kojima prvi izvod ne postoji. Obično su za funkcije kod kojih je argument zatvoren u znaku modula i za funkcije stepena s razlomkom racionalni indikator. Ako ove tačke nedostaju, možete preći na sljedeći korak.
3. Sada određujemo koje stacionarne tačke spadaju u dati interval. Prvo, izjednačimo izvod sa 0, riješimo jednačinu i pronađemo odgovarajuće korijene. Ako nemamo ni jednu stacionarnu tačku ili ne spadaju u zadati interval, odmah idemo na dalja akcija. Oni su određeni tipom intervala.

• Ako interval izgleda kao [ a ; b) , tada trebamo izračunati vrijednost funkcije u tački x = a i jednostranoj granici lim x → b - 0 f (x) .
• Ako interval ima oblik (a ; b ] , onda trebamo izračunati vrijednost funkcije u tački x = b i jednostranoj granici lim x → a + 0 f (x) .
• Ako interval ima oblik (a ; b) , tada trebamo izračunati jednostrane granice lim x → b - 0 f (x), lim x → a + 0 f (x) .
• Ako interval izgleda kao [ a ; + ∞) , tada je potrebno izračunati vrijednost u tački x = a i granicu na plus beskonačnost lim x → + ∞ f (x) .
• Ako interval izgleda kao (- ∞ ; b ] , izračunavamo vrijednost u tački x = b i granicu u minus beskonačnosti lim x → - ∞ f (x) .
• Ako je - ∞ ; b , tada razmatramo jednostranu granicu lim x → b - 0 f (x) i granicu na minus beskonačnost lim x → - ∞ f (x)
• Ako je - ∞ ; + ∞ , tada razmatramo granice na minus i plus beskonačnost lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. Na kraju treba izvući zaključak na osnovu dobijenih vrijednosti funkcije i granica. Ovdje postoji mnogo opcija. Dakle, ako je jednostrana granica jednaka minus beskonačnosti ili plus beskonačnosti, onda je odmah jasno da se ništa ne može reći o najmanjoj i najvećoj vrijednosti funkcije. U nastavku ćemo razmotriti jedan tipičan primjer. Detaljni opisi pomoći da shvatite šta je šta. Ako je potrebno, možete se vratiti na slike 4 - 8 u prvom dijelu materijala.

Uslov: data je funkcija y = 3 e 1 x 2 + x - 6 - 4 . Izračunajte njegovu najveću i najmanju vrijednost u intervalima - ∞ ; - 4 , - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; +∞) .

Odluka

Prije svega, nalazimo domenu funkcije. Imenilac razlomka je kvadratni trinom, koji se ne bi trebao pretvoriti u 0:

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Dobili smo opseg funkcije kojem pripadaju svi intervali navedeni u uvjetu.

Sada ćemo razlikovati funkciju i dobiti:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

Prema tome, derivati ​​funkcije postoje u cijelom domenu njene definicije.

Pređimo na pronalaženje stacionarnih tačaka. Derivat funkcije postaje 0 na x = - 1 2 . Ovo je stacionarna tačka koja se nalazi u intervalima (- 3 ; 1 ] i (- 3 ; 2) .

Izračunajmo vrijednost funkcije na x = - 4 za interval (- ∞ ; - 4 ] , kao i granicu na minus beskonačnost:

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

Pošto je 3 e 1 6 - 4 > - 1 , onda je m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. Ovo nam ne dozvoljava da jedinstveno odredimo najmanju vrijednost funkcije. Možemo samo zaključiti da postoji granica ispod -1, budući da se ovoj vrijednosti funkcija približava asimptotski na minus beskonačnosti.

Karakteristika drugog intervala je da nema niti jednu stacionarnu tačku niti jednu strogu granicu. Stoga ne možemo izračunati ni najveću ni najmanju vrijednost funkcije. Definiranjem granice na minus beskonačnost i kako argument teži - 3 na lijevoj strani, dobijamo samo raspon vrijednosti:

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

To znači da će se vrijednosti funkcije nalaziti u intervalu - 1; +∞

Da bismo pronašli maksimalnu vrijednost funkcije u trećem intervalu, odredimo njenu vrijednost u stacionarnoj tački x = - 1 2 ako je x = 1 . Također moramo znati jednostrano ograničenje za slučaj kada argument teži - 3 na desnoj strani:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Pokazalo se da će funkcija poprimiti najveću vrijednost u stacionarnoj tački m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4. Što se tiče najmanje vrijednosti, ne možemo je odrediti. Sve to možemo znam , je prisustvo donje granice do - 4 .

Za interval (- 3 ; 2), uzmimo rezultate prethodnog izračunavanja i još jednom izračunajmo čemu je jednaka jednostrana granica kada težimo 2 s lijeve strane:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Dakle, m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 , a najmanja vrijednost se ne može odrediti, a vrijednosti funkcije su ograničene odozdo brojem - 4 .

Na osnovu onoga što smo uradili u prethodna dva proračuna, možemo tvrditi da na intervalu [ 1 ; 2) funkcija će poprimiti najveću vrijednost pri x = 1, a najmanju je nemoguće pronaći.

Na intervalu (2 ; + ∞) funkcija neće dostići ni najveću ni najmanju vrijednost, tj. uzimat će vrijednosti iz intervala - 1; +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Nakon što smo izračunali kojoj će biti vrijednost funkcije pri x = 4, saznajemo da je m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , a data funkcija na plus beskonačno će se asimptotski približiti pravoj y = - 1 .

Uporedimo ono što smo dobili u svakom proračunu sa grafikom date funkcije. Na slici su asimptote prikazane isprekidanim linijama.

To je sve o čemu smo hteli da pričamo o pronalaženju najveće i najmanje vrednosti funkcije. Ovi nizovi radnji koje smo dali pomoći će vam da izvršite potrebne proračune što je brže i jednostavnije moguće. Ali zapamtite da je često korisno prvo saznati u kojim intervalima će se funkcija smanjiti, a u kojim intervalima će se povećati, nakon čega se mogu izvući daljnji zaključci. Tako možete preciznije odrediti najveću i najmanju vrijednost funkcije i opravdati rezultate.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter