Os problemas que envolvem a construção de seções de poliedros ocupam um lugar significativo como curso escolar geometria para o ensino médio e em exames de diversos níveis. A resolução deste tipo de problemas contribui para a assimilação dos axiomas da estereometria, a sistematização de conhecimentos e competências, o desenvolvimento da compreensão espacial e das competências construtivas. São conhecidas as dificuldades que surgem na resolução de problemas que envolvem a construção de secções.

Desde a infância nos deparamos com seções. Cortamos pão, salsicha e outros produtos, cortamos com um palito ou lápis com uma faca. O plano de corte em todos esses casos é o plano da faca. As seções (cortes de peças) acabam sendo diferentes.

Uma seção de um poliedro convexo é um polígono convexo, cujos vértices, no caso geral, são os pontos de intersecção do plano de corte com as arestas do polígono, e os lados são as linhas de intersecção do plano de corte com as faces .

Para construir a reta de intersecção de dois planos, basta encontrar dois pontos comuns esses planos e desenhe uma linha reta através deles. Isso se baseia nas seguintes afirmações:

1. se dois pontos de uma reta pertencem a um plano, então toda a reta pertence a este plano;

2. se dois planos diferentes têm um ponto comum, então eles se cruzam ao longo de uma linha reta que passa por esse ponto.

Como já disse, a construção de seções de poliedros pode ser realizada com base nos axiomas da estereometria e nos teoremas do paralelismo de retas e planos. Ao mesmo tempo, existem certos métodos para construir seções planas de poliedros. Os mais eficazes são os três métodos a seguir:

Método de rastreamento

Método de Design Interno

Método combinado.

No estudo da geometria e, em particular, nas seções onde são consideradas imagens de figuras geométricas, as imagens de figuras geométricas são auxiliadas pelo uso de apresentações de computador. Com a ajuda de um computador, muitas aulas de geometria tornam-se mais visuais e dinâmicas. Axiomas, teoremas, provas, problemas de construção, problemas de construção de seções podem ser acompanhados por construções sucessivas na tela do monitor. Desenhos feitos em computador podem ser salvos e inseridos em outros documentos.

Gostaria de mostrar alguns slides sobre o tema: “Construindo seções em corpos geométricos”

Para construir o ponto de intersecção de uma reta e um plano, encontre uma reta no plano que intercepta a reta dada. Então o ponto requerido é o ponto de intersecção da linha encontrada com aquela dada. Vamos ver isso nos próximos slides.

Tarefa 1.

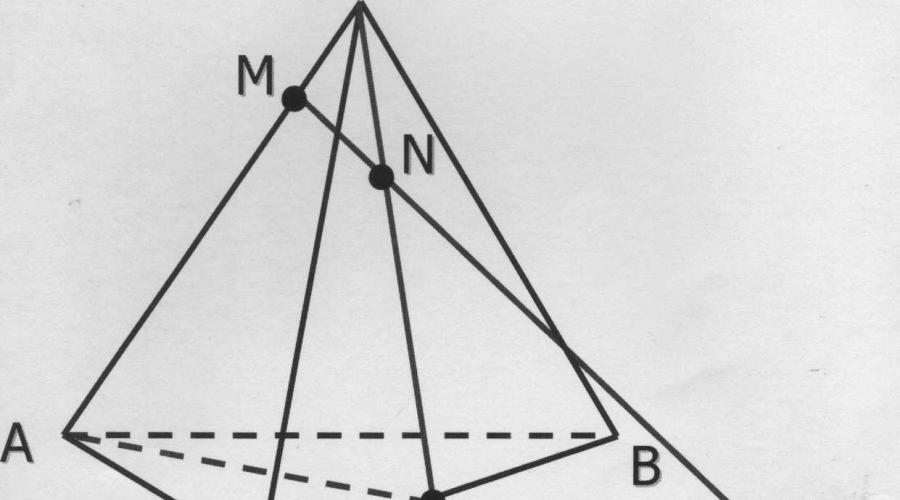
Dois pontos M e N estão marcados nas bordas do tetraedro DABC; M GAD, N b DC. Especifique o ponto de intersecção da reta MN com o plano base.

Solução: para encontrar o ponto de intersecção da reta MN com o plano

Continuaremos a base com AC e o segmento MN. Marquemos o ponto de intersecção dessas retas por X. O ponto X pertence à reta MN e à face AC, e AC está no plano da base, o que significa que o ponto X também está no plano da base. Consequentemente, o ponto X é o ponto de intersecção da reta MN com o plano da base.

Vamos considerar o segundo problema. Vamos complicar um pouco.

Tarefa 2.

Dado um tetraedro DABC de pontos M e N, onde M € DA, N C (DBC). Encontre o ponto de intersecção da reta MN com o plano ABC.

Solução: o ponto de intersecção da reta MN com o plano ABC deve estar no plano que contém a reta MN e no plano da base. Continuemos o segmento DN até o ponto de intersecção com a aresta DC. Marcamos o ponto de intersecção através de E. Continuamos a linha AE e MN até o ponto de sua intersecção. Marquemos X. O ponto X pertence a MN, o que significa que está no plano que contém a reta MN e X pertence a AE, e AE está no plano ABC. Isso significa que X também está no plano ABC. Portanto X é o ponto de intersecção da reta MN e do plano ABC.

Vamos complicar a tarefa. Consideremos a seção de figuras geométricas por planos que passam por três pontos dados.

Problema 3

Os pontos M, N e P estão marcados nas arestas AC, AD e DB do tetraedro DABC. Construa uma seção do tetraedro usando o plano MNP.

Solução: construa uma linha reta ao longo da qual o plano é MNP. Intersecta o plano da face ABC. O ponto M é o ponto comum desses planos. Para construir outro ponto comum, continuamos o segmento AB e NP. Marcamos o ponto de intersecção através de X, que será o segundo ponto comum dos planos MNP e ABC. Isso significa que esses planos se cruzam ao longo da linha reta MX. MX cruza a aresta BC em algum ponto E. Como E está em MX, e MX é uma linha pertencente ao plano MNP, então PE pertence a MNP. Quadrangle MNPE é a seção obrigatória.

Problema 4

Vamos construir uma seção de um prisma reto ABCA1B1C1 com um plano passando pelos pontos P , P,R, onde R pertence a ( A.A. 1C 1C),R pertence EM 1C1,

Q pertence a AB

Solução: Todos três pontos P,Q,R estão em faces diferentes, portanto ainda não podemos construir a linha de intersecção do plano de corte com qualquer face do prisma. Vamos encontrar um ponto intersecções do PR com o ABC. Vamos encontrar as projeções dos pontos P e R no plano base PP1 perpendicular a BC e RR1 perpendicular a AC. A linha P1R1 cruza a linha PR no ponto X. X é o ponto de intersecção da linha PR com o plano ABC. Encontra-se no plano desejado K e no plano da base, como o ponto Q. XQ é uma linha reta que cruza K com o plano da base. XQ intercepta AC no ponto K. Portanto, KQ é o segmento de intersecção do plano X com a face ABC. K e R estão no plano X e no plano da face АА1С1С. Vamos traçar uma linha reta KR e marcar o ponto de intersecção com A1Q E. KE é a linha de intersecção do plano X com esta face. Vamos encontrar a linha de intersecção do plano X com o plano das faces BB1A1A. KE cruza com A1A no ponto Y. A linha QY é a linha de intersecção do plano de corte com o plano AA1B1B. FPEKQ é a seção obrigatória.

O método das seções de poliedros em estereometria é utilizado em problemas de construção. Baseia-se na capacidade de construir uma seção de um poliedro e determinar o tipo de seção.

Este material é caracterizado pelas seguintes características:

1. O método das seções é usado apenas para poliedros, uma vez que vários tipos complexos (oblíquos) de seções de corpos de rotação não estão incluídos no currículo do ensino médio.
2. Os problemas utilizam principalmente os poliedros mais simples.
3. Os problemas são apresentados principalmente sem dados numéricos, a fim de criar a possibilidade de seu uso múltiplo.

Para resolver o problema de construção de uma seção de um poliedro, o aluno deve saber:

• o que significa construir uma seção de um poliedro com um plano;
• como um poliedro e um plano podem ser posicionados um em relação ao outro;
• como o plano é definido;
• quando o problema de construir uma seção de um poliedro por um plano é considerado resolvido.

Porque o plano está definido:

• três pontos;
• linha reta e ponto;
• duas linhas paralelas;
• duas linhas que se cruzam,

A construção do plano de corte depende da especificação deste plano. Portanto, todos os métodos de construção de seções de poliedros podem ser divididos em métodos.

Existe três métodos principais construindo seções de poliedros:

1. Método de rastreamento.
2. Método de seções auxiliares.
3. Método combinado.

Os dois primeiros métodos são variações Método axiomático construção de seções.

Também podemos distinguir os seguintes métodos para construir seções de poliedros:

• construindo uma seção de um poliedro com um plano passando por determinado ponto paralelo a um determinado plano;
• construir uma seção que passa por uma determinada linha paralela a outra determinada linha;
• construir uma seção que passa por um determinado ponto paralelo a duas retas que se cruzam;
• construir uma seção de um poliedro com um plano passando por uma determinada linha perpendicular a um determinado plano;
• construir uma seção de um poliedro com um plano que passa por um determinado ponto perpendicular a uma determinada linha reta.

A lista federal de livros didáticos de geometria para as séries 10 a 11 inclui livros dos seguintes autores:

• Atanasyan L.S., Butuzova V.F., Kadomtseva S.B. e outros (Geometria, 10-11);
• Pogorelova A.V. (Geometria, 7-11);
• Alexandrova A.D., Vernera A.L., Ryzhik V.I. (Geometria, 10-11);
• Smirnova I.M. (Geometria, 10-11);
• Sharygina I.F. (Geometria, 10-11).

Vamos dar uma olhada nos livros de L.S., Atanasyan e A.V.

No livro L.S. Atanasyan no tema “Construção de seções de poliedros” teve duas horas alocadas. No 10º ano, no tópico “Paralelismo de retas e planos”, após o estudo do tetraedro e do paralelepípedo, é reservada uma hora para apresentação do parágrafo “Problemas de construção de secções”. São consideradas seções de um tetraedro e de um paralelepípedo. E o tópico “Paralelismo de retas e planos” termina com a resolução de problemas em uma ou duas horas (são oito problemas no total para construção de seções no livro didático).

No livro Pogorelov A.V. Cerca de três horas são alocadas para a construção de seções do capítulo “Poliedros”: uma para estudar o tema “Imagem de um prisma e construção de suas seções”, a segunda para estudar o tema “Construindo uma pirâmide e suas seções planas”, e a terceira para resolver problemas. Na lista de problemas fornecida após o tópico, existem apenas cerca de dez problemas transversais.

Oferecemos um sistema de aulas sobre o tema “Construção de seções de poliedros” para o livro didático de Pogorelov A.V.

Propõe-se organizar o material na sequência em que ele pode ser utilizado para ensinar os alunos. Da apresentação do tema “Poliedros” propõe-se excluir os seguintes parágrafos: “Construção de seções de um prisma” e “Construção de seções de uma pirâmide” para sistematizar este material no final deste tópico “Poliedros”. Pode ser classificado de acordo com o objeto das tarefas com observância aproximada do princípio “do simples ao complexo” da seguinte forma:

1. Determinação da seção de poliedros.
2. Construção de seções de uma pirâmide prismática, paralelepípeda, pelo método trace. (Via de regra, em um curso escolar de estereometria, são utilizados problemas para construir seções de poliedros, resolvidos por métodos básicos. Outros métodos, por serem mais alto nível dificuldades, o professor pode deixá-lo para consideração em aulas optativas ou para estudo independente. Em problemas de construção, os métodos básicos requerem a construção de um plano de seção que passa por três pontos).
3. Encontrar a área da seção transversal em poliedros (sem usar o teorema da área da projeção ortogonal de um polígono).
4. Encontrar a área da seção transversal em poliedros (usando o teorema da área da projeção ortogonal de um polígono).

PROBLEMAS ESTEREOMÉTRICOS PARA CONSTRUÇÃO DE SEÇÕES DE POLIEDROS E MÉTODOS PARA SEU USO NAS AULAS DO 10º ao 11º ano.

(sistema de aulas e aulas eletivas sobre o tema “Construção de seções de poliedros”)

LIÇÃO 1.

Tópico da lição: “Construção de seções de poliedros”.

Objetivo da lição: familiarização com métodos de construção de seções de poliedros.

Etapas da lição:

1. Atualizando conhecimentos básicos.
2. Formulação do problema.
3. Aprendendo novo material:

A) Definição da seção.

B) Métodos de construção de seções:

a) método de rastreamento;

b) método das seções auxiliares;

c) método combinado.

1. Fixando o material.

Exemplos de construção de seções usando o método trace.

1. Resumindo a lição.

Durante as aulas.

1. Atualizando conhecimentos básicos.

Vamos lembrar:
- intersecção de uma linha reta com um plano;
- intersecção de planos;
- propriedades de planos paralelos.

2. Formulação do problema.

Perguntas para a aula:
- O que significa construir uma seção de um poliedro com um plano?
- Como um poliedro e um plano podem ser posicionados um em relação ao outro?
- Como o plano é definido?
- Quando se considera resolvido o problema de construir uma seção de um poliedro por um plano?

3. Aprendendo novo material.

A) Assim, a tarefa é construir a intersecção de duas figuras: um poliedro e um plano (Fig. 1). Podem ser: uma figura vazia (a), um ponto (b), um segmento (c), um polígono (d). Se a intersecção de um poliedro e um plano for um polígono, então esse polígono é chamado seção de um poliedro por um plano.

Consideraremos apenas o caso em que o plano intercepta o poliedro ao longo do seu interior. Neste caso, a intersecção deste plano com cada face do poliedro será um determinado segmento. Assim, o problema é considerado resolvido se forem encontrados todos os segmentos ao longo dos quais o plano intercepta as faces do poliedro.

Examine as seções do cubo (Fig. 2) e responda às seguintes perguntas:

Que polígonos são obtidos quando um cubo é cortado por um plano? (O número de lados do polígono é importante);

[Respostas sugeridas: triângulo, quadrilátero, pentágono, hexágono.]

Um cubo pode ser cortado por um plano em um heptágono? E quanto ao octógono, etc.? Por que?

Vejamos o prisma e suas possíveis seções por plano (no modelo). Que tipo de polígonos são obtidos?

O que pode ser concluído? Qual é o maior número de lados de um polígono obtido cortando um poliedro com um plano?

[ Maior número lados de um polígono obtido cortando um poliedro por um plano é igual ao número de faces do poliedro.]

BA) Método de rastreamento consiste em construir traços de um plano de corte no plano de cada face do poliedro. A construção de uma seção de um poliedro pelo método do traço geralmente começa com a construção do chamado traço principal do plano de corte, ou seja, traço do plano de corte no plano da base do poliedro.

b) Método de seções auxiliares construir seções de poliedros é bastante universal. Nos casos em que o traço (ou traços) desejado do plano de corte está fora do desenho, este método ainda apresenta algumas vantagens. Ao mesmo tempo, deve-se ter em mente que as construções realizadas com este método muitas vezes ficam “lotadas”. No entanto, em alguns casos, o método das seções auxiliares acaba sendo o mais racional.

O método de rastreamento e o método de seção auxiliar são variações método axiomático construção de seções de poliedros com um plano.

c) A essência método combinado a construção de seções de poliedros consiste na aplicação de teoremas sobre o paralelismo de retas e planos no espaço em combinação com o método axiomático.

Agora, usando um exemplo de resolução de problemas, vejamos método de rastreamento

4. Fixação do material.

Tarefa 1.

Construa uma seção do prisma ABCDA 1 B 1 C 1 D 1 com um plano passando pelos pontos P, Q, R (os pontos estão indicados no desenho (Fig. 3)).

Solução.

Arroz. 3

1. Vamos construir um traço do plano de corte no plano da base inferior do prisma. Considere a face AA 1 B 1 B. Os pontos de seção P e Q estão nesta face. Vamos traçar uma linha reta PQ.
2. Continuemos a reta PQ, que pertence ao trecho, até cruzar a reta AB. Obtemos um ponto S 1 pertencente ao traço.
3. Da mesma forma, obtemos o ponto S 2 pela intersecção das linhas QR e BC.
4. Linha reta S 1 S 2 - traço do plano de corte no plano da base inferior do prisma.
5. A linha reta S 1 S 2 cruza o lado AD no ponto U, o lado CD no ponto T. Conectemos os pontos P e U, pois eles estão no mesmo plano da face AA 1 D 1 D. Da mesma forma, obtemos TU e RT.
6. PQRTU é a seção obrigatória.

Construa uma seção do paralelepípedo ABCDA 1 B 1 C 1 D 1 com um plano passando pelos pontos M, N, P (os pontos estão indicados no desenho (Fig. 4)).

Solução.

1. Os pontos N e P estão no plano da seção e no plano da base inferior do paralelepípedo. Vamos construir uma linha reta passando por esses pontos. Esta linha reta é o traço do plano de corte sobre o plano da base do paralelepípedo.
2. Continuemos a linha reta de que lado AB está o paralelepípedo. As linhas AB e NP se cruzam em algum ponto S. Este ponto pertence ao plano de seção.
3. Como o ponto M também pertence ao plano de seção e cruza a linha AA 1 em algum ponto X.
4. Os pontos X e N estão no mesmo plano da face AA 1 D 1 D, conecte-os e obtenha uma linha reta XN.
5. Como os planos das faces do paralelepípedo são paralelos, então através do ponto M podemos traçar uma reta na face A 1 B 1 C 1 D 1 paralela à reta NP. Esta linha reta cruzará o lado B 1 C 1 no ponto Y.
6. Da mesma forma, traçamos a linha reta YZ, paralela à linha reta XN. Conectamos Z com P e obtemos a seção desejada - MYZPNX.

Problema 3 (para solução independente).

Construa uma seção do tetraedro DACB com um plano passando pelos pontos M, N, P (os pontos estão indicados no desenho (Fig. 5)).

5. Resumindo a lição.

Responda à pergunta: as figuras sombreadas são seções dos poliedros representados pelo plano PQR? E faça a construção correta (Fig. 6).

Opção 1.

Opção 2.

Tópico da lição: ENCONTRANDO A ÁREA SECCIONAL.

Objetivo da lição: apresentar métodos para encontrar a área da seção transversal de um poliedro.

Etapas da lição:

1. Atualizando conhecimentos básicos.

Lembre-se do teorema da área da projeção ortogonal de um polígono.

2. Resolvendo problemas para encontrar a área da seção transversal:

Sem usar o teorema da área da projeção ortogonal de um polígono;

Usando o teorema da área da projeção ortogonal de um polígono.

3. Resumindo a lição.

Durante as aulas.

1. Atualizando conhecimentos básicos.

Vamos lembrar teorema sobre a área da projeção ortogonal de um polígono: A área da projeção ortogonal de um polígono em um plano é igual ao produto de sua área e o cosseno do ângulo entre o plano do polígono e o plano de projeção.

2. Solução de problemas.

ABCD - correto pirâmide triangular com lado da base AB igual A e altura DH igual h. Construa uma seção da pirâmide com um plano passando pelos pontos D, C e M, onde M é o meio do lado AB, e encontre sua área (Fig. 7).

A seção transversal da pirâmide é o triângulo MCD. Vamos encontrar sua área.

S = 1/2 DH CM = 1/2 =

Encontre a área da seção transversal de um cubo ABCDA 1 B 1 C 1 D 1 com uma aresta A plano passando pelo vértice D e pelos pontos E e F nas arestas A 1 D 1 e C 1 D 1, respectivamente, se A 1 E = k D 1 E e C 1 F = k D 1 F.

Construção da seção:

1. Como os pontos E e F pertencem ao plano de seção e ao plano da face A 1 B 1 C 1 D 1, e os dois planos se cruzam ao longo de uma linha reta, então a linha reta EF será um traço do plano de seção no plano da face A 1 B 1 C 1 D 1 (Fig. 8).
2. ED e FD diretos são obtidos da mesma maneira.
3. EDF é a seção obrigatória.

Problema 3 (para solução independente).

Construa uma seção do cubo ABCDA 1 B 1 C 1 D 1 com lado A um plano que passa pelos pontos B, M e N, onde L é o meio da aresta AA 1 e N é o meio da aresta CC 1.

Construímos a seção usando o método trace.

Encontramos a área da seção transversal usando o teorema da área da projeção ortogonal de um polígono. Resposta: S = 1/2 · um 2.

CONSTRUÇÃO DE SEÇÕES E SEÇÕES EM DESENHOS

A formação de um desenho de peça é realizada adicionando sequencialmente as projeções, seções e seções necessárias. Inicialmente, é criada uma vista personalizada com o modelo especificado pelo usuário, e é definida a orientação do modelo mais adequada para a vista principal. A seguir, usando esta e as seguintes vistas, são criados os cortes e seções necessárias.

A vista principal (vista frontal) é selecionada de forma a dar a ideia mais completa das formas e dimensões da peça.

Seções em desenhos

Dependendo da posição do plano de corte, existem os seguintes tipos cortes:

A) horizontal, se o plano de corte estiver paralelo ao plano horizontal das projeções;

B) vertical, se o plano de corte for perpendicular ao plano horizontal de projeções;

C) inclinado - o plano de corte está inclinado em relação aos planos de projeção.

As seções verticais são divididas em:

· frontal - o plano de corte é paralelo ao plano frontal das projeções;

· perfil - o plano de corte é paralelo ao plano do perfil das projeções.
Dependendo do número de planos de corte, os cortes são:

· simples - com um plano de corte (Fig. 107);

· complexo - com dois ou mais planos de corte (Fig. 108)
A norma prevê os seguintes tipos de cortes complexos:

· escalonado, quando os planos de corte são paralelos (Fig. 108 a) e quebrados - os planos de corte se cruzam (Fig. 108 b)

Fig. 107 Seção simples

A) b)

Fig. 108 Cortes complexos

Designação de cortes

No caso em que num corte simples o plano secante coincide com o plano de simetria do objeto, o corte não é indicado (Fig. 107). Em todos os outros casos, os cortes são indicados em letras maiúsculas do alfabeto russo, começando com a letra A, por exemplo A-A.

A posição do plano de corte no desenho é indicada por uma linha de corte - uma linha grossa e aberta. No caso de um corte complexo, os traços também são feitos nas curvas da linha de corte. As setas devem ser colocadas nos traços iniciais e finais indicando a direção de visão; as setas devem estar a uma distância de 2-3 mm das extremidades externas dos traços; Na parte externa de cada seta que indica a direção de visão, a mesma letra maiúscula é aplicada.

Para designar cortes e seções no sistema KOMPAS, o mesmo botão é utilizado A linha de corte localizada na página Designação (Fig. 109).

Fig. 109 Botão de linha de corte

Conectando meia vista com meia seção

Se a vista e a seção forem figuras simétricas (Fig. 110), então você pode conectar metade da vista e metade da seção, separando-as com uma linha pontilhada fina, que é o eixo de simetria. Parte da seção geralmente está localizada à direita do eixo de simetria, que separa parte da vista da parte da seção, ou abaixo do eixo de simetria. As linhas de contorno ocultas nas partes de conexão de uma vista e seção geralmente não são mostradas. Se a projeção de qualquer linha, por exemplo, a borda de uma figura facetada, coincide com a linha axial que separa a vista e a seção, então a vista e a seção são separadas por uma linha sólida ondulada desenhada à esquerda do eixo de simetria se a borda estiver superfície interior, ou mais para a direita se a borda for externa.

Arroz. 110 Conectando parte de uma vista e uma seção

Construção de seções

Estudaremos a construção de seções no sistema KOMPAS usando o exemplo de construção do desenho de um prisma, cuja tarefa é mostrada na Fig.

A sequência do desenho é a seguinte:

1. Com base nas dimensões fornecidas, construiremos um modelo sólido do prisma (Fig. 109 b). Vamos salvar o modelo na memória do computador em um arquivo chamado “Prisma”.

Fig.112 Painel Linhas

3. Para construir uma seção de perfil (Fig. 113) vamos traçar uma linha seção A-A na visualização principal usando o botão Linha de corte.

Fig. 113 Construção de uma seção de perfil

A direção de visualização e o texto do símbolo podem ser selecionados no painel de controle de comando na parte inferior da tela (Fig. 114). A construção da linha de corte é finalizada clicando no botão Criar objeto.

Fig. 114 Painel de controle do comando para construir seções e seções

4. No painel Vistas associativas (Fig. 115), selecione o botão Linha de corte e use a captura que aparece na tela para indicar a linha de corte. Se tudo for feito corretamente (a linha de corte deve ser desenhada na forma ativa), a linha de corte ficará vermelha. Após especificar a linha de corte A-A, uma imagem fantasma na forma de um retângulo geral aparecerá na tela.

Fig. 115 Vistas Associativas do Painel

Usando o botão Seção/seção na barra de propriedades, você seleciona o tipo de imagem – Seção (Fig. 116) e a escala da seção exibida.

Fig. 116 Painel de controle do comando para construir seções e seções

A seção do perfil será construída automaticamente em conexão de projeção e com designação padrão. Se necessário, a comunicação da projeção pode ser desligada com um interruptor Conexão de projeção (Fig. 116). Para configurar os parâmetros de hachura que serão utilizados na seção (seção) criada, utilize os controles da aba Hachura.

Fig. 117 Construção de uma horizontal seção B-B e seções B-B

Se o plano de corte selecionado durante a construção de uma seção coincidir com o plano de simetria da peça, então, de acordo com a norma, tal seção não será designada. Mas se você simplesmente apagar a designação de uma seção, devido ao fato de a visualização e a seção na memória do computador estarem interligadas, toda a seção será apagada. Portanto, para eliminar uma designação, é necessário primeiro destruir a ligação entre a vista e o corte. Para fazer isso, clique com o botão esquerdo do mouse para selecionar a seção e, a seguir, clique com o botão direito do mouse para abrir o menu de contexto, a partir do qual selecione o item Destruir Visualização (Fig. 97). O símbolo de corte agora pode ser removido.

5. Para construir uma seção horizontal, desenhe uma linha de corte B-B através do plano inferior do furo na vista frontal. Você deve primeiro tornar a vista frontal atual clicando duas vezes com o botão esquerdo do mouse. Em seguida, é construída uma seção horizontal (Fig. 117).

6. Ao construir um corte frontal, combinamos parte da vista e parte do corte, pois estas são figuras simétricas. A borda externa do prisma é projetada na linha que divide a vista e a seção, então vamos distinguir vista e corte com uma linha sólida e fina ondulada desenhada à direita do eixo de simetria, porque costela externa. Para desenhar uma linha ondulada, use o botão Curva de Bézier localizada no painel Geometria, desenhada com o estilo For break line (Fig. 118). Especifique consistentemente os pontos pelos quais a curva de Bézier deve passar. Você pode terminar de executar o comando clicando no botão Criar objeto.

Fig. 118 Selecionando um estilo de linha para uma quebra

Construção de seções

Uma seção é uma imagem de um objeto obtida dissecando mentalmente o objeto com um plano. A seção mostra apenas o que está localizado no plano de corte.

A posição do plano de corte, com o qual o corte é formado, é indicada no desenho pela linha de corte, assim como nos cortes.

As seções, dependendo de sua localização nos desenhos, são divididas em estendidas e sobrepostas. As seções retiradas geralmente estão localizadas no campo livre do desenho e são contornadas por uma linha principal. As seções sobrepostas são colocadas diretamente na imagem do objeto e contornadas com linhas finas (Fig. 119).

Fig. 119 Construção de seções

Consideremos a sequência de construção do desenho de um prisma com deslocamento inclinado seção B-B(Fig. 117).

1. Faça uma vista frontal clicando duas vezes com o botão esquerdo do mouse na vista e desenhe uma linha de seção usando o botão Linha de corte . Selecione o texto da inscrição В-В.

2. Usando o botão Cut Line localizado no painel Associative Views (Fig. 115), a armadilha que aparece indicará a linha secante avião B-B. Usando o botão Seção/seção na barra de propriedades, selecione o tipo de imagem – Seção (Fig. 116), a escala da seção exibida é selecionada na janela Escala.

O trecho construído está localizado em um link de projeção, o que limita seu movimento no desenho, mas o link de projeção pode ser desabilitado através do botão Comunicação de projeção.

No desenho finalizado você deve desenhar linhas axiais e, se necessário, adicionar dimensões.

Toda a história da geometria e de alguns outros ramos da matemática está intimamente ligada ao desenvolvimento da teoria das construções geométricas. Os axiomas mais importantes da geometria, formados por Euclides por volta de 300 a.C., mostram claramente o papel que as construções geométricas desempenharam na formação da geometria.

Existem tópicos especiais em geometria escolar que você espera ansiosamente, antecipando um encontro com incríveis belo material. Esses tópicos incluem “Poliedros e a construção de suas seções”. Mundo maravilhoso corpos geométricos com propriedades únicas, mas também interessantes hipóteses científicas. E então a aula de geometria se torna uma espécie de estudo de aspectos inesperados de uma matéria escolar familiar.

Nas aulas de geometria deste ano abordamos o tópico “Construindo seções de poliedros”. Como parte do programa, estudamos um método para construir seções, mas fiquei interessado em saber quais outros métodos existem.

O propósito do meu trabalho: Aprenda todos os métodos para construir seções de poliedros.

Nenhum corpo geométrico tem tanta perfeição e beleza quanto os poliedros. “Há um número chocantemente pequeno de poliedros”, escreveu certa vez L. Carroll, “mas esse distanciamento em número muito modesto conseguiu penetrar nas profundezas de várias ciências”.

Atualmente, a teoria das construções geométricas representa uma vasta e profundamente desenvolvida área da matemática associada à solução de diversas questões fundamentais que se estendem a outros ramos da matemática.

1. História da geometria descritiva

Mesmo nos tempos antigos, as pessoas desenhavam e desenhavam imagens de coisas, árvores, animais e pessoas em rochas, pedras, paredes e utensílios domésticos. Ele fez isso para satisfazer suas necessidades, inclusive estéticas. Além disso, o principal requisito para tais imagens era que a imagem evocasse uma ideia visual correta da forma do objeto representado.

Com o crescimento da prática e aplicações técnicas imagens (na construção de edifícios e outras estruturas civis e militares, etc.) passaram a estar sujeitas a tais requisitos que a imagem pudesse ser utilizada para julgar as propriedades geométricas, dimensões e posição relativa elementos individuais um determinado assunto. Tais requisitos podem ser avaliados por muitos monumentos antigos que sobreviveram até hoje. No entanto, regras e métodos estritos de base geométrica para representar figuras espaciais (no que diz respeito à perspectiva) começaram a ser desenvolvidos sistematicamente por artistas, arquitetos e escultores apenas na Renascença: Leonardo da Vinci, Durer, Rafael, Michelangelo, Ticiano e outros.

A geometria descritiva como ciência foi criada em final do XVIII século pelo grande geômetra e engenheiro francês Gaspard Monge (1746 – 1818). Em 1637, o geômetra e filósofo francês René Descartes (1596 - 1650) criou o método de coordenadas e lançou as bases da geometria analítica, e seu compatriota, engenheiro e matemático Girard Desages (1593 - 1662), usou este método de coordenadas para construir projeções em perspectiva e fundamentou a teoria das projeções axonométricas.

No século XVII, desenhos técnicos, feitos na forma de plantas e perfis em escala, desenvolveram-se com sucesso na Rússia. Aqui, em primeiro lugar, devemos mencionar os desenhos do notável mecânico e inventor russo I.P. Kulibin (1735 – 1818). Seu projeto para uma ponte em arco de madeira fez o primeiro uso de projeções ortogonais (1773). (A projeção ortogonal de um plano em uma linha situada nele ou do espaço em um plano é caso especial projeção paralela, em que a direção da projeção é perpendicular à linha reta ou plano no qual estão se projetando.)

Uma contribuição importante para o desenvolvimento de projeções ortogonais foi feita pelo engenheiro francês A. Frezier (1682-1773), que foi o primeiro a considerar a projeção de um objeto em dois planos - horizontal e frontal.

O maior mérito de G. Monge foi a generalização de todos os trabalhos científicos de seus antecessores, toda a teoria dos métodos de representação de figuras espaciais e a criação de uma ciência matemática unificada de projeção ortogonal - a geometria descritiva.

O nascimento deste nova ciência quase coincidiu com a fundação em São Petersburgo do primeiro transporte superior da Rússia instituição educacional– Instituto do Corpo de Engenheiros Ferroviários (2 de dezembro de 1809)

Os graduados deste instituto, seus professores e cientistas deram um contributo significativo para o desenvolvimento dos métodos geométricos de representação, para a teoria e prática da geometria descritiva.

1. Definições de poliedros

Na estereometria, estudam-se figuras no espaço, chamadas corpos . Um corpo visual (geométrico) deve ser imaginado como uma parte do espaço ocupado corpo físico e limitado pela superfície.

Poliedro - este é um corpo cuja superfície consiste em vários polígonos planos. O poliedro é chamado convexo , se estiver localizado em um lado do plano de cada polígono plano em sua superfície. A parte comum de tal plano e a superfície de um poliedro convexo é chamada borda . As faces de um poliedro convexo são polígonos convexos planos. Os lados das faces são chamadosarestas do poliedro, e os vértices são vértices do poliedro.

Seção um poliedro é chamado de plano figura geométrica, que é o conjunto de todos os pontos do espaço que pertencem simultaneamente a um determinado poliedro e plano; o plano é chamado de plano de corte.

A superfície de um poliedro consiste em arestas, segmentos e faces de polígonos planos. Como uma linha reta e um plano se cruzam em um ponto, e dois planos se cruzam ao longo de uma linha reta, então a seção de um poliedro por um plano épolígono plano; os vértices deste polígono são os pontos de intersecção do plano de corte com as arestas do poliedro, e os lados são os segmentos ao longo dos quais o plano de corte cruza suas faces. Isso significa que para construir a seção desejada de um determinado poliedro com o plano α, basta construir os pontos de sua intersecção com as arestas do poliedro. Em seguida, conecte esses pontos sequencialmente com segmentos, destacando com linhas sólidas os lados visíveis e invisíveis tracejados da seção poligonal resultante.

III. Métodos para construir seções de poliedros

O método das seções de poliedros em estereometria é utilizado em problemas de construção. Baseia-se na capacidade de construir uma seção de um poliedro e determinar o tipo de seção.

Este material é caracterizado pelas seguintes características:

• O método das seções é usado apenas para poliedros, uma vez que vários tipos complexos (oblíquos) de seções de corpos de rotação não estão incluídos no currículo do ensino médio.
• Os problemas utilizam principalmente os poliedros mais simples.
• Os problemas são apresentados principalmente sem dados numéricos, a fim de criar a possibilidade de seu uso múltiplo.

Para resolver o problema de construção de uma seção de um poliedro, o aluno deve saber:

• O que significa construir uma seção de um poliedro com um plano;
• Como um poliedro e um plano podem ser posicionados um em relação ao outro?
• Como o plano é definido;
• Quando o problema de construir uma seção de um poliedro por um plano é considerado resolvido.

Porque o plano está definido:

• Três pontos;
• Reto e ponto;
• Duas linhas paralelas;
• Duas linhas que se cruzam

A construção do plano de corte depende da especificação deste plano. Portanto, todos os métodos de construção de seções de poliedros podem ser divididos em métodos.

3.1 Construção de seções de poliedros com base no sistema de axiomas estereométricos

Problema 1 . Construa uma seção da pirâmide RABC com o plano α = (MKH), onde M, K e H são os pontos internos das arestas RS, PB e AB, respectivamente (Fig. 1, a).

Solução.

1º passo . Os pontos M e K estão em cada um dos dois planos α e RVS. Portanto, de acordo com o axioma da intersecção de dois planos, o plano α intercepta o plano RVS ao longo da linha MK. Consequentemente, o segmento MK é um dos lados da seção desejada (Fig. 1, b).

2º passo . Da mesma forma, o segmento KN é o outro lado da seção desejada (Fig. 1, c).

3º passo . Os pontos M e H não estão simultaneamente em nenhuma das faces da pirâmide RABC, portanto o segmento MH não é um lado da seção desta pirâmide. As linhas retas KN e RA estão no plano da face AVR e se cruzam. Vamos construir o ponto T= KH ∩AP (Fig. 1, d).

Como a linha reta KN está no plano α, então o ponto T está no plano α. Agora vemos que os planos α e APC têm pontos comuns M e T. Consequentemente, de acordo com o axioma da intersecção de dois planos, o plano α e o plano APC se cruzam ao longo da linha reta MT, que, por sua vez, cruza a aresta AC no ponto R ( Figura 1, d).

4º passo . Agora, da mesma forma que no passo 1, estabelecemos que o plano α intercepta as faces ACP e ABC ao longo dos segmentos MR e HR, respectivamente. Consequentemente, a seção necessária é o quadrilátero MKHR (Fig. 1, f).

Arroz. 2

Tarefa 2. Construa uma seção da pirâmide MABCD com o plano α = (CN), onde K, H e P são os pontos internos das arestas MA, MV e MD, respectivamente (Fig. 2, a).

Solução. As duas primeiras etapas são semelhantes às etapas 1 e 2 do problema anterior. Como resultado, obtemos os lados KR e KN (Fig. 2, b) da seção desejada. Vamos construir os vértices e lados restantes do polígono - seções.

3º passo . Continuemos o segmento KR até cruzar com a reta AD no ponto F (Fig. 2, c). Como a reta KR está no plano de corte α, o ponto F= KR ∩ AD = KR ∩ (ABC) é comum aos planos α e ABC.

4º passo . Continuemos o segmento KH até cruzar com a reta AB no ponto L (Fig. 2, d). Como a linha КН está no plano de corte α, o ponto L = КН ∩ АВ = КН ∩ (АВС) é comum para os planos α e АВС.

Por isso , os pontos F e L são comuns aos planos α e ABC. Isso significa que o plano α intercepta o plano ABC da base da pirâmide ao longo da linha reta FL.

5º passo . Vamos traçar uma linha reta FL. Esta reta cruza as arestas BC e DC, respectivamente, nos pontos R e T (Fig. 2, e), que servem como vértices da seção desejada. Isso significa que o plano α cruza a face da base ABCD ao longo do segmento RT - o lado da seção desejada.

6º passo . Agora desenhamos os segmentos RH e PT (Fig. 2, f), ao longo dos quais o plano α cruza as faces do BMC e MCD desta pirâmide. Obtemos o pentágono PKHRT - a seção desejada da pirâmide MABCD (Fig. 2, f).

Vamos considerar um problema mais complexo.

Problema 3 . Construa uma seção da pirâmide pentagonal PABCDE com o plano α = (KQR), onde K, Q são os pontos internos das arestas RA e RS, respectivamente, e o ponto R fica dentro da face DPE (Fig. 3, a).

Solução . As retas (QK e AC estão no mesmo plano ACP (de acordo com o axioma da reta e do plano) e se cruzam em algum ponto T1, (Fig. 3 b), enquanto T1 є α, já que QK є α.

A reta PR cruza DE em algum ponto F (Fig. 3, c), que é o ponto de intersecção do plano ARR e do lado DE da base da pirâmide. Então as retas KR e AF estão no mesmo plano ARR e se cruzam em algum ponto T2 (Fig. 3, d), enquanto T2 є α, como um ponto da reta KR є α (de acordo com o axioma da reta linha e o plano).

Pegou: a reta T1 T2 encontra-se no plano secante α e no plano da base da pirâmide (de acordo com o axioma da reta e do plano), enquanto a reta intercepta os lados DE e AE da base ABCDE da pirâmide, respectivamente, nos pontos M e N (Fig. 3, e), que são os pontos de intersecção do plano α com as arestas DE e AE da pirâmide e servem como vértices da seção desejada.

Avançar , a reta MR encontra-se no plano da face DPE e no plano de corte α (de acordo com o axioma da reta e do plano), enquanto cruza a aresta PD em algum ponto H - outro vértice da seção desejada (Fig. 3 , f).

Avançar, Vamos construir um ponto T3 - T1T2 ∩ AB (Fig. 3, g), que, como ponto da reta T1T2 є α, está no plano a (segundo o axioma da reta e do plano). Já o plano da face RAB pertence a dois pontos T3 e K ao plano de corte α, o que significa que a reta T3K é a reta de intersecção desses planos. A reta T3K cruza a aresta PB no ponto L (Fig. 3, h), que serve como o próximo vértice da seção desejada.

Arroz. 3

Assim, a “cadeia” da sequência de construção do trecho desejado é a seguinte:

1. T1 = QK ∩AC;

2. F = PR ∩ DE;

3. T2 = KR ∩ AF;

4. М = Т1Т2 ∩ DE;

5. N = T1T2 ∩ AE;

6. H = MR ∩ PD;

7. T3 = T1T2 ∩AB;

8. L = T3K ∩ PB.

Hexágono MNKLQH é a seção necessária.

Seção da pirâmide na Fig. 1 e a seção do cubo na Fig. 2 são construídos com base apenas nos axiomas da estereometria.

Ao mesmo tempo, uma seção de um poliedro com faces paralelas (prisma, paralelepípedo, cubo) pode ser construída usando as propriedades dos planos paralelos.

3.2 O método trace na construção de seções planas de poliedros

A linha reta ao longo da qual o plano de corte α cruza o plano da base do poliedro é chamada de traço do plano α no plano desta base.

Da definição de traço obtemos: em cada um de seus pontos se cruzam retas, uma das quais está no plano secante e a outra no plano da base. É esta propriedade do traço que é usada na construção de seções planas de poliedros usando o método traço. Além disso, no plano secante é conveniente usar linhas retas que cruzam as arestas do poliedro.

Primeiramente, definimos o plano secante pelo seu traço no plano da base do prisma (pirâmide) e por um ponto pertencente à superfície do prisma (pirâmide).

Problema 1 . Construa uma seção do prisma АВСВЭА1В1С1D1Э1 pelo plano α, que é especificado pelo traço l no plano ABC da base do prisma e pelo ponto M pertencente à aresta DD1.

Solução. Análise . Suponhamos que o pentágono MNPQR seja a seção desejada (Fig. 4). Para construir este pentágono plano, basta construir seus vértices N, P, Q, R (o ponto M é dado) - os pontos de intersecção do plano de corte α com as arestas CC1, BB1, AA1, EE1 do prisma dado, respectivamente.

E1 D1

Para construir o ponto N =α ∩ CC1, basta construir a reta de intersecção do plano de corte α com o plano da face СDD1C1. Para isso, por sua vez, basta construir outro ponto no plano desta face, pertencente ao plano de corte α. Como construir tal ponto?

Como a reta l está no plano da base do prisma, ela pode cruzar o plano da face СDD1C1 apenas em um ponto que pertence à reta CD = (CDD1) ∩ (АВС), ou seja, o ponto X = l ∩ СD = l ∩ (CDD1) pertence ao plano de corte α. Assim, para construir o ponto N = α ∩ CC1, basta construir o ponto X = l ∩ CD.

Da mesma forma, para construir os pontos P = α ∩ BB1, Q = α ∩ AA1 e R = α ∩ EE1, basta construir os pontos respectivamente: Y = l ∩ BC, Z = 1 ∩ AB e T =1 ∩ AE .

Construção. Nós construímos (Fig. 5):

1. X = l ∩ CD (Fig. 5, b);

2. N = MX ∩ CC1 (Fig. 5, c);

3. У = l ∩ ВС (Fig. 5, d);

4. P = NY ∩ BB1 (Fig. 5, e);

5. Z = 1 ∩ AB (Fig. 5, f);

6. Q= PZ ∩ AA1 (Fig. 5, g);

7. T= eu ∩ AE (Fig. 5, h);

8. R= QT ∩ EE1 (Fig. 5, i).

Pentágono MNPQR é a seção desejada (Fig. 5, j).

Prova. Como a reta l é o traço do plano de corte α, então os pontos X = l ∩ CD, Y = l ∩ BC, Z = 1 ∩ AB e T= l ∩ AE pertencem a este plano.

Portanto temos:

М Є α, X Є α => МХ є α, então МХ ∩ СС1 = N є α, o que significa N = α ∩ СС1;

N Є α, Y Є α => NY Є α, então NY ∩ BB1= P Є α, o que significa P = α ∩ BB1;

Р Є α, Z Є α => РZ Є α, então PZ ∩ AA1 = Q Є α, o que significa Q = α ∩ AA1;

Q Є α, T Є α => QТ Є α, então QТ ∩ EE1 =R Є α, o que significa R = α ∩ EE1.

Portanto, MNPQR é a seção obrigatória.

Estudar. O traço l do plano de corte α não intercepta a base do prisma, e o ponto M do plano de corte pertence à aresta lateral DD1 do prisma. Portanto, o plano de corte α não é paralelo às arestas laterais. Consequentemente, os pontos N, P, Q e R de intersecção deste plano com as arestas laterais do prisma (ou extensões destas arestas) existem sempre. E como, além disso, o ponto M não pertence ao traço l, então o plano α definido por eles é único. Isso significa que o problema (sempre) tem uma solução única.

3.3 Método de projeto interno para construção de seções planas de poliedros

Em alguns livros didáticos, o método de construção de seções de poliedros, que consideraremos agora, é chamado de método de projeção interna ou método de correspondências, ou método de seções diagonais.

Problema 1 . Construa uma seção da pirâmide PABCDE com o plano α = (MFR), se os pontos M, F e R forem pontos internos das arestas RA, RS e PE, respectivamente. (Fig. 6)

Solução . Vamos denotar o plano da base da pirâmide como β. Para construir a seção desejada, construiremos os pontos de intersecção do plano de corte α com as arestas da pirâmide.

Vamos construir o ponto de intersecção do plano de corte com a aresta PD desta pirâmide.

Os planos APD e CPE cruzam o plano β ao longo das retas AD e CE, respectivamente, que se cruzam em algum ponto K. A reta РК = (АРD) ∩(СPE) cruza a reta FR є α em algum ponto К1: К1 = РК ∩ FR, neste K1 є α. Então: M є α, K1 є α => linha reta MK є a. Portanto, o ponto Q = MK1 ∩ PD é o ponto de intersecção da aresta PD e do plano de corte: Q =α ∩ PD. O ponto Q é o vértice da seção desejada. Da mesma forma, construímos o ponto de intersecção do plano α e a aresta PB. Os planos BPE e АD cruzam o plano β ao longo das retas BE e AD, respectivamente, que se cruzam no ponto H. A reta РН = (ВРЭ) ∩ (АРD) cruza a reta МQ no ponto Н1 Então a reta РН1 cruza a aresta РВ no ponto N. = α ∩ РВ - o topo da seção.

Por isso , a sequência de etapas para a construção da seção desejada é a seguinte:

1. K = AD ∩ CE; 2. К1 = РК ∩ RF;

3. Q = MK1 ∩РD; 4. H = BE ∩ AD;

5. Н1 = РН ∩ МQ; 6. N = RН1 ∩ РВ.

Pentágono MNFQR é a seção obrigatória.

3.4 Método combinado na construção de seções planas de poliedros

A essência do método combinado para construir seções de poliedros é a seguinte. Em algumas etapas da construção de um trecho, utiliza-se o método de traçado ou o método de dimensionamento interno, e em outras etapas da construção do mesmo trecho, são utilizados os teoremas estudados sobre paralelismo, perpendicularidade de retas e planos.

Para ilustrar a aplicação deste método, considere o seguinte problema.

Tarefa 1.

Construa uma seção do paralelepípedo ABCDA1B1C1D1 pelo plano α especificado pelos pontos P, Q e R, se o ponto P estiver na diagonal A1C1, o ponto Q na aresta BB1 ​​e o ponto R na aresta DD1. (Fig. 7)

Solução

Vamos resolver este problema usando o método trace e teoremas sobre o paralelismo de retas e planos.

Primeiramente, vamos construir o traço do plano de corte α = (РQR) no plano ABC. Para isso, construímos os pontos Т1 = РQ ∩ Р1В (onde PP1 ║AA1,P1є AC) e T2 = RQ ∩ ВD. Construído o traço T1T2, notamos que o ponto P está no plano A1B1C1, que é paralelo ao plano ABC. Isso significa que o plano α intercepta o plano A1B1C1 ao longo de uma linha reta que passa pelo ponto P e é paralelo à linha reta T1T2. Vamos traçar esta linha e denotar por M e E os pontos de sua intersecção com as arestas A1B1 e A1D1, respectivamente. Obtemos: M = α ∩ A1B1, E = α∩ A1D1. Então os segmentos ER e QM são os lados da seção desejada.

Além disso, como o plano BCC1 é paralelo ao plano da face ADD1A1, então o plano α cruza a face BCC1B1 ao longo do segmento QF (F= α ∩ CC1), paralelo à linha reta ER. Assim, o pentágono ERFQM é a seção necessária. (O ponto F pode ser obtido executando RF║ MQ)

Vamos resolver este problema usando o método da projeção interna e teoremas sobre o paralelismo de retas e planos.(Fig. 8)

Arroz. 8

Seja H = AC ∩ BD. Desenhando uma linha reta НН1 paralela à aresta ВВ1 (Н1 є RQ), construímos o ponto F: F=РН1 ∩ CC1 O ponto F é o ponto de intersecção do plano α com a aresta CC1, pois РН1 є α. Então os segmentos RF e QF ao longo dos quais o plano α cruza as faces CC1D1D e ВСС1В1 deste paralelepípedo, respectivamente, são os lados de sua seção desejada.

Como o plano ABB1 é paralelo ao plano CDD1, a intersecção do plano α e da face ABB1A1 é o segmento QM (M Є A1B1), paralelo ao segmento FR; segmento QM - lado da seção. Além disso, o ponto E = MP ∩ A1D1 é o ponto de intersecção do plano α e a aresta A1D1, pois MP є α. Portanto, o ponto E é outro vértice da seção desejada. Assim, o pentágono ERFQM é a seção necessária. (O ponto E pode ser construído traçando a reta RE ║ FQ. Então M = PE ∩ A1B1).

4. Conclusão

Graças a este trabalho, resumi e sistematizei os conhecimentos adquiridos durante o curso de geometria deste ano, familiarizei-me com as regras de execução trabalho criativo, adquiriu novos conhecimentos e os aplicou na prática.

Gostaria de colocar em prática meus novos conhecimentos adquiridos com mais frequência.

Infelizmente, não considerei todos os métodos de construção de seções de poliedros. Existem muitos outros casos especiais:

• construir uma seção de um poliedro com um plano passando por um determinado ponto paralelo a um determinado plano;
• construir uma seção que passa por uma determinada linha paralela a outra determinada linha;
• construir uma seção que passa por um determinado ponto paralelo a duas retas que se cruzam;
• construir uma seção de um poliedro com um plano passando por uma determinada linha perpendicular a um determinado plano;
• construir uma seção de um poliedro com um plano passando por um determinado ponto perpendicular a uma determinada linha, etc.

No futuro, pretendo expandir a minha investigação e complementar o meu trabalho com uma análise dos casos especiais listados acima.

Acredito que meu trabalho é relevante porque pode ser utilizado por alunos do ensino fundamental e médio para auto estudo para o Exame Estadual Unificado de matemática, para o estudo aprofundado de matérias eletivas e para a autoformação de jovens professores. Os graduados do ensino médio não devem apenas dominar o material programas escolares, mas também ser capaz de aplicá-lo de forma criativa e encontrar uma solução para qualquer problema.

V. Literatura

1. Potoskuev E.V., Zvavich L.I. Geometria. 10ª série: Livro didático para instituições educacionais com estudo aprofundado e especializado de matemática. - M.: Abetarda, 2008.
2. Potoskuev E.V., Zvavich L.I. Geometria. 10º ano: Livro de problemas para instituições de ensino geral com estudo aprofundado e especializado de matemática. - M.: Abetarda, 2008.
3. Potoskuev E.V. Imagem de figuras espaciais em um plano. Construção de seções de poliedros. Tutorial para alunos da Faculdade de Física e Matemática de uma Universidade Pedagógica. - Togliatti: TSU, 2004.
4. Revista científica e prática para alunos do ensino médio “Matemática para Alunos”, 2009, nº 2/Nº 3, 1-64.
5. Geometria em tabelas - Livro didático para alunos do ensino médio - Nelin E.P.
6. Geometria, 7ª a 11ª séries, Materiais de referência, Bezrukova G.K., Litvinenko V.N., 2008.
7. Matemática, Guia de referência, Para estudantes do ensino médio e ingressantes nas universidades, Ryvkin A.A., Ryvkin A.Z., 2003.
8. Álgebra e geometria em tabelas e diagramas, Roganin A.N., Dergachev V.A., 2006.

Os problemas que envolvem a construção de seções de um cubo utilizando um plano são, via de regra, mais simples do que, por exemplo, problemas que envolvem seções de uma pirâmide.

Podemos traçar uma linha reta passando por dois pontos se eles estiverem no mesmo plano. Ao construir seções de um cubo, outra opção é possível para construir um traço de um plano de corte. Como o terceiro plano cruza dois planos paralelos ao longo de linhas paralelas, então se uma linha reta já foi construída em uma das faces, e na outra há um ponto por onde passa a seção, então podemos traçar uma linha paralela a esta aponte através deste ponto.

Vamos olhar para exemplos específicos, como construir seções de um cubo usando um plano.

1) Construa uma seção do cubo com um plano passando pelos pontos A, C e M.

Problemas deste tipo são os mais simples de todos os problemas para a construção de seções de um cubo. Como os pontos A e C estão no mesmo plano (ABC), podemos traçar uma linha reta através deles. Seu traço é o segmento AC. É invisível, então representamos AC com um traço. Da mesma forma, conectamos os pontos M e C, que estão no mesmo plano (CDD1), e os pontos A e M, que estão no mesmo plano (ADD1). O triângulo ACM é a seção necessária.

2) Construa uma seção do cubo com um plano passando pelos pontos M, N, P.

Aqui apenas os pontos M e N estão no mesmo plano (ADD1), então traçamos uma linha reta através deles e obtemos um traço MN (invisível). Como as faces opostas do cubo estão em planos paralelos, então o plano de corte intercepta planos paralelos (ADD1) e (BCC1) ao longo de linhas paralelas. Já construímos uma das linhas paralelas - esta é MN.

Através do ponto P traçamos uma linha paralela a MN. Ele cruza a aresta BB1 ​​no ponto S. PS é o traço do plano de corte na face (BCC1).

Traçamos uma linha reta através dos pontos M e S situados no mesmo plano (ABB1). Recebemos um traço de MS (visível).

Os planos (ABB1) e (CDD1) são paralelos. Já existe uma reta MS no plano (ABB1), então através do ponto N do plano (CDD1) traçamos uma reta paralela a MS. Esta linha intercepta a aresta D1C1 no ponto L. Seu traço é NL (invisível). Os pontos P e L estão no mesmo plano (A1B1C1), então traçamos uma linha reta através deles.

Pentágono MNLPS é a seção necessária.

3) Construa uma seção do cubo com um plano passando pelos pontos M, N, P.

Os pontos M e N estão no mesmo plano (ВСС1), portanto uma linha reta pode ser traçada através deles. Obtemos o traço MN (visível). O plano (BCC1) é paralelo ao plano (ADD1), portanto, através do ponto P situado em (ADD1), traçamos uma linha paralela a MN. Ele cruza a aresta AD no ponto E. Obtivemos um traço PE (invisível).

Não há mais pontos no mesmo plano, nem linha reta e pontos em planos paralelos. Portanto, precisamos continuar uma das linhas existentes para conseguir um ponto adicional.

Se continuarmos a reta MN, então, por estar no plano (BCC1), precisamos procurar o ponto de intersecção de MN com uma das retas deste plano. Já existem pontos de intersecção com CC1 e B1C1 - são M e N. O que resta são as retas BC e BB1. Vamos continuar BC e MN até que se cruzem no ponto K. O ponto K está na linha BC, o que significa que pertence ao plano (ABC), então podemos traçar uma linha reta através dele e do ponto E, que está neste plano. Ele cruza a aresta CD no ponto H. EH é seu traço (invisível). Como H e N estão no mesmo plano (CDD1), uma linha reta pode ser traçada através deles. Obtemos um traço HN (invisível).

Os planos (ABC) e (A1B1C1) são paralelos. Em um deles existe uma reta EH, no outro existe um ponto M. Podemos traçar uma reta paralela a EH passando por M. Obtemos o traço MF (visível). Desenhe uma linha reta passando pelos pontos M e F.

O hexágono MNHEPF é a seção necessária.

Se continuássemos a reta MN até que ela cruzasse com outro plano reto (BCC1), BB1, obteríamos o ponto G pertencente ao plano (ABB1). Isso significa que através de G e P podemos traçar uma reta cujo traço é PF. A seguir, traçamos linhas retas através de pontos situados em planos paralelos e chegamos ao mesmo resultado.

Trabalhar com PE direto dá a mesma seção MNHEPF.

4) Construa uma seção do cubo com um plano passando pelo ponto M, N, P.

Aqui podemos traçar uma linha reta através dos pontos M e N situados no mesmo plano (A1B1C1). A pegada dela é MN (visível). Não existem mais pontos no mesmo plano ou em planos paralelos.

Vamos continuar a linha reta MN. Encontra-se no plano (A1B1C1), portanto só pode cruzar com uma das retas deste plano. Já existem pontos de intersecção com A1D1 e C1D1 - N e M. Mais duas retas deste plano - A1B1 e B1C1. O ponto de intersecção de A1B1 e MN é S. Por estar na linha A1B1, pertence ao plano (ABB1), o que significa que uma linha reta pode ser traçada através dele e do ponto P, que está no mesmo plano. A linha PS cruza a aresta AA1 no ponto E. PE é o seu traço (visível). Através dos pontos N e E, situados no mesmo plano (ADD1), pode-se traçar uma linha reta, cujo traço é NE (invisível). No plano (ADD1) existe uma reta NE, no plano paralelo a ela (BCC1) existe um ponto P. Através do ponto P podemos traçar uma reta PL paralela a NE. Ela cruza a aresta CC1 no ponto L. PL é o traço desta linha (visível). Os pontos M e L estão no mesmo plano (CDD1), o que significa que uma linha reta pode ser traçada através deles. A trilha dela é ML (invisível). Pentágono MLPEN é a seção necessária.

Foi possível continuar a reta NM em ambas as direções e buscar seus pontos de intersecção não só com a reta A1B1, mas também com a reta B1C1, que também está no plano (A1B1C1). Neste caso, através do ponto P traçamos duas retas ao mesmo tempo: uma no plano (ABB1) passando pelos pontos P e S, e a segunda no plano (BCC1), passando pelos pontos P e R. Depois disso, resta conectar o pontos situados no mesmo plano: M c L, E - com N.