Nierówności z logarytmami na przykładach Jednolitego Egzaminu Państwowego. Nierówności logarytmiczne – Hipermarket Wiedzy
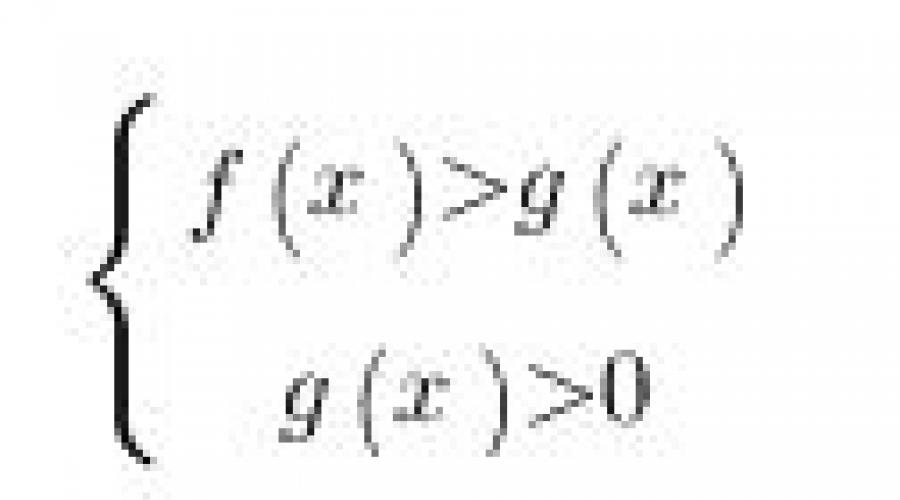
Przeczytaj także
Nierówności logarytmiczne
Na poprzednich lekcjach zapoznaliśmy się z równaniami logarytmicznymi i teraz wiemy, czym są i jak je rozwiązać. Dzisiejsza lekcja poświęcona będzie badaniu nierówności logarytmicznych. Czym są te nierówności i jaka jest różnica między rozwiązaniem równania logarytmicznego a nierównością?
Nierówności logarytmiczne to nierówności, w których zmienna pojawia się pod znakiem logarytmu lub u jego podstawy.
Można też powiedzieć, że nierówność logarytmiczna to nierówność, w której jej nieznana wartość, jak w równaniu logarytmicznym, pojawi się pod znakiem logarytmu.
Pierwotniaki nierówności logarytmiczne wygląda jak to:
gdzie f(x) i g(x) to pewne wyrażenia zależne od x.
Spójrzmy na to na przykładzie: f(x)=1+2x+x2, g(x)=3x−1.
Rozwiązywanie nierówności logarytmicznych
Przed rozwiązaniem nierówności logarytmicznych warto zauważyć, że po rozwiązaniu są one podobne nierówności wykładnicze, a mianowicie:
Po pierwsze, przechodząc od logarytmów do wyrażeń pod znakiem logarytmu, musimy także porównać podstawę logarytmu z jednością;
Po drugie, rozwiązując nierówność logarytmiczną za pomocą zmiany zmiennych, musimy rozwiązywać nierówności ze względu na zmianę, aż otrzymamy najprostszą nierówność.
Ale ty i ja rozważaliśmy podobne aspekty rozwiązywania nierówności logarytmicznych. Zwróćmy teraz uwagę na dość istotną różnicę. Ty i ja wiemy, że funkcja logarytmiczna ma ograniczony obszar definicje, dlatego przechodząc od logarytmów do wyrażeń pod znakiem logarytmu, należy wziąć pod uwagę obszar dopuszczalne wartości(ODZ).
Oznacza to, że należy wziąć pod uwagę, że rozwiązując równanie logarytmiczne, ty i ja możemy najpierw znaleźć pierwiastki równania, a następnie sprawdzić to rozwiązanie. Ale rozwiązanie nierówności logarytmicznej nie będzie działać w ten sposób, ponieważ przy przejściu od logarytmów do wyrażeń pod znakiem logarytmu konieczne będzie zapisanie ODZ nierówności.
Ponadto warto pamiętać, że teoria nierówności składa się z liczb rzeczywistych, które są dodatnie i liczby ujemne, a także cyfrę 0.
Na przykład, gdy liczba „a” jest dodatnia, należy zastosować następującą notację: a >0. W tym przypadku zarówno suma, jak i iloczyn tych liczb również będą dodatnie.
Główną zasadą rozwiązywania nierówności jest zastąpienie jej prostszą nierównością, ale najważniejsze jest to, aby była ona równoważna podanej. Ponadto uzyskaliśmy również nierówność i ponownie zastąpiliśmy ją inną, która ma prostszą formę itp.
Rozwiązując nierówności ze zmienną, musisz znaleźć wszystkie jej rozwiązania. Jeżeli dwie nierówności mają tę samą zmienną x, to nierówności takie są równoważne, pod warunkiem, że ich rozwiązania są zbieżne.
Wykonując zadania dotyczące rozwiązywania nierówności logarytmicznych należy pamiętać, że gdy a > 1 to funkcja logarytmiczna rośnie, a gdy 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Metody rozwiązywania nierówności logarytmicznych
Przyjrzyjmy się teraz niektórym metodom stosowanym przy rozwiązywaniu nierówności logarytmicznych. Dla lepszego zrozumienia i przyswojenia postaramy się je zrozumieć na konkretnych przykładach.
Wszyscy wiemy, że najprostsza nierówność logarytmiczna ma postać:
W tej nierówności V – jest jednym z następujących znaków nierówności:<,>, ≤ lub ≥.
Gdy podstawa danego logarytmu jest większa od jedności (a>1), dokonując przejścia od logarytmów do wyrażeń pod znakiem logarytmu, to w tej wersji znak nierówności zostaje zachowany i nierówność będzie miała postać:
co jest równoważne temu systemowi:

W przypadku, gdy podstawa logarytmu jest większa od zera i mniejsza od jedności (0 Jest to równoważne temu systemowi: Przyjrzyjmy się kolejnym przykładom rozwiązywania najprostszych nierówności logarytmicznych pokazanych na poniższym obrazku: Ćwiczenia. Spróbujmy rozwiązać tę nierówność: Rozwiązywanie zakresu wartości dopuszczalnych. Spróbujmy teraz pomnożyć jego prawą stronę przez: Zobaczmy, co możemy wymyślić: Przejdźmy teraz do konwersji wyrażeń sublogarytmicznych. Ponieważ podstawa logarytmu wynosi 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; I z tego wynika, że uzyskany przez nas przedział w całości należy do ODZ i jest rozwiązaniem takiej nierówności. Oto odpowiedź jaką otrzymaliśmy: Spróbujmy teraz przeanalizować, czego potrzebujemy, aby skutecznie rozwiązać nierówności logarytmiczne? Najpierw skup całą swoją uwagę i staraj się nie popełnić błędów podczas wykonywania przekształceń podanych w tej nierówności. Należy również pamiętać, że przy rozwiązywaniu takich nierówności należy unikać rozszerzania i kurczenia ODZ nierówności, co może prowadzić do utraty lub nabycia obcych rozwiązań. Po drugie, rozwiązując nierówności logarytmiczne, trzeba nauczyć się myśleć logicznie i rozumieć różnicę między pojęciami takimi jak system nierówności i zbiór nierówności, aby móc łatwo wybierać rozwiązania nierówności, kierując się jej DL. Po trzecie, aby skutecznie rozwiązać takie nierówności, każdy z Was musi doskonale znać wszystkie właściwości funkcje elementarne i jasno rozumiem ich znaczenie. Takie funkcje obejmują nie tylko logarytmiczne, ale także wymierne, potęgowe, trygonometryczne itp., Jednym słowem wszystkie te, które studiowałeś przez cały czas szkolenie algebra. Jak widać, po przestudiowaniu tematu nierówności logarytmicznych, nie ma nic trudnego w rozwiązaniu tych nierówności, pod warunkiem, że będziesz ostrożny i wytrwały w osiąganiu swoich celów. Aby uniknąć problemów w rozwiązywaniu nierówności, należy jak najwięcej ćwiczyć przy rozwiązywaniu różnych zadań, a jednocześnie pamiętać o podstawowych metodach rozwiązywania takich nierówności i ich układach. Jeśli nie uda Ci się rozwiązać nierówności logarytmicznej, powinieneś dokładnie przeanalizować swoje błędy, aby nie wracać do nich ponownie w przyszłości. Aby lepiej zrozumieć temat i utrwalić omawiany materiał, rozwiąż następujące nierówności: Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania. Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią. Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami. Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać. Jakie dane osobowe zbieramy: Jak wykorzystujemy Twoje dane osobowe: Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim. Wyjątki: Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem. Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności. Nierówność nazywa się logarytmiczną, jeśli zawiera funkcję logarytmiczną. Metody rozwiązywania nierówności logarytmicznych nie różnią się od, z wyjątkiem dwóch rzeczy. Po pierwsze, przy przejściu od nierówności logarytmicznej do nierówności poniżej funkcje logarytmiczne powinien podążaj za znakiem powstałej nierówności. Przestrzega następującej zasady. Jeżeli podstawa funkcji logarytmicznej jest większa niż 1$, to przy przejściu od nierówności logarytmicznej do nierówności funkcji sublogarytmicznych znak nierówności zostaje zachowany, natomiast jeśli jest mniejszy niż 1$, to zmienia się na przeciwny . Po drugie, rozwiązaniem dowolnej nierówności jest przedział, dlatego na końcu rozwiązywania nierówności funkcji sublogarytmicznych konieczne jest utworzenie układu dwóch nierówności: pierwszą nierównością tego układu będzie nierówność funkcji sublogarytmicznych, a drugi będzie przedziałem dziedziny definicji funkcji logarytmicznych zawartych w nierówności logarytmicznej. Rozwiążmy nierówności: 1.
$\log_(2)((x+3)) \geq 3.$ $D(y): \x+3>0.$ $x \in (-3;+\infty)$ Podstawą logarytmu jest $2>1$, więc znak się nie zmienia. Korzystając z definicji logarytmu otrzymujemy: $x+3 \geq 2^(3),$ $x\in\) Bardzo ważne! W dowolnej nierówności przejście z postaci \(\log_a(f(x)) ˅ \log_a(g(x))\) do porównywania wyrażeń pod logarytmami można wykonać tylko wtedy, gdy: Przykład
. Rozwiąż nierówność: \(\log\)\(≤-1\) Rozwiązanie:
\(\dziennik\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) Napiszmy ODZ. ODZ: \(\frac(3x-2)(2x-3)\) \(>0\) \(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) Otwieramy nawiasy i przynosimy . \(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) Mnożymy nierówność przez \(-1\), nie zapominając o odwróceniu znaku porównania. \(\frac(3x-7)(2x-3)\) \(≤\) \(0\) \(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) Skonstruujmy oś liczbową i zaznaczmy na niej punkty \(\frac(7)(3)\) i \(\frac(3)(2)\). Należy pamiętać, że kropka jest usuwana z mianownika, mimo że nierówność nie jest ścisła. Faktem jest, że ten punkt nie będzie rozwiązaniem, ponieważ podstawiony do nierówności doprowadzi nas do dzielenia przez zero. Teraz wykreślamy ODZ na tej samej osi liczbowej i w odpowiedzi zapisujemy przedział mieszczący się w ODZ. Zapisujemy ostateczną odpowiedź. Przykład
. Rozwiąż nierówność: \(\log^2_3x-\log_3x-2>0\) Rozwiązanie:
\(\log^2_3x-\log_3x-2>0\) Napiszmy ODZ. ODZ: \(x>0\) Przejdźmy do rozwiązania. Rozwiązanie: \(\log^2_3x-\log_3x-2>0\) Mamy tu typową nierówność logarytmiczną kwadratową. Zróbmy to. \(t=\log_3x\) \(D=1+8=9\) Teraz musimy wrócić do pierwotnej zmiennej - x. Aby to zrobić, przejdźmy do , który ma to samo rozwiązanie i dokonajmy odwrotnego podstawienia. \(\left[ \begin(zebrane) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2\\\log_3x<-1 \end{gathered} \right.\) Przekształć \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). \(\left[ \begin(zebrane) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) Przejdźmy do porównywania argumentów. Podstawy logarytmów są większe niż \(1\), więc znak nierówności się nie zmienia. \(\left[ \begin(zebrane) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) Połączmy rozwiązanie nierówności i ODZ na jednym rysunku. Zapiszmy odpowiedź. Cele Lekcji: Dydaktyczny: Edukacyjny: rozwijać pamięć, uwagę, logiczne myślenie, umiejętność porównywania, umiejętność uogólniania i wyciągania wniosków Edukacyjny: kultywuj dokładność, odpowiedzialność za wykonywane zadanie i wzajemną pomoc. Metody nauczania:
werbalny ,
wizualny ,
praktyczny ,
wyszukiwanie częściowe ,
samorządność ,
kontrola. Formy organizacji aktywność poznawcza studenci:
czołowy ,
indywidualny ,
pracować w parach. Sprzęt:
zestaw zadań testowych, notatki referencyjne, czyste arkusze rozwiązań. Typ lekcji: nauka nowego materiału. Podczas zajęć 1. Moment organizacyjny. Ogłaszany jest temat i cele lekcji, plan lekcji: każdy uczeń otrzymuje kartę oceny, którą wypełnia w trakcie lekcji; dla każdej pary uczniów – drukowane materiały z zadaniami należy wykonać w parach; puste arkusze rozwiązań; arkusze pomocnicze: definicja logarytmu; wykres funkcji logarytmicznej, jej własności; właściwości logarytmów; algorytm rozwiązywania nierówności logarytmicznych. Wszelkie decyzje po dokonaniu samooceny przekazywane są nauczycielowi. Arkusz ocen ucznia 2. Aktualizowanie wiedzy. Instrukcje nauczyciela. Przypomnij sobie definicję logarytmu, wykres funkcji logarytmicznej i jej właściwości. Aby to zrobić, przeczytaj tekst na s. 88–90, 98–101 podręcznika „Algebra i początki analizy 10–11” pod redakcją Sh.A Alimova, Yu.M Kolyagina i innych. Uczniowie otrzymują arkusze, na których zapisano: definicję logarytmu; pokazuje wykres funkcji logarytmicznej i jej własności; właściwości logarytmów; algorytm rozwiązywania nierówności logarytmicznych, przykład rozwiązania nierówności logarytmicznej sprowadzającej się do kwadratowej. 3. Studiowanie nowego materiału. Rozwiązywanie nierówności logarytmicznych opiera się na monotoniczności funkcji logarytmicznej. Algorytm rozwiązywania nierówności logarytmicznych: A) Znajdź dziedzinę definicji nierówności (wyrażenie sublogarytmiczne jest większe od zera). Element edukacyjny nr 1. Cel: skonsolidować rozwiązanie najprostszych nierówności logarytmicznych Forma organizacji aktywności poznawczej studentów: praca indywidualna. Zadania dla niezależna praca za 10 minut. Dla każdej nierówności istnieje kilka możliwych odpowiedzi; należy wybrać właściwą i sprawdzić ją za pomocą klawisza. Element edukacyjny nr 2. Cel: skonsolidować rozwiązanie nierówności logarytmicznych za pomocą właściwości logarytmów. Instrukcje nauczyciela. Zapamiętaj podstawowe własności logarytmów. W tym celu zapoznaj się z tekstem podręcznika na s. 92, 103–104. Zadania do samodzielnej pracy przez 10 minut. KLUCZ: 2113, maksymalna liczba punktów – 8 punktów. Element edukacyjny nr 3. Cel: badanie rozwiązania nierówności logarytmicznych metodą redukcji do kwadratu. Instrukcja nauczyciela: metoda sprowadzenia nierówności do kwadratu polega na przekształceniu nierówności do takiej postaci, że pewna funkcja logarytmiczna jest oznaczona przez nową zmienną, uzyskując w ten sposób nierówność kwadratową względem tej zmiennej. Skorzystajmy z metody interwałowej. Przeszedłeś pierwszy poziom opanowania materiału. Teraz musisz wybrać własną metodę rozwiązania równania logarytmiczne wykorzystując całą swoją wiedzę i możliwości. Element edukacyjny nr 4. Cel: utrwalić rozwiązanie nierówności logarytmicznych samodzielnie wybierając racjonalną metodę rozwiązania. Zadania do samodzielnej pracy przez 10 minut Element edukacyjny nr 5. Instrukcje nauczyciela. Dobrze zrobiony! Opanowałeś rozwiązywanie równań drugiego stopnia złożoności. Celem Twojej dalszej pracy jest zastosowanie wiedzy i umiejętności w bardziej złożonych i niestandardowych sytuacjach. Zadania do samodzielnego rozwiązania: Instrukcje nauczyciela. Świetnie, jeśli wykonałeś całe zadanie. Dobrze zrobiony! Ocena z całej lekcji uzależniona jest od ilości punktów zdobytych za wszystkie elementy edukacyjne: Prześlij arkusze ocen nauczycielowi. 5. Praca domowa: jeśli zdobyłeś nie więcej niż 15 punktów, popracuj nad swoimi błędami (rozwiązania można pobrać od nauczyciela), jeśli zdobyłeś więcej niż 15 punktów, wykonaj kreatywne zadanie na temat „Nierówności logarytmiczne”.

Rozwiązywanie przykładów
![]()



3x > 24;
x > 8. ![]()
Co jest potrzebne do rozwiązania nierówności logarytmicznych?
Praca domowa

Gromadzenie i wykorzystywanie danych osobowych
Ujawnianie informacji osobom trzecim
Ochrona danych osobowych
Szanowanie Twojej prywatności na poziomie firmy
Ćwiczyć.
Odpowiedź:
\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

Odpowiedź:
\((0; \frac(1)(3))∪(9;∞)\)
\(t^2-t-2>0\) Układ lewa strona nierówności na.
\(t_1= \frac(1+3)(2)=2\)
\(t_2=\frac(1-3)(2)=-1\)
\((t+1)(t-2)>0\)

B) Przedstaw (jeśli to możliwe) lewą i prawą stronę nierówności jako logarytmy o tej samej podstawie.
C) Określ, czy funkcja logarytmiczna jest rosnąca czy malejąca: jeśli t>1, to rosnąca; jeśli 0
D) Przejdź do więcej prosta nierówność(wyrażenia sublogarytmiczne), biorąc pod uwagę, że znak nierówności pozostanie, jeśli funkcja wzrośnie, i zmieni się, jeśli funkcja maleje.
KLUCZ: 13321, maksymalna liczba punktów – 6 punktów.



