Dodatna svojstva logaritama. Logaritamski izrazi. primjeri

Šta je logaritam?

Pažnja!
Postoje dodatni
materijal u Posebnom dijelu 555.
Za one koji snažno "ne baš..."
I za one koji "jako...")

Šta je logaritam? Kako riješiti logaritme? Ova pitanja zbunjuju mnoge diplomce. Tradicionalno, tema logaritama se smatra složenom, nerazumljivom i zastrašujućom. Posebno - jednadžbe sa logaritmima.

Ovo apsolutno nije istina. Apsolutno! Ne vjerujete? Dobro. Sada, nekih 10-20 minuta vi:

1. Razumjeti šta je logaritam.

2. Naučite riješiti cijeli razred eksponencijalne jednačine. Čak i ako niste čuli za njih.

3. Naučite izračunati jednostavne logaritme.

Štoviše, za to ćete morati znati samo tablicu množenja i kako se broj podiže na stepen ...

Osećam da sumnjaš... Pa, zadrži vreme! Idi!

Prvo u mislima riješite sljedeću jednačinu:

Ako vam se sviđa ovaj sajt...

Inače, imam još par zanimljivih stranica za vas.)

Možete vježbati rješavanje primjera i saznati svoj nivo. Testiranje sa trenutnom verifikacijom. Učenje - sa interesovanjem!)

možete se upoznati sa funkcijama i izvedenicama.

Glavna svojstva prirodnog logaritma, graf, domen definicije, skup vrijednosti, osnovne formule, izvod, integral, proširenje u snaga serije i predstavlja funkciju ln x u terminima kompleksnih brojeva.

Definicija

prirodni logaritam je funkcija y = ln x, inverzno eksponentu, x \u003d e y , a koji je logaritam bazi broja e: ln x = log e x.

Prirodni logaritam se široko koristi u matematici jer njegov izvod ima najjednostavniji oblik: (ln x)′ = 1/ x.

Na osnovu definicije, baza prirodnog logaritma je broj e:
e ≅ 2.718281828459045...;
.

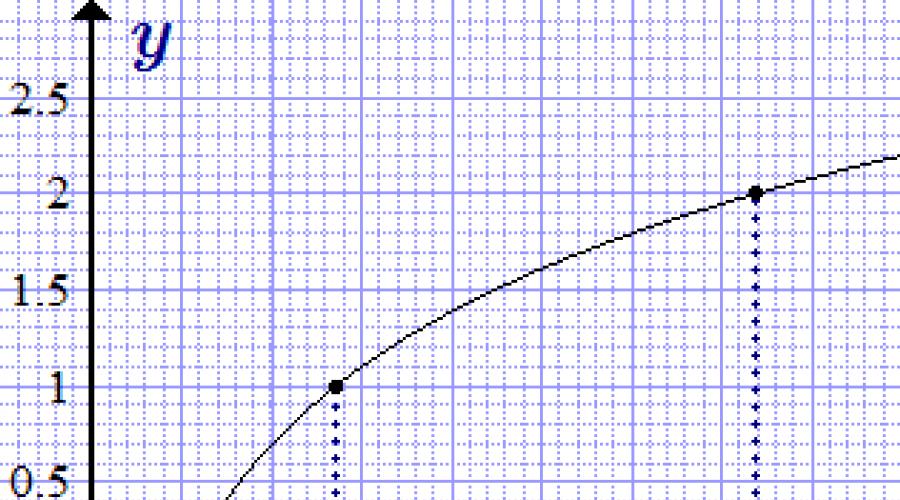
Grafikon funkcije y = ln x.

Grafikon prirodnog logaritma (funkcije y = ln x) se dobija iz dijagrama eksponenta odraz ogledala u odnosu na pravu liniju y = x .

Prirodni logaritam je definiran za pozitivne vrijednosti x. Ona se monotono povećava u svom domenu definicije.

Kao x → 0 granica prirodnog logaritma je minus beskonačnost ( - ∞ ).

Kako je x → + ∞, granica prirodnog logaritma je plus beskonačnost ( + ∞). Za veliki x, logaritam raste prilično sporo. Bilo koji funkcija snage x a sa pozitivnim eksponentom a raste brže od logaritma.

Svojstva prirodnog logaritma

Domen definicije, skup vrijednosti, ekstremi, povećanje, smanjenje

Prirodni logaritam je monotono rastuća funkcija, tako da nema ekstrema. Glavna svojstva prirodnog logaritma prikazana su u tabeli.

ln x vrijednosti

log 1 = 0

Osnovne formule za prirodne logaritme

Formule koje proizlaze iz definicije inverzne funkcije:

Glavno svojstvo logaritama i njegove posljedice

Formula zamjene baze

Bilo koji logaritam se može izraziti prirodnim logaritmima koristeći formulu promjene baze:

Dokazi ovih formula su predstavljeni u odjeljku "Logaritam".

Inverzna funkcija

Recipročna vrijednost prirodnog logaritma je eksponent.

Ako onda

Ako onda .

Derivat ln x

Derivat prirodnog logaritma:
.
Derivat prirodnog logaritma modula x:
.
Derivat n-tog reda:
.
Izvođenje formula > > >

Integral

Integral se izračunava integracijom po dijelovima:
.
dakle,

Izrazi u terminima kompleksnih brojeva

Razmotrimo funkciju kompleksne varijable z:
.
Izrazimo kompleksnu varijablu z preko modula r i argument φ :
.
Koristeći svojstva logaritma, imamo:
.
Or
.
Argument φ nije jednoznačno definiran. Ako stavimo
, gdje je n cijeli broj,
tada će to biti isti broj za različite n.

Dakle, prirodni logaritam, kao funkcija kompleksne varijable, nije jednoznačna funkcija.

Proširenje serije snaga

Za , proširenje se odvija:

Reference:
I.N. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente visokoškolskih ustanova, Lan, 2009.

Nastavljamo da proučavamo logaritme. U ovom članku ćemo govoriti o izračunavanje logaritama, ovaj proces se zove logaritam. Prvo ćemo se pozabaviti izračunavanjem logaritama po definiciji. Zatim razmotrite kako se vrijednosti logaritama pronalaze pomoću njihovih svojstava. Nakon toga ćemo se zadržati na izračunavanju logaritama kroz početno date vrijednosti drugih logaritama. Na kraju, naučimo kako koristiti tablice logaritama. Cijela teorija je opskrbljena primjerima sa detaljnim rješenjima.

Navigacija po stranici.

Računanje logaritama po definiciji

U najjednostavnijim slučajevima moguće je brzo i lako izvesti nalaženje logaritma po definiciji. Pogledajmo bliže kako se ovaj proces odvija.

Njegova suština je da se broj b predstavi u obliku a c , odakle je, prema definiciji logaritma, broj c vrijednost logaritma. To jest, po definiciji, pronalaženje logaritma odgovara sljedećem lancu jednakosti: log a b=log a a c =c .

Dakle, izračunavanje logaritma, po definiciji, svodi se na pronalaženje takvog broja c da je a c \u003d b, a sam broj c je željena vrijednost logaritma.

S obzirom na informacije iz prethodnih paragrafa, kada je broj pod znakom logaritma dat nekim stepenom osnove logaritma, tada možete odmah naznačiti čemu je logaritam jednak - jednak je eksponentu. Hajde da pokažemo primere.

Primjer.

Pronađite log 2 2 −3 , a također izračunajte prirodni logaritam od e 5.3 .

Odluka.

Definicija logaritma nam omogućava da odmah kažemo da je log 2 2 −3 = −3 . Zaista, broj pod znakom logaritma jednak je osnovici 2 na stepen −3.

Slično, nalazimo drugi logaritam: lne 5,3 =5,3.

odgovor:

log 2 2 −3 = −3 i lne 5,3 =5,3 .

Ako broj b pod znakom logaritma nije dat kao stepen osnove logaritma, onda morate pažljivo razmisliti da li je moguće doći do prikaza broja b u obliku a c. Često je ovaj prikaz sasvim očigledan, posebno kada je broj pod znakom logaritma jednak bazi na stepen od 1, ili 2, ili 3, ...

Primjer.

Izračunajte logaritme log 5 25 , i .

Odluka.

Lako je vidjeti da je 25=5 2 , ovo vam omogućava da izračunate prvi logaritam: log 5 25=log 5 5 2 =2 .

Nastavljamo s izračunavanjem drugog logaritma. Broj se može predstaviti kao stepen od 7: (pogledajte ako je potrebno). dakle, .

Prepišimo treći logaritam sljedeći obrazac. Sada to možete vidjeti , odakle to zaključujemo . Dakle, po definiciji logaritma .

Ukratko, rješenje bi se moglo napisati na sljedeći način:

odgovor:

log 5 25=2 , i .

Kada je pod znakom logaritma dovoljno velika vrijednost prirodni broj, onda ne škodi razložiti ga na primarni faktori. Često pomaže da se takav broj predstavi kao neki stepen baze logaritma, i stoga, izračunati ovaj logaritam po definiciji.

Primjer.

Pronađite vrijednost logaritma.

Odluka.

Neka svojstva logaritama vam omogućavaju da odmah odredite vrijednost logaritama. Ova svojstva uključuju svojstvo logaritma jedinice i svojstvo logaritma broja jednakog bazi: log 1 1=log a a 0 =0 i log a a=log a a 1 =1 . Odnosno, kada je broj 1 ili broj a pod znakom logaritma, jednak osnovici logaritma, tada su u ovim slučajevima logaritmi 0 i 1, respektivno.

Primjer.

Koji su logaritmi i lg10?

Odluka.

Budući da , to slijedi iz definicije logaritma .

U drugom primjeru, broj 10 pod znakom logaritma poklapa se sa njegovom bazom, pa je decimalni logaritam od deset jednak jedan, odnosno lg10=lg10 1 =1.

odgovor:

I lg10=1 .

Imajte na umu da izračunavanje logaritama po definiciji (o čemu smo raspravljali u prethodnom paragrafu) podrazumijeva korištenje jednakosti log a a p =p , što je jedno od svojstava logaritama.

U praksi, kada se broj pod znakom logaritma i baza logaritma lako mogu predstaviti kao stepen nekog broja, vrlo je zgodno koristiti formulu , što odgovara jednom od svojstava logaritma. Razmotrimo primjer pronalaženja logaritma koji ilustruje upotrebu ove formule.

Primjer.

Izračunajte logaritam od .

Odluka.

odgovor:

.

Svojstva logaritama koja nisu spomenuta također se koriste u proračunu, ali ćemo o tome govoriti u sljedećim paragrafima.

Pronalaženje logaritama u terminima drugih poznatih logaritama

Informacije u ovom odlomku nastavljaju na temu korištenja svojstava logaritama u njihovom proračunu. Ali ovdje je glavna razlika u tome što se svojstva logaritma koriste za izražavanje originalnog logaritma u terminima drugog logaritma čija je vrijednost poznata. Uzmimo primjer za pojašnjenje. Recimo da znamo da je log 2 3≈1,584963, onda možemo pronaći, na primjer, log 2 6 tako što ćemo napraviti malu transformaciju koristeći svojstva logaritma: log 2 6=log 2 (2 3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .

U gornjem primjeru bilo nam je dovoljno koristiti svojstvo logaritma proizvoda. Međutim, mnogo češće morate koristiti širi arsenal svojstava logaritama da biste izračunali originalni logaritam u smislu datih.

Primjer.

Izračunajte logaritam od 27 do baze 60 ako je poznato da je log 60 2=a i log 60 5=b .

Odluka.

Dakle, moramo pronaći log 60 27 . Lako je vidjeti da je 27=3 3 , a originalni logaritam, zbog svojstva logaritma stepena, može se prepisati kao 3·log 60 3 .

Sada da vidimo kako se log 60 3 može izraziti u terminima poznatih logaritma. Svojstvo logaritma broja jednakog bazi omogućava vam da zapišete log jednakosti 60 60=1 . S druge strane, log 60 60=log60(2 2 3 5)= log 60 2 2 +log 60 3+log 60 5= 2 log 60 2+log 60 3+log 60 5 . dakle, 2 log 60 2+log 60 3+log 60 5=1. dakle, log 60 3=1−2 log 60 2−log 60 5=1−2 a−b.

Konačno, izračunavamo originalni logaritam: log 60 27=3 log 60 3= 3 (1−2 a−b)=3−6 a−3 b.

odgovor:

log 60 27=3 (1−2 a−b)=3−6 a−3 b.

Odvojeno, vrijedi spomenuti značenje formule za prijelaz na novu bazu logaritma oblika . Omogućuje vam prelazak sa logaritma s bilo kojom bazom na logaritme s određenom bazom, čije su vrijednosti poznate ili ih je moguće pronaći. Obično se sa originalnog logaritma, prema formuli tranzicije, prelaze na logaritme u jednoj od baza 2, e ili 10, jer za ove baze postoje tablice logaritama koje omogućavaju izračunavanje njihovih vrijednosti ​​​​​tačnosti. U sljedećem odjeljku ćemo pokazati kako se to radi.

Tablice logaritama, njihova upotreba

Za približno izračunavanje vrijednosti logaritama, može se koristiti logaritamske tablice. Najčešće korištene su tablica logaritama baze 2, tablica prirodnog logaritma i tablica decimalnog logaritma. Kada radite u decimalnom brojevnom sistemu, zgodno je koristiti tablicu logaritama na osnovu deset. Uz njegovu pomoć naučit ćemo pronaći vrijednosti logaritama.

Prikazana tabela omogućava, sa tačnošću od jedne desethiljaditinke, pronalaženje vrednosti decimalnih logaritama brojeva od 1.000 do 9.999 (sa tri decimale). Princip nalaženja vrijednosti logaritma pomoću tablice decimalnih logaritama analizirat će se u konkretan primjer- mnogo jasnije. Nađimo lg1,256 .

U lijevom stupcu tablice decimalnih logaritama nalazimo prve dvije cifre broja 1.256, odnosno nalazimo 1.2 (ovaj broj je zaokružen plavom bojom radi jasnoće). Treća znamenka broja 1.256 (broj 5) nalazi se u prvom ili posljednjem redu lijevo od dvostrukog reda (ovaj broj je zaokružen crvenom bojom). Četvrta znamenka originalnog broja 1.256 (broj 6) nalazi se u prvom ili posljednjem redu desno od dvostrukog reda (ovaj broj je zaokružen zelenom bojom). Sada nalazimo brojeve u ćelijama tabele logaritama na preseku označenog reda i označenih kolona (ovi brojevi su istaknuti narandžasta). Zbir označenih brojeva daje željenu vrijednost decimalnog logaritma do četvrte decimale, tj. log1.236≈0.0969+0.0021=0.0990.

Da li je moguće, koristeći gornju tabelu, pronaći vrijednosti decimalnih logaritama brojeva koji imaju više od tri znamenke iza decimalnog zareza, a također prelaze granice od 1 do 9.999? Da, možeš. Pokažimo kako se to radi na primjeru.

Izračunajmo lg102.76332 . Prvo treba da napišete broj u standardni obrazac : 102.76332=1.0276332 10 2 . Nakon toga, mantisu treba zaokružiti na treću decimalu, imamo 1.0276332 10 2 ≈1.028 10 2, dok je originalni decimalni logaritam približno jednak logaritmu rezultirajućeg broja, odnosno uzimamo lg102.76332≈lg1.028·10 2 . Sada primijenite svojstva logaritma: lg1.028 10 2 =lg1.028+lg10 2 =lg1.028+2. Konačno, nalazimo vrijednost logaritma lg1.028 prema tabeli decimalnih logaritama lg1.028≈0.0086+0.0034=0.012. Kao rezultat, cijeli proces izračunavanja logaritma izgleda ovako: lg102.76332=lg1.0276332 10 2 ≈lg1.028 10 2 = lg1.028+lg10 2 =lg1.028+2≈0.012+2=2.012.

U zaključku, vrijedno je napomenuti da pomoću tablice decimalnih logaritama možete izračunati približnu vrijednost bilo kojeg logaritma. Da biste to učinili, dovoljno je koristiti formulu prijelaza za prelazak na decimalne logaritme, pronaći njihove vrijednosti u tablici i izvršiti preostale proračune.

Na primjer, izračunajmo log 2 3 . Prema formuli za prijelaz na novu bazu logaritma, imamo . Iz tablice decimalnih logaritama nalazimo lg3≈0,4771 i lg2≈0,3010. dakle, .

Bibliografija.

• Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. i dr. Algebra i počeci analize: udžbenik za 10-11 razred opšteobrazovnih ustanova.
• Gusev V.A., Mordkovich A.G. Matematika (priručnik za polaznike tehničkih škola).

\(a^(b)=c\) \(\Strelica ulevo\) \(\log_(a)(c)=b\)

Hajde da to lakše objasnimo. Na primjer, \(\log_(2)(8)\) je jednako snazi ​​\(2\) na koju se mora podići da bi se dobilo \(8\). Iz ovoga je jasno da je \(\log_(2)(8)=3\).

Argument i baza logaritma

Svaki logaritam ima sljedeću "anatomiju":

Argument logaritma se obično piše na njegovom nivou, a baza se upisuje u indeksu bliže predznaku logaritma. I ovaj unos se čita ovako: "logaritam od dvadeset pet do osnove od pet."

Kako izračunati logaritam?

Da biste izračunali logaritam, morate odgovoriti na pitanje: do kojeg stepena treba podići bazu da biste dobili argument?

na primjer, izračunajte logaritam: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Na koji stepen treba podići \(4\) da bi se dobilo \(16\)? Očigledno drugi. dakle:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Na koji stepen treba podići \(\sqrt(5)\) da bi se dobilo \(1\)? I koji stepen čini bilo koji broj jedinicom? Nula, naravno!

\(\log_(\sqrt(5))(1)=0\)

d) Na koji stepen treba podići \(\sqrt(7)\) da bi se dobio \(\sqrt(7)\)? U prvom - bilo koji broj u prvom stepenu jednak je samom sebi.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Na koji stepen treba podići \(3\) da bi se dobilo \(\sqrt(3)\)? Odatle znamo da je to razlomak, što znači Kvadratni korijen je stepen \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Primjer : Izračunajte logaritam \(\log_(4\sqrt(2))(8)\)

Odluka :

Odgovori : \(\log_(4\sqrt(2))(8)=1,2\)

Zašto je izmišljen logaritam?

Da bismo ovo razumjeli, riješimo jednačinu: \(3^(x)=9\). Samo uparite \(x\) da bi jednakost funkcionirala. Naravno, \(x=2\).

Sada riješite jednačinu: \(3^(x)=8\).Čemu je x jednako? To je poenta.

Najgenijalniji će reći: "X je malo manje od dva." Kako tačno napisati ovaj broj? Da bi odgovorili na ovo pitanje, smislili su logaritam. Zahvaljujući njemu, odgovor se ovdje može napisati kao \(x=\log_(3)(8)\).

Želim da naglasim da \(\log_(3)(8)\), kao i svaki logaritam je samo broj. Da, izgleda neobično, ali je kratak. Jer ako bismo to htjeli napisati u formi decimalni razlomak, tada bi to izgledalo ovako: \(1.892789260714.....\)

Primjer : Riješite jednačinu \(4^(5x-4)=10\)

Odluka :

Odgovori : \(\frac(\log_(4)(10)+4)(5)\)

Decimalni i prirodni logaritmi

Kao što je navedeno u definiciji logaritma, njegova baza može biti bilo koji pozitivan broj osim jednog \((a>0, a\neq1)\). I među svima mogućim razlozima postoje dva koja se javljaju tako često da je izmišljen poseban kratki zapis za logaritme s njima:

Prirodni logaritam: logaritam čija je osnova Ojlerov broj \(e\) (jednak približno \(2,7182818…\)), a logaritam je zapisan kao \(\ln(a)\).

tj. \(\ln(a)\) je isto što i \(\log_(e)(a)\)

Decimalni logaritam: Logaritam čija je baza 10 piše se \(\lg(a)\).

tj. \(\lg(a)\) je isto što i \(\log_(10)(a)\), gdje je \(a\) neki broj.

Osnovni logaritamski identitet

Logaritmi imaju mnoga svojstva. Jedan od njih se zove "Glavni logaritamski identitet' i izgleda ovako:

Ovo svojstvo slijedi direktno iz definicije. Pogledajmo kako je nastala ova formula.

Prisjetite se kratke definicije logaritma:

ako je \(a^(b)=c\), onda \(\log_(a)(c)=b\)

To jest, \(b\) je isto što i \(\log_(a)(c)\). Tada možemo napisati \(\log_(a)(c)\) umjesto \(b\) u formuli \(a^(b)=c\) . Ispostavilo se \(a^(\log_(a)(c))=c\) - glavni logaritamski identitet.

Ostala svojstva logaritama možete pronaći. Uz njihovu pomoć možete pojednostaviti i izračunati vrijednosti izraza logaritmima, koje je teško direktno izračunati.

Primjer : Pronađite vrijednost izraza \(36^(\log_(6)(5))\)

Odluka :

Odgovori : \(25\)

Kako napisati broj kao logaritam?

Kao što je gore spomenuto, svaki logaritam je samo broj. I obrnuto: bilo koji broj se može napisati kao logaritam. Na primjer, znamo da je \(\log_(2)(4)\) jednako dva. Tada možete napisati \(\log_(2)(4)\) umjesto dva.

Ali \(\log_(3)(9)\) je također jednako \(2\), tako da možete napisati i \(2=\log_(3)(9)\) . Slično sa \(\log_(5)(25)\), i sa \(\log_(9)(81)\), itd. Odnosno, ispostavilo se

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Dakle, ako trebamo, možemo to dvoje napisati kao logaritam sa bilo kojom bazom bilo gdje (čak i u jednadžbi, čak iu izrazu, čak i u nejednakosti) - samo napišemo kvadratnu bazu kao argument.

Isto je i sa trojkom - može se napisati kao \(\log_(2)(8)\), ili kao \(\log_(3)(27)\), ili kao \(\log_(4)( 64) \) ... Ovdje pišemo bazu u kocki kao argument:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

I sa četiri:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

I sa minus jedan:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\)\(...\)

I sa jednom trećinom:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Bilo koji broj \(a\) može se predstaviti kao logaritam sa bazom \(b\): \(a=\log_(b)(b^(a))\)

Primjer : Pronađite vrijednost izraza \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Odluka :

Odgovori : \(1\)

Logaritam broja N razumom a naziva se eksponent X , na koji trebate podići a da dobijem broj N

Pod uslovom da
,
,

Iz definicije logaritma slijedi da
, tj.
- ova jednakost je osnovni logaritamski identitet.

Logaritmi na osnovu 10 nazivaju se decimalni logaritmi. Umjesto
pisati
.

osnovni logaritmi e nazivaju se prirodnim i denotiranim
.

Osnovna svojstva logaritama.

Logaritam jedinice za bilo koju bazu je nula

Logaritam proizvoda jednak je zbiru logaritama faktora.

3) Logaritam količnika jednak je razlici logaritama

Faktor
naziva se modulom prijelaza iz logaritma na bazi a na logaritme u osnovi b .

Koristeći svojstva 2-5, često je moguće svesti logaritam složenog izraza na rezultat jednostavnih aritmetičkih operacija nad logaritmima.

Na primjer,

Takve transformacije logaritma nazivaju se logaritmi. Transformacije recipročne od logaritama nazivaju se potenciranje.

Poglavlje 2. Elementi više matematike.

1. Ograničenja

ograničenje funkcije
je konačan broj A ako, kada se teži xx 0 za svaku unapred određenu
, postoji broj
da čim
, onda
.

Funkcija koja ima ograničenje razlikuje se od nje za beskonačno mali iznos:
, gdje je - b.m.w., tj.
.

Primjer. Razmotrite funkciju
.

Kada težite
, funkcija y ide na nulu:

1.1. Osnovne teoreme o granicama.

Granica konstantne vrijednosti jednaka je ovoj konstantnoj vrijednosti

.

Granica zbira (razlike) konačnog broja funkcija jednaka je zbiru (razlici) granica ovih funkcija.

Granica proizvoda konačnog broja funkcija jednaka je proizvodu granica tih funkcija.

Granica kvocijenta dvije funkcije jednaka je količniku granica ovih funkcija ako granica nazivnika nije jednaka nuli.

Izvanredne granice

,
, gdje

1.2. Primjeri izračuna ograničenja

Međutim, nisu sve granice izračunate tako lako. Češće se izračun granice svodi na otkrivanje nesigurnosti tipa: ili .

.

2. Derivat funkcije

Neka imamo funkciju
, kontinuirano na segmentu
.

Argument dobio malo pojačanja
. Tada će se funkcija povećati
.

Vrijednost argumenta odgovara vrijednosti funkcije
.

Vrijednost argumenta
odgovara vrijednosti funkcije .

Dakle, .

Nađimo granicu ove relacije na
. Ako ova granica postoji, onda se naziva derivacijom date funkcije.

Definicija 3derivacije date funkcije
argumentacijom naziva se granica omjera prirasta funkcije i prirasta argumenta, kada inkrement argumenta proizvoljno teži nuli.

Derivat funkcije
može se označiti na sljedeći način:

; ; ; .

Definicija 4 Operacija pronalaženja derivacije funkcije se zove diferencijaciju.

2.1. Mehaničko značenje izvedenice.

Razmotrimo pravolinijsko kretanje nekog krutog tijela ili materijalne tačke.

Neka u nekom trenutku pokretna tačka
bio na distanci sa početne pozicije
.

Nakon nekog vremena
odmaknula se
. Stav =- prosječna brzina materijalna tačka
. Nađimo granicu ovog omjera, uzimajući to u obzir
.

Shodno tome, određivanje trenutne brzine materijalne tačke se svodi na pronalaženje derivacije putanje u odnosu na vrijeme.

2.2. Geometrijska vrijednost derivacije

Pretpostavimo da imamo grafički definiranu neku funkciju
.

Rice. 1. Geometrijsko značenje izvedenice

Ako a
, zatim poenta
, će se kretati duž krive, približavajući se tački
.

Dakle
, tj. vrijednost izvoda s obzirom na vrijednost argumenta numerički jednak tangentu ugla koji formira tangenta u datoj tački sa pozitivnim smerom ose
.

2.3. Tabela osnovnih formula diferencijacije.

Funkcija napajanja

Eksponencijalna funkcija

logaritamska funkcija

trigonometrijska funkcija

Inverzna trigonometrijska funkcija

2.4. Pravila diferencijacije.

Derivat od

Derivat zbira (razlike) funkcija

Derivat proizvoda dvije funkcije

Derivat kvocijenta dvije funkcije

2.5. Derivat od složena funkcija.

Neka funkcija
tako da se može predstaviti kao

i
, gdje je varijabla onda je srednji argument

Derivat kompleksne funkcije jednak je proizvodu izvoda date funkcije u odnosu na međuargument na derivaciju međuargumena u odnosu na x.

Primjer1.

Primjer 2.

3. Funkcijski diferencijal.

Neka bude
, diferencibilan na nekom intervalu
pusti to at ova funkcija ima izvod

,

onda možeš pisati

(1),

gdje - beskonačno mala količina,

jer at

Množenje svih pojmova jednakosti (1) sa
imamo:

Gdje
- b.m.v. višeg reda.

Vrijednost
naziva se diferencijal funkcije
i označeno

.

3.1. Geometrijska vrijednost diferencijala.

Neka funkcija
.

Fig.2. Geometrijsko značenje diferencijala.

.

Očigledno, diferencijal funkcije
jednak je inkrementu ordinate tangente u datoj tački.

3.2. Derivati ​​i diferencijali različitih redova.

Ako tamo
, onda
naziva se prvim izvodom.

Izvod prvog izvoda naziva se izvod drugog reda i piše se
.

Derivat n-tog reda funkcije
naziva se derivacija (n-1) reda i piše se:

.

Diferencijal diferencijala funkcije naziva se drugi diferencijal ili diferencijal drugog reda.

.

.

3.3 Rješavanje bioloških problema pomoću diferencijacije.

Zadatak1. Istraživanja su pokazala da je rast kolonije mikroorganizama u skladu sa zakonom
, gdje N – broj mikroorganizama (u hiljadama), t – vrijeme (dani).

b) Hoće li se populacija kolonije povećati ili smanjiti tokom ovog perioda?

Odgovori. Kolonija će rasti.

Zadatak 2. Voda u jezeru se periodično ispituje radi kontrole sadržaja patogenih bakterija. Kroz t dana nakon testiranja, koncentracija bakterija se određuje omjerom

.

Kada će minimalna koncentracija bakterija doći u jezero i kada će se u njemu moći kupati?

Rješenje Funkcija dostiže maksimum ili min kada je njen izvod nula.

,

Odredimo max ili min će biti za 6 dana. Da bismo to učinili, uzimamo drugi izvod.

Odgovor: Nakon 6 dana bit će minimalna koncentracija bakterija.